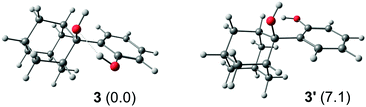Photogeneration of quinone methide from adamantylphenol in an ultrafast non-adiabatic dehydration reaction

Abstract

The ultrafast photochemical reaction of quinone methide (QM) formation from adamantylphenol was monitored in real time using femtosecond transient absorption spectroscopy and fluorescence upconversion in solution at room temperature. Experiments were complemented by theoretical studies simulating the reaction pathway and elucidating its mechanism. Excitation with sub-20 fs UV pulses and broadband probing revealed ultrafast formation of the long-lived QM intermediate directly in the ground state, occurring with a time constant of around 100 fs. UV-vis transient absorption data covering temporal dynamics from femtoseconds to hundreds of milliseconds revealed persistence of the absorption band assigned to QM and partially overlapped with other contributions tentatively assigned to triplet excited states of the adamantyl derivative and the phenoxyl radical that are clearly distinguished by their evolution on different time scales. Our data, together with the computations, provide evidence of a non-adiabatic photodehydration reaction, which leads to the formation of QM in the ground state via a conical intersection, circumventing the generation of a transient QM excited state.

---

Introduction

Quinone methides (QMs), important intermediates in the chemistry and photochemistry of phenols,¹ attracted attention owing to their biological activity^2–4 and increasing number of applications in organic synthesis.^5–8 However, the polar structure of QMs, which results in their high electrophilic and nucleophilic reactivity,⁹ makes them usually short-lived,¹⁰ so they cannot be stored and have to be generated in situ. Furthermore, QMs react with dienophiles in Diels–Alder reactions,^5–8 which are commonly used in modifications of surfaces.^11–13 Among the methods for the generation of QMs, photochemical reactions are particularly appealing due to their ability to temporally and spatially control the activation event.¹⁴ For the applications of QMs in biological systems, it is pivotal to fully unravel all details of the photochemical reaction mechanisms and characterize all intermediates that exist from the moment of photoactivation to the generation of QMs in the ground state. In fact, biological molecules may interact with these intermediates and thereby change reaction pathways and products.¹⁵

The most commonly used photochemical method to generate QMs in biological systems is photodeamination of suitably substituted phenols.¹⁶ The mechanism of photodeamination has therefore been investigated by a variety of approaches, including nanosecond laser flash photolysis (LFP),¹⁷ computations,¹⁸ and femtosecond transient absorption (fs-TA) spectroscopy.¹⁹ The major discovery was that photodeamination takes place in an adiabatic ultrafast photochemical reaction on the S₁ potential energy surface, delivering QMs in the excited state and without any detectable intermediate en route.¹⁹ However, one serious drawback of photodeamination reactions is the fact that QMs react efficiently with water molecules,^20,21 resulting in hydration products and loss of the starting material.

Photodehydration reactions^22,23 are therefore a better option, since the reaction of QMs with water regenerates the starting molecules and therefore does not act as a material loss channel. For this reason, photodehydration reactions have been studied on several substrates, extended by investigations of antiproliferative activity of photogenerated QMs^24–27 that highlighted some anthracene derivatives as potent agents against cancer stem cells.²⁸ The mechanism of the photodehydration reaction has been fully unraveled on the simple o-hydroxymethylphenol (1) by computations and fs-TA measurements. It was demonstrated that the corresponding QM 2 (Scheme 1) is generated in an ultrafast adiabatic reaction on the S₁ potential energy surface, taking place in less than 1 ps and generating the QM intermediate in its excited S₁ state.²⁹ However, it is not a general mechanism for the photodehydration, since the formation of QMs may involve benzoxete derivatives as intermediates,²³ or it may proceed via phenoxyl radicals that undergo a homolytic cleavage of the alcohol OH group.²⁷

Scheme 1 Photodehydration of o-hydroxymethylphenol (1) delivering quinone methide 2.

Here we present a joint experimental and computational investigation of the photodehydration mechanism of the adamantyl derivative 3 (Scheme 2). A previous photochemical investigation demonstrated that 3 undergoes dehydration more efficiently (Φ_R = 0.51)³⁰ when compared to 1 (Φ_R = 0.23),²² which raises questions about the mechanism and the timescale for the formation of the corresponding QM 4. Investigation of the photoreactivity of adamantylphenol derivatives is particularly important since the corresponding QMs generally show better antiproliferative activity compared to non-substituted QMs.^24–27 To this end we combine fs-TA and fs fluorescence upconversion (FlUC) measurements performed on 3 in CH₃CN : H₂O (1 : 1) with time-dependent density functional theory (TD-DFT) computations which support the observations and fully elucidate the photochemical reaction mechanism. Our main finding is that 1 and 3 do not follow the same photochemical pathway. Unlike the parent molecule 1, photodehydration of 3 appears to be a non-adiabatic reaction that proceeds via a conical intersection (CI), delivering directly QM in its ground electronic state, 4(S₀). Our results demonstrate that changes in the molecular structure not altering the actual chromophore may nevertheless result in a profound change of the photochemical reactivity.

Scheme 2 Photochemical formation of quinone methide 4(S₀).

Experimental and computational methods

Femtosecond transient absorption (fs-TA) experiments

We investigated the ultrafast photochemistry of QM formation from adamantylphenol 3 using two different and complementary fs-TA setups. The first setup had a lower time resolution (≈500 fs) and a longer scan range (≈1 ns) and was used to obtain an overall view of the photoinduced dynamics; the second setup had higher time resolution (<50 fs) and was employed to zoom in on the early steps of the photochemical reaction. Initial measurements were performed on a home-built femtosecond pump–probe spectrometer based on Ti:sapphire regenerative amplifier system (Spitfire, Spectra-Physics). Part of the fundamental (120 fs, 0.8 mJ pulses at 800 nm with a 1 kHz repetition rate) is split into two beams. UV pump pulses with 10 μJ energy are generated using a “double-mixing” scheme in which first fundamental beam is frequency doubled in a 0.5 mm thick type 1 β-barium borate (BBO) crystal (θ = 29.3° φ = 0°), and the resultant 400 nm light is mixed with the remaining 800 nm light in a second 0.5 mm thick type 1 BBO crystal (θ = 44.5° φ = 0°) to generate the sum frequency at 267 nm. Before the second BBO crystal, a quartz waveplate (half-waveplate for 800 nm and full-waveplate for 400 nm) is used to rotate the 800 nm beam polarization by 90 degrees. An additional 3.0 mm thick α-BBO crystal (θ = 66° φ = 0°) is inserted after the second harmonic generation (SHG) BBO, acting as group delay compensation plate. Broadband white-light continuum (WLC) probe pulses in the visible (340–610 nm) are obtained by focusing a small portion of the 800 nm fundamental, after retro reflection on a computer-controlled delay line, into a c-cut 3 mm thick CaF₂ plate that is continuously rotated to avoid the accumulation of color centers. A variable attenuator and an iris are used to optimize the beam quality, spectral shape, and stability of the continuum. The continuum is collimated with a 90 degree off-axis parabolic mirror (MPD129-F01; Thorlabs) and split into two roughly equal parts with a broadband beam splitter (BS). As beam splitter, we use an UV fused silica reflective neutral density filter with a nominal optical density of 0.5 transmission (NDUV505B; Thorlabs). These two beams serve as reference (transmitted) and probe (reflected) beam and are both focused in the flow cell using another 90 degree off-axis parabolic mirror (MPD169-F01; Thorlabs). By adding sufficient path length to the optical path of the reflected beam we ensure that for the entire range of the delay stage used (approximately 20 cm) the transmitted beam will arrive at the overlap in the flow cell before the pump pulse. Both continua are recollimated using f = 125 mm spherical mirror which is chosen to ensure that the distance between two beams matches the distance (14 mm) between two Hamamatsu S8381-1024Q photodiode array sensors mounted on a single PCB (Entwicklungsbuero EB Stresing, Berlin, Germany) with line rate >1 kHz and 16bit AD conversion. Finally, reference and probe beams are dispersed onto separate photodiode arrays by a fused silica prism with an apex angle of 60°, with horizontal polarization to work at Brewster condition at the central wavelength in order to minimize reflection losses. The spectrally resolved intensities of both continua at the cameras can be read out at single-shot regime. This allows an operation at the full 1 kHz repetition rate. The temporal resolution of the setup was determined from optical Kerr effect measurements in pure solvent and found to be around 500 fs. This was confirmed by the width of the two-photon absorption signal in fs-TA data. For the measurements, pump and probe polarizations were set at magic angle, and approximately 10 μJ of pump beam was focused to a spot size with a 400 μm diameter, resulting in fluence of 8 mJ cm⁻².

The second, high temporal resolution broadband fs-TA spectrometer used in these experiments has been described in detail elsewhere.³¹ Briefly, the setup is based on an amplified Ti:sapphire laser (Coherent Libra). The pump pulses are generated by SHG of a visible non-collinear optical parametric amplifier (NOPA) in a 20 μm-thick BBO crystal, resulting in sub-20 fs pulses in the UV tunable between 260 and 290 nm. A 35 μJ fraction of the laser output is sent to a computer-controlled delay line, followed by the WLC generation stage. The energy for WLC generation is adjusted to ∼1 μJ. For WLC a small fraction of the fundamental laser output is focused onto a 3 mm-thick CaF₂ plate. Optionally, the WLC can be driven by the SH of Ti:sapphire, generated in a 1 mm-thick type 1 BBO crystal (θ = 29°). To avoid optical damage, a two-axis translation stage (Zaber Technologies, Vancouver, Canada, model T-LS28M) is used to slowly scan the plate in a plane perpendicular to the propagation direction. The pump and the probe beams are separately and non-collinearly focused on the sample at approximately 5° by two UV enhanced aluminum spherical mirrors with focal lengths f_pump = 250 mm and f_probe = 200 mm, corresponding to focal spot diameters of 120 and 80 μm, respectively. The fluence of the pump beam with energy of 113 nJ was therefore 1 mJ cm⁻².

Parallel polarizations of pump and probe beams were used for early time fs-TA measurements. The transmitted probe, selected by an iris, is focused on the entrance slit of a spectrometer (SP2300 Princeton Instruments, Acton, MA, USA) equipped with a CCD detector, with the spectral resolution of 0.5 nm, and a read-out electronics (Entwicklungsbuero EB Stresing, Berlin, Germany) capable of single-shot measurement of the probe spectrum at the full 1 kHz laser repetition rate.

In both experimental setups the pump is modulated by a mechanical chopper at 500 Hz and the absorbance difference spectrum as a function of probe wavelength λ_pr and pump–probe delay t is calculated as:

where offset and background have been previously subtracted. Measurements were taken by overlapping the pump and probe pulses on a 1 mm optical path-length spectrophotometric quartz flow cell. The flow cell system was pumped at a rate that ensured a fresh sample volume for each pump pulse.

Synthesis of 3 has been described previously.³⁰ For the first measurements over longer timescales, adamantylphenol 3 was dissolved in CH₃CN–H₂O (1 : 1) in the concentration c = 5.0 × 10⁻⁴ M and the absorbance at the 267 nm excitation wavelength measured in a cuvette with 1 cm path was 0.7, while for the second set of measurements where sub-20 fs NOPA pump pulse resulted in lower fluence in order to have a reasonable level of the fs-TA signal the concentration was increased to c = 5.0 × 10⁻³ M. In these and subsequent time resolved fluorescence and laser flash photolysis measurements acetonitrile used for the measurements was of HPLC purity. Additionally, mQ H₂O (Millipore) was used. All measurements were performed at ambient temperature (22 °C).

Femtosecond fluorescence upconversion (FlUC) experiment

Time resolved fluorescence is recorded by gating the emitted light with a NIR laser in an upconversion scheme. The experimental setup follows the apparatus of N. Ernsting.³² Pulses from an 8 kHz repetition rate amplified Ti:sapphire laser system (LIBRA, Coherent Inc.) of ∼80 fs are split into two beams of 250 μJ of energy. One part pumps the gate NIR laser. The NIR laser is a double pass OPA.³³ It delivers 230 mW at 1250 nm. The excitation laser is an in house constructed two-stage NOPA. The pulses are compressed with a set of chirped mirrors. The output is doubled in a β-BBO crystal and used for excitation of the samples. After a delay stage the excitation beam is spatially filtered and focused into a 200 μm flow cell. For the FlUC measurements, adamantylphenol 3 was dissolved in CH₃CN–H₂O (1 : 1) in a concentration c = 5.0 × 10⁻³ M. The absorbance at the 260 nm excitation wavelength measured in a cuvette with a 1 mm path was 0.7 OD. An absorption spectrum before and after the FlUC measurement was recorded to monitor possible degradation of the sample. Circulation of the solution was achieved with a peristaltic pump. The fluorescence is collected in an off-axis Schwarzschild objective. Most of the excitation wavelength is removed with a longpass filter and the polarizations are separated with a calcite prism. Eventually, the fluorescence is focused into the type 2 β-BBO crystal. Type 2 was chosen as phase matching can be better achieved, however with the drawback of conversion efficiency. The interaction angle of gate pulse and fluorescence is 21°. To obtain a satisfying time resolution, the pulse front of the gate beam is tilted after compression with a SF11 prism. The relatively large interaction angle of gate and fluorescence reduces background signal (scatted light from the pump and doubled NIR). The power of the gate pulse was 70 mW at the interaction zone in front of the β-BBO crystal. After upconversion, the signal is coupled into a 0.7 mm single mode fiber and enters a spectrograph. The spectrum is recorded with an Andor intensified CCD camera. The illumination time was 0.5 s which resulted, for the case of adamantylphenol 3, in up to 300 counts. To cope with instabilities of the laser system, a series of 20 scans was recorded. The data were averaged, despiked and chirp corrected. The time resolution, measured with the upconverted scattered fundamental excitation wavelength (377 nm) was 650 fs. This is due to the fact that the system is optimized for visible fluorescence and the interaction and cutting angles of the β-BBO crystal were not optimal. Comparing the UV fluorescence to a standard (anisole) yielded a time resolution of 0.7 ps.

Laser flash photolysis (LFP)

The measurements were performed on a LP980 Edinburgh Instruments spectrometer. For the excitation a Qsmart Q450 Quantel YAG laser was used with the fourth harmonic at 266 nm. The energy of the laser pulse was set to 20 mJ. Adamantylphenol 3 was dissolved in CH₃CN–H₂O (1 : 1) in the concentration c = 2.0 × 10⁻⁴ M and the absorbance at the 266 nm excitation wavelength measured in a cuvette with 1 cm path was 0.3. Prior to the measurements, the solution was purged with a stream of argon or oxygen for 20 min. The measurements were performed in static cells which were frequently exchanged to remove potential artifacts from the photoproducts.

Time-correlated single photon counting (TC-SPC)

Fluorescence decays were measured by TC-SPC method on an Edinburgh Instruments FS5 spectrometer equipped with a pulsed LED at 280 nm. The duration of the pulse was ≈800 ps. Fluorescence signals at 310 nm were monitored over 1023 channels with the time increment of ≈20 ps per channel. The decays were collected until they reached 3000 counts in the peak channel. In addition, time resolved emission spectra were collected with excitation at 280 nm. Adamantylphenol 3 was dissolved in CH₃CN–H₂O (1 : 1) in the concentration c = 5.0 × 10⁻⁵ M and the absorbance at the 280 nm excitation wavelength measured in a cuvette with 1 cm path was 0.07. Prior to the measurements, the solution was purged with a stream of nitrogen for 20 min.

Computational methods

Geometry optimizations were performed with the GAUSSIAN16³⁴ program package using the PCM(water)/ωB97XD/6-311++G(d,p) level of theory^35,36 and the obtained minima were verified by frequency computations. The PCM(water)/TD-ωB97XD/6-311++G(d,p) level of theory was used for excited state optimizations and computations of vertical excitation energies for 20 energetically lowest excited singlet states. The viability of the used TD-DFT method was supported by the benchmarking performed in our previous work where computational results were further verified by comparison with experimental data.^19,29 Conical intersection optimization scan for QM 4(S₀) formation was performed on the same level of theory using ORCA 4.2.0.^37,38

Results and discussion

Transient absorption measurements

Initial fs-TA measurements were performed with 500 fs temporal resolution up to 1.1 ns in time delay. Fig. 1(A) shows a 2D TA map as a function of probe wavelength and pump–probe delay. Around time zero, we observe the instantaneous appearance of the two-photon absorption artifact, which involves the absorption of one pump and one probe photon and occurs only during the temporal overlap of the pulses, superimposed onto the measured transient absorption spectra and is more prominent at shorter wavelengths (340–400 nm). This is followed by a broad, nearly featureless positive signal that appears at a slightly slower rate and decays on the nanosecond timescale (panel B). The signal consists of a clear photoinduced absorption (PA) band centered around 425 nm, with a strong shoulder rising at longer wavelengths and extending into the infrared region (panel C). Assigning the PA band to the vibrationally relaxed S₁ state of 3 would be the most obvious choice. To verify this potential assignment, we have computed the excited state absorption (ESA) spectrum for 3(S₁), corresponding to transitions S₁ → S_n. Several transitions were found in the visible part of the spectrum, albeit with negligible oscillator strengths (see Fig. S26a and Table S2 in the ESI†). Based on the computed ESA spectrum, experimentally detectable absorption for 3(S₁) is not anticipated at wavelengths longer than 350 nm. Although computation of the ESA spectra using TD-DFT is known to be rather coarse, in our case it precluded assignment of the PA band at 425 nm to 3(S₁). On the other hand, the PA band at 425 nm may tentatively also be assigned to a radical cation obtained by one or two-photon ionization of the phenolic molecule 3. However, in aqueous solvent phenolic radical cations deprotonate to phenoxyl radicals,³⁹ which is not supported by our measurements, since the same signal at 425 nm persists over ns time scale and can be detected by LFP over hundreds of milliseconds (vide infra).³⁰

Fig. 1 (A) fs-TA data for the photochemistry of 3 in CH₃CN–H₂O (1 : 1) using THG pump pulse together with (B) kinetic traces and (C) spectra for the selected wavelengths and time delays, respectively. Note that the time delay is given on a logarithmic scale.

Based on previously published spectra for QM 4, the PA band at 425 nm most probably results from a transition from the ground state (S₀) of the intermediate 4.³⁰ This assignment is also in agreement with the results of our TD-DFT simulations that reveal a corresponding peak in the photoproduct absorption spectrum at 368 nm (see ESI,† Fig. S25c and Table S1). Although it is common that the computed spectra often do not precisely match the experimental spectra (here 368 nm vs. 425 nm) due to the nature of the used TD-DFT method, the qualitative match is in our case sufficient to reliably assign the photoactive species.

At longer wavelengths, a second PA band peaking at wavelengths longer than 600 nm is observed. Based on previous results,²⁷ we assign it to solvated electrons. Transients due to the solvated electrons decay faster and with two characteristic time constants. From the bi-exponential fitting of data for this wavelength range, we obtain an initial fast decay of around 35 ps, followed by a slower decay of around 1.5 ns (see ESI† Fig. S4 to S6). Comparison with results of other studies focused on photochemistry of solvated electrons in different solvents is not straightforward since in our case we have a mixture of two different solvents and a solute. However, it was reported previously that in pure acetonitrile excess electrons take on two distinct forms – solvated electrons and solvated molecular anions – that are in equilibrium with each other.⁴⁰ It is known that the timescale for ground-state solvated electrons to convert into solvated dimer anions is around 80 ps.⁴¹ These two forms have distinct absorption spectra and relaxation dynamics which in our case could be further modified by the presence of water and solute. To clarify the origin of solvated electrons, we measured excitation intensity dependence on the transient absorption spectra for both the sample and pure solvent at fixed delay of 10 ps that show quadratic dependence in the case of pure solvent, as expected for two-photon ionization (see ESI† Fig. S12). Intensity dependence for sample is almost linear, suggesting that it stems from free electrons resulting from one photon radical cation formation with only minor contribution of two-photon ionization of solvent molecules (see ESI† Fig. S11). Absence of signature of radical cation formation in our fs-TA experiments could be explained by the overlap with stronger solvated electron PA signal.

The observation of exclusively positive TA signal in the whole spectral range is due to the fact that the ground state absorption of 3 lies below 300 nm (see ESI† Fig. S13) and suggests that stimulated emission (SE) from the S₁ state of 3 is either overlapped with a stronger PA signal, or decays on an ultrafast, sub-picosecond timescale.

The absence of short-lived spectral features that would correspond to the initially populated Franck–Condon state of the reactant 3 or to the excited state S₁ of the photoproduct QM prompted us to perform another set of measurements with a higher, sub-50 fs temporal resolution. Fig. 2 shows kinetic traces at selected wavelengths following photoexcitation with sub-20 fs pulses at 280 nm. Due to the short duration of the pump pulses, strong artifacts (two-photon absorption, cross phase modulation) could not be avoided that complicated the analysis of the early reaction dynamics. The analysis of kinetics at relevant wavelengths showed that, apart from a faster rise of spectral features due to the increased temporal resolution, no evidence of intermediates was found. Measurements with WLC probe driven by SH of Ti:sapphire at 400 nm, extending the probed spectral range deeper into UV, revealed no spectral signatures either of additional photoexcited states or SE, and showed only the ground state bleach signal from adamantylphenol 3 in the 265–285 nm spectral range (see ESI† Fig. S14). The lack of any clear evidence of a SE, despite a detected steady-state emission, agrees with a signal dominated by the PA contributions, likely due to non-emissive species, and urges on carrying out time resolved fluorescence measurements.

Fig. 2 Kinetic traces for the selected wavelengths using sub-20 fs UV NOPA pump pulse revealing early photochemistry of 3 in CH₃CN–H₂O (1 : 1).

Careful analysis of the TA dynamics at selected wavelengths convinced us that it is not possible to reveal any intermediate state with sub-picosecond dynamics. We therefore decided to perform detailed fitting of single wavelengths using the sum of two exponential functions convoluted with a Gaussian instrument response function (IRF), where the first exponential function describes a fast rise, while the second one is connected with a slow decay (fixed at 1 ns). This procedure, which was employed to analyse the results of both experiments, allowed the use of a minimum number of free parameters. Details on the fitting procedure are given in the ESI.†

Results of fits of kinetic traces at several relevant wavelengths for the sub-50 fs TA measurements are summarized in Table 1. We further verified rise time of the TA signal obtained with sub-20 fs pumping by fitting the signal integrated in the 400–500 nm spectral window, which corresponds to the PA band ascribed to the QM (see ESI† Fig. S10). This procedure is justified by the fact that our analysis indicates absence of intermediate species with rapid dynamics but it also reduces the noise, resulting in better fitting of the rise time. In addition, in this spectral range the contribution from solvated electrons is less pronounced than at longer wavelengths. The 100 fs rise time obtained for the integrated signal is in good agreement with the rise times from single wavelength kinetic profiles (Table 1).

Table 1 Values of deconvoluted rise time at several prominent wavelengths from the fs-TA data shown in Fig. 2

Wavelength [nm]	Rise time [fs]
425	78 ± 4
500	82 ± 6
600	125 ± 10

---

To provide additional evidence for assignment of the PA band at 425 nm to the ground state of the QM 4 and to confirm the absence of any prior intermediates, we collected nanosecond transient absorption data covering broad time-window up to hundreds of milliseconds.

Transient absorption spectra of 3 in Ar-purged and O₂-purged CH₃CN–H₂O (1 : 1), shown in Fig. 3, revealed additional transient species absorbing in the 300–450 nm spectral range. On the nanosecond time-scale, in the Ar-purged solution a short-lived transient was detected absorbing at 300–420 nm that was fitted to unimolecular kinetics at 400 nm with the decay time τ = 750 ± 30 ns (to be compared to the previously reported value τ = 3 μs).²⁶ The transient was quenched by O₂; in the O₂-purged solution the decay time is 30 ± 10 ns. Based on the quenching by O₂, this transient species may tentatively be assigned to the triplet excited state of 3.

Fig. 3 Nanosecond transient absorption spectra of 3 (c = 2.0 × 10⁻⁴ M) in Ar-purged (left) and O₂-purged (right) CH₃CN–H₂O (1 : 1). The energy of the laser pulse at 266 nm was set to 17 mJ per pulse.

On a long time-scale, two transients were detected, a shorter-lived one absorbs at 350–400 nm and decays at 400 nm with the lifetime τ = 260 ± 10 μs in Ar-purged solution and τ = 420 ± 20 μs in O₂-purged solution (Fig. 4). Since it is not quenched by O₂, and according to the comparison with the published spectrum,³⁹ it is assigned to phenoxyl radical (previously not detected). A radical cation could be formed in an ionization process, which would also explain the presence of solvated electrons detected as a red positive absorption band in fs-TA. Deprotonation of the radical cation then leads to the phenoxyl radical formation. However, since we found no evidence of radical formation in fs-TA measurements, it seems that more plausible interpretation is that the radical cation decays via back electron transfer while the phenoxyl radical could be formed directly in a H-transfer reaction that is known to evolve on nanosecond time scales.⁴² In this case, formation of phenoxyl radical cannot be resolved with fs-TA that covers only nanosecond time-window or in LFP measurements that use 10 ns excitation pulses.

Fig. 4 Microsecond transient absorption spectra of 3 (c = 2.0 × 10⁻⁴ M) in Ar-purged (left) and O₂-purged (right) CH₃CN–H₂O (1 : 1). The energy of the laser pulse at 266 nm was set to 17 mJ per pulse.

The longer-lived transient in CH₃CN–H₂O has an absorption maximum at ≈420 nm, and decays to the baseline with the lifetime of τ = 600 ± 50 ms in Ar-purged solution and τ = 470 ± 20 ms in O₂-purged solution (see ESI† Fig. S17). Based on previous reports, it is assigned to QM. Note that the transient is formed within the laser pulse (10 ns), since at longer wavelengths (500 nm) no growth of the transient absorption was detected on a short time-scale. More details on fitting results are given in the ESI.†

Results of nanosecond laser flash photolysis suggest that in fs-TA experiments at wavelengths below 425 nm transient absorption spectra probably contain contributions from the triplet excited state of 3 and the radical cation whose dynamics is too slow to be observed in fs-TA. However, the PA band at 425 nm, which remains visible in the entire time-window spanning from fs to hundreds of milliseconds, stems from the QM 4 in the ground state and not from a slowly depleting singlet excited state of 3, which should decay radiatively with nanosecond time constant.

We can give a tentative explanation for the absence of a negative signal in absorption transients. At a first glance, the apparent absence of SE of 3 seems to be in disagreement with its fluorescence quantum yield (Φ_F = 0.13).³⁰ However, it should be noted that the starting phenol derivative can adopt two distinct conformer orientations in the ground state that are energetically quite different (Fig. 5). Performed computations indicate that the conformer that forms an intramolecular bond between the two alcohol groups (3) is by 7.1 kcal mol⁻¹ more stable than the conformer where such hydrogen bonding does not occur (3′). It is probable that the hydrogen-bonded conformer 3 is reactive and undergoes the QM formation reaction that quenches fluorescence on the 100-fs timescale. On the other hand, the less stable conformer 3′ is unreactive and therefore emissive, which would account for the observed fluorescence quantum yield. Note, however, that in an aqueous environment the conformer distribution can shift somewhat in favor of the less stable conformer since water molecules, with their hydrogen bonding network, can compete with the solute, influence the energetic stabilization and thereby increase the fluorescence efficiency, as was demonstrated previously.³⁰ In addition, decay of fluorescence measured by TC-SPC for 3 in CH₃CN–H₂O (1 : 1 v/v) was fitted to a sum of two exponents with decay times τ₁ = 0.20 ± 0.03 ns and τ₂ = 3.26 ± 0.01 ns. The detection of short and long decay times is also in agreement with the existence of both reactive and non-reactive conformers.

Fig. 5 Two optimized geometries (3 and 3′) of the starting phenol derivative computed at the PCM(water)/ωB97XD/6-311++G(d,p) level of theory. Relative energies in the parentheses are given in kcal mol⁻¹ and hydrogen bonding is indicated with a dashed line.

It is expected that the fluorescence of both conformers should be observed at wavelengths slightly higher compared to the absorption band of 3, around 300 nm. Indeed, this was confirmed by fluorescence upconversion measurements described in the next paragraph. The absence of SE signal in this wavelength range, that was covered by additional UV transient absorption measurements, can be explained by overlap of a weaker SE signal with a stronger PA signal.

Fluorescence upconversion measurements

We already mentioned TC-SPC fluorescence measurement on the nanosecond time scale for 3 where short and long decay times were detected, in agreement with the existence of reactive and non-reactive conformers.³⁰ Fast decay time was imprecisely determined on the setup used, while the slower one was on a nanosecond time-scale, in line with the measured fluorescence quantum yield. Evidence for heterogeneity of fluorescence due to emission from two species (dual emission) was expected to emerge in measured time resolved emission spectra (TRES), ESI† Fig. S24. At very early time-scale when we still see the rise of fluorescence, results show that there may be an additional band in the fluorescence spectra at shorter wavelength, at 300 nm. Unfortunately, it appears at the limits of the detection of the setup used, and it has a low contribution. This might be due to the emission from more stable conformer 3, emitting from the hot vibrational level close to the Franck–Condon state. Determination of time-resolved emission kinetics and spectra using femtosecond FlUC was expected to provide further details on the photoreaction of adamantylphenol 3 in the singlet excited state. Fluorescence band peaking at 307 nm was observed without any detectable spectral change (Fig. 6), within our time resolution and detection range, namely slower than ∼100 fs and at λ > 290 nm. Note that time-resolved spectra are in good agreement with the steady-state one reported in Fig. S22 (ESI†). Tail of the fluorescence signal at longer wavelengths could not be detected as the detection efficiency was optimized for the maximum of the emission at 310 nm and unavoidably decreases moving further from this wavelength. We ascribe this fluorescence band mainly to the unreactive conformer (3′) that accounts for the observed fluorescence quantum yield of adamantylphenol 3 and decay time of 3.26 ns. The analysis of these data reveals the existence of a 460 fs rise component and two decays: a faster 22 ± 2 ps decay and a slower decay on the ns time scale, unresolved within the available scan range of 50 ps.

Fig. 6 (A) and (B) Temporal evolution of fluorescence spectra of 3 (c = 5.0 × 10⁻⁴ M) in CH₃CN–H₂O (1 : 1). (C) Fluorescence intensity decay at 307 nm fitted using sum of two decaying exponentials convoluted with IRF of 630 fs: added rise component was necessary to account for the observed rise of fluorescence. The last component is set to 2 ns (infinity in our spanned time window).

To give further evidence of the rise component, we measured also the FlUC data for anisole in acetonitrile (see ESI,† Fig. S21), which is the non-photoreactive model for adamantylphenol 3. It is confirmed that 0.46 ps rise is not an instrumental artifact, since it is absent in the reference system and present only in the adamantylphenol 3. As we do not see any change in the shape, pure vibrational relaxation mechanism (energy redistribution and cooling) can be ruled out. Instead, a pure rise of a band without a change in shape would point to an indirect population mechanism, which probably stems from a conformational change, since for a simple phenol chromophore absorption and emission transition dipole moments should be co-linear. Based on the available information related to the photochemistry of this molecule, the most plausible explanation for the time-resolved rise of fluorescence is the rotation around the C–C single bond connecting the adamantane and the phenol, converting 3′ into 3 and vice versa, or the rotation of the phenolic OH group resulting in a different spatial approach of the two OH groups. Both species 3 and 3′ are present in the solution prior to the laser excitation. We assume that the excited reactive conformer 3 would undergo dehydration to QM 4 (100 fs, as indicated by fs-TA), and inefficiently convert to the emissive 3′, with the time constant of 460 fs. This difference in dynamics is also in agreement with the difference in quantum yields for dehydration (Φ_R = 0.51) and fluorescence (Φ_F = 0.13) from adamantylphenol.³⁰ On the contrary, the emissive conformer 3′, which is higher in energy, may convert into 3 with 200 ps time constant, and that would account for the observed dual decay from 3′ (200 ps and 3.26 ns) detected by TC-SPC.

Moving to the interpretation of decay components, slow decay that was fixed to 2 ns in our analysis is ascribed to nonreactive emissive conformer 3′ in line with its fluorescence quantum yield (Φ_F = 0.13).³⁰ Even if we would have set the value from fluorescence decay measured with TC-SPC (3.26 ns), the only effect would have been on the relative amplitude of the two contributions but not on the values of the time constants. Interpretation of much faster decay that was clearly resolved within the available scan range of 50 ps is less trivial. Here, we cannot exclude that it reflects an anisotropy relaxation since the FLUC measurements could not have been performed at magic angle (see ESI† for more details). The fact that we found the same component in the reference system (see ESI,† Fig. S21), which does not undergo any conformational change, confirms the diffusional origin of the 22 ps component and rules out that it might describe any conformational relaxation. Details on IRF measurements, global analysis and FlUC data for the anisole reference molecule can be found in the ESI.† To summarize, temporal evolution of fluorescence can be explained by conversion between the two conformers 3′ and 3 appearing on different time scales without any need to invoke additional species.

Computations

A TD-DFT computational study was performed to elucidate the results obtained by fs-TA spectroscopy and explain the lack of observed intermediates in the formation of 4(S₀) (Scheme 2). We successfully identified stationary points for 3 and 4 in the ground state and in the first excited state using the PCM(water)/(TD-)ωB97XD/6-311++G(d,p) level of theory (Fig. 7). To clarify, a stationary point is a geometry of the molecule such that the derivative of its energy with respect to all displacements of the nuclei is zero. A local energy minimum is a stationary point where all such displacements lead to an increase in energy. The obtained energetics for both hydrogen-bonded 3 and QM 4 are in line with our previous findings for QM systems.¹⁹ However, note that adiabatic computation for the considered transition structure (TS) did not yield a minimum for the S₁ state and only the corresponding vertical excitation energy from the optimized S₀ to the excited state was available.

Fig. 7 Mechanism considerations of quinone methide formation from 3. Stationary points for the ground and the first excited state were computed at the PCM(water)/(TD-)ωB97XD/6-311++G(d,p) level of theory. Relative energies are given in kcal mol⁻¹. Vertical excitation energy from S₀ to S₁ corresponds to 243 nm for 3 and to 380 nm for 4.

Since the fs-TA experimental results indicate that 4(S₀) is formed directly from 3(S₁) without an intermediate structure, a CI pathway is the most probable one. Moreover, the failure to adiabatically optimize TS(S₁) also indirectly points toward a presence of a CI since TD-DFT methods in general encounter problems when faced with CI geometries. However, a new implementation in the Orca 4.2.0 program³⁸ enables simultaneous optimization of the ground and first excited state of the target structure in a way that facilitates approach toward the CI region, essentially confirming a reaction pathway towards a CI. In order to scan the potential energy surface of adamantylphenol 3 for such a path, we performed a CI optimization of the ground and the first excited state geometries and found the energy difference between them to amount to only 3.3 kcal mol⁻¹, which is small enough to confirm the presence of the CI (see ESI,† Table S5).

Conclusions

In this work, we utilized several complementary time-resolved laser spectroscopy techniques to measure photoinduced dynamical processes on different time scales from femtoseconds to seconds and to monitor the photochemistry of QM formation from adamantylphenol 3via an ultrafast photodehydration reaction. To elucidate the initial reaction pathway in fs-TA sub-20 fs UV pump pulses were used. These measurements lacked any signature in transient spectra of intermediate 3(S₁) state or of the formation of the photoproduct 4(S₁), QM in the excited state. Absence of 3(S₁) transients can be explained by a very weak excited state absorption which in addition could be located at shorter wavelengths. On the other hand, our computational results confirmed the presence of a conical intersection leading to direct formation of quinone methide (QM) in the ground state. This is in contrast to previously investigated mechanism of the photodehydration reaction where adiabatic QM formation from o-hydroxymethylphenol was established.

Moreover, we indirectly resolved the passage of the wave packet formed at the Franck–Condon point in 3(S₁) to the 4(S₀) ground state via a conical intersection by fitting the kinetic traces at several chosen wavelengths where rise time of spectral features was longer (∼100 fs) than the time resolution of the measurement (∼50 fs). Femtosecond FlUC was employed with the goal to resolve temporal evolution of adamantylphenol 3 in its excited state revealing the existence of a nonreactive conformer 3′ with temporal evolution distinctive from the conformer involved in QM formation. Appearance of non-emissive QM could not be tracked with fluorescence measurements but lack of any changes related to photochemical reaction, also absent in transient absorption, indicates that ultrafast measurements are in line with direct formation of QM in the ground state. In addition, in the LFP experiment, transient spectra associated with absorption from QM in the ground state were tracked from nanoseconds up to hundreds of milliseconds, further supporting our interpretation of fs-TA results. These results, providing unifying picture on investigated photochemical reaction of QM formation, are summarized in Scheme 3.

Scheme 3 Summary of revealed photochemical reaction pathways and characteristic time constants observed with different time resolved spectroscopic techniques backed up by theoretical computations. The rotational diffusional process (22 ps from FlUC) is not listed in the figure, since it showcases only the processes relevant to the photochemical reactions.

The results shed new light on the photochemical reactivity of phenols. We have demonstrated that a change of the molecular structure, while not altering the chromophore, nevertheless changes the photochemical reaction pathway. This principle should be taken into account when designing molecules for particular reaction schemes.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported in part by the Croatian Science Foundation's funding of the project UIP-05-2017-5831. The research was sponsored in part by European Union's Horizon 2020 research and innovation programme under grant agreement no. 654148 Laserlab-Europe. M. Š. thanks Professor Peter R. Schreiner for kindly providing computational resources of the Justus-Liebig-University, Giessen, Germany. We thank N. P. Ernsting for the FLUPS equipment and its installation. M. N. H. P., H. M. F. and A. C. acknowledge funding from the Swiss NSF through the NCCR MUST “Molecular Ultrafast Science and Technology”.

Notes and references

1. Quinone Methides, ed. S. E. Rokita, Wiley, Hoboken, 2009.
2. M. Freccero, Mini-Rev. Org. Chem., 2004, 1, 403–415.
3. P. Wang, Y. Song, L. Zhang, H. He and X. Zhou, Curr. Med. Chem., 2005, 12, 2893–2913.
4. F. Dufrasne, M. Gelbecke, J. Nève, R. Kiss and J.-L. Kraus, Curr. Med. Chem., 2011, 18, 3995–4011.
5. R. Van De Water and T. R. R. Pettus, Tetrahedron, 2002, 58, 5367–5405.
6. T. P. Pathak and M. S. Sigman, J. Org. Chem., 2011, 76, 9210–9215.
7. M. S. Singh, A. Nagaraju, N. Anand and S. Chowdhury, RSC Adv., 2014, 4, 55924–55959.
8. W.-J. Bai, J. G. David, Z.-G. Feng, M. G. Weaver, K.-L. Wu and T. R. R. Pettus, Chem. Res., 2014, 47, 3655–3664.
9. M. M. Toteva and J. P. Richard, Adv. Phys. Org. Chem., 2011, 45, 39–91.
10. P. Wan, B. Barker, L. Diao, M. Fischer, Y. Shi and C. Yang, Can. J. Chem., 1996, 74, 465–475.
11. S. Arumugam and V. V. Popik, J. Am. Chem. Soc., 2011, 133, 5573–5579.
12. S. Arumugam and V. V. Popik, J. Am. Chem. Soc., 2011, 133, 15730–15736.
13. S. Arumugam, S. V. Orski, J. Locklin and V. V. Popik, J. Am. Chem. Soc., 2012, 134, 179–182.
14. N. Basarić, K. Mlinarić-Majerski and M. Kralj, Curr. Org. Chem., 2014, 18, 3–18.
15. C. Percivalle, F. Doria and M. Freccero, Curr. Org. Chem., 2014, 18, 19–43.
16. E. Modica, R. Zanaletti, M. Freccero and M. Mella, J. Org. Chem., 2001, 66, 41–52.
17. Đ. Škalamera, C. Bohne, S. Landgraf and N. Basarić, J. Org. Chem., 2015, 80, 10817–10828.
18. Y. Yang, Y. Ma, Y. Zhao, Y. Zhao and Y. Li, J. Phys. Chem. A, 2018, 122, 1011–1018.
19. J. Ma, M. Šekutor, Đ. Škalamera, N. Basarić and D. L. Phillips, J. Org. Chem., 2019, 84, 8630–8637.
20. Y. Chiang, A. J. Kresge and Y. Zhu, J. Am. Chem. Soc., 2000, 122, 9854–9855.
21. Y. Chiang, A. J. Kresge and Y. Zhu, J. Am. Chem. Soc., 2001, 123, 8089–8094.
22. L. Diao, C. Yang and P. Wan, J. Am. Chem. Soc., 1995, 117, 5369–5370.
23. S. Arumugam and V. V. Popik, J. Am. Chem. Soc., 2009, 131, 11892–11899.
24. N. Basarić, N. Cindro, D. Bobinac, K. Mlinarić-Majerski, L. Uzelac, M. Kralj and P. Wan, Photochem. Photobiol. Sci., 2011, 10, 1910–1925.
25. N. Basarić, N. Cindro, D. Bobinac, K. Mlinarić-Majerski, L. Uzelac, M. Kralj and P. Wan, Photochem. Photobiol. Sci., 2012, 11, 381–396.
26. J. Veljković, L. Uzelac, K. Molčanov, K. Mlinarić-Majerski, M. Kralj, P. Wan and N. Basarić, J. Org. Chem., 2012, 77, 4596–4610.
27. Đ. Škalamera, K. Mlinarić-Majerski, I. Martin-Kleiner, M. Kralj, J. Oake, P. Wan, C. Bohne and N. Basarić, J. Org. Chem., 2017, 82, 6006–6021.
28. L. Uzelac, Đ. Škalamera, K. Mlinarić-Majerski, N. Basarić and M. Kralj, Eur. J. Med. Chem., 2017, 137, 558–574.
29. Đ. Škalamera, I. Antol, K. Mlinarić-Majerski, H. Vančik, D. L. Phillips, J. Ma and N. Basarić, Chem. – Eur. J., 2018, 24, 9426–9435.
30. N. Basarić, I. Žabčić, K. Mlinarić-Majerski and P. Wan, J. Org. Chem., 2010, 75, 102–116.
31. R. Borrego-Varillas, L. Ganzer, G. Cerullo and C. Manzoni, Appl. Sci., 2018, 8, 989.
32. M. Gerecke, G. Bierhance, M. Gutmann, N. P. Ernsting and A. Rosspeintner, Rev. Sci. Instrum., 2016, 87, 053115.
33. P. Hamm, R. A. Kaindl and J. Stenger, Opt. Lett., 2000, 25, 1798–1800.
34. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford, CT, 2016.
35. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
36. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
37. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
38. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327.
39. G. Siano, S. Crespi and S. M. Bonesi, J. Org. Chem., 2020, 85, 14012–14025.
40. S. C. Doan and B. J. Schwartz, J. Phys. Chem. Lett., 2013, 4, 1471–1476.
41. S. C. Doan and B. J. Schwartz, J. Phys. Chem. B, 2013, 117, 4216–4221.
42. E. J. Land and G. Porter, Trans. Faraday Soc., 1963, 59, 2016–2026.

---

Footnote

† Electronic supplementary information (ESI) available: Additional information regarding the theoretical computations and analysis of experimental data. See DOI: 10.1039/d1cp05690e

---