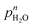Quantifiable models for surface protonic conductivity in porous oxides – case of monoclinic ZrO2†
Received
12th December 2021
, Accepted 8th April 2022
First published on 5th May 2022
Abstract
The surface protonic conductivity of porous monoclinic ZrO2 sintered at temperatures in the range 700–1100 °C yielding relative densities of around 60% and grain sizes of approximately 160 nm has been studied using impedance spectroscopy as a function of temperature well below the sintering temperature in wet atmospheres (pH2O = 0.03 bar). The sum of two high-frequency impedance responses is argued to represent surface conductance according to a new model of impedance over curved surfaces. A simple brick layer model is applied to compare the measured macroscopic conductivities with predicted surface conductances. The well-faceted samples sintered at the highest temperatures exhibited activation enthalpies up to 58 kJ mol−1 of surface protonic conduction in wet atmospheres at temperatures above 300 °C. We attribute this to the mobility of dissociated protons over surface oxide ions, and the high preexponential is in good agreement with a model comprising relatively strong dissociative chemisorption. With decreasing sintering temperature, the particles appear more rounded, with less developed facets, and we obtain activation enthalpies of surface protonic conduction in the chemisorbed layer down to around 30 kJ mol−1, with correspondingly smaller preexponentials and an observed 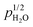 dependency. Supported by the thermogravimetry of adsorption, we attribute this to weaker and more molecular chemisorption on the more randomly terminated less faceted surfaces, providing water layers with fewer dissociated charge carrying protons, but also smaller activation enthalpies of mobility. Below 200 °C, all samples exhibit a strongly inverse temperature dependency characteristic of conduction in the 1st physisorbed layer with increasing coverage. The preexponentials correspond well to the models of physisorption, with dissociation to and proton migration between physisorbed water molecules. The enthalpies fit well to physisorption and with enthalpies of dissociation and proton mobility close to those of liquid water. We have by this introduced models for proton conduction in chemisorbed and physisorbed water on ZrO2, applicable to other oxides as well, and shown that preexponentials are quantitatively assessable in the order-of-magnitude level to discriminate models via a simple brick layer model based topographical analysis of the ceramic microstructure.
dependency. Supported by the thermogravimetry of adsorption, we attribute this to weaker and more molecular chemisorption on the more randomly terminated less faceted surfaces, providing water layers with fewer dissociated charge carrying protons, but also smaller activation enthalpies of mobility. Below 200 °C, all samples exhibit a strongly inverse temperature dependency characteristic of conduction in the 1st physisorbed layer with increasing coverage. The preexponentials correspond well to the models of physisorption, with dissociation to and proton migration between physisorbed water molecules. The enthalpies fit well to physisorption and with enthalpies of dissociation and proton mobility close to those of liquid water. We have by this introduced models for proton conduction in chemisorbed and physisorbed water on ZrO2, applicable to other oxides as well, and shown that preexponentials are quantitatively assessable in the order-of-magnitude level to discriminate models via a simple brick layer model based topographical analysis of the ceramic microstructure.
1 Introduction
Adsorption of water on the outer and inner surfaces of dense and porous ceramics is well known and studied, which enables humidity sensors (see e.g. ref. 1 and references therein) and gives rise to protonic conduction that in combination with various airborne contamination decreases the performance of electrical insulators.2 Surface protonic conduction in water adsorbed in porous nano-grained ceramics has more recently received renewed interest as potential electrolytes for fuel cells,3–5 while it is also realised that it plays significant roles in kinetics of catalysts, photocatalysts, and electrocatalysts.6,7
Surface protonics is particularly well studied for pure and doped dioxides of tetravalent cations. Much of our present knowledge on the adsorption of water and surface protonics in porous nano-grained ceramic oxides stems from studies of undoped monoclinic and cubic ZrO2,8–11 and cubic Y-stabilised ZrO2 (YSZ).12–18 Miyoshi et al.19,20 showed that the room temperature (RT) protonic conductivity of YSZ increased by 3 orders of magnitude when the grain size was reduced from 100 to 13 nm, while the concentration of Y2O3 did not have a significant effect on the surface protonic conductivity. They attributed the proton conductivity to water adsorbed at grain boundaries and surfaces. CeO2 is of particular importance in catalysis; the water adsorption has been well characterised,21,22 and surface protonic conduction has been measured,23,24 but it exhibits a complex surface chemistry with slow equilibria and considerable hysteresis.25–27 TiO2 has also been well studied28–30 lately because protonic migration in adsorbed water appears to be central for the use of TiO2 photocatalysts.31,32 Recently, Kang et al.33 investigated the role of surface orientation on water adsorption and surface protonic conduction in anatase TiO2 materials synthesised under conditions that favour different surface facets. They found by in situ FT-IR and conductivity measurements that simple {100} and {001} surfaces with accessible cations and anions favour dissociative chemisorption and the conductivity suggested that the subsequent physisorbed water layer was rigidly bonded and solid (ice-like). In comparison, the {101} surface favours molecular (associative) chemisorption, with a more loosely bonded subsequent physisorbed layer. The two types of surfaces have characteristic differences in surface protonic conductivity – especially its temperature dependency.
Gregori et al.23 proposed a brick layer model that qualitatively estimates the surface protonic conductivity of porous oxides based on the pore size, volume fraction of the open porosity, and thickness and bulk conductivity of the adsorbed water layer. They further assumed that dissociation into charge carriers follows autoprotolysis of water. Stub et al.15,16 suggested that proton transport can occur over grain surfaces (intra) and over grain boundary intersects (inter). They treated surface protonic conduction quantitatively based on their own measurements, standard models for adsorption, and transport terms for YSZ developed by Raz et al.12
These recent studies and the growing understanding of the phenomena involved have led us to propose a quantitative approach to parameterise models of adsorption, dissociation, and migration, which can also be applied to other porous materials. This in turn leads to prediction and interpretation of the macroscopic surface protonic conductivity of the porous sample, employing both enthalpies and, unlike non-quantitative approaches, the preexponentials. To do this, we define and employ a defect chemical notation for surface species, merge adsorption theory and defect equilibrium thermodynamics, apply normal theory of proton diffusion and migration, and link the surface conductance through the macroscopic sample conductivity by a simple topographical analysis – a brick layer model (BLM) – of the microstructure.
The surfaces of monoclinic ZrO2 show a preferred termination along the {111} plane after sintering at high temperatures.34 The literature on adsorption is limited to a review and study of CO adsorption35 in addition to the aforementioned studies on the adsorption of water and stability of hydroxylated ZrO2 surfaces.8,11 Surface protonic conductivity has not been reported for porous monoclinic ZrO2 and only scarcely from the perspective of volume conduction in undoped ZrO2 with a relatively high density (>80%) and a coarse microstructure.36 We herein report the surface protonic conductivity in adsorbed water layers in nano-grained porous monoclinic ZrO2, with focus on the effect of sintering temperature and hence small differences in the microstructure and degree of faceting of the surfaces. Samples are characterised by X-ray diffraction (XRD), scanning electron microscopy (SEM), thermogravimetry (TG) and electrochemical impedance spectroscopy (EIS). Results are interpreted according to the model for activation enthalpies and preexponentials of protonic conduction in chemisorbed and physisorbed water layers, supported by the observed isothermal pH2O dependence of conductivity, and the effect of faceting is considered. A discussion on the appearance of two high-frequency time responses in the impedance spectra is provided, which our samples have in common with most porous materials with surface protonic conduction.
2 Experimental
In order to prepare ZrO2 ceramic pellets, ZrO2 powder (99.99% metal basis except Hf, CAS no. 1314-23-4, Aladdin Industrial Corporation, China) and a binder (a mixture of polyvinyl, glycerol, ethanol and DI water) were mixed in the weight ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and pressed into disks with a diameter of 12.7 mm and a thickness of approx. 2.0 mm under a pressure of 760 MPa. They were sintered for 24 h at 600, 700, 800, 900, 1000, or 1100 °C, with a heating and cooling ramp rate of 5 °C min−1. Samples sintered at 600 °C were of insufficient mechanical strength for conductivity measurements, and only samples sintered at 700–1100 °C were characterised further and were denoted as ST700-ST1100 accordingly, see Table 1.
1 and pressed into disks with a diameter of 12.7 mm and a thickness of approx. 2.0 mm under a pressure of 760 MPa. They were sintered for 24 h at 600, 700, 800, 900, 1000, or 1100 °C, with a heating and cooling ramp rate of 5 °C min−1. Samples sintered at 600 °C were of insufficient mechanical strength for conductivity measurements, and only samples sintered at 700–1100 °C were characterised further and were denoted as ST700-ST1100 accordingly, see Table 1.
Table 1 Sample notation with sintering and microstructural parameters. Factor ψ is the ratio between the macroscopic conductivity of the porous sample and the grain surface conductance according to the brick layer model (BLM) that we will come back to later in eqn (3) with a percolation power ξ = 1. Also, volumetric, gravimetric, and molar specific surface areas are estimated to first approximation based on the BLM (see ESI 5, ESI)
| Sample |
ST700 |
ST800 |
ST900 |
ST1000 |
ST1100 |
| Sintering temperature, °C |
700 |
800 |
900 |
1000 |
1100 |
| FWHM, ° |
0.175 |
0.178 |
0.177 |
0.181 |
0.177 |
| Relative density, % |
60 |
60 |
60 |
65 |
70 |
| Average grain size from SEM, nm |
150 |
150 |
160 |
170 |
190 |
|
ψ, cm−1 (eqn (3) with ξ = 1) |
6.4 × 104 |
6.4 × 104 |
6.0 × 104 |
5.4 × 104 |
4.4 × 104 |
| SSAv, cm2 cm−3 |
9.6 × 104 |
9.6 × 104 |
9.0 × 104 |
8.1 × 104 |
6.6 × 104 |
| SSAg, cm2 g−1 |
2.7 × 104 |
2.7 × 104 |
2.6 × 104 |
2.1 × 104 |
1.6 × 104 |
| SSAM, cm2 mol−1 |
3.4 × 106 |
3.4 × 106 |
3.2 × 106 |
2.6 × 106 |
2.0 × 106 |
Powder XRD patterns were collected using a Bruker D8 Advance Diffractometer (Laguna Hills, CA, USA) with Cu Kα radiation (λ = 1.5418 Å). Microstructures were observed by SEM using a Hitachi SU 8010 Boerne (Hitachi, Tokyo, Japan).
Thermogravimetric data were acquired using a Netzsch 449 F1 Jupiter® thermal analyser (GmbH, Germany) on ST700 and ST1000, representing samples sintered at low and high temperatures, respectively. Samples were first degassed during heating to 650 °C (ST700) or 900 °C (ST1000) at 3 K min−1 using bottle-dry 99.999% N2 as both the carrier and protective gas, and further held at the given temperature for 2 h. (In our experience, even very dry gases typically end up with 30 ppm H2O in high-temperature apparatus.37) Then, the uptake of water was measured by flowing wet (pH2O = 0.026 bar) N2 over the samples during stepwise cooling to 26 °C. The water uptake was obtained by subtracting the background measurements in dry N2 gas carried out under otherwise identical conditions.
For electrical measurements, silver paste (SOFCMAN, China) was painted on both sides of the pellets, and heat-treated at 800 °C in an ambient atmosphere for 2 h, except for the sample sintered at 700 °C for which the heat-treatment was made at 600 °C. The pellets were mounted in a ProboStat™ (NORECS, Norway) sample holder with a 4-wire 2-electrode configuration. AC impedance spectra were collected in the range 1 MHz–1 Hz at 0.7 V rms applied voltage with a CHI604E electrochemical workstation (Shanghai Chenhua Instruments Ltd, Shanghai, China) or at 3 V rms using a Solartron SI 1260 frequency response analyser (Solartron Analytical, Farnborough, UK). For both, the ProboStat™ base unit chassis was connected to instrument ground to reduce noise and eliminate parasitic parallel conduction, and it was controlled that both instruments yielded equivalent spectra. The atmosphere was flowing Ar (99.999%) either bottle-dry or wetted to pH2O ≈ 0.03 bar by bubbling through de-ionized water at room temperature or using a HumiStat gas-mixer and humidifier (NORECS, Norway). The impedance spectra were collected after keeping the sample at each temperature for at least 1 h during cooling and analysed with ZView software (Scribner Associates, Inc. NC, USA). The electrical conductivity of each porous sample is calculated from its resistance, thickness, and electrode area.
3 Results
3.1 Microstructure characterisation
The geometrical dimensions after sintering were close to those of green bodies, i.e., little sintering takes place. From the dimensions and weight, the relative densities were calculated to vary only between 60% and 70% for the samples sintered at 700 and 1100 °C, respectively, see Table 1.
Fig. 1 shows the XRD results for the precursor powder and powder ground off the sintered samples. They all correspond to the monoclinic polymorph of ZrO2. Analyses of the main peaks shows that the full width at half maximum (FWHM) values are close, at about 0.180° for the samples annealed at 700–1100 °C, see Table 1, indicating from the Debye–Scherrer formula average crystallite sizes around 50 nm.38
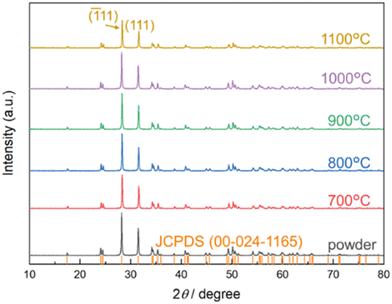 |
| | Fig. 1 X-ray diffractograms collected at RT for the ZrO2 powder and samples sintered at the given temperatures, compared with peak locations of the monoclinic ZrO2 structure (JCPDS). | |
Fig. 2 shows the SEM images of the precursor powder and sintered samples, revealing the openly porous microstructure in agreement with the densities from geometry and weight. From the statistical analyses of the images, we estimate average grain sizes of 150 nm for the precursor powder and 150–190 nm for the ST700–ST1100 samples. Hence, both sintering and grain growth are modest at the sintering temperatures applied here.
 |
| | Fig. 2 SEM images of the precursor powder and fracture surfaces of the samples sintered at the given temperatures. | |
Closer inspection of the grains suggests no differences in the aspect ratio and modest differences in connectivity (necks). However, while the mostly spherical shape of the precursor particles has been retained in the samples sintered at low temperatures (below 900 °C), the particles of samples sintered at higher temperatures show more faceted surfaces, apparently a distribution over normal {100}, {110}, and {111} surfaces (in cubic framework) as the regular aspect of the crystallite is maintained.
3.2 Thermogravimetry (TG)
Fig. 3 shows the TG result in terms of the amount of water (chemisorbed and physisorbed) adsorbed on ZrO2 ST700 and ST1000, with area specific coverage calculated based on the estimates of specific surface areas listed in Table 1. The uptake of chemisorbed water saturates towards 200 °C at around 4–5 H2O molecules per nm2, which is considered a monolayer.8 We note that the coverage is not yet complete at 400 °C for the ST700 sample, suggesting relatively weak and hence molecular chemisorption, while the ST1000 sample achieves coverage at somewhat higher temperatures, indicating stronger chemisorption on its more developed (facetted) surfaces, as observed also for CeO2.39
 |
| | Fig. 3 The area specific uptake of water obtained from TG analysis for ST700 and ST1000 in wet (pH2O = 0.026 bar) N2vs. 1/T. | |
Physisorption sets in below 200 °C, and a first physisorbed layer is complete around 80 °C. Qualitatively, the water uptake modelled as the sum of a completed chemisorbed layer and physisorbed layers yields adsorption enthalpies similar to that of condensation to liquid water,12 as expected. The total water uptake corresponds well to one reported in the literature, when its surface area of 80 m2 g−1, a factor of 4 higher than in our samples is taken into account.40
3.3 Electrical properties
3.3.1 Electrochemical impedance spectroscopy (EIS).
Representative impedance spectra are displayed in ESI 2 and Fig. S1 (ESI†). All samples exhibited two overlapping semicircles in the high frequency domain, with capacitances in the lower and higher end of the 10−11 F range, irrespective of sintering and measurement temperature or atmosphere (dry or wet). The literature does not provide a consistent rationalisation of this, but in our present understanding, it reflects surface conduction over the curved surface of the porous microstructure, namely concave regions with small capacitance of the gas phase over the gap and convex regions with higher capacitance due to the dielectric solid phase. We provide a more detailed discussion of the origin and capacitances of the two responses in ESI 3 (ESI†), but here take it that the sum of the two resistances represents the total resistance of the surface transport.
The two responses are present also in dry atmospheres at the highest measurement temperatures. This suggests that also the native, non-protonic conduction is dominated by surface transport, which is reasonable in these fine-grained porous samples.
At the highest measurement temperatures, there is an additional response at the lowest frequencies, with characteristic capacitances of the order of magnitude of 10−8 F, both in wet and dry atmospheres. This may be a grain boundary impedance as reported by Stub et al.16 for YSZ, but it may also be an electrode response. The contact area between the adsorbed water layer and the metal electrode is small compared with a normal solid electrolyte, hence the normal capacitance of 10−6 F for samples of this size attributed to the double layer in parallel with charge transfer may be reduced by orders of magnitude and be what we observe.
3.3.2 Surface protonic conductivities.
An Arrhenius plot of the electrical conductivity of all samples under wet and dry Ar (separated) is provided in ESI 4 and Fig. S2 (ESI†). The conductivities in wet atmosphere generally behave like typical surface protonic isobars with considerable conductivities at high temperatures, a minimum at around 200 °C, and conductivities increasing with decreasing temperature towards room temperature. In bottle-dry atmospheres, the measured conductivities were similar for all samples, with activation energies of around 100 kJ mol−1 at the highest temperatures, typical of oxide vacancy mobility in ZrO2 materials.36,41 We attribute this to native conductivity of the sample, apparently dominated by surface transport based on the above-mentioned interpretation of the impedance spectra in dry atmospheres.
Fig. 4 shows the surface protonic conductivities obtained in wet atmospheres after subtraction of native conductivity, plotted as log(σT) vs. 1/T as we shall use that for extracting enthalpies and preexponentials, listed in Table 2.
 |
| | Fig. 4 Plot of log(σT) vs. 1/T measured in wet (pH2O = 0.03 bar) Ar, after subtraction of the dry atmosphere native conductivities, as explained in the text. | |
Table 2 Preexponentials and activation enthalpies of the macroscopic conductivity of the porous sample material fitted from log(σT) vs. 1/T plots
| Conditions |
Type of conduction |
Sample |
ST700 |
ST800 |
ST900 |
ST1000 |
ST1100 |
| Parameter |
| High T, dry |
Native conductivity |
σ
M 0, SK cm−1 |
2 × 101 |
1 × 101 |
1 × 102 |
1 × 102 |
7 × 101 |
| ΔH, kJ mol−1 |
95 |
92 |
109 |
105 |
104 |
| High T, wet |
Surface protonic, chemisorbed |
σ
M 0, SK cm−1 |
5 × 10−3 |
1 × 10−1 |
2 × 10−2 |
4 × 10−1 |
1 × 10−1 |
| ΔH, kJ mol−1 |
27 |
41 |
34 |
58 |
57 |
| Low T, wet |
Surface protonic, 1st physisorbed |
σ
M 0, SK cm−1 |
6 × 10−9 |
1 × 10−9 |
5 × 10−9 |
7 × 10−12 |
4 × 10−13 |
| ΔH, kJ mol−1 |
−22 |
−32 |
−25 |
−40 |
−47 |
The surface protonic conductivities in wet atmospheres above 200 °C are typical of conduction in the chemisorbed water layer, which according to adsorption thermodynamics of ZrO28 should approach full coverage below 400 °C at pH2O = 0.03 bar. The enthalpies in this region are approaching 60 kJ mol−1 for ST1000 and ST1100, which we for now note is comparable to the enthalpy of mobility of protons in the lattices of MO2 oxides, e.g. 58 kJ mol−1 for polycrystalline rutile TiO242, and 43 kJ mol−1 as an estimate for 50% La-doped CeO2.43 With lower sintering temperatures, the enthalpies decrease, to around 30 kJ mol−1 for ST700, and conductivities are higher suggesting that the enthalpy of migration is lower and/or the exothermic adsorption is at play, i.e., the layer is not complete and still filling up with decreasing temperature for these samples, in agreement with the TG results, and to be discussed further later.
Below 150 °C, we have a strong increase in conductivity, as a first molecular physisorbed water layer starts to build on top of the chemisorbed layer, providing easier transfer of protons. The activation enthalpies are now found to be in the range of −40 to −20 kJ mol−1. This is qualitatively dominated by the exothermic enthalpy of the condensation of water vapour, and we shall quantify it when we discuss models for transport in this layer later.
As the physisorbed layer builds, it expectedly gets more liquid-like and the physisorption enthalpy approaches that of pure liquid water. This gives rise to an additional strong increase in the surface protonic conductivity in many porous ceramics,15,28 including some facets of TiO233 as we approach RT and relative humidity (RH) surpasses 60%. For our monoclinic ZrO2 samples, however, there is no such secondary increase in conductivity. This is similar to the {101} facet of TiO233 and our on-going work on undoped CeO239 where it even increases less steeply above RHs of 60%. As our data do not extensively explore the region at RH > 60%, we refrain from analysing that region further and it is not part of Table 2.
3.3.3 Isothermal pH2O dependencies.
Fig. 5 shows the pH2O dependence of surface protonic conductivity obtained for the ST700 sample recorded at 400 and 100 °C, reflecting the chemisorbed and first physisorbed water layer, respectively. A close to  dependency is revealed at 400 °C, in agreement with the results for 4 mol% Y2O3-stabilised ZrO2 (4YSZ) at 250–400 °C19 and more recently for undoped CeO2 at 400 °C.39 This may be interpreted to reflect a weak molecular and hence incomplete chemisorbed layer with only partial dissociation to conductive protons. At 100 °C, we obtained close to
dependency is revealed at 400 °C, in agreement with the results for 4 mol% Y2O3-stabilised ZrO2 (4YSZ) at 250–400 °C19 and more recently for undoped CeO2 at 400 °C.39 This may be interpreted to reflect a weak molecular and hence incomplete chemisorbed layer with only partial dissociation to conductive protons. At 100 °C, we obtained close to  dependency, same as that of undoped nanoscopic CeO2 sintered at 550 °C and measured at 100 °C.39 We will discuss models that may rationalise it below.
dependency, same as that of undoped nanoscopic CeO2 sintered at 550 °C and measured at 100 °C.39 We will discuss models that may rationalise it below.
 |
| | Fig. 5
p
H2O dependence of surface protonic conductivity for ST700 at 400 and 100 °C recorded in N2 gas, representing the chemisorbed and physisorbed regions, respectively. | |
4 Models and quantitative interpretation
In the following, we provide a deeper theoretical analysis of the preexponentials and activation enthalpies of surface conduction in porous oxides, with focus on MO2 type oxides and ZrO2 and the actual samples and data presented here. For this, we will go through some definitions and clarifications of conductivity contributions, considerations of geometrical factors for surface conduction in porous materials, estimation of charge mobility of protonic species, nomenclature for surface species, and thermodynamics of adsorption and dissociation, leading up to expressions for surface conduction and sample macroscopic conductivity. A list of symbols and subscripts is provided in the ESI† (ESI 1 and Table S1).
4.1 Conductivity and geometry
The total macroscopic conductivity of a porous material σM can be taken to have bulk and surface contributions. Under our experimental conditions, we take it that the bulk conductivity of ZrO2 is due to native oxide ion transport, and while it appears that this is negligible, the surface conductivity also has a contribution from oxide ions in addition to protonic conduction. The latter may be taken to arise from migration in chemisorbed, first rigid physisorbed, and second liquid-like physisorbed water layers:| |  | (1) |
We will treat the three water layers as one, dominated by the outermost one, in the sense that the layers adsorb one by one, to a first approximation, and that the conductivity of the outermost layer for the purpose of modelling totally outcompetes that of any layers underneath.
The conductivities in dry atmospheres at high temperatures exhibit activation energies of around 100 kJ mol−1, attributable to inherent conduction by oxide ions in gross agreement with literature data for bulk conductivity of monoclinic ZrO2.36,41 If it is a bulk conduction process, the measured conductivity is empirically proportional to the square of the relative density, making factors such as 0.652 = 0.42, but this does not change the comparison significantly. As mentioned earlier, impedance spectra suggest that the inherent conduction is also a surface process due to the presence of the overlapping high-frequency semicircles with capacitances of the order of 10−11 F (see ESI 2 and Fig. S1(e, f), ESI†). Dual time constants have also been reported for YSZ, suggested to reflect intra- and inter-grain surface protonic resistances.16 It is anyway not of our interest here, and we subtract it where it is significant at high temperatures and can neglect it at lower temperatures, so that Fig. 4 represents σM = σM,s,H+.
The macroscopic protonic surface conductivity σM,s,H+ of the sample material must be related to the adsorbed water surface layer volume conductivity σs,H+ along an appropriate geometric model. For this, we need the protonic surface layer conductance, Gs,H+. It has unit S (Siemens) and is the in-plane conductance of a square of a surface layer with thickness t. It is independent of the width w and the length l of the square, since they are equal and cancel. The surface protonic conductance Gs,H+ with average volume concentration cH+ and charge mobility uH+ in the water layer is then related to the protonic surface layer volume conductivity σs,H+ by
| |  | (2) |
where we have also replaced the protonic surface layer volume concentration
cH+ (in mol cm
−3) with surface concentration
γH+ (in mol cm
−2) and layer thickness
t in
cH+ =
γH+/
t. As stated above, we here treat the surface layer as one, and we have deliberately used subscript s to distinguish conductance and conductivity of the surface layer from other geometries, while we have omitted the superscript s for concentration and mobility terms to avoid build-up of too many subscripts later on.
From a simple brick layer model (BLM, see ESI 5, ESI†), we may make an order-of-magnitude approximation to the macroscopic conductivity contribution σM,s of a porous material from the surface conductance Gs, the relative density ρr, and assumed equal grain and pore size dg:
| | 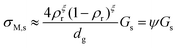 | (3) |
The exponent
ξ adjusts for percolation. For materials of regular and equal shapes of grains and pores, and densities around 50%, it will be
ξ = 1–2 and we here use
ξ = 1. The effect is still less than half an order of magnitude for densities around 50%. The factor
ψ =
σM,s/
Gs in
eqn (3) calculated on this basis is listed for our samples in
Table 1. In this work, we hence calculate the predicted macroscopic sample surface protonic conductivity from
σM,s,H+ =
ψGs,H+.
4.2 Charge mobility of protonic species
We now consider the diffusivity and charge mobility of protons, which we will need to couple thermodynamics and concentrations with conductance and conductivity. Since the proton is a defect on oxide surfaces, its random diffusivity is in the classic approximation we will use here a simple activated function, multiplied by the chance XO that the oxide ion it jumps to is available to accept the proton:| |  | (4) |
XO is the fractional occupancy of any oxide-ion containing species, O2−, OH−, or H2O, that can accept a proton, depending on the mechanism. The charge mobility is via the Nernst–Einstein relation then:| |  | (5) |
Generally, the preexponential of diffusivity is given by  where A is a geometrical factor of the order of unity, s is the jump distance, ω0 is the vibrational attempt frequency, and ΔSm is the entropy part of the energy barrier. The proton always jumps from its host oxide ion to a nearest one, so we may take the effective jump distance to be 2.8 ≈ 3 Å. The vibrational attempt frequency is in practice that of the oxide ion host, of the order of 1012 s−1 (not the 1013 s−1 of the proton itself). With this, we get DH+0 ≈ 1 × 10−3 cm2 s−1 as an order of magnitude estimate, irrespective of the mechanism or host system, and in turn,
where A is a geometrical factor of the order of unity, s is the jump distance, ω0 is the vibrational attempt frequency, and ΔSm is the entropy part of the energy barrier. The proton always jumps from its host oxide ion to a nearest one, so we may take the effective jump distance to be 2.8 ≈ 3 Å. The vibrational attempt frequency is in practice that of the oxide ion host, of the order of 1012 s−1 (not the 1013 s−1 of the proton itself). With this, we get DH+0 ≈ 1 × 10−3 cm2 s−1 as an order of magnitude estimate, irrespective of the mechanism or host system, and in turn,  .
.
4.3 Nomenclature for surface species
Now that we start our thermodynamic analysis with the aim to combine it with charge mobility to get conductivity, we choose to use a Kröger–Vink compatible notation for surface chemistry in which superscripts ×, ′, and ˙ denote, respectively, neutral, negative, and positive effective charges compared to the charge of the clean, “perfect” surface. For compatibility with other binary oxides, we furthermore choose to denote cations by the general symbol M, so that here M = Zr and surface cation and oxide ion sites are hence denoted as Ms and Os.
4.4 The chemisorbed layer
We start by attempting to predict the level and behaviour of surface protonic conductivity in the chemisorbed layer, which dominates typically in wet atmospheres at high temperatures down to around 200 °C. The samples behave differently in terms of activation enthalpy and preexponentials, and we will derive two models that can rationalise the two. One is based on weak, molecular chemisorption, and it divides further into two sub-models with different dissociation and migration behaviours, of which one will be shown to be applicable to sample sintered at the lowest temperatures. The other model is based on strong, dissociative chemisorption, which appears to apply to the samples sintered at higher temperatures. The models are schematically depicted in Fig. 6.
 |
| | Fig. 6 Schematic illustration of the five models derived for adsorption, dissociation and protonic migration in this work. “Surface” shows the bare MO2 surface. “chm” shows weak molecular chemisorption and dissociation (for reasons of space limitations shown as half covered and half dissociated) with resulting protonic migration (arrows) in the molecular dissociated layer. “chm-s” is similar, but protons are dissociated to and migrate with the help of surface oxide ions. “chd” shows strong dissociative chemisorption with proton migration on surface oxide ions. “chm-ph1” shows partial coverage of the 1st physisorbed layer with protons dissociated from a molecular chemisorbed layer underneath. “ph1” shows partial coverage of the 1st physisorbed layer with weak dissociation over a strongly adsorbed and dissociated chemisorbed layer underneath. | |
4.4.1 Weak, molecular chemisorption.
A previous in situ FTIR study shows that a high surface concentration of hydroxyl groups is missing from water chemisorption on monoclinic ZrO2 between RT and 1173 K over a pressure range of 10−5–24 mbar, in contrast to highly hydroxylated YSZ and Y2O3.18 Room temperature IR measurements on high surface area ZrO2 after annealing at 873 K reveal a single broad peak at 3690 cm−1, attributed to the O–H stretch mode of H2O molecules, in addition to a characteristic molecular water band at ∼1630 cm−1 due to H–O–H bending.40Ab initio molecular dynamics calculations suggest that while only dissociative adsorption is observed on tetragonal ZrO2{110} surfaces,44 both undissociated and dissociated water species coexist on the two most stable surfaces of monoclinic ZrO2, i.e. {101} and {111}.11
These experimental and computational studies lead us to propose that H2O adsorbs on a surface M4+ cation but does not easily dissociate protons H+ onto surface oxide ions O2− or to other water molecules. The lack of dissociation, i.e., an endothermic dissociation enthalpy, leaves the overall chemisorption weak (only modestly exothermic adsorption enthalpy, dominated by unfavourable entropy) and makes an only partly covered and largely molecular layer (“chm” and “chm-s” in Fig. 6). The molecular chemisorption is in our nomenclature written as follows:
| |  | (6) |
with equilibrium coefficient
| |  | (7) |
Here,
X represents the fractional occupancy (which ideally corresponds to activity and also to surface site coverage),
p is the partial pressure, and
γ is the surface concentration
e.g. in mol cm
−2. The concentration of adsorbed molecular water according to this model follows simple adsorption isotherm treatments. We are interested in partial dissociation, either protonating other adsorbed molecules (“chm”) or surface oxide ions (“chm-s”) and thereby providing protonic conductivity. We shall derive expressions for both, and compare with the experimental data.
Dissociation within molecular water
As suggested by e.g. Raz et al.,12 chemisorbed water molecules may dissociate into adsorbed OH− ions and H3O+ ions, in our nomenclature according to| | 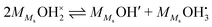 | (8) |
and the equilibrium constant can then be written as follows:| |  | (9) |
If this dominates, we have the following simple electroneutrality:| |  | (10) |
Moreover, cation surface site balance requires 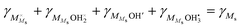 , but under the assumption of weak molecular adsorption (low coverage and limited dissociation), we have
, but under the assumption of weak molecular adsorption (low coverage and limited dissociation), we have 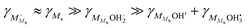 , and we can insert and simplify to get
, and we can insert and simplify to get| |  | (11) |
In estimating the surface conductance based on this dissociation model, we assume that jumps of protons from dissociated protons H3O+ to H2O and jumps from H2O to dissociated OH− contribute equally, and from the electroneutrality the surface protonic conductance in the chemisorbed layer according to eqn (2) can be expressed as the product of charge, surface concentration, and charge mobility:| |  | (12) |
The charge mobility of the charged defects contains the chance that a proton in an H3O+ group finds an adjacent water molecule to jump to, or that a water molecule is there to offer a proton to jump to OH−. Hence, we get| |  | (13) |
which, by combination with eqn (7) and (11), yields| |  | (14) |
We rewrite this as| |  | (15) |
with| |  | (16) |
where  is the standard preexponential of surface protonic conductance at pH2O = 1 bar. We emphasize that
is the standard preexponential of surface protonic conductance at pH2O = 1 bar. We emphasize that  is hence the most fundamental parameter specific for a surface and a particular adsorption and transport model, in this case weak molecular adsorption with dissociation and transport in the molecular layer. To derive such a fundamental parameter is only meaningful once a model is chosen, so that the pH2O dependency is clear.
is hence the most fundamental parameter specific for a surface and a particular adsorption and transport model, in this case weak molecular adsorption with dissociation and transport in the molecular layer. To derive such a fundamental parameter is only meaningful once a model is chosen, so that the pH2O dependency is clear.
Now, we attempt to estimate  ,
,  , and eventually
, and eventually  . The standard entropy change
. The standard entropy change 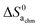 plays a major role and represents the biggest uncertainty. Condensation of water vapour to liquid water has a standard entropy change of −109 J mol−1 K−1 at 100 °C.45 It decreases strongly with temperature, e.g., to −44 J mol−1 K−1 at 300 °C which is relevant for our chemisorption temperature range. On the other hand, the entropy of condensation to ice is larger than that to water (−144 vs. −118 J mol−1 K−1 at RT) and the entropy of molecular adsorption to hydroxylated α-Fe2O3, i.e., physisorption, has been reported to be −138 J mol−1 K−1.46 We will hence in this work for the most part use −109 J mol−1 K−1 from the entropy of condensation to water at 100 °C45 as our value for the standard entropy of molecular adsorption
plays a major role and represents the biggest uncertainty. Condensation of water vapour to liquid water has a standard entropy change of −109 J mol−1 K−1 at 100 °C.45 It decreases strongly with temperature, e.g., to −44 J mol−1 K−1 at 300 °C which is relevant for our chemisorption temperature range. On the other hand, the entropy of condensation to ice is larger than that to water (−144 vs. −118 J mol−1 K−1 at RT) and the entropy of molecular adsorption to hydroxylated α-Fe2O3, i.e., physisorption, has been reported to be −138 J mol−1 K−1.46 We will hence in this work for the most part use −109 J mol−1 K−1 from the entropy of condensation to water at 100 °C45 as our value for the standard entropy of molecular adsorption 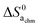 , both here for chemisorption and later for physisorption. This implies uncertainties of several orders of magnitude in our calculations for conductances, but helps to emphasise differences between different models.
, both here for chemisorption and later for physisorption. This implies uncertainties of several orders of magnitude in our calculations for conductances, but helps to emphasise differences between different models.
We next assume  for dissociation (since it does not involve gas species or solvation of ions). Using furthermore an adsorption site surface concentration γMs ≈ 5 nm−2 = 8 × 10−10 mol cm−2, and uH+0 ≈ 10 cm2 K V−1 s−1 as derived earlier, we get
for dissociation (since it does not involve gas species or solvation of ions). Using furthermore an adsorption site surface concentration γMs ≈ 5 nm−2 = 8 × 10−10 mol cm−2, and uH+0 ≈ 10 cm2 K V−1 s−1 as derived earlier, we get  for pH2O = 1 bar and
for pH2O = 1 bar and  at pH2O = 0.03 bar. By applying
at pH2O = 0.03 bar. By applying  from eqn (3) and values of ψ from Table 1, we get predicted preexponentials for macroscopic conductivity of around
from eqn (3) and values of ψ from Table 1, we get predicted preexponentials for macroscopic conductivity of around  for our samples at pH2O = 0.03 bar. This low value, dominated by the variable and uncertain but grossly negative entropy of adsorption, is several orders of magnitude below the experimental ones for the surface protonic conductivity in the chemisorbed layer at higher temperatures (Table 2) and the “chm” model can be ruled out.
for our samples at pH2O = 0.03 bar. This low value, dominated by the variable and uncertain but grossly negative entropy of adsorption, is several orders of magnitude below the experimental ones for the surface protonic conductivity in the chemisorbed layer at higher temperatures (Table 2) and the “chm” model can be ruled out.
Dissociation to surface oxide ions
In the other possibility of dissociation, the molecule dissociates into an adsorbed hydroxide ion and a surface hydroxide ion, i.e., it protonates a surface oxide ion (“chm-s” in Fig. 6), as suggested by AIMD simulations on cubic ZrO2{110} surfaces9:| |  | (17) |
| |  | (18) |
The same analysis as above now yields| |  | (19) |
We may further assume that the proton on surface oxide in the  defect may migrate by jumping to other surface oxide ions, since MMsOH′ it left behind from the dissociation is rare to find. The surface protonic conductance will then be
defect may migrate by jumping to other surface oxide ions, since MMsOH′ it left behind from the dissociation is rare to find. The surface protonic conductance will then be| | 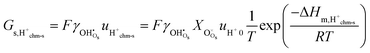 | (20) |
Since we have little adsorption and little dissociation, surface oxide ions are generally available,  , so that we by inserting eqn (19) get
, so that we by inserting eqn (19) get| |  | (21) |
and hence| | 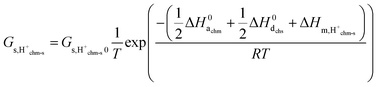 | (22) |
with| |  | (23) |
Considering that the concentration of surface oxide adsorption sites in ZrO2 is twice that of cation sites, i.e., γOs = 2γMs, and other parameters are the same as before, we predict now  ,
,  , and
, and  . Sample ST700 has a preexponential of macroscopic conductivity of around 5 × 10−3 S K cm−1 (Table 2), i.e., within an order of magnitude of prediction, suggesting that weak molecular adsorption and dissociation to protons transported along surface oxide ions may apply. In this case, the experimental enthalpy should be interpreted according to
. Sample ST700 has a preexponential of macroscopic conductivity of around 5 × 10−3 S K cm−1 (Table 2), i.e., within an order of magnitude of prediction, suggesting that weak molecular adsorption and dissociation to protons transported along surface oxide ions may apply. In this case, the experimental enthalpy should be interpreted according to  . The standard enthalpy of molecular chemisorption has been determined calorimetrically as
. The standard enthalpy of molecular chemisorption has been determined calorimetrically as  for YSZ relatively independent of the Y content.13 If we adopt a dissociation enthalpy of 22.1 kJ mol−1 from ref. 47 used by Raz et al.12 for YSZ, we get an enthalpy for surface mobility of protons of
for YSZ relatively independent of the Y content.13 If we adopt a dissociation enthalpy of 22.1 kJ mol−1 from ref. 47 used by Raz et al.12 for YSZ, we get an enthalpy for surface mobility of protons of  .
.
The model proposes a proportionality to  of surface protonic conduction for weakly adsorbed and dissociated chemisorbed water according to eqn (21). This is in line with the experimental results obtained for the ST700 sample at 400 °C (Fig. 5).
of surface protonic conduction for weakly adsorbed and dissociated chemisorbed water according to eqn (21). This is in line with the experimental results obtained for the ST700 sample at 400 °C (Fig. 5).
All in all, partial coverage of molecularly chemisorbed water, partially dissociated into mobile protonic species, forms a credible model for the surface protonic conductivity at temperatures above 200 °C for samples sintered at the lowest temperatures. Involvement of surface hydroxide as a dissociation product and mobile species fits much better with the observed preexponentials than transport between adsorbed water species. We suggest that this may apply also to other oxides where a similar behaviour is observed, and is a result of surfaces that are relatively amorphous or rounded (vs. faceted) or have terminations where dissociation is unfavourable. While the transfer of a proton to a surface oxide ion is not very favourable, the transfer between oxide ions may be correspondingly easier.
4.4.2 Strong, dissociative chemisorption.
Next, we assume as before that H2O adsorbs on a surface M4+ cation (here Zr4+) and dissociates one proton H+ onto a surface oxide ion O2−. However, now this dissociation step is favourable (exothermic) and strengthens the overall chemisorption (making it more exothermic) and makes a fully covered and dissociated layer at relatively high temperatures (low RH). Dissociative chemisorption (“chd” in Fig. 6) is then a combination of eqn (6) and (17):| |  | (24) |
with equilibrium coefficient being the product of eqn (7) and (9):| |  | (25) |
While we earlier used data for weak molecular chemisorption on ZrO2, there exist data also for strong dissociative adsorption. From first principles calculations, the enthalpy of dissociative chemisorption on the {001} surface of monoclinic ZrO2 has been reported to be −165 kJ mol−1 for half-monolayer coverage, and −109 kJ mol−1 for full-monolayer coverage48. Radha et al.8 measured the amount of chemisorbed water on monoclinic ZrO2 and found that full coverage corresponds to 3.8–5 H2O per nm2. From high-temperature oxide melt solution calorimetry on samples annealed at 600 and 800 °C, they found integral enthalpies of dissociative chemisorption at half monolayer coverage (2.2 H2O per nm2) and full monolayer coverage of −142 kJ mol−1 and −119.5 ± 1.7 kJ mol−1, respectively. With this and aforementioned estimates of the entropy, eqn (25) and the electroneutrality and site balances yield the coverage of cation adsorption sites at pH2O = 0.03 bar varying from above 90% at the lower end of the temperature range considered for strong dissociative chemisorption here to 50% at higher temperatures. For the interpretation of the exponential changes in conductivity with temperature, these variations are minor (of the order of a factor of 2) in the range where we assign conductivity to transport in the chemisorbed layer. The Arrhenius plots of the surface protonic conductivity for the samples sintered at higher temperatures are indeed linear in the range above 300 °C (Fig. 4). The electroneutrality and assumption of full coverage leads directly to| |  | (26) |
indicating that the concentration of dissociated protons is independent of temperature as well as RH and pH2O, and that the temperature dependence is attributable solely to the mobility of dissociated protons. We assume that the dominating transport mechanism for dissociated protons on ZrO2 surfaces within the chemisorbed water layer is their jump between their surface oxide host sites, and that these have an average occupancy of  since half of them are occupied with dissociated protons. The surface protonic conductance then becomes
since half of them are occupied with dissociated protons. The surface protonic conductance then becomes| |  | (27) |
with| |  | (28) |
With the same assumptions as before, this yields  , and
, and 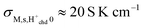 , to be compared with the corresponding experimental preexponentials (Table 2) for the chemisorbed layer of 0.1–0.4 S K cm−1 for the samples sintered at the highest temperatures. The two orders of magnitude difference may be ascribed to the many approximations along the way, but may also mean that the assumptions of the model comprising fully covered and dissociated chemisorbed water are not fully met. However, we may assign the activation enthalpies of up to 60 kJ mol−1 to the diffusion barrier for protons migrating between oxide ions on the faceted surfaces of monoclinic ZrO2 covered with dissociatively chemisorbed water. The aforementioned comparison to the enthalpy of mobility of protons of 58 kJ mol−1 for polycrystalline rutile TiO242 and 43 kJ mol−1 as an estimate for 50% La-doped CeO243 is reasonable if the concentration of carriers is constant as in a fully covered chemisorbed layer, which based on the TG result seems reasonable for the samples sintered at the highest temperatures.
, to be compared with the corresponding experimental preexponentials (Table 2) for the chemisorbed layer of 0.1–0.4 S K cm−1 for the samples sintered at the highest temperatures. The two orders of magnitude difference may be ascribed to the many approximations along the way, but may also mean that the assumptions of the model comprising fully covered and dissociated chemisorbed water are not fully met. However, we may assign the activation enthalpies of up to 60 kJ mol−1 to the diffusion barrier for protons migrating between oxide ions on the faceted surfaces of monoclinic ZrO2 covered with dissociatively chemisorbed water. The aforementioned comparison to the enthalpy of mobility of protons of 58 kJ mol−1 for polycrystalline rutile TiO242 and 43 kJ mol−1 as an estimate for 50% La-doped CeO243 is reasonable if the concentration of carriers is constant as in a fully covered chemisorbed layer, which based on the TG result seems reasonable for the samples sintered at the highest temperatures.
The samples sintered at intermediate temperatures show preexponentials and enthalpies between those sintered at the lowest and highest temperatures, and we may expect that they (or in fact all samples) have mixed presence of surface areas with weak molecular and strong dissociated chemisorption.
4.5 Physisorbed layers
4.5.1 Physisorption.
Below 150 °C, the conductivities of the samples show a steep increase. This is attributed to the effect of water molecules physisorbed on top of its complete chemisorbed layer. It starts with a structured, relatively rigid (ice-like) first physisorbed layer:| |  | (29) |
with equilibrium coefficient| |  | (30) |
and in a second step builds further, increasingly liquid-like layers:The enthalpy of physisorption starts out a bit more exothermic than condensation into liquid water due to the stronger hydrogen bonds to the chemisorbed layer, and becomes less exothermic and eventually reaches the heat of condensation of water, which is −44.0 kJ mol−1 at RT and decreases with increasing temperature, e.g. −40.7 kJ mol−1 at 100 °C. The number of monolayers of physisorbed water is given by the BET isotherm49| | 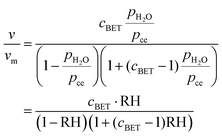 | (32) |
where v is the volume of adsorbed water, vm is the volume of one monolayer such that v/vm gives the surface coverage in number of monolayers, cBET is the so-called BET constant, pH2O is the partial pressure of water, pce is the temperature-dependent condensation–evaporation equilibrium partial pressure, and  . The BET constant is approximated by
. The BET constant is approximated by| |  | (33) |
where E1 is the heat of adsorption for the first layer and EL for the second and higher layers. EL is usually more or less equal to the heat of condensation, −44 kJ mol−1 at RT and −40.7 kJ mol−1 at 100 °C. Here, when the chemisorbed layer is treated separately and we deal only with the physisorbed layers, the energy difference between the first and second physisorbed water layer is expected to be small, but still non-zero; a typical estimate is E1 − EL = −4 kJ mol−1.
The equilibrium pressure pe is a strong function of temperature, which can be expressed by the thermodynamics of vaporisation or condensation as
| |  | (34) |
At RT we have approximate thermodynamic parameters of condensation of

and

, while at 100 °C, we have
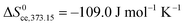
and
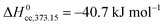
.
45 In the low coverage region of the first physisorbed layer,
eqn (30) can be simplified to yield the coverage as
| |  | (35) |
We express this in many ways and using many parameters to stress its significance and simplicity. Here, Δ
S0ph1 and Δ
H0ph1 are temperature dependent parameters for the first physisorbed layer, expressing the temperature dependency of
cBET/
pce. They are close to those of condensation to bulk water, enhanced by the extra few kJ mol
−1 of exothermic enthalpy because of the extra hydrogen bonds in the first layer bonding to the chemisorbed layer underneath.
Eqn (35) is an alternative representation of
eqn (32) and (33), more useful for our purpose. From this, we will later on use an estimate that the enthalpy of physisorption for the first physisorbed layer around 100 °C will be Δ
H0ph1 ≈ −(40.7 + 4) kJ mol
−1 ≈ −45 kJ mol
−1.
4.5.2 Dissociation and conduction in the first physisorbed water layer.
Dissociation of physisorbed water has different possibilities; we will consider and evaluate two of them here.
Dissociation from chemisorbed to physisorbed water
In the first, we assume that chemisorbed molecular water dissociate protons into the physisorbed layer forming H3O+ (“chm-ph1” in Fig. 6) so that we have| |  | (36) |
with equilibrium constant| |  | (37) |
If this dominates, we have the following simple electroneutrality:| |  | (38) |
Moreover, the cation surface site balance assuming full coverage in the chemisorbed layer and low dissociation  allows us to insert and combine with physisorption thermodynamics, and get
allows us to insert and combine with physisorption thermodynamics, and get| |  | (39) |
which is rearranged into| |  | (40) |
The surface protonic conductance in the 1st physisorbed layer will by this model be| |  | (41) |
which we may write as follows:| |  | (42) |
with| |  | (43) |
If we assume that uH+0 is still of the order of magnitude of 10 cm2 K V−1 s−1, and that the standard entropy of physisorption is −109 J mol−1 K−1, and that of dissociation is negligible, we obtain  ,
,  , and
, and  . If we assign a negative standard entropy to dissociation, like a small part of what it is in liquid water, the preexponentials decrease further. This is in rough agreement with the experimentally observed preexponentials of conductivity in the 1st physisorbed layer for the samples sintered at the lowest temperatures (∼10−9 SK cm−1, see Table 2). The corresponding apparent activation enthalpies of around −30 kJ mol−1 contain in this case 3/2 times the standard adsorption enthalpy estimated at −45 kJ mol−1 as explained earlier, plus half the dissociation enthalpy, which as a first estimate now may be taken as that in water at 100 °C of +42 kJ mol−1, leaving the activation enthalpy of proton mobility at around +17 kJ mol−1, credible in being just somewhat higher than that in liquid water of 12 kJ mol−1.
. If we assign a negative standard entropy to dissociation, like a small part of what it is in liquid water, the preexponentials decrease further. This is in rough agreement with the experimentally observed preexponentials of conductivity in the 1st physisorbed layer for the samples sintered at the lowest temperatures (∼10−9 SK cm−1, see Table 2). The corresponding apparent activation enthalpies of around −30 kJ mol−1 contain in this case 3/2 times the standard adsorption enthalpy estimated at −45 kJ mol−1 as explained earlier, plus half the dissociation enthalpy, which as a first estimate now may be taken as that in water at 100 °C of +42 kJ mol−1, leaving the activation enthalpy of proton mobility at around +17 kJ mol−1, credible in being just somewhat higher than that in liquid water of 12 kJ mol−1.
Furthermore, ST700 revealed an approximate 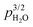 dependence of conductivity in the physisorbed region (Fig. 5), in agreement with the predicted results from the current model, suggesting that dissociated protons come from the chemisorbed water layer underneath.
dependence of conductivity in the physisorbed region (Fig. 5), in agreement with the predicted results from the current model, suggesting that dissociated protons come from the chemisorbed water layer underneath.
Dissociation within physisorbed water
In a second model, we assume instead that the chemisorbed water is already fully dissociated into surface protons, and that dissociation into the physisorbed layer must originate from physisorbed water molecules themselves (“ph1” in Fig. 6):| |  | (44) |
with equilibrium constant| |  | (45) |
If this dominates, we have the following simple electroneutrality:| | 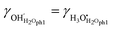 | (46) |
Assuming low coverage and low degree of dissociation and that the surface concentration of physisorption sites is the same as that for chemisorption, γH2Oph1 ≈ γMs, we may insert and combine with physisorption thermodynamics to get| |  | (47) |
The surface protonic conductance in the 1st physisorbed layer will by this model, assuming contributions of jumps from both H3O+ and to OH−, be| |  | (48) |
The surface protonic conductance from this process is then| |  | (49) |
where the preexponential of surface protonic conductance is| |  | (50) |
Under the same assumptions as above, we obtain  ,
, 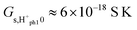 , and
, and  , possibly somewhat lower if the entropy of dissociation is negative like in liquid water. This corresponds well with the experimentally observed preexponentials for the samples sintered at the highest temperatures, see Table 2. The corresponding apparent activation enthalpies approaching −50 kJ mol−1 are to compare with twice the estimated standard adsorption enthalpy of −45 kJ mol−1 plus half the dissociation enthalpy, which as a first estimate may be taken as that in liquid water at 100 °C of +42 kJ mol−1, leaving the activation enthalpy of proton mobility at 19 kJ mol−1, again a credible assessment. The difference to the preceding model is the expected effect of half the adsorption enthalpy.
, possibly somewhat lower if the entropy of dissociation is negative like in liquid water. This corresponds well with the experimentally observed preexponentials for the samples sintered at the highest temperatures, see Table 2. The corresponding apparent activation enthalpies approaching −50 kJ mol−1 are to compare with twice the estimated standard adsorption enthalpy of −45 kJ mol−1 plus half the dissociation enthalpy, which as a first estimate may be taken as that in liquid water at 100 °C of +42 kJ mol−1, leaving the activation enthalpy of proton mobility at 19 kJ mol−1, again a credible assessment. The difference to the preceding model is the expected effect of half the adsorption enthalpy.
There is a  -dependency of this latter model vs. a
-dependency of this latter model vs. a  -dependency of the preceding one. Sun et al.39 report
-dependency of the preceding one. Sun et al.39 report  -dependency for surface conduction in the 1st physisorbed layer on undoped more facetted CeO2, supporting our assumption that ZrO2 samples sintered at high temperatures take place by this last model, i.e., by dissociation and migration in the physisorbed layer.
-dependency for surface conduction in the 1st physisorbed layer on undoped more facetted CeO2, supporting our assumption that ZrO2 samples sintered at high temperatures take place by this last model, i.e., by dissociation and migration in the physisorbed layer.
4.6 Summarising discussion
Table 3 summarises the derived pH2O dependencies along with the predicted estimates of preexponentials we have arrived at in this work for surface protonic conduction in the chemisorbed and 1st physisorbed layer of water of porous oxides. The experimental values for ST700 and ST1100, representing samples sintered at low and high temperatures, representatively, are included in the same table for easier comparison.
Table 3 Derived pH2O dependencies and predicted preexponentials for the five models of protonic surface transport in the chemisorbed layer and 1st physisorbed layer, for porous MO2 oxides in general, and in the case of conditions and microstructures employed in this study, compared with the experimental values of the same parameters for ST700 and ST1100. The preexponentials are rounded off to one significant digit, but the realistic predictive power is much less accurate, rather within 1–2 orders of magnitude due to the many assumptions mainly in adsorption thermodynamics and transport parameters
| Derived values according to the five models |
| Layer of adsorption |
Chemisorbed layer |
1st physisorbed layer |
| Model notation |
chm |
chm-s |
chd |
chm-ph1 |
ph1 |
p
H2O dependency, n in 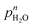 |
2 |
1/2 |
0 |
3/2 |
2 |
 , pH2O = 1 bar , pH2O = 1 bar |
7 × 10−15 |
2 × 10−6 |
4 × 10−4 |
2 × 10−12 |
6 × 10−15 |
 , pH2O = 0.03 bar , pH2O = 0.03 bar |
6 × 10−18 |
3 × 10−7 |
4 × 10−4 |
1 × 10−14 |
6 × 10−18 |
 , pH2O = 0.03 bar, ψ = 6 × 104 cm−1 , pH2O = 0.03 bar, ψ = 6 × 104 cm−1 |
4 × 10−13 |
2 × 10−2 |
2 × 101 |
7 × 10−10 |
3 × 10−13 |
| Experimental values (pH2O = 0.03 bar) |
| Layer of adsorption |
Chemisorbed layer |
1st physisorbed layer |
|
σ
M 0 (S K cm−1), ST700 |
5 × 10−3 |
6 × 10−9 |
|
σ
M 0 (S K cm−1), ST1100 |
1 × 10−1 |
4 × 10−13 |
n in  for ST700 for ST700 |
0.6 |
1.5 |
For the sake of completion, we mention here again that as RH surpasses 60%, i.e., below 50 °C at pH2O = 0.03 bar, a 2nd liquid-like physisorbed layer is expected with strong increase in conductivity as temperature decreases further, as observed for, e.g., porous YSZ15 and TiO2,33 but this was not evidenced in this study of monoclinic ZrO2.
The temperature dependency of the conductivity can be measured and modelled at constant RH instead of constant pH2O. With the exception of the modest effect of cBET, a constant RH yields a constant coverage, as one may see in the mathematics derived here. All models, except strong dissociative chemisorption, then come out with an activation enthalpy given by half the dissociation enthalpy plus the migration enthalpy:  . Stub et al.15 did this for YSZ in the region of physisorption, and for constant RHs in the range of 20–60% obtained enthalpies of 43–34 kJ mol−1. Colomer50 studied the proton conductivity of nanoporous anatase TiO2 thin films as a function of temperature (from 25 to 80 °C) at different RH values, and found the activation enthalpies to be 36 kJ mol−1 at RH of 33%, and 33 kJ mol−1 at RH of 58%. These results are in agreement with our assessment for ZrO2 of 38–40 kJ mol−1 measured at constant pH2O after subtraction of the estimated enthalpies of adsorption according to the two models applied for surface protonic conduction in the 1st physisorbed layer.
. Stub et al.15 did this for YSZ in the region of physisorption, and for constant RHs in the range of 20–60% obtained enthalpies of 43–34 kJ mol−1. Colomer50 studied the proton conductivity of nanoporous anatase TiO2 thin films as a function of temperature (from 25 to 80 °C) at different RH values, and found the activation enthalpies to be 36 kJ mol−1 at RH of 33%, and 33 kJ mol−1 at RH of 58%. These results are in agreement with our assessment for ZrO2 of 38–40 kJ mol−1 measured at constant pH2O after subtraction of the estimated enthalpies of adsorption according to the two models applied for surface protonic conduction in the 1st physisorbed layer.
It appears that the surface protonic conductivity in the porous samples of ZrO2 sintered at low and high temperatures can be rationalised with simple models of adsorption, dissociation, and transport. But why do well-sintered and presumably well-faceted surfaces show a stronger more dissociative chemisorption, while the less developed surfaces show weaker, molecular chemisorption? During annealing at high temperatures, the system lowers its excess surface and grain boundary energies by sintering and grain growth, but the type of surface and hence area-specific surface energy and adsorption behaviour may still be the same. In faceting, on the other hand, random surfaces from particle growth during synthesis, or from milling, transform into more stable, usually low-index surfaces. However, the lower-energy facets should adsorb water less strongly, so this explanation seems not to hold. But if the low-sintered samples have a large amount of amorphous surfaces, not yet faceted at all, they are believed from general adsorption theory to have low surface energies by the freedom to arrange terminations variably along the surface, with less gain in adsorbing gases like water. This would explain our observations. But why do amorphous surfaces crystallise and facet if they already have low energies? This would be because the subsurface lattice decreases its energy in crystallisation, while the surface itself may increase in energy.
If our interpretations hold, the samples sintered at low temperatures, exhibiting weak molecular chemisorption, have physisorbed water that dissociates protons from the chemisorbed water underneath (“chm-ph1” in Fig. 6). In comparison, the samples sintered at high temperatures have dissociation from the physisorbed water itself (“ph1” in Fig. 6), because the strongly dissociated chemisorbed water on the high temperature sintered samples has no more protons to offer; they have all gone to the oxide surface, where they are immobile due to their high activation energy and the now low temperature. Hence, the conduction in the physisorbed layer can now only arise from dissociation within the physisorbed layer itself. It appears intuitive that the steep increase in conductivity with increasing coverage of this layer then must imply that mobility has less activation enthalpy here than on the oxide surface, and indeed the derived enthalpies of mobility go from those typical of solid-state proton mobility towards those typical of liquid water. We note that both still reflect Grotthuss proton jumps.
5 Conclusions
Our impedance spectrometric study of the surface protonic conductivity vs. temperature in wet atmospheres of porous undoped monoclinic ZrO2 sintered at five different temperatures has allowed us to forward models for interpretation and parameterisation of surface protonic conduction that may be applied to porous oxides in general. The dual time constants in the high frequency part of the impedance spectra with capacitances in the geometric (bulk) range are omnipresent and attributable to different capacitances over concave and convex surface paths of porous microstructures. A simple brick layer model (BLM) connects measured preexponentials of macroscopic surface protonic conductivity σM,s,H+0 to the predicted values from credible models of preexponentials Gs,H+0 of surface protonic conductance. Along with pH2O dependencies and credible enthalpies, this enables discrimination between models.
The surface protonic conductivity in wet atmospheres above 200 °C is attributed to the chemisorbed water monolayer. Samples sintered at low temperatures have activation enthalpies as low as 30 kJ mol−1, along with an observed 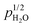 dependency, and preexponentials expected for water weakly chemisorbed to surface cations and weakly dissociated into protons on and migrating between surface oxide ions. (Dissociation to and migration between adsorbed water molecules have a predicted preexponential orders of magnitude away from experimental values, and can be ruled out.) Samples sintered at higher temperatures display higher activation energies and preexponentials, expected for strong, near complete dissociative chemisorption, driven by a more exothermic dissociation to surface oxide ions. The activation enthalpy of conductivity of up to 58 kJ mol−1 can then be interpreted as that of mobility of protons on surface oxide ions. The smaller enthalpy for the samples sintered at low temperatures can be understood as a combination of incomplete exothermic molecular adsorption, unfavourable endothermic dissociation, and easier mobility of protons on surface oxide ions than in the case of the surface with strong dissociative chemisorption. In other words, the well-faceted surfaces are relaxed by protons that bond strongly and are hard to move, while the random surfaces have less affinity for protons, allowing those that are there to move more easily.
dependency, and preexponentials expected for water weakly chemisorbed to surface cations and weakly dissociated into protons on and migrating between surface oxide ions. (Dissociation to and migration between adsorbed water molecules have a predicted preexponential orders of magnitude away from experimental values, and can be ruled out.) Samples sintered at higher temperatures display higher activation energies and preexponentials, expected for strong, near complete dissociative chemisorption, driven by a more exothermic dissociation to surface oxide ions. The activation enthalpy of conductivity of up to 58 kJ mol−1 can then be interpreted as that of mobility of protons on surface oxide ions. The smaller enthalpy for the samples sintered at low temperatures can be understood as a combination of incomplete exothermic molecular adsorption, unfavourable endothermic dissociation, and easier mobility of protons on surface oxide ions than in the case of the surface with strong dissociative chemisorption. In other words, the well-faceted surfaces are relaxed by protons that bond strongly and are hard to move, while the random surfaces have less affinity for protons, allowing those that are there to move more easily.
The surface protonic conductivity in wet atmospheres below around 150 °C and down to around 50 °C can be attributed to the first physisorbed water monolayer. The apparent negative enthalpies are readily attributed to a lower activation energy of mobility now overtaken by the negative enthalpy of physisorption contributing strongly because more than one water molecule is now involved to dissociate and migrate a proton. The samples sintered at low temperatures have preexponentials and 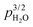 dependency suggesting that the dissociated protons come from the chemisorbed layer, while for the samples sintered at high temperatures, they seem to come from the physisorbed layer itself (autoprotolysis), supported by the difference in enthalpies. The measured enthalpies fit to the models if physisorption is assumed to have an enthalpy of −45 kJ mol−1, dissociation has +42 kJ mol−1 like in water, and mobility has around 17 kJ mol−1, close to that in liquid water. To our understanding, the difference between samples of ZrO2 sintered at low and high temperatures must be related to crystallisation and faceting from a more amorphous state of the surface.
dependency suggesting that the dissociated protons come from the chemisorbed layer, while for the samples sintered at high temperatures, they seem to come from the physisorbed layer itself (autoprotolysis), supported by the difference in enthalpies. The measured enthalpies fit to the models if physisorption is assumed to have an enthalpy of −45 kJ mol−1, dissociation has +42 kJ mol−1 like in water, and mobility has around 17 kJ mol−1, close to that in liquid water. To our understanding, the difference between samples of ZrO2 sintered at low and high temperatures must be related to crystallisation and faceting from a more amorphous state of the surface.
All in all, surface protonic conductivity data can be credibly modelled with simple thermodynamics and transport. It is noteworthy how all thermodynamics of adsorption and dissociation and proton mobility terms change completely from the chemisorbed to the physisorbed layers, giving them their widely different temperature dependencies. In the chemisorbed layer, we have favourable adsorption, weakly or strongly favourable dissociation, and difficult migration. In the physisorbed layer, adsorption is weak and dissociation is hard, but migration is easy. We point out how preexponentials and isothermal pH2O dependencies of conductivity can discriminate between models.
Author contributions
JG and XS fabricated the samples and performed characterisation and electrical measurements. XS and JG interpreted and plotted the results and fitted them to the models. XS performed and interpreted TG. DH and TN conceived and supervised the experimental study. XS and TN developed the models and wrote the first manuscript draft. All authors contributed to revision and checking of the final manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
JG and DH acknowledge support from the Natural Science Foundation of Jiangsu Province (Grant No. BK20211071) and the Key Technology Initiative of Suzhou Municipal Science and Technology Bureau (Grant No. SYG202011). XS and TN acknowledge support from The Research Council of Norway (RCN) through projects MoZEES (257653) and SUPROX (280868). The authors acknowledge valuable experimental support from MSc. Lulu Jiang, Soochow University.
References
- L. Almar,
et al., Mesoporous ceramic oxides as humidity sensors: A case study for gadolinium-doped ceria, Sens. Actuators, B, 2015, 216, 41–48 CrossRef CAS.
- J. Y. Li, C. X. Sun and S. A. Sebo, Humidity and contamination severity impact on the leakage currents of porcelain insulators, Gener. Transm. Distrib. IET, 2011, 5, 19–28 CrossRef.
- M. T. Colomer, Nanoporous anatase ceramic membranes as fast-proton-conducting materials, J. Eur. Ceram. Soc., 2006, 26(7), 1231–1236 CrossRef CAS.
- S. Kim,
et al., Unprecedented room-temperature electrical power generation using nanoscale fluorite-structured oxide electrolytes, Adv. Mater., 2008, 20(3), 556–559 CrossRef CAS.
- L. Malavasi, C. A. Fisher and M. S. Islam, Oxide-ion and proton conducting electrolyte materials for clean energy applications: Structural and mechanistic features, Chem. Soc. Rev., 2010, 39(11), 4370–4387 RSC.
- D. Poetzsch, R. Merkle and J. Maier, Proton uptake in the H+-SOFC cathode material Ba0.5Sr0.5Fe0.8Zn0.2O3-delta: Transition from hydration to hydrogenation with increasing oxygen partial pressure, Faraday Discuss., 2015, 182, 129–143 RSC.
- Y. Hisai,
et al., Enhanced activity of catalysts on substrates with surface protonic current in an electrical field – A review, Chem. Commun., 2021, 57(47), 5737–5749 RSC.
- A. V. Radha,
et al., Surface enthalpy, enthalpy of water adsorption, and phase stability in nanocrystalline monoclinic zirconia, J. Am. Ceram. Soc., 2009, 92(1), 133–140 CrossRef CAS.
- R. Sato,
et al., Proton migration on hydrated surface of cubic ZrO2: Ab initio molecular dynamics simulation, J. Phys. Chem. C, 2015, 119(52), 28925–28933 CrossRef CAS.
- R. Sato,
et al., Effects of CO2 adsorption on proton migration on a hydrated ZrO2 surface: An ab initio molecular dynamics study., Phys. Chem. Chem. Phys., 2017, 19(30), 20198–20205 RSC.
- S. T. Korhonen, M. Calatayud and A. O. I. Krause, Stability of hydroxylated (111) and (101) surfaces of monoclinic zirconia: A combined study by DFT and infrared spectroscopy, J. Phys. Chem. C, 2008, 112(16), 6469–6476 CrossRef CAS.
- S. Raz,
et al., Characterization of adsorbed water layers on Y2O3-doped ZrO2, Solid State Ionics, 2001, 143(2), 181–204 CrossRef CAS.
- G. C. C. Costa,
et al., Calorimetric measurement of surface and interface enthalpies of yttria-stabilized zirconia (YSZ), Chem. Mater., 2010, 22(9), 2937–2945 CrossRef CAS.
- B. Scherrer,
et al., On proton conductivity in porous and dense yttria stabilized zirconia at low temperature, Adv. Funct. Mater., 2013, 23(15), 1957–1964 CrossRef CAS.
- S. Ø. Stub, E. Vøllestad and T. Norby, Mechanisms of protonic surface transport in porous oxides: Example of YSZ, J. Phys. Chem. C, 2017, 121(23), 12817–12825 CrossRef CAS.
- S. Ø. Stub, E. Vøllestad and T. Norby, Protonic surface conduction controlled by space charge of intersecting grain boundaries in porous ceramics, J. Mater. Chem. A, 2018, 6(18), 8265–8270 RSC.
- S. Kim,
et al., On the conduction pathway for protons in nanocrystalline yttria-stabilized zirconia, Phys. Chem. Chem. Phys., 2009, 11(17), 3035–3038 RSC.
- E. M. Kock,
et al., Structural and electrochemical properties of physisorbed and chemisorbed water layers on the ceramic oxides Y2O3, YSZ, and ZrO2, ACS Appl. Mater. Interfaces, 2016, 8(25), 16428–16443 CrossRef PubMed.
- S. Miyoshi,
et al., Water uptake and conduction property of nano-grained yttria-doped zirconia fabricated by ultra-high pressure compaction at room temperature, Solid State Ionics, 2012, 207, 21–28 CrossRef CAS.
- S. Miyoshi,
et al., Low-temperature protonic conduction based on surface protonics: An example of nanostructured yttria-doped zirconia, Chem. Mater., 2014, 26(18), 5194–5200 CrossRef CAS.
- S. Hayun, T. Y. Shvareva and A. Navrotsky, Nanoceria – Energetics of surfaces, interfaces and water adsorption, J. Am. Ceram. Soc., 2011, 94(11), 3992–3999 CrossRef CAS.
- P. A. Thiel and T. E. Madey, The interaction of water with solid-surfaces – Fundamental-aspects, Surf. Sci. Rep., 1987, 7(6–8), 211–385 CrossRef CAS.
- G. Gregori, M. Shirpour and J. Maier, Proton conduction in dense and porous nanocrystalline ceria thin films, Adv. Funct. Mater., 2013, 23(47), 5861–5867 CrossRef CAS.
- M. Shirpour,
et al., On the proton conductivity in pure and gadolinium doped nanocrystalline cerium oxide, Phys. Chem. Chem. Phys., 2011, 13(3), 937–940 RSC.
- K. Murakami,
et al., Key factor for the anti-Arrhenius low-temperature heterogeneous catalysis induced by H+ migration: H+ coverage over support, Chem. Commun., 2020, 56(23), 3365–3368 RSC.
- P. Simons, K. P. Torres and J. L. M. Rupp, Careful choices in low temperature ceramic processing and slow hydration kinetics can affect proton conduction in ceria, Adv. Funct. Mater., 2021, 31(31), 2009630 CrossRef CAS.
- D. R. Mullins, The surface chemistry of cerium oxide, Surf. Sci. Rep., 2015, 70(1), 42–85 CrossRef CAS.
- S. Ø. Stub,
et al., The influence of acceptor and donor doping on the protonic surface conduction of TiO2, Phys. Chem. Chem. Phys., 2018, 20(23), 15653–15660 RSC.
- I. G. Tredici,
et al., Mechanism of low-temperature protonic conductivity in bulk, high-density, nanometric titanium oxide, Adv. Funct. Mater., 2014, 24(32), 5137–5146 CrossRef CAS.
- J. Gao,
et al., Insights into the proton transport mechanism in TiO2 simple oxides by in situ Raman spectroscopy, ACS Appl. Mater. Interfaces, 2020, 12(34), 38012–38018 CrossRef CAS PubMed.
- A. Y. Nosaka,
et al., Characteristics of water adsorbed on TiO2 photocatalytic systems with increasing temperature as studied by solid-state 1H NMR spectroscopy, J. Phys. Chem. B, 2004, 108(26), 9121–9125 CrossRef CAS.
- X. W. Sun,
et al., Photocatalytic generation of gas phase reactive oxygen species from adsorbed water: Remote action and electrochemical detection, J. Environ. Chem. Eng., 2021, 9(2), 104809 CrossRef CAS.
- X. L. Kang,
et al., Facet-engineered TiO2 nanomaterials reveal the role of water-oxide interactions in surface protonic conduction., J. Mater. Chem. A, 2022, 10(1), 218–227 RSC.
- G. Cerrato,
et al., A surface study of monoclinic zirconia (m-ZrO2), Surf. Sci., 1997, 377(1–3), 50–55 CrossRef.
- S. Kouva,
et al., Review: Monoclinic zirconia, its surface sites and their interaction with carbon monoxide, Catal. Sci. Technol., 2015, 5(7), 3473–3490 RSC.
- O. H. Kwon,
et al., Investigation of the electrical conductivity of sintered monoclinic zirconia (ZrO2), Ceram. Int., 2017, 43(11), 8236–8245 CrossRef CAS.
- T. Norby, Direct-current conductivity of Y2O3 as a function of water vapor pressure, J. Am. Ceram. Soc., 1986, 69(11), 780–783 CrossRef CAS.
- A. Weibel,
et al., The big problem of small particles: A comparison of methods for determination of particle size in nanocrystalline anatase powders, Chem. Mater., 2005, 17(9), 2378–2385 CrossRef CAS.
-
X. Sun, N. G. Kalantzopoulos, E. Vøllestad, A. Chatzitakis and T. Norby, Surface protonic conductivity in chemisorbed and physisorbed water layers in porous nanoscopic CeO2, to be submitted.
- E. Mamontov, Dynamics of surface water in ZrO2 studied by quasielastic neutron scattering, J. Chem. Phys., 2004, 121(18), 9087–9097 CrossRef CAS PubMed.
- E. N. S. Muccillo and M. Kleitz, Impedance spectroscopy of Mg-partially stabilized zirconia and cubic phase decomposition, J. Eur. Ceram. Soc., 1996, 16(4), 453–465 CrossRef CAS.
- S. Erdal,
et al., Hydration of rutile TiO2: Thermodynamics and effects on n- and p-type electronic conduction, J. Phys. Chem. C, 2010, 114(19), 9139–9145 CrossRef CAS.
- L. E. Kalland,
et al., Structure, hydration, and proton conductivity in 50% La and Nd doped CeO2–La2Ce2O7 and Nd2Ce2O7 – and their solid solutions, Solid State Ionics, 2020, 354, 115401 CrossRef CAS.
- R. Anez,
et al., Stabilization of the (110) tetragonal zirconia surface by hydroxyl chemical transformation, Surf. Sci., 2009, 603(16), 2526–2531 CrossRef CAS.
-
A. H. Harvey, Thermodynamic Properties of Water: Tabulation from the lAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use, U.S.D.o. Commerce, Editor. 1998, National Institute of Standards and Technology: Technology Administration.
- E. McCafferty and A. Zettlemoyer, Entropy of adsorption and the mobility of water vapor on α-Fe2O3, J. Colloid Interface Sci., 1970, 34(3), 452–460 CrossRef CAS.
- M. A. Blesa, A. J. G. Maroto and A. E. Regazzoni, Surface acidity of metal oxides immersed in water: A critical analysis of thermodynamic data, J. Colloid Interface Sci., 1990, 140(1), 287–290 CrossRef CAS.
- I. M. Iskandarova,
et al., First-principle investigation of the hydroxylation of zirconia and hafnia surfaces, Microelectron. Eng., 2003, 69(2), 587–593 CrossRef CAS.
- S. Brunauer, P. H. Emmett and E. Teller, Adsorption of gases in multimolecular layers, J. Am. Chem. Soc., 1938, 60(2), 309–319 CrossRef CAS.
- M. T. Colomer, Nanoporous anatase thin films as fast proton-conducting materials, Adv. Mater., 2006, 18(3), 371–374 CrossRef CAS.
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Jie
Gu‡
b,
Donglin
Han
a,
Jie
Gu‡
b,
Donglin
Han
 *b and
Truls
Norby
*ab
*b and
Truls
Norby
*ab
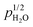 dependency. Supported by the thermogravimetry of adsorption, we attribute this to weaker and more molecular chemisorption on the more randomly terminated less faceted surfaces, providing water layers with fewer dissociated charge carrying protons, but also smaller activation enthalpies of mobility. Below 200 °C, all samples exhibit a strongly inverse temperature dependency characteristic of conduction in the 1st physisorbed layer with increasing coverage. The preexponentials correspond well to the models of physisorption, with dissociation to and proton migration between physisorbed water molecules. The enthalpies fit well to physisorption and with enthalpies of dissociation and proton mobility close to those of liquid water. We have by this introduced models for proton conduction in chemisorbed and physisorbed water on ZrO2, applicable to other oxides as well, and shown that preexponentials are quantitatively assessable in the order-of-magnitude level to discriminate models via a simple brick layer model based topographical analysis of the ceramic microstructure.
dependency. Supported by the thermogravimetry of adsorption, we attribute this to weaker and more molecular chemisorption on the more randomly terminated less faceted surfaces, providing water layers with fewer dissociated charge carrying protons, but also smaller activation enthalpies of mobility. Below 200 °C, all samples exhibit a strongly inverse temperature dependency characteristic of conduction in the 1st physisorbed layer with increasing coverage. The preexponentials correspond well to the models of physisorption, with dissociation to and proton migration between physisorbed water molecules. The enthalpies fit well to physisorption and with enthalpies of dissociation and proton mobility close to those of liquid water. We have by this introduced models for proton conduction in chemisorbed and physisorbed water on ZrO2, applicable to other oxides as well, and shown that preexponentials are quantitatively assessable in the order-of-magnitude level to discriminate models via a simple brick layer model based topographical analysis of the ceramic microstructure.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and pressed into disks with a diameter of 12.7 mm and a thickness of approx. 2.0 mm under a pressure of 760 MPa. They were sintered for 24 h at 600, 700, 800, 900, 1000, or 1100 °C, with a heating and cooling ramp rate of 5 °C min−1. Samples sintered at 600 °C were of insufficient mechanical strength for conductivity measurements, and only samples sintered at 700–1100 °C were characterised further and were denoted as ST700-ST1100 accordingly, see Table 1.
1 and pressed into disks with a diameter of 12.7 mm and a thickness of approx. 2.0 mm under a pressure of 760 MPa. They were sintered for 24 h at 600, 700, 800, 900, 1000, or 1100 °C, with a heating and cooling ramp rate of 5 °C min−1. Samples sintered at 600 °C were of insufficient mechanical strength for conductivity measurements, and only samples sintered at 700–1100 °C were characterised further and were denoted as ST700-ST1100 accordingly, see Table 1.




 dependency is revealed at 400 °C, in agreement with the results for 4 mol% Y2O3-stabilised ZrO2 (4YSZ) at 250–400 °C19 and more recently for undoped CeO2 at 400 °C.39 This may be interpreted to reflect a weak molecular and hence incomplete chemisorbed layer with only partial dissociation to conductive protons. At 100 °C, we obtained close to
dependency is revealed at 400 °C, in agreement with the results for 4 mol% Y2O3-stabilised ZrO2 (4YSZ) at 250–400 °C19 and more recently for undoped CeO2 at 400 °C.39 This may be interpreted to reflect a weak molecular and hence incomplete chemisorbed layer with only partial dissociation to conductive protons. At 100 °C, we obtained close to  dependency, same as that of undoped nanoscopic CeO2 sintered at 550 °C and measured at 100 °C.39 We will discuss models that may rationalise it below.
dependency, same as that of undoped nanoscopic CeO2 sintered at 550 °C and measured at 100 °C.39 We will discuss models that may rationalise it below.


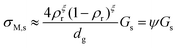


 where A is a geometrical factor of the order of unity, s is the jump distance, ω0 is the vibrational attempt frequency, and ΔSm is the entropy part of the energy barrier. The proton always jumps from its host oxide ion to a nearest one, so we may take the effective jump distance to be 2.8 ≈ 3 Å. The vibrational attempt frequency is in practice that of the oxide ion host, of the order of 1012 s−1 (not the 1013 s−1 of the proton itself). With this, we get DH+0 ≈ 1 × 10−3 cm2 s−1 as an order of magnitude estimate, irrespective of the mechanism or host system, and in turn,
where A is a geometrical factor of the order of unity, s is the jump distance, ω0 is the vibrational attempt frequency, and ΔSm is the entropy part of the energy barrier. The proton always jumps from its host oxide ion to a nearest one, so we may take the effective jump distance to be 2.8 ≈ 3 Å. The vibrational attempt frequency is in practice that of the oxide ion host, of the order of 1012 s−1 (not the 1013 s−1 of the proton itself). With this, we get DH+0 ≈ 1 × 10−3 cm2 s−1 as an order of magnitude estimate, irrespective of the mechanism or host system, and in turn,  .
.


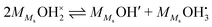


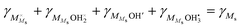 , but under the assumption of weak molecular adsorption (low coverage and limited dissociation), we have
, but under the assumption of weak molecular adsorption (low coverage and limited dissociation), we have 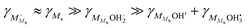 , and we can insert and simplify to get
, and we can insert and simplify to get





 is the standard preexponential of surface protonic conductance at pH2O = 1 bar. We emphasize that
is the standard preexponential of surface protonic conductance at pH2O = 1 bar. We emphasize that  is hence the most fundamental parameter specific for a surface and a particular adsorption and transport model, in this case weak molecular adsorption with dissociation and transport in the molecular layer. To derive such a fundamental parameter is only meaningful once a model is chosen, so that the pH2O dependency is clear.
is hence the most fundamental parameter specific for a surface and a particular adsorption and transport model, in this case weak molecular adsorption with dissociation and transport in the molecular layer. To derive such a fundamental parameter is only meaningful once a model is chosen, so that the pH2O dependency is clear.
 ,
,  , and eventually
, and eventually  . The standard entropy change
. The standard entropy change  plays a major role and represents the biggest uncertainty. Condensation of water vapour to liquid water has a standard entropy change of −109 J mol−1 K−1 at 100 °C.45 It decreases strongly with temperature, e.g., to −44 J mol−1 K−1 at 300 °C which is relevant for our chemisorption temperature range. On the other hand, the entropy of condensation to ice is larger than that to water (−144 vs. −118 J mol−1 K−1 at RT) and the entropy of molecular adsorption to hydroxylated α-Fe2O3, i.e., physisorption, has been reported to be −138 J mol−1 K−1.46 We will hence in this work for the most part use −109 J mol−1 K−1 from the entropy of condensation to water at 100 °C45 as our value for the standard entropy of molecular adsorption
plays a major role and represents the biggest uncertainty. Condensation of water vapour to liquid water has a standard entropy change of −109 J mol−1 K−1 at 100 °C.45 It decreases strongly with temperature, e.g., to −44 J mol−1 K−1 at 300 °C which is relevant for our chemisorption temperature range. On the other hand, the entropy of condensation to ice is larger than that to water (−144 vs. −118 J mol−1 K−1 at RT) and the entropy of molecular adsorption to hydroxylated α-Fe2O3, i.e., physisorption, has been reported to be −138 J mol−1 K−1.46 We will hence in this work for the most part use −109 J mol−1 K−1 from the entropy of condensation to water at 100 °C45 as our value for the standard entropy of molecular adsorption  , both here for chemisorption and later for physisorption. This implies uncertainties of several orders of magnitude in our calculations for conductances, but helps to emphasise differences between different models.
, both here for chemisorption and later for physisorption. This implies uncertainties of several orders of magnitude in our calculations for conductances, but helps to emphasise differences between different models. for dissociation (since it does not involve gas species or solvation of ions). Using furthermore an adsorption site surface concentration γMs ≈ 5 nm−2 = 8 × 10−10 mol cm−2, and uH+0 ≈ 10 cm2 K V−1 s−1 as derived earlier, we get
for dissociation (since it does not involve gas species or solvation of ions). Using furthermore an adsorption site surface concentration γMs ≈ 5 nm−2 = 8 × 10−10 mol cm−2, and uH+0 ≈ 10 cm2 K V−1 s−1 as derived earlier, we get  for pH2O = 1 bar and
for pH2O = 1 bar and  at pH2O = 0.03 bar. By applying
at pH2O = 0.03 bar. By applying  from eqn (3) and values of ψ from Table 1, we get predicted preexponentials for macroscopic conductivity of around
from eqn (3) and values of ψ from Table 1, we get predicted preexponentials for macroscopic conductivity of around  for our samples at pH2O = 0.03 bar. This low value, dominated by the variable and uncertain but grossly negative entropy of adsorption, is several orders of magnitude below the experimental ones for the surface protonic conductivity in the chemisorbed layer at higher temperatures (Table 2) and the “chm” model can be ruled out.
for our samples at pH2O = 0.03 bar. This low value, dominated by the variable and uncertain but grossly negative entropy of adsorption, is several orders of magnitude below the experimental ones for the surface protonic conductivity in the chemisorbed layer at higher temperatures (Table 2) and the “chm” model can be ruled out.


 defect may migrate by jumping to other surface oxide ions, since MMsOH′ it left behind from the dissociation is rare to find. The surface protonic conductance will then be
defect may migrate by jumping to other surface oxide ions, since MMsOH′ it left behind from the dissociation is rare to find. The surface protonic conductance will then be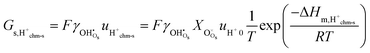
 , so that we by inserting eqn (19) get
, so that we by inserting eqn (19) get
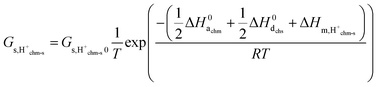

 ,
,  , and
, and  . Sample ST700 has a preexponential of macroscopic conductivity of around 5 × 10−3 S K cm−1 (Table 2), i.e., within an order of magnitude of prediction, suggesting that weak molecular adsorption and dissociation to protons transported along surface oxide ions may apply. In this case, the experimental enthalpy should be interpreted according to
. Sample ST700 has a preexponential of macroscopic conductivity of around 5 × 10−3 S K cm−1 (Table 2), i.e., within an order of magnitude of prediction, suggesting that weak molecular adsorption and dissociation to protons transported along surface oxide ions may apply. In this case, the experimental enthalpy should be interpreted according to  . The standard enthalpy of molecular chemisorption has been determined calorimetrically as
. The standard enthalpy of molecular chemisorption has been determined calorimetrically as  for YSZ relatively independent of the Y content.13 If we adopt a dissociation enthalpy of 22.1 kJ mol−1 from ref. 47 used by Raz et al.12 for YSZ, we get an enthalpy for surface mobility of protons of
for YSZ relatively independent of the Y content.13 If we adopt a dissociation enthalpy of 22.1 kJ mol−1 from ref. 47 used by Raz et al.12 for YSZ, we get an enthalpy for surface mobility of protons of  .
.
 of surface protonic conduction for weakly adsorbed and dissociated chemisorbed water according to eqn (21). This is in line with the experimental results obtained for the ST700 sample at 400 °C (Fig. 5).
of surface protonic conduction for weakly adsorbed and dissociated chemisorbed water according to eqn (21). This is in line with the experimental results obtained for the ST700 sample at 400 °C (Fig. 5).


 since half of them are occupied with dissociated protons. The surface protonic conductance then becomes
since half of them are occupied with dissociated protons. The surface protonic conductance then becomes

 , and
, and  , to be compared with the corresponding experimental preexponentials (Table 2) for the chemisorbed layer of 0.1–0.4 S K cm−1 for the samples sintered at the highest temperatures. The two orders of magnitude difference may be ascribed to the many approximations along the way, but may also mean that the assumptions of the model comprising fully covered and dissociated chemisorbed water are not fully met. However, we may assign the activation enthalpies of up to 60 kJ mol−1 to the diffusion barrier for protons migrating between oxide ions on the faceted surfaces of monoclinic ZrO2 covered with dissociatively chemisorbed water. The aforementioned comparison to the enthalpy of mobility of protons of 58 kJ mol−1 for polycrystalline rutile TiO242 and 43 kJ mol−1 as an estimate for 50% La-doped CeO243 is reasonable if the concentration of carriers is constant as in a fully covered chemisorbed layer, which based on the TG result seems reasonable for the samples sintered at the highest temperatures.
, to be compared with the corresponding experimental preexponentials (Table 2) for the chemisorbed layer of 0.1–0.4 S K cm−1 for the samples sintered at the highest temperatures. The two orders of magnitude difference may be ascribed to the many approximations along the way, but may also mean that the assumptions of the model comprising fully covered and dissociated chemisorbed water are not fully met. However, we may assign the activation enthalpies of up to 60 kJ mol−1 to the diffusion barrier for protons migrating between oxide ions on the faceted surfaces of monoclinic ZrO2 covered with dissociatively chemisorbed water. The aforementioned comparison to the enthalpy of mobility of protons of 58 kJ mol−1 for polycrystalline rutile TiO242 and 43 kJ mol−1 as an estimate for 50% La-doped CeO243 is reasonable if the concentration of carriers is constant as in a fully covered chemisorbed layer, which based on the TG result seems reasonable for the samples sintered at the highest temperatures.



 . The BET constant is approximated by
. The BET constant is approximated by

 and
and  , while at 100 °C, we have
, while at 100 °C, we have 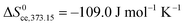 and
and 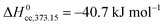 .45 In the low coverage region of the first physisorbed layer, eqn (30) can be simplified to yield the coverage as
.45 In the low coverage region of the first physisorbed layer, eqn (30) can be simplified to yield the coverage as



 allows us to insert and combine with physisorption thermodynamics, and get
allows us to insert and combine with physisorption thermodynamics, and get




 ,
,  , and
, and  . If we assign a negative standard entropy to dissociation, like a small part of what it is in liquid water, the preexponentials decrease further. This is in rough agreement with the experimentally observed preexponentials of conductivity in the 1st physisorbed layer for the samples sintered at the lowest temperatures (∼10−9 SK cm−1, see Table 2). The corresponding apparent activation enthalpies of around −30 kJ mol−1 contain in this case 3/2 times the standard adsorption enthalpy estimated at −45 kJ mol−1 as explained earlier, plus half the dissociation enthalpy, which as a first estimate now may be taken as that in water at 100 °C of +42 kJ mol−1, leaving the activation enthalpy of proton mobility at around +17 kJ mol−1, credible in being just somewhat higher than that in liquid water of 12 kJ mol−1.
. If we assign a negative standard entropy to dissociation, like a small part of what it is in liquid water, the preexponentials decrease further. This is in rough agreement with the experimentally observed preexponentials of conductivity in the 1st physisorbed layer for the samples sintered at the lowest temperatures (∼10−9 SK cm−1, see Table 2). The corresponding apparent activation enthalpies of around −30 kJ mol−1 contain in this case 3/2 times the standard adsorption enthalpy estimated at −45 kJ mol−1 as explained earlier, plus half the dissociation enthalpy, which as a first estimate now may be taken as that in water at 100 °C of +42 kJ mol−1, leaving the activation enthalpy of proton mobility at around +17 kJ mol−1, credible in being just somewhat higher than that in liquid water of 12 kJ mol−1.
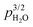 dependence of conductivity in the physisorbed region (Fig. 5), in agreement with the predicted results from the current model, suggesting that dissociated protons come from the chemisorbed water layer underneath.
dependence of conductivity in the physisorbed region (Fig. 5), in agreement with the predicted results from the current model, suggesting that dissociated protons come from the chemisorbed water layer underneath.

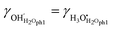




 ,
, 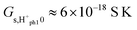 , and
, and  , possibly somewhat lower if the entropy of dissociation is negative like in liquid water. This corresponds well with the experimentally observed preexponentials for the samples sintered at the highest temperatures, see Table 2. The corresponding apparent activation enthalpies approaching −50 kJ mol−1 are to compare with twice the estimated standard adsorption enthalpy of −45 kJ mol−1 plus half the dissociation enthalpy, which as a first estimate may be taken as that in liquid water at 100 °C of +42 kJ mol−1, leaving the activation enthalpy of proton mobility at 19 kJ mol−1, again a credible assessment. The difference to the preceding model is the expected effect of half the adsorption enthalpy.
, possibly somewhat lower if the entropy of dissociation is negative like in liquid water. This corresponds well with the experimentally observed preexponentials for the samples sintered at the highest temperatures, see Table 2. The corresponding apparent activation enthalpies approaching −50 kJ mol−1 are to compare with twice the estimated standard adsorption enthalpy of −45 kJ mol−1 plus half the dissociation enthalpy, which as a first estimate may be taken as that in liquid water at 100 °C of +42 kJ mol−1, leaving the activation enthalpy of proton mobility at 19 kJ mol−1, again a credible assessment. The difference to the preceding model is the expected effect of half the adsorption enthalpy.
 -dependency of this latter model vs. a
-dependency of this latter model vs. a  -dependency of the preceding one. Sun et al.39 report
-dependency of the preceding one. Sun et al.39 report  -dependency for surface conduction in the 1st physisorbed layer on undoped more facetted CeO2, supporting our assumption that ZrO2 samples sintered at high temperatures take place by this last model, i.e., by dissociation and migration in the physisorbed layer.
-dependency for surface conduction in the 1st physisorbed layer on undoped more facetted CeO2, supporting our assumption that ZrO2 samples sintered at high temperatures take place by this last model, i.e., by dissociation and migration in the physisorbed layer. . Stub et al.15 did this for YSZ in the region of physisorption, and for constant RHs in the range of 20–60% obtained enthalpies of 43–34 kJ mol−1. Colomer50 studied the proton conductivity of nanoporous anatase TiO2 thin films as a function of temperature (from 25 to 80 °C) at different RH values, and found the activation enthalpies to be 36 kJ mol−1 at RH of 33%, and 33 kJ mol−1 at RH of 58%. These results are in agreement with our assessment for ZrO2 of 38–40 kJ mol−1 measured at constant pH2O after subtraction of the estimated enthalpies of adsorption according to the two models applied for surface protonic conduction in the 1st physisorbed layer.
. Stub et al.15 did this for YSZ in the region of physisorption, and for constant RHs in the range of 20–60% obtained enthalpies of 43–34 kJ mol−1. Colomer50 studied the proton conductivity of nanoporous anatase TiO2 thin films as a function of temperature (from 25 to 80 °C) at different RH values, and found the activation enthalpies to be 36 kJ mol−1 at RH of 33%, and 33 kJ mol−1 at RH of 58%. These results are in agreement with our assessment for ZrO2 of 38–40 kJ mol−1 measured at constant pH2O after subtraction of the estimated enthalpies of adsorption according to the two models applied for surface protonic conduction in the 1st physisorbed layer.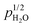 dependency, and preexponentials expected for water weakly chemisorbed to surface cations and weakly dissociated into protons on and migrating between surface oxide ions. (Dissociation to and migration between adsorbed water molecules have a predicted preexponential orders of magnitude away from experimental values, and can be ruled out.) Samples sintered at higher temperatures display higher activation energies and preexponentials, expected for strong, near complete dissociative chemisorption, driven by a more exothermic dissociation to surface oxide ions. The activation enthalpy of conductivity of up to 58 kJ mol−1 can then be interpreted as that of mobility of protons on surface oxide ions. The smaller enthalpy for the samples sintered at low temperatures can be understood as a combination of incomplete exothermic molecular adsorption, unfavourable endothermic dissociation, and easier mobility of protons on surface oxide ions than in the case of the surface with strong dissociative chemisorption. In other words, the well-faceted surfaces are relaxed by protons that bond strongly and are hard to move, while the random surfaces have less affinity for protons, allowing those that are there to move more easily.
dependency, and preexponentials expected for water weakly chemisorbed to surface cations and weakly dissociated into protons on and migrating between surface oxide ions. (Dissociation to and migration between adsorbed water molecules have a predicted preexponential orders of magnitude away from experimental values, and can be ruled out.) Samples sintered at higher temperatures display higher activation energies and preexponentials, expected for strong, near complete dissociative chemisorption, driven by a more exothermic dissociation to surface oxide ions. The activation enthalpy of conductivity of up to 58 kJ mol−1 can then be interpreted as that of mobility of protons on surface oxide ions. The smaller enthalpy for the samples sintered at low temperatures can be understood as a combination of incomplete exothermic molecular adsorption, unfavourable endothermic dissociation, and easier mobility of protons on surface oxide ions than in the case of the surface with strong dissociative chemisorption. In other words, the well-faceted surfaces are relaxed by protons that bond strongly and are hard to move, while the random surfaces have less affinity for protons, allowing those that are there to move more easily.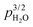 dependency suggesting that the dissociated protons come from the chemisorbed layer, while for the samples sintered at high temperatures, they seem to come from the physisorbed layer itself (autoprotolysis), supported by the difference in enthalpies. The measured enthalpies fit to the models if physisorption is assumed to have an enthalpy of −45 kJ mol−1, dissociation has +42 kJ mol−1 like in water, and mobility has around 17 kJ mol−1, close to that in liquid water. To our understanding, the difference between samples of ZrO2 sintered at low and high temperatures must be related to crystallisation and faceting from a more amorphous state of the surface.
dependency suggesting that the dissociated protons come from the chemisorbed layer, while for the samples sintered at high temperatures, they seem to come from the physisorbed layer itself (autoprotolysis), supported by the difference in enthalpies. The measured enthalpies fit to the models if physisorption is assumed to have an enthalpy of −45 kJ mol−1, dissociation has +42 kJ mol−1 like in water, and mobility has around 17 kJ mol−1, close to that in liquid water. To our understanding, the difference between samples of ZrO2 sintered at low and high temperatures must be related to crystallisation and faceting from a more amorphous state of the surface.