Open Access Article
Open Access ArticlePolymer degradation through chemical change: a quantum-based test of inferred reactions in irradiated polydimethylsiloxane
Matthew P.
Kroonblawd
 *,
Nir
Goldman
*,
Nir
Goldman
 ,
Amitesh
Maiti
,
Amitesh
Maiti
 and
James P.
Lewicki
and
James P.
Lewicki

Physical and Life Sciences Directorate, Lawrence Livermore National Laboratory, Livermore, CA 94550, USA. E-mail: kroonblawd1@llnl.gov
First published on 17th March 2022
Abstract
Chemical reaction schemes are key conceptual tools for interpreting the results of experiments and simulations, but often carry implicit assumptions that remain largely unverified for complicated systems. Established schemes for chemical damage through crosslinking in irradiated silicone polymers comprised of polydimethylsiloxane (PDMS) date to the 1950's and correlate small-molecule off-gassing with specific crosslink features. In this regard, we use a somewhat reductionist model to develop a general conditional probability and correlation analysis approach that tests these types of causal connections between proposed experimental observables to reexamine this chemistry through quantum-based molecular dynamics (QMD) simulations. Analysis of the QMD simulations suggests that the established reaction schemes are qualitatively reasonable, but lack strong causal connections under a broad set of conditions that would enable making direct quantitative connections between off-gassing and crosslinking. Further assessment of the QMD data uncovers a strong (but nonideal) quantitative connection between exceptionally hard-to-measure chain scission events and the formation of silanol (Si–OH) groups. Our analysis indicates that conventional notions of radiation damage to PDMS should be further qualified and not necessarily used ad hoc. In addition, our efforts enable independent quantum-based tests that can inform confidence in assumed connections between experimental observables without the burden of fully elucidating entire reaction networks.
1 Introduction
Chemical degradation of polymer materials is thought to arise from atomic-scale chemical reactions that alter networks through a range of processes including formation of crosslinks, chain scission, rearrangement, and abstraction/alteration of side groups. These reactions can adversely impact macroscale properties leading to irreversible changes in mechanical moduli, permanent set, embrittlement, or breaking under load that ultimately render components unfit for purpose.1,2 Polydimethylsiloxane (PDMS) is the primary constituent of silicones, which are ubiquitous in commercial, industrial, and medical contexts as oils, elastomers, and foams.3 The wide adoption of PDMS-based materials owes to their highly tunable mechanical response with favorable long-time characteristics, chemical inertness, thermal stability, and shape-filling factor. Despite these characteristics, PDMS is not impervious to chemical damage and it can interact with other materials. Common vectors for degradation arise from the ready uptake of environmental water4–7 or absorption of radiation.7–12 Understanding the degradation responses of PDMS has enormous practical applications, ranging from assessing environmental impacts13–15 to establishing models for the aging and lifetime prediction of silicone components.4–12,16,17Ionizing radiation is a common cause for polymer degradation that can arise during component sterilization,1,18,19 as a consequence of planned operation conditions, and as a driver in accelerated aging studies.7–12 In 1955, Charlesby proposed20 a set of reaction schemes for crosslinking in irradiated PDMS that were quickly refined by others21,22 and were based on IR vibrational spectroscopy, titration, mass spectra of off-gassing species, and chromatography (see Fig. 1). These reactions respectively connect the evolution of hydrogen (H2), methane (CH4), and ethane (C2H6) with the formation of silethylene (Si–C–C–Si), silmethylene (Si–C–Si), and silicon–silicon (Si–Si) crosslinks. Here, Si–C–C–Si links are thought to form from the joining of two under-coordinated methyl side groups (Si–CH2). Producing these sites emits two H atoms (Si–CH3 → Si–CH2 + H) that combine stoichiometrically to make H2. Similarly, producing Si–C–Si links emits an H atom (Si–CH3 → Si–CH2 + H) and a CH3 group (Si–CH3 → Si + CH3) that combine stoichiometrically to make CH4. Direct Si–Si linking can arise from the loss of two CH3 side groups (Si–CH3 → Si + CH3) that combine stoichiometrically to make C2H6.
The reaction schemes of Charlesby have formed the basis for interpreting a wide range of experiments and modeling results in the ensuing decades and are generally uncontested. A recent comprehensive review by Palsule et al.2 highlights these reactions among other chemical routes to different crosslinking and backbiting motifs. The reaction schemes in Fig. 1 indeed form a chemically reasonable hypothesis for interpreting experiments. At the same time, it is well understood that imprecision in the available experimental diagnostics can lead to large uncertainties in the quantification of crosslinking and other network alterations. Consequently, while this simple reaction scheme is pragmatic, its unqualified use neglects the possibility for systematic errors in the assumption that this mechanism comprises the main routes to evolution of observed gases and crosslinks.
Vibrational spectra offer a sensitive test for the presence of crosslinking groups, but it is difficult to quantify crosslink populations with high precision. Interpreting IR or Raman intensities invokes considerations of absorptivity and optical path lengths along with concentration (the quantity of interest). Complicated spectra with overlapping peaks can further exacerbate these difficulties. Modern NMR methods also suffer from some of these drawbacks. Mass spectra peak intensities are typically reconciled to a standard, giving only reliable relative measurements. Thus, making quantitative comparisons between mass, vibrational, and NMR spectra to count crosslinking events is fraught with unknowns.
In addition, unlike polymer crosslinking, it is comparatively difficult to directly detect and quantify chain scission events in experiments. Radiation damage leads to a net formation of crosslinks in PDMS, measured as a decrease in average chain length, onset of gellation, or enhancement of mechanical modulus. However, scission reactions not directly connected to the proposed crosslinking schemes can also take place. Scission events also open alternative channels for network alterations23 and can combine with crosslinking to result in complex dynamic changes in molecular weight distributions.8,9 Most experimental routes to estimate crosslinking and scission rely on fitting bulk-integrated data to rigid model forms,8,9,24–26 such as Tobolsky's two-network model,27 and thus do not provide a direct route to quantify populations of specific crosslink types nor their possible correlation with scission reactions. Some of the most advanced experiments that quantify scissions do so via isotopic tagging of silanol groups, which are treated as a proxy for the event of interest.28
Direct comparison of populations is far cleaner in computer-based simulations of reactions based on quantum-mechanical descriptions of atomic interactions. These simulations have uncovered a number of complicated reactive processes in PDMS materials including potential synergies between multiple degradation factors.7,10,11,17,29–35 Quantum-based molecular dynamics (QMD) takes as input a suitable initial-boundary value problem and evolves the system trajectory according to the dynamically evolving Born–Oppenheimer potential energy surface given by the electronic structure. This captures the ensuing chemical reactions as a direct consequence, with the primary difficulty resting on analyzing these simulations and interpreting underlying events for chemical significance.
In this work, we focus on characterizing chemical changes in pure PDMS through an atomistic modeling approach utilizing chains of dodecamethylpentasiloxane (DMPS), a methyl-terminated PDMS backbone with five silicon centers as an analog for the amorphous polymer. DMPS has previously been chosen as a somewhat simplified model as it includes enough monomer units to provide physical–chemical insights on local chemical reactivity while allowing for the reactive phase space to be explored more effectively on the timescales of our simulations.17 In using this approach, we can help bound the actual PDMS degradation chemistry in the context of Charlesby's reaction schemes for crosslink formation in Fig. 1. Hundreds of QMD simulations are used to predict the dynamic reaction cascades that follow from initial ionization events, which are modeled with a primary knock-on atom (PKA) approach36 using an established simulation protocol.11 Integrating QMD trajectories starting from a PKA event explicitly models the reaction cascades that result from secondary and tertiary knock-on atom events that occur over picosecond timescales.11,36,37 The simulations probe reaction cascades under ideal vacuum conditions and in the presence of environmental water, which is a common and potentially reactive contaminant7,10,17,31,38,39 that is difficult to eliminate in experiments.
Simulations in this work are assessed from two perspectives. The first is an ensemble-based time history analysis and the second a probabilistic analysis. The first approach quantifies the production of reaction intermediates, stable small molecules, and populations of polymer network features such as crosslinks and scissions. These ensemble-averaged response functions are analogous to “bulk” or system-integrated measures of the sort probed in most experiments, yielding for instance the amount of gas evolved. While this is useful information, QMD simulations can provide a direct exploration of the chemical reaction networks including causal dependencies, which is neglected by the ensemble time history analysis approach.
We therefore develop here a complimentary second approach, which takes the form of a general event-based conditional probability and correlation analysis framework. It casts QMD data in a way that provides a straightforward route to test the underlying assumptions of an established hypothesis and make direct connections to experimental observables. This allows one to quantify causal connections between reactive events without fully deducing the complete reaction network and also test the suitability of treating specific events as proxies for other events. Our method allows us to quantitatively assess reliance on the Charlesby scheme for experimental analysis. Application of this analysis framework reveals that Charlesby's schemes are qualitatively correct, but also shows that causal linking of events may be insufficient to quantitatively determine the number of crosslinks formed from off-gassing data. Further extension of the method yields a possible proxy for difficult-to-measure chain scission events under certain circumstances. The present results are discussed in the context of the extensive body of literature for PDMS radiolytic chemistry.
2 Methods
2.1 QMD simulations
High-throughput QMD simulations40 were performed using the self-consistent charge (SCC) DFTB method41,42 as implemented in the DFTB+ code.43 The DFTB total energy is derived from an expansion of the Kohn–Sham energy44 about a reference electronic density to second order in charge fluctuations and is evaluated as| EDFTB = EBS + ECoul + ERep + EDisp. | (1) |
Our simulations consisted of a cubic 3D-periodic cell that contained four chains of DMPS, where dry and wet conditions were considered. The wet case simulation cell included 10 H2O molecules that were initially randomly distributed among the four DMPS chains. A multistep procedure was used to bring the system to the PDMS average bulk density of 0.965 g cm−3 and to equilibrate it at 300 K prior to simulations to predict primary radiation damage. First, the four DMPS chains (and H2O for the wet case) were placed in a cubic cell with side length 20 Å. This cell was then isotropically compressed by reducing the cell length to 13.836 Å (14.356 Å with H2O) at a constant rate of 1.0 Å ps−1. Following this, a 20 ps isothermal–isochoric (NVT) simulation was performed and 100 configurations were extracted every 100 fs during the last 10 ps as starting points for simulations of radiation damage. This sampling timescale is sufficient for decorrelation of per-atom forces but is smaller than other structural relaxation timescales in this system such as the chain end-to-end vector decorrelation time, which approaches hundreds of picoseconds. QMD trajectories for system preparation were integrated using the LAMMPS code52 with forces and stresses evaluated by DFTB+. The temperature was set to 300 K through a Nosé–Hoover-style thermostat,53,54 the electron temperature was set equal to the instantaneous ionic temperature, and the XL-BOMD dynamics were integrated with a 0.2 fs time step and four SCC cycles per step.
We verified that the water molecules, introduced in the simulation cell as un-clustered single molecules, remain dispersed throughout the simulation cell during the entire simulation time. We checked this both through visual inspection of the trajectory and through the O–O radial distribution function for the water oxygen atoms. In future work, it will be interesting to introduce H-bonded clusters of water molecules in the simulation cell and explore their effects on the resulting reaction cascade.
Similar to our previous work,11 we adopted a PKA approach to initiate chemical reactions of the form given in Fig. 1. With this approach, a randomly selected atom or group of atoms in a thermal configuration is imparted with a large “recoil” kinetic energy through assignment of a random velocity of set magnitude. We take a representative recoil energy to be 50 eV, which is ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10) times greater than typical bond dissociation energies in PDMS and is similar in magnitude to ultraviolet radiation. Three types of PKA groups were considered including (1) entire methyl side groups (denoted “Me”), (2) single hydrogen atoms on a methyl side group (denoted “Me–H”), and (3) single hydrogen atoms on an H2O molecule (denoted “H2O–H”). We do not consider PKA events that induce chain scission directly via recoil of backbone atoms as our focus is on testing Charlesby's reaction schemes. Such event were recently explored in our earlier work11 and are predicted to lead to qualitatively similar reaction cascades. By simulating the above three types of PKA events, we can effectively explore all possible irradiation events in the context of Charlesby's reaction schemes without performing direct calculation of absorption cross-sections, which can require substantial effort55 and is the subject of future work.
(10) times greater than typical bond dissociation energies in PDMS and is similar in magnitude to ultraviolet radiation. Three types of PKA groups were considered including (1) entire methyl side groups (denoted “Me”), (2) single hydrogen atoms on a methyl side group (denoted “Me–H”), and (3) single hydrogen atoms on an H2O molecule (denoted “H2O–H”). We do not consider PKA events that induce chain scission directly via recoil of backbone atoms as our focus is on testing Charlesby's reaction schemes. Such event were recently explored in our earlier work11 and are predicted to lead to qualitatively similar reaction cascades. By simulating the above three types of PKA events, we can effectively explore all possible irradiation events in the context of Charlesby's reaction schemes without performing direct calculation of absorption cross-sections, which can require substantial effort55 and is the subject of future work.
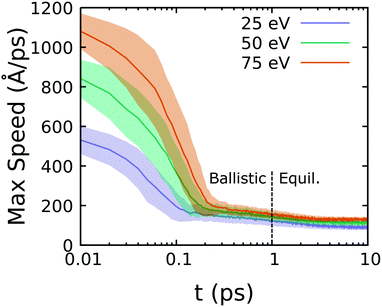
Reaction cascades following from a PKA event were sampled through ensembles of statistically independent, 21 ps long NVE simulations. The reaction cascade is characterized by an initial ballistic portion followed by establishment of local thermal equilibrium at a high temperature. Thermal relaxation due to conduction of the resulting heat spike in nm-sized regions is expected to be on the order of 10 s of picoseconds or more for materials with a glass-like thermal conductivity (≈0.5 W m−1 K−1) such as PDMS.56,57Fig. 2 shows ensemble-average maximum atom speeds reached following hydrogen atom PKA excitation at three different recoil energies in PDMS. The initial ballistic portion of the trajectory only lasts a few hundred femtoseconds and is followed by the onset of local equilibrium within 1 ps. Hydrogen excitation leads to the highest maximum atom speeds as this PKA group has the lowest mass. Energy conserving integration of the ballistic portion requires a very small time step, which is unnecessary and computationally expensive for the equilibrium portion. Based on Fig. 2 and an assessment of energy conservation, we set the time step to 0.05 fs for H-atom excitation and 0.10 fs for Me-group excitation during the first 1 ps of the trajectory and used a larger 0.20 fs time step for the remaining 20 ps.
 | ||
| Fig. 2 Ensemble-average maximum atom speed in simulations exciting hydrogen at three different PKA recoil energies. | ||
A given ensemble had 100 independent simulations, each starting from one of the 100 independent starting configurations, and had one specific group type (Me, Me–H, or H2O–H) selected for PKA excitation. The single excited group was chosen at random from among those of the chosen type in a given simulation. (There were 60 unique Me groups, 180 unique Me–H atoms, and 20 unique H2O–H atoms in the system.) Five ensembles were considered, one for each PKA group type under dry and wet conditions, leading to 500 independent trajectories and a total of 10.5 ns of combined QMD trajectory. All cascade QMD simulations were performed with the standalone DFTB+ code using NVE XL-BOMD dynamics. The electron temperature was set to 2000 K, consistent with the system-average kinetic energy, and full SCC convergence was enforced each time step. Trajectory snapshots were recorded every 10 fs for subsequent chemical analysis.
2.2 Chemical analysis
Dynamic changes to chemical bonding were determined through post-processing of trajectories in the PKA simulations using separation distance cutoffs and a time-symmetric lifetime criteria. Bond distance cutoffs are collected in Table 1 and were chosen to be somewhat larger than equilibrium lengths for single bonds of a given interaction type obtained from DFTB-optimized geometries of representative small molecules. The lifetime criterion was set to τB = 50 fs, which is several times larger than the typical oscillation period of the fastest bond vibrations in the system.| Si | O | C | H | |
|---|---|---|---|---|
| Si | 2.55 | 2.00 | 2.20 | 1.80 |
| O | 2.00 | 1.80 | 1.80 | 1.30 |
| C | 2.20 | 1.80 | 1.80 | 1.30 |
| H | 1.80 | 1.30 | 1.30 | 1.00 |
Bonding between atoms was tracked through time and was recorded at each time step as an adjacency graph. (The adjacency graph was initialized based on pre-PKA thermalization runs.) Changes to the system's adjacency graph were recorded only when certain criteria were met. A bond was considered to be broken between two atoms at a given time step if the pair were considered bonded on the previous time step and the atoms were separated by more than the cutoff distance for the past τB = 50 fs. Similarly, a bond was considered to have formed between two atoms at a given time step if the pair were considered unbonded on the previous time step and the atoms were separated by less than the cutoff distance for the past τB = 50 fs. Forwards and backwards application of lifetime criteria serves to filter out transients and is essential for detailed balance.58 A more rigorous yet computationally demanding definition of bonding could assess the trajectory for oscillatory behaviors59 or explicitly connect to the electronic structure via bond orders.60
We considered both all-atom and backbone-only adjacency graphs. The former is useful for identifying small molecules and the latter specifically isolates the polymer network. The backbone-only adjacency graph was determined from the all-atom one by first removing all hydrogen atom nodes and their corresponding bonds (edges), followed by deleting any remaining nodes (atoms) that had only one bond.11 This serves to effectively remove side groups and other highly undercoordinated terminal atoms. Individual molecules and backbones were identified as connected components of the respective (undirected) adjacency graphs through a depth-first search.
A reduced-order descriptor was used to identify small molecules of specific types. These descriptors were integer-valued length-14 vectors with components corresponding to the population of each atom type and bond type contained in a given molecular connected component. That is,
| D = (NSi,…,NH, NSi–Si, NSi–O,…,NH–H), | (2) |
The reaction scheme in Fig. 1 yields specific backbone crosslinking motifs. Rapid screening for these features on the backbone adjacency graphs can be performed efficiently without rigorous differentiation of unique backbone topologies through isomorphism checks. We identify methyl and ethyl links by finding 3-center angles and 4-center dihedrals with specific features on the backbone adjacency graphs following Fig. 3. Methyl (Si–C–Si) links were found as angles between connected atoms A, B, and C with the requisite ordering of element types and where atom B had exactly two bonds to heavy atoms NB = 2. Atoms A and C could have one or more bonds to heavy atoms, but A and C were required to not be bonded to each other. Ethyl (Si–C–C–Si) links were found as proper dihedrals between connected atoms A, B, C, and D with the requisite ordering of element types and where atoms B and C had exactly two bonds to heavy atoms NB = 2. Atoms A and D could have one or more bonds to heavy atoms, but the following bond pairs were prohibited: A–C, B–D, and A–D. Silicon–silicon crosslinking (Si–Si) was quantified through counting the number of Si–Si bonds on the backbone adjacency graphs.
 | ||
| Fig. 3 Topology definitions and examples for identification of methyl (Si–C–Si) and ethyl (Si–C–C–Si) carbon-containing crosslink junctions. Snapshots of example backbones were rendered using the OVITO code63 and the approach described in ref. 11. Atoms are colored yellow, red, and cyan for Si, O, and C. | ||
2.3 Statistical analysis
Statistics were gathered on specific chemical changes through ensemble-average time history analysis and event-based probabilities. We define fsimα(ti) as the time history for some property α in a given independent simulation with discrete time stepping (e.g., the number of CH4molecules). The ensemble-average time history is then obtained as | (3) |
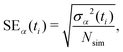 | (4) |
We define time-independent events E and their probabilities P based on the complete time histories of individual simulations. The definition for event A is
 | (5) |
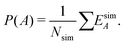 | (6) |
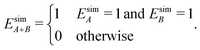 | (7) |
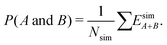 | (8) |
 | (9) |
| P(A and B) = P(A)P(B), | (10) |
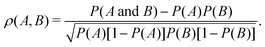 | (11) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 resamplings of a given 100-simulation ensemble.
000 resamplings of a given 100-simulation ensemble.
Event-based conditional probability analysis applied to QMD simulations offers a route to independently test whether assumptions regarding causal linking are well-founded, such as the simplified reaction schemes in Fig. 1. In particular, eqn (9) can help justify using certain events (or quantities) as proxies for different events (or quantities). Event B is a good proxy for event A if |ρ(A, B)| is sufficiently high, which expressed in terms of conditional probabilities is P(A) < P(A|B) and P(A|B) → 1.0. A perfect proxy pair is one for which |ρ(A, B)| = 1.0, or equivalently if P(A|B) = 1.0 and P(B|A) = 1.0. Given some initial chemical intuition or hypothesis to define pertinent events, an event-based probability analysis is substantially less complicated than constructing a full reaction network and facilitates making direct connections to experimental observables.
2.4 DFTB validation
The accuracy DFTB and its description of key reactions explored in this work were validated against DFT calculations. DFT calculations were performed using the CP2K code64 with the Perdew–Burke–Ernzerhof (PBE) functional,65 Grimme D3 dispersion corrections,66 and the core electrons represented by the Geodecker-Teter-Hutter pseudopotentials.67 CP2K is a mixed Gaussian/plane-wave code; we used a double-ζ plus polarization Gaussian basis set (DZVP) and a 200 Ha plane wave energy cutoff for expansion of the charge density. The electronic structure was evaluated without spin polarization. Both the DFT and DFTB calculations considered isolated gas-phase molecules. Gas-phase conditions were imposed in our DFT calculations through the nonperiodic Martyna–Tuckerman Poisson electrostatic solver68 using a cubic simulation cell with side length 30 Å, which is more than twice the maximum cluster size. All structures were optimized with a force-based tolerance of 2 × 10−2 eV Å−1.Fig. 4 shows the four key reactions considered in our validation testing. These are all based on a trisiloxane analog molecule and include the three crosslink forming reactions due to Charlesby and a fourth reaction involving the water-mediated substitution of a methyl group for a silanol (Si–OH) group. Ordering of the reaction energies is in excellent agreement between DFT and DFTB, indicating that DFTB accurately captures the relative favorability of these reactions. The largest difference between DFT and DFTB is for reaction (1), with DFTB predicting a reaction energy that is 0.595 eV (13.7 kcal mol−1) higher. Similar magnitude differences were noted for other reactions in siloxanes with this DFTB parameterization10 and with other off-the-shelf parameter sets for organic molecules.40 The reaction energies indicate that the formation of methyl bridges and methyl → silanol substitutions are both energetically favorable processes. We note that while some of the crosslinking reactions are endothermic, the energy involved is substantially lower than the PKA energy, so we would expect all four reactions to occur in irradiated silicones.
3 Results and discussion
3.1 Crosslinking events
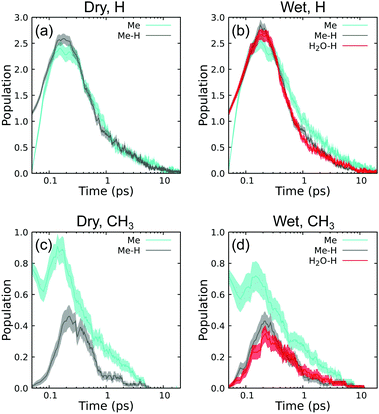
Exciting whole methyl groups (Me) is expected to make CH3 and exciting hydrogen atoms on methyl groups (Me–H) is expected to make H. The last type with excited hydrogen atoms on environmental water (H2O–H) is expected to initially generate an H/OH pair. In all cases, the populations at t = 0.05 ps are consistent with excitation group. Exciting Me–H and H2O–H leads to an initial H population of ≈1 and CH3 population of ≈0. Similarly, exciting Me leads to initial CH3 population of ≈1 and H population of ≈0. Note that these values are not precisely 0 and 1 as the recoil event is sufficiently strong to induce secondary reactions within the first 10 fs. For instance, in H excitation cases, the population of H is slightly more than 1 at 0.05 ps due to initial ballistic scattering that knocks additional H atoms free. Following this, all cases exhibit a maximum in 0.1 ≤ t ≤ 1.0 ps, coinciding with the end of the ballistic regime. Populations of these species decay practically to zero within the timescale of the simulations.
Perhaps surprisingly, all three excitation types are very effective at producing H, yielding an average maximum of 2.5 per simulation regardless of excitation group. All three excitation types can also produce CH3, although in this case Me excitation is more effective. Taking the dry case as an example in panel (c), Me excitation leads to a maximum CH3 population of 0.9 whereas Me–H leads to a maximum CH3 population of 0.4. Interpreted as a probability, nearly every Me excitation makes a stable (if short-lived) CH3. The double CH3 peaks for Me excitation and single delayed CH3 peak for H excitation for both wet and dry conditions indicates that CH3 is also an intermediate product of subsequent reactions that follow the very initial reactive states induced by PKA recoil.
Water has only one subtle effect on these intermediate time histories. Comparison of panels (c) and (d) shows that environmental water modestly suppresses CH3 production when exciting Me groups. In contrast, the presence of water does not seem to suppress H populations relative to the dry case. There is largely no difference in initial production between exciting H on Me compared to H on H2O. Both H-excitation types lead to H and CH3 population curves that agree within standard error bounds in panels (b) and (d).
The lifetimes for CH3 predicted here are very short compared to electron spin resonance measurements in cryogenic (77 K) radiolysis experiments using both X-ray69 and γ-ray sources.70 At such low temperatures, these species can exist as radicals for hours.69 Subsequent warming to 195 K and room temperature led to rapid disappearance of these radicals,70 indicating a very strong temperature-dependent kinetics. Spin trapping chemical agents are needed to observe CH3 radicals above 77 K.71 Considering that our system is closed and the local temperature is in excess of 1000 K, picosecond-scale kinetics is not unreasonable and in qualitative agreement with the available experiments.
There is a high degree of similarity among the H2 time histories for the different cases shown in panels (a) and (b). Exciting Me is approximately twice as effective at generating H2 than exciting H atoms under both wet and dry conditions. Water has negligible impact on final populations for a given excitation type within computed errors. We also determine no difference between exciting Me–H or H2O–H. The ability of Me excitation to produce more H2 than H excitation is perhaps surprising, but this indicates that a significant quantity of H2 is produced from secondary and tertiary events in the ensuing reaction cascades.
In contrast, time histories for CH4 in panels (c) and (d) show distinctly different trends than H2. Under dry conditions, both Me and Me–H excitation generate the same amounts of CH4. Under wet conditions, CH4 production is unchanged when exciting Me compared to dry conditions, but is modestly suppressed when exciting Me–H. H2O–H yields quite different trends than exciting Me–H, and is the most effective excitation type for generating CH4. Insensitivity of CH4 populations with excitation type, especially in the H-excitation cases, indicates that secondary and tertiary events are responsible for a significant portion of CH4 production.
Experimental measurements of small molecule off-gassing were made in a number of independent studies that considered different radiation sources and PDMS molecular weights.20–22,70,72–74 Relative concentrations of H2, CH4, and C2H6 referenced to the H2 concentration [H2] measured in these experiments are collected in Table 2, along with information on the form of the PDMS material sample, the radiation source (reactor piles, 60Co γ-rays, or high-energy electrons e−), and headspace gases exposed to the sample (if known). These are compared to analogous values predicted here from QMD, which correspond to the ensemble-average results at time t = 21 ps in Fig. 6. Recent experiments on engineering silicones with complex compositions can off-gas additional volatile species,16 though we restrict our discussion to pure PDMS materials here.
| QMD (this work) | ||||
|---|---|---|---|---|
| Material | Excitation | Headspace | [CH4]/[H4] | [C2H6]/[H2] |
| a Reported in reference from private communications with W. Davison and D. Lloyd. b Values correspond to measurements at 25 °C. | ||||
| Pentamer | Me | Vacuum (ideal) | 1.24 | 0.12 |
| Pentamer | Me–H | Vacuum (ideal) | 2.10 | 0.03 |
| Pentamer | Me | H2O | 0.94 | 0.05 |
| Pentamer | Me–H | H2O | 2.21 | 0.05 |
| Pentamer | H2O–H | H2O | 2.62 | 0.00 |
| Experiment | |||||
|---|---|---|---|---|---|
| Material | Rad. source | Headspace | [CH4]/[H4] | [C2H6]/[H2] | Ref. |
| Dimer | 60Co | Vacuum (<10−6 atm) | 2.23 | 0.00 | Zach et al.72 |
| Dimer | Pile | Vacuum (<10−6 atm) | 2.33 | 0.01 | Zach et al.72 |
| Dimer | 800 kvp e− | N2 | 2.00 | 0.57 | Dewhurst and St. Pierre22 |
| Pentamer | 800 kvp e− | N2 | 1.52 | 0.71 | St. Pierre et al.73 |
| Cyclotetramer | 60Co | Sealed (unspecified) | 1.76 | 0.14 | Warrick et al.74 |
| Silicone | Pile | Sealed (unspecified) | 1.16 | 0.30 | Charlesby20 |
| Silicone | 2 MeV e− | Unknown | 1.38 | 0.24 | Ormerod and Charlesbya![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 70 |
| Silicone | 800 kvp e− | N2 | 0.86 | 0.61 | Millerb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 21 |
Quantitative trends among the experiments are difficult to discern. Results from Zack et al.72 on hexamethyldisiloxane oil show little difference in off-gassing products between a 60Co γ-ray source and the environment of a reactor pile. At the same time, the results of Zack et al. differ from the measurements by Warrick et al.74 of 60Co-irradiated octamethylcyclotetrasiloxane and those by Charlesby20 of pile-irradiated high-molecular-weight silicone. The results of Warrick et al. and Charlesby also differ from each other.
Significant spread is seen for relative CH4 production despite similar radiation sources and inert N2 atmosphere, as seen by comparing the experiments of St. Pierre et al.,73 Dewhurst and St. Pierre,22 and Miller.21 Perhaps interestingly, those experiments show similar relative production of C2H6. The original source documenting the MeV-range electron irradiation experiments noted in ref. 70 could not be located, but those results clearly fall within the spread of the other studies.
The present QMD modeling results and experiments are broadly consistent, exhibiting a significant (yet similar) spread of values. The minimum [CH4]/[H4] and [C2H6]/[H2] populations over the five QMD ensembles are respectively 0.95 and 0.00, while the corresponding maximums are 2.62 and 0.12. This is quite similar to the respective experimental minima (0.86 and 0.00) and maxima (2.33 and 0.71). In particular, there are some experiments in which large amounts of H2 and CH4 form with no detectable C2H6 whereas large quantities of C2H6 form in others.
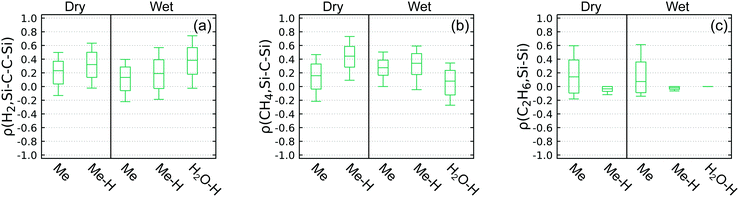
The time history response is characterized by well-converged plateaus under wet conditions and more slowly converging plateaus in dry conditions for all three crosslink types. The apparent rate of convergence is slower than those for the H2, CH4, and C2H6 populations. Methyl and ethyl links are rapidly formed in 30% or fewer PKA events and Si–Si links are produced in 10% or fewer PKA events. These crosslink populations are approximately half the size of the corresponding small molecule species populations in Fig. 6.
Wet conditions suppress both types of carbon crosslinking, consistent with earlier DFTB modeling results of radiation-induced reactions in phenylated siloxanes10 and arguments based on DFT-computed reaction barriers.7 Direct Si–Si linking is also lower in wet simulations, although these differences are similar in magnitude to the computed errors. Water suppresses Si–C–Si formation more than Si–C–C–Si formation. Exciting Me–H under dry conditions is the most effective combination for producing both Si–C–Si and Si–C–C–Si links; this is at least twice as effective as exciting Me groups directly. Conversely, exciting Me under dry conditions is the most effective combination for producing Si–Si links.
It is substantially more difficult to accurately quantify the different types of crosslinking in experiments than it is to measure small-molecule off-gassing. The small subset of experiments that quantified relative Si–C–C–Si, Si–C–Si, and Si–Si crosslink populations are listed in Table 3. These are compared to analogous values predicted here from QMD, which correspond to the ensemble-average results at time t = 21 ps in Fig. 7.
| QMD (this work) | ||||
|---|---|---|---|---|
| Material | Excitation | Headspace | [Si–C–Si]/[Si–C–C–Si] | [Si–Si]/[Si–C–C–Si] |
| a Values correspond to measurements at 25 °C. | ||||
| Pentamer | Me | Vacuum (ideal) | 3.25 | 2.50 |
| Pentamer | Me–H | Vacuum (ideal) | 1.26 | 0.13 |
| Pentamer | Me | H2O | 2.33 | 1.67 |
| Pentamer | Me–H | H2O | 0.63 | 0.06 |
| Pentamer | H2O–H | H2O | 0.38 | 0.15 |
Among the experiments, the measurements of Dewhurst and St. Pierre22 are perhaps the most direct. They analyzed nonvolatile products of irradiated hexamethyldisiloxane through liquid chromatography to deduce crosslink populations. In comparison, Miller21 deduced these ratios from a combination of relative IR intensities (sensitive to Si–C–Si and Si–C–C–Si) and titration with bromine Br2, which reacts quickly with Si–Si bonds. Bueche24 quantified radiation-induced changes to average molecular weights in dodecamethylpentasiloxane oil as a measure for crosslinking, but their technique did not yield specific crosslink type ratios. Their complimentary IR measurements did not detect Si–C–C–Si links.
Modern NMR techniques provide what is perhaps the most direct experimental route to quantify crosslinking in PDMS. Chemically specific crosslinking motifs were elucidated in γ-irradiated PDMS through a series of 13C and 29Si NMR experiments by Hill et al.23,75 in samples under vacuum at cryogenic (77 K) and room temperature. Two principle findings from these studies were that (1) many of the crosslinks in PDMS arose from formation of Si–O–Si crosslinks (following main chain scission) that are not considered in the Charlseby mechanism, and (2) there was no evidence for Si–Si linking. While their experiments did detect Si–C–Si and Si–C–C–Si links, overlaps in spectral peaks prevented quantifying populations of the latter. These results indicate that caution should be exercised in interpreting crosslinking ratios from experiments such as sol-dose that measure only populations of generic “mechanically relevant” crosslinks with no chemical specificity.
The above experiments were performed under vacuum or N2 atmosphere, so the QMD results without water are the cleanest point for comparison. As discussed above, QMD predicts that environmental water will have a substantial impact on crosslinking, which manifests markedly in the relative ratios. The QMD ensemble with Me excitation in vacuum yielded ratios very similar to the tabulated experiments. In contrast, H excitation yields results closer to Hill et al. that found little to no Si–Si linking. The wide (and sometimes conflicting) range of experimental results highlights the complexity of chemistry in this system. One interpretation of the present modeling results for small molecule production and crosslinking suggests that both environmental factors—it is difficult to completely eliminate water in samples—and the chemical groups initially excited by radiation could play a role in this spread.
Focusing first on Fig. 8(a), the comparison is structured to test connections between H2 off-gassing and Si–C–C–Si crosslinking. The unconditional probabilities follow P(H2) > P(Si–C–C–Si) and differ by a factor of six for Me excitation and 1.5 for either type of H excitation, which could indicate many other reaction channels for H2 production with Me excitation. The conditional probability P(H2|Si–C–C–Si) is as much as 0.86, indicating that many H2 molecules are connected to Si–C–C–Si crosslinking events. Conversely, while the conditional probability P(Si–C–C–Si) < P(Si–C–C–Si|H2) and thus meets our criteria for a proxy, the value of P(Si–C–C–Si|H2) is never greater than 0.47 (e.g., much less than the ideal value of 1). This implies there must be many other chemical events that produce H2 without ever generating a Si–C–C–Si cross link. Thus, H2 formation may not be a good proxy for Si–C–C–Si formation. Additional correlation analysis described below is required to determine whether a statistically significant relationship exists between these two events.
Fig. 8(b) is structured to test connections between CH4 off-gassing and Si–C–Si crosslinking. For all cases P(CH4) > P(Si–C–Si), with difference factors ranging from 1.9 to 8.3 that are greatest in wet conditions. The conditional probability P(CH4|Si–C–Si) is no less than 0.71 and is 1.0 for the case with wet conditions and Me excitation. Forming Si–C–Si makes forming CH4 much more likely, and there is an even stronger causal relationship than was seen for H2 and Si–C–C–Si links. In contrast, the conditional probability P(Si–C–Si|CH4) is never greater than 0.46, indicating that CH4 is formed through other routes besides crosslink formation. As with H2, so to we find that CH4 formation may not be a good proxy for Si–C–Si formation, with the relationship requiring further interrogation.
Lastly, Fig. 8(c) tests connections between C2H6 off-gasing and Si–Si crosslinking. The unconditional probability to form C2H6 is much lower than H2 or CH4 and is zero in the case of H2O–H excitation. In contrast, the unconditional formation probability for Si–Si crosslinking is more similar to the Si–C–Si and Si–C–C–Si formation probabilities within the predicted spread. The conditional probability follows P(C2H6|Si–Si) > P(C2H6) for Me excitation, but both probabilities are very low. The direction for the inequality is reversed for Me–H excitation. While the conditional probability P(Si–Si|C2H6) > P(Si–Si) for Me excitation, it is never greater than 0.43, indicating that only some crosslinks are connected to C2H6 off-gassing. With H excitation, P(Si–Si|C2H6) = 0 even though P(Si–Si) ≈ 0.1, suggesting that none of the evolved C2H6 is tied to Si–Si crosslinking. Thus, C2H6 and Si–Si formation are almost certainly not good proxies for each other and there must be other chemical events that produce Si–Si crosslinks.
Correlation coefficients for the events defined in Fig. 8 were computed using eqn (11) and are collected in Fig. 9. Confidence intervals for the correlation coefficients were computed via bootstrapping with 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 resamplings of each 100-simulation ensemble. In this representation, there exists a statistically significant positive (negative) correlation between events A and B with 95% certainty if the entire 95% confidence interval indicated by the box is above (below) zero. For instance, focusing on panel (a), one can see that there exists a statistically significant correlation between H2 and Si–C–C–Si links with Me excitations in dry environments, but not in wet environments.
000 resamplings of each 100-simulation ensemble. In this representation, there exists a statistically significant positive (negative) correlation between events A and B with 95% certainty if the entire 95% confidence interval indicated by the box is above (below) zero. For instance, focusing on panel (a), one can see that there exists a statistically significant correlation between H2 and Si–C–C–Si links with Me excitations in dry environments, but not in wet environments.
From the correlation confidence intervals, it is clear that there is a modest positive and statistically significant correlation between H2 and CH4 off-gassing and their respective crosslinking events for the majority of the conditions studied. This is unlike the correlation between C2H6 off-gassing and Si–Si linking, which shows no statistical significance for any excitation/humidity combination and is formally undefined for H2O–H excitation given that some of the underlying probabilities are zero. We note that even for the apparent positive relationship between H2 and CH4 gases and crosslinks, there are some excitation/humidity combinations that yield insignificant correlations. In the case of H2, it is the two wet cases with excitations centered on PDMS that have insignificant correlations. In contrast, there is no systematic trend for which cases exhibit significant correlations between CH4 and Si–C–Si links; two cases are insignificant, one being Me excitation in dry environment and the other between H2O–H excitation in wet environment.
As P(link|gas) > P(link) and ρ(gas, link) is statistically significant in the majority of cases involving H2 and CH4, it is clear that these specific off-gassing products are causally connected to specific crosslinks. However, P(link|gas) and ρ(gas, link) are rarely unity, which is what one would expect if every gas molecule were traced to a crosslink-forming event and vice versa. Taken together with the fact that there are some excitation/humidity conditions that yield insignificant correlations, the conditional probabilities P(link|gas) computed for the present QMD data indicates caution is warranted in using H2 and CH4 off-gassing to directly quantify Si–C–C–Si and Si–C–Si crosslink populations. The complete lack of significant correlations between C2H6 and Si–Si links further underscores the wide variance in the experimental and predicted concentrations for those two features reflected in Tables 2 and 3.
A pragmatic interpretation of the set of statistically significant correlations indicates that it should be possible to construct a regression model linking off-gassing and crosslinking under certain circumstances. Regression models linking H2 and Si–C–C–Si links may work well in perfectly desiccated systems. It is less clear whether the same will hold for CH4 and Si–C–Si links. Importantly, such regression models will need to be trained against data with high chemical specificity, such as that generated from QMD simulations. A more sophisticated analysis of the QMD data that considers other trace gases might yield more robust models for quantification of crosslinking through small molecule off-gassing measurements. From a chemical perspective, our results indicate that a qualitative interpretation of Charlesby's reaction schemes may be most reasonable, as they miss important (if still poorly characterized) branches in a larger reaction network.
3.2 Scission events
Inspection of panels (a) and (b) shows that fewer than one Si–O bond is scissioned per PKA event on average. Excitation of Me groups is the most effective route to chain scission among the cases considered. These scission events occur very early in the trajectory following PKA excitation, typically within the first few picoseconds. Chain scissions slowly anneal following Me excitation under dry conditions, whereas the scissions are persistent in the other four cases. Environmental water does not change the initial number of Si–O bonds broken, but it does impede recovery following Me excitation seen in the dry case.
There is a very large difference between wet and dry conditions in terms of silanol formation. Up to four times as many silanols are formed when water is present. The excitation group does not impact silanol production under dry conditions, but has a strong bearing on silanol production in wet conditions. We note that the silanol populations are only partly converged on the timescale of our simulations with Me and H2O–H excitation under wet conditions. Longer simulations were not considered as they would require a careful (and likely ad hoc) treatment of thermal relaxation of the heat spike. Picosecond-scale silanol formation reactions were predicted to occur in QMD simulations following loss of a phenyl side group in a model siloxane copolymer.10 In that case it was found that loss of a side group leaves an undercoordinated Si atom, which is highly reactive and readily scavenges OH groups from nearby water. A similar reaction likely occurs here in pure PDMS following loss of a methyl group. Excitation of H2O–H is also highly effective at generating silanols. Perhaps surprisingly, while Me–H excitation is the least effective at producing silanols, it is still twice as effective under wet conditions as compared to dry conditions.
As was seen in the time-dependent analysis, unconditional probabilities show silanols are formed about 20% of the time in dry conditions and up to 60% of the time in wet conditions. The conditional probability P(Si–OH|Si–/–O) is always larger than P(Si–OH) and it is never smaller than 0.44. In addition, knowledge of Si–O scission reactions increases the probability of silanol formation by a factor of 1.3 to 3.6, as indicated by the ratio of P(Si–OH|Si–/–O) to P(Si–OH).
Unconditional scission probabilities vary most with excitation group and are somewhat larger than 0.5 with Me excitation and closer to 0.3 with H excitation. The conditional probability P(Si–/–O|Si–OH) is always larger than P(Si–/–O). Here, P(Si–/–O|Si–OH) = 1.0 under dry conditions, indicating that every Si–O bond scission is closely connected to silanol formation. These results imply that silanol formation is an excellent proxy for chain scission under dry conditions. Conditional probabilities are somewhat lower under wet conditions (0.59 < P(Si–/–O|Si–OH) < 0.77). Thus, while Si–O bond scission is likely if silanols are detected, there are other chemical events leading to both silanol formation and Si–O bond scission when water is present.
Correlation coefficients for silanol formation and main chain scission were computed using eqn (11) and are plotted in Fig. 12. Similar to the analysis of off-gassing and croslinking in the previous section, confidence intervals for the correlation coefficients were computed via bootstrapping with 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 resamplings of each 100-simulation ensemble. A statistically significant positive correlation exists with 95% certainty if the entire 95% confidence interval indicated by the box is above zero.
000 resamplings of each 100-simulation ensemble. A statistically significant positive correlation exists with 95% certainty if the entire 95% confidence interval indicated by the box is above zero.
 | ||
| Fig. 12 Box and whisker plots of the correlation coefficients ρ(A, B) for chain scission (Si–/–O) and silanol (Si–OH) formation events in PKA simulations with different excitation types and system conditions. We follow the same box-and-whisker convention as in Fig. 9. | ||
As anticipated from Fig. 11, the correlation analysis shows that a positive and statistically significant correlation exists between chain scissions and silanol formation under all of the conditions studied. The correlation strength here is quite unlike that computed for small molecule off-gassing and crosslinking in Fig. 9. Despite this relative increase in strength, the correlation between silanol formation and scission is still much less than unity, indicating that these events are not fully coupled. The strength of the correlation is generally greater for H excitations than for Me excitations and the presence of water systematically lowers the strength relative to dry conditions.
There have been numerous attempts to quantify scissions through experiments, although few can be directly compared to the present work. Comparisons are difficult to make as the experiments either measure “mechanically relevant” crosslinks and scissions or else tie the scission probability to assumed models or complex sets of products. For instance, Squire and Turner25 estimated ratios of crosslinking and scissioning from sol-dose experiments through an analysis with a probabilistic model that makes a number of assumptions, including that the starting molecular weight distribution is random. Similarly, Tanny and St. Pierre26 estimated scissioning indirectly through two routes, namely with Tobolsky's two-network model and as a ratio to crosslinks in sol-dose experiments. The latter makes use of the so-called “Charlesby-Pinner” analysis,76 which has proven to return similar results as obtained through fitting constitutive models for siloxane elastomer stress–strain responses.77 These approaches that rely on mechanical data necessarily only account for scissioning and crosslinking that alters mechanical response. Multi-quantum NMR can measure detailed changes in molecular weight distributions, but scissioning and crosslinking are again inferred indirectly through fitting to probabilistic models.8,9 Hill et al.23,75 presented an alternative means to measure scissioning through NMR, which can quantify populations for a host of chemical structures that are reasonably interpreted as resulting from chemistry with scissioned chain ends.
Consideration of silanol production as a measure for scissioning dates to early experiments by Miller,78 who made the (chemically reasonable) assumption that these features were directly related in the analysis of IR spectra for irradiated PDMS loaded with hydrogen donors. More recent experiments by Alam38 and Patel et al.39 used 17O-labeled water to identify the formation of silanols and incorporation of water oxygen atoms into the main chain during radiolysis. A new approach to detect silanols through NMR via tagging with 19F-labeled groups that react with silanols offers what is perhaps the cleanest spectroscopic measure for these features.28 In this context, the present QMD simulations with water suggest that many (but not all) silanols can be traced to chain scissions while the discrepancy in unconditional probabilities for scissioning and silanol formation in dry conditions indicates there are more scissions than silanols. Thus, a population count for silanols in experiments might underrepresent the true number of chain scissions. Calibrated regression models based on QMD data that link scissioning and silanol formation hold promise as a means to systematically correct these underestimates. The production of silanol groups in irradiated silicones may also have consequences beyond their connection to changes in modulus through scissioning of chains as these groups are known to alter the dielectric properties of related systems.79–81
4 Conclusions
We develop here a general in silico analysis framework to test proposed reaction schemes for polymer degradation processes and apply this to characterize the radiolytic chemistry of polydimethylsiloxane (PDMS), the primary constituent of silicones. Here, we use a model system of dodecamethylpentasiloxane (DMPS) in order make simulation of the amorphous polymer more tractable with our quantum calculations. In addition, we model all types of atomic excitations relevant to siloxane systems in the context of long-standing reaction schemes for irradiation of PDMS. In doing so, we can place reasonable bounds on the types of chemical events that can occur as well as their intercorrelations. Our approach combines ensembles of quantum-based molecular dynamics (QMD) simulations to generate statistics for radiation-induced reaction cascades with an event-based conditional probability and correlation analysis to uncover causal connections between experimental observables. In this context, we test a long-standing set of reaction schemes for crosslinking in irradiated PDMS that link small molecule off-gassing products with formation of specific crosslinking motifs. The effects of water as a commonly unavoidable experimental contaminant are also assessed.The established reaction schemes for crosslinking and off-gassing chemistry in irradiated PDMS date to Charlesby's experiments from the 1950's and are based on highly integrated data. These schemes respectively connect the evolution of hydrogen (H2), methane (CH4), and ethane (C2H6) with the formation of silethylene (Si–C–C–Si), silmethylene (Si–C–Si), and silicon–silicon (Si–Si) crosslinks. Our independent analysis of this chemistry through QMD simulations suggests that these reaction schemes are qualitatively reasonable, but lack strong statistically significant connections under a broad set of conditions that would enable making quantitative connections between off-gassing and crosslinking without careful consideration. Conditional probability analysis shows that many Si–C–C–Si and Si–C–Si crosslinks are connected to formation of H2 and CH4, but the reverse is not necessarily true. Large quantities of these gases are produced without any direct connection to these specific crosslinks. The relationship between Si–Si linking and C2H6 production is found to be statistically insignificant under all conditions considered and yields much smaller populations compared to the other crosslink and gas types.
Water is shown to alter relative and absolute product yields for crosslinks and gases, with the results being consistent with the spread in available experiments. In particular, water suppresses the formation of Si–C–C–Si and Si–C–Si crosslinks by up to a factor of three, while it has a largely negligible influence on the production rate of H2 and CH4 gases. No significant differences were found between wet and dry environments for the populations of Si–Si crosslinks and C2H6 gas.
Application of our analysis framework to our QMD data uncovers a strong (but nonideal) quantitative connection between exceptionally hard-to-measure scission events and the formation of silanol (Si–OH) groups. These connections have long been assumed and even exploited as an indirect measure for chain scissioning in experimental diagnostics. We find that under perfectly desiccated conditions, every silanol formed is connected to scission of the main polysiloxane chain. Water has a noticeable effect in opening alternative reaction pathways to silanol formation that are not causally linked to scission. We find that water does not appreciably alter the number of chain scissions relative to dry conditions, but water does lead to a nearly four-fold increase in the production of silanols. Even under perfectly desiccated conditions, more scissions occur than are accounted for in the silanol populations. These results imply that one cannot count silanols as a means to directly count the number chain scission events, but the statistically significant correlations identified here indicate that a regression model trained on QMD data could offer a route to systematically correct these underestimates.
Implications of our efforts inform confidence in the underlying assumptions used to interpret PDMS radiolysis experiments. In particular, skewness in conditional probability measures cast doubt on using comparatively easy-to-measure small molecule off-gassing products as a quantitatively accurate proxy for hard-to-measure crosslink populations. It also suggests that significant branches are missing in the proposed reaction schemes that would provide other routes to small molecule gases.
The main practical benefit of this analysis approach is that one can independently inform confidence in connections between experimental observables without the burden of fully elucidating entire reaction networks. While the present example considers well-studied PDMS chemistry, our approach is general. Given a suitable initial-boundary value problem for QMD simulations, it can be applied to test any proposed reaction scheme. Our analysis method could thus be applied to any number of reactive degradation processes, including other radiation damage studies where the connection between easy- and hard-to-quantify observables is difficult to determine from experiments alone.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. Released under document number LLNL-JRNL-829305.Notes and references
- I. R. Williams, M. B. Mayor and J. P. Collier, Clin. Orthop. Relat. Res., 1998, 356, 170–180 CrossRef PubMed.
- A. S. Palsule, S. J. Clarson and C. W. Widenhouse, J. Inorg. Organomet. Polym. Mater., 2008, 18, 207–221 CrossRef CAS.
- B. Arkles, CHEMTECH, 1983, 13, 542–555 CAS.
- S. J. Harley, E. A. Glascoe and R. S. Maxwell, J. Phys. Chem. B, 2012, 116, 14183–14190 CrossRef CAS PubMed.
- Y. Sun, S. J. Harley and E. A. Glascoe, ChemPhysChem, 2015, 16, 3072–3083 CrossRef CAS PubMed.
- H. N. Sharma, L. N. Dinh, J. H. Leckey, R. S. Maxwell and W. McLean, Ind. Eng. Chem. Res., 2020, 59, 19510–19521 CrossRef CAS.
- P.-C. Wang, N. Yang, D. Liu, Z.-M. Qin, Y. An and H.-B. Chen, Mater. Des., 2020, 195, 108998 CrossRef CAS.
- L. N. Dinh, B. P. Mayer, A. Maiti, S. C. Chinn and R. S. Maxwell, J. Appl. Phys., 2011, 109, 094905 CrossRef.
- A. Maiti, T. Weisgraber, L. N. Dinh, R. H. Gee, T. Wilson, S. Chinn and R. S. Maxwell, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 031802 CrossRef CAS PubMed.
- M. P. Kroonblawd, N. Goldman and J. P. Lewicki, J. Phys. Chem. B, 2018, 122, 12201–12210 CrossRef CAS PubMed.
- M. P. Kroonblawd, N. Goldman, A. Maiti and J. P. Lewicki, J. Chem. Theory Comput., 2021, 17, 463–473 CrossRef CAS PubMed.
- Q. Liu, W. Huang, B. Liu, P.-C. Wang and H.-B. Chen, ACS Appl. Mater. Interfaces, 2021, 13, 41287–41302 CrossRef PubMed.
- E. F. Griessbach and R. Lehmann, Chemosphere, 1999, 38, 1461–1468 CrossRef CAS PubMed.
- D. Graiver, K. W. Farminer and R. Narayan, J. Polym. Environ., 2003, 11, 129–136 CrossRef CAS.
- C. Rücker and K. Kümmerer, Chem. Rev., 2015, 115, 466–524 CrossRef PubMed.
- A. Labouriau, C. Cady, J. Gill, D. Taylor, A. Zocco, J. Stull, K. Henderson and D. Wrobleski, Polym. Degrad. Stab., 2015, 117, 75–83 CrossRef CAS.
- M. P. Kroonblawd, N. Goldman and J. P. Lewicki, J. Phys. Chem. B, 2019, 123, 7926–7935 CrossRef CAS PubMed.
- S. D. Bruck and E. P. Mueller, J. Biomed. Mater. Res. Appl. Biomater, 1988, 22, 133–144 CrossRef CAS PubMed.
- J. C. Almeida, J. Lancastre, M. H. V. Fernandes, F. M. A. Margaça, L. Ferreira and I. M. M. Salvado, Mater. Sci. Eng., C, 2015, 48, 354–358 CrossRef CAS PubMed.
- A. Charlesby and F. A. Freeth, Proc. R. Soc. Lond. A, 1955, 230, 120–135 CAS.
- A. A. Miller, J. Am. Chem. Soc., 1960, 82, 3519–3523 CrossRef CAS.
- H. A. Dewhurst and L. E. S. Pierre, J. Phys. Chem., 1960, 64, 1063–1065 CrossRef CAS.
- D. J. Hill, C. M. Preston and A. K. Whittaker, Polymer, 2002, 43, 1051–1059 CrossRef CAS.
- A. M. Bueche, J. Polym. Sci., 1956, 19, 297–306 CrossRef CAS.
- D. R. Squire and D. T. Turner, Macromolecules, 1972, 5, 401–404 CrossRef CAS.
- G. B. Tanny and L. E. S. Pierre, Int. J. Polym. Mater., 1972, 1, 279–293 CrossRef.
- A. V. Tobolsky, Silicon in organic, organometallic, and polymer chemistry, Wiley, New York, USA, 1960 Search PubMed.
- J. N. Rodriguez, C. T. Alviso, C. A. Fox, R. S. Maxwell and J. P. Lewicki, Macromolecules, 2018, 51, 1992–2001 CrossRef CAS.
- E. A. Nikitina, V. D. Khavryutchenko, E. F. Sheka, H. Barthel and J. Weis, J. Phys. Chem. A, 1999, 103, 11355–11365 CrossRef CAS.
- G. V. Gibbs, D. Jayatilaka, M. A. Spackman, D. F. Cox and K. M. Rosso, J. Phys. Chem. A, 2006, 110, 12678–12683 CrossRef CAS PubMed.
- E. M. Lupton, F. Achenbach, J. Weis, C. Bräuchle and I. Frank, J. Phys. Chem. B, 2006, 110, 14557–14563 CrossRef CAS PubMed.
- E. M. Lupton, F. Achenbach, J. Weis, C. Bräuchle and I. Frank, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 125420 CrossRef.
- S. Nangia and B. J. Garrison, J. Phys. Chem. A, 2008, 112, 2027–2033 CrossRef CAS PubMed.
- E. M. Lupton, F. Achenbach, J. Weis, C. Bräuchle and I. Frank, ChemPhysChem, 2009, 10, 119–123 CrossRef CAS PubMed.
- J. M. Rimsza, J. Yeon, A. C. T. van Duin and J. Du, J. Phys. Chem. C, 2016, 120, 24803–24816 CrossRef CAS.
- K. Nordlund, S. J. Zinkle, A. E. Sand, F. Granberg, R. S. Averback, R. E. Stoller, T. Suzudo, L. Malerba, F. Banhart, W. J. Weber, F. Willaime, S. L. Dudarev and D. Simeone, J. Nucl. Mater., 2018, 512, 450–479 CrossRef CAS.
- F. Saiz and M. Gamero-Castaño, AIP Adv., 2016, 6, 065319 CrossRef.
- T. M. Alam, Radiat. Phys. Chem., 2001, 62, 145–152 CrossRef CAS.
- M. Patel, P. Morrell, J. Cunningham, N. Khan, R. S. Maxwell and S. C. Chinn, Polym. Degrad. Stab., 2008, 93, 513–519 CrossRef CAS.
- M. P. Kroonblawd, F. Pietrucci, A. M. Saitta and N. Goldman, J. Chem. Theory Comput., 2018, 14, 2207–2218 CrossRef CAS PubMed.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268 CrossRef CAS.
- P. Koskinen and V. Mäkinen, Comput. Mater. Sci., 2009, 47, 237–253 CrossRef CAS.
- B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678–5684 CrossRef CAS PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- J. C. Slater and G. F. Koster, Phys. Rev., 1954, 94, 1498–1524 CrossRef CAS.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- N. D. Mermin, Phys. Rev., 1965, 137, A1441–A1443 CrossRef.
- A. M. N. Niklasson, C. J. Tymczak and M. Challacombe, Phys. Rev. Lett., 2006, 97, 123001 CrossRef PubMed.
- A. M. N. Niklasson, Phys. Rev. Lett., 2008, 100, 123004 CrossRef PubMed.
- A. M. N. Niklasson, P. Steneteg, A. Odell, N. Bock, M. Challacombe, C. J. Tymczak, E. Holmström, G. Zheng and V. Weber, J. Chem. Phys., 2009, 130, 214109 CrossRef PubMed.
- G. Zheng, A. M. N. Niklasson and M. Karplus, J. Chem. Phys., 2011, 135, 044122 CrossRef PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- J. Lehtola, M. Hakala, J. Vaara and K. Hämäläinen, Phys. Chem. Chem. Phys., 2011, 13, 5630–5641 RSC.
- M. P. Kroonblawd and T. D. Sewell, J. Phys. Chem. C, 2016, 120, 17214–17223 CrossRef CAS.
- M. P. Kroonblawd, B. W. Hamilton and A. Strachan, J. Phys. Chem. C, 2021, 125, 20570–20582 CrossRef CAS.
- E. Chen, Q. Yang, V. Dufour-Décieux, C. A. Sing-Long, R. Freitas and E. J. Reed, J. Phys. Chem. A, 2019, 123, 1874–1881 CrossRef CAS PubMed.
- B. M. Rice, W. D. Mattson, J. P. Larentzos and E. F. C. Byrd, J. Chem. Phys., 2020, 153, 064102 CrossRef CAS PubMed.
- M. Hutchings, J. Liu, Y. Qiu, C. Song and L.-P. Wang, J. Chem. Theory Comput., 2020, 16, 1606–1617 CrossRef CAS PubMed.
- M. N. Sakano, A. Hamed, E. M. Kober, N. Grilli, B. W. Hamilton, M. M. Islam, M. Koslowski and A. Strachan, J. Phys. Chem. A, 2020, 124, 9141–9155 CrossRef CAS PubMed.
- F. Pietrucci and W. Andreoni, Phys. Rev. Lett., 2011, 107, 085504 CrossRef PubMed.
- A. Stukowski, Model. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöss, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- G. J. Martyna and M. E. Tuckerman, J. Chem. Phys., 1999, 110, 2810–2821 CrossRef CAS.
- L. N. Pankratova, E. V. Saenko, V. L. Bugaenko and V. V. Makhlyarchuk, Mendeleev Commun., 2011, 21, 157–159 CrossRef CAS.
- M. Ormerod and A. Charlesby, Polymer, 1963, 4, 459–470 CrossRef CAS.
- H. Menhofer and H. Heusinger, Int. J. Radiat. Appl. Instrum. C, 1987, 29, 243–251 CAS.
- J. F. Zack, E. L. Warrick and G. Knoll, J. Chem. Eng. Data, 1961, 6, 279–281 CrossRef CAS.
- L. E. St. Pierre, H. A. Dewhurst and A. M. Bueche, J. Polym. Sci., 1959, 36, 105–111 CrossRef CAS.
- E. L. Warrick, Ind. Eng. Chem., 1955, 47, 2388–2393 CrossRef CAS.
- D. J. Hill, C. M. Preston, D. J. Salisbury and A. K. Whittaker, Radiat. Phys. Chem., 2001, 62, 11–17 CrossRef CAS.
- A. Charlesby, S. H. Pinner and F. P. Bowden, Proc. R. Soc. Lond. A, 1959, 249, 367–386 CAS.
- A. Maiti, W. Small, M. P. Kroonblawd, J. P. Lewicki, N. Goldman, T. S. Wilson and A. P. Saab, J. Phys. Chem. B, 2021, 125, 10047–10057 CrossRef CAS PubMed.
- A. A. Miller, J. Am. Chem. Soc., 1961, 83, 31–36 CrossRef CAS.
- L. Peng, W. Qisui, L. Xi and Z. Chaocan, Colloids Surf., A, 2009, 334, 112–115 CrossRef.
- M. Praeger, I. L. Hosier, A. S. Vaughan and S. G. Swingler, 2015 IEEE Electrical Insulation Conference (EIC), 2015, pp. 201–204 Search PubMed.
- F. Saiz and N. Quirke, Phys. Chem. Chem. Phys., 2018, 20, 27528–27538 RSC.
| This journal is © the Owner Societies 2022 |