Ultralow work function of the electride Sr₃CrN₃

Abstract

Electrides have valence electrons that occupy free space in the crystal structure, making them easier to extract. This feature can be used in catalysis for important reactions that usually require a high-temperature and high-pressure environments, such as ammonia synthesis. In this paper, we use density functional theory to investigate the behaviour of interstitial electrons of the 1-dimensional electride Sr₃CrN₃. We find that the bulk excess electron density persists on introduction of surface terminations, that the crystal termination perpendicular to the 1D free-electron channel is highly stable and we confirm an extremely low work function with hybrid functional methods. Our results indicate that Sr₃CrN₃ is a potentially important novel catalyst, with accessible, directional and extractable free electron density.

---

Introduction

Modern society is enabled by chemical industries. For example, it is estimated that current crop production could only sustain half of the global population without artificial fertilisers.¹ However, this manufacture alone (the Haber–Bosch process) is estimated to consume up to 2% of the global energy supply.² As a result, the identification of new catalysts that can improve the efficiency of chemical processes has enormous potential to improve quality of life and mitigate climate change.

Independent electrons have long been sought as activating species for catalysis in chemical industries. Being not bound to any nuclei, such electrons would extract easily, i.e. have a low work function and diffuse easily i.e. have a high conductivity.³ In solution, they have been studied for over a century,^4,5 but attempts to crystallise them to solids were met with mixed success until the first single crystal was reported in 1982.⁶ Even still, the crown ether complex in question was highly unstable at room temperature, even in inert atmosphere.⁷ In 2003, mayenite (Ca₁₂Al₁₄O₃₂) was reported as the first wholly inorganic electride and it was found to be stable at ambient conditions.⁸ Since then, so called inorganic electrides that have valence electron density located in the interstitial space of the crystal structure have attracted increasing attention.^9–14

Electrides can be considered as 0-dimensional (0D), 1-dimensional (1D) and 2-dimensional (2D), according to the degree of freedom of the anionic electron in the crystal lattice. For example, Mayenite (Ca₁₂Al₁₄O₃₂)⁸ can be considered 0D because the excess electrons exists in pores, Y₅Si₃¹⁵ can be considered 1D¹⁶ because they are in a channel and Ca₂N can be considered 2D because they are in a plane.¹⁷ The excess electron density for each of these materials has been observed in experiment not just predicted in theory; see ref. 18–20 respectively.

The lower the dimensionality of the electrides, the more stable they are expected to be because the crystal structure helps shield the anionic electronic density from electrophilic attack. On the other hand, access to the excess electron density is relevant to catalytic performance. As a result, the 1D electrides may represent an ideal compromise between available electron density and stability.¹⁶ Indeed, to date, the only known water stable electride is the 1D Y₅Si₃.²¹ Yet still, Ru-loaded Y₅Si₃ has shown an obvious catalytic effect on ammonia synthesis, which is attributed to the strong electron donating ability of Y₅Si₃ to the Ru metal.

Recently Chanhom et al. confirmed Sr₃CrN₃ as a new one-dimensional electride.²² The excess electron density originates from the Cr and aggregates in a channel through the crystal, giving an overall charge assignment of Sr²⁺₃Cr⁴⁺N³⁻₃:e⁻.²³ Earlier theoretical work has placed the bulk material on the convex hull for the Sr–Cr–N phase space, meaning that the material is thermodynamically stable, and confirmed the delocalised electron density within the 1-dimensional channel up to GW level of theory.²⁴ To the knowledge of the authors, Sr₃CrN₃ is the only experimentally confirmed electride that has a transition metal component with partially filled 3d-shells. This is unusual as the redox-active chromium could accept the excess electron with a decrease in the formal oxidation state from +4 to +3.²³ While this has been confirmed to not occur for the bulk material, the extent to which the excess electron density is ro-bust to structural modification, especially the breaking of 3D periodicity, has yet to be demonstrated.

We investigate the non-polar surface terminations of Sr₃CrN₃ based on density functional theory (DFT). We find that the interstitial electron density persists, even upon introduction of a surface termination. We also find that the surface perpendicular to the one-dimensional channel of Sr₃CrN₃ is the most stable despite exposing the excess electron density to the external system. Finally, we find the work function of this surface to be extremely low, which means that the electrons should be able to transfer to almost any reactant or intermediary species, such as Ru. Overall, Sr₃CrN₃ is an exciting new material, of interest for fundamental and applied reasons, and deserving of further research.

Methods

We used density functional theory as implemented in the Vienna Ab Initio Simulation Package (VASP).^25,26 For the exchange–correlational functional, we employ a mix of Generalized Gradient Approximation (GGA) within the Perdew–Burke–Enzerhof (PBE) formulation of the exchange–correlation functional.²⁷ We use the Projector Augmented Wave (PAW) method for modelling core electrons with an energy cut-off of 520 eV;^28,29 at least 1.3 times higher than the recommended cut-off. All computations are performed with spin polarization on and with magnetic ions in a high-spin ferromagnetic initialization (the system can relax to a low spin state during the DFT relaxation). We use a k-point mesh of 6 × 6 × 9, with the Monkhorst–Pack method.³⁰ The energy difference for ionic convergence is set to 2 × 10⁻⁵ eV.

To calculate the surface energies and work function we create slab models. The method of Hinuma et al. is used to expand the cell and obtain a non-polar supercell of the crystal, with a vacuum region of around 15 Å between faces.³¹ This way we obtain Sr₃CrN₃(001), (100), (101) and (110) as slab models that are non polar.

Surface energy, γ, is defined as the difference between surface free energy and bulk free energy.^32–34 The surface energy of each surface is calculated according to eqn (1),³⁵ in which, E_total is the total energy of the constructed slab, E_bulk is the energy the bulk material unit cell, n is the number of formula units contained in the slab model and A is the surface area of the slab. The factor of 2 accounts for the surfaces at either end of one slab model calculation.

γ = (E_total − nE_bulk)/2A (1)

To obtain an accurate work function (ϕ) we use the hybrid functional HSE06^36–39 with a shielding distance of 0.207 Å⁻¹ and 25% Hartree–Fock exchange. We use eqn (2) to calculate the work function,^40,41 in which ΔV is the difference in electrostatic potential between the vacuum and the macroscopic average electrostatic potential of the material,⁴¹ and E_F is the Fermi level calculated from the bulk, periodic material, also at HSE06 level of theory.

ϕ = ΔV − E_F (2)

Results and discussion

The lattice constants obtained from ionic relaxation of the bulk material are shown in Table 1, which are within 3% error of the experimentally reported case.⁴² The structure is composed of trigonal units of CrN₃ that are planar in the a–b axis and the Sr ions form distorted trigonal bipyramidal coordination environments with N anions. A hypothetical sixth coordination towards the anionic electrons in the 1 dimensional channels of the y-axis can also be inferred for Sr, indeed it has been shown that these cations are much closer together spatially than would be stable in the absence of interstitial electrons.²⁴ The crystal structure belongs to the P6₃/m space group (symmetry number 176), and is shown in Fig. 1.

Table 1 The lattice constants of Sr₃CrN₃ from DFT ionic relaxation and the values reported from experiment in the literature⁴²

Sr3CrN3	a	b	c	α	β	γ
DFT	7.839	7.839	5.243	90	90	120
Experiment	7.724	7.724	5.249	90	90	120

---

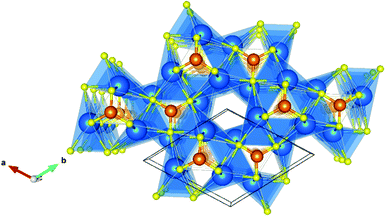Fig. 1 Sr₃CrN₃ crystal structure with spheres representing atoms of Sr (blue), Cr (orange) and N (yellow). The unit cell is shown with a black box and the 1D channel is at the centre of the image.

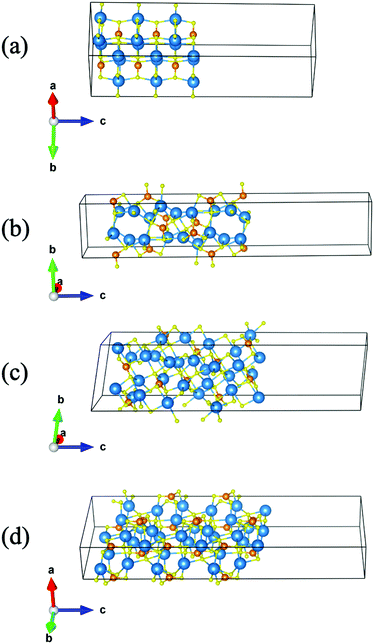
The (001), (100), (101) and (110) slab models of Sr₃CrN₃ are shown in Fig. 2. The chosen terminations of Sr₃CrN₃ belong to the Tasker type II interface classification,⁴³ meaning that the slab is non-polar due to the symmetrical sequence of atomic charges at the surface. As a result, a periodic surface will not affect the ions inside the crystal, and thereby are more likely to be stable and preserve the internal excess electron behaviour.

Fig. 2 (a)–(d) display the constructed (001), (100), (101) and (110) surfaces of Sr₃CrN₃ respectively. The Sr atoms are blue, Cr atoms are orange and N atoms are yellow. The unit cell is outlined, showing the relative size of the vacuum layer.

The surface energy of the different crystal terminations, calculated according to eqn (1),³⁵ are shown in Table 2. We find that Sr₃CrN₃(001) has the smallest surface energy and is therefore the most stable. In fact, there is a large discrepancy between the surface energies, showing the Sr₃CrN₃(001) surface is highly preferred in spite of the cleavage plane bisecting the 1D electron channel. Such a relatively low surface energy is likely to have a strong impact on crystal growth and nanoparticle morphology. Conversely the (100) termination that would cleave the structure along the anionic electron channel is much higher in energy and is by far the least stable.

Table 2 The calculated surface energy of different crystal planes of Sr₃CrN₃

Sr3CrN3 termination	Surface energy (J m^−2)
001	0.67
100	2.40
101	0.93
110	1.11

---

The origin of the particularly low 0.67 J m⁻² surface energy for the (001) surface likely arises from the trigonal planar CrN₃ units that uniformly align in the a–b plane. This ubiquitous structural unit lends itself to a natural (001) termination that can preserve the internal physics of the material. By comparison, the lowest surface energy value calculated for silicon on the Materials Project is 1.28 J m⁻², more than twice our lowest calculated surface energy of 0.67 J m⁻².⁴⁴ On the other hand, the 2-dimensional van der Waals material MoS₂ has an estimated surface energy for cleavage parallel to the bonded plane of 0. 15–0.22 J m⁻².⁴⁵ These values suggest that Sr₃CrN₃ is closer in nature to 2-dimensional materials in the c-axis, than to bulk, 3-dimensional bonded materials.

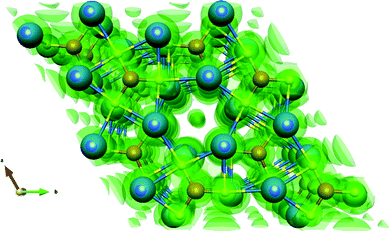
Fig. 3 shows the valence charge density of the Sr₃CrN₃(001) slab model from the converged calculation. It can be seen that there are still excess electrons in the closed channel, indicating that the defining feature of electrides persists even in the slab model. While the free electron density was predicted and observed experimentally for this material in bulk, this is the first time it has been observed to be robust with respect to such dramatic alteration to the crystal structure.

Fig. 3 Valence electron density of the Sr₃CrN₃(001) slab model shown as a transparent green isosurface. The spheres in the centre of the image evince the existence of excess electrons in the 1D channel even in the presence of a perpendicular crystal termination and vacuum region. Again, Sr are blue, Cr orange and N yellow.

We continue to analyse the most stable Sr₃CrN₃(001) surface by calculating the work function. Catalysts usually work by transferring electron density to chemical bonds in reactants from higher energy states. While catalytic performance depends on a range of factors,⁴⁶ it has been shown empirically that the work function of the catalyst relates directly to activity,⁴⁷ and has been used elsewhere in the literature as an indicator of likely catalytic performance.⁴⁸

ϕ is usually estimated by the energy difference between the Fermi level (E_F) and the vacuum level (E_vac).⁴⁹Fig. 4 is the calculated electrostatic potential using the slab model of Sr₃CrN₃ (001). The average electrostatic potential in the empty region corresponds with the vacuum electrostatic potential, and the difference between this and the average electrostatic potential gives (ΔV) for eqn (2). The work function of Sr₃CrN₃(001) is therefore calculated to be 2.14 eV.

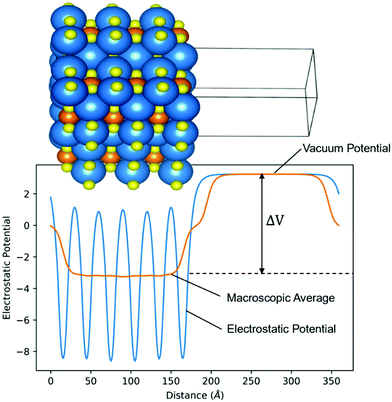Fig. 4 Slab model electrostatic potential diagram. The difference (ΔV) between the average electrostatic potential and the vacuum potential is used to calculate the work function from eqn (2).

We compare the work function of Sr₃CrN₃(001) with the work function of other electrides from various references in Table 3. We find that even among electrides, which are known for their low work function, Sr₃CrN₃(001) is lower. By comparison, the same theoretical method previously applied to chalcogenides finds typical values of twice or even three times the amount reported here.⁵⁰ Finally, we also compared this value with the work functions of elements found in experiment.⁵¹ The Sr₃CrN₃(001) work function is smaller than that found for all elements except for that of cesium, which is reported to be 1.95 eV from photoelectric effect experiments. These results highlight a relative ease of electron extraction for Sr₃CrN₃ compared to other materials.

Table 3 Comparison of the work function of Sr₃CrN₃ (001) and those of other electride materials in descending order

Compound	Work function (eV)
Sr3CrN3	2.14
Ca12Al14O32	2.4^49
Ca2N	2.6^52
Ca5Pb3	2.6^53
Sr5P3	2.8^54
Y5Si3	3.5^21

---

We believe that the low work function of this material originates from 2 sources. Firstly, the electrons already being detached from their parent atom mean that less energy is required to remove them from the host material. This is a property that will be present to some extent for all electrides.³

Secondly, the one dimensional channel that permeates the material perpendicular to the lowest-energy termination will raise the electrostatic potential uniformly, and thereby affect the macroscopic average strongly in the relevant direction. The anionic electrons being adjacent to one another should also facilitate removal of electrons assuming they can delocalise over empty anion sites.

In summary, we have obtained and analysed the non-polar (001), (100), (101) and (110) crystal surfaces of Sr₃CrN₃. The (001) surface that bisects the 1D electron density in the crystal structure is highly stable, and does not destroy the anionic electron density of the electride. This result suggests that the unique properties of the bulk electride will be present even in (nano)particulate form, indeed there appears to be a strong thermodynamic driving force preserving the anionic electron behaviour, as evidenced by the much higher (100) termination surface energy. Using the hybrid functional HSE06 method, it is determined that the (001) crystal termination has a very small work function of 2.14 eV, which means that the excess electron density of Sr₃CrN₃ should able to activate the chemical bonds of external reactants. What's more, the uni-directionality of the electron density allows for the possibility of additional control in deploying this material as a catalyst.

Future study of this material could follow the development of other electrides currently being deployed as catalysts elsewhere,⁹ such as investigating the intercalation of extrinsic species in to the anionic electron cavity,³ or decorating the material with Ru for reaction.²¹ DFT studies can contribute with phonon calculations to predict the temperature up to which Sr₃CrN₃ is stable or screening molecular species to determine stability in the presence of various common environments used for chemical reactions. Beyond catalysis, electrides are also being investigated as electron emitters,⁵⁵ superconductors,⁵⁶ battery anodes,⁵⁷ lamps,⁵⁸ and even radio-active waste storage,⁵⁹ which all offer alternative avenues of research.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

L. A. B acknowledges support by the Shanghai Municipal Science and Technology Commission Program, 19010500500, and the Natural National Science Foundation of China (NSFC), 51950410585.

References

1. J. W. Erisman, M. A. Sutton, J. Galloway, Z. Klimont and W. Winiwarter, Nat. Geosci., 2008, 1, 636–639.
2. V. Smil, Enriching the Earth: Fritz Haber, Carl Bosch, and the Transformation of World Food Production, MIT Press, 2001.
3. C. Liu, S. A. Nikolaev, W. Ren and L. A. Burton, J. Mater. Chem. C, 2020, 8, 10551–10567.
4. C. A. Kraus, J. Am. Chem. Soc., 1907, 29, 1557–1571.
5. J. Jortner and N. R. Kestner, Electrons in Fluids: The Nature of Metal—Ammonia Solutions, Springer-Verlag, Berlin, Heidelberg, 1973.
6. D. Issa and J. L. Dye, J. Am. Chem. Soc., 1982, 104, 3781–3782.
7. J. L. Dye, Science, 1990, 247, 663–668.
8. S. Matsuishi, et al. , Science, 2003, 301, 626–629.
9. M. Kitano, Y. Inoue, Y. Yamazaki, F. Hayashi, S. Kanbara, S. Matsuishi, T. Yokoyama, S. W. Kim, M. Hara and H. Hosono, Nat. Chem., 2012, 4, 934–940.
10. W. Zou, K. Khan, X. Zhao, C. Zhu, J. Huang, J. Li, Y. Yang and W. Song, Mater. Res. Express, 2017, 4, 036408.
11. J. L. Dye, Acc. Chem. Res., 2009, 42, 1564–1572.
12. J. L. Dye, Science, 2003, 626–629.
13. K. Karim, T. A. Khan, E. Sayed, M. Naseer, J. Li, A. Israa, B. Luigi, Y. Ashish, R. Ur and K. Usman, RSC Adv., 2018, 8, 24276–24285.
14. K. Khan, A. K. Tareen, J. Li, U. Khan and A. Nairan, et al. , Dalton Trans., 2018, 47, 13498–13506.
15. Q. Zheng, T. Feng, J. A. Hachtel, R. Ishikawa, Y. Cheng, L. Daemen, J. Xing, J. C. Idrobo, J. Yan, N. Shibata, Y. Ikuhara, B. C. Sales, S. T. Pantelides and M. Chi, Sci. Adv., 2021, 7, eabe6819.
16. Y. Zhang, Z. Xiao, T. Kamiya and H. Hosono, J. Phys. Chem. Lett., 2015, 6, 4966–4971.
17. K. Lee, S. W. Kim, Y. Toda, S. Matsuishi and H. Hosono, Nature, 2013, 494, 336–340.
18. L. Palacios, A. Cabeza, S. Bruque, S. García-Granda and M. A. G. Aranda, Inorg. Chem., 2008, 47, 2661–2667.
19. Q. Zheng, T. Feng, J. A. Hachtel, R. Ishikawa, Y. Cheng, L. Daemen, J. Xing, J. C. Idrobo, J. Yan, N. Shibata, Y. Ikuhara, B. C. Sales, S. T. Pantelides and M. Chi, Sci. Adv., 2021, 7, eabe6819.
20. J. S. Oh, C.-J. Kang, Y. J. Kim, S. Sinn, M. Han, Y. J. Chang, B.-G. Park, S. W. Kim, B. I. Min, H.-D. Kim and T. W. Noh, J. Am. Chem. Soc., 2016, 138, 2496–2499.
21. Y. Lu, J. Li, T. Tada, Y. Toda, S. Ueda, T. Yokoyama, M. Kitano and H. Hosono, J. Am. Chem. Soc., 2016, 138, 3970–3973.
22. P. Chanhom, K. E. Fritz, L. A. Burton, J. Kloppenburg, Y. Filinchuk, A. Senyshyn, M. Wang, Z. Feng, N. Insin, J. Suntivich and G. Hautier, J. Am. Chem. Soc., 2019, 141, 10595–10598.
23. Y. Ding, Y. Kumagai, F. Oba and L. A. Burton, J. Phys. Chem. Lett., 2020, 11, 8264–8267.
24. L. A. Burton, F. Ricci, W. Chen, G.-M. Rignanese and G. Hautier, Chem. Mater., 2018, 30, 7521–7526.
25. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
26. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
28. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
29. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
30. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
31. Y. Hinuma, Y. Kumagai, F. Oba and I. Tanaka, Comput. Mater. Sci., 2016, 113, 221–230.
32. Q. Jiang, H. X. Shi and M. Zhao, Acta Mater., 1999, 47, 2109–2112.
33. Q. Jiang, D. S. Zhao and M. Zhao, Acta Mater., 2001, 49, 3143–3147.
34. F. P. Buff, J. Chem. Phys., 1951, 19, 1591–1594.
35. X. Tian, T. Wang, L. Fan, Y. Wang, H. Lu and Y. Mu, Appl. Surf. Sci., 2018, 427, 357–362.
36. J. Heyd and G. E. Scuseria, J. Chem. Phys., 2004, 121, 1187–1192.
37. J. Heyd and G. E. Scuseria, J. Chem. Phys., 2004, 120, 7274–7280.
38. J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, J. Chem. Phys., 2005, 123, 174101.
39. J. E. Peralta, J. Heyd, G. E. Scuseria and R. L. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 073101.
40. J. D. Jackson, Classical Electrodynamics, John Wiley, 1975.
41. K. T. Butler, J. Buckeridge, C. R. A. Catlow and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 231–236.
42. M. G. Barker, M. J. Begley, P. P. Edwards, D. H. Gregory and S. E. Smith, ChemInform, 1996, 27, 1–5.
43. P. W. Tasker, J. Phys. C: Solid State Phys., 1979, 12, 4977–4984.
44. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
45. Y. Guo, Z. Wang, L. Zhang, X. Shen and F. Liu, Phys. Chem. Chem. Phys., 2016, 18, 14449–14453.
46. E. Roduner, Chem. Soc. Rev., 2014, 43, 8226–8239.
47. C. G. Vayenas, S. Bebelis and S. Ladas, Nature, 1990, 343, 625–627.
48. F. Calle-Vallejo, M. T. M. Koper and A. S. Bandarenka, Chem. Soc. Rev., 2013, 42, 5210–5230.
49. Y. Toda, H. Yanagi, E. Ikenaga, J. J. Kim, M. Kobata, S. Ueda, T. Kamiya, M. Hirano, K. Kobayashi and H. Hosono, Adv. Mater., 2007, 19, 3564–3569.
50. L. A. Burton, Y. Kumagai, A. Walsh and F. Oba, J. Mater. Chem. A, 2017, 5, 9132–9140.
51. W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC Press, 2016.
52. M. M. Menamparambath, J.-H. Park, H.-S. Yoo, S. P. Patole, J.-B. Yoo, S. W. Kim and S. Baik, Nanoscale, 2014, 6, 8844–8851.
53. K. Li, Y. Gong, J. Wang and H. Hosono, J. Am. Chem. Soc., 2021, 143, 8821–8828.
54. J. Wang, K. Hanzawa, H. Hiramatsu, J. Kim, N. Umezawa, K. Iwanaka, T. Tada and H. Hosono, J. Am. Chem. Soc., 2017, 139, 15668–15680.
55. R. H. Huang and J. L. Dye, Chem. Phys. Lett., 1990, 166, 133–136.
56. H. Hosono, S.-W. Kim, S. Matsuishi, S. Tanaka, A. Miyake, T. Kagayama and K. Shimizu, Philos. Trans. R. Soc., A, 2015, 373, 20140450.
57. D. L. Druffel, J. T. Pawlik, J. D. Sundberg, L. M. McRae, M. G. Lanetti and S. C. Warren, J. Phys. Chem. Lett., 2020, 11, 9210–9214.
58. S. Watanabe, T. Watanabe, K. Ito, N. Miyakawa, S. Ito, H. Hosono and S. Mikoshiba, Sci. Technol. Adv. Mater., 2011, 12, 034410.
59. N. Kuganathan, A. Chroneos and R. W. Grimes, Sci. Rep., 2019, 9, 13612.

---