The pH-dependent gating of the human voltage-gated proton channel from computational simulations

Abstract

Gating of the voltage-gated proton channel H_V1 is strongly controlled by pH. There is evidence that this involves the sidechains of titratable amino acids that change their protonation state with changes of the pH. Despite experimental investigations to identify the amino acids involved in pH sensing only few progress has been made, including one histidine at the cytoplasmic side of the channel that is involved in sensing cellular pH. We have used constant pH molecular dynamics simulations in symmetrical and asymmetrical pH conditions across the membrane to investigate the pH- and ΔpH-dependent gating of the human H_V1 channel. Therefore, the pK_a of every titratable amino acids has been assessed in single simulations. Our simulations captured initial conformational changes between a deactivated and an activated state of the channel induced solely by changes of the pH. The pH-dependent gating is accompanied by an outward displacement of the three S4 voltage sensing arginines that moves the second arginine past the hydrophobic gasket (HG) which separates the inner and outer pores of the channel. H_V1 activation, when outer pH increases, involves amino acids at the extracellular entrance of the channel that extend the network of interactions from the external solution down to the HG. Whereas, amino acids at the cytoplasmic entrance of the channel are involved in activation, when inner pH decreases, and in a network of interactions that extend from the cytoplasm up to the HG.

---

Introduction

Voltage-gated proton channels H_V1 are unique ion channels expressed in most eukaryotic species. They play fundamental roles in a pleiora of physiological tasks including charge compensation during the respiratory burst,^1,2 innate immune response,³ human sperm maturation,^4,5 proton extrusion from the cytosol,⁶ malignancy of cancer,^7–10 glucose homeostasis,^11,12 migration of granulocytes,¹³ the calcification of coccolithophores,¹⁴ and pH regulation.^14–16 In all cells, H_V1 channels conduct exclusively protons (H⁺) through the cell membranes. To perform this task, H_V1s adopt (at least) two main configurations. The open configuration conducts protons through the channel, the closed configuration stops any permeation of protons. Their specific function requires that they open and conduct current only under certain conditions, typically when the electrochemical gradient for H⁺ is outwards. In the open state, the single (monomeric) channel allows up to 10⁵ H⁺ to cross the membrane per second. An obvious function of H_V1 is thus acid extrusion. H_V1s are voltage-gated channels, meaning that they open when the membrane potential is depolarized, i.e. when it is made more positive. Unlike other voltage-gated ion channels, such as potassium, sodium and calcium channels, H_V1 has lost the last two S5–S6 of the typical six transmembrane alpha helices (TMH) usually composing the pore region. H_V1 consists of only one pore (S1–S4) that is responsible for both voltage sensing and the conduction of protons.¹⁷ The conduction pathway includes a typical negatively charged aspartate in S1 as proton selectivity filter.^18,19 Three arginines in the S4 proton channel signature motif RxWRxxR are assumed to be responsible for voltage-sensing.^20,21 The three arginines are located along the inner wall, spaced at every third position so that they almost perfectly line the pore. It is generally believed that voltage-sensing results in parts of the protein moving to produce a conduction pathway.^22–24 Rearrangements in the S1²³ and S4 helices were shown to play critical roles in this process.^24–27 Voltage gating in the open state occurs when S4 moves outwards.

Few is known about the mechanism of pH-sensing. H_V1 channels are regulated by pH so that they open, with rare exceptions, to extrude H⁺ from cells. Indirect evidences support a model for ΔpH-dependent gating that involves titratable sites. The Wild-Type (WT) human H_V1 (hH_V1) was shown to exhibit saturation of ΔpH dependence at intracellular pH (pH_i) or extracellular pH (pH_o) higher than 8.0,²⁸ which might be expected if the ambient pH is approaching the pK_a of one or more titratable groups. Mutations of several dozen individual titratable residues in a previous work failed to eliminate or even attenuate ΔpH-dependent gating.²⁹ More recently however, replacement of histidine H168 by glutamine in the intracellular S2–S3 loop of human H_V1 diminished pH_i sensitivity.³⁰ Selective impairment in pH_i sensing is consistent with distinct internal and external pH sensors, as opposed to a centrally located sensor that would sense pH on both sides of the membrane. Additional evidence that distinct external and internal sensors exist is that mutation of an unusual tryptophan residue in the hH_V1 pore, Trp207, modifies pH_o sensing without affecting pH_i sensing.²⁸

One of the most distinctive properties of H_V1's gating is its ΔpH-dependence,³¹ where ΔpH represents the pH gradient across the cell membrane (ΔpH = pH_o − pH_i). This property is consistent in all species studied thus far and is essential to H_V1's function.³² The ΔpH regulation of the voltage-dependent activation is known as the “Rule of forty”:^21,31

V_treshold = −40 (pH_o − pH_i) + 20 mV. (1)

According to (1), increasing pH_o or lowering pH_i promotes channel opening by shifting the activation threshold to more negative potentials by 40 mV per unit change in pH. On the contrary, changing ΔpH to values that promote proton influx (by lowering pH_o or increasing pH_i) shifts the voltage dependence of activation to more depolarized potentials, making the channel less likely to open. Low pH_o shifts the voltage-activation curves of H⁺ channels toward positive potentials and slows activation at a given voltage.³³ A common finding in hH_V1 and H_V1 of other organisms is that, regardless of the side at which pH is changed, gating is influenced only by the absolute value of ΔpH, so changing either solution's pH value alters ΔpH. The symmetry involved in this pH gating phenomenology has led to quantitative models in which proton-binding sites with alternating accessibilities exist at both intra- and extracellular sides of the channel.³¹

How H_V1 channels sense the inner and outer pH is so far largely not elucidated. Obtaining information about the pH-dependent activity of a protein from experimental methods is a long and expensive task. For example, potential amino acids (AAs) candidates to the pH-sensing must be tested individually (e.g. by mutating each AA individually) for their effect on H_V1 activity. It is also not possible experimentally to assess the acid–base constants (pK_a) of all putative titratable AA sidechains in one single experiment. During the last few years several computational studies successfully provided details at the molecular level of the pH-dependent mechanism of transmembrane proteins, among them also some proton channels, see e.g. ref. 34–37, by applying the constant pH (CpH) molecular dynamics (MD) technique that offers atomic description of the pH-coupled conformational dynamics of proteins. H_V1's activity depends on the pH and even more on the pH gradient across the membrane (see above). Here, we applied this technique to investigate the atomistic details of hH_V1's response to different pH conditions in explicit solvent and lipid bilayer. Using this approach, the pH-induced conformational change from a deactivated to an activated state of the channel was directly observed and amino acids that play an essential role in H_V1 gating were identified. None of these aspects have been investigated in previous simulations studies of H_V1 channels due to the limitations of conventional MD simulations which assume fixed protonation states. A Table summarizing the effects of the titratable amino acids on H_V1's activity is given in the ESI† (Table S1, ESI†).

Computational methods

System preparation

The first structure of a H_V1 proton channel was determined in 2014 for a mouse H_V1/Ci-VSD/GNC4 chimera;³⁸ denoted mH_V1 hereafter. More recently, the structure of the human proton channel hH_V1 was published.³⁹ Inspection of both structures reveals structural pecularities. In the crystal structure of mH_V1, the TMH S3 is obviously shifted downward by approximately one helical turn. It results in a hydrophobic gasket (HG) that separates the inner and outer vestibules of the channel with F146 (F182 in mH_V1) instead of V177 and V178 (see ref. 40 for a detailed description). A downward shift of helix S2 and upward shift of helix S3 by one helical turn would match the experimental structure with the model⁴¹ and the results of.⁴⁰ The NMR structure of hH_V1 is distorted. It results in S1 being apart from the other transmembrane helices S2 to S4 and a distorted HG. Furthermore, several AA sidechains including the selectivity filter D112, E119, D123, and V109 and F150 (HG), have their sidechain improperly oriented outside the pore in most of the NMR models. The two experimental structures are thus very complex for accurate investigation of hH_V1 at the molecular level.

Our group utilized a “minimal” human H_V1 channel that is fully functional (not published yet). We refer to it as hH_V1m later on. The minimal channel contains essentially the transmembrane domain and lacks most of the N- and C-termini. It starts at the codon for M91 (cytoplasmic part of helix S1), and ends at S224 (cytoplasmic part of S4). In the present work we used a structural model of hH_V1m. The construction of the model followed the protocol described in ref. 42, details are given in the ESI.† A representation of the model is given in Fig. 1.

Fig. 1 Structural model of the hH_V1m proton channel. The three S4 arginines (R1 to R3) are shown as sticks; R2 backbone Cα atom as sphere. Sidechains of the amino acids discussed in the text are also shown as sticks. The hydrophobic gasket (HG: V109, F150, V177 and V178) that separates the inner (below) and outer (above) vestibules of hH_V1 is depicted as yellow surface. In the model, R2 Cα atom lies almost in the HG and the sidechain is orientated towards the outer vestibule.

The initial protonation state of the titratable sidechains was determined using Propka⁴⁴ at the crystallization pH of Ci-VSD (pH = 5.5). Choosing this pH also allows us to compare the results of our simulations to most of the available experimental data. The protein was orientated in the membrane using the PPM Server⁴⁵ and inserted into a preassembled POPC lipid bilayer using Membrane Builder⁴⁶ in CHARMM-GUI.⁴⁷ The resulting number of lipids is 84 for the cytoplasmic leaflet and 81 for the extracellular leaflet. The system was solvated with water layers of 15 Å on both sides of the membrane and 150 mM NaCl. At the end of the procedure, input files were generated for AMBER.

Molecular dynamics simulations

All the molecular dynamics (MD) simulations were done using AMBER 18.⁴⁸ To prepare the system for the constant pH MD (CpHMD) simulations dummy hydrogen atoms were added to the carboxylate groups of the titratable acidic AAs as required for the different pH-conditions simulated (see below), following the documentation of AMBER 18 for constant pH calculations in explicit solvent. AMBER uses the ff10 force field for proteins for constant pH simulations. The lipid14 force field was used for lipids.⁴⁹ The Cheatham–Joung parameters⁵⁰ and the TIP3P model⁵¹ were used for ions and water respectively. The systems were first minimized and equilibrated using the default multi-step protocol of CHARMM-GUI.⁵² During the minimization and equilibration, the protonation state of the titratable sidechains was kept as determined by Propka for pH 5.5. The structure at the end of the equilibration was used for the CpHMD simulations.

Constant pH MD simulations with pH replica exchange (CpHRE MD simulations)

The protonation state distribution of titratable sidechains is affected by the ambient pH. In the CpHMD simulation scheme of AMBER the pH is set as an external parameter and attempts to change the protonation state (PS) of the titratable sidechains are done at regular time intervals to take account of the conformational changes. Between PS changes attempts, conventional molecular dynamics is done to allow the protein structure to adapt to the new PSs. We used explicit solvent and lipid bilayer during the conventional conformational dynamics. For PS changes attempts the water and ions were replaced with a Generalized Born (GB) implicit solvent model.⁵³

The human proton channel hH_V1 opens very slowly, on the order of the second.⁵⁴ Classical MD simulations are usually run for hundreds to thousands nanoseconds (ns) and might not be able to capture the complete transition to an open conformation of the channel. In order to improve the protonation and conformational states sampling, we combined CpHMD with the pH replica exchange (pHRE) protocol as suggested by the authors of AMBER. pHRE MD simulations considerably speed up the conformational changes induced by PS changes. In the pHRE scheme, several copies (replicas) of the same system are simulated each at a different solution pH and the replicas attempt to exchange their solution pH at regular time intervals. This strategy has successfully captured the conformational changes between closed and open states of several membrane channel proteins including the M2 proton channel of influenza virus,^34,35 the NhaA sodium–proton antiporter of E. coli³⁶ or the AcrB transporter of E. coli.³⁷ In ref. 34, the proton-coupled conformational activation of the M2 channel of the influenza virus was observed in reasonable simulation time during CpHRE MD simulations. This would have been inaccessible with conventional MD simulations. In ref. 35, use of this approach in AMBER revealed the conformational switch from the C-terminal closed to the C-terminal open conformers of the M2 channel. The charge of the His tetrad involved in proton conduction was determined in good agreement with the experimental data. And details were gained at the molecular level about the pH-dependent interactions between titratable sidechains relevant for the conduction of protons across the membrane. Our CpHRE MD simulations were done in the NVT ensemble to take profit of the GPU implementation of pmemd.cuda in AMBER 18. The temperature was maintained at 300 K using the Berendsen thermostat.⁵⁵ The van der Waals interactions were smoothly switched to zero between 10 and 12 Å. The particle mesh Ewald method⁵⁶ was used to calculate long-range electrostatics, with a cut-off of 12 Å. The SHAKE algorithm⁵⁷ was used to constrain bonds involving hydrogen atoms and enable a 2 fs time step.

Three simulations were done to represent different pH conditions. Two simulations aimed at representing a pH gradient across the membrane. In these two simulations, since the ambient pH is defined as an external parameter, the titratable sidechains on the one side of the membrane were allowed to change their PS during the PS changes attempts, whereas those on the other side were not and thus conserved their initial PS. In one of the two simulations, only the sidechains of titratable AAs on the extracellular side were allowed to change their PS. This situation is referred to as ΔpH_i=cst. The opposite was applied in the other simulation, ΔpH_o=cst. To differentiate intra- from extracellular AAs we considered the HG that separates the inner and outer vestibules (V109, F150, V177 and V178). According to conventional representations where the intracellular side is depicted below the membrane and the extracellular side above the membrane, we will sometimes refer to intracellular AAs as “below” the HG and to extracellular AAs as “above” the HG. Due to our computational limitations, for the two simulations, the pH-range was 3.5–8.0 with an interval of 0.5 unit of pH resulting in 10 replicas in each simulation. From the ‘reference’ pH 5.5, the solution pH was thus lowered to more acidic (down to 3.5) and increased to more basic (up to 8.0) values, representing positive and negative pH gradients (ΔpH = pH_o − pH_i) across the membrane. Each replica was simulated for 95.8 ns in the ΔpH_i=cst simulation, resulting in an aggregate sampling time of 958.0 ns, and for 97.84 ns in the ΔpH_o=cst simulation, resulting in an aggregate sampling time of 978.4 ns. PS changes were attempted every 0.01 ps and replica exchanges every 0.2 ps. We note here, that in these two simulations, since all the sidechains on one or the other side have a fixed PS, the actual pH on this side of the membrane is not exactly 5.5 but rather represent the pH range around 5.5 at which no AA titrates. A second issue is that AAs which should change their PS in this pH-range, e.g. because of the conformational changes occurring during the conventional MD, cannot. Despite these issues, the results of these two simulations were consistent with those of the third simulation, where all titratable sidechains on both sides of the membrane were allowed to change their PS. We refer to this simulation as pH_sym. Here, a larger pH range (1.0–10.5) was used to get a better estimation of the pK_a of AAs titrating at very low and very high pH, with an interval of 0.5 resulting in 20 replicas. Due to the higher computational cost of this simulation, the replicas were simulated for 50.0 ns each, resulting in an aggregate sampling time of 1 μs. In the three simulations, all the aspartates (Asp), glutamates (Glu), histidines (His) and lysines (Lys) on either side of the membrane (ΔpH_i=cst or ΔpH_o=cst) or on both (pH_sym) were able to titrate. In preliminary simulations we also considered the tyrosines (Tyr). Tyr has a standard pK_a of 10.98, close to the standard pK_a of Lys (10.68⁵⁸). However, all Tyr sidechains remained fully protonated, whereas some of the lysines exhibited highly depressed pK_a values. We thus conserved lysines, but not tyrosines, as titratable AAs later on. Arginines (Arg) are not defined as titratable AA in AMBER. Arg has a pK_a value above 12, so that the sidechain is predominantly, if not always, protonated. A recent study determined the pK_a of Arg to be 13.8 or even higher which would explain why deprotonated arginine sidechains have never been observed in proteins.⁵⁹ Consequently, Tyr and Arg were always protonated in our simulations. Finally, hH_V1 has one cysteine, C107, in the transmembrane domain. C107 lies deep in the membrane with its sidechain oriented towards the lipid bilayer, not accessible to the solvent, and was thus also not considered as a titratable AA.

pK_a calculations

The deprotonated fraction P of each individual titratable amino acid at all pH conditions was calculated during the CpHRE MD simulations and the amino acid-specific microscopic pK_a values were obtained by fitting P to the generalized Hill equation, where n is the Hill coefficient:

Figures

In the figures, the following colouring scheme was adopted: at pH conditions that promote a deactivated channel, results are depicted in grey to green (over blue) at pH conditions that promote an activated channel. The MD trajectories were visualized with VMD.⁶⁰ Structures of hH_V1 were rendered in VMD and post-processed with POV-Ray. Other plots like the RMSDs, probability distributions and so forth were generated with Gnuplot. The final graphics were prepared with GIMP.

Results and discussion

H_V1 channels are generally in a resting state and activate in order to extrude protons from the cell when the pH-gradient across the membrane is positive (pH_o > pH_i). Increasing symmetrical pH across the membrane (when pH_i = pH_o, also denoted pH_i//o) also enhances H_V1 activation.^27,61,62 In our group, preliminary measurements of the conductance of hH_V1m at symmetrical pH conditions show that the channel already opens at pH 5.5 and confirm a higher probability for the channel to open with increasing pH (Fig. S1, ESI†).

The results are consistent between the three CpHRE MD simulations: (1) The conformational changes observed in the three simulations are similar at pH conditions that expectedly confer a similar pH-dependent response of the channel, when ΔpH is negative in the ΔpH_i,o=cst simulations and when pH is low in the pH_sym simulation respectively, or when ΔpH is positive in ΔpH_i,o=cst and pH is high in pH_sym, and (2) the calculated pK_a of the titratable AAs are also similar in the different simulations, as will be shown below. Overall, the results were more significant in the ΔpH_i=cst simulation. Therefore, unless otherwise noted, the results and discussion will generally refer to this simulation, except when dealing with features that depend on pH_i changes (ΔpH_o=cst simulation). Otherwise, the results for the other simulations (ΔpH_o=cst and pH_sym) are generally presented in the ESI.†

While the replicas walked across the pH ladder during the course of the CpHRE MD simulations (Fig. S2, ESI†) the sampling of the protonation state was generally converged and remained in equilibrium at the end of the simulations for almost all titratable AAs in all replicas (Fig. S3, ESI†). Observation of the time-dependent evolution of the protein backbone RMSD suggested that the replicas fluctuated between two ensembles more or less populated depending on the value of pH_o (Fig. 2A). One ensemble is centred around 3 Å from the starting structure and is essentially populated at pH_o values 5.5–6.5 (Fig. 2B and Fig. S4, ESI†). Lowering pH_o (negative ΔpH) or increasing pH_o (positive ΔpH), ensembles with higher RMSDs around 3.5–4.5 Å and 4.0–4.5 Å respectively become more populated, representing conformations that deviate more from the starting structure. As already mentioned in Methods, our model of hH_V1m was constructed on the structure of Ci-VSD in the down state solved at pH 5.5. According to our setting the pH gradient is nearly zero at pH_o values around 5.5. It is thus reasonable that the replicas at pH_o around 5.5 deviate less from the starting structure than those at positive ΔpH values that should promote an activated state of the channel. But how can we explain the ensemble at negative ΔpHs (pH_o < 5.5) that also deviate more from the starting structure? We reasoned that the ensemble with the lowest RMSD represents an intermediate between two distinct conformations at larger negative and positive ΔpH respectively. In order to verify this hypothesis, we analysed the pH-dependence of several structural features of hH_V1m (see below).

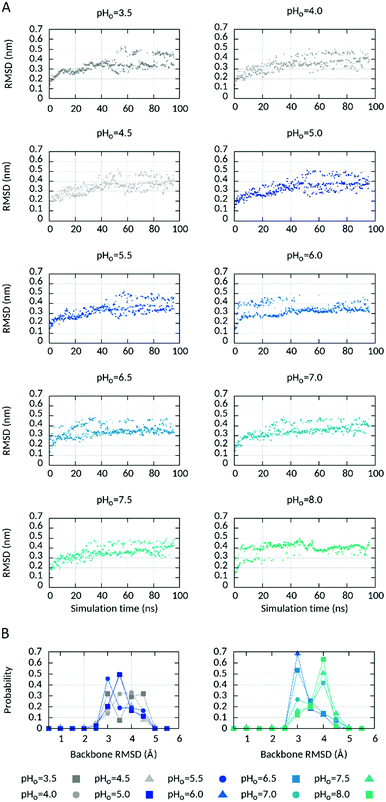Fig. 2 Protein backbone changes at different pH_o values. (A) Time evolution of the protein backbone RMSD at different pH_o values in the ΔpH_i=cst CpHRE MD simulation and (B) probability distribution of the protein backbone RMSD at different pH_o values during the last 20 ns of the ΔpH_i=cst CpHRE MD simulation. The RMSD values were binned in bins with intervals of 0.5 Å. For example, a pic centered at 3.0 Å contains all the snapshots accumulated during the simulated time with 3.0 ≤ RMSD (Å) < 3.5. See also Fig. S4 (ESI†) for the ΔpH_o=cst and pH_sym CpHRE MD simulations.

Visual inspection of the pH_o-specific trajectories revealed that the sidechain of the central S4 Arg, R2 (R208 in hH_V1), shuttled recurrently between the outer and inner vestibules, while in our structural model R2 (Cα atom) lies almost in the HG with the sidechain pointing in the outer vestibule (Fig. 1). The tendency of R2 sidechain (R2sc) being above, respectively below, the HG appeared to be higher as ΔpH increased, respectively decreased. In order to quantify this feature, we calculated the probability of R2sc to be above or below the HG as a function of pH_o by assessing the dihedral angle of R2sc with respect to the plane formed by the HG in the pH_o-specific trajectories. As shown in Fig. 3A (Fig. S5 (ESI†) for the ΔpH_o=cst and pH_sym simulations), R2sc is preferentially above the HG when ΔpH is positive (high pH_o or low pH_i), with higher probabilities at pH_o 7.0–8.0. On the contrary, it is almost only below the HG when ΔpH is negative (low pH_o or high pH_i), with higher probabilities at pH_o 3.5–4.5. At small |ΔpH|, when pH_o = 5.0–6.5, the dihedral angle is more broadly distributed over negative and positive values with lower probabilities, in agreement with the observation that R2sc shuttles repeatedly between the inner and outer vestibules with no or little preference.

Fig. 3 Fraction of activated state in the ΔpH_i=cst CPHRE MD simulation. (A) Probability distribution of R208 sidechain (R2sc) dihedral angle with respect to the hydrophobic gasket (HG) in the ΔpH_i=cst CpHRE MD simulation. The dihedral angle was defined as V177(Cβ)–F150(Cγ)–V109(Cβ)–R208(Cζ). With this definition, R2sc is below the HG at positive dihedral angles and above at negative angles. (B) Density of states of R2 Cα atom axial position with respect to the hydrophobic gasket during the last 20 ns of the ΔpH_i=cst CpHRE MD simulation. The sidechain heavy atoms of V109, F150, V178 and V179 were used to calculate the axial position of the center of mass of the HG. (C) Fraction of activated state at different pH_o values in the ΔpH_i=cst CpHRE MD simulation. R2sc orientation during the last 20 ns of the simulation was used to discriminate the deactivated (R2sc below HG) and the activated (R2sc above HG) states. See also Fig. S5 (ESI†) for the ΔpH_o=cst and pH_sym CpHRE MD simulations.

We also observed that R2sc interacts with different AAs when it is orientated below or above the HG. Furthermore, due to R2 position in S4 only one helix turn below R1 and one helix turn above R3, rearrangement of R2 interactions below and above the HG should most probably affect the interactions of the other two Arg, R1 and R3. Therefore, we looked at the time evolution of the interactions involving the three Arg during the course of the simulation (Fig. 4).

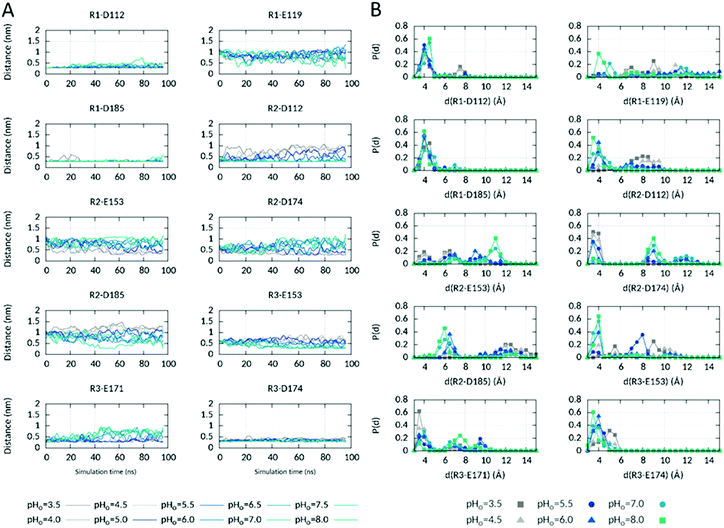Fig. 4 Electrostatic interactions of the three S4 arginines in the ΔpH_i=cst CpH RE MD simulation. (A) Time evolution of salt-bridged interactions involving the three S4 Arg R205 (R1), R208 (R2) and R211 (R3) at different pH_o values in the ΔpH_i=cst CpHRE MD simulation. The minimal distance between the oxygen atoms of the aspartates and glutamates sidechain carboxyl group and the nitrogen atoms of the arginine sidechain amino group is plotted using the acspline smooth function of Gnuplot. (B) Probability distribution of the distances during the last 20 ns of the simulation at different selected pH_o values. See also Fig. S7 (ESI†) for the ΔpH_o=cst and pH_sym CpHRE MD simulations.

In the structural model, R2 interacts via a salt-bridged interaction in the extracellular vestibule with D112 (selectivity filter of hH_V1) only, as shown in Fig. 1. This interaction is strongly conserved at high pH_o values (Fig. 4). An interaction with D185 in S3, that lies higher in the outer vestibule than D112, is additionally formed at some times of the simulation at pH_o 8.0. As pH_o decreases, the R2–D112 interaction loosens and is definitively lost when pH_o becomes lower than 5.0. While the R2–D112 distance increases up to 9–10 Å, the R2–E153 and R2–D174 distances, originally of 9.2 and 7.3 Å respectively, decrease down to 2.7 Å, in agreement with the reorientation of R2sc below the HG and the formation of new interactions in the intracellular vestibule with E153 in S2 and D174 in S3. At intermediate pH_o values (5.0–6.0), the three distances fluctuate in between the extrema, consistent with R2sc shuttling repeatedly between the inner and outer vestibules when the pH gradient across the membrane is around zero. R3's interactions network is dependent on the orientation of R2sc. In the structural model, R3 interacts with E171 and D174 in the intracellular part of S3. When R2sc is below the HG, only the interaction with E171 is conserved. When R2sc is above the HG, R3 loses the interaction with E171, tightens the interaction with D174 and forms a new one with E153 in S2. E153 lies higher in the intracellular part of the channel, closer to the HG than E171. Thus, R3sc interacts with an upper part of the channel, directly below the HG, when R2sc is above the HG, at high pH_o. The interactions of R1 with D112 and D185 in the starting structure are conserved at almost all pH_o values during the whole simulation. In the second part of the simulation however, they sometimes become slightly looser at pH_o 7.5–8.0, while R1sc appears to get closer to E119. E119 lies in the upper part of S1. Like R3sc, R1sc interacts with an upper part of the channel when R2sc is above the HG, at high pH_o. Evidently, distinct conformations are promoted when the pH gradient across the membrane is highly negative or positive. Essentially, the sidechains of the three S4 Arg interact with AAs located lower in the channel at negative ΔpH and with AAs located higher in the channel at positive ΔpH. We also checked if further salt-bridged interactions are correspondingly affected by the pH (Fig. S6, ESI†). In the inner vestibule, one interaction that is stable at all pH_o values was identified between K157 in S3 and E153. A looser interaction is found with E171 in S3 essentially at high pH_o (8.0). An interaction between H168 in the S2–S3 intracellular loop and E171 appears to be relatively tight at the highest but not at the intermediate and lowest pH_o values. At almost all pH_o values, E119 interacts with H140 in the higher part of the outer vestibule at various times of the simulation. Altogether, our simulations suggest substantial participation of the voltage sensor during the pH-dependent gating, in agreement with.⁶³ Furthermore, our analyses suggest a more extended network of interactions when ΔpH is highly positive than when it is highly negative. The intracellular network extends from the cytoplasm up to the HG via H168 → E171 → K157/R3 → D174/E153. Note here, that no interaction partner in the intracellular pore is found for H167 (Fig. S6, ESI†), located directly before H168 in the S2–S3 loop. This might explain why H168, but not H167, was identified as a potential sensor of intracellular pH.³⁰ On the extracellular side, H140 might correspondingly participate in the network of interactions that extends from the HG up to H140 via R2 → D112/D185 → R1 → E119 → H140 at high pH_o. Upon activation, H_V1 channels undergo conformational changes that result in gate opening and proton conduction.^22–24 Changes in membrane potential drive S4 to move from its position in the resting ‘down’ state outwards to its ‘up’ position in the activated state. In contrast to S4, the S1–S3 helices appear to form a relatively immobile scaffold.^64–70 Estimates of the magnitude of S4 outward displacement vary widely from ∼5 to ∼20 Å, depending on the experimental technique used^{43,65,71–76} or the approach used to construct the structural models. However, such models were often based on experimental structures of low homology potassium or sodium channels and often reflect preconceived notions of their creators.^29,77–85 Per extrapolation of S4 movement in K⁺ or Na⁺ channels where S4 moves at least three –of up to seven- basic AAs past the HG, a larger displacement was proposed that moves all three Arg past the HG during H_V1 gating, as e.g. in ref. 29, 77, 78, 80, 82–86. However, the experimental structures of mH_V1 and hH_V1 in the resting (closed) state seem to contradict this model. Both show R1 on the extracellular side of the channel, R2 backbone below or nearly in the HG (in mH_V1 and hH_V1 respectively) with the sidechain interacting extracellularly with D108 in mH_V1 (equivalent to D112 in hH_V1) and intracellularly with D174 in hH_V1, and R3 entirely in the intracellular vestibule. MD simulations using mH_V1 as template to track Ci-H_V1 gating suggested that the crystal structure of mH_V1 may either be an intermediate state more closely resembling the open state.⁸³ In the structure of Ci-VSD in the down state, R2 backbone is located almost in the HG and R2sc points to the outer vestibule.⁴³ However, only the backbone scaffold was determined and the sidechains were modelled using their orientation in the up state (PDB 4G7V⁴³). In a subsequent publication about the resting state of hH_V1, the same authors depict R2sc in the intracellular vestibule.⁴¹ Based on the down and up structures of Ci-VSD, they also propose that S4 moves only one turn of the helix outward allowing only R2 to pass the HG. As a matter of fact, independently of the extent of S4 movement in the different studies, at least R2 should pass the HG during H_V1 gating. In order to determine if S4 moved in our simulation as a function of pH_o, and to which extent, we looked at the axial position of R2 Cα atom with respect to the HG during the last 20 ns of the simulation. As shown in Fig. 3B, R2 Cα is preferentially below the HG at low pH_o and almost exclusively above at high pH_o. Thus, a pH-induced movement of S4 was captured in our simulation that, starting with the structural model, moves S4 inwards at negative and outwards at positive ΔpHs. We note here, that on the time scale of the CpHRE MD simulations, we did not identify a larger movement of S4 than the one only moving R2 past the HG.

The two states identified in the CpHRE MD simulations are in accordance with the results from others in discriminating deactivated/resting^22,41 (unpolarised configuration at 0 mV) from activated/open states of H_V1.^81,82 We thus assume that our simulations captured the pH-induced transition between a deactivated and an activated state of the hH_V1 proton channel.

Interestingly, the relative population of the two states shows a nearly sigmoïdal pH dependence (Fig. 3C), similar to that observed for the M2 proton channel.^34,35 The fraction of activated state increases more sharply at pH_o 4.5 to 6.5 when ΔpH is small or zero, indicating a pH-induced conformational activation of the channel. The transition midpoint is at pH ∼5.5 corresponding to ΔpH approximately zero. Experimentally, increasing currents are measured with increasing pH gradients (even without electrical gradient across the membrane like in our simulations), the channel shows a progressively faster activation as pH_i decreases or pH_o increases as well as shifts of the voltage-activation curves to more negative potentials, and slower activation (at a given voltage) at low pH_o.³¹ The previous result is thus of good acceptance, especially if we consider that pH_i in the present simulation might not exactly be 5.5 but rather represent a pH range around this value (see computational method). We did not attain fractions of 0 and 1 respectively, which suggests that the conformations were not fully converged and that further structural changes are possible, e.g. multiple closed and open states without further impact on function. Indeed, sigmoïdal activation kinetics and biexponential decay of tail currents near threshold potentials indicate that H⁺ channels pass through at least two closed states before opening.³¹ Furthermore, a coupling between the chemical energy stored in the pH gradient and the electrical energy of the voltage gradient across the membrane is required to fully activate the homolog CiH_V1 channel.^63,87 The contribution of the electrical potential is not taken into account in our simulations. However, the decreased steepness at pH_o 8.0 in Fig. 3C might also correlate with the saturation of the effect starting at pH_o 8.0 observed in proton channels.³¹

The deactivated and activated states

Because our simulation was not completely converged, we took the conformations of the two replicas at pH_o 3.5 (deactivated) and 8.0 (activated) and submitted them to 200 ns of CpH MD simulations without replica exchange to better characterize the deactivated and activated states. The results are summarized in Fig. 5. No crucial conformational change was observed during the simulation of the two replicas (in comparison to the conformations at the end of the CpHRE MD simulation). R2 was consistently below, respectively above, the HG in the deactivated and activated states respectively (Fig. 5A and B). The previously identified interactions were generally stable, confirming the three Arg clusters D112–R1–D185, E153–R2–D174 (with K157), and R3–E171 as stabilizing elements of the deactivated state (Fig. 5A left panel). As already suggested by the CpHRE MD simulations, the clusters expand to larger networks of interactions in the inner and outer vestibules of the activated state (Fig. 5A right panel). On the extracellular side it consists, from the HG to the extracellular medium, of R2–D112/D185–R1–E119–H140. The interaction of H140 with E119 on the extracellular side of the channel becomes tighter in the CpH MD of the activated state (non-existent in the deactivated state). In the activated state, we also observed H193 interacting repeatedly with H140, and E119 or D185, extending the network on the extracellular side of the channel, from the HG up to the entrance of the pore. In the inner vestibule the network involves R3–E153/D174–K157–E171–E168, from the HG down to the cytoplasm. Interestingly, E171 interacts with H168 in the S3–S4 intracellular loop in the activated but not in the deactivated state. E171 and H168 extend the network down to the cytoplasmic entrance of the channel in the activated state. H167 was not observed to interact with any AA neither at pH_o 3.5 nor at 8.0, which again might explain the identification of H168, but not H167 as a sensor of the inner pH.³⁰ The previous result for H168 is elusive because, like all other AAs on the intracellular side, it cannot titrate in the two simulations. This indicates that H168's interaction with E171 depends only on the outer pH value in the ΔpH_i=cst simulations. H140 and H193 might play an essential role in sensing the outer pH on the extracellular side of hH_V1m, as counterpart to H168 on the intracellular side. Interestingly, the two histidines H140 and H193 are essential contributors to the two zinc binding sites in monomeric hH_V1.⁴²

Fig. 5 The deactivated and activated states in the constant pH MD simulations. (A) Representative snapshots of the deactivated (left panel) and activated (right panel) states in the CpH MD simulations at pH_o = 3.5 and 8.0 respectively. The three S4 voltage sensing arginines are shown in lila. The hydrophobic gasket separating the inner and outer vestibules is depicted as a yellow surface. The electrostatic interactions stabilizing the deactivated and activated states are depicted as orange lines. The dashed boxes in the left and right panels indicate the region depicted in the middle panel. (A, middle panel) Overlay of the central region of the pore in the deactivated (grey) and activated (green) states. The arrows show the outward displacement of the backbone Cα atoms (shown as spheres) of the three S4 arginines during activation. (B) Density of states of R2 Cα atom axial position with respect to the HG (defined as the center of mass of the sidechain heavy atoms of V109, F150, V177 and V178) in the constant pH MD simulations of the deactivated (grey) and activated states (green). A displacement of the R2 Cα atom of approximately 4.3 Å during activation is calculated from the two simulations, corresponding to a S4 outward displacement of approximately one helix turn. (C) The radius of gyration of the HG as well as (D) the pore radius along the whole z axis increase with activation promoting a broader permeation pathway in the activated state (grey: deactivated state; green: activated state; z = 0 at the HG).

H_V1 channels are generally supposed to be slightly more open in the proton conducting state. We thus first looked at the radius of gyration of the HG. As shown in Fig. 5C, the radius of gyration of HG increases in the activated state. A comparable amplitude has been noted for the opening of the cytoplasmic gate of the sodium–proton antiporter NhaA channel.³⁶ Then, we looked at the size of the pore along the membrane axis. As can be seen in Fig. 5D, the pore is more open in the activated state. However, it is similarly constricted directly above the HG in the region of R1 and R2 as well as below the HG in the regions of R3 and K157. In summary here, our constant pH MD simulations captured the conformational change induced by the ΔpH-dependent (without electrical gradient) gating, as summarized in Fig. 5. Despite the longer time of the CpH MD simulations we did not observe further inward or outward displacement of S4. We assessed again the axial position of C2 Cα atom with respect to the HG and calculated an approximate outward S4 displacement of 4.3 Å. This value corresponds to approximately one helix turn, although it is smaller (∼5.4 Å for an α-helix, Fig. 5B). The two states might differ from the states induced by the voltage-dependent gating. However, our simulations suggest that during the pH (only)-dependent activation of hH_V1 only the second S4 arginine passes the HG from the intra- to the extracellular side of the channel, in agreement with the “one-click” model (as illustrated in ref. 88 and 62). The activated state identified in our simulations is consistent with experimental accessibility data of the three S4 Arg, indicating that the two outermost Arg (R1 and R2) are accessible to the solvent, but R3 is accessible only to the internal solution after gating.⁸²

pK_a of the titratable amino acids

We calculated the microscopic pK_a values for the stepwise titration of the Asp, Glu, His and Lys AAs (Fig. S8 (ESI†) and Table 1). Note here that AAs on the intracellular side, respectively extracellular side, of the channel did not titrate during the ΔpH_i=cst, resp. ΔpH_o=cst, simulations so that pK_a values cannot be calculated in the respective cases. The calculated pK_a values are consistent and generally within less than 0.5 units of pK_a in the different simulations. The calculated pK_a are generally close to the standard value (within ∼1 unit of pK_a). Most importantly, the individual AAs deviate from the ‘standard’ value in the same direction in the different simulations.

Table 1 ‘Standard’ and calculated pK_a values of the titratable amino acids. The ‘standard’ values are (a) from the PKAD database based on experimentally measured pK_as of 1350 ionizable AAs in 157 wild-type proteins (408 Asp, 4177 Glu, 253 His, and 155 Lys),⁵⁸ (b) the values normally used in protein pK_a calculations and (c) the model or ‘intrinsic’ pK_a values when all other groups are fixed in their neutral state

Amino acids	‘Standard’ pKas a/b/c	pKa (pHsym)	pKa (ΔpHi=cst)	pKa (ΔpHo=cst)
Lys 94	10.68/10.5/10.4	9.16	—	9.24
His 99	6.45/6.08/6.4	7.17	—	7.20
Asp 112	3.43/3.9/4.0	2.05	3.24	—
Glu 119	4.14/4.3/4.5	6.85	6.18	—
Asp 123	3.43/3.9/4.0	5.85	6.37	—
Lys 125	10.68/10.5/10.4	10.62	12.15	—
Asp 130	3.43/3.9/4.0	7.25	6.28	—
Lys 131	10.68/10.5/10.4	8.54	7.26	—
His 140	6.45/6.08/6.4	5.35	4.96	—
Glu 153	4.14/4.3/4.5	4.67	—	5.00
Lys 157	10.68/10.5/10.4	5.57	—	4.99
Glu 164	4.14/4.3/4.5	5.11	—	5.23
His 167	6.45/6.08/6.4	7.00	—	7.15
His 168	6.45/6.08/6.4	6.16	—	5.72
Lys 169	10.68/10.5/10.4	10.59	—	8.84
Glu 171	4.14/4.3/4.5	3.73	—	3.52
Asp 174	3.43/3.9/4.0	2.49	—	3.09
Asp 185	3.43/3.9/4.0	2.46	3.17	—
Glu 192	4.14/4.3/4.5	6.51	6.04	—
His 193	6.45/6.08/6.4	6.96	6.82	—
Glu 196	4.14/4.3/4.5	8.34	7.5	—
Lys 221	10.68/10.5/10.4	9.78	—	9.25

---

Based on the deviation of their pK_a with respect to their intrinsic value we distinguish two groups of AAs. The first one includes AAs located outside the pore in the N-terminus (K94, H99), the extracellular loops S1–S2 and S3–S4 (D123, D130, K131, E192, H193, E196), the intracellular loop (H167, K169), and in the C-terminus (K221). Basic AAs in these regions exhibit depressed pK_as whereas acidic AAs have elevated pK_as in comparison to their standard values. These AAs were observed to form only unspecific and transient (if any) interactions with other AAs within this group. By changing their PS near the activation pH-range, some of these residues might contribute to modify the charge at the internal (H99, H167) or external (D123, D130, E192) membrane that is perceived by the voltage-sensor (the three S4 arginines) in the voltage-dependent gating, as proposed in the electrostatic model of ΔpH gating in ref. 62. The second group consists of the AAs in the channel pore. Contrarily to the acidic AAs outside of the pore, the acidic AAs in the vicinity of HG, D174 and D112 and D185 exhibit depressed pK_a, below 4. This is not surprising since these AAs are buried in the channel pore and interact with the positively charged S4 Arg which stabilizes the three AAs and decreases their pK_as. They are thus always fully deprotonated at pH conditions when activity can be experimentally detected. Curiously, E153 exhibit pK_a within the standard value (5.00 and 4.67 in the ΔpH_o and pH_sym simulations respectively). Indeed, E153 was observed to interact tightly via a salt bridge with R2 in the deactivated and with R3 in the activated state in the ΔpH_i=cst, but only slightly in the ΔpH_o=cst and pH_sym simulations where this AA titrates. However, the transient interactions of E153 with R2 in the deactivated and with R3 in the activated state observed in the pH_sym CpHRE MD simulation became tighter in CpH (without RE) MD simulations of the deactivated and activated states suggesting that its pK_a, likewise D174, D112 and D185, might be more depressed in converged simulations. With values of 4.67/5.00, K157's pK_a is largely depressed and close to the pK_a of E171 (3.52/3.73). In the activated state, K157 interconnects E171 (that interacts also with H168 and R3), E153 and D174 (that interact with R3). A low pK_a for K157 would be essential to the proton transfer in an intracellular proton pathway extending from the cytoplasm (via H168) up to the HG. Interestingly, both H140 and E119 at the entrance of the extracellular channel pore and K157, E171 and H168 at the entrance of the intracellular channel pore have pK_as close to the activation pH determined formerly (∼5.5 for the ΔpH_i=cst, ∼6.7 for the ΔpH_o=cst simulation, Fig. 3C and Fig. S5B, ESI†). Because H193 also interacts with H140 in the latter CpH MD simulation, we included it to form a H140–E119–H193 triad and calculated the fraction of activated state as a function of the charge carried by the H140–E119–H193 and K157–E171–H168 triads. As shown in Fig. 6, the fraction of activated state varies with the charge of the H140–E119–H103 triad on the extracellular side, as well as with the charge of the K157–E164–H168 triad on the intracellular side. On the extracellular side, a +2 charge (2 times His⁺¹ and one Glu⁰) dominates in the pH_o-range 3.5–4.5 with a fraction of activated state lower than 24%. The fraction increases up to 41% in the pH_o-range 5.0–6.0 with charge +1 after deprotonation of H140, 51% at pH_o 6.5 with charge 0 with deprotonation of E119, and 88% in the pH_o-range 7.0–8.0 with charge −1 after deprotonation of H193. On the intracellular side, the fraction of activated state increases when pH_i decreases. It is less than 20% for pH_i above 6.0 with charge −1, increases up to 49% with charge 0 in the pH_i-range 6.0–5.5 after protonation of H168, 70% with charge +1 after protonation of K157 in the pH_i-range 4.5–4.0, and 85% with charge +2 at pH_i 3.5 after protonation of E171. Here, the transition occurs between charge 0 and +1 with deprotonation of K157. Again, this is in line with the conformational changes. At higher pH_i, when it is deprotonated, K157 sidechain is confined in the E153–R2–D174 cluster (without E153 in the ΔpH_o CpHREMD simulation). But at lower pH_i, K157 activates the inner network of interactions by bridging D174 and E153 with E171. With its low pK_a (4.00 and 5.57 in the ΔpH_o and pH_sym simulations respectively) near that of D174 (3.09/2.49) and E171 (3.52/3.73), K157 might participate in a proton transfer pathway activated a low pH_i that extend from the entrance of the cytoplasmic channel pore up to the HG via D174/E153 and R2.

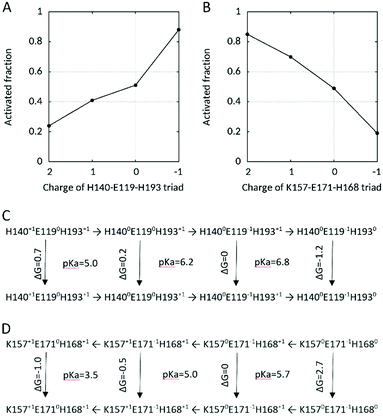Fig. 6 (A and B) Fraction of activated state as a function of the charge on the H140-E119-H168 and K157-E171-H168 triads and (C and D) thermodynamic linkage to channel activation.

Free energies of conformational transition

A salient feature of pHRE MD simulations is the ability to quantify thermodynamic linkage between protonation steps and conformational changes.⁸⁹ For hH_V1, on the extracellular side, there are a total of 8 microscopic states, i.e. 4 charge states for the triad (H140⁺¹–E119⁰–H193⁺¹, H140⁰–E119⁰–H193⁺¹, H140⁰–E119⁻¹–H193⁺¹ and H140⁰–E119⁻¹–H193⁰), each of which can be either deactivated or activated (Fig. 6C). Based on the population of each state (in the ΔpH_i=cst CpHRE MD simulation, Fig. 6A), free energies of the conformational transition from the deactivated to the activated state can be calculated for each charge state. Accordingly, the calculated free energy required for channel activation decreases from positive to negative as the triad becomes less charged: 0.8 kcal mol⁻¹ for +2, 0.2 kcal mol⁻¹ for +1, nearly zero for 0 and +1.2 kcal mol⁻¹ for −1. Remarkably, the free energy switches from positive to negative with E119 deprotonating suggesting an important role of E119 in the outer pH-dependent activation of hH_V1. This is in line with the conformational changes because when E119 deprotonates, it engages in salt-bridged interactions with R1 and H140. Based on this triad charge model, the latter deprotonation of H193 allowing its interaction with H140 and D185/E119, would contribute to further activation of the channel at higher positive ΔpH. On the intracellular side, there are also a total of 8 microscopic states, i.e. 4 charge states for the triad (K157⁺¹–E171⁰–H168⁺¹, K157⁺¹–E171⁻¹–H168⁺¹, K157⁰–E171⁻¹–H168⁺¹ and K157⁰–E171⁻¹–H168⁰), again each of which can be either deactivated or activated (Fig. 6D). Here, the free energy required for channel activation, calculated from the population of each state in the ΔpH_o=cst CpHRE MD simulation (Fig. 6B), decreases from positive to negative as the triad becomes more charged: 2.7 kcal mol⁻¹ for −1, nearly zero kcal mol⁻¹ for 0, −0.5 kcal mol⁻¹ for +1 and −1.0 for +2. The free energy switches from positive to negative with K157 protonation suggesting a strong involvement of K157 in inner pH-dependent activation of hH_V1. The calculated free energies of protonation are small in comparison to the experimentally measured activation energies of gating.⁹⁰ Our MD simulations are limited to calculating the free energy of protonation of the triads which might more reflect the initiation of gating than the complete process. Furthermore, the triads are not fully populated with charge +2 or −1 which otherwise would drastically increase the free energy.

Our results support in several lines the model described in ref. 91 for the observed ΔpH dependence of hH_V1 gating. This model suggests that protonation sites at the entrance of the intra- and extracellular cavities regulate the position of the S4 helix. Accordingly, we can extend this model with our results. In the deactivated state, the three S4 Arg are engaged each in separated clusters of interactions, D112–R1–D185, E153–R2–D174 (with K157), and R3–E171. Deprotonation of the H140–E119–H193 site at the extracellular pore entrance, when the outer pH increases, or protonation of the K157–E171–H168 site at the intracellular entrance, when the inner pH decreases, destabilize the interactions in the deactivated state. When E119 deprotonates, it can interact electrostatically (salt bridge) with R1 that moves (and with it the whole S4 helix) outwards. This is accompanied with rearrangements of the interactions both in the extra- and the intracellular vestibules. On the extracellular side, the deprotonated E119 further engages in an electrostatic interaction with H140. Interestingly, E119 and H140 are the two main contributors to one of the zinc binding sites that block the monomeric channel into a non-active conformation. And H193 participates to the second binding site.⁴² On the intracellular side, protonation of K157 might destabilize the electrostatic interaction between R2 and D174/E153, resulting in S4 outward movement to displace R2 above the HG. As a consequence, R3 comes closer to D174 and E153, possibly destabilizing the electrostatic interaction between K157 and D174/E153. In turn, K157 engages in a new interaction with E171 that is almost always deprotonated. Although we cannot confirm this hypothesis, rearrangements resulting in an extensive network of interactions in the intracellular vestibule take place with gating, from the cytoplasm up to the HG. In the extracellular vestibule it also results in an extensive network of interactions from the HG up to the extracellular medium. As we already mentioned, de-/protonation of titratable sidechains at the intra- and extracellular entrances of the channel change the potential sensed by the voltage-sensing Arg in S4. Transmembrane voltage contributes to S4 inward and outward movement.

Conclusions

Constant pH replica-exchange simulations were applied to investigate the pH dependent conformational behaviour of the human proton channel H_V1. Starting from a structure based on the crystal structure of Ci-VSD in a putative closed state, conformational changes to a deactivated and to an activated state were observed. Our simulations successfully captured the pH-dependent gating of the hH_V1 channel under different pH conditions. Despite our computational limitations resulting in simulations that were generally not sufficiently converged to confidently assess all the conformational changes, the results were consistent between simulations representing different pH conditions. The pH profiles of the activated state fraction agree with our expectation of a deactivated (non-conducting) state at negative ΔpH and low symmetrical pH and of an activated (proton conducting) state at positive ΔpH and high symmetrical pH, confirming conformational change during the pH-dependent gating of hH_V1. Our data support a small outward displacement (approximately one helix turn) of the S4 helix during gating. This moves only the central of the three S4 voltage-sensing Arg past the hydrophobic gasket that separates the inner and outer cavities of the channel. Importantly, constant pH simulations with replica exchange provide the pK_a of all titratable sidechains in one single experiment. With this information, we were able to determine that S4 motion is coupled to the deprotonation of the H140–E119–H193 site at the extracellular entrance of the channel when the outer pH increases. When the inner pH decreases, it is coupled to the protonation of the K157–E171–H168 site at the intracellular entrance. De-/protonation of titratable sidechains outside the pore might further contribute to S4 movement by modifying the charge perceived near the extra- and intracellular membrane by the voltage-sensing Arg in S4. Finally, the structural rearrangements accompanying the gating provide extensive networks of electrostatic interactions. These rise from the cytoplasm up to the hydrophobic gasket on the intracellular side and from the hydrophobic gasket up to the extracellular medium where the titratable sidechains may participate to the proton conduction pathway.

Author contributions

B. M. and C. J. conceived the project. C. J. and N. O. did the simulations. A. F. designed and generated the “minimal” hH_V1 channel. G. C. recorded the patch-clamp experimental measurements. C. J. wrote the manuscript. All the authors read and approved the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the Förderverein der Paracelsus Medizinische Privatuniversität (PMU) Nürnberg for financial support.

Notes and references

1. L. M. Henderson, J. B. Chappell and O. T. G. Jones, Biochem. J., 1987, 246, 325–329.
2. T. E. DeCoursey, D. Morgan and V. V. Cherny, Nature, 2003, 422, 531–534.
3. M. Sasaki, A. Tojo, Y. Okochi, N. Miyawaki, D. Kamimura, A. Yamaguchi, M. Murakami and Y. Okamura, Biochem. J., 2013, 450, 295–301.
4. P. V. Lishko, I. L. Botchkina, A. Fedorenko and Y. Kirichok, Cell, 2010, 140, 327–337.
5. P. V. Lishko and Y. Kirichok, J. Physiol., 2010, 588, 4667–4672.
6. M. E. Barish and C. Baud, J. Physiol., 1984, 352, 243–263.
7. Y. Wang, S. J. Li, J. Pan, Y. Che, J. Yin and Q. Zhao, Biochem. Biophys. Res. Commun., 2011, 412, 353–359.
8. Y. Wang, S. J. Li, X. Wu, Y. Che and Q. Li, J. Biol. Chem., 2012, 287, 13877–13888.
9. Y. Wang, X. Wu, Q. Li, S. Zhang and S. J. Li, PLoS One, 2013, 8, e70550.
10. Y. Wang, S. Zhang and S. J. Li, Biochem. Biophys. Res. Commun., 2013, 438, 312–317.
11. T. Kawai, K. Kayama, S. Tatsumi, S. Akter, N. Miyawaki, Y. Okochi, M. Abe, K. Sakimura, H. Yamamoto, S. Kihara and Y. Okamura, FASEB J., 2020, 34, 15805–15821.
12. W. Xudong, Biochem. Biophys. Res. Commun., 2018, 498, 975–980.
13. A. El Chemaly, Y. Okochi, M. Sasaki, S. Arnaudeau, Y. Okamura and N. Demaurex, J. Exp. Med., 2009, 207, 129–139.
14. A. R. Taylor, A. Chrachri, G. Wheeler, H. Goddard and C. Brownlee, PLoS Biol., 2011, 9, e1001085.
15. D. Iovannisci, B. Illek and H. Fischer, J. Gen. Physiol., 2010, 136, 35–46.
16. D. Morgan, M. Capasso, B. Musset, V. V. Cherny, E. Ríos, M. J. S. Dyer and T. E. DeCoursey, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18022–18027.
17. S. Y. Lee, J. A. Letts and R. MacKinnon, J. Mol. Biol., 2009, 387, 1055–1060.
18. B. Musset, S. M. Smith, S. Rajan, D. Morgan, V. V. Cherny and T. E. Decoursey, Nature, 2011, 480, 273–277.
19. T. Dudev, B. Musset, D. Morgan, V. V. Cherny, S. M. E. Smith, K. Mazmanian, T. E. DeCoursey and C. Lim, Sci. Rep., 2015, 5, 10320.
20. F. Bezanilla, Physiol. Rev., 2000, 80, 555–592.
21. T. E. DeCoursey, J. R. Soc., Interface, 2018, 15, 20180108.
22. A. D. Geragotelis, M. L. Wood, H. Göddeke, L. Hong, P. D. Webster, E. K. Wong, J. A. Freites, F. Tombola and D. J. Tobias, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 13490–13498.
23. F. Qiu, S. Rebolledo, C. Gonzalez and H. P. Larsson, Neuron, 2013, 77, 288–298.
24. L. Mony, D. Stroebel and E. Y. Isacoff, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 20898–20907.
25. C. Gonzalez, S. Rebolledo, M. E. Perez and H. P. Larsson, J. Gen. Physiol., 2013, 141, 275–285.
26. F. Qiu, A. Chamberlin, B. M. Watkins, A. Ionescu, M. E. Perez, R. Barro-Soria, C. González, S. Y. Noskov and H. P. Larsson, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E5962–E5971.
27. T. M. Schladt and T. K. Berger, Sci. Rep., 2020, 10, 21293.
28. V. V. Cherny, D. Morgan, B. Musset, G. Chaves, S. M. E. Smith and T. E. DeCoursey, J. Gen. Physiol., 2015, 146, 343–356.
29. I. S. Ramsey, Y. Mokrab, I. Carvacho, Z. A. Sands, M. S. P. Sansom and D. E. Clapham, Nat. Struct. Mol. Biol., 2010, 17, 869–875.
30. V. V. Cherny, D. Morgan, S. Thomas, S. M. E. Smith and T. E. DeCoursey, J. Gen. Physiol., 2018, 150, 851–862.
31. V. V. Cherny, V. S. Markin and T. E. DeCoursey, J. Gen. Physiol., 1995, 105, 861–896.
32. T. E. DeCoursey and J. Hosler, J. R. Soc., Interface, 2013, 11, 20130799.
33. V. V. Cherny and T. E. DeCoursey, J. Gen. Physiol., 1999, 114, 819–838.
34. W. Chen, Y. Huang and J. Shen, J. Phys. Chem. Lett., 2016, 7, 3961–3966.
35. Y. Zhang, H. Zhang and Q. Zheng, Phys. Chem. Chem. Phys., 2019, 21, 2984–2991.
36. Y. Huang, W. Chen, D. L. Dotson, O. Beckstein and J. Shen, Nat. Commun., 2016, 7, 12940.
37. Z. Yue, W. Chen, H. I. Zgurskaya and J. Shen, J. Chem. Theory Comput., 2017, 13, 6405–6414.
38. K. Takeshita, S. Sakata, E. Yamashita, Y. Fujiwara, A. Kawanabe, T. Kurokawa, Y. Okochi, M. Matsuda, H. Narita, Y. Okamura and A. Nakagawa, Nat. Struct. Mol. Biol., 2014, 21, 352–357.
39. M. Bayrhuber, I. Maslennikov, W. Kwiatkowski, A. Sobol, C. Wierschem, C. Eichmann, L. Frey and R. Riek, Biochemistry, 2019, 58, 4017–4027.
40. R. Banh, V. V. Cherny, D. Morgan, B. Musset, S. Thomas, K. Kulleperuma, S. M. E. Smith, R. Pomès and T. E. DeCoursey, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 18951–18961.
41. Q. Li, R. Shen, J. S. Treger, S. S. Wanderling, W. Milewski, K. Siwowska, F. Bezanilla and E. Perozo, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E5926–5935.
42. C. Jardin, G. Chaves and B. Musset, Biophys. J., 2020, 118, 1221–1233.
43. Q. Li, S. Wanderling, M. Paduch, D. Medovoy, A. Singharoy, R. McGreevy, C. A. Villalba-Galea, R. E. Hulse, B. Roux, K. Schulten, A. Kossiakoff and E. Perozo, Nat. Struct. Mol. Biol., 2014, 21, 244–252.
44. M. H. Olsson, C. R. Søndergaard, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 525–537.
45. M. A. Lomize, I. D. Pogozheva, H. Joo, H. I. Mosberg and A. L. Lomize, Nucleic Acids Res., 2012, 40, D370–376.
46. E. L. Wu, X. Cheng, S. Jo, H. Rui, K. C. Song, E. M. Dávila-Contreras, Y. Qi, J. Lee, V. Monje-Galvan, R. M. Venable, J. B. Klauda and W. Im, J. Comput. Chem., 2014, 35, 1997–2004.
47. S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865.
48. D. A. Case, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham, III, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, D. Ghoreishi, M. K. Gilson, H. Gohlke, A. W. Goetz, D. Greene, R. Harris, N. Homeyer, Y. Huang, S. Izadi, A. Kovalenko, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, D. J. Mermelstein, K. M. Merz, Y. Miao, G. Monard, C. Nguyen, H. Nguyen, I. Omelyan, A. Onufriev, F. Pan, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, J. Smith, R. Salomon-Ferrer, J. Swails, R. C. Walker, J. Wang, H. Wei, R. M. Wolf, X. Wu, L. Xiao, D. M. York and P. A. Kollman, AMBER 2018, University of California, San Francisco, 2018.
49. C. J. Dickson, B. D. Madej, Å. A. Skjevik, R. M. Betz, K. Teigen, I. R. Gould and R. C. Walker, J. Chem. Theory Comput., 2014, 10, 865–879.
50. I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2009, 113, 13279–13290.
51. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
52. S. Jo, T. Kim and W. Im, PLoS One, 2007, 2, e880.
53. J. M. Swails, D. M. York and A. E. Roitberg, J. Chem. Theory Comput., 2014, 10, 1341–1352.
54. T. E. DeCoursey and V. V. Cherny, Biophys. J., 1993, 65, 1590–1598.
55. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684.
56. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
57. J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
58. S. Pahari, L. Sun and E. Alexov, Database: the journal of biological databases and curation, 2019, 2019.
59. C. A. Fitch, G. Platzer, M. Okon, B. Garcia-Moreno, E. Bertrand and L. P. McIntosh, Protein Sci., 2015, 24, 752–761.
60. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
61. T. K. Berger, D. M. Fußhöller, N. Goodwin, W. Bönigk, A. Müller, N. Dokani Khesroshahi, C. Brenker, D. Wachten, E. Krause, U. B. Kaupp and T. Strünker, J. Physiol., 2017, 595, 1533–1546.
62. V. S. Sokolov, V. V. Cherny, A. G. Ayuyan and T. E. DeCoursey, Biochim. Biophys. Acta, Bioenerg., 2021, 1862, 148480.
63. E. M. Carmona, M. Fernandez, J. J. Alvear-Arias, A. Neely, H. P. Larsson, O. Alvarez, J. A. Garate, R. Latorre and C. Gonzalez, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2025556118.
64. S. B. Long, E. B. Campbell and R. Mackinnon, Science, 2005, 309, 897–903.
65. E. Vargas, V. Yarov-Yarovoy, F. Khalili-Araghi, W. A. Catterall, M. L. Klein, M. Tarek, E. Lindahl, K. Schulten, E. Perozo, F. Bezanilla and B. Roux, J. Gen. Physiol., 2012, 140, 587–594.
66. C. A. Ahern and R. Horn, Neuron, 2005, 48, 25–29.
67. F. Tombola, M. M. Pathak, P. Gorostiza and E. Y. Isacoff, Nature, 2007, 445, 546–549.
68. M. Jensen, V. Jogini, D. W. Borhani, A. E. Leffler, R. O. Dror and D. E. Shaw, Science, 2012, 336, 229–233.
69. L. Delemotte, M. Tarek, M. L. Klein, C. Amaral and W. Treptow, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6109–6114.
70. D. Balleza, M. E. Rosas and S. Romero-Romero, Channels, 2019, 13, 455–476.
71. J. Guo, W. Zeng, Q. Chen, C. Lee, L. Chen, Y. Yang, C. Cang, D. Ren and Y. Jiang, Nature, 2016, 531, 196–201.
72. D. J. Posson, P. Ge, C. Miller, F. Bezanilla and P. R. Selvin, Nature, 2005, 436, 848–851.
73. V. Ruta, J. Chen and R. MacKinnon, Cell, 2005, 123, 463–475.
74. A. Banerjee, A. Banerjee and R. MacKinnon, J. Mol. Biol., 2008, 381, 569–580.
75. H. P. Larsson, O. S. Baker, D. S. Dhillon and E. Y. Isacoff, Neuron, 1996, 16, 387–397.
76. A. Cha, G. E. Snyder, P. R. Selvin and F. Bezanilla, Nature, 1999, 402, 809–813.
77. A. L. Randolph, Y. Mokrab, A. L. Bennett, M. S. P. Sansom and I. S. Ramsey, eLife, 2016, 5, e18017.
78. S. C. van Keulen, E. Gianti, V. Carnevale, M. L. Klein, U. Rothlisberger and L. Delemotte, J. Phys. Chem. B, 2017, 121, 3340–3351.
79. B. Musset, S. M. E. Smith, S. Rajan, V. V. Cherny, S. Sujai, D. Morgan and T. E. DeCoursey, J. Physiol., 2010, 588, 1435–1449.
80. M. L. Wood, E. V. Schow, J. A. Freites, S. H. White, F. Tombola and D. J. Tobias, Biochim. Biophys. Acta, Biomembr., 1818, 2012, 286–293.
81. K. Kulleperuma, S. M. E. Smith, D. Morgan, B. Musset, J. Holyoake, N. Chakrabarti, V. V. Cherny, T. E. DeCoursey and R. Pomès, J. Gen. Physiol., 2013, 141, 445–465.
82. D. Morgan, B. Musset, K. Kulleperuma, S. M. E. Smith, S. Rajan, V. V. Cherny, R. Pomès and T. E. DeCoursey, J. Gen. Physiol., 2013, 142, 625–640.
83. A. Chamberlin, F. Qiu, S. Rebolledo, Y. Wang, S. Y. Noskov and H. P. Larsson, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E273–E282.
84. A. Chamberlin, F. Qiu, Y. Wang, S. Y. Noskov and H. Peter Larsson, J. Mol. Biol., 2015, 427, 131–145.
85. E. Gianti, L. Delemotte, M. L. Klein and V. Carnevale, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E8359–E8368.
86. A. Pupo, D. Baez-Nieto, A. Martínez, R. Latorre and C. González, Channels, 2014, 8, 180–192.
87. E. M. Carmona, H. P. Larsson, A. Neely, O. Alvarez, R. Latorre and C. Gonzalez, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9240–9245.
88. T. E. DeCoursey, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 13430–13431.
89. C. Shi, J. A. Wallace and J. K. Shen, Biophys. J., 2012, 102, 1590–1597.
90. T. E. DeCoursey and V. V. Cherny, J. Gen. Physiol., 1998, 112, 503–522.
91. L. D. Islas, J. Gen. Physiol., 2018, 150, 781–782.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp05609c

---