Open Access Article
Open Access ArticleUsing adsorption kinetics to assemble vertically aligned nanorods at liquid interfaces for metamaterial applications†
S. O.
Morgan
a,
A.
Muravitskaya
a,
C.
Lowe
a,
A. M.
Adawi
 a,
J.-S. G.
Bouillard
a,
J.-S. G.
Bouillard
 a,
T. S.
Horozov
a,
T. S.
Horozov
 b,
G. J.
Stasiuk
b,
G. J.
Stasiuk
 c and
D. M. A.
Buzza
c and
D. M. A.
Buzza
 *a
*a
aDepartment of Physics & Mathematics, University of Hull, Hull HU6 7RX, UK. E-mail: d.m.buzza@hull.ac.uk
bDepartment of Chemistry & Biochemistry, University of Hull, Hull HU6 7RX, UK
cImaging Chemistry & Biology, King's College London, Strand, London WC2R 2LS, UK
First published on 25th April 2022
Abstract
Vertically aligned monolayers of metallic nanorods have a wide range of applications as metamaterials or in surface enhanced Raman spectroscopy. However the fabrication of such structures using current top-down methods or through assembly on solid substrates is either difficult to scale up or have limited possibilities for further modification after assembly. The aim of this paper is to use the adsorption kinetics of cylindrical nanorods at a liquid interface as a novel route for assembling vertically aligned nanorod arrays that overcomes these problems. Specifically, we model the adsorption kinetics of the particle using Langevin dynamics coupled to a finite element model, accurately capturing the deformation of the liquid meniscus and particle friction coefficients during adsorption. We find that the final orientation of the cylindrical nanorod is determined by their initial attack angle when they contact the liquid interface, and that the range of attack angles leading to the end-on state is maximised when nanorods approach the liquid interface from the bulk phase that is more energetically favorable. In the absence of an external field, only a fraction of adsorbing nanorods end up in the end-on state (≲40% even for nanorods approaching from the energetically favourable phase). However, by pre-aligning the metallic nanorods with experimentally achievable electric fields, this fraction can be effectively increased to 100%. Using nanophotonic calculations, we also demonstrate that the resultant vertically aligned structures can be used as epsilon-near-zero and hyperbolic metamaterials. Our kinetic assembly method is applicable to nanorods with a range of diameters, aspect ratios and materials and therefore represents a versatile, low-cost and powerful platform for fabricating vertically aligned nanorods for metamaterial applications.
1. Introduction
The adsorption of colloids at liquid interfaces has generated increasing interest in recent years because of potential applications in areas such as emulsification,1 encapsulation,2 nanostructured materials3,4 and reconfigurable systems.5 More fundamentally, interfacial colloids have paved the way for the creation of exotic new states of matter such as liquid marbles, bijels and ‘dry’ water.6–8 Up to now, most of the research in this area has focused on spherical or nearly spherical particles. However, advances in synthetic methods have made possible the fabrication of anisotropic particles such as ellipsoids,9–14 cylinders,15–17 cubes18–22 and more complex shapes.23,24 The behaviour of such shape anisotropic particles at fluid interfaces is richer than that of spherical particles as anisotropic particles can adopt multiple locally stable orientations at the liquid interface.15,17–22,25 The possible stable orientations of anisotropic particles at liquid interfaces are strongly dependent on the shape of the anisotropic particle. For example, ellipsoidal particles are always ‘side-on’ (particle long axis parallel to liquid interface),12,14 cylindrical particles can be either ‘side-on’ or ‘end-on’ (particle long axis perpendicular to liquid interface)15,17 while cubes can be face-up, edge-up or corner-up.18–22The fact that cylindrical colloids can adopt the end-on state at the liquid interface is particularly interesting for many novel applications since arrays of vertically aligned nanorods can be used as epsilon-near-zero or hyperbolic metamaterials,26–31 plasmonic cavity resonators32 or in surface enhanced Raman spectroscopy (SERS) for sensing applications.27,33–36 Vertically aligned nanorod arrays are particularly versatile platforms for sensing and enhanced spectroscopies since the nanorods can be constructed from a wide variety of materials, including metals (e.g., gold, silver, aluminium, copper etc.) and dielectrics (e.g., polymers, silica etc.), providing maximum flexibility for tuning the frequency range over which the array has desired properties.28,37–40 One option for creating vertical nanorod arrays is to use nanolithograph,41 but such top-down methods have low throughput, complex fabrication protocols and low scalability. An alternative approach is to use bottom-up self-assembly on solid substrates such as electrodeposition38–40,42 or evaporation driven assembly.35,43–45 These approaches allow one to create high quality vertically aligned nanorod monolayers over large areas (cm-scale), but the solid nature of the substrates used to template the array limits the possibilities for post-processing to vary monolayer properties such as the spacing between nanorods.
In recent years, the self-assembly of particles at liquid interfaces has emerged as a powerful method for creating dimensionally confined nanostructures.5,46–50 Once these structures have been assembled at the liquid interface, the spacing between particles can be tuned through compression or the use of coated nanoparticles and the final structures can be transferred to a solid substrate and immobilised to create functional nanomaterials.48–52 For example, Kim et al. have recently demonstrated that they can prepare vertically aligned nanorod monolayers through the adsorption of gold nanorods (GNRs) at a liquid interface.36 Specifically, by exploiting the differential surface chemistry between the tips and sides of their GNRs and by a suitable choice of the two bulk liquid phases, they were able to engineer the end-on state to be the thermodynamic ground state so that the GNRs spontaneously formed a vertically aligned monolayer at the liquid interface. However, while this assembly method is very attractive due to its simplicity, it is extremely challenging in general to engineer nanoparticles to have specific patchy particle surface chemistries, so this method may be challenging to generalize to other nanorod systems.
A more generic method for assembling vertically aligned nanorods at a liquid interface has been proposed by de Graaf et al. which is based on adsorption kinetics rather than thermodynamics.53 Using a simple viscous-based Langevin model, these authors showed that the final orientation of cylindrical colloids at a liquid interface is determined by the ‘attack’ angle of the cylinder, i.e., the initial orientation of the cylinder when it first contacts the liquid interface. In particular, they showed that for a range of attack angles, the final orientation of the cylinder is the end-on state, even if the side-on state is the thermodynamic ground state. The range of attack angles which lead to the end-on state in turn depends on system parameters such as particle contact angle and aspect ratio and which bulk phase the cylinder approaches the liquid interface from. Because this assembly method relies on adsorption kinetics rather than the nanoparticles having a specific surface chemistry, it is applicable to nanorod systems made from a wide range of materials and therefore represents a versatile platform for engineering vertically aligned nanorods for specific applications.
While the viscous-based model of de Graaf serves as a useful initial guide to experiments, it does not include a number of important effects. Firstly, the model uses a physically unrealistic ratio for the translational to rotational friction coefficients.53,54 Secondly, it neglects the deformation of the liquid meniscus around the adsorbing particle which are significant for particle adsorption in the low capillary number regime.10–12,16,17,20 Finally, the model neglects the effect of contact line pinning which has been shown to lead to adsorption kinetics which are orders of magnitude slower than what is predicted by viscous-based models.55–57 In principle, some of these limitations can be addressed using particle-based simulations such as Lattice-Boltzmann simulations.58 However, it is not possible for current simulations to simultaneously achieve the very long timescales required to access the low capillary and Reynolds number regimes that are relevant to the experiments.
In a previous study, we extended the Langevin model of de Graaf et al. to incorporate interfacial deformation, the correct ratio for particle friction coefficients and contact line pinning.54 Specifically, interfacial deformation was accurately captured in our model by coupling Langevin dynamics to a finite element model for the interface. Using this model, we were able to reproduce much of the reported experimental phenomenology for the adsorption of ellipsoidal particles. For example, we were able to quantitatively model the evolution of particle orientation with time in some experimental systems,57 and even for systems where this was not possible, we were able to accurately model the adsorption trajectory (i.e., particle orientation vs. particle height) of the ellipsoids.56 Since the range of attack angles giving rise to the end-on state is controlled by the adsorption trajectory rather than the dynamics of the individual adsorption coordinates per se (see later), our model allows us to accurately determine the final orientation nanorods at a liquid interface.
The aim of this paper is to use our Langevin model to study the adsorption kinetics of cylinders at a liquid interface in order to quantitatively determine the conditions required to prepare cylindrical nanorods in the end-on state. We further use nanophotonic calculations to demonstrate that an ensemble of such vertically aligned nanorods can be used as zero refractive index and hyperbolic metamaterials. Our calculations will help guide experiments to use adsorption kinetics as a low cost and versatile method for preparing vertically aligned nanorod monolayers as metamaterials.
The rest of the paper is organised as follows. In Section 2, we provide details of the Langevin model we use to study the adsorption kinetics of cylindrical particles at a liquid interface and the nanophotonic model we use to calculate the optical response of an ensemble of such nanorods. In Section 3, we use these theoretical models to determine the conditions required to kinetically assemble cylindrical nanorods into vertically aligned monolayers and calculate the metamaterial response of such monolayers. Based on these theoretical results, in Section 4 we discuss the feasibility of using our kinetic assembly method to experimentally prepare vertically aligned cylindrical nanorods at the liquid interface. Finally, in Section 5 we present our conclusions.
2. Theoretical model
2.1 Thermodynamics of nanorod adsorption
We consider a cylindrical particle adsorbing at a liquid interface with long and short axis a, b respectively and aspect ratio (Fig. 1). For definiteness, we refer to the top and bottom liquid phases as oil and water respectively. The configuration of the cylinder at any instant during its adsorption is described by two degrees of freedom, namely the height of the particle center relative to the height of the undisturbed interface h, and the angle between the particle's long axis and the normal to the undisturbed interface ϕ. Note that we use the sign convention where the particle centre is in the water phase for h < 0 and in the oil phase for h > 0. Note also that due to symmetry, we only need to consider ϕ values in the range 0° ≤ ϕ ≤ 90°.
(Fig. 1). For definiteness, we refer to the top and bottom liquid phases as oil and water respectively. The configuration of the cylinder at any instant during its adsorption is described by two degrees of freedom, namely the height of the particle center relative to the height of the undisturbed interface h, and the angle between the particle's long axis and the normal to the undisturbed interface ϕ. Note that we use the sign convention where the particle centre is in the water phase for h < 0 and in the oil phase for h > 0. Note also that due to symmetry, we only need to consider ϕ values in the range 0° ≤ ϕ ≤ 90°.
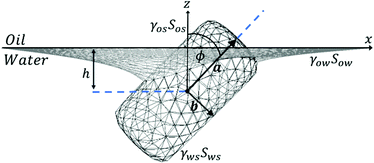 | ||
| Fig. 1 Geometry of cylindrical nanorod adsorbing at a liquid interface. The illustrated nanorod has aspect ratio m = 2.5 and sharpness parameter η = 20. | ||
For sub-micron particles, which is the focus of this paper, gravity is negligible and the free energy of the system is primarily due to interfacial energy and is therefore given by14,54
| F(h,ϕ) = γowSow + γosSos + γwsSws | (1) |
| F(h,ϕ) = γow(Sow + cosθwSos). | (2) |
For a given particle configuration (h,ϕ), the free energy given by eqn (2) is calculated using the finite element package Surface Evolver.14,17,60 One problem with using finite element methods to study cylinders is that they become numerically unstable when the three phase contact line crosses the sharp edge of the cylinder.17 To overcome this problem, we approximate the cylinder using the super-ellipsoid equation61
 | (3) |
 and eqn (3) allows us to find the coordinates of the contact point and hc(ϕ) is given by the z contact coordinate.
and eqn (3) allows us to find the coordinates of the contact point and hc(ϕ) is given by the z contact coordinate.
The interfacial areas and free energy in eqn (2) depend sensitively on the boundary condition at the three phase contact line. The original study by de Graaf et al. assumed that the liquid meniscus remains flat.53 A more realistic boundary condition is that the liquid meniscus is deformed due to the constant contact angle requirement.10–12,16,17,20,54 We call these boundary conditions ‘flat interface’ and ‘deformed interface’ respectively and consider both limiting cases in our study. For both cases, the interfacial energy F(h,ϕ) is first calculated for (h,ϕ) values on a 101 × 37 non-equidistant grid for h ∈ [−hc(ϕ),hc(ϕ)] and ϕ ∈ [0, π/2]; the data on this grid are then interpolated with a third order interpolation scheme to yield the full energy landscape. To check that this grid resolution is sufficient, for selected cases we performed calculations on a higher resolution 202 × 180 grid and found no discernable differences in the final result.
2.2 Kinetics of nanorod adsorption
The adsorption trajectory of the cylinder is found by solving the Langevin equation for the particle at the liquid interface. In the low Reynolds number regime where inertial forces are negligible, this is given by the coupled differential equations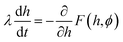 | (4) |
 | (5) |
To simplify our discussion and following ref. 53 and 54, we assume that both λ and μ are independent of h, ϕ to a first approximation. In this case, we can rescale eqn (4) and (5) to
 | (6) |
 | (7) |
 ,
,  which corresponds to
which corresponds to  ; we call this choice of scale factors Scaling 1. However, these authors point out that this choice is unphysical for a viscous-based model because it does not approximate to the sphere value of
; we call this choice of scale factors Scaling 1. However, these authors point out that this choice is unphysical for a viscous-based model because it does not approximate to the sphere value of 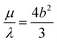 for m = 1.53 To overcome this problem, we also consider the scale factors
for m = 1.53 To overcome this problem, we also consider the scale factors  ,
,  which corresponds to
which corresponds to 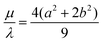 ; we call this choice of scale factors Scaling 2 and we expect this scaling to be more accurate as we do recover the sphere value for
; we call this choice of scale factors Scaling 2 and we expect this scaling to be more accurate as we do recover the sphere value for  for m = 1 in this case.54
for m = 1 in this case.54
By solving eqn (6) and (7), we obtain the adsorption trajectory (h(t), ϕ(t)) for different attack angles, i.e., the initial orientations of the cylinder when it first contacts the liquid interface. In ref. 54, we showed that the most accurate results for the adsorption trajectories of ellipsoids were obtained for the deformed interface boundary condition and Scaling 2. However, in order to compare our results with the previous work of de Graaf et al. and to study the impact of different contact line boundary conditions and dynamical scalings on the adsorption kinetics of cylinders, in what follows we calculate the adsorption trajectories for three scenarios: flat interface with Scaling 1; deformed interface with Scaling 1; deformed interface with Scaling 2. In what follows, we refer to these three scenarios as models 1, 2 and 3 respectively.
2.3 Nanophotonic calculations
The optical properties of the metamaterial which consists of the vertically aligned nanorod array can be described analytically using a local effective medium theory (EMT) in the Maxwell-Garnett approximation.31,64–66 In this approximation the in-plane and out-of-plane components of the permittivity are defined as | (8) |
| εEMTz = εm(1 − p) + pεAu | (9) |
We compare the results of the EMT with numerical calculations performed using Lumerical FDTD (finite difference time domain method).68 In this case, the optical parameters (refractive index, impedance, permittivity, and permeability) were extracted from the calculations of the complex reflection/transmission coefficients.69,70 We set periodic boundary conditions on the four vertical sides and a perfectly matched layer on the top and bottom sides of the simulation box.
3. Results
3.1 Stable states of cylinders at a liquid interface
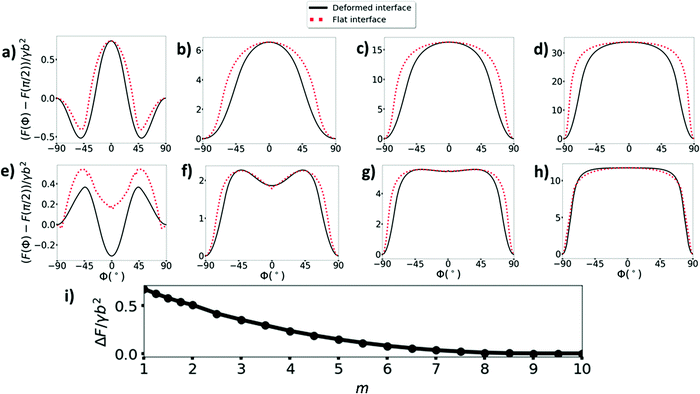
Before calculating the adsorption trajectories of cylindrical particles, we first calculate the stable states of the particles at a liquid interface (i.e., local or global energy minima) as these represent the end points of the adsorption trajectories. In Fig. 2(a)–(h), we show the interfacial energy as a function of tilt angle ϕ for cylinders with η = 20 and different contact angles and aspect ratios, where the interfacial energy at each ϕ is minimised with respect to the particle height h. The top and bottom rows respectively show results for neutrally wetting cylinders (θw = 90°) and hydrophobic cylinders (illustrated by θw = 120°), while the first, second, third and fourth columns respectively show results for aspect ratios m = 1, 2.5, 5, 9.5. The dashed red lines and solid black lines are calculated using the flat interface model and deformed interface model respectively; we see that the deformed interface model generally yields a lower energy compared to the flat interface model at any given value of ϕ. This is not surprising since the constant contact angle condition comes from minimizing interfacial energy. Note that the stable states of the system are independent of the assumed dynamical scaling model.For neutrally wetting cylinders (Fig. 2(a)–(d)), both the flat and deformed interface models predict that there is only one stable orientation for the cylinder. Specifically, for m = 2.5, 5 and 9.5, the equilibrium state is the side-on state ϕ = ±90° while for m = 1, the equilibrium state is the tilted state, with a tilt angle ϕ = ±49.6° for the deformed interface model (note that positive and negative ϕ represent equivalent states). These results are in good agreement with our previous study17 where we showed that below a critical aspect ratio of mc = 2.3, the equilibrium orientation of neutrally wetting cylinders at a liquid interface transitions from the side-on state to the tilted state.
In contrast, for hydrophobic cylinders (Fig. 2(e)–(h)), both models predict that, provided the aspect ratio is not too large, there are two stable cylinder orientations, namely the side on state ϕ = ±90° and the end-on state ϕ = 0° with the cylinders being mainly immersed in the oil phase in both states, i.e., h > 0, see Fig. 3(b)–(d). For small aspect ratio cylinders m = 1, the deformed interface model predicts that the end-on state is the ground state and the side-on state is metastable. For larger aspect ratio cylinders m = 2.5, 5, both models predict that the side-on state is the ground state and the end-on state is metastable. In Fig. 2(i), we plot the energy barrier stabilising the end-on state against the side-on state as a function of aspect ratio calculated using the deformed interface model. We see that the energy barrier decreases with increasing aspect ratio and indeed disappears altogether for m = 9.5 (Fig. 2(h)) so that only the side-on state is stable for m ≥ 9.5. Finally, we note that a hydrophilic cylinder whose contact angle is the same distance away from the neutrally wetting condition (i.e., θw = 60° in this case) would have exactly the same orientational energy landscape as shown in Fig. 2(d)–(f) except for the fact that the stable states of the cylinder would now be mainly immersed in the water phase, i.e., h < 0.
3.2 Adsorption kinetics of cylinders at a bare liquid interface
From the previous section, we saw that only non-neutrally wetting cylinders can exist in the end-on state that we are targeting in this study. For the rest of the paper we will therefore focus on the adsorption trajectories of non-neutrally wetting cylinders. However, for completeness the adsorption of neutrally wetting cylinders is discussed in ESI.† For definiteness, we consider hydrophobic particles with contact angle θw = 120°, but as we shall see later, our results can be readily generalized to hydrophilic particles. In this section, we consider the idealized case of a cylinder with a relatively sharp edges (sharpness parameter η = 20) adsorbing at a bare liquid interface. In the next section, we will extend this simple model to include experimentally relevant factors such as the rounding of the cylinder edge and interactions with other nanorods for nanorods adsorbing at an interface with pre-adsorbed nanorods.For convenience, we represent the adsorption trajectories of the cylindrical system using phase plane diagrams.53,54,71 This is illustrated in Fig. 3(a) where we show the adsorption trajectories for a hydrophobic cylinder with aspect ratio m = 2.5 for model 3 (deformed interface + Scaling 2) in the h vs. ϕ plane for h ∈ [−hc(ϕ),hc(ϕ)] and ϕ ∈ [0,π/2]. The solid red curves represent the height of the cylinder when it first contacts the liquid interface as a function of particle orientation hc(ϕ), with the left and right curve representing contact from the water and oil side respectively. The two black dots represent the stable states of the cylinder calculated in the previous section, with the dots at ϕ = 0°, 90° representing the end-on and side-on states respectively. The solid black curves are parametric plots of the adsorption trajectories of the cylinder (h(t),ϕ(t)), with all trajectories starting from the contact curves and flowing towards one of the two stable states as indicated by the arrows. To help visualize what these trajectories mean physically, in Fig. 3(a), we have highlighted three trajectories in bold and show snapshots of the cylinder at different stages of the adsorption process along these trajectories in Fig. 3(b)–(d). The dashed green line represents the ‘dynamical attractor’ to which many adsorption trajectories are attracted at the later stages of the adsorption process.
All the features in the phase plane that have been discussed so far also appear for the adsorption of ellipsoids.53,54,58 However, as non-neutrally-wetting cylinders possess two stable states rather than just one, a new feature emerges called the ‘separatrix’ which is given by the dashed purple line. The separatrix divides the phase plane into two attractive regions such that all flow lines originating from points in a given region will flow towards the stable point associated with that region, see Fig. 3. Recall that the main aim of this paper is to use adsorption kinetics to prepare cylinders in the end-on state. We are therefore particularly interested in where the separatrix intersects the two contact lines. These intersections are the boundary attack angles ϕ0 which tell us the range of particle attack angles which will lead to the end-on state.
In principle, the attractor and the separatrix lines are defined as the locus of points in (h,ϕ) space where the eigenvectors of the Hessian matrix ∇∇TF* with positive and negative eigen values respectively (i.e., with positive and negative principle curvatures respectively) are parallel to the gradient of the free energy ∇F*, where  is the grad operator in (h*,ϕ*) space.53,54 However, since calculating second derivatives is very noisy numerically, we instead calculate these lines by calculating the adsorption trajectories for multiple attack angles in order to identify the boundary attack angles at each of the two contact lines. The trajectories starting from attack angles just above and just below these boundary angles will then essentially trace out the separatrix and attractor lines.
is the grad operator in (h*,ϕ*) space.53,54 However, since calculating second derivatives is very noisy numerically, we instead calculate these lines by calculating the adsorption trajectories for multiple attack angles in order to identify the boundary attack angles at each of the two contact lines. The trajectories starting from attack angles just above and just below these boundary angles will then essentially trace out the separatrix and attractor lines.
Having outlined the key features in typical phase plane diagrams, in Fig. 4, we present the adsorption trajectories for hydrophobic cylinders with different aspect ratios calculated using different assumptions. Specifically, the top, middle and bottom row show results for aspect ratios m = 1, 2.5 and 5 respectively. On the other hand, the left, middle and right columns show the results for model 1 (flat interface + Scaling 1), model 2 (flat interface + Scaling 2) and model 3 (deformed interface + Scaling 2) respectively (see Section2 for details of these models).
We first consider the impact of the calculational model used on the adsorption process of cylinders. For all the aspect ratios shown in Fig. 4, we see that for model 1, there is generally strong non-monotonic variation of the particle orientation ϕ along the adsorption trajectory, with ϕ initially moving away from the stable state orientation before moving towards the stable state value at the later stages of the adsorption. However, as we go to model 2 then to model 3, the non-monotonic variation of ϕ is either strongly reduced or disappears altogether. This trend was also seen in our earlier study of ellipsoids where we found that the non-monotonic variation in ϕ was strongly suppressed in going from model 1 to model 3.54 We also note that model 3 agrees best with experiments on ellipsoid adsorption which found that particle orientation varied monotonically with time during the adsorption process.56,57
Interestingly, for the aspect ratios shown in Fig. 4, all three models showed very similar dynamic attractor lines. This result is again consistent with our earlier results for ellipsoids where we found that, far from the neutrally wetting regime, the attractor line becomes essentially insensitive to the assumed dynamic scaling model or contact line boundary condition.54 In contrast, the specific calculational model used has a strong impact on the shape of the separatrix line. Specifically, in going from model 1 to model 2, the boundary attack angle on the left contact line (i.e., particle attaching from water side) is significantly increased, while in going from model 2 to model 3, that boundary angle is significantly decreased again. On the other hand, there is very little change in the boundary attack angle on the right contact line (i.e., particle attaching from the oil side) in going from model 1 to model 2 to model 3. The net result is that when we change both the dynamical scaling model from Scaling 1 to Scaling 2 and the contact line boundary condition from flat to deformed interface, there is little change in the left and right boundary attack angles, suggesting that there is a cancellation of errors between these two model assumptions.
We next consider the impact of particle aspect ratio on the adsorption process of cylinders. Since we have shown previously that model 3 yields the most accurate results,54 we will focus on model 3 for this discussion (i.e., right column of Fig. 4). From Fig. 4, we note that for all aspect ratios, the left boundary attack angle is always smaller than the right boundary attack angle. Furthermore, as we increase the aspect ratio from m = 1 to m = 5, the left boundary attack angle is reduced from ϕ0 ≈ 10° at m = 1 to ϕ0 ≈ 0° for m = 5. In contrast there is very little change in the right boundary attack angle, with the attack remaining essentially constant at ϕ0 ≈ 50° as we increase the aspect ratio from m = 1 to m = 5. Finally, we note that although our discussion so far has focussed on hydrophobic cylinders, all our conclusions also apply to hydrophilic cylinders so long as we recognise that the phase plane diagrams in this case should be reflected about the h = 0 line. In particular, this means that in order to maximize the range of attack angles leading to the end-on state, hydrophilic cylinders should be adsorbed onto the liquid interface from the water side.
Based on our discussion above, we conclude that the optimum condition for preparing cylindrical nanorods in the end-on state is to adsorb the nanorods from their energetically favorable phase, i.e. hydrophobic particles should be dispersed in the oil phase and hydrophilic particles in the water phase. Surprisingly, when particles adsorb from the energetically favorable phase, the range of attack angles giving rise to the end-on state is only weakly dependent on the aspect ratio of the cylinders. This means that it should be possible to use the kinetic assembly method to prepare vertically aligned cylindrical nanorods with different aspect ratios, giving us the flexibility to tune the aspect ratio for different application (e.g., tune plasmonic modes for sensing applications). The caveat is that, while the aspect ratio may not be limited by adsorption kinetics, the end-on state becomes kinetically unstable when the aspect ratio of the cylinders m ≳ 10 (see previous section). This effect sets the main limiting factor for the cylinder aspect ratios that can be assembled using our kinetic method.
3.3 Adsorption kinetics of experimentally realistic nanorods
In the previous section we considered the adsorption of cylinders with sharp edges at a bare liquid interface. In real experimental systems, the nanorods generally have more rounded edges and adsorption often occurs at a crowded monolayer where interactions with other pre-adsorbed nanorods could be important. In this section, we study the impact of these factors on nanorod adsorption.We first consider the effect of edge rounding. In Fig. 5(a), we show a transmission electron micrograph of a GNR from ref. 72 with diameter 48 nm, length 120 nm and aspect ratio m = 2.5. We also superpose on the micrograph outlines calculated from the super-ellipsoid equation eqn (3) for the same aspect ratio and various sharpness parameter values η. From Fig. 5(a), we see that the edges of the GNR are more rounded than η = 20. Although it is difficult to assign a unique η value to the GNR because it does not fully conform to the super-ellipsoid shape (indeed there is evident faceting of the GNR ends in for this system), we can see that the GNR has an effective sharpness parameter lying between 4 ≤ η ≤ 12. In what follows we set η = 4 to give us an upper bound estimate for the influence of edge rounding on the adsorption trajectory of cylindrical nanorods and we compare these results to the case η = 20 that we considered in the previous section.
 | ||
| Fig. 5 (a) Transmission electron micrograph image of experimental GNR with aspect ratio m = 2.5 from ref. 72 together with outlines calculated from the super-ellipsoid equation eqn (3) for the same aspect ratio and various sharpness parameter values η. (b) interfacial energy as a function of tilt angle ϕ for cylindrical nanorods with aspect ratio m = 2.5, contact angle θw = 120° and sharpness parameter η = 4 (solid black line) or η = 20 (dashed red line), where the interfacial energy at each ϕ is minimised with respect to the particle height h. (c) Adsorption trajectories of nanorods with m = 2.5, θw = 120° and η = 4 (solid lines) or η = 20 (dashed lines). The black and open dots represent the stable states for η = 4 and 20 respectively, while the black, green and purple lines are respectively the adsorption trajectories, dynamic attractor and separatrix. | ||
In Fig. 5(b), we show the interfacial energy as a function of tilt angle ϕ for cylindrical nanorods with aspect ratio m = 2.5, contact angle θw = 120° and sharpness parameter η = 4 (solid black line) and η = 20 (dashed black line) where the interfacial energy at each ϕ is once again minimised with respect to the particle height h. Surprisingly, even though the edge is strongly rounded for η = 4 (see Fig. 5(a)), the end-on state is still a metastable state. In addition, although edge rounding clearly reduces the energy barrier stabilising the end-on state, the barrier for η = 4 is still significant. For example, for a nanorod system with η = 4, m = 2.5, θw = 120°, γow ≈ 30 mN m−1 and b = 25 nm, the energy barrier is ΔF ≈ 1000kT so that the end-on state is still kinetically stable. Evidently even for η = 4, the nanorod end is sufficiently flattened to stabilize the end-on state. In contrast, the end-on state is unstable for ellipsoids due to the absence of a flattened end.53,54,58
In Fig. 5(c), we show the phase plane diagram for the adsorption of nanorods with m = 2.5, θw = 120° and η = 4 (solid lines) or η = 20 (dashed lines). The black and open dots represent the stable states for η = 4 and 20 respectively and we see that increasing the rounding of the edges reduces the heights of both the side-on stable state (dots at ϕ = π/2) and end-on stable state (dots at ϕ = 0). This reduction is not surprising since when the edges are rounded, the hydrophobic nanorod can satisfy the constant contact angle condition by being immersed in the lower water phase more (see Fig. 5(a)). We also see that changing the rounding of the edges leads to discernable changes in the adsorption trajectories (black lines), dynamic attractor (green lines) and separatrix (pink lines). In particular, the range of attack angles leading to the end-on state is slightly decreased and increased respectively for particles approaching from the oil side and the water side. However, the changes in Fig. 5(c) are relatively small and none of the key features in in the phase plane diagram are changed qualitatively when we decrease η. We therefore conclude that the adsorption process is not significantly affected by edge-rounding and the sharp cylinders we have considered in the previous section therefore provide a good description for the adsorption kinetics of nanorods with experimentally realistic rounding.
Next, we consider the effect of interactions with pre-adsorbed nanorods on the adsorption kinetics. In principle, we can calculate this effect by including many pre-adsorbed nanorods in our simulation and doing an ensemble average over the configurations of these nanorods. However, since such a calculation is too expensive in Surface Evolver, we instead use a simplified model to mimic the effect of the other nanorods. Specifically, as shown in Fig. 6(a), we assume that the x,y-coordinate of the centre of the adsorbing nanorod (coloured in green) is in the centre of a hexagonal lattice with lattice constant S while the pre-adsorbed nanorods (coloured in yellow), assumed to be in the end-on state, are represented by the nearest and next-nearest neighbours in the hexagonal lattice. For definiteness, we further assume that the projection of the long axis of the adsorbing particle on the x,y-plane is parallel to one of the lattice vectors of the hexagonal lattice and consider a moderately dense monolayer with S = 3a.
Note that the open lattice shown in Fig. 6(a) is not the final equilibrium state of the system but represents a transient arrangement of the rods during the adsorption process. For vertical GNRs with b = 25 nm, a = 60 nm interacting through water, we estimate that the dispersion forces between the GNRs only become significant for nanorod separation ≲200 nm (see ESI†). Dispersion forces therefore do not play a significant role in the initial and intermediate stages of the adsorption process when the typical separation between nanorods is much greater than this value. Similarly, for a hydrophilic GNR approaching the oil–water interface from the water side, we estimate that the dispersion force between the GNR and the oil phase is significant only for surface-to-surface separations ≲40 nm (see ESI†). Dispersion forces therefore only attract the GNR towards the interface when the GNR is quite close to the interface. They are also sub-dominant compared capillary forces once the nanorods have adsorbed onto the interface47 and therefore do not play a significant role in determining the adsorption trajectory of the nanorods. However, dispersion forces will play a significant role in the final stages of the adsorption process as the final equilibrium separation is determined by balancing the attractive dispersion forces and repulsive forces (e.g., steric forces due to polymeric coatings) between nanorods. Finally, we note that since the energy barrier stabilizing the end-on state of typical nanorods is much greater than the thermal energy as discussed earlier, we anticipate that the effect of orientational fluctuations of the neighbouring nanorods on our calculations will be small.
In Fig. 6(b), we show the phase plane diagram for particle adsorption at the monolayer described above (solid lines) and at a bare liquid interface (dashed lines). The stable states for the monolayer and the bare interface cases are represented by the red and green dots respectively, but note that only the red dots are visible as the stable states in both cases are either very close or the same; the fact that the end-on state is the same for both monolayers and bare interfaces is as we expect since nanorods in the end-on state do not generate any interfacial deformations and hence no capillary interactions between the adsorbed and pre-adsorbed rods. We also see that interactions with pre-adsorbed nanorods lead to discernable changes in the adsorption trajectories (black lines) but hardly any changes to the dynamic attractor (green lines) and separatrix (pink lines). In particular, the range of attack angles leading to the end-on state is essentially unchanged for particles approaching from either the oil side or the water side, and none of the key features in in the phase plane diagram are changed qualitatively for nanorod adsorption at a dense monolayer. From our analysis in this section, we therefore conclude that the adsorption of cylinders with sharp edges at a bare liquid interface serves as an accurate predictive model for particle adsorption in experimentally realistic nanorod systems.
3.4 Metamaterial response of array of vertically aligned nanorods
We consider the optical properties of vertically aligned nanorods of 100 nm height and 20 nm radius (aspect ratio 2.5) organized in a hexagonal lattice. The aspect ratio of the nanorods was chosen to be the same for the nanorod adsorption calculations. The interparticle distance was chosen to be S = 80 nm while the refractive index and permittivity of the host medium was chosen to be n = 1.5 and εm = 2.25 respectively as we are considering a metamaterial consisting of an array of nanorods coated with a thick polymeric shell in their final close-packed configuration after they have been transferred to a solid substrate and immobilised. The main optical parameters of the array with interparticle distance are shown in Fig. 7(a). Here, the real (Re) and imaginary (Im) parts of the effective permittivity tensor components were calculated using the analytical expressions in eqn (8). The array has anisotropic behaviour with εx > 0 for the whole visible range, while εz shows epsilon-near-zero (ENZ) behaviour around 710 nm followed by negative εz. When εx > 0 and εz < 0, the metamaterial is in the hyperbolic regime and can support bulk electromagnetic states. We also evaluated numerically the εx for the exact model of the array of nanorods using Lumerical FDTD. The two methods give a similar shape and intensity of the spectra (see Fig. 7(a)).One can see in Fig. 7(b) that the spectral position of the ENZ behaviour depends on the interparticle distance S (and, thus, the fill factor p); note that S can be varied by adjusting the thickness of the dielectric shell around the nanorod.49,50 The array with the S = 3a (150 nm) still features the hyperbolic metamaterial characteristics with the ENZ point at 850 nm. Fig. 7(c) shows the electric field distribution at the ENZ region of εz for the polarization of the excitation light aligned along the z axis. The field reaches the highest values near the tips of the nanorods, but also part of the near-field is distributed between the nanorods and around them indicating that they are coupled at this wavelength. High electric fields and sensitivity of the optical response (ENZ point and hyperbolic modes) to the local refractive index make the aligned nanorod array a promising substrate for the sensing applications and surface-enhanced spectroscopies.
4. Discussion
Based on our results in the previous section, we now discuss the feasibility of using adsorption kinetics to experimentally prepare vertically aligned cylindrical nanorods at the liquid interface. As we shall see later, it is easier to use an external electric field to align metallic nanorods when they are in the more polar medium. In our following discussion, we therefore consider hydrophilic GNRs with long and short axis a = 60 nm and b = 25 nm respectively (i.e., m ≈ 2.5) approaching the interface from the water side. Our earlier calculations showed that the final state of such GNRs is the end-on state for initial attack angles less than ϕ0 ≈ 50°. We can visualise the initial orientation of the GNR as a point on a hemisphere with radius unity (hemisphere since the range of ϕ is 0° ≤ ϕ ≤90°). Since the initial orientation of these sub-micron particles is essentially random due to Brownian motion, the ensemble of initial GNR orientations can be represented by points which are uniformly distributed over the hemisphere. The fraction of particles contacting the interface that will end up in the end-on state f0 is therefore the fraction of the hemisphere occupied by a spherical cap which subtends an angle of ϕ0 at the centre of the hemisphere, i.e., | (10) |
We can increase this fraction by pre-aligning the GNRs in the bulk phase with an external electric field that is perpendicular to the liquid interface (see Fig. 8) so that more GNRs have attack angles less than ϕ0 when they approach the interface. In the presence of such a field, the energy of a GNR as a function of its orientation is given by73
 | (11) |
 | (12) |
 | (13) |
 is the volume of the ellipsoid, n‖, n⊥ are depolarizing factors along the long and short axis given by
is the volume of the ellipsoid, n‖, n⊥ are depolarizing factors along the long and short axis given by | (14) |
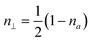 | (15) |
 is the eccentricity of the ellipsoid.
is the eccentricity of the ellipsoid.
In the presence of an electric field, the fraction of GNRs with attack angles in the range ϕ to ϕ + dϕ is given by the Boltzmann factor
 | (16) |
 and U (ϕ) is given by eqn (11). The fraction of GNRs with attack angles less than ϕ0 is therefore given by
and U (ϕ) is given by eqn (11). The fraction of GNRs with attack angles less than ϕ0 is therefore given by | (17) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, the fraction of GNRs contacting the interface that end up in the end-on state as a function of the applied electric field is therefore given by
ϕ, the fraction of GNRs contacting the interface that end up in the end-on state as a function of the applied electric field is therefore given by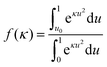 | (18) |
 | (19) |
From eqn (19), since Δα ∝ εr, for a given electric field E we obtain stronger alignment of the nanorods in the more polar medium. This is why we have considered hydrophilic GNRs approaching the liquid interface from the water side in this section. Specifically, for κ = 10, b = 25 nm, m = 2.5, εr = 80 (permittivity of water) and T = 300 K, from eqn (19) we find E ≈ 104 V m−1, i.e., applying this field in the water phase allows us to achieve 99.5% vertical alignment for the final state of the adsorbed nanorods. This is a modest electric field which is orders of magnitude smaller than the dielectric strength of de-ionised water (70 × 106 V m−1)75 and is easily achievable experimentally. Note that a common way to enhance the local electric field near a liquid–liquid interface is to add electrolytes to the two bulk phases and polarise the interface using an external field.76–78 Using this so-called interface between two immiscible electrolyte solutions (ITIES) arrangement would allow us to lower the external field required to pre-align the GNRs even further. We therefore conclude that it is feasible experimentally to use our kinetic assembly method to prepare high quality vertically aligned cylindrical nanorod monolayers at the liquid interface.
Finally, we note that applying an external electric field (either in the absence or presence of added electrolytes) will create polarization charges at the liquid interface which may significantly modify the interfacial tension of the liquid interface.76–78 However, since interfacial tension only affects the timescale of the adsorption (via the scaling factor β, see Section 2.2) but not the adsorption trajectory itself (i.e., particle orientation vs. particle height), applying an external electric field across the liquid interface should not in principle affect the main result of our free energy calculation, namely the range of particle attack angles which will lead to the end-on state of GNRs.
5. Conclusions
We have used Langevin dynamics coupled to a finite element model to study the adsorption kinetics of cylindrical nanorods at an oil/water interface in order to determine the optimum conditions for using adsorption kinetics to assemble nanorods into vertically aligned monolayers. Our Langevin model is more accurate compared to previous models as it captures the deformation of the liquid meniscus during particle adsorption and uses the correct ratio for the rotational to translational friction coefficients for the nanorod.We find that the end-on state is stable only for non-neutrally wetting cylindrical nanorods. We also find that the final orientation of the nanorods at the oil/water interface is determined by their initial attack angle when they contact the liquid interface. In particular, the range of attack angles leading to the end-on state is maximised when nanorods adsorb onto the liquid interface from the energetically favorable phase, i.e. hydrophobic particles from the oil phase and hydrophilic particles from the water phase. Surprisingly, we find that the range of attack angles is only weakly dependent on particle aspect ratio, thus allowing us to use adsorption kinetics to assemble vertically aligned nanorods for a wide range of aspect ratios. However, we also find that the energy barrier stabilizing the (metastable) end-on state decreases with increasing aspect ratio m. This effect sets a practical limit of m ≲ 10 on the cylindrical nanorods that can be assembled into vertically aligned monolayers using our kinetic assembly method.
Since only attack angles smaller than a threshold value lead to the end-on state, in the absence of an external field, only a fraction of nanorods that contact the liquid interface end up in the end-on state (typically ≲40% under optimum conditions). However, by pre-aligning the nanorods in the more polar bulk phase with experimentally achievable electric fields, we can increase this fraction to be effectively 100%. Finally, using nanophotonic calculations, we demonstrate that by tuning particle diameter and spacing, an ensemble of vertically aligned nanorods can be used as zero refractive index and hyperbolic metamaterials. Our kinetic assembly method is generic and can be used to assemble nanorods with a range of diameters, aspect ratios and materials (e.g., gold, silver, aluminium, copper, polymer, silica etc.). As such, it represents a versatile, low-cost and powerful platform for fabricating vertically aligned monolayers of nanorods for metamaterial applications.
Author contributions
SOM performed the Surface Evolver and adsorption trajectory calculations; AM performed the nanophotonic calculations; DMAB performed all other analytical calculations; SOM and DMAB wrote the manuscript with the help of AM, AMA and JSGB; TSH and all the other authors commented on the manuscript; DMAB, AMA and JSGB supervised the study; DMAB conceptualized the study.Conflicts of interest
There are no conflicts to declare.Acknowledgements
SOM and CL acknowledge funding from the University of Hull PhD Scholarship Scheme. SOM and DMAB acknowledge the Viper High Performance Computing facility of the University of Hull and it support team. We also thank Jens Harting and Luis Liz-Marzan for helpful discussions.References
- R. Aveyard, B. P. Binks and J. H. Clint, Adv. Colloid Interface Sci., 2003, 100, 503–546 CrossRef.
- A. D. Dinsmore, M. F. Hsu, M. G. Nikolaides, M. Marquez, A. R. Bausch and D. A. Weitz, Science, 2002, 298, 1006–1009 CrossRef CAS PubMed.
- K. P. Velikov and O. D. Velev in Colloidal Particles at Liquid Interfaces, ed. B. Binks, T. S. Horozov, Cambridge University Press, Cambridge, 2006 Search PubMed.
- O. D. Velev and S. Gupta, Adv. Mater., 2009, 21, 1897–1905 CrossRef CAS.
- J. Forth, P. Y. Kim, G. Xie, X. Liu, B. A. Helms and T. P. Russell, Adv. Mater., 2019, 31, 2678–2690 Search PubMed.
- P. Aussillous and D. Quéré, Nature, 2001, 411, 924–927 CrossRef CAS PubMed.
- E. M. Herzig, K. A. White, A. B. Schofield, W. C. K. Poon and P. S. Clegg, Nat. Mater., 2007, 6, 966–971 CrossRef CAS PubMed.
- B. P. Binks and R. Murakami, Nat. Mater., 2006, 5, 865–869 CrossRef CAS PubMed.
- C. C. Ho, A. Keller, J. A. Odell and R. H. Ottewill, Colloid Polym. Sci., 1993, 271, 469–479 CrossRef CAS.
- J. C. Loudet, A. M. Alsayed, J. Zhang and A. G. Yodh, Phys. Rev. Lett., 2005, 94, 018301 CrossRef CAS PubMed.
- J. C. Loudet, A. G. Yodh and B. Pouligny, Phys. Rev. Lett., 2006, 97, 018304 CrossRef CAS PubMed.
- H. Lehle, E. Noruzifar and M. Oettel, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 26, 151 CrossRef CAS PubMed.
- B. Madivala, J. Fransaer and J. Vermant, Langmuir, 2009, 25, 2718–2728 CrossRef CAS PubMed.
- B. J. Newton, K. A. Brakke and D. M. A. Buzza, Phys. Chem. Chem. Phys., 2014, 16, 26051–26058 RSC.
- E. P. Lewandowski, P. C. Searson and K. J. Stebe, J. Phys. Chem. B, 2006, 110, 4283 CrossRef CAS PubMed.
- E. P. Lewandowski, M. Cavallaro Jr., L. Botto, J. C. Bernate, V. Garbin and K. J. Stebe, Langmuir, 2010, 26, 15142 CrossRef CAS PubMed.
- B. J. Newton and D. M. A. Buzza, Soft Matter, 2016, 12, 5285 RSC.
- Q. Song, M. Steuber, S. I. Druzhinin and H. Schonherr, Angew. Chem., Int. Ed., 2019, 58, 5246 CrossRef CAS PubMed.
- Q. Song and H. Schonherr, Langmuir, 2019, 35, 6742 CrossRef CAS PubMed.
- G. Soligno, M. Dijkstra and R. van Roij, Phys. Rev. Lett., 2016, 116, 258001 CrossRef PubMed.
- G. Soligno, M. Dijkstra and R. van Roij, Soft Matter, 2018, 14, 42 RSC.
- C. Anzivino, G. Soligno, R. van Roij and M. Dijkstra, Soft Matter, 2021, 17, 965 RSC.
- S. Sacanna and D. J. Pine, Curr. Opin. Colloid Interface Sci., 2011, 16(2), 96–105 CrossRef CAS.
- Z. Gong, T. Hueckel, G. R. Yi and S. Sacanna, Nature, 2017, 550(7675), 234–238 CrossRef PubMed.
- S. Dasgupta, M. Katava, M. Faraj, T. Auth and G. Gompper, Langmuir, 2014, 30, 11873 CrossRef CAS PubMed.
- D. Vestler, I. Shishkin, E. A. Gurvitz, M. E. Nasir, A. Ben-Moshe, A. P. Slobozhanyuk, A. V. Krasavin, T. Levi-Belenkova, A. S. Shalin, P. Ginzburg, G. Markovich and A. V. Zayats, Opt. Express, 2018, 26, 17841 CrossRef CAS PubMed.
- A. V. Kabashin, P. Evans, S. Pastkovsky, W. Hendren, G. A. Wurtz, R. Atkinson, R. Pollard, V. A. Podolskiy and A. V. Zayats, Nat. Mater., 2009, 8, 867–871 CrossRef CAS PubMed.
- J. Gao, X. Wu, Q. Li, S. Du, F. Huang, L. Liang, H. Zhang, F. Zhuge, H. Cao and Y. Song, Adv. Mater., 2017, 29, 1605324 CrossRef PubMed.
- G. A. Wurtz, R. Pollard, W. Hendren, G. P. Wiederrecht, D. J. Gosztola, V. A. Podolskiy and A. V. Zayats, Nat. Nanotechnol., 2011, 6, 107–111 CrossRef CAS PubMed.
- G. A. Wurtz, W. Dickson, D. O’Connor, R. Atkinson, W. Hendren, P. Evans, R. Pollard and A. V. Zayats, Opt. Express, 2008, 16, 7460 CrossRef CAS PubMed.
- D. J. Roth, A. V. Krasavin, A. Wade, W. Dickson, A. Murphy, S. Kéna-Cohen, R. Pollard, G. A. Wurtz, D. Richards, S. A. Maier and A. V. Zayats, ACS Photonics, 2017, 4, 2513–2521 CrossRef CAS.
- D. P. Lyvers, J. M. Moon, A. V. Kildishev, V. M. Shalaev and A. Wei, ACS Nano, 2008, 2, 2569–2576 CrossRef CAS PubMed.
- X.-D. Tian, Y. Lin, J.-C. Dong, Y.-J. Zhang, S.-R. Wu, S.-Y. Liu, Y. Zhang, J.-F. Li and Z.-Q. Tian, Adv. Opt. Mater., 2017, 5, 1700581 CrossRef.
- Z. Zhang and M. Lin, J. Mater. Chem. C, 2014, 2, 4545–4551 RSC.
- R. A. Alvarez-Puebla, A. Agarwal, P. Manna, B. P. Khanal, P. Aldeanueva-Potel, E. Carbó-Argibay, N. Pazos-Pérez, L. Vigderman, E. R. Zubarev, N. A. Kotov and L. M. Liz-Marzán, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 8157–8161 CrossRef CAS PubMed.
- K. Kim, H. S. Han, I. Choi, C. Lee, S. Hong, S.-H. Suh, L. P. Lee and T. Kang, Nat. Commun., 2013, 4, 2182 CrossRef PubMed.
- G. A. Wurtz, P. R. Evans, W. Hendren, R. Atkinson, W. Dickson and R. J. Pollard, Nano Lett., 2007, 7(5), 1297–1303 CrossRef CAS PubMed.
- A. D. Neira, N. Olivier, M. E. Nasir, W. Dickson, G. A. Wurtz and A. V. Zayats, Nat. Commun., 2015, 6, 1–8 Search PubMed.
- P. R. Evans, G. A. Wurtz, R. Atkinson, W. Hendren, D. O’Connor, W. Dickson, R. J. Pollard and A. V. Zayats, J. Phys. Chem. C, 2007, 111, 12522–12527 CrossRef CAS.
- K. Takahashi, S. J. Limmer, Y. Wang and G. Cao, J. Phys. Chem. B, 2004, 108, 9795–9800 CrossRef CAS.
- D. Zschech, D. H. Kim, A. P. Milenin, R. Scholz, R. Hillebrand, C. J. Hawker, T. P. Russell, M. Steinhart and U. Gösele, Nano Lett., 2007, 7, 1516–1520 CrossRef CAS PubMed.
- M. E. Nasir, A. V. Krasavin, R. M. Córdova-Castro, C. P. T. McPolin, J. G. Bouillard, P. Wang and A. V. Zayats, Adv. Opt. Mater., 2021, 9, 2001467 CrossRef CAS.
- Y. Xie, S. Guo, Y. Ji, C. Guo, X. Liu, Z. Chen, X. Wu and Q. Liu, Langmuir, 2011, 27, 11394–11400 CrossRef CAS PubMed.
- B. Peng, Z. Li, E. Mutlugun, P. L. Hernández Martínez, D. Li, Q. Zhang, Y. Gao, H. V. Demir and Q. Xiong, Nanoscale, 2014, 6, 5592–5598 RSC.
- A. Guerrero-Martínez, J. Pérez-Juste, E. Carbó-Argibay, G. Tardajos and L. M. Liz-Marzán, Angew. Chemie, 2009, 121, 9648–9652 CrossRef.
- A. D. Law, D. M. A. Buzza and T. S. Horozov, Phys. Rev. Lett., 2011, 106, 128302 CrossRef PubMed.
- A. D. Law, M. Auriol, D. Smith, T. S. Horozov and D. M. A. Buzza, Phys. Rev. Lett., 2013, 110, 138301 CrossRef PubMed.
- M. Rey, A. D. Law, D. M. A. Buzza and N. Vogel, J. Am. Chem. Soc., 2017, 139, 17464–17473 CrossRef CAS PubMed.
- M. Rey, T. Yu, K. Bley, K. Landfester, D. M. A. Buzza and N. Vogel, Langmuir, 2018, 34, 9990–10000 CrossRef CAS PubMed.
- J. Menath, J. Eatson, R. Brilmayer, A. Andrieu-Brunsen, D. M. A. Buzza and N. Vogel, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2113394118 CrossRef CAS PubMed.
- T. Kraus, D. Brodoceanu, N. Pazos-Perez and A. Fery, Adv. Funct. Mater., 2013, 23, 4529–4541 CrossRef CAS.
- M. E. Hummel, C. Stelling, B. A. Kopera, F. A. Nutz, M. Karg, M. Retsch and S. Förster, Langmuir, 2019, 35, 973–979 CrossRef CAS PubMed.
- J. de Graaf, M. Dijkstra and R. van Roij, J. Chem. Phys., 2010, 132, 164902 CrossRef PubMed.
- S. O. Morgan, J. Fox, C. Lowe, A. M. Adawi, J.-S. G. Bouillard, G. J. Stasiuk, T. S. Horozov and D. M. A. Buzza, Phys. Rev. E, 2021, 103, 042604 CrossRef CAS PubMed.
- D. M. Kaz, R. McGorty, M. Mani, M. P. Brenner and V. N. Manoharan, Nat. Mater., 2012, 11, 138 CrossRef CAS PubMed.
- A. Wang, W. B. Rogers and V. N. Manoharan, Phys. Rev. Lett., 2017, 119, 108004 CrossRef PubMed.
- S. Coertjens, R. De Dier, P. Moldenaers, L. Isa and J. Vermant, Langmuir, 2017, 33, 2689 CrossRef CAS PubMed.
- F. Gunther, S. Frijters and J. Harting, Soft Matter, 2014, 10, 4977 RSC.
- S. Coertjens, P. Moldenaers, J. Vermant and L. Isa, Langmuir, 2014, 30, 4289 CrossRef CAS PubMed.
- K. A. Brakke, Exp. Math, 1992, 1, 141–165 CrossRef.
- G. Morris, S. J. Neethling and J. J. Cilliers, J. Colloid Interface Sci., 2011, 354(1), 380–385 CrossRef CAS PubMed.
- B. J. Newton, R. Mohammed, G. B. Davies, L. Botto and D. M. A. Buzza, ACS Omega, 2018, 3, 14962 CrossRef CAS PubMed.
- G. Boniello, C. Blanc, D. Fedorenko, M. Medfai, N. B. Mbarek, M. In, M. Gross, A. Stocco and M. Nobili, Nat. Mater., 2015, 14, 908 CrossRef CAS PubMed.
- R. J. Pollard, A. Murphy, W. R. Hendren, P. R. Evans, R. Atkinson, G. A. Wurtz, A. V. Zayats and V. A. Podolskiy, Phys. Rev. Lett., 2009, 102, 127405 CrossRef CAS PubMed.
- J. Elser, R. Wangberg, V. A. Podolskiy and E. E. Narimanov, Appl. Phys. Lett., 2006, 89, 5–7 CrossRef.
- R. Atkinson, W. R. Hendren, G. A. Wurtz, W. Dickson, A. V. Zayats, P. Evans and R. J. Pollard, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 1–8 CrossRef.
- P. B. Johnson and R. W. Christy, Phys. Rev. B: Condens. Matter Mater. Phys., 1972, 6, 4370–4379 CrossRef CAS.
- https://www.lumerical.com/tcad-products/fdt .
- D. R. Smith, D. C. Vier, T. Koschny and C. M. Soukoulis, Phys. Rev. E: Stat. Nonlinear, Soft Matter Phys., 2005, 71, 1–11 Search PubMed.
- R. W. Ziolkowski, IEEE Trans. Antennas Propag., 2003, 51, 1516–1529 CrossRef.
- P. Collins, Differential and Integral Equations, Oxford University Press, 2006 Search PubMed.
- G. González-Rubio, V. Kumar, P. Llombart, P. Díaz-Núñez, E. Bladt, T. Altantzis, S. Bals, O. Peña-Rodríguez, E. G. Noya, L. G. MacDowell, A. Guerrero-Martínez and L. M. Liz-Marzán, ACS Nano, 2019, 13, 4424–4435 CrossRef PubMed.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, 1986 Search PubMed.
- L. D. Landau, E. M. Lifshitz and L. P. Pitaevskii, Electrodynamics of Continious Media, 2nd Edn, Elsevier Butterworth-Heinemann, 1984 Search PubMed.
- Dielectric Strength of Insulating Materials, in CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Taylor and Francis, Boca Raton, FL, 88th Edition, CD-ROM Version, 2008 Search PubMed.
- E. J. W. Verwey and K. F. Niessen, Philos. Mag., 1939, 28, 435–446 CAS.
- Z. Samec, Chem. Rev., 1988, 88, 617–632 CrossRef CAS.
- G. I. Guerrero-García and M. Olvera de la Cruz, J. Chem. Theory Comput., 2013, 9, 1–7 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d1cp05484h |
| This journal is © the Owner Societies 2022 |