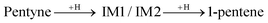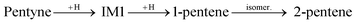An ab initio study of size-selected Pd nanocluster catalysts for the hydrogenation of 1-pentyne

Abstract

The hydrogenation of alkynes is an important reaction in the synthesis of both fine and bulk chemicals. Palladium-based catalysts are widely used and therefore size-selected Pd nanoclusters may provide enhanced performance. An investigation of the adsorption and desorption of the molecules involved in the reaction can shed light on the activity and selectivity of the catalysts. We employ ab initio calculations to investigate the binding energies of all the molecules related to the hydrogenation of 1-pentyne (1-pentyne, 1-pentene, cis-2-pentene, trans-2-pentene and pentane) on a comprehensive set of possible binding sites of two Pd₁₄₇ and Pd₅₆₁ cuboctahedral nanoclusters. We extract the site and size dependence of these binding energies. We find that the adsorption of 1-pentyne occurs preferably on the (100) facets of the nanoclusters, followed by their (111) facets, their edges and their vertices. The molecule binds more strongly on the larger nanoclusters, which are therefore expected to display higher activity. The binding energies of the pentenes are found to be lower on the smaller nanoclusters. Therefore, these molecules are expected to desorb more easily and the small clusters should display better selectivity, i.e., partial hydrogenation to 1-pentene, compared with large clusters. Our results provide guidelines for the optimal design of Pd nanocatalysts.

---

Introduction

The selective hydrogenation of alkynes is extremely important in both the fine and bulk chemicals sectors. Therefore, efficient and selective heterogenous catalysts are highly needed to improve the productivity of these industrial reactions. The interplay between activity (yield) and selectivity, specifically, partial hydrogenation to alkenes, depends on the atomic and chemical structure of the catalyst, which is often based on Pd, as the Lindlar catalyst,¹ which served as the industry standard for the selective hydrogenation of alkynes for several decades. Due to its inherent disadvantages, there has been an effort during the past decade for developing new more economic, active and selective catalysts for the production of alkenes.² The availability of size-selected metal nanoclusters provides catalysis research with a new toolbox. In model studies, such nanostructured catalysts can outperform conventional catalysts in terms of activity, selectivity and overall efficiency.^3,4 Recent advances in nanofabrication provide many options for the production of novel, selective nanocatalysts for the partial hydrogenation of alkynes.^5–7 The synthesis of nanocatalysts by deposition of nanoparticles from a cluster beam source, can offer unparalleled size control and shows promise for various applications^8,9 and routes to scale-up of this technique are now being explored.^10–12

In the case of alkyne hydrogenations, specifically that of 1-pentyne, 3–8 nm Pd nanoparticles (NPs) and nanoalloys synthesised in the gas phase and deposited on conventional metal-oxide support powders, such as alpha alumina, gamma alumina and titania, resulted in Pd materials that performed as well as those made by the typical catalyst manufacturing methods of impregnation and deposition¹³ and alloy materials that outperformed them.¹⁴ Small Pd nanoparticles (55–400 atoms) deposited on graphite powders also performed well for the same reaction.¹⁵ Importantly, they showed very good stability against sintering, important due to the suppression of the melting point at the nanoscale and the elevated temperatures at which the hydrogenation reactions take place, and a size-dependent activity and selectivity, which no doubt relates to probable active sites for the reaction. A size-dependent activity for nanocluster catalysts has also been reported for the selective hydrogenation of 1-hexyne on large (6–14 nm) NPs, where a 15-fold turnover frequency increase was observed when the size of the NP increased from 11 to 14 nm.¹⁶

These experimental works on the hydrogenation of 1-alkyne on metal nanocluster catalysts call for theoretical support. Such a study was recently performed for the hydrogenation of 1-pentyne on small Cu₂₀ model nanoclusters,¹⁷ where the active sites, formation barriers and reaction paths were determined. Ab initio works are important in the study of catalysis, since they can provide an understanding of the interactions between the reactants and the catalysts, reveal the mechanisms behind the catalytic reaction and reveal variations between different catalysts.^4,18,19 In this work, we report an ab initio computational study of the hydrogenation of 1-pentyne on free Pd₁₄₇ and Pd₅₆₁ cuboctahedral NPs. We perform a detailed examination of the binding energies of the stable molecules involved in the hydrogenation and extract the dependencies of these binding energies on the binding area and size of the NP. We conclude with critical considerations for the design of efficient Pd nanocatalysts for the hydrogenation of 1-pentyne.

Theoretical methods

The Density Functional Theory (DFT) calculations were performed using the Vienna Ab initio Simulation Package (VASP)^20,21 under the Perdew–Burke–Ernzerhof derivation of the Generalized Gradient Approximation (GGA-PBE),²² with Projector Augmented-Wave (PAW) pseudopotentials.^23,24 The energy cut-off of the plane-wave basis set was 400 eV. The Brillouin zone was sampled at the Γ point and the break condition for the electronic self-consistent loop was 1 meV. The width of the vacuum surrounding the nanoclusters was more than 15 Å in all directions, which ensured that there was no interaction between the nanoclusters and their nearest image. van der Waals interactions were taken into account through the DFT-D3 method²⁵ with Becke–Jonson damping.²⁶

We built models of 147-atom and 561-atom cuboctahedral Pd NPs on which the hydrocarbon molecules were deposited. The choice of the cuboctahedral structural motif was based on the presence of both (100) and (111) facets: cuboctahedral NPs comprise six (100) facets and eight (111) facets. This facilitated the comparison between different binding sites. It has also been shown to be the dominant shape of large, 923- and 2057-atom, Pd NPs before and after the vapor-phase 1-pentyne hydrogenation treatment.²⁷ The Pd clusters were fully relaxed before the placement of the hydrocarbon molecules. The hydrocarbon molecules were then placed on the binding spots under examination and the models were fully relaxed again to obtain the true lowest energy configurations.

The binding energies E_binding of the hydrocarbon molecules were calculated according to:

E_{binding =}E_{particle+molecule} − E_particle − E_molecule

where E_particle, E_molecule and E_{particle+molecule} are the total energies after relaxation of the free NP, the free hydrocarbon molecule and the NP-molecule combination, respectively.

The charge density difference Δρ was calculated according to:

Δρ = ρ_{cluster+molecule} − ρ_cluster − ρ_molecule

where ρ_{cluster+molecule}, ρ_cluster and ρ_molecule are the electron charge densities obtained from static runs of the relaxed models of the NP–molecule combination, the free NP and the free molecule, respectively. The imaging of the results was performed with the VESTA visualization program.²⁸

Results and discussion

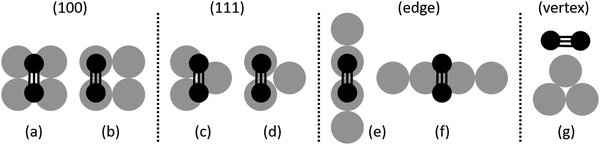
The surface of a cuboctahedral NP presents (100) facets, (111) facets, edges and vertices. These NP facets present structural differences compared to the respective bulk surfaces, especially in the smaller NPs. For example, the atoms of the (100) facets of a Pd₁₄₇ NP are 2–3% closer compared to bulk (100) surfaces (1–3% for the Pd₅₆₁ NP). The shells are generally closer by 1–2% compared to the bulk.

A comprehensive set of molecule binding sites and orientations on these different areas was examined for all the molecules related to the hydrogenation of 1-pentyne (1-pentyne, 1-pentene, cis-2-pentene, trans-2-pentene and pentane). The examined configurations are shown in Fig. 1. For the facets we placed the unsaturated bonds of the molecules between two Pd atoms or a Pd triangle in the case of the (111) facet and a quadruplet of Pd atoms in the (100) facet (Fig. 1(a–d)). For the edges we performed relaxations with each molecule's unsaturated bond parallel and perpendicular to the edge and always between two Pd atoms (Fig. 1(e and f)). For the vertex we placed the molecules directly on top of the Pd atom (Fig. 1(g)). The resulting binding energies for the Pd₁₄₇ and Pd₅₆₁ NPs, as well as the respective binding energies on bulk Pd(100) and (111) surfaces, are given in Table 1.

Fig. 1 The different orientations of the molecules on the four possible binding areas of the Pd NPs. From left to right: top-down views of the 1-pentyne molecule's triple bond on (a and b) the (100) facet; (c and d) the (111) facet; (e and f) the edge between the two facets; and (g) side view of the molecule on the NP vertex. Grey circles represent Pd atoms and black circles represent C atoms.

Table 1 The binding energies in eV of the molecules involved in the hydrogenation of 1-pentyne on the four surface regions of a Pd₁₄₇ cuboctahedral NP, a Pd₅₆₁ cuboctahedral NP and the (100) and (111) Pd surface slabs

	Pd147				Pd561				Pd
	(100)	(111)	Edge	Vertex	(100)	(111)	Edge	Vertex	(100)	(111)
1-Pentyne	−3.25	−2.27	−1.95	−1.27	−3.44	−2.63	−2.00	−1.38	−3.28	−2.45
1-Pentene	−1.41	−1.19	−1.46	−1.28	−1.61	−1.44	−1.53	−1.32	−1.57	−1.50
cis-2-Pentene	−1.35	−1.19	−1.48	−1.41	−1.49	−1.44	−1.52	−1.37	−1.55	−1.44
trans-2-Pentene	−1.40	−1.17	−1.42	−1.38	−1.58	−1.40	−1.50	−1.12	−1.58	−1.23
Pentane	−0.47	−0.45	−0.47	−0.36	−0.55	−0.50	−0.50	−0.33	−0.58	−0.62

---

We find a clear preference for 1-pentyne to bind on the (100) facets, with the 1-pentyne triple bond exactly between a quadruplet of Pd atoms, as shown in Fig. 1(a). The binding energies on the (100) facet are 0.98 (0.81) eV larger for the Pd₁₄₇ (Pd₅₆₁) NPs compared with the next preferable sites on the (111) facet between a triplet of Pd atoms. The binding energies on the NP edge are of the same scale as these of the (111) facet, but somewhat smaller. For the edges, there is a small preference for the configuration of Fig. 1(f) compared with Fig. 1(e), equal to 0.02 (0.07) eV for the Pd₁₄₇ (Pd₅₆₁) NPs. The two C atoms of the unsaturated bond interact with two Pd atoms in both cases. The binding energy of the molecule on the NP vertex is much smaller, lower than half of the binding energy on the (100) facets for both NPs. The relaxed models for the lowest energy sites on each of the four surface regions are shown in Fig. 2.

Fig. 2 The energetically preferable configurations of the 1-pentyne molecule on the four possible binding areas of a Pd₅₆₁ NP. Side views of the 1-pentyne molecule (a) on a (100) facet, (b) on a (111) facet, (c) on the edge between the two facets and (d) on the NP vertex.

1-Pentene and the 2-pentenes preferably orient themselves with their double bond on top of two Pd atoms (Fig. 1(b)). In order to find how easily a 1-pentene molecule transitions between the two sites of Fig. 1(a and b), we calculated the related transition barrier, for which the results are shown in the ESI.† We found that even if one starts from a 1-pentene molecule centered between the quadruplet of Pd atoms (as it might come from the hydrogenation of a 1-pentyne molecule on this exact site) it will slide laterally towards a lower energy site on top of a pair of two Pd atoms, and the barrier for this translation is either 0 or a minimal 0.05 eV. The differences between the two movements are attributed to the asymmetrical shape of the 1-pentene molecule. Again, on the (111) facets, while 1-pentyne will prefer the configuration of Fig. 1(c), being associated with three Pd atoms, 1-pentene will prefer the configuration of Fig. 1(d) being on top of two Pd atoms.

The binding energies reported for pentane in Table 1 refer to the molecule on top of two Pd atoms, in a configuration similar to Fig. 1(b), assuming the pentene results from the hydrogenation of 1-pentene. Pentane would otherwise preferably lie in the center of the quadruplet, like 1-pentyne, showing a binding energy of 0.54 (0.61) eV for the Pd₁₄₇ (Pd₅₆₁) NPs. On the (111) facet, there is virtually no difference in energy between the orientations of Fig. 1(c and d).

Regarding the dependence upon the NP size, 1-pentyne always binds more strongly to the larger NP, a trend retained for all the other molecules. In general, the binding energies of the molecules on the Pd₅₆₁ NP will be up to 30–40 meVs higher than the binding energies on the Pd₁₄₇ NPs. These results are consistent with previous experimental results showing an increased 1-pentyne hydrogenation activity of Pd nanoclusters with cluster size,¹⁵ since (a) 1-pentyne will bind more strongly on large NPs and (b) the area of the (100) facets increases at an exponential rate with the size of the nanoclusters, whereas the length of edges increases linearly and the number of vertices remains the same.

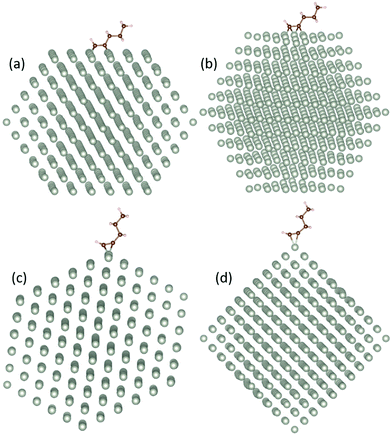
For 1-pentyne, the four C–Pd bonds have a length of 2.02–2.05 Å. Similarly, the two bonds of 1-pentene have a length of 2.09–2.11 Å. Pentane is further removed from the facet; the respective bond length is 2.89–3.01 Å. The nature of the bonding of the molecules on the Pd nanoparticles is visualized by the charge density differences in Fig. 3. The charge densities illustrate the formation of chemical bonds between the hydrocarbon molecule and four Pd atoms in 1-pentyne, two Pd atoms in 1-pentene and a very weak bonding with two Pd atoms in pentane.

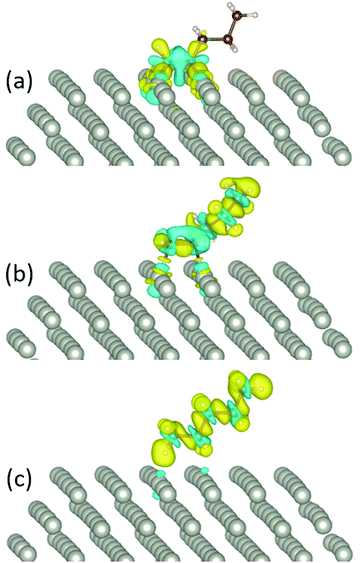Fig. 3 The charge density difference of (a) 1-pentyne, (b) 1-pentene, and (c) pentane on a Pd₁₄₇ nanocluster. Blue and yellow colours represent charge depletion and accumulation, respectively.

A Bader charge analysis illustrates the charge exchange between the hydrocarbon molecules and the NP. For 1-pentyne, we observe a charge transfer of 0.2 e from each C atom towards the 4 Pd atoms beneath it. In 1-pentene, 0.1 e from each C atom is transferred to the 2 Pd atoms under the molecule. Lastly, for pentane, the charge transfer is negligible. These charge exchanges are marginally higher (∼0.01 e) for Pd₁₄₇ compared to Pd₅₆₁.

Structural changes occur to all the molecules when bound on the Pd NP facets and the scale of these changes depends on the molecule and on the binding site. The triple bond is stretched to 1.42 Å from 1.21 Å in the free 1-pentyne molecule (+17%) when it binds on the (100) facet of the Pd₅₆₁ nanocluster. The C atoms participating in the bond and the third C atom are at an angle of 120°, although almost collinear in the free molecule (177°). Importantly, we observe a preference for a pentane-like configuration of the last three C atoms of the molecule (Fig. 1(a)). This particular configuration is 0.16 eV (0.19) eV lower in energy for the (100) facets of the Pd₁₄₇ (Pd₅₆₁) NPs compared with the original configuration. It persists for the (111) facets (Fig. 2(b)), whereas for the edge and vertex cases the original configuration of the 1-pentyne molecule becomes preferable again (Fig. 1(c and d)).

The 1-pentyne triple bond length change correlates with the binding strength of the molecule to a specific site. We obtain a distance of 1.39 Å for the (111) facet, 1.31–1.32 Å for the edges and 1.27 Å for the vertex of a Pd₅₆₁ NP. In the last case, the 1-pentyne molecule is almost structurally unchanged. In the three pentenes (1-, trans-2- and cis-2-), the double bonds are stretched from 1.34 Å in the free molecules to 1.44, 1.45 and 1.46 Å, respectively, for the chemisorbed molecules (+7–9%), while the angles of the C triplets containing the double bonds change by 2–8°. Pentane is very weakly bonded to the NP, independent of the binding site, and this fact is reflected in its structure: the length of the single bond between the two first C atoms only stretches to 1.52–1.53 Å from 1.50 Å depending on the orientation, and the angles between the C triplets of the molecule change by only ∼1°.

The first H atom to bind to the 1-pentyne molecule can either connect to the 1st C atom of 1-pentyne resulting in a H2C⋯C⋯CH2–R semi-hydrogenated intermediate (IM1) or the 2nd C atom resulting in a HC⋯CH⋯CH2–R semi-hydrogenated intermediate (IM2). Of these two, IM1 is lower in energy by 0.21 eV (0.15 eV) on the Pd₁₄₇ (Pd₅₆₁) NP. Two possibilities arise from this point: (i) the IM1 and IM2 intermediates accept one more H atom which binds with their 2nd or 1st C atoms, respectively, to form H2C=CH–CH2–R (1-pentene), or (ii) IM1 undergoes an isomerization to H2C⋯CH⋯CH–R (IM3), where a H atom moves from the 3rd C atom to the 2nd.

IM3 is more stable than IM1. It is lower in energy by 0.11 eV (0.25 eV) on the Pd₁₄₇ (Pd₅₆₁) NP. IM3 will hydrogenate to a pentene depending on where the next H atom binds: 1-pentene if it binds to the 2nd C atom or 2-pentene to the 1st C atom. Alternatively, 1-pentene may isomerise to 2-pentene.

Summarising the above, the simplest reaction path for the formation of 1-pentene is:

and the alternative paths for the formation of 2-pentene are:
and
Both transitions from IM1 to IM3 and from 1-pentene to 2-pentene are favoured since the resulting molecules are more stable. trans-Like IM3 is lower in energy by 0.09 eV (0.15 eV) on Pd₁₄₇ (Pd₅₆₁) compared to cis-like IM3. Likewise, trans-2-pentene is lower in energy by 0.07 eV (0.11 eV) compared to cis-2-pentene on Pd₁₄₇ (Pd₅₆₁) NP. These results are in accordance with the experiments showing an amount of trans-2-pentene comparable with that of 1-pentene, and a smaller but still significant amount of cis-2-pentene.¹³

The binding energies of the molecules dictate the rate at which a specific molecule adsorbs and desorbs and, therefore, play a significant role in predicting the selectivity of the Pd catalysts. The tailoring of the catalyst's properties can be achieved through the manipulation of these binding energies. For partial hydrogenation, the pentyne molecule must strongly bind to the surface in order to be hydrogenated to pentene and then must easily desorb instead of further hydrogenating to pentane. Ideally, one would want to control the size and shape of the nanoclusters, to show high binding energies for 1-pentyne and low binding energies for 1-pentene and 2-pentene. The desorption rates of the molecules can be estimated using a harmonic approximation to transition state theory, with the rate constant expressed as:

_{k = ve}^−E_b/k_BT

where v is a pre-exponential factor, E_b is the binding energy, k_B is the Boltzmann constant, and T is the temperature.²⁹ The v factor is taken to be 10¹³ s⁻¹ site⁻¹, but may be scaled down by 1–4 orders of magnitude due to the fact that the molecules will not be always present at all active sites. This scale down changes the calculated rates only minimally, and is equivalent to a 0.1 eV change in the binding energies.

The exponential nature of the rate constants means that very small changes in the binding energies translate to big effects on the rate constants. A comparison of the desorption rate constants based on our calculated binding energies of 1-pentene on the (100) and (111) facets of the two NPs is given in Table 2. The rate increases 290- to 80-fold in favour of the (111) facets, with the change being smaller in the bigger NP. Most importantly, depending on the binding site, the smaller NP shows a 170- to 630-fold increase in the desorption rate constant compared with the larger NP.

Table 2 The desorption rate constants in s⁻¹ site⁻¹ for v = 10¹⁰ for 1-pentene on the (100) and (111) facets of a Pd₁₄₇ and a Pd₅₆₁ cuboctahedral NP at 450 K

	(100)	(111)
Pd147	1.6 × 10^−6	4.7 × 10^−4
Pd561	9.3 × 10^−9	7.5 × 10^−7

---

Of course, to better evaluate the parameters for desorption one would also have to take into account the number of active sites, since the real desorption rate at a reactive site on the surface are the rate constant times the probability a molecule is present at such a site. This number is of course dependent on the structure and size of the NP. For example, a cuboctahedral Pd₅₆₁ NP has 2.74 times more surface atoms than a Pd₁₄₇ NP (252 compared to 92). However, even if we assume this many more binding sites for the bigger NP, the desorption rate of the Pd₁₄₇ NP will still be at least a hundred times higher than the desorption rate of the Pd₅₆₁NP. Lastly, we should also mention that, in general, the semi-hydrogenated intermediates show very high binding energies (∼3–4 eV). Therefore, it is very unlikely for a molecule to desorb at these points.

Conclusions

To explore the partial hydrogenation of 1-pentyne on Pd nanoclusters, we have investigated the adsorption of 1-pentyne, 1-pentene, cis-2-pentene, trans-2-pentene and pentane on Pd₁₄₇ and Pd₅₆₁ nanoclusters via ab initio calculations. The energetically preferable sites for the adsorption of all the molecules are the (100) facets of the nanoclusters, followed by their (111) facets, the edges and the vertices. All molecules bind more strongly on larger nanoclusters, which are therefore expected to display higher activity. The binding energies of the pentenes are found to be lower on the smaller nanoclusters. These small clusters should be more selective to 1-pentene: enhanced desorption reduces the chance of over hydrogenation to pentane or isomerisation to cis- and trans-2-pentene.

Our results provide guidelines for the fabrication of Pd nanocluster catalysts with control of their activity and selectivity:

(i) very active nanocatalysts must comprise large NPs with (100) facets. Big, crystalline, cubic NPs are ideal.

(ii) very selective catalysts must comprise small NPs with (111) facets. These may be either crystalline (octahedral) or non-crystalline (icosahedral).

To control the shape of the NPs one can take advantage of the fact that different NP size regimes may be dominated by different energetically preferable shapes, a hot topic for theoretical studies during the past 15 years.^30–32 Cluster beam sources provide promise of such manipulation since they offer unparalleled size control. Indeed, shape control of noble metal NPs has been achieved via shape control³³ or control of gas-phase formation parameters³⁴ in conventional cluster beam sources.

The Sabatier principle states that the best catalysts should interact with molecules strongly enough so that the reactants bind to its surface, but weakly enough so that the products are able to desorb.³⁵ We believe that a future look into sizes and shapes of NPs, which will compare between NPs comprising only (100) facets and only (111) facets over a range of sizes, will identify the system that would fulfils these conditions.

Author contributions

Conceptualization, T. P., J. K. and R. E. P.; methodology, T. P. and J. K.; software, T. P. and J. K.; validation, T. P.; formal analysis, T. P.; investigation, T. P.; resources, T. P. and R. E. P.; data curation, T. P.; writing – original draft preparation, T. P.; writing – review and editing, T. P.; J. K. and R. E. P.; visualization, T. P.; supervision, R. E. P.; project administration, T. P. and R. E. P.; funding acquisition, T. P. and R. E. P. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This work was financially supported by the Engineering and Physical Sciences Research Council through [EP/K006061/2]. TP received financial support from the European Union's Horizon 2020 program and the Welsh Government through the Marie Skłodowska-Curie Actions Sêr Cymru II COFUND [fellowship 663830-SU165]. We acknowledge the support of the Supercomputing Wales project, which is part-funded by the European Regional Development Fund (ERDF) via the Welsh Government.

References

1. H. Lindlar, Ein Neuer Katalysator Für Selektive Hydrierungen, HCA, 1952, 35(2), 446–450,  DOI:10.1002/hlca.19520350205.
2. C. Lederhos, C. Betti, D. Liprandi, E. Cagnola and M. Quiroga, Alkyne Selective Hydrogenation with Mono- and Bimetallic- Anchored Catalysts, New Advances in Hydrogenation Processes – Fundamentals and Applications, InTech, 2017.  DOI:10.5772/64866.
3. G. Vilé, D. Albani, N. Almora-Barrios, N. López and J. Pérez-Ramírez, Advances in the Design of Nanostructured Catalysts for Selective Hydrogenation, ChemCatChem, 2015, 8(1), 21–33,  DOI:10.1002/cctc.201501269.
4. E. C. Tyo and S. Vajda, Catalysis by Clusters with Precise Numbers of Atoms, Nat. Nanotechnol., 2015, 10(7), 577–588,  DOI:10.1038/nnano.2015.140.
5. J. Hori, K. Murata, T. Sugai, H. Shinohara, R. Noyori, N. Arai, N. Kurono and T. Ohkuma, Highly Active and Selective Semihydrogenation of Alkynes with the Palladium Nanoparticles-Tetrabutylammonium Borohydride Catalyst System, Adv. Synth. Catal., 2009, 351(18), 3143–3149,  DOI:10.1002/adsc.200900721.
6. S. Carenco, A. Leyva-Pérez, P. Concepción, C. Boissière, N. Mézailles, C. Sanchez and A. Corma, Nickel Phosphide Nanocatalysts for the Chemoselective Hydrogenation of Alkynes, Nano Today, 2012, 7(1), 21–28,  DOI:10.1016/j.nantod.2011.12.003.
7. J. A. Delgado, O. Benkirane, C. Claver, D. Curulla-Ferré and C. Godard, Advances in the Preparation of Highly Selective Nanocatalysts for the Semi-Hydrogenation of Alkynes Using Colloidal Approaches, Dalton Trans., 2017, 46(37), 12381–12403,  10.1039/c7dt01607g.
8. P. Grammatikopoulos, S. Steinhauer, J. Vernieres, V. Singh and M. Sowwan, Nanoparticle Design by Gas-Phase Synthesis, Adv. Phys.: X, 2016, 1(1), 81–100,  DOI:10.1080/23746149.2016.1142829.
9. R. E. Palmer, R. Cai and J. Vernieres, Synthesis without Solvents: The Cluster (Nanoparticle) Beam Route to Catalysts and Sensors, Acc. Chem. Res., 2018, 51(9), 2296–2304,  DOI:10.1021/acs.accounts.8b00287.
10. R. E. Palmer, L. Cao and F. Yin, Note: Proof of Principle of a New Type of Cluster Beam Source with Potential for Scale-Up, Rev. Sci. Instrum., 2016, 87(4), 046103,  DOI:10.1063/1.4947229.
11. R. Cai, F. Martelli, J. Vernieres, S. Albonetti, N. Dimitratos, C. Tizaoui and R. E. Palmer, Scale-Up of Cluster Beam Deposition to the Gram Scale with the Matrix Assembly Cluster Source for Heterogeneous Catalysis (Catalytic Ozonation of Nitrophenol in Aqueous Solution), ACS Appl. Mater. Interfaces, 2020, 12(22), 24877–24882,  DOI:10.1021/acsami.0c05955.
12. R. Cai, L. Cao, R. Griffin, S. Chansai, C. Hardacre and R. E. Palmer, Scale-up of Cluster Beam Deposition to the Gram Scale with the Matrix Assembly Cluster Source for Heterogeneous Catalysis (Propylene Combustion), AIP Adv., 2020, 10(2), 025314,  DOI:10.1063/1.5142836.
13. P. R. Ellis, C. M. Brown, P. T. Bishop, D. Ievlev, J. Yin, K. Cooke and R. E. Palmer, High-Selectivity Palladium Catalysts for the Partial Hydrogenation of Alkynes by Gas-Phase Cluster Deposition onto Oxide Powders, Catal., Struct. React., 2018, 4(2), 1–8,  DOI:10.1080/2055074x.2018.1477315.
14. P. R. Ellis, C. M. Brown, P. T. Bishop, J. Yin, K. Cooke, W. D. Terry, J. Liu, F. Yin and R. E. Palmer, The Cluster Beam Route to Model Catalysts and Beyond, Faraday Discuss., 2016, 188, 39–56,  10.1039/c5fd00178a.
15. V. Habibpour, M. Y. Song, Z. W. Wang, J. Cookson, C. M. Brown, P. T. Bishop and R. E. Palmer, Novel Powder-Supported Size-Selected Clusters for Heterogeneous Catalysis under Realistic Reaction Conditions, J. Phys. Chem. C, 2012, 116(50), 26295–26299,  DOI:10.1021/jp306263f.
16. N. Semagina, A. Renken and L. Kiwi-Minsker, Palladium Nanoparticle Size Effect in 1-Hexyne Selective Hydrogenation, J. Phys. Chem. C, 2007, 111(37), 13933–13937,  DOI:10.1021/jp073944k.
17. L. Ma, M. Melander, T. Weckman, S. Lipasti, K. Laasonen and J. Akola, DFT Simulations and Microkinetic Modelling of 1-Pentyne Hydrogenation on Cu20 Model Catalysts, J. Mol. Graphics Modell., 2016, 65, 61–70,  DOI:10.1016/j.jmgm.2016.02.007.
18. J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Towards the Computational Design of Solid Catalysts, Nat. Chem., 2009, 1(1), 37–46,  DOI:10.1038/nchem.121.
19. L. Liu and A. Corma, Metal Catalysts for Heterogeneous Catalysis: From Single Atoms to Nanoclusters and Nanoparticles, Chem. Rev., 2018, 118(10), 4981–5079,  DOI:10.1021/acs.chemrev.7b00776.
20. G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6(1), 15–50,  DOI:10.1016/0927-0256(96)00008-0.
21. G. Kresse and J. Furthmüller, Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186,  DOI:10.1103/physrevb.54.11169.
22. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/physrevlett.77.3865.
23. P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979,  DOI:10.1103/physrevb.50.17953.
24. G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775,  DOI:10.1103/physrevb.59.1758.
25. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104,  DOI:10.1063/1.3382344.
26. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32(7), 1456–1465,  DOI:10.1002/jcc.21759.
27. K.-J. Hu, S. R. Plant, P. R. Ellis, C. M. Brown, P. T. Bishop and R. E. Palmer, The Effects of 1-Pentyne Hydrogenation on the Atomic Structures of Size-Selected AuNand PdN(N = 923 and 2057) Nanoclusters, Phys. Chem. Chem. Phys., 2014, 16(48), 26631–26637,  10.1039/c4cp02686a.
28. K. Momma and F. Izumi, VESTA 3for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data, J. Appl. Crystallogr., 2011, 44(6), 1272–1276,  DOI:10.1107/s0021889811038970.
29. J. Hussain, H. Jónsson and E. Skúlason, Calculations of Product Selectivity in Electrochemical CO2 Reduction, ACS Catal., 2018, 8(6), 5240–5249,  DOI:10.1021/acscatal.7b03308.
30. F. Baletto, R. Ferrando, A. Fortunelli, F. Montalenti and C. Mottet, Crossover among Structural Motifs in Transition and Noble-Metal Clusters, J. Chem. Phys., 2002, 116(9), 3856–3863,  DOI:10.1063/1.1448484.
31. J. M. Rahm and P. Erhart, Beyond Magic Numbers: Atomic Scale Equilibrium Nanoparticle Shapes for Any Size, Nano Lett., 2017, 17(9), 5775–5781,  DOI:10.1021/acs.nanolett.7b02761.
32. A. L. Garden, A. Pedersen and H. Jónsson, Reassignment of ‘Magic Numbers’ for Au Clusters of Decahedral and FCC Structural Motifs, Nanoscale, 2018, 10(11), 5124–5132,  10.1039/c7nr09440j.
33. D. Pearmain, S. J. Park, A. Abdela, R. E. Palmer and Z. Y. Li, The Size-Dependent Morphology of Pd Nanoclusters Formed by Gas Condensation, Nanoscale, 2015, 7(46), 19647–19652,  10.1039/c5nr06473b.
34. S. R. Plant, L. Cao and R. E. Palmer, Atomic Structure Control of Size-Selected Gold Nanoclusters during Formation, J. Am. Chem. Soc., 2014, 136(21), 7559–7562,  DOI:10.1021/ja502769v.
35. A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, From the Sabatier principle to a predictive theory of transition-metal heterogeneous catalysis, J. Catal., 2015, 328, 36–42,  DOI:10.1016/j.jcat.2014.12.033.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1: Energy barrier for the migration of the 1-pentene molecule on a (100) facet of a Pd₅₆₁ NP. See DOI: 10.1039/d1cp05470h

---