Open Access Article
Open Access ArticleBODIPY–pyrene donor–acceptor sensitizers for triplet–triplet annihilation upconversion: the impact of the BODIPY-core on upconversion efficiency†
Natalia
Kiseleva
a,
Mikhail A.
Filatov
 b,
Jan C.
Fischer
a,
Milian
Kaiser
a,
Marius
Jakoby
a,
Dmitry
Busko
a,
Ian A.
Howard
b,
Jan C.
Fischer
a,
Milian
Kaiser
a,
Marius
Jakoby
a,
Dmitry
Busko
a,
Ian A.
Howard
 ac,
Bryce S.
Richards
ac,
Bryce S.
Richards
 *ac and
Andrey
Turshatov
*ac and
Andrey
Turshatov
 *a
*a
aInstitute of Microstructure Technology, Karlsruhe Institute of Technology, Hermann-von-Helmholtz-Platz 1, 76344, Eggenstein-Leopoldshofen, Germany. E-mail: bryce.richards@kit.edu; andrey.turshatov@kit.edu
bSchool of Chemical and Pharmaceutical Sciences, Technological University Dublin, City Campus, Grangegorman, Dublin 7, Ireland
cLight Technology Institute, Karlsruhe Institute of Technology, Engesserstrasse 13, 76131 Karlsruhe, Germany
First published on 14th January 2022
Abstract
Triplet–triplet annihilation upconversion (TTA-UC) is an important type of optical process with applications in biophotonics, solar energy harvesting and photochemistry. In most of the TTA-UC systems, the formation of triplet excited states takes place via spin–orbital interactions promoted by heavy atoms. Given the crucial role of heavy atoms (especially noble metals, such as Pd and Pt) in promoting intersystem crossing (ISC) and, therefore, in production of UC luminescence, the feasibility of using more readily available and inexpensive sensitizers without heavy atoms remains a challenge. Here, we investigated sensitization of TTA-UC using BODIPY–pyrene heavy-atom-free donor–acceptor dyads with different numbers of alkyl groups in the BODIPY scaffold. The molecules with four and six alkyl groups are unable to sensitize TTA-UC in the investigated solvents (tetrahydrofuran (THF) and dichloromethane (DCM)) due to negligible ISC. In contrast, the dyad with two methyl groups in the BODIPY scaffold and the dyad with unsubstituted BODIPY demonstrate efficient intersystem crossing (ISC) of 49–58%, resulting in TTA-UC with quantum yields of 4.7% and 6.9%, respectively. The analysis of the elementary steps of the TTA-UC process indicates that heavy-atom-free donor–acceptor dyads are less effective than their noble metal counterparts, but may equal them in the future if the right combination of solvent, donor–acceptor sensitizer structure, and new luminescent molecules as TTA-UC emitters can be found.
Introduction
Anti-Stokes luminescence based on triplet–triplet annihilation upconversion (TTA-UC) has recently attracted much interest in various applications such as biophotonics,1–5 photovoltaics,6–9 photochemistry,10–14 production of solar fuels,15 and anticounterfeiting.16 There are two underpinning reasons motivating TTA-UC research. First, recent studies have demonstrated a wide variety of TTA-UC systems – from purely organic to hybrid organic/inorganic materials – which leads to many options for their application.17 Second, TTA-UC provides broader and stronger absorption18 as well as affords efficient UC luminescence under lower light intensities19–22 when compared to other prominent UC systems based on lanthanide ions.23,24The typical process of TTA-UC is illustrated in Fig. 1a. After absorption of a photon, the sensitizer undergoes intersystem crossing (ISC). The generated triplet state (localized on the sensitizer) transmits energy to a triplet state of an emitter molecule via triplet–triplet energy transfer (TTET). When two emitter molecules meet, triplet–triplet annihilation (TTA) occurs and results in the occupancy of an excited singlet state of one emitter; thus, the maximum possible quantum yield of the UC process is 50%. The emitter then undergoes radiative relaxation, emitting a new photon with an energy greater than the energy of the absorbed photons.
Benchmark TTA-UC systems are based on Pd and Pt-porphyrin sensitizers,25 enabling very high ISC. When combined with organic emitter molecules like diphenylanthracene (DPA),26 perylene,27 and rubrene,28 they afford uncorrected TTA-UC quantum yields (ϕUC) of 22%, 38%, and 8%, respectively. The correction of multiplying the ϕUC by a factor of 2 (given the theoretical UC limit of 50%) is somewhat commonplace in the literature; however, according to recent recommendations29–31 such multiplication should be avoided.
In addition to the metalloporphyrins, 4,4-difluoro-4-bora-3a,4a-diaza-s-indacene (BODIPY) derivatives bearing iodine atoms32 also proved to be popular sensitizers.33 In the case of the metalloporphyrins and the BODIPY derivatives, the presence of Pt, Pd, and I enhances ISC due to the spin–orbit interaction (heavy-atom effect).34 Many other new sensitizers have been studied over the past few years including quantum dots,35–40 perovskite nanocrystals and films,41–45 lanthanide complexes,46 molecules showing TADF (thermally activated delayed fluorescence),47–49 and electron donor–acceptor dyads.50–56
Among these classes of photosensitizers, heavy-atom-free donor–acceptor dyads are of particular interest for a new generation of TTA-UC systems. To promote the formation of long-lived triplet excited states, the BODIPY unit is combined with electron-donating aromatic subunits, such as anthracene,57 phenoxazine,53 perylene,52 and pyrene.58 Intramolecular electron transfer in these dyads leads to efficient formation of triplet excited states by SOCT-ISC. As it is indicated in Fig. 1b, the lowest singlet excited state of the sensitizer transforms into a charge transfer (CT) state, which further undergoes radiative/non-radiative decay or charge recombination into the lowest triplet excited state (SOCT-ISC). Usually, this process leads to population of the triplet state localized on the BODIPY subunit (3BODIPY) with an energy in the range of 1.58–1.69 eV53,54 that, for instance, is sufficient to enable TTET to the triplet state of the perylene emitter having an energy of 1.53 eV,59 but is insufficient for TTET to DPA (another effective TTA-UC emitter) with an energy of 1.72 eV.60
We recently demonstrated that the BODIPY–pyrene dyad (BPD1, Fig. 1c) together with perylene in THF exhibits a high ϕUC of 6.9%,31 which is among the highest values obtained for heavy-atom-free sensitizers so far. For example, a BODIPY–anthracene dyad paired with perylene as an emitter exhibited ϕUC up to 15.8% in dichloromethane (DCM)50 and a group of BODIPY–phenoxazine dyads exhibited UC luminescence in a nonpolar solvent (hexane) with a ϕUC of 12.3%53 (note that all data for ϕUC in ref. 50 and 53 should be divided by 2 as they were given with an additional factor of 2).
Furthermore, we observed a strong correlation between ϕUC and the solvent polarity (quantified via parameter ET(30)61). We found the highest ϕUC of 6.9% for the BPD1 sensitizer in THF with ET(30) = 37.4, whereas in less polar (toluene, ET(30) = 33.9) and more polar (DCM, ET(30) = 42.2) solvents the quantum yields are reduced down to 1.4% and 2.5%, respectively, although the reason for this peak-like behaviour is not clear. Moreover, the highest ϕUC of 6.9% obtained with perylene as the emitter is much lower than the theoretical TTA-UC limit of 50%, which also needs to be rationalized.
To understand the aforementioned results, herein we performed a more detailed study of corresponding TTA-UC systems in order to determine the efficiencies of the elementary steps of the TTA-UC process which contribute to the integral value of ϕUC (eqn (1)):
| ϕUC = 0.5 × ϕISC × ϕTTET × fTTA × ϕTTA × ϕF | (1) |
We investigated the effect of the number of alkyl substituents in the BODIPY scaffold (Fig. 1c) on the ability to sensitize TTA-UC in DCM and THF. Furthermore, we applied methods of transient absorption and transient and variable-temperature photoluminescence (PL) spectroscopy to assess the efficiency of ISC, TTET and TTA for BPD sensitizers in solvents of different polarity in order to identify the limiting step of TTA-UC sensitized using this donor–acceptor dyad.
Experimental
Chemicals
Deoxygenated tetrahydrofuran (THF) and dichloromethane (DCM) were purchased from Sigma-Aldrich (Merck). Compounds BPD 1–4 were prepared following a previously published procedure.62Preparation of samples for UC measurements
The UC-systems (BPDs – perylene) in deoxygenated solvents were prepared inside a N2-filled glovebox (GS Glovebox Systemtechnik GmbH) with a concentration of oxygen less than 0.1 ppm. The solutions were placed in a quartz cuvette and sealed inside the glovebox with a plastic cap and two layers of a sealing tape (Parafilm “M”).Photoluminescence characterization
The ultraviolet-visible (UV-vis) absorption spectra were recorded using a spectrophotometer (PerkinElmer Lambda 950). Steady-state PL spectra in THF and DCM were measured with 355 nm excitation (the third harmonic of an actively Q-switched laser (Innolas picolo-AOT MOPA)). Steady-state PL spectra in ethanol in the temperature range of 40–300 K were recorded using a closed-cycle cryostat (Oxford Instruments Optistat Dry TLEX) and a temperature-stabilized laser diode (Roithner LaserTechnik, 405 nm). The absolute quantum yields (ϕF) of perylene in DCM and THF were determined using a previously-described technique,31 with a 3-port integrating sphere (CSTM-QE-060-SL, Labsphere, diameter of ∅15 cm). The first port (∅0.6 cm) was used as the laser (the temperature stabilized laser diode, 405 nm) entrance, while the second port (∅0.3 cm in diameter) was used for detection of luminescence with a fibre-coupled irradiance calibrated CCD spectrometer (AvaSpec-ULS2048x64-TEC, Avantes Inc.). A sample holder with the sample to be investigated was inserted through the third (∅5.1 cm) port. The ϕF value was estimated as the ratio between the numbers of emitted and absorbed photons.TTA-UC PL characterization
The steady-state UC spectra were measured using a custom-built optical system. A Ti:sapphire laser with an external doubling unit (Solstis + ECD-X, M-Squared Ltd) with a wavelength of 498 nm was used as the excitation source. The UC luminescence signal was recorded using a spectrometer (Avantes, AvaSpec-ULS2048 × 64TEC) and a slightly tilted notch-filter (NF03-532E-25, Semrock) to reject scattered excitation light.The ϕUC value was calculated using the relative method according to a previously reported procedure.31 Briefly, the luminescence from the CT state of BPD1, which is independent of oxygen presence and emitter (perylene) concentration, was used as a reference with ϕref = 7.0% in DCM and ϕref = 8.0% in THF. Using the relative method, the ϕUC value was calculated using eqn (2):
| ϕUC = ϕref(Aref/AUC)(EUC/Eref)(nUC/nref)2 | (2) |
PL transient characterization
For UC PL lifetime measurements (μs time-scale), a multichannel scaling (MCS) card (TimeHarp 260, PicoQuant) was used. The laser modulation was performed to achieve a regime with 5 ms laser on and 5 ms laser off (100 Hz, 50% duty cycle). The modulation of the 525 nm laser diode (Roithner LaserTechnik) was performed using a built-in function generator in the laser diode driver. To detect the rise and fall times of the UC emission, the transistor–transistor logic (TTL) signal from the laser diode controller was delayed by the use of a delay generator (DG645, Stanford Research Systems). The intensity of the laser was measured without the applied modulation. The spectral separation of the photoluminescence was achieved with a double monochromator (DTMS300, Bentham) and the emission at a specific wavelength was detected via a photomultiplier tube (R928P, Hamamatsu), mounted in temperature-cooled housing (CoolOne, Horiba). A more detailed description of the experimental setups for measurements of steady-state and time resolved UC spectra, as well as ϕUC, can be found in previous publications.31,51PL lifetimes on the ns time-scale were measured with a streak camera system. The third harmonic of an actively Q-switched laser (Innolas picolo-AOT MOPA) with a wavelength of 355 nm, a repetition rate of 1 kHz, and a pulse length of 500 ps was used as the excitation source. The streak camera (Hamamatsu Universal Streak Camera C10910) was used in the single-sweep mode to allow for a time-base of 20 ns and an instrumental-response function width of 310 ps. The PL kinetics were measured with an excitation fluence of 120 nJ cm−2.
Transient absorption characterization
Transient absorption (TA) spectra were recorded by using a custom-built pump–probe setup with a resolution of ∼500 ps. Pump pulses (355 nm, 1 kHz) were provided by the third harmonic of an actively Q-switched Nd:YVO laser (Innolas picolo-AOT MOPA). White light continuum pulses (450–1000 nm) were generated by pumping a 2 mm thick sapphire crystal using the output of a commercial femtosecond laser (Light Conversion Pharos, 1030 nm, 10 μJ, 2 kHz, 260 fs). The white light pulses were dispersed onto a linear CCD image sensor and read out at 2 kHz. The adjacent spectra correspond to the transmission of the sample with and without the pump pulse and were used to calculate ΔT/T. The long delay (>4 ns) between the pump and white light pulses was controlled using an electronic delay generator (Stanford Research Systems DG535). For short pump–probe delay times smaller than 4 ns, the chopped optical output of a collinear optical parametric amplifier with a second harmonic generator (Light Conversion Orpheus, Lyra) was used. The pump–probe delay is adjusted using a linear translation stage (Thorlabs DDS600/M).Results and discussion
In all donor–acceptor dyads (BPDs), examined in this work, BODIPY plays the role of an electron acceptor and pyrene acts as an electron donor (Fig. 1c), providing ultrafast electron transfer from pyrene to the BODIPY subunit. To achieve an effective PET, the donor subunit is attached directly in the meso-position of the BODIPY which results in orthogonal geometry (dihedral angles of 81°–89°). The formation of triplet states in these dyads via SOCT-ISC can take place in solvents of different polarity (from non-polar hexane to strongly polar acetonitrile).63 Recently, the efficiency of triplet state generation in these dyads was investigated by measuring the singlet oxygen quantum yield (ΦΔ).62 Dyad BPD1 displayed the highest ΦΔ value of 0.75 in ethanol, whereas dyads BPD2 and BPD3 displayed lower ΦΔ values (0.25–0.34). Dyad BPD4 bearing six alkyl groups showed a much lower ΦΔ value of 0.04. This trend can be explained by a decrease in the driving force of PET with an increase in the number of alkyl groups. Buck et al. demonstrated that the presence of four methyl groups in the BODIPY core makes electron transfer in BPD3 thermodynamically unfavourable even in very polar acetonitrile (ΔGPET = 0.083 eV). The presence of two additional ethyl groups in BPD4 further reduces the driving force of the process (ΔGPET = 0.27 eV).58Since perylene, which was employed in this work as the TTA-UC emitter, is poorly soluble in highly polar solvents (ethanol and acetonitrile), we performed spectroscopic characterization of dyads in less polar solvents like DCM and THF.
Optical characterization of BPDs
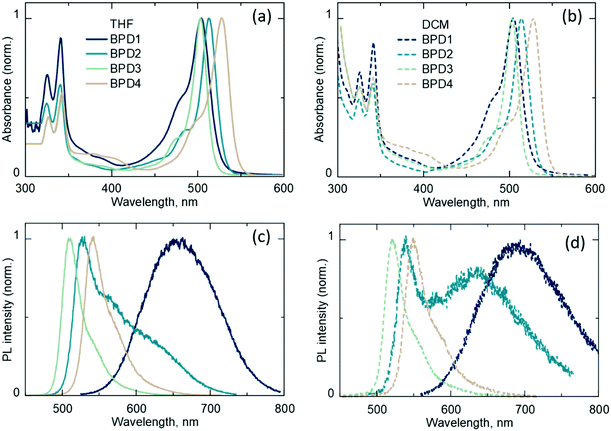
The UV-Vis absorption (Fig. 2a and b) and emission (Fig. 2c and d) spectra of BPDs in DCM and THF are presented in Fig. 2. The absorption spectra of all dyads exhibit a pyrene band at around 300–400 nm and a BODIPY band at around 450–550 nm for all four BPD molecules. For BPD1 and BPD3, the BODIPY band lies around 505 nm, whereas BPD4 shows a red-shifted band at around 528 nm. The position of the absorption peak of BPD2 (with the maximum at 515 nm) is intermediate between BPD1 and BPD4. The absorption maxima are independent of solvent polarity. However, the polarity has a strong effect on the emission spectra as it is presented in Fig. 2c and d.BPD1 demonstrates a strongly red-shifted emission band compared to regular BODIPYs. The emission is centred at 680 nm in THF and 700 nm in DCM. This emission originates from the CT state and exhibits moderate ϕF values of 8.0% and 7.0%,31 with decay times of 4 ns and 3.3 ns in THF and DCM (see Fig. S1a and S2a, ESI†), respectively. Although CT states are generally considered to be dark, recent results have indicated enhanced emissivity of CT states in dyads based on the alkyl-unsubstituted BODIPY scaffold, proposed to be caused by increased electronic coupling between the electron donor and acceptor subunits.64
The dyad with two methyl groups (BPD2) in DCM displays an emission peak around 540 nm, which corresponds to the radiative transition S1 → S0 and an additional red-shifted shoulder peak at around 640 nm, which corresponds to the emission of the CT state (1CT → S0). The transitions have a similar decay time of 4.6 ns in DCM and slightly different decay times of 7.4 ns and 6.6 ns in THF solvent (Fig. S2b, ESI†), respectively. In contrast to alkyl-unsubstituted and dialkyl-substituted BODIPY scaffolds, BPD3 and BPD4 dyads with four and six alkyl groups display typical BODIPY emission spectra for both solvents with peaks in the region of 500–550 nm and decay times of 5.6 ns and 6.7 ns in DCM, and 10.2 ns and 11.2 ns in THF, respectively. Thus, it can be assumed that BPD3 and BPD4 do not undergo PET in solvents with moderate polarity (DCM and THF) as opposed to BPD1 and BPD2, or their charge-transfer states (1CT) are not emissive.
The decay times of the charge-transfer emission for dyads BPD1 and BPD2, which are in the range of 3–6.6 ns, shed light on the kinetics of the intersystem crossing. It can be assumed that ISC in these molecules is a relatively slow process with a rate constant in the range of ns−1. ISC in these systems can in principle lead to the formation of two different triplet states: charge transfer (TCT) and local triplet (TBODIPY) states formed by radical-pair ISC (RP-ISC) and SOCT-ISC, respectively, whereas a second local triplet state (TPyr) is unlikely to be attainable due to its high energy of 2.09 eV.65 It should be noted that the formation of the TCT state via RP-ISC is also quite debatable, since recently Buck et al. have provided experimental evidence for the absence of RP-ISC in similar electron-donor–acceptor dyads.58 It is known that BODIPY triplet states are poorly emissive; however, the corresponding phosphorescence can be detected in a glassy solvent matrix at low temperatures.66 Therefore, the PL spectra of the BPDs dissolved in ethanol at low temperatures (down to 40 K) were investigated in detail. It was expected that highly polar ethanol can additionally facilitate the formation of triplet states and provide a good glassy matrix for detection of the triplet emission.
Fig. 3a demonstrates the PL spectra of BPD1 at different temperatures. At less than 140 K, the appearance of a new peak in the near-infrared (NIR) range was observed, with a maximum of 735 nm (1.69 eV).
The decay time of the peak exceeds the 1 ms time window of the streak camera, and it is therefore concluded that these must be long-lived triplet states formed by SOCT-ISC. It should be pointed out that the triplet energy of the BODIPY molecule reported in the literature (1.7 eV)66 is close to the 735 nm peak and, thus, this triplet level can be assigned to the TBODIPY state. The low temperature PL spectrum of the BPD2 dyad reveals a NIR peak with a maximum of 765 nm (1.62 eV), which probably also belongs to the TBODIPY state. Low-temperature PL measurements for dyads BPD3 and BPD4 (Fig. 3c and d) do not display any additional peaks and, therefore, it can be concluded that these molecules possess inefficient ISC.
TTA-UC with BPDs used as sensitizers
Using variable-temperature PL measurements, triplet states with energies of >1.62 eV were detected for BPD1 and BPD2 dyads. Therefore, these dyads can be paired with perylene (with a lower triplet energy of 1.53 eV) to realize TTA-UC. Indeed, the BPD1 dyad mixed with perylene in solvents with moderate polarity (deoxygenated THF and DCM) demonstrated bright UC luminescence with characteristic features of perylene luminescence (420–500 nm) and broad luminescence from the CT state (550–900 nm) (Fig. 4a). The BPD2 dyad paired with perylene also demonstrated strong UC PL in DCM, whereas the THF solution only exhibited strong luminescence of BPD2 and only an extremely weak UC signal (Fig. 5a). To quantify TTA-UC intensity, measurements of ϕUC were performed using a relative method.31 The calculated ϕUC values are presented in Table 1. The highest ϕUC value of 6.9% was observed for the BPD1 dyad in THF solution. The same dyad in DCM demonstrates a lower ϕUC value of 2.5%. The opposite trend was found for BPD2, where the highest ϕUC of 4.7% was measured in DCM and only extremely weak UC luminescence is observed in THF. It should be noted that no UC luminescence was detected for dyads BPD3 and BPD4 in either DCM or THF.| BPD1 (DCM) | BPD1 (THF) | BPD2 (DCM) | |
|---|---|---|---|
| a Measured at an intensity of 5 W cm−2 (498 nm laser) using eqn (2) for BPD and perylene concentrations of 10−5 M and 10−4 M, respectively. b Estimated for a BPD concentration of 10−5 M. c Estimated using eqn (5) for BPD and perylene concentrations of 10−5 M and 10−4 M, respectively. d Estimated using eqn (6) with BPD and perylene concentrations of 10−5 M and 10−4 M, respectively. The reported values correspond to intensities (525 nm laser) of 12 W cm−2 and 3.6 W cm−2 for BPD1 and BPD2, respectively. e Estimated using an integrating sphere for a perylene concentration of 10−4 M. f Calculated using eqn (1). | |||
| ϕ UC,a % | 2.5 | 6.9 | 4.7 |
| ϕ ISC,b % | 49 | 58 | 56 |
| ϕ TTET,c % | 99 | 99 | 99 |
| ϕ TTA,d % | 92 | 83 | 94 |
| ϕ F,e % | 71 | 85 | 71 |
| f TTA | 0.15 | 0.33 | 0.25 |
To shed light on TTA-UC with heavy-atom-free sensitizers, the efficiency of each individual step (as illustrated earlier in eqn 1) was investigated. Efficiencies of intersystem crossing (ϕISC) for BPD1 and BPD2 dyads were assessed using TA spectroscopy. As depicted in Fig. 4b and 5b, we were able to measure the time evolution of the ground-state bleaching with short (ps–ns) and long (ns–μs) delays using the same setup and the same excitation settings. It was assumed that ground state bleaching is the dominant signal at 505 nm and 515 nm (for BPD1 and BPD2, respectively), while the other signals attributed to excited state absorption are much less prominent at these wavelengths. Therefore, after normalization of the TA transients, the amplitude value of the long component (in the μs range) should be proportional to the efficiency of ISC:
| ϕISC≈A × 100%, | (3) |
The estimated ϕISC values are presented in Table 1. The highest value of ϕISC of 58% was observed for BPD1 in THF. A similar value of 56% was calculated for BPD2 in DCM, while BPD1 exhibited a slightly lower value of ϕISC = 49% in this solvent. It can be assumed that the parameter ϕISC is independent of both intensity and concentration, and therefore the obtained values can be directly used in eqn (1).
Measurements of TA with long delay (ns–μs) also assist in estimating TTET efficiency from the triplet state of dyads to the perylene triplet state. For instance, Fig. S3–S5 (ESI†) demonstrate the TA spectra for pure BPD1 and BPD2, as well as for BPD1–perylene and BPD2–perylene mixtures. In these results, transients of the ground state bleach (505 nm and 515 nm for BPD1 and BPD2, respectively) follow the mono-exponential kinetics and their decay times are equal to the decay time of the triplet state (TBODIPY). Thus, the values of 37 μs, 37 μs, and 44 μs were obtained for BPD1 in DCM, BPD1 in THF and BPD2 in DCM, respectively. The τ0 values for BPD1 are consistent with earlier measurements performed in DMF, where a value of 36 μs was reported.62
A series of measurements of triplet state lifetime at different concentrations of the triplet quencher (perylene) allow assessment of the Stern–Volmer constant (KSV) using the equation:
| τ0/τ = 1 +KSV [perylene], | (4) |
Stern–Volmer plots for the BPD1 dyad measured in DCM and THF are presented in Fig. 4c. The linear fit of the data results in Stern–Volmer constants of KSV = 3.1 × 106 M−1 in THF and KSV = 1.5 × 106 M−1 in DCM. These values of KSV are in line with the earlier found KSV constants for quenching of BODIPY–phenoxazine dyads by perylene (1.06 × 106 M−1 and 1.59 × 106 M−1).53 The values of τ0 allow us to additionally calculate the quenching constant kq = KSV/τ0, which leads to the values of kq = 8.4 × 1010 M−1 s−1 and kq = 4.1 × 1010 M−1 s−1. These values, in turn, are very close to diffusion-controlled bimolecular quenching rate constants of ∼1010–1011 M−1 s−1 (calculated for BODIPY–phenoxazine dyads in toluene and hexane, respectively).53 The obtained KSV values ensure that, at an emitter concentration of 10−5 M, perylene almost completely quenches the triplet states of BPD1 with efficiencies of 93.7% and 97.2% (eqn (5)) in DCM and THF, respectively.
| ϕq = ϕTTET = (1 − τ/τ0) × 100%, | (5) |
To estimate ϕTTA, UC decays at different excitation intensities were measured. These decays measured in the intensity range of 0.03–15 W cm−2 are plotted in Fig. S6–S8 (ESI†). According to the method proposed by Cheng et al.,67 the global fitting of these decays using eqn (6) enables determining the parameters kEM and β:
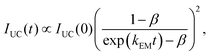 | (6) |
This method was originally developed for a pulsed excitation (with a short fs-pulse) where ϕTTA < β. However, for the method used in our work (with cw-laser modulated with a frequency of 100 Hz and a duty cycle of 50%, see the experimental part for details) the β value obtained with eqn (6) can be converted to ϕTTA using a simple approximation ϕTTA ≈ β.
It is necessary to note that that ϕUC values were measured using 498 nm excitation (close to the absorption maximum of BPD sensitizers). However, this laser cannot be modulated to measure UC transients. Therefore, a laser diode with a wavelength of 525 nm was used to measure UC lifetimes. Given the difference in absorption at 498 and 525 nm, the correction factor should be introduced for comparison of ϕUC and ϕTTA. Assuming an equal flux of absorbed photons, ϕUC measured at 5 W cm−2 of a 498 nm laser corresponds to ϕTTA measured at 12 W cm−2 for BPD1 in DCM and THF, as well as at 3.6 W cm−2 for BPD2 in DCM. Fig. 4d displays the rise of β = ϕTTA up to 92% (at 12 W cm−2) in DCM and up to 83% (at 12 W cm−2) in THF. Furthermore, global fitting of the data obtained for the BPD1–perylene mixtures in DCM (Fig. S6, ESI†) and THF (Fig. S7, ESI†) gives kEM values of 0.78 ms−1 and 1.59 ms−1, respectively. This corresponds to the lifetimes of the perylene triplet state of τTperylene = 1/kEM = 1.3 ms and 0.65 ms, respectively. Global fitting of UC decays for the BPD2–perylene mixture in DCM (Fig. S8, ESI†) results in τTperylene = 1.1 ms and the intensity dependence of β (Fig. 5d) which gives ϕTTA = 94% (at 3.6 W cm−2).
To estimate further the yield of singlet states generated via the TTA process, ϕTTA needs to be multiplied by the statistical factor fTTA, which considers spin statistics of TTA.67 The TTA is usually assumed to occur through the formation of a complex between the two emitters in their triplet states. The complexes can have different multiplicity, and the probability of forming complexes with a certain multiplicity (singlet, triplet, or quintet) should correspond to the ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, respectively. This statistic predicts fTTA = 0.11, if TTA occurs via complexes with all possible multiplicity; fTTA = 0.4, if TTA occurs via complexes with singlet and triplet multiplicity; and fTTA = 1, if only the complex with singlet multiplicity is involved in the TTA process.
5, respectively. This statistic predicts fTTA = 0.11, if TTA occurs via complexes with all possible multiplicity; fTTA = 0.4, if TTA occurs via complexes with singlet and triplet multiplicity; and fTTA = 1, if only the complex with singlet multiplicity is involved in the TTA process.
The rise and saturation of β have a strong relationship to a figure-of-merit UC parameter – UC threshold (Ith). At intensities far greater than Ith, bimolecular TTA dominates over monomolecular decays and ϕTTA approaches a constant value. The Ith value can be roughly estimated by approximating the dependency of UC intensity vs. excitation intensity (ln(IUC) ∝ ln(Pexc)) by two straight lines (for low and high excitation intensities) and finding their intersection point. However, it is not always possible to investigate UC in a very broad excitation intensity range to identify quadratic (with slope n = 2) and linear (with slope n = 1) regimes. For instance, Fig. S9a (ESI†) illustrates the UC behaviour of the BPD1/perylene pair measured in DCM using various excitation intensities. The slope gradually changes from n = 1.5 (at 0.1 W cm−2) down to n = 1.15 (at 8 W cm−2), which makes the Ith estimate rather arbitrary. On the other side, a ratio of UC intensity to excitation intensity (IUC/I) changes proportionally to ϕUC (Fig. S9b, ESI†). We assumed that the values of ϕUC > 0.5 × ϕmaxUC can be relevant for practical applications.68 Thus, the value of excitation intensity corresponding to ϕUC ≈ 0.5 × ϕmaxUC was used as Ith and the values of 0.3 W cm−2 and 0.03 W cm−2 were estimated for BPD1 (Fig. S9b, ESI†) and BPD2 (Fig. S10b, ESI†) in DCM, respectively.
To complete measurements of the parameters included in eqn (1), the photoluminescence quantum yields (ϕF) of perylene in THF and DCM were measured using the absolute method in an integrating sphere resulting in values of ϕF = 71% in DCM and ϕF = 85% in THF.
Comparison of BPDs as sensitizers for TTA-UC
It has been previously demonstrated that BPDs bearing tetra- and hexa-substituted BODIPY scaffolds are not able to efficiently generate singlet oxygen.62 The results from this work agree with this in that neither BPD3 nor BPD4 dyads are not able to sensitize TTA-UC in THF or DCM. More polar solvents (ethanol or acetonitrile) were not investigated here due to the limited solubility of perylene in these solvents. The lack of TTA-UC with BPD3 and BPD4 sensitizers can be explained by the very limited ISC in these molecules due to thermodynamically unfavoured PET.58 Unlike BPD3 and BPD4, the dyad with two alkyl groups (BPD2) and the unsubstituted dyad (BPD1) exhibit sensitization of TTA-UC in DCM, while only the BPD1 dyad demonstrates efficient UC in THF.Comparing the results (Table 1) obtained for the BPD1 dyad in DCM and THF provides several important observations. The UC sensitized with the BPD1 dyad demonstrates comparable values of ϕTTA and ϕTTET in both solvents. Therefore, at first glance, the rather significant difference in ϕUC (2.5% in DCM vs. 6.9% in THF) can be explained by the differences in ϕISC and ϕF. However, accounting for the rather small difference in these parameters our attention was focused on the values of fTTA.
It has previously been demonstrated that for UC with the highest quantum yield the perylene dimer (ϕUC = 42%, emitter concentration of 5 × 10−4 M) and perylene (ϕUC = 38%, emitter concentration of 1 × 10−4 M) sensitized by Pd(II)- and Pt(II)-tetrabenzoporphyrin complexes in THF exhibit values of fTTA = 1 and saturated ϕTTA close to 100%.27,69 In our work we extracted fTTA = 0.33 (using eqn (1) and the results presented in Table 1) for UC in THF with the concentration of BPD1 and perylene (10−5 M and 10−4 M, respectively). On the other side, Wei et al.70 reported 0.11 < fTTA < 0.4 for perylene paired with the BODIPY-phenyl-C60 dyad in THF (perylene concentration of 4.5 × 10−3 M). Thus, the literature reports quite different values for fTTA even for the same solvent (THF), while our result of fTTA = 0.32 is closer to the results reported by Wei et al.69 Furthermore, the fTTA values of 0.15 and 0.25 were obtained for UC sensitized with BPD1 and BPD2 in DCM, respectively. Several recent papers have discussed a number of reasons explaining additional loss channels in TTA-UC, which may manifest as a false reduction in fTTA.71–73 For example, it was noticed that singlet and triplet energy landscapes can change in a conformationally flexible emitter (9,10-bis(phenylethynyl)anthracene) and the energetic requirement 2 × ET1 > ES1 for efficient TTA-UC is not fulfilled for all rotational conformers.71 In addition, in the case of the perylene emitter, triplet excimer formation in solution may also change the triplet and singlet state energies, which may lead to less efficient UC and is reflected in the apparent change of fTTA in different solvents and at different emitter concentrations.72 However, the perylene used as the emitter in this study shows no evidence of excimer formation (observed as a sharp fluorescence peak with a maximum at 565 nm73). Thus, the observed discrepancies in the fTTA values for perylene cannot be still explained unambiguously.
Importantly, the high values of ϕTTA found for BPD2 in DCM are evident in the low Ith (Fig. S9 and S10, ESI†). However, the value of Ith ∼ 30 mW cm−2 is still high to be considered useful for applications requiring an intensity of 1 Sun equivalent (∼3–5 mW cm−2). Both Ith and ϕUC can be further improved by tuning the chemical structure of the sensitizer and emitter, as well as finding the best solvent and optimizing the sensitizer and emitter concentrations.
The BPD1 and BPD2 sensitizers in THF and DCM demonstrate ϕISC ≈ 0.5 which is significantly lower than ϕISC ≈ 1 for benchmark photosensitizer–porphyrin complexes of noble metals (Pd(II) or Pt(II)). We assume that the efficiency of intersystem crossing for the investigated sensitizers can be improved by finding an optimal solvent to enhance formation of the CT state and SOCT-ISC. For example, the luminescence of the BPD1 CT state in DCM and THF is an important deactivation channel that competes with relatively slow SOCT-ISC. This luminescence is significantly reduced in the polar solvent (DMF)62 which indicates an increase of SOCT-ISC efficiency.
However, even more attention should be paid to the choice of the emitter, as perylene is insoluble in polar solvents and demonstrates in our experiments very low fTTA values (in the range of 0.15–0.32). Recently, Bossanyi et al.74 demonstrated that fTTA can vary from 0.4 to 1 depending on the orientation of molecules in the triplet dimers (TT), the energy gap between E(TT) and ET2, as well as the reverse intersystem crossing T2 → S1. Thus, a fine modification of the chemical structure of perylene could probably improve its solubility and enable an increase in fTTA and the rate of TTA, increasing ϕUC in general.
Conclusions
In this work we investigated the photosensitization of TTA-UC using heavy-atom-free donor–acceptor BODIPY–pyrene dyads (BPDs) paired with perylene as the emitter. Dyads with four and six alkyl substituents in the BODIPY scaffold (BPD3 and BPD4) are not capable of producing UC luminescence, whereas dyads with two methyl groups and an unsubstituted BODIPY scaffold (BPD1 and BPD2) exhibit UC with quantum efficiencies up to 6.9% (at 498 nm laser excitation intensity of 5 W cm−2) and a low UC threshold (down to ∼ 30 mW cm−2). This efficient UC was explained through evaluation of elementary step efficiencies contributing to the ϕUC integral value. The BPD1 and BPD2 dyads demonstrate SOCT-ISC in moderate polarity solvents (THF and DCM) with efficiencies of 49–58%. We found that SOCT-ICS populates BODIPY triplet states with energies of 1.69 and 1.62 eV for BPD1 and BPD2, respectively. Furthermore, both dyads allow energy transfer to perylene triplet states at transfer rates (quenching constants in the range of 2.2–8.8 × 1010 M−1 s−1) close to the diffusion limit. The TTA efficiency values estimated from UC transitions measured at different intensities are high (up to 94% at an excitation (488 nm) intensity of 5 W cm−2) and these measurements confirm a spin statistical factor (fTTA) close to 0.4. Thus, ISC (with efficiency of ∼50%) and the poor statistics of the TTA step currently limit the effectiveness of TTA-UC. We hope to overcome these limitations in the future by finding better solvents as well as emitters with higher fTTA.Author contributions
The manuscript was written through the contributions of all authors. N. K., J. C. F., M. K., M. J. and D. B. conducted spectroscopic experiments and N. K. wrote the paper. M. F. synthesized the BPD molecules. B. S. R. and A. T. developed the original concept of the paper. A. T., I. A. H. and B. S. R. contributed equally to scoping and structuring the paper and provided additional guidance on experimental methods. All authors have approved the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the following funding from the Helmholtz Association: (i) the Recruitment Initiative for B.S.R.; (ii) Research Field Energy – Program Materials and Technologies for the Energy Transition – Topic 1 Photovoltaics; and (iii) the Helmholtz Energy Material Foundry (HEMF). N. K. gratefully acknowledges the PhD scholarship provided by the German Academic Exchange Service (DAAD).References
- C. Wohnhaas, A. Turshatov, V. Mailänder, S. Lorenz, S. Baluschev, T. Miteva and K. Landfester, Macromol. Biosci., 2011, 11, 772–778 CrossRef CAS PubMed.
- Q. Liu, T. Yang, W. Feng and F. Li, J. Am. Chem. Soc., 2012, 134, 5390–5397 CrossRef CAS PubMed.
- S. H. C. Askes, M. S. Meijer, T. Bouwens, I. Landman and S. Bonnet, Molecules, 2016, 21, 1460 CrossRef PubMed.
- Q. Liu, M. Xu, T. Yang, B. Tian, X. Zhang and F. Li, ACS Appl. Mater. Interfaces, 2018, 10, 9883–9888. CrossRef CAS PubMed.
- H.-L. Lee, J. H. Park, H.-S. Choe, M.-S. Lee, J.-M. Park, N. Harada, Y. Sasaki, N. Yanai, N. Kimizuka, J. Zhu, S. H. Bhang and J.-H. Kim, ACS Appl. Mater. Interfaces, 2019, 11, 26571–26580 CrossRef CAS PubMed.
- T. F. Schulze and T. W. Schmidt, Energy Environ. Sci., 2015, 8, 103–125 RSC.
- L. Frazer, J. K. Gallaher and T. W. Schmidt, ACS Energy Lett., 2017, 2, 1346–1354 CrossRef CAS.
- T. Dilbeck and K. Hanson, J. Phys. Chem. Lett., 2018, 9, 5810–5821 CrossRef CAS PubMed.
- Y. Zhou, C. Ruchlin, A. J. Robb and K. Hanson, ACS Energy Lett., 2019, 4, 1458–1463 CrossRef CAS.
- J.-H. Kim and J.-H. Kim, J. Am. Chem. Soc., 2012, 134, 17478–17481 CrossRef CAS PubMed.
- H.-i. Kim, O. S. Kwon, S. Kim, W. Choi and J.-H. Kim, Energy Environ. Sci., 2016, 9, 1063–1073. RSC.
- O. S. Kwon, J.-H. Kim, J. K. Cho and J.-H. Kim, ACS Appl. Mater. Interfaces, 2015, 7, 318–325 CrossRef CAS PubMed.
- B. Pfund, D. M. Steffen, M. R. Schreier, M.-S. Bertrams, C. Ye, K. Börjesson, O. S. Wenger and C. Kerzig, J. Am. Chem. Soc., 2020, 142, 10468–10476 CrossRef CAS PubMed.
- J. Isokuortti, K. Kuntze, M. Virkki, Z. Ahmed, E. Vuorimaa-Laukkanen, M. A. Filatov, A. Turshatov, T. Laaksonen, A. Priimagi and N. A. Durandin, Chem. Sci., 2021, 12, 7504–7509 RSC.
- M. Barawi, F. Fresno, R. Pérez-Ruiz and V. A. de la Peña O’Shea, ACS Appl. Energy Mater., 2019, 2, 207–211 CrossRef CAS.
- A. L. Hagstrom, H.-L. Lee, M.-S. Lee, H.-S. Choe, J. Jung, B.-G. Park, W.-S. Han, J.-S. Ko, J.-H. Kim and J.-H. Kim, ACS Appl. Mater. Interfaces, 2018, 10, 8985–8992 CrossRef CAS PubMed.
- S. Wen, J. Zhou, P. J. Schuck, Y. D. Suh, T. W. Schmidt and D. Jin, Nat. Photonics, 2019, 13, 828–838 CrossRef CAS.
- J. Pedrini and A. Monguzzi, J. Photonics Energy, 2017, 8, 022005 Search PubMed.
- M. Oldenburg, A. Turshatov, D. Busko, S. Wollgarten, M. Adams, N. Baroni, A. Welle, E. Redel, C. Wöll, B. S. Richards and I. A. Howard, Adv. Mater., 2016, 28, 8477–8482 CrossRef CAS PubMed.
- F. Meinardi, M. Ballabio, N. Yanai, N. Kimizuka, A. Bianchi, M. Mauri, R. Simonutti, A. Ronchi, M. Campione and A. Monguzzi, Nano Lett., 2019, 19, 2169–2177 CrossRef CAS PubMed.
- E. Radiunas, S. Raišys, S. Jurėnas, A. Jozeliūnaitė, T. Javorskis, U. inkevičiūtė, E. Orentas and K. Kazlauskas, J. Mater. Chem. C, 2020, 8, 5525–5534 RSC.
- M. Wu, T.-A. Lin, J. O. Tiepelt, V. Bulović and M. A. Baldo, Nano Lett., 2021, 21, 1011–1016 CrossRef CAS PubMed.
- J. Zhou, Q. Liu, W. Feng, Y. Sun and F. Li, Chem. Rev., 2015, 115, 395–465 CrossRef CAS PubMed.
- W. Zou, C. Visser, J. A. Maduro, M. S. Pshenichnikov and J. C. Hummelen, Nat. Photonics, 2012, 6, 560–564 CrossRef CAS.
- J. Zhao, W. Wu, J. Sun and S. Guo, Chem. Soc. Rev., 2013, 42, 5323–5351 RSC.
- D. Dzebo, K. Moth-Poulsen and B. Albinsson, Photochem. Photobiol. Sci., 2017, 16, 1327–1334 CrossRef CAS PubMed.
- S. Hoseinkhani, R. Tubino, F. Meinardi and A. Monguzzi, Phys. Chem. Chem. Phys., 2015, 17, 4020–4024 RSC.
- Y. Y. Cheng, T. Khoury, R. G. C. R. Clady, M. J. Y. Tayebjee, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, Phys. Chem. Chem. Phys., 2010, 12, 66–71 RSC.
- N. Yanai, K. Suzuki, T. Ogawa, Y. Sasaki, N. Harada and N. Kimizuka, J. Phys. Chem. A, 2019, 123, 10197–10203 CrossRef CAS PubMed.
- Y. Zhou, F. N. Castellano, T. W. Schmidt and K. Hanson, ACS Energy Lett., 2020, 5, 2322–2326 CrossRef CAS.
- N. Kiseleva, D. Busko, B. S. Richards, M. A. Filatov and A. Turshatov, J. Phys. Chem. Lett., 2020, 11, 6560–6566 CrossRef CAS PubMed.
- T. Yogo, Y. Urano, Y. Ishitsuka, F. Maniwa and T. Nagano, J. Am. Chem. Soc., 2005, 127, 12162–12163 CrossRef CAS PubMed.
- K. Chen, Y. Dong, X. Zhao, M. Imran, G. Tang, J. Zhao and Q. Liu, Front. Chem., 2019, 7, 821 CrossRef CAS PubMed.
- K. N. Solov'ev and E. A. Borisevich, Phys.-Usp., 2005, 48, 231–253 CrossRef.
- V. Gray, P. Xia, Z. Huang, E. Moses, A. Fast, D. A. Fishman, V. I. Vullev, M. Abrahamsson, K. Moth-Poulsen and M. Lee Tang, Chem. Sci., 2017, 8, 5488–5496 RSC.
- L. Nienhaus, M. Wu, N. Geva, J. J. Shepherd, M. W. B. Wilson, V. Bulović, T. Van Voorhis, M. A. Baldo and M. G. Bawendi, ACS Nano, 2017, 11, 7848–7857 CrossRef CAS PubMed.
- M. Mahboub, Z. Huang and M. L. Tang, Nano Lett., 2016, 16, 7169–7175 CrossRef CAS PubMed.
- N. Nishimura, J. R. Allardice, J. Xiao, Q. Gu, V. Gray and A. Rao, Chem. Sci., 2019, 10, 4750–4760 RSC.
- E. M. Gholizadeh, S. K. K. Prasad, Z. L. Teh, T. Ishwara, S. Norman, A. J. Petty, J. H. Cole, S. Cheong, R. D. Tilley, J. E. Anthony, S. Huang and T. W. Schmidt, Nat. Photonics, 2020, 14, 585–590 CrossRef CAS.
- Z. A. VanOrman, C. R. Conti, G. F. Strouse and L. Nienhaus, Chem. Mater., 2021, 33, 452–458 CrossRef CAS.
- K. Mase, K. Okumura, N. Yanai and N. Kimizuka, Chem. Commun., 2017, 53, 8261–8264 RSC.
- S. He, X. Luo, X. Liu, Y. Li and K. Wu, J. Phys. Chem. Lett., 2019, 10, 5036–5040 CrossRef CAS PubMed.
- K. Okumura, N. Yanai and N. Kimizuka, Chem. Lett., 2019, 48, 1347–1350 CrossRef CAS.
- S. He, R. Lai, Q. Jiang, Y. Han, X. Luo, Y. Tian, X. Liu and K. Wu, Angew. Chem., Int. Ed., 2020, 59, 17726–17731 CrossRef CAS PubMed.
- Z. A. VanOrman, H. K. Drozdick, S. Wieghold and L. Nienhaus, J. Mater. Chem. C, 2021, 9, 2685–2694 RSC.
- N. Kiseleva, P. Nazari, C. Dee, D. Busko, B. S. Richards, M. Seitz, I. A. Howard and A. Turshatov, J. Phys. Chem. Lett., 2020, 11, 2477–2481 CrossRef CAS PubMed.
- W. Chen, F. Song, S. Tang, G. Hong, Y. Wu and X. Peng, Chem. Commun., 2019, 55, 4375–4378 RSC.
- T. C. Wu, D. N. Congreve and M. A. Baldo, Appl. Phys. Lett., 2015, 107, 031103 CrossRef.
- N. Yanai, M. Kozue, S. Amemori, R. Kabe, C. Adachi and N. Kimizuka, J. Mater. Chem. C, 2016, 4, 6447–6451 RSC.
- Z. Wang and J. Zhao, Org. Lett., 2017, 19, 4492–4495 CrossRef CAS PubMed.
- N. Kiseleva, M. A. Filatov, M. Oldenburg, D. Busko, M. Jakoby, I. A. Howard, B. S. Richards, M. O. Senge, S. M. Borisov and A. Turshatov, Chem. Commun., 2018, 54, 1607–1610 RSC.
- Z. Wang, J. Zhao, M. Di Donato and G. Mazzone, Chem. Commun., 2019, 55, 1510–1513 RSC.
- Y. Dong, A. A. Sukhanov, J. Zhao, A. Elmali, X. Li, B. Dick, A. Karatay and V. K. Voronkova, J. Phys. Chem. C, 2019, 123, 22793–22811 CrossRef CAS.
- H. Liang, S. Sun, M. Zafar, Z. Yuan, Y. Dong, S. Ji, Y. Huo, M.-D. Li and J. Zhao, Dyes Pigm., 2020, 173, 108003 CrossRef CAS.
- Y. Dong, A. Elmali, J. Zhao, B. Dick and A. Karatay, ChemPhysChem, 2020, 21, 1388–1401 CrossRef CAS PubMed.
- Y. Hou, J. Liu, N. Zhang and J. Zhao, J. Phys. Chem. A, 2020, 124, 9360–9374 CrossRef CAS PubMed.
- M. A. Filatov, S. Karuthedath, P. M. Polestshuk, S. Callaghan, K. J. Flanagan, M. Telitchko, T. Wiesner, F. Laquai and M. O. Senge, Phys. Chem. Chem. Phys., 2018, 20, 8016–8031 RSC.
- J. T. Buck, A. M. Boudreau, A. DeCarmine, R. W. Wilson, J. Hampsey and T. Mani, Chem, 2019, 5, 138–155 CAS.
- D. Meroni, A. Monguzzi and F. Meinardi, J. Chem. Phys., 2020, 153, 114302 CrossRef CAS PubMed.
- V. Gray, D. Dzebo, A. Lundin, J. Alborzpour, M. Abrahamsson, B. Albinsson and K. Moth-Poulsen, J. Mater. Chem. C, 2015, 3, 11111–11121 RSC.
- J. P. Cerón-Carrasco, D. Jacquemin, C. Laurence, A. Planchat, C. Reichardt and K. Sraïdi, J. Phys. Org. Chem., 2014, 27, 512–518 CrossRef.
- M. A. Filatov, S. Karuthedath, P. M. Polestshuk, S. Callaghan, K. J. Flanagan, T. Wiesner, F. Laquai and M. O. Senge, ChemPhotoChem, 2018, 2, 606–615 CrossRef CAS.
- M. A. Filatov, Org. Biomol. Chem., 2020, 18, 10–27 RSC.
- Y. Hou, I. Kurganskii, A. Elmali, H. Zhang, Y. Gao, L. Lv, J. Zhao, A. Karatay, L. Luo and M. Fedin, J. Chem. Phys., 2020, 152, 114701 CrossRef CAS PubMed.
- W. Zhao and F. N. Castellano, J. Phys. Chem. A, 2006, 110, 11440–11445 CrossRef CAS PubMed.
- X.-F. Zhang, X. Yang, K. Niu and H. Geng, J. Photochem. Photobiol., A, 2014, 285, 16–20 CrossRef CAS.
- Y. Y. Cheng, B. Fückel, T. Khoury, R. G. C. R. Clady, M. J. Y. Tayebjee, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, J. Phys. Chem. Lett., 2010, 1, 1795–1799 CrossRef CAS.
- N. A. Durandin, J. Isokuortti, A. Efimov, E. Vuorimaa-Laukkanen, N. V. Tkachenko and T. Laaksonen, J. Phys. Chem. C, 2019, 123, 22865–22872 CrossRef CAS.
- W. Sun, A. Ronchi, T. Zhao, J. Han, A. Monguzzi and P. Duan, J. Mater. Chem. C, 2021, 9, 14201–14208 RSC.
- Y. Wei, Y. Wang, Q. Zhou, S. Zhang, B. Zhang, X. Zhou and S. Liu, Phys. Chem. Chem. Phys., 2020, 22, 26372–26382 RSC.
- V. Gray, A. Dreos, P. Erhart, B. Albinsson, K. Moth-Poulsen and M. Abrahamsson, Phys. Chem. Chem. Phys., 2017, 19, 10931–10939 RSC.
- C. Ye, V. Gray, J. Mårtensson and K. Börjesson, J. Am. Chem. Soc., 2019, 141, 9578–9584 CrossRef CAS PubMed.
- C. Ye, V. Gray, K. Kushwaha, S. Kumar Singh, P. Erhart and K. Börjesson, Phys. Chem. Chem. Phys., 2020, 22, 1715–1720 RSC.
- D. G. Bossanyi, Y. Sasaki, S. Wang, D. Chekulaev, N. Kimizuka, N. Yanai and J. Clark, JACS Au, 2021, 1, 2188–2201 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Luminescence and UC luminescence transients, transient absorption spectra, and dependencies of UC luminescence on excitation intensity. See DOI: 10.1039/d1cp05382e |
| This journal is © the Owner Societies 2022 |