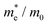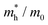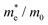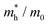Lone pair driven anisotropy in antimony chalcogenide semiconductors

Abstract

Antimony sulfide (Sb₂S₃) and selenide (Sb₂Se₃) have emerged as promising earth-abundant alternatives among thin-film photovoltaic compounds. A distinguishing feature of these materials is their anisotropic crystal structures, which are composed of quasi-one-dimensional (1D) [Sb₄X₆]_n ribbons. The interaction between ribbons has been reported to be van der Waals (vdW) in nature and Sb₂X₃ are thus commonly classified in the literature as 1D semiconductors. However, based on first-principles calculations, here we show that inter-ribbon interactions are present in Sb₂X₃ beyond the vdW regime. The origin of the anisotropic structures is related to the stereochemical activity of the Sb 5s lone pair according to electronic structure analysis. The impacts of structural anisotropy on the electronic, dielectric and optical properties relevant to solar cells are further examined, including the presence of higher dimensional Fermi surfaces for charge carrier transport. Our study provides guidelines for optimising the performance of Sb₂X₃-based photovoltaics via device structuring based on the underlying crystal anisotropy.

---

1 Introduction

Solar photovoltaic (PV) technology which converts the solar energy into electricity provides a clean and sustainable solution to the energy crisis. Current commercial thin-film light absorber materials such as cadmium telluride (CdTe) and copper indium gallium selenide (CIGS) have achieved certified PV efficiencies of over 22% under laboratory conditions.¹ These are tetrahedral semiconductors based on expansions of the diamond structure. However, CdTe and CIGS have limitations of the scarcity of the Te element, the toxicity of the Cd element and the high cost of In and Ga elements.^2–6

As potential alternatives, antimony chalcogenides (Sb₂X₃; X = S, Se) have attracted growing attention. Their associated ground-state crystal structures are orthorhombic with a range of locally distorted coordination environments. Sb₂X₃ have advantages of long-term stability, optimal bandgaps and high absorption coefficients (>10⁵ cm⁻¹) with abundant, non-toxic and low-cost constituents.^7–9 The PV conversion efficiencies of Sb₂X₃ devices have increased rapidly during the last decade. The current record efficiencies for pure Sb₂S₃ and Sb₂Se₃ have reached 7.5% and 9.2% respectively.^10,11 However, these values are still far below the maximum theoretical efficiency of ∼30% predicted by the Shockley–Queisser (SQ) model¹² which is an idealised model only based on band gaps of solar absorbers.

Intensive efforts have been devoted to improve the efficiencies in Sb₂X₃ solar cells. One research direction is the orientation control of Sb₂X₃ films.^13,14 Based on the understanding that Sb₂X₃ are composed of one-dimensional (1D) [Sb₄X₆]_n ribbons which are held together by vdW forces,^15–19 it has been reported that higher PV efficiency could be achieved when the Sb₂X₃ films are oriented more perpendicular to the substrate due to more efficient carrier transport along ribbons than between them.²⁰ Consequently, researchers have focused on tailoring the growth orientation of Sb₂X₃ films in order to achieve high efficiencies.^11,21–24 However, the origin of anisotropic crystal structures and the connection and the extent of the anisotropy in the physical properties remain unclear. Building on recent work that has shown a tolerance to structural reconstructions,²⁵ understanding how film orientations affect the conversion efficiency in Sb₂X₃ is crucial to designing high-performance devices.

In this study, we investigate the anisotropic structural, electronic and optical properties of Sb₂X₃ using first-principles calculations. The dimensionality of Sb₂X₃ is studied by consideration of the chemical binding energies, carrier effective masses, and Fermi surfaces. Electronic structure analysis further confirms that the orthorhombic crystal structures of Sb₂X₃ result from the stereochemical activity of the Sb 5s lone pair. Moreover, anisotropic optical properties including dielectric constants and optical absorption spectra are reported.

2 Methods

Analysis of the total energy and electronic structure was performed within the framework of Kohn–Sham density-functional theory (DFT).^26,27 Calculations were performed based on DFT as implemented in the Vienna Ab initio Simulation Package (VASP).²⁸ As these materials are non-magnetic, with an even number of electrons, all calculations were spin restricted. The projector augmented-wave (PAW) method²⁹ was employed with a plane-wave energy cutoff of 400 eV. All calculations were carried out using the Heyd–Scuseria–Ernzerhof hybrid functional (HSE06)^30,31 except for the calculation of ionic contribution of dielectric constants, as a lower-level functional is sufficient for this high-cost calculation.³²

To account for the weak inter-ribbon interactions, the optB86b-vdW functional³³ was used to calculate the ionic contribution to the static dielectric constant, and the D3 dispersion correction³⁴ was used for HSE06 calculations. The coefficients used for the zero-damping D3 correction are consistent with the previous research.³⁵ In order to obtain well-converged structures, the atomic positions were optimised until the Hellman–Feynman forces on each atom were below 0.0005 eV Å⁻¹, and the energy convergence criterion was set to 10⁻⁸ eV. According to convergence tests (shown in Table S2, ESI†), the total energies of Sb₂S₃ and Sb₂Se₃ converge to within 1 meV per atom at a k-point mesh of 7 × 2 × 2. Therefore, Γ-centered k-point meshes were set to 7 × 2 × 2 for geometry optimisation with primitive unit cells, and 14 × 4 × 4 for projected density of states (PDOS) and crystal orbital Hamilton populations (COHP) calculations. For calculations of effective masses, dielectric constants and optical absorption coefficients which are more sensitive to k-point density, detailed settings and the proof of convergence are shown in the ESI† (Tables S3–S6).

COHP calculations were performed using the LOBSTER package.³⁶ The conductivity effective mass tensors were calculated by the AMSET package.³⁷ Sb₂S₃ and Sb₂Se₃ have complex band structures with multiple band pockets close in energy to the band edges (Fig. S2, ESI†). This means that (i) the high symmetry band structure path does not pass through the true conduction band maximum (CBM) and valence band maximum (VBM) and (ii) picking the effective masses of a single minima/maxima will not be a meaningful metric as multiple band extrema will be occupied even at low temperatures. Therefore, the conventional definitions of effective mass for parabolic bands (such as the curvature effective mass,³⁸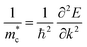) are no longer applicable for such systems. The conductivity effective mass (m*) has the advantage that it incorporates effects arising from multiple band extrema and incorporates the full Brillouin zone instead of just the k-points on the high symmetry path. This definition of conductivity effective mass has been widely used to assess materials with complex band structures where the typical picture of effective mass breaks down.^39–43 The ionic contribution to the static dielectric constants was calculated by density functional perturbation theory (DFPT),⁴⁴ while the electronic part was calculated using the approach developed by Furthmüller et al.⁴⁴ The optical absorption coefficients (α) were calculated from the dielectric function by the sumo package.⁴⁵ The thickness-dependent radiative limit of solar conversion efficiencies were determined using the calculated optical absorption coefficients, which uses a similar metric to the radiative limit of spectroscopic limited maximum efficiency (SLME).⁴⁶ We note that excitonic effects are not included in this analysis. More details about the calculations of the effective masses, optical absorption coefficients and radiative limit of solar conversion efficiencies are provided in the ESI.†

The crystal structures and partial charge densities were plotted using CrystalMaker®.⁴⁷ The PDOS and optical absorption spectra were plotted using the sumo package.⁴⁵ Fermi surfaces were plotted using the IFermi package.⁴⁸ The figures of distance histograms, COHP, dielectric constants, optical absorption spectra and thickness-dependent maximum efficiencies were plotted using matplotlib.⁴⁹

3 Results and discussions

We first consider the anisotropy of the crystal structures found from structural relaxation within DFT, followed by analysis of the orientation-dependence of the associated electronic structure and optical properties.

3.1 Structural properties

The ground-state crystal structures of Sb₂S₃ and Sb₂Se₃ (Pnma space group) are shown in Fig. 1a. They are composed of strongly bonded quasi-1D [Sb₄X₆]_n ribbons units stacked together by weak interactions. In order to better reproduce the crystal structures, different vdW dispersion correction methods were applied in the geometry optimisation process. Lattice parameters calculated by different functionals and different vdW correction methods and obtained by experiments^50–55 are shown in Table 1. The c parameter (the direction between ribbons) is significantly overestimated (>7.0%) with no dispersion correction included for both PBE and HSE06 functionals. Including dispersion corrections, the accuracy of lattice parameter in the c direction is greatly improved regardless of the correction methods. This demonstrates the presence of significant vdW interactions between ribbons, which are much weaker than the bonding within ribbons, and thus the necessity of dispersion corrections when modelling Sb₂X₃. For both systems, HSE06 + D3 gives the best agreement with experimental measurements (an average difference of 0.7% and 0.9% for Sb₂S₃ and Sb₂Se₃ from the experimental lattice constants, respectively), which is in agreement with previous studies,^35,56 followed by optB86b performing the next best (1.0% and 1.4% difference for Sb₂S₃ and Sb₂Se₃, respectively). Thus, the HSE06 functional with the D3 Grimme dispersion correction was used for most of the following calculations and the optB86b functional was used for most convergence tests.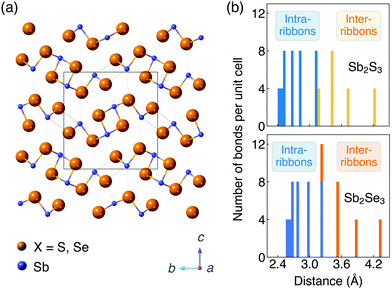

Fig. 1 (a) Crystal structures (Pnma space group) and (b) histogram of Sb–X distances of Sb₂S₃ and Sb₂Se₃. The unit cell is represented by a rectangle.

Table 1 Lattice parameters (Å) of Sb₂S₃ and Sb₂Se₃ as calculated by different functionals and different vdW dispersion correction methods. The percentage error (%) relative to the experimental average is given in parentheses

System		PBE	PBE + D3	PBE + TS	optB86b	HSE06	HSE06 + D3	HSE06 + TS	Experimental data
									Ref. 50 and 51	Ref. 52 and 53	Ref. 54 and 55	Average
Sb2S3	a	3.87	3.84	3.88	3.86	3.80	3.80	3.81	3.84	3.82	3.84	3.83
		(1.0)	(0.3)	(1.3)	(0.8)	(−0.8)	(−0.8)	(−0.5)
	b	11.22	10.92	11.09	11.04	11.39	11.20	11.22	11.22	11.27	11.29	11.26
		(−0.4)	(−3.1)	(−1.5)	(−2.0)	(1.1)	(−0.5)	(−0.4)
	c	12.14	11.15	11.54	11.32	12.09	11.39	11.54	11.31	11.30	11.27	11.29
		(7.0)	(−1.3)	(2.2)	(0.3)	(6.6)	(0.9)	(2.2)
Sb2Se3	a	4.03	3.99	4.04	4.02	3.96	3.95	3.97	3.98	3.99	3.96	3.98
		(1.2)	(0.3)	(1.5)	(1.0)	(−0.5)	(−0.8)	(−0.3)
	b	11.53	11.33	11.41	11.46	11.73	11.55	11.54	11.65	11.65	11.62	11.64
		(−1.0)	(−2.7)	(−2.0)	(−1.6)	(0.8)	(−0.8)	(−0.9)
	c	12.84	11.68	12.31	11.90	12.65	11.93	12.18	11.80	11.79	11.77	11.79
		(8.2)	(−0.9)	(4.2)	(0.9)	(6.8)	(1.2)	(3.2)

---

Histograms of distances between Sb and X ions are shown in Fig. 1b. The widely distributed bond lengths indicate the anisotropic connectivity of Sb₂X₃. The bond lengths of Sb₂Se₃ are slightly larger than those of Sb₂S₃ due to the increased anion radius. In the study of Deringer et al.,⁵⁷ analysis of the integrated COHP and the harmonic force constants showed a clear separation between strong intra-ribbon and weaker inter-ribbon interactions in Sb₂Se₃. In order to quantify the interaction between ribbons, inter-ribbon binding energies per atom (E_b) and binding energies per bond along the b (E_b(b)) and c (E_b(c)) directions are calculated by

E_b = (2E_2D − E_t)/20 (1)

E_b(b) = (E_1D − E_2D)/2 (2)

E_b(c) = (2E_2D − E_t)/16 (3)

where E_1D and E_2D are total energies of one 1D [Sb₄X₆]_n ribbon in isolation and one 2D [Sb₄X₆]_n ribbon periodically repeated along a and b directions, respectively (the 1D and 2D substructures are given in Fig. S1, ESI†). E_t is the total energy of the unit cell. The denominators of 20, 2 and 16 in eqn (1)–(3) are due to the fact that one unit cell of Sb₂X₃ contains twenty atoms, two Sb–X bonds along the b direction and sixteen Sb–X bonds along the c direction, respectively. Note that the substructures were directly taken from the optimised structures and kept unrelaxed in order to avoid structural distortion effects, as is typical for binding energy calculations.^58,59 The effect of optimisation was also tested and the total energies of the substructures were ∼10 kJ mol⁻¹ lower after relaxation. Table 2 shows the calculated inter-ribbon binding energies using the HSE06 functional and D3 dispersion correction. It can be seen that binding energies of Sb₂S₃ and Sb₂Se₃ are both over 10 kJ mol⁻¹, which are both beyond the typical vdW regime (0.4–4 kJ mol⁻¹).⁶⁰ This is consistent with previous research that the distance of Sb–S between ribbons in Sb₂S₃ is shorter than the sum of Sb and S vdW radii at 293 K.⁵⁰ Moreover, E_b(b) is larger than E_b(c) due to the elongation of ribbons along b, and the binding energies of Sb₂Se₃ is slightly larger than that of Sb₂S₃. The calculated values agree well with previous calculations⁶¹ and indicate that the inter-ribbon interactions of Sb₂S₃ and Sb₂Se₃ are both between the vdW and covalent regime. This type of inter-ribbon binding energies can also be found in other systems.^62,63 The results of inter-ribbon binding energies without vdW corrections are given in Table S1 (ESI†).

Table 2 Inter-ribbon binding energies (kJ mol⁻¹) of Sb₂S₃ and Sb₂Se₃

System	E b	E b(b)	E b(c)
Sb2S3	12.77	27.44	15.96
Sb2Se3	14.36	31.13	17.95

---

3.2 Electronic properties

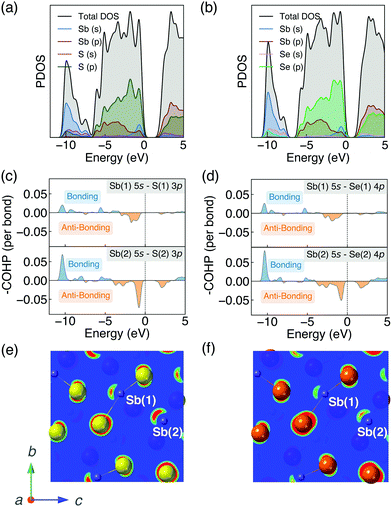
The strength of the interaction between ribbons is closely related to the distortion of Sb atomic environment which originates from the stereochemically active Sb 5s lone pairs. Before going further into the lone pair analysis, the density of states and orbital overlaps are first investigated.

The PDOS are shown in Fig. 2a and b. The valence band (VB) can be divided into two main parts. The highest occupied VB between −1 and 0 eV consists of S 3p/Se 4p, Sb 5s and Sb 5p states. While the states between −10 and −7 eV mainly consists of Sb 5s orbitals, alongside some small contributions from S 3s/Se 4s and S 3p/Se 4p states. A valley at about 2 eV below the valence band maximum (VBM) is demonstrated to be one of the major characteristics of energy distribution curves for Sb₂Se₃ according to the photoemission measurements.⁵⁵ Our calculated PDOS of Sb₂Se₃ also shows a valley at ∼−2 eV which is in good agreement with the experimental results. The conduction band (CB) are dominated by Sb 5p and S 3p/Se 4p states. These results agree well with earlier studies of PDOS on Sb₂X₃.^57,64–66

Fig. 2 (a) and (b) Projected density of states (PDOS), (c) and (d) crystal orbital Hamilton populations (COHP) and (e) and (f) partial charge densities of antimony chacogenides. The range of isosurface value for partial charge densities is set to 0.05–0.10 e Å⁻³ for both Sb₂S₃ and Sb₂Se₃. The VBM is set to 0 in each case.

The bonding and antibonding interactions are further studied by COHP³⁶ (shown in Fig. 2c and d). Two separate cases are plotted since Sb has two distinct chemical environments. The interaction is weaker in Sb(1)–X(1) than Sb(2)–X(2) which agrees with the longer bond lengths of Sb(1)–X(1). Combined with the results of PDOS, the energy range from −10 to −7 eV corresponds to a bonding interaction between Sb 5s and S 3p/Se 4p states, whereas the region at the top of the VB corresponds to an antibonding state, which is similar to other quasi-1D systems with stereochemically active lone pairs.⁶⁷ The photoemission measurements for Sb₂Se₃⁵⁵ show that the lower part of VB below ∼−6 eV is contributed by bonding states which agrees well with our results. Moreover, the interaction is stronger in Sb₂S₃ than Sb₂Se₃ which will be discussed in detail later.

The different inter-ribbon interactions in Sb₂S₃ and Sb₂Se₃ result from the Sb 5s lone pair formation. In the revised lone pair model,⁶⁸ the interaction between the antibonding states of cation s–anion p and cation p states results in the formation of stereochemically active lone pairs. Smaller energy difference between cation s and anion p states will facilitate stronger interaction and thus a more asymmetric electron density. In our systems, for the Sb(III) oxidation state found in Sb₂X₃, the formal electronic configuration of Sb is 5s²5p⁰. Based on the discussions above, the Sb 5s states interact with the S 3p/Se 4p states in the VB forming filled bonding and antibonding states. The additional interaction of the nominally empty Sb 5p orbitals stabilises the system by lowering the total energy, which is similar to other lone pair systems.^68–71 The resulting stereochemically active lone pair results in an asymmetric electronic density at the top of VB which can be visualised by the contour plot of partial charge density. Partial charge densities for the states between −1 and 0 eV (with respect to the VBM) are shown in Fig. 2e and f. They are obtained by cutting the (100) plane through Sb atoms. The lone pair is stronger in Sb₂S₃ compared with Sb₂Se₃ due to the smaller energy separation and increased overlap of Sb 5s and S 3p.

To connect the electronic structure to transport properties, effective masses of electrons and holes were calculated (shown in Table 3). According to the electronic band structures of Sb₂S₃ and Sb₂Se₃ (shown in Fig. S2, ESI†), the band dispersions around the extrema are relatively flat which are far from parabolic. Therefore, effective masses in Sb₂X₃ are quite sensitive to calculation parameters (particularly the k-point density), and effective masses larger than 2 are rounded to the nearest whole numbers in Table 3 and Table S3 (ESI†). The harmonic mean is used to average the values for a polycrystalline sample with random orientations, and the anisotropy ratio (a_r) is defined as the ratio of maximum to minimum effective mass. The average effective masses of holes are larger than those of electrons for both Sb₂S₃ and Sb₂Se₃, indicating that Sb₂S₃ and Sb₂Se₃ may be better n-type semiconductors. Nevertheless, the electron effective masses show a stronger anisotropy. a_r is larger in Sb₂Se₃ than Sb₂S₃ for both electron and hole effective masses, suggesting Sb₂Se₃ has stronger anisotropy which agrees with the weaker lone pair and longer bond lengths in Sb₂Se₃. The electron and hole effective masses are the largest along [001] for both Sb₂S₃ and Sb₂Se₃, indicating the conductivity along [001] will be lower than along the other two directions. This is also consistent with the low inter-ribbon binding energies along the [001] direction and the direction of the Sb 5s lone pair (Fig. 2e and f). In general the values follow the trend x < y < z, with the exception of the hole effective mass for Sb₂Se₃, which is discussed later. Moreover, the 2D nature of transport (with small effective masses in two directions and large effective mass in the other direction) is similar to other so-called “quasi-1D” systems such as BiSI and BiSeI.⁷² Our calculated effective masses deviate largely from other studies on Sb₂X₃.^73,74 One possible reason of the discrepancy could be the use of simple parabolic fitting or the consideration of solely the Γ point in other computational investigations. The choice of functionals could be another important factor, as demonstrated by Whalley et al.⁷⁵ It has been demonstrated that semi-local functionals would not only underestimate the bandgap, but also would influence the shape of band structures, resulting in overestimated nonparabolicity.

Table 3 Effective masses of Sb₂S₃ and Sb₂Se₃. The harmonic mean is represented by m̄*. The anisotropy ratio (a_r) is defined as the ratio of maximum to minimum effective mass

System		x	y	z	m̄*	a r
Sb2S3		0.16	0.92	5	0.40	31.25
		0.47	0.65	0.97	0.64	2.06
Sb2Se3		0.14	0.81	7	0.35	50.00
		0.85	0.55	3	0.90	5.45

---

To further illustrate the dimensionality of the electronic structure, Fermi surfaces were plotted at 0.1 eV below (above) the VBM (CBM) using the IFermi package⁴⁸ (shown in Fig. 3). 0.1 eV is an arbitrary value intended to indicate the shape of the Fermi surface close to the band edge. Due to the tails of the Fermi–Dirac distribution, this energy range will be occupied at room temperature and the Fermi surface is therefore reflective of the states that govern transport properties. The Fermi surfaces of 0.08 and 0.12 eV below (above) the VBM (CBM) were also shown in Fig. S3 and S4 (ESI†) which qualitatively show the same behaviour. An ellipsoidal Fermi surface is found for holes in Sb₂S₃ (Fig. 3a), indicating dispersion in three dimensions.^76,77 The shape of warped cylinders (considering the periodic boundary conditions) found for electrons in Sb₂S₃ (Fig. 3c) can be classified as quasi-2D with small dispersion in the [001] direction.^76,77 These agree well with observation that the hole effective mass of Sb₂S₃ is much smaller than the electron effective mass in the [001] direction. In contrast, for Sb₂Se₃, due to the relatively large hole and electron effective masses in the [001] direction, the hole and electron Fermi surfaces of Sb₂Se₃ are quasi-2D (with the shape of warped cylinders) (shown in Fig. 3b and d). Moreover, it can be seen that the electron Fermi surfaces of Sb₂S₃ and Sb₂Se₃ have similar topology, which is consistent with the similar values of effective masses and indicates similar transport behaviours, whereas their hole Fermi surfaces have a significant difference in terms of the dimensionality. Indeed, for Sb₂S₃ the three components of the effective masses are all below one, while for Sb₂Se₃ the z component is greater than 3. We link this behaviour to the stronger lone pair distortion of Sb₂S₃ and the resulting shorter inter-ribbon Sb–S bonds along the [001] direction.

Fig. 3 Fermi surfaces of Sb₂S₃ and Sb₂Se₃. (a) and (c) are hole Fermi surfaces (0.1 eV below the valence band maximum), while (b) and (d) are electron Fermi surfaces (0.1 eV above the conduction band minimum). The different colors represent the magnitude of group velocity (m s⁻¹).

3.3 Optical properties

The dielectric constants are important descriptors for the optical properties of crystals. The static dielectric constant (ε₀) is defined as the sum of the ionic and high-frequency response to an external electric field. The complex dielectric function ε(ω) is given by:

ε(ω) = ε₁(ω) + iε₂(ω) (4)

where ε₁ and ε₂ are the real part and imaginary part of the frequency-dependent dielectric function, respectively. For orthorhombic structures, the dielectric tensor has three distinct non-zero components. As shown in Table 4, the dielectric constants of Sb₂X₃ are anisotropic and relatively large, which is common in lone-pair containing crystals.^67,71 Large dielectric constants indicate the potential for strong screening to charged defects and low recombination losses.^2,78 It can be seen that the dielectric constants are larger in the x and y directions than the z direction, indicating the screening is stronger in the ab plane. Moreover, the dielectric screening in Sb₂X₃ is shown to be dominated by the lattice polarization as the ionic contribution is much larger than the electronic contribution. The large ionic dielectric constants can be attributed to large Born effective charges in Sb₂X₃.^79,80 The anisotropy ratio (a_r) (defined as the ratio of maximum to minimum dielectric constant) is larger in Sb₂Se₃ than Sb₂S₃ for both static and high-frequency dielectric constants, indicating Sb₂Se₃ has stronger anisotropy which is consistent with previous discussions.

Table 4 Calculated static (ε₀) and high-frequency (ε_∞) dielectric constants of Sb₂S₃ and Sb₂Se₃. The anisotropy ratio (a_r) is defined as the ratio of maximum to minimum dielectric constant

System	ε 0				ε ∞
	x	y	z	a r	x	y	z	a r
Sb2S3	98.94	94.21	13.14	7.53	11.55	10.97	8.25	1.40
Sb2Se3	85.64	128.18	15.00	8.54	15.11	14.92	10.53	1.43

---

The real and imaginary parts of the high-frequency (ε_∞) dielectric functions are plotted in Fig. 4. Combined with the results of PDOS, the peaks in the imaginary parts of dielectric functions mainly correspond to the optical transition from the S 3p/Se 4p states in the valence band to the Sb 5p states in the conduction band. Our calculated dielectric constants are in excellent agreement with ellipsometry measurements on polycrystalline thin films (ε_∞,x, ε_∞,y and ε_∞,z of 12.5, 10.8 and 7.0 for Sb₂S₃,⁸¹ respectively, and an averaged ε_∞ of 14.3 for Sb₂Se₃⁷). Furthermore, our results are inline with previous theoretical studies.^65,82–85

Fig. 4 Calculated high-frequency dielectric functions of (a) Sb₂S₃ and (b) Sb₂Se₃.

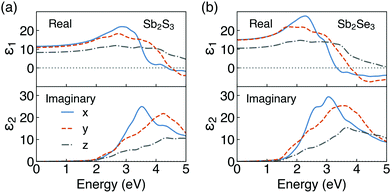
The calculated optical absorption spectra, and radiative limit of solar conversion efficiency, for Sb₂S₃ and Sb₂Se₃ are shown in Fig. 5. As can be seen in Fig. 5a, both Sb₂S₃ and Sb₂Se₃ possess high optical absorption coefficients above the band edge (in the range of 10⁵ cm⁻¹) which could more effectively absorb photons and generate electron–hole pairs. This agrees well with experimental UV-vis measurements on Sb₂X₃, which observed large absorption coefficients of ∼10⁵ cm⁻¹ in the visible region.^2,9,86,87 Possible reasons for such high optical absorption coefficients in these indirect gap semiconductors could be attributed to their unique electronic band structures (shown in Fig. S2, ESI†). On the one hand, the difference between indirect and direct gaps of Sb₂X₃ is small (0.16 eV for Sb₂S₃ and 0.06 eV for Sb₂Se₃) which makes them still suitable for strong absorption near the band edges.⁸⁸ On the other hand, the relatively flat dispersions near the band extrema will lead to high DOS near the VBM and CBM and thus strong absorption.⁸⁹ Moreover, there is slight difference in absorption coefficients along different directions. The thickness-dependent radiative limit of conversion efficiencies (Fig. 5b) along different orientations were further determined using the calculated optical absorption coefficients. The efficiencies show a strong dependence on the film thickness in the 0–2 μm range, and rise rapidly with the increase of the film thickness due to the large magnitude of optical absorption coefficients. We note that our simplified model assumes that all generated carriers are collected, which means the mobility is assumed to be infinitely high. Under this assumption, for both Sb₂S₃ and Sb₂Se₃, the radiative limit of efficiencies approach the SQ limit at a thickness of 2 μm. Within our model, which incorporates the electronic structure and direction-dependent optical absorption, the solar conversion efficiencies are equivalent in each different orientation. The efficiencies are larger in Sb₂Se₃ than Sb₂S₃ since the band gap of Sb₂Se₃ is closer to the optimal band gap predicted by the SQ model. These results indicate that absorption does not lead to orientation dependence in the conversion efficiencies in Sb₂S₃ and Sb₂Se₃. We note that our predictions of anisotropic crystal structure and anisotropic effective masses indicate that real devices will likely show orientation-dependent efficiencies, due to favourable (benign) grain boundary orientations²⁰ and anisotropic carrier mobilities (and thus charge collection efficiencies). Beyond this, the presence of defects in Sb₂X₃^{10,35,56,90–93} also reduces conversion efficiencies from the idealised theoretical limit to that obtained in real devices.

Fig. 5 (a) Calculated optical absorption spectra of Sb₂S₃ and Sb₂Se₃ arising from direct valence to conduction band transitions. The fundamental band gaps are shown in grey dotted lines. (b) Thickness-dependent maximum efficiencies based on the radiative limit of Sb₂S₃ and Sb₂Se₃.

4 Conclusions

The standard description of Sb₂X₃ in the literature refers to them as 1D semiconductors, where electrons and holes can readily diffuse along, but not between, ribbons in the crystal. This has lead to a focus on thin-film synthesis to achieve optimal [100] orientations. Our first-principles investigation has shown that the chemical binding energies between ribbons (>10 kJ mol⁻¹) fall between the vdW and ionic/covalent regime. Analysis of the carrier effective masses does reveal a strong anisotropy, but the behaviour is not 1D, with stronger dispersion found in [010] compared to [001]. The Fermi surfaces for electrons and holes illustrate this complexity with a combination of 3D (holes in Sb₂S₃) and quasi-2D transport. The anisotropy carries through to the dielectric response of the crystals with much stronger screening in the ab plane compared to along the c axis. However, the resulting optical absorption profiles are less sensitive and yield the same radiative limit of conversion efficiencies for photovoltaic applications. The origin of these anisotropic effects is linked to lone pair formation associated with the filled Sb 5s orbitals which distorts the Sb coordination environment. Beyond the bulk crystal properties, the orientation-dependence should extend to the crystal terminations where the associated surface polarisation will influence electron and hole extraction by electrical contacts.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1 and EP/T022213/1). Xinwei Wang acknowledges Imperial College London for the funding of a President's PhD Scholarship. Seán R. Kavanagh acknowledges the EPSRC Centre for Doctoral Training in the Advanced Characterisation of Materials (CDT-ACM) (EP/S023259/1) for funding a PhD studentship. Alex M. Ganose was supported by EPSRC Fellowship EP/T033231/1. Xinwei Wang thanks Chengcheng Xiao and Sunghyun Kim for advice on the computational analysis.

References

1. M. A. Green, E. D. Dunlop, J. Hohl-Ebinger, M. Yoshita, N. Kopidakis and A. W. Ho-Baillie, Prog. Photovolt. Res. Appl., 2020, 28, 3–15.
2. K. Zeng, D.-J. Xue and J. Tang, Semicond. Sci. Technol., 2016, 31, 063001.
3. H. Lei, J. Chen, Z. Tan and G. Fang, Sol. RRL, 2019, 3, 1900026.
4. R. Kondrotas, C. Chen and J. Tang, Joule, 2018, 2, 857–878.
5. A. Mavlonov, T. Razykov, F. Raziq, J. Gan, J. Chantana, Y. Kawano, T. Nishimura, H. Wei, A. Zakutayev and T. Minemoto, et al. , Sol. Energy, 2020, 201, 227–246.
6. J. T. Dufton, A. Walsh, P. M. Panchmatia, L. M. Peter, D. Colombara and M. S. Islam, Phys. Chem. Chem. Phys., 2012, 14, 7229–7233.
7. C. Chen, W. Li, Y. Zhou, C. Chen, M. Luo, X. Liu, K. Zeng, B. Yang, C. Zhang and J. Han, et al. , Appl. Phys. Lett., 2015, 107, 043905.
8. C. Ghosh and B. Varma, Thin Solid Films, 1979, 60, 61–65.
9. Y. Zhou, M. Leng, Z. Xia, J. Zhong, H. Song, X. Liu, B. Yang, J. Zhang, J. Chen and K. Zhou, et al. , Adv. Energy Mater., 2014, 4, 1301846.
10. Y. C. Choi, D. U. Lee, J. H. Noh, E. K. Kim and S. I. Seok, Adv. Funct. Mater., 2014, 24, 3587–3592.
11. Z. Li, X. Liang, G. Li, H. Liu, H. Zhang, J. Guo, J. Chen, K. Shen, X. San and W. Yu, et al. , Nat. Commun., 2019, 10, 1–9.
12. W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519.
13. J. Kim, S. Ji, Y. Jang, G. Jeong, J. Choi, D. Kim, S.-W. Nam and B. Shin, Sol. RRL, 2021, 5, 2100327.
14. T. D. Hobson, L. J. Phillips, O. S. Hutter, H. Shiel, J. E. Swallow, C. N. Savory, P. K. Nayak, S. Mariotti, B. Das and L. Bowen, et al. , Chem. Mater., 2020, 32, 2621–2630.
15. F. Caruso, M. R. Filip and F. Giustino, Phys. Rev. B, 2015, 92, 125134.
16. H. Song, T. Li, J. Zhang, Y. Zhou, J. Luo, C. Chen, B. Yang, C. Ge, Y. Wu and J. Tang, Adv. Mater., 2017, 29, 1700441.
17. L. Guo, B. Zhang, Y. Qin, D. Li, L. Li, X. Qian and F. Yan, Sol. RRL, 2018, 2, 1800128.
18. W. Yang, J. Ahn, Y. Oh, J. Tan, H. Lee, J. Park, H.-C. Kwon, J. Kim, W. Jo and J. Kim, et al. , Adv. Energy Mater., 2018, 8, 1702888.
19. R. Gusmão, Z. Sofer, J. Luxa and M. Pumera, ACS Sustain. Chem. Eng., 2019, 7, 15790–15798.
20. Y. Zhou, L. Wang, S. Chen, S. Qin, X. Liu, J. Chen, D.-J. Xue, M. Luo, Y. Cao and Y. Cheng, et al. , Nat. Photonics, 2015, 9, 409–415.
21. S. Yuan, H. Deng, D. Dong, X. Yang, K. Qiao, C. Hu, H. Song, H. Song, Z. He and J. Tang, Sol. Energy Mater. Sol. Cells, 2016, 157, 887–893.
22. L. Wang, D.-B. Li, K. Li, C. Chen, H.-X. Deng, L. Gao, Y. Zhao, F. Jiang, L. Li and F. Huang, et al. , Nat. Energy, 2017, 2, 1–9.
23. R. Kondrotas, J. Zhang, C. Wang and J. Tang, Sol. Energy Mater. Sol. Cells, 2019, 199, 16–23.
24. Y. Zeng, K. Sun, J. Huang, M. P. Nielsen, F. Ji, C. Sha, S. Yuan, X. Zhang, C. Yan and X. Liu, et al. , ACS Appl. Mater. Interfaces, 2020, 12, 22825–22834.
25. K. P. McKenna, Adv. Electron. Mater., 2021, 7, 2000908.
26. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
27. R. M. Dreizler and E. K. Gross, Density Functional Theory, Springer, 1990, pp. 245–271.
28. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
29. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
30. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
31. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
32. S. R. Kavanagh, A. Walsh and D. O. Scanlon, ACS Energy Lett., 2021, 6, 1392–1398.
33. J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131.
34. S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
35. C. N. Savory and D. O. Scanlon, J. Mater. Chem. A, 2019, 7, 10739–10744.
36. R. Dronskowski and P. E. Blöchl, J. Phys. Chem., 1993, 97, 8617–8624.
37. A. M. Ganose, J. Park, A. Faghaninia, R. Woods-Robinson, K. A. Persson and A. Jain, Nat. Commun., 2021, 12, 1–9.
38. N. W. Ashcroft and N. D. Mermin, Solid State Physics, Harcourt College Publishers, Fort Worth, 1976.
39. G. Hautier, A. Miglio, G. Ceder, G.-M. Rignanese and X. Gonze, Nat. Commun., 2013, 4, 1–7.
40. G. Hautier, A. Miglio, D. Waroquiers, G.-M. Rignanese and X. Gonze, Chem. Mater., 2014, 26, 5447–5458.
41. A. Bhatia, G. Hautier, T. Nilgianskul, A. Miglio, J. Sun, H. J. Kim, K. H. Kim, S. Chen, G.-M. Rignanese and X. Gonze, et al. , Chem. Mater., 2016, 28, 30–34.
42. L. Lykke, B. B. Iversen and G. K. Madsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195121.
43. D. S. Parker, A. F. May and D. J. Singh, Phys. Rev. Appl., 2015, 3, 064003.
44. M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112.
45. A. M. Ganose, A. J. Jackson and D. O. Scanlon, J. Open Source Softw., 2018, 3, 717.
46. L. Yu and A. Zunger, Phys. Rev. Lett., 2012, 108, 068701.
47. CrystalMaker, CrystalMaker Software Ltd, Oxford, England, (http://www.crystalmaker.com).
48. A. M. Ganose, A. Searle, A. Jain and S. M. Griffin, J. Open Source Softw., 2021, 6, 3089.
49. J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95.
50. A. Kyono, M. Kimata, M. Matsuhisa, Y. Miyashita and K. Okamoto, Phys. Chem. Miner., 2002, 29, 254–260.
51. O. Savadogo and K. Mandal, Sol. Energy Mater. Sol. Cells, 1992, 26, 117–136.
52. A. Salem and M. S. Selim, J. Phys. D, 2001, 34, 12.
53. I. Efthimiopoulos, J. Zhang, M. Kucway, C. Park, R. C. Ewing and Y. Wang, Sci. Rep., 2013, 3, 1–8.
54. G. Voutsas, A. Papazoglou, P. Rentzeperis and D. Siapkas, Z. Kristallogr. Cryst. Mater., 1985, 171, 261–268.
55. Z. Hurych, D. Davis, D. Buczek, C. Wood, G. Lapeyre and A. Baer, Phys. Rev. B: Condens. Matter Mater. Phys., 1974, 9, 4392.
56. A. Stoliaroff, A. Lecomte, O. Rubel, S. Jobic, X. Zhang, C. Latouche and X. Rocquefelte, ACS Appl. Energy Mater., 2020, 3, 2496–2509.
57. V. L. Deringer, R. P. Stoffel, M. Wuttig and R. Dronskowski, Chem. Sci., 2015, 6, 5255–5262.
58. N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti and G. Pizzi, et al. , Nat. Nanotechnol., 2018, 13, 246–252.
59. T. Björkman, A. Gulans, A. V. Krasheninnikov and R. M. Nieminen, Phys. Rev. Lett., 2012, 108, 235502.
60. R. H. Garrett and C. M. Grisham, Biochemistry, Brooks/Cole, Boston, 2010.
61. M. R. Filip, C. E. Patrick and F. Giustino, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 205125.
62. L. Xian, A. P. Paz, E. Bianco, P. M. Ajayan and A. Rubio, 2D Mater., 2017, 4, 041003.
63. D. Wines, J. A. Kropp, G. Chaney, F. Ersan and C. Ataca, Phys. Chem. Chem. Phys., 2020, 22, 6727–6737.
64. R. Caracas and X. Gonze, Phys. Chem. Miner., 2005, 32, 295–300.
65. H. Koç, A. M. Mamedov, E. Deligoz and H. Ozisik, Solid State Sci., 2012, 14, 1211–1220.
66. A. Radzwan, R. Ahmed, A. Shaari, A. Lawal and Y. X. Ng, Malays. J. Fundam. Appl. Sci., 2017, 13, 285–289.
67. A. M. Ganose, K. T. Butler, A. Walsh and D. O. Scanlon, J. Mater. Chem. A, 2016, 4, 2060–2068.
68. A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455–4463.
69. A. Walsh and G. W. Watson, J. Solid State Chem., 2005, 178, 1422–1428.
70. J. P. Allen, J. J. Carey, A. Walsh, D. O. Scanlon and G. W. Watson, J. Phys. Chem. C, 2013, 117, 14759–14769.
71. S. R. Kavanagh, C. N. Savory, D. O. Scanlon and A. Walsh, Mater. Horiz., 2021, 8, 2709–2716.
72. A. M. Ganose, S. Matsumoto, J. Buckeridge and D. O. Scanlon, Chem. Mater., 2018, 30, 3827–3835.
73. T. B. Nasr, H. Maghraoui-Meherzi and N. Kamoun-Turki, J. Alloys Compd., 2016, 663, 123–127.
74. W. Qiu, C. Zhang, S. Cheng, Q. Zheng, X. Yu, H. Jia and B. Wu, J. Solid State Chem., 2019, 271, 339–345.
75. L. D. Whalley, J. M. Frost, B. J. Morgan and A. Walsh, Phys. Rev. B, 2019, 99, 085207.
76. I. Matsuda and S. Hasegawa, J. Phys.: Condens. Matter, 2007, 19, 355007.
77. S. G. Albert, PhD thesis, Technische Universität München, 2015.
78. A. Walsh and A. Zunger, Nat. Mater., 2017, 16, 964–967.
79. Y. Liu, K. T. E. Chua, T. C. Sum and C. K. Gan, Phys. Chem. Chem. Phys., 2014, 16, 345–350.
80. Y. Cheng, O. Cojocaru-Mirédin, J. Keutgen, Y. Yu, M. Küpers, M. Schumacher, P. Golub, J.-Y. Raty, R. Dronskowski and M. Wuttig, Adv. Mater., 2019, 31, 1904316.
81. M. Schubert, T. Hofmann, C. Herzinger and W. Dollase, Thin Solid Films, 2004, 455, 619–623.
82. T. B. Nasr, H. Maghraoui-Meherzi, H. B. Abdallah and R. Bennaceur, Phys. B, 2011, 406, 287–292.
83. M. H. Lakhdar, B. Ouni and M. Amlouk, Mater. Sci. Semicond. Process., 2014, 19, 32–39.
84. H. Maghraoui-Meherzi, T. B. Nasr and M. Dachraoui, Mater. Sci. Semicond. Process., 2013, 16, 179–184.
85. A. Lawal, A. Shaari, R. Ahmed and L. Taura, Curr. Appl. Phys., 2018, 18, 567–575.
86. M. Y. Versavel and J. A. Haber, Thin Solid Films, 2007, 515, 7171–7176.
87. Y. Lai, Z. Chen, C. Han, L. Jiang, F. Liu, J. Li and Y. Liu, Appl. Surf. Sci., 2012, 261, 510–514.
88. R. Kondrotas, C. Chen, X. Liu, B. Yang and J. Tang, J. Semicond., 2021, 42, 031701.
89. M. Kumar, N. Umezawa and M. Imai, Appl. Phys. Express, 2014, 7, 071203.
90. X. Liu, X. Xiao, Y. Yang, D.-J. Xue, D.-B. Li, C. Chen, S. Lu, L. Gao, Y. He and M. C. Beard, et al. , Prog. Photovolt., 2017, 25, 861–870.
91. X. Hu, J. Tao, G. Weng, J. Jiang, S. Chen, Z. Zhu and J. Chu, Sol. Energy Mater. Sol. Cells, 2018, 186, 324–329.
92. Z. Cai, C.-M. Dai and S. Chen, Sol. RRL, 2020, 4, 1900503.
93. M. Huang, Z. Cai, S. Wang, X.-G. Gong, S.-H. Wei and S. Chen, Small, 2021, 17, 2102429.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp05373f

---