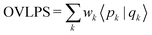Energy decomposition analysis method for metallic systems†
Received
8th November 2021
, Accepted 17th December 2021
First published on 21st December 2021
Abstract
In this work, we present the first extension of an energy decomposition analysis (EDA) method to metallic systems. We extend the theory of our Hybrid Absolutely Localized Molecular Orbitals (HALMO) EDA to take into account that molecular orbitals in metallic systems are partially occupied, which is done by weighted orthogonalization (WO) of the molecular orbitals using their associated fractional occupancies as weights in the construction of the projection operators. These operators are needed for the self-consistent field for molecular interaction (SCF MI) computation of the polarization-energy contribution to the interaction. The method gives more weight to orbitals that have higher occupancies and treats each fragment as metallic. The resulting HALMO EDA for metallic systems naturally reduces to the insulator version and produces the same results when applied to an insulating system. We present the theory and implementation of our new approach, and we demonstrate it with sample calculations of relevance to industrial materials. This work provides a new EDA paradigm and tool for the study and analysis of interactions in metallic systems within large-scale DFT calculations.
1 Introduction
Density-functional theory (DFT) aims to estimate the total energy of a system. Complementing DFT or wave-function methods, the main objective of energy decomposition analysis (EDA) is to partition the interaction energy of a supermolecule into its chemical origins in a similar vein to mono- and diatomic centers1,2 but for fragments containing an arbitrary number of atoms instead. Examples of the components of an EDA scheme often include electrostatics, exchange–correlation contributions, polarization, and any other relevant chemical phenomena. Hence, EDA is an analytical tool that partitions the interaction energy into chemically interpretable components.
EDA is a family of decomposition methods, each of which is known as an EDA scheme. EDA schemes can be categorized according to the nature of their underlying theory,3 of which there are two major categories: variational-based and perturbation-based. Variational-based schemes are typically derived from the early forms of EDA, where the interaction energy is decomposed by the use of intermediate wave functions. Localized Molecular Orbitals (LMO),4 Absolutely Localized Molecular Orbitals (ALMO),5 and Block-Localized Wavefunction (BLW)6,7 schemes are in this category. Perturbation-based schemes approach EDA from symmetry-adapted perturbation theory (SAPT) scheme,8,9 where the interactions among the fragments are seen as perturbations to the non-interacting description and are constructed as corrections resulting from different physical effects. EDA can also facilitate the creation of new force fields in molecular mechanics by parameterization against EDA data, thereby yielding force fields that are more accurate and transferable.10,11
Whenever the interaction energy is concerned, basis set superposition error (BSSE) must be taken into account. There are many approaches to addressing BSSE,12 but a common approach taken by some EDA schemes is the self-consistent field for molecular interaction (SCF MI), which optimizes the molecular orbitals in the presence of all fragments without BSSE.13 Essentially, SCF MI expands the molecular orbitals of each fragment in the basis functions of the fragment only, which minimizes the amount of charge transfer that occurs among the fragments.14 As such, SCF MI can also be used for computing the energy arising from charge transfer, which is evaluated by taking the difference between applying and not applying SCF MI. In the context of EDA, charge transfer is a useful and interpretable component that indicates the amount of charge that is transferred from one fragment to another.5 While different approaches to SCF MI have been proposed, the method of localized molecular orbitals (LMO) SCF MI15 is chosen here for its amenability to fractional occupancies inherent in species with sufficiently small band gaps at finite electronic temperatures.
In the family of finite-temperature DFT methods, various approaches have been employed to study systems under finite electronic temperatures,16,17 at excited states,18,19 or open systems that have fractional electron numbers.20 For the validation of metallic systems presented in this work, the finite-temperature DFT algorithm of ensemble DFT (EDFT)21,22 in the ONETEP software package23,24 is used to optimize a set of sample non-excited metallic systems with sufficiently small band gaps that produces fractional occupancies at specific electronic temperatures. Without EDA, metallic systems can be fragmented into subsystems in order to obtain the interaction energy, but nothing beyond such a coarse-grained energy value would be available. EDA methods serve to decompose the interaction energy but are normally developed for the pure state where the occupancies are integral. EDA schemes, particularly those that require SCF MI as in ALMO/HALMO EDA, pose difficulties in decomposing the interaction energy of a metallic system due to the fractional occupancies that are part of the optimization process in EDFT. Hence, fractional occupancies must also be incorporated in the SCF-MI optimization process of the fragmented system.
Although EDA is normally developed and applied to non-conducting species at the pure state, developing EDA for species that have a conduction band or have fragments that interact with each other through the conduction of charge necessitates the incorporation of EDA in EDFT, such that the interactions (which could possibly involve covalent bonding) can be dissected into contributing factors as EDA components. Other than EDFT in ONETEP,22 the methods presented in this work are applicable to wave-function-based approaches as well. Separate and independent from ONETEP, the implementation of HALMO EDA makes no distinction between DFT and wave-function methods. EDA and EDFT are first given an overview. The problem of extending SCF MI to fractional occupancies in EDA for each fragment with weighted orthogonalization (WO)25 is then discussed. WO is essential in orthogonalizing the molecular orbitals based on their differing fractional occupancies for the projection operators needed by SCF MI. Finally, motivation of and results from EDA with EDFT applied to sample metallic systems with small band gaps are presented.
2 Methods
2.1 Energy decomposition analysis
The EDA scheme used in this work is Hybrid Absolutely Localized Molecular Orbitals (HALMO),26,27 which decomposes the interaction energy into three major components based on the first-generation ALMO EDA:5 frozen density, polarization, and charge transfer. Further decomposition of the frozen-density component is based on LMO EDA4 and is discussed below. HALMO is a hybrid EDA scheme that has components sharing some names for similar, though not identical, components in LMO, whereas HALMO is compatible with and has the same corresponding component names as ALMO. The interaction energy, ΔEint, is decomposed into the three major components of HALMO EDA as| | | ΔEint = ΔEHALMOfrz + ΔEHALMOpol + ΔEHALMOct | (1) |
in the same manner as ALMO EDA. Frozen density, ΔEHALMOfrz, is further decomposed as| | | ΔEHALMOfrz = ΔEHALMOes + ΔEHALMOex + ΔEHALMOrep + ΔEHALMOcorr | (2) |
which is based on, but not identical to, LMO EDA. Each HALMO-EDA component is given a brief description, but the reader is referred to the original development of HALMO EDA for an extensive review of its components and formulation as an EDA scheme.26
Electrostatics component, ΔEHALMOes, is the change in classical-like terms of the Kohn–Sham (KS) energy containing the Coulombic repulsions when going from isolated fragments to the supermolecule without orbital orthogonalization. Letting Ψ be the wave function of any intermediate quantum state, the electrostatics component is defined4,26 as
| |  | (3) |
where
Ecl is the energy functional for the classical-like part of the KS energy, and
![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif)
is the set of fragments whose molecular orbitals are localized and variationally optimized within their respective fragments in isolation of other fragments. Exchange component, Δ
EHALMOex, is the change in exchange energy when going from isolated fragments to the supermolecule without orbital orthogonalization. It is defined
4,26 as
| |  | (4) |
where
Ex is the energy functional for the exchange part of the KS energy. Pauli-repulsion component, Δ
EHALMOrep, is the change in energy upon orbital orthogonalization excluding correlation. It is defined
4,26 as
| | ΔEHALMOrep = (Ecl[ΨX*] + Ex[ΨX*]) − (Ecl[Ψ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) ] + Ex[Ψ ] + Ex[Ψ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) ]) ]) | (5) |
where
X* is the set of fragments whose molecular orbitals are localized and were first variationally optimized within their respective fragments in isolation of other fragments and are then orthogonalized across the supermolecule. Correlation component, Δ
EHALMOcorr, is the change in correlation energy when going from isolated fragments to the supermolecule with orthogonalized molecular orbitals. It is defined
26 as
| |  | (6) |
where
Ec is the energy functional for the correlation part of the KS energy.
HALMO polarization component, ΔEHALMOpol, is the change in energy when going from the supermolecule with orthogonalized molecular orbitals to the supermolecule with SCF-MI optimized13–15 molecular orbitals. It is defined5,26 as
| | 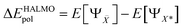 | (7) |
where

is the set of fragments whose molecular orbitals are optimized under SCF-MI constraints. Charge-transfer component, Δ
EHALMOct, is the change in energy when going from the supermolecule with SCF-MI optimized molecular orbitals to the supermolecule with optimized delocalized molecular orbitals. It is defined
5,26 as
| | | ΔEHALMOct = ΔEHALMOdeloc + ΔEBSSE | (8) |
where
| |  | (9) |
is the delocalization term,
X is the set of fragments whose molecular orbitals are expanded in all nonorthogonal generalized Wannier functions (NGWFs)
28 and variationally optimized across the supermolecule, and Δ
EBSSE is the BSSE-correction term.
HALMO EDA has some fundamental differences with LMO EDA, making them incompatible with each other in terms of the decomposition of interaction energy into EDA components. For instance, the LMO-EDA scheme itself does not have an explicit component for charge transfer,4 whereas HALMO EDA does and requires SCF MI or at least some other method that can describe charge-transfer states.29 In contrast, an important component for indicating dispersion effects exists in LMO EDA4 but not in HALMO EDA.26 This in turn makes LMO EDA more suitable for post-HF methods and Grimme dispersion corrections than HALMO EDA.
To determine the components of HALMO EDA, various quantum states are evaluated that represent the intermediate wave functions used in defining each component. The steps for evaluating such quantum states are depicted in Fig. 1.
 |
| | Fig. 1 Steps for evaluating the quantum states for the corresponding components in HALMO EDA. | |
2.2 Ensemble DFT
Ensemble DFT (EDFT) as in ONETEP treats a supermolecule as a whole without the concept of fragmentation as in EDA. EDFT involves occupancies that are fractional, since a species is no longer evaluated at the pure state and, hence, the density operator is no longer idempotent. The lack of idempotency complicates SCF MI due to the fact that SCF-MI methods were originally developed under the pervasive assumption of the pure state. Therefore, SCF MI must be extended to include fractional occupancies. Before considering EDFT with fragmentation and under the constraints of SCF MI, an overview of EDFT is given first.
A system of interacting electrons22 satisfies the Kohn–Sham (KS) equation,
where {
ψi} are molecular orbitals, {
εi} are orbital energies as eigenvalues, and
Ĥ is the Hamiltonian as
| | Ĥ = ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) + + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ext + ext + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) H[n] + H[n] +![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) xc[n] xc[n] | (11) |
Here,
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
is the kinetic energy operator,
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ext
ext is the potential operator due to the field of the nucleus,
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) H
H is the Hartree potential operator,
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) xc
xc is the exchange–correlation potential operator, and
| | 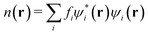 | (12) |
is the electron density with {
fi} as the occupancies of the molecular orbitals.
The occupancy, f, of a molecular orbital is determined from the Fermi–Dirac distribution as a function of its orbital energy, ε:
| |  | (13) |
where
kB is the Boltzmann constant,
T is a non-zero electronic temperature, and
μ is the Fermi level as a parameter. Also called chemical potential, a Fermi level is determined algorithmically (as in ONETEP
22) from a known number of electrons and a given set of orbital energies. For a fixed set of orbital energies at a specified electronic temperature, the search begins with an initial guess of the Fermi level and calculates the occupancies of the molecular orbitals using
eqn (13). If the sum of the occupancies differs from the expected number of electrons, the search adjusts the Fermi level in the appropriate direction and recalculates the occupancies. The algorithm repeats and adjusts the Fermi level until the occupancies computed from the Fermi–Dirac distribution sum to the number of electrons, thereby determining the Fermi level of the species. Fractional occupancies resulting from finite electronic temperature should be distinguished from correlation-induced fractional occupancies in strongly correlated systems. Higher temperature translates to higher kinetic energy of the electrons, causing them to partially occupy orbitals of greater energies. In strongly correlated systems, electrons cannot be treated as non-interacting, since Coulomb repulsion is no longer an insignificant factor and could cause higher energy levels to be partially occupied due to the strong repulsion.
The entropy,  , depends on the occupancies by
, depends on the occupancies by
| |  | (14) |
The Helmholtz free energy,
A, relates the KS energy and the entropy
via the electronic temperature,
T, by
| |  | (15) |
where
EH is the Hartree energy functional, and
Exc is the exchange–correlation energy functional.
Eqn (15) can be expressed in terms of NGWFs, {
ϕk}, and expansion coefficients, {
Mki}, as
| |  | (16) |
In minimizing the energy, the process of optimizing the Hamiltonian is performed by a line-search algorithm described in the ESI.†
2.3 Self-consistent field for molecular interaction
Basis set superposition error (BSSE) is a problem that has been widely studied with many methods and variations thereof being proposed in eliminating it.12,30 A family of methods for describing and dealing with such error used by some EDA schemes is self-consistent field for molecular interaction (SCF MI).13–15,30–33 SCF MI constructs molecular orbitals using basis functions from each corresponding fragment only, which reduces charge transfer among fragments.14 LMO SCF MI is chosen as the SCF-MI method for HALMO EDA due to its mathematical amenability of incorporating fractional occupancies. For ONETEP, BSSE is not exhibited,34 since the NGWFs that ONETEP uses for expanding the molecular orbitals are themselves expanded in terms of a plane-wave basis set defined as periodic sinc (psinc) functions.35 The psinc functions homogeneously span the simulation cell and are not biased by the atomic positions. As such for ONETEP, SCF MI is used exclusively for the purpose of separating out the charge-transfer component.26,36
LMO SCF MI15 uses localized molecular orbitals and constrained minimization of energy to ensure orthogonality within each fragment. It has no relations to LMO EDA.4 Localized molecular orbitals are expressed as
| | 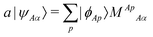 | (17) |
where
A is a fragment,
Ap is the index of a basis function in
A,
Aα is the index of a molecular orbital in
A, and
| |  | (18) |
are the expansion coefficients for some Fragment
B.
The lowest energy can be constructed15 from the molecular orbitals in eqn (17) by evaluating
for each fragment, where {
ψAα} are the localized molecular orbitals on Fragment
A, {
εAα} are the orbital energies as eigenvalues, and
Ĥ is the Hamiltonian. Each dual molecular orbital is defined as
| | 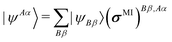 | (20) |
where
| | | ΨJ = (|ΨJ,1〉 |ΨJ,2〉⋯) | (24) |
In LMO SCF MI,
Ψ†JΨJ is constrained to be an identity matrix for Fragment
J for all
J. The dual molecular orbitals localized to Fragment
J are expressed as
where (
σMI)
J is the matrix of column vectors from
σMI that correspond to Fragment
J. Extending
eqn (25) to include all localized molecular orbitals becomes
| |  | (26) |
Performing LMO SCF MI involves finding the energy minimum using the first derivative of the energy with respect to the expansion coefficients, {MJqJβ}:15
| | 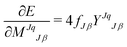 | (27) |
for all
J, where
| | YJqJβ = 〈ϕJq|(1 − ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) )Ĥ|ψJβ〉 )Ĥ|ψJβ〉 | (28) |
| |  | (29) |
| |  | (30) |
and
fJβ is the occupancy of
ψJβ. The stationary point can be determined by solving an eigenvalue problem casted from
eqn (27) set to 0. By solving an eigenvalue problem, molecular orbitals and their orbital energies are obtained, and an effective Hamiltonian can then be constructed from the projection operators. The process repeats until the energy is minimized (
Fig. 2). This allows solving the expansion coefficients,
MJ, for the molecular orbitals localized to Fragment
J to be part of the optimization process.
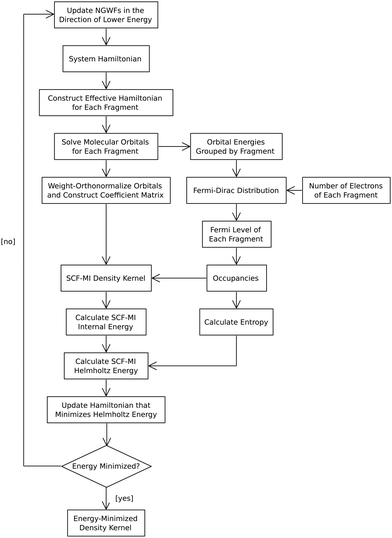 |
| | Fig. 2 LMO SCF MI with occupancies from EDFT. EDFT uses the Fermi–Dirac distribution to calculate the occupancies of the molecular orbitals. Once calculated, the occupancies are incorporated into the density kernel. From the density kernel and occupancies, the internal and Helmholtz energies are evaluated. The Helmholtz energy is used in the line search of EDFT to find the energy minimum. | |
Attaining the energy minimum results in eqn (27) becoming zero:
which can be extended to all dual molecular orbitals localized to Fragment
J as
| | Φ†J(1 − ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) )ĤΨJ = 0 )ĤΨJ = 0 | (32) |
To rewrite
eqn (32) as an eigenvalue problem with an effective Hamiltonian that is Hermitian, the partial projection operator for Fragment
J is defined as
| |  | (33) |
and has the property that
| |  | (34) |
for some Fragment
K. Using the partial projection operator, the effective Hamiltonian for Fragment
J in LMO SCF MI
15 is
| |  | (35) |
whose matrix representation
37 in NGWFs can be obtained by distributing the operators on the right-hand side and then multiplying by
Φ†J and
FJ from the left and right, respectively:
| | 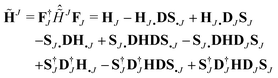 | (36) |
with the definitions of
During the line-search algorithm of EDFT, the constrains of SCF MI are imposed, thereby affecting the search direction in the Hamiltonian space and, in turn, the molecular orbitals solved from it (Fig. 2). The resulting molecular orbitals, expanded in the NGWFs of the corresponding fragments, would therefore satisfy the constraints of SCF MI. Along with the fractional occupancies determined from the Fermi–Dirac distribution during the line search of EDFT, the density kernel can thus be constructed and used in calculating the electron density.
2.3.1 Incorporating fractional occupancies.
Many EDA schemes were developed for the pure state. By assuming the pure state, an EDA scheme and its implementation can simplify what otherwise could be a complicated scheme. Recent developments of the ALMO EDA scheme allow for excited systems38 but involves accommodating the EDA components for the system at an excited state into the same EDA scheme by including a difference term for each EDA component. While this has advantages such as being able to compare the same system at pure and excited states, it introduces complexities to an existing EDA scheme in the interpretation and in the implementation. While excited systems are not studied in this work, EDA with EDFT is applied to systems in ensemble states at finite electronic temperatures without modifying the EDA scheme itself.
For incorporating ensemble-state calculations into EDA, the fractional occupancies that are part of the density kernel are included in the implementation of SCF MI. The problem of performing ensemble-state calculations as part of an EDA scheme then becomes a problem of determining the fractional occupancies during the energy decomposition. Determining the fractional occupancies themselves is performed by the existing implementation of EDFT in ONETEP22 using the Fermi–Dirac distribution, and the HALMO-EDA scheme itself remains unmodified with the same components.
The density kernel varies depending on the quantum state of the system. Specifically, the molecular orbitals differ via the expansion coefficients, and the molecular orbitals would have another set of orbital energies. In turn, occupancies depend on the orbital energies.22,39,40 Therefore, the density kernel must be reconstructed along with a changing set of occupancies throughout an EDA calculation. According to the Fermi–Dirac distribution for fragmented systems, the occupancy, fJi, of a molecular orbital localized to Fragment J as a function of its orbital energy, εJi, is
| |  | (43) |
where
μJ is the Fermi level of Fragment
J as the parameter. The number of electrons in each fragment is known from the optimization of the fragments in isolation. For each fragment, its own Fermi level is determined, followed by calculating the desired occupancies. By evaluating the Fermi–Dirac distribution for each fragment, the SCF-MI constraint of disallowing charge transfer to take place is satisfied, and the occupancies of the molecular orbitals in a fragment are calculated without the orbital energies from other fragments. Despite the different Fermi levels across fragments, charge flow does not occur among fragments, since SCF MI restricts charge transfer. The process of incorporating occupancies from EDFT in SCF MI is diagrammed in
Fig. 2.
2.4 Weighted orthogonalization
Treating all molecular orbitals equally during orthogonalization would be inconsistent with their relative importance when the associated occupancies vary. As a result, some of the orthogonalized molecular orbitals should take higher priority in minimizing their displacements from their nonorthogonalized counterparts in a least-squares fashion. Such orthogonalization can be done using weighted orthogonalization (WO).25 In general, the priority of a molecular orbital in relation to others depends on the context and the application. For this work, molecular orbitals are orthogonalized using occupancies as weights. Using occupancies for weights lends consistency to how molecular orbitals are orthogonalized in the construction of the projection operators for SCF MI under EDFT. The weight-orthogonalized molecular orbitals would have greater-occupied orbitals closer to the corresponding original (nonorthogonal) orbitals according to least squares and lesser-occupied orbitals would be less so, thereby imposing dependency on orbital occupancies and the molecular orbitals being solved from an effective Hamiltonian.41
WO is an orthogonalization process that depends on a preliminary orthogonalization process. Preliminary orthogonalization does not involve weights in any way (otherwise a circular dependency would occur), and it can be one25 of Gram-Schmidt process, symmetric orthogonalization, or canonical orthogonalization. Symmetric orthogonalization was the default choice due to it being readily available in ONETEP.
Starting with P = (|p1〉|p2〉⋯) as a nonorthogonal and normalized matrix of orbitals, it is preliminarily orthogonalized to yield  which is an intermediate matrix that is orthogonal. The goal of WO is to transform Q′ to Q by rotations such that the weighted overlap sum, OVLPS, is maximized:
which is an intermediate matrix that is orthogonal. The goal of WO is to transform Q′ to Q by rotations such that the weighted overlap sum, OVLPS, is maximized:
| | 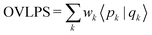 | (44) |
where
wk is the weight associated with |
pk〉. Orthogonalization weights are predefined (which in this work are occupancies determined from the Fermi–Dirac distribution) and must be provided to WO. Maximizing OVLPS is achieved by performing sweeps of 2-by-2 rotations on all pairs of orbitals until convergence is attained.
Eqn (44) is essentially a reformulation of the least-squares problem for orbitals with weights. The derivation for the algorithm of WO is provided in the ESI.
†
SCF MI with WO bears some similarities and important differences to the related method of molecular-orbital localization with intrinsic fragment orbitals (IFOs).42,43 Both approaches utilize orbitals that are expanded in the basis functions localized on respective fragments and perform 2-by-2 rotations to maximize an objective function. However, an SCF-MI method formulates14,15 a solution to the expansion coefficients of the fragment-localized orbitals and the needed orbital energies by affecting the eigenvalue spectrum,41 whereas the approach of IFOs does not and simply specifies the general form of the resulting orbitals. Another distinguishing nature of IFOs is that the projector matrices implicitly assume symmetric orthogonalization (SO) of some reference fragment orbitals based on how the overlap matrices are used in their definitions, while LMO SCF MI has its projection operators naturally arising from the derivation of energy minimization.15 Finally, the objective function being maximized is different in WO compared to the construction of localized molecular orbitals (LMOs) from IFOs. Specifically, the LMOs formed from IFOs have the number of electrons in each fragment raised to the fourth power maximized,43 but WO has the more general aim of maximizing the weighted overlap sum defined by (44). Hence, WO and SCF MI remain more applicable than IFOs by allowing orbital occupancies to serve as orthogonalization weights in the construction of a projection operator.
3 Results and discussion
HALMO EDA with EDFT was performed for Pt13–CO(atop), Pt55–CO(atop), anatase-Pt13–CO(atop), Pt210–phenol, and Li12-graphite. These systems have sufficiently small band gaps that they exhibit fractional occupancies at finite electronic temperatures and, therefore, serve as test systems for HALMO EDA with EDFT. All systems were analyzed at the electronic temperature of 0.1 eV except Pt210–phenol, which was analyzed at the electronic temperature of 1000 K. Furthermore, in relevance to the interactions that occur in heterogeneous catalysis, fragmentation of each system for EDA occurs at the bonds between the adsorbate and the catalyst.
The frozen-density component of HALMO EDA contains electrostatics, exchange, Pauli repulsion, and correlation as its subcomponents. For all species in this study, the frozen-density components exhibit similar characteristics. Energy values of electrostatics, exchange, and correlation are negative, indicating that the interactions from these factors are favorable. Energy values of Pauli repulsion, however, are positive and large, which stems from the unfavorable exclusion repulsions caused by overlapping molecular orbitals.
For Pt13–CO(atop), Pt55–CO(atop), and anatase-Pt13–CO(atop), a carbon-monoxide molecule is bonded to the platinum portion of the system. In anatase-Pt13–CO(atop), the platinum nanoparticle is supported by titanium dioxide (TiO2, also called titania).44 These systems are depicted in Fig. 3. HALMO EDA at the electronic temperature of 0.1 eV was performed for each of the species fragmented at the bond between carbon monoxide and the platinum nanoparticle (Table 1) except anatase-Pt13–CO(atop), which has an additional fragmentation scheme between the platinum nanoparticle and the anatase support (Table 2). HALMO-EDA results for these systems demonstrate some trends among them (Table 1). Unlike Helmholtz interaction energy, internal interaction energy does not contain the entropic term due to electronic temperature. As such, any fractional occupancies result in the two types of interaction energies being different. Indeed, the three platinum species are expected to have fractional occupancies at the specified finite electronic temperature and have unequal internal and Helmholtz interaction energies. From SCF MI, the large charge-transfer energies suggest that the covalency between the carbon monoxide and the platinum is substantial,5 which is to be expected for heterogeneous catalysis in general.
 |
| | Fig. 3 Pt13–CO(atop), Pt55–CO(atop), and anatase-Pt13–CO(atop). Red atom is oxygen, light blue atom is carbon, gold atom is platinum, and pink atom is titanium. | |
Table 1 HALMO EDA with EDFT of Pt13–CO(atop), Pt55–CO(atop), and anatase-Pt13–CO(atop) using the RPBE exchange–correlation functional at electronic temperature of 0.1 eV. Fragmentation is indicated by the bracketing. All energy values are in kcal mol−1
| EDA component |
[Pt13][CO(Atop)] |
[Pt55][CO(Atop)] |
[Anatase-Pt13][CO(Atop)] |
| Electrostatics |
−36.1 |
−38.3 |
−39.7 |
| Exchange |
−56.3 |
−53.9 |
−56.6 |
| Pauli repulsion |
214.2 |
216.9 |
220.1 |
| Correlation |
−22.1 |
−22.1 |
−22.8 |
| Polarization |
−78.2 |
−68.4 |
−45.6 |
| Charge transfer |
−92.3 |
−90.9 |
−87.8 |
| Internal interaction energy |
−70.9 |
−56.7 |
−32.5 |
| Helmholtz interaction energy |
−67.5 |
−54.0 |
−30.5 |
Table 2 HALMO EDA with EDFT of anatase-Pt13–CO(atop) using the RPBE exchange–correlation functional at electronic temperature of 0.1 eV. Fragmentation is between the platinum nanoparticle and the anatase support, indicated by the bracketing. All energy values are in kcal mol−1
| EDA Component |
[Anatase][Pt13–CO(Atop)] |
| Electrostatics |
−130.0 |
| Exchange |
−87.2 |
| Pauli repulsion |
418.2 |
| Correlation |
−61.0 |
| Polarization |
−88.6 |
| Charge transfer |
−145.2 |
| Internal interaction energy |
−93.9 |
| Helmholtz interaction energy |
−92.4 |
To get a sense of the charge distribution in relation to the charge-transfer energy, Mulliken population analysis was also performed for each of the platinum-nanoparticle systems in the last part of their respective calculations where charge transfer has occurred (Table 3). Charges of the atoms in each subspecies were summed to give the charge of the subspecies. For the HALMO polarized state from SCF MI, the Mulliken charge of each fragment is zero (data not shown), which is in accordance with a constraint of SCF MI where the delocalization of electrons among fragments is disallowed. Pt13–CO(atop) has a charge-transfer energy of −92.3 kcal mol−1, and Pt55–CO has a less negative value of −90.9 kcal mol−1. This correlates with the Mulliken charge of carbon monoxide not being as negative in Pt55–CO(atop) (−0.126) as compared to Pt13–CO(atop) (−0.130). Anatase-Pt13–CO(atop), however, does not agree with the trend. A possible explanation is that some of the charge has transferred from anatase to carbon monoxide and made the covalent bonding between carbon monoxide and the platinum nanoparticle less stable. If instead the fragmentation is between the platinum nanoparticle and anatase (Table 2), the charge-transfer energy is much more negative than any of the species in Table 1, and the Mulliken charge on anatase agrees with the charge-transfer energy being more negative.
Table 3 Mulliken population analyses of Pt13–CO(atop), Pt55–CO(atop), and anatase-Pt13–CO(atop) for the optimized supermolecule state after charge transfer has occurred
| Subspecies |
Pt13–CO(Atop) |
Pt55–CO(Atop) |
Anatase-Pt13–CO(Atop) |
| Carbon monoxide |
−0.130 |
−0.126 |
−0.137 |
| Platinum nanoparticle |
0.130 |
0.126 |
0.558 |
| Anatase |
N/A |
N/A |
−0.421 |
Visualizing the major EDA components can be done with electron-density differences (EDD).45Fig. 4 illustrates the polarization and charge-transfer components for Pt13–CO(atop). Polarization can be thought of as the change in quantum state where the fragments in the supermolecule are preparing for electron transfer among each other. This can be visualized as an increase in the electron density close to the nucleophilic carbon atom on the side facing the electrophilic platinum atom. During charge transfer, the region between the carbon atom and the platinum atom experiences an increase in electron density as the two atoms form a covalent bond. A corresponding decrease in electron density is observed at the face of the carbon atom, indicating that the electrons migrated from the carbon atom toward the bonding region with the platinum atom. This suggests that the energy decomposition of Pt13–CO(atop) is qualitatively reasonable with the covalency between the Pt nanoparticle and carbon monoxide.
 |
| | Fig. 4 Difference in electron densities for polarization (left) and for charge transfer (right) of Pt13–CO(atop). Red atom is oxygen, light blue atom is carbon, and gold atom is platinum. Red wireframe indicates an increase in electron density; blue wireframe, decrease. Isovalue is set at ±0.05 e Å−3. | |
Pt210–phenol is another heterogeneous catalysis system (Fig. 5) that was tested with HALMO EDA at an electronic temperature of 1000 K (Table 4). Fragmentation is along the binding between Pt210 (the slab) and phenol (the adsorbate). Similar to the other systems tested, Pt210–phenol exhibits large negative charge-transfer energy (−238.1 kcal mol−1) according to HALMO EDA, indicating that there is significant transfer of electrons and, hence, covalency between the two fragments. The relatively small difference (1.3 kcal mol−1) between the internal and Helmholtz interaction energies implies that the interaction due to entropic effects from electronic temperature is not very substantial. This in turn indicates that the interaction between Pt210 and phenol stems significantly from their binding. From this HALMO EDA, the improvement of a catalysis system similar to Pt210–phenol would benefit from optimizing the interaction between the slab and the adsorbate such that the interaction is more favorable for catalysis.
 |
| | Fig. 5 Pt210–phenol with its periodic unit cell. | |
Table 4 HALMO EDA with EDFT of Pt210–phenol using the optB88 exchange–correlation functional at electronic temperature of 1000 K. Fragmentation is indicated by the bracketing. All energy values are in kcal mol−1
| EDA component |
[Pt210][Phenol] |
| Electrostatics |
−139.3 |
| Exchange |
−307.7 |
| Pauli repulsion |
756.6 |
| Correlation |
−39.0 |
| Polarization |
−147.8 |
| Charge transfer |
−238.1 |
| Internal interaction energy |
−115.3 |
| Helmholtz interaction energy |
−114.0 |
As a final example, HALMO EDA with EDFT of lithium nucleation at graphite models of battery electrodes was performed. Lithium metal plating is an undesired side effect in lithium-ion cells and decreases the lifetime of the battery.46 Plating is caused by the nucleation of lithium ions on the graphite. Increasing the nucleation barrier would be desirable in the design of lithium-ion cells so that a battery's lifetime can be improved. Since lithium nucleation can be viewed as an interaction between lithium ions and graphite, EDA is suitable for examining the factors that contribute to such interaction and could offer some insight on which factors are more prevalent compared to others, otherwise the overall interaction energy would be too coarse-grained. Furthermore, competing designs of lithium-ion cells can also be compared using EDA as part of a methodology that aims to increase the nucleation barrier where some of the EDA components could have an effect on the overall lifetime.
Table 5 lists the HALMO-EDA components of graphite and a cluster of 12 lithium atoms (Fig. 6) in vacuum, with graphite as one fragment and the lithium cluster as the other. Similar to the other species in this work, the Li12-graphite system exhibits large negative charge-transfer energy (−308.8 kcal mol−1) from the interaction between the graphite and lithium cluster. The possibility of making the charge-transfer component less negative could suggest a candidate design that can mitigate the lithium-nucleation effect, which in turn cannot be gleaned from the interaction energy alone. Effects of the finite electronic temperature (0.1 eV) are also exhibited in the difference of 13.7 kcal mol−1 between internal (−230.6 kcal mol−1) and Helmholtz (−216.9 kcal mol−1) interaction energies. Electronic temperature lessens the interaction between the lithium ions and graphite due to entropic effects.
Table 5 HALMO EDA with EDFT of Li12-graphite in vacuum using the PBE exchange–correlation functional at electronic temperature of 0.1 eV. Fragmentation is indicated by the bracketing. All energy values are in kcal mol−1
| EDA component |
[Li12][Graphite] |
| Electrostatics |
−298.9 |
| Exchange |
−288.4 |
| Pauli repulsion |
951.4 |
| Correlation |
−59.5 |
| Polarization |
−170.1 |
| Charge transfer |
−308.8 |
| DFT-D2 |
−56.2 |
| Internal interaction energy |
−230.6 |
| Helmholtz interaction energy |
−216.9 |
 |
| | Fig. 6 Li12-graphite. | |
4 Conclusions
Energy decomposition analysis (EDA) has been extended to metallic systems using an implementation alongside a patched version of ONETEP that can dissect the interaction energy of a species at an ensemble state. EDA and self-consistent field for molecular interaction (SCF MI) methods have usually been developed and applied to systems at the pure state. In this work, EDA and SCF MI were expanded to species that are studied with ensemble DFT (EDFT).
SCF MI was combined with EDFT by removing the assumptions of the pure state and incorporating fractional occupancies into the implementation of SCF MI. Fractional occupancies determined by EDFT are normally for the supermolecule as a whole using the Fermi–Dirac distribution. However, in order for SCF MI to accommodate the occupancies into its process, the evaluation of Fermi–Dirac distribution was restricted to individual fragments, resulting in each fragment having a different Fermi level.
Throughout the line search of EDFT in finding the minimum energy, the constraints of SCF MI were imposed such that the molecular orbitals and the associated orbital energies are solved from the effective Hamiltonian of LMO SCF MI.15 The effective Hamiltonian of LMO SCF MI contains projection operators that require weighted orthogonalization (WO) to be constructed due to the fractional occupancies from the ensemble state. Constructing the projection operators was adapted to orthogonalizing the molecular orbitals with fractional occupancies as orthogonalization weights. Using WO, the construction of such SCF-MI projection operators and the level of occupancy of each molecular orbital are therefore made consistent in the formulation and implementation of SCF MI.
The adaptations of EDA and SCF MI to metallic systems were validated using samples from catalysis and batteries, such as carbon-monoxide-bound platinum nanoparticle systems (in vacuum and supported on titania), platinum slab with phenol adsorbed, and graphite with lithium cluster that have sufficiently small band gaps. Across these sample metallic systems, HALMO EDA has provided reasonable decompositions of interactions energies and revealed some trends from SCF MI that correlate with charge distributions and chemical intuition.
This work has provided a new paradigm and tool for the study and analysis of metallic systems using a combination of EDA and EDFT within large-scale quantum chemistry calculations. HALMO EDA has shown to be a useful tool in decomposing the interaction energy into components for comparisons and analysis of systems at ensemble states that require EDFT. It has been demonstrated by this work that EDA with SCF MI can be extended and applied to metallic systems at finite electronic temperatures. With such advancement, EDA and SCF MI are no longer restricted to species at the pure state. Future work can involve more in-depth study of the nature of interactions in some technologically important systems, such as conductors, semiconductors, heterogeneous catalysts, and lithium-ion batteries.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
The authors acknowledge the use of the IRIDIS 5 High Performance Computing Facility, and associated support services at the University of Southampton. The authors are also grateful for computational support from the UK Materials and Molecular Modelling Hub, which is partially funded by EPSRC (EP/T022213/1). This work is part of University of Southampton's Centre for Doctoral Training in Next Generation Computational Modelling (NGCM).
Notes and references
- I. Mayer, Chem. Phys. Lett., 2000, 332, 381–388 CrossRef CAS.
- I. Mayer, Chem. Phys. Lett., 2003, 382, 265–269 CrossRef CAS.
- M. J. S. Phipps, T. Fox, C. S. Tautermann and C.-K. Skylaris, Chem. Soc. Rev., 2015, 44, 3177–3211 RSC.
- P. Su and H. Li, J. Chem. Phys., 2009, 131, 014102–1-014102-15 CrossRef PubMed.
- R. Khaliullin, E. Cobar, R. Lochan, A. Bell and M. Head-Gordon, J. Phys. Chem., 2007, 111, 8753–8765 CrossRef CAS PubMed.
- Y. Mo, J. Gao and S. D. Peyerimhoff, J. Chem. Phys., 2000, 112, 5530–5538 CrossRef CAS.
- Y. Mo, P. Bao and J. Gao, Phys. Chem. Chem. Phys., 2011, 13, 6760–6775 RSC.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930 CrossRef CAS.
- K. Patkowski, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1452 CAS.
- J. McDaniel and J. Schmidt, Annu. Rev. Phys. Chem., 2016, 67, 467–488 CrossRef CAS PubMed.
- R. Qi, Q. Wang and P. Ren, Bioorg. Med. Chem., 2016, 24, 4911–4919 CrossRef PubMed.
- M. Gutowski and G. Chałasiński, J. Chem. Phys., 1993, 98, 5540–5554 CrossRef CAS.
- E. Gianinetti, M. Raimondi and E. Tornaghi, Int. J. Quantum Chem., 1996, 60, 157–166 CrossRef CAS.
- T. Nagata, O. Takahashi, K. Saito and S. Iwata, J. Chem. Phys., 2001, 115, 3553–3560 CrossRef CAS.
- H. Stoll, G. Wagenblast and H. Preuβ, Theor. Chim. Acta, 1980, 57, 169–178 CrossRef CAS.
- S. Pittalis, C. R. Proetto, A. Floris, A. Sanna, C. Bersier, K. Burke and E. K. U. Gross, Phys. Rev. Lett., 2011, 107, 163001 CrossRef CAS PubMed.
- J. C. Smith, A. Pribram-Jones and K. Burke, Phys. Rev. B, 2016, 93, 245131 CrossRef.
- T. Gould, J. Phys. Chem. Lett., 2020, 11, 9907–9912 CrossRef CAS PubMed.
- T. Gould, G. Stefanucci and S. Pittalis, Phys. Rev. Lett., 2020, 125, 233001 CrossRef CAS PubMed.
- B. Senjean and E. Fromager, Int. J. Quantum Chem., 2020, 120, e26190 CrossRef CAS.
- N. Marzari, D. Vanderbilt and M. C. Payne, Phys. Rev. Lett., 1997, 79, 1337 CrossRef CAS.
- A. Ruiz-Serrano and C.-K. Skylaris, J. Chem. Phys., 2013, 139, 054107-1–054107-8 Search PubMed.
- C.-K. Skylaris, P. Haynes, A. Mostofi and M. Payne, J. Chem. Phys., 2005, 122, 084119-1–084119-10 CrossRef PubMed.
- J. Prentice,
et al.
, J. Chem. Phys., 2020, 152, 174111-1–174111-36 Search PubMed.
- A. West, Comput. Theor. Chem., 2014, 1045, 73–77 CrossRef CAS.
- M. J. S. Phipps, T. Fox, C. S. Tautermann and C.-K. Skylaris, J. Chem. Theory Comput., 2016, 12, 3135–3148 CrossRef CAS PubMed.
- H. Chen and C.-K. Skylaris, Phys. Chem. Chem. Phys., 2021, 23, 8891 RSC.
- C.-K. Skylaris, A. Mostofi, P. Haynes, O. Diéguez and M. Payne, Phys. Rev., 2002, 66, 035119-1–035119-12 Search PubMed.
- E. Rosta and P. R. Surján, J. Chem. Phys., 2002, 116, 878–890 CrossRef CAS.
- F. Jensen, J. Chem. Phys., 2017, 146, 184109-1–184109-7 CrossRef.
- P. Politzer and H. Weinstein, J. Chem. Phys., 1979, 71, 4218–4220 CrossRef CAS.
- G. Del, Re, P. Otto and J. Ladik, Isr. J. Chem., 1980, 19, 265–271 CrossRef.
- Z. Szekeres and P. Surján, Chem. Phys. Lett., 2003, 369, 125–130 CrossRef CAS.
- P. Haynes, C.-K. Skylaris, A. Mostofi and M. Payne, Chem. Phys. Lett., 2006, 422, 345–349 CrossRef CAS.
- A. Mostofi, P. Haynes, C.-K. Skylaris and M. Payne, J. Chem. Phys., 2003, 119, 8842–8848 CrossRef CAS.
- R. Khaliullin, M. Head-Gordon and A. Bell, J. Chem. Phys., 2006, 124, 204105–1-204105-11 CrossRef PubMed.
- C. Sanderson and R. Curtin, J. Open Source Software, 2016, 1, 26 CrossRef.
- Q. Ge, Y. Mao and M. Head-Gordon, J. Chem. Phys., 2018, 148, 064105-1–064105-13 CrossRef PubMed.
- J. F. Janak, Am. Phys. Soc., 1978, 18, 7165–7168 CAS.
-
R. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, 1989 Search PubMed.
- S. Huzinaga,
et al.
, J. Chem. Phys., 1971, 55, 5543–5549 CrossRef CAS.
- G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843 CrossRef CAS PubMed.
- B. Senjean, S. Sen, M. Repisky, G. Knizia and L. Visscher, J. Chem. Theory Comput., 2021, 17, 1337–1354 CrossRef CAS PubMed.
- T. Ellaby, L. Briquet, M. Sarwar, D. Thompsett and C.-K. Skylaris, J. Chem. Phys., 2019, 151, 114702 CrossRef PubMed.
- M. J. S. Phipps, T. Fox, C. S. Tautermann and C.-K. Skylaris, J. Chem. Theory Comput., 2017, 13, 1837–1850 CrossRef CAS PubMed.
- C. Peng, J. Mater. Chem. A, 2021, 9, 16798–16804 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp05112a |
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Chris-Kriton
Skylaris
and
Chris-Kriton
Skylaris
 *
*

![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) is the set of fragments whose molecular orbitals are localized and variationally optimized within their respective fragments in isolation of other fragments. Exchange component, ΔEHALMOex, is the change in exchange energy when going from isolated fragments to the supermolecule without orbital orthogonalization. It is defined4,26 as
is the set of fragments whose molecular orbitals are localized and variationally optimized within their respective fragments in isolation of other fragments. Exchange component, ΔEHALMOex, is the change in exchange energy when going from isolated fragments to the supermolecule without orbital orthogonalization. It is defined4,26 as
![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) ] + Ex[Ψ
] + Ex[Ψ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) ])
])
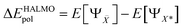
 is the set of fragments whose molecular orbitals are optimized under SCF-MI constraints. Charge-transfer component, ΔEHALMOct, is the change in energy when going from the supermolecule with SCF-MI optimized molecular orbitals to the supermolecule with optimized delocalized molecular orbitals. It is defined5,26 as
is the set of fragments whose molecular orbitals are optimized under SCF-MI constraints. Charge-transfer component, ΔEHALMOct, is the change in energy when going from the supermolecule with SCF-MI optimized molecular orbitals to the supermolecule with optimized delocalized molecular orbitals. It is defined5,26 as
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) +
+ ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ext +
ext + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) H[n] +
H[n] +![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) xc[n]
xc[n]![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is the kinetic energy operator,
is the kinetic energy operator, ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ext is the potential operator due to the field of the nucleus,
ext is the potential operator due to the field of the nucleus, ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) H is the Hartree potential operator,
H is the Hartree potential operator, ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) xc is the exchange–correlation potential operator, and
xc is the exchange–correlation potential operator, and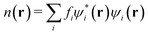

 , depends on the occupancies by
, depends on the occupancies by


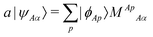

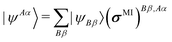

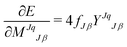
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) )Ĥ|ψJβ〉
)Ĥ|ψJβ〉

![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) )ĤΨJ = 0
)ĤΨJ = 0


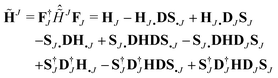

 which is an intermediate matrix that is orthogonal. The goal of WO is to transform Q′ to Q by rotations such that the weighted overlap sum, OVLPS, is maximized:
which is an intermediate matrix that is orthogonal. The goal of WO is to transform Q′ to Q by rotations such that the weighted overlap sum, OVLPS, is maximized: