Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Integration of global ring currents using the Ampère–Maxwell law†
Raphael J. F.
Berger
 *a,
Maria
Dimitrova
*a,
Maria
Dimitrova
 ab,
Rinat T.
Nasibullin
c,
Rashid R.
Valiev
bc and
Dage
Sundholm
ab,
Rinat T.
Nasibullin
c,
Rashid R.
Valiev
bc and
Dage
Sundholm
 *b
*b
aChemistry of Materials, Paris-Lodron University of Salzburg, Jakob-Haringerstr. 2A, A-5020 Salzburg, Austria. E-mail: raphael.berger@plus.ac.at
bDepartment of Chemistry, Faculty of Science, P.O. Box 55, A. I. Virtasen aukio 1, FI-00014 University of Helsinki, Finland. E-mail: sundholm@chem.helsinki.fi
cTomsk State University, 36 Lenin Avenue, Tomsk 634050, Russia
First published on 10th December 2021
Abstract
Magnetically induced ring currents are calculated from the magnetic shielding tensor by employing the Ampère–Maxwell law. The feasibility of the method is demonstrated by integrating the zz component of the shielding tensor along the symmetry axis of highly symmetric ring-shaped aromatic, antiaromatic and nonaromatic molecules. The calculated ring-current strengths agree perfectly with the ones obtained by integrating the current-density flux passing through a plane cutting half the molecular ring. The method can be used in combination with all electronic structure codes capable of calculating nuclear magnetic resonance (NMR) shielding tensors in general points in space. We also show that nucleus independent chemical shifts (NICS) along the symmetry axis are related to the spatial derivative of the strength of the global ring-current along the z axis.
An external magnetic field perpendicular to the molecular plane of a planar ring-shaped molecule may induce a ring current around the molecule.1–6 The strength of the ring current is often used for investigating the aromatic character of the molecule and its degree of aromaticity.7,8 The ring-current strength can be estimated from the isotropic magnetic shielding calculated in discrete points in the vicinity of the molecule.9–13 Methods based on the nucleus independent chemical shifts have been extended to two and three dimensions using the isotropic shielding constant or the zz component of the shielding tensor.14–18 Ring-current strengths can be directly calculated by integrating the current-density flux passing through a surface S that cuts the molecular ring current.19–21
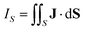 | (1) |
Here, we propose an alternative method to determine ring-current strengths. The presented approach is based on the integral form of the Ampère–Maxwell law that relates the integrated magnetic field around the boundary of a surface to the strength of the current passing through it. The integral form of the Ampère–Maxwell law reads
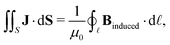 | (2) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) enclosing S and μ0 = 1.256 637 062 12(19) × 10−6 N A−2 is the vacuum permeability. We investigate planar molecules such as benzene that lie in the x, y plane and have an axial symmetry with the z axis coinciding with the main symmetry axis. The chosen molecules belong to point groups having a main symmetry axis of the order of ≥3 or to the D2h point group, since this class of molecules has a vertical ring-current vortex for symmetry reasons and the central vortex stagnation line coincides in such molecules exactly with the z axis. The external magnetic field is perpendicular to the molecular ring.
enclosing S and μ0 = 1.256 637 062 12(19) × 10−6 N A−2 is the vacuum permeability. We investigate planar molecules such as benzene that lie in the x, y plane and have an axial symmetry with the z axis coinciding with the main symmetry axis. The chosen molecules belong to point groups having a main symmetry axis of the order of ≥3 or to the D2h point group, since this class of molecules has a vertical ring-current vortex for symmetry reasons and the central vortex stagnation line coincides in such molecules exactly with the z axis. The external magnetic field is perpendicular to the molecular ring.
According to eqn (2) the strength of the ring current can be obtained by numerically integrating the σzz component of the magnetic shielding tensor along the z axis. Since the induced magnetic field vanishes at a very long distance from the molecule, the integration path can be closed by bending it far away from the molecule where it approaches the z axis from the other side of the molecule. The induced magnetic field is obtained from the position dependent chemical shielding tensor σ by contracting with the external magnetic field Bexternal that is set parallel to the z axis in this work.
| Binduced = −σBexternal | (3) |
The shielding tensor is computed in a number of discrete point along the z axis and integrated numerically. For the studied molecules, the non-parallel components of the induced magnetic field vanishes. Thus, the method involves numerical integration of only the zz component of the aromatic ring-current shielding (ARCS) function, whose shape has previously been used for estimating ring-current strengths.10,11,25–27 The ARCS idea has later been adopted, extended and generalized.28–30 For molecules whose x and y components of the induced magnetic field do not vanish along the z axis, the present approach leads to a small numerical deviation from the exact ring-current strength because the path integration does not follow the stagnation line of the central vortex. The current–density integration scheme employing a rectangular integration domain suffers from similar problems, because the boundary of integration domain does not always coincide with the center of the current–density vortex implying that whole ring current is not obtained or some of the returning ring current is considered.31 The deviations are usually small and can in both approaches be accounted for by using a slightly extended scheme.
The method is demonstrated by calculating the strength of the ring current of cyclobutadiene, benzene, cyclohexadiene, borazine, p-benzoquinone, hexadehydro12 annulene, porphyrin and isophlorin. The profile of the ring current of benzene is compared to the one obtained by integrating the current density.
The molecular structures were optimized at the density functional theory (DFT) level using the B3LYP functional,32–34 the def2-TZVP basis set,35 and the semiempirial D3-BJ dispersion correction.36 DFT optimizations of the ground-state molecular structures were performed with Turbomole.37 The Cartesian coordinates of the optimized molecular structures are given in the ESI.†
Nuclear magnetic shielding tensors were calculated with the mpshift module of Turbomole.38 Magnetically induced current densities were calculated with the GIMIC program using basis-set data and density matrices obtained in the NMR shielding calculations.19,21,39 Reference values for the ring-current strengths were obtained with GIMIC by numerically integrating the current-density flux passing the rectangular cross-section area through half the ring.
The ring-current strengths were also obtained from Ampère–Maxwell's circuital law by numerically integrating the zz component of the nuclear magnetic shielding tensor along the z axis. We use the five-point Boole's rule 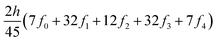 to approximate the integral in each five-point element.40,41 We used an equidistant step length h of 0.25 bohr between the grid points and fi are the σzz value calculated in each grid point. We used 1001 equidistant integration points with the first one at z = −100 bohr and the last one at z = 100 bohr from the molecular plane, because the induced magnetic field declines very slowly for large molecular rings sustaining a strong ring current.
to approximate the integral in each five-point element.40,41 We used an equidistant step length h of 0.25 bohr between the grid points and fi are the σzz value calculated in each grid point. We used 1001 equidistant integration points with the first one at z = −100 bohr and the last one at z = 100 bohr from the molecular plane, because the induced magnetic field declines very slowly for large molecular rings sustaining a strong ring current.
The ring-current strengths obtained by integrating the current-density flux circling around the ring and the ones obtained using Ampère–Maxwell's law in Table 1 agree very well showing that the ring-current strength can be obtained with high accuracy from the magnetic shielding tensor. The deviation between the two values are less then 0.2 nA T−1 for most of the studied molecules. The deviations are 0.4–0.6 nA T−1 for the porphyrinoids with very strong ring currents.
| Molecule | I Ampère | I flux |
|---|---|---|
| Cyclobutadiene | −20.00 | −19.82 |
| Benzene | 11.94 | 12.04 |
| Cyclohexadiene | −0.65 | −0.47 |
| Borazine | 3.25 | 3.23 |
| p-Benzoquinone | −0.01 | 0.21 |
| Hexadehydro[12]annulene | −24.16 | −23.98 |
| Porphyrin | 27.59 | 27.03 |
| Isophlorin | −63.99 | −63.34 |
The ring-current strength of isophlorin is overestimated, because we use the B3LYP functional with only 20% Hartree–Fock (HF) exchange. A smaller paratropic ring current would be obtained when using a functional with at least 50% HF exchange or when using a range-separated functional.42,43 However, this does not affect the conclusions, since the two ring-current strengths for isophlorin agree well.
Application of Ampère–Maxwell's law to evaluate total induced ring current strengths also sheds light on the physical meaning of NICS values9,13 and their relation to the magnetically induced current density. For convenience, we define the integral over the path ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) between the points a and b in the right-hand-side of eqn (2) as
between the points a and b in the right-hand-side of eqn (2) as
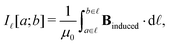 | (4) |
Evaluating the line integral in eqn (2) along a general rectangular path shown in Fig. 1 yields the strength of the magnetically induced current density passing through the surface enclosed by it. The contribution from the first part (l1) of the integration path starting at r0 = (0,0, −z0) on the symmetry axis and ending at r1 = (0,0,z0) is given by
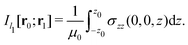 | (5) |
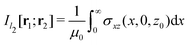 | (6) |
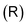 in Fig. 1 is given by
in Fig. 1 is given by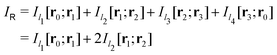 | (7) |
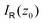 as
as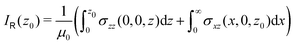 | (8) |
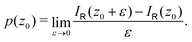 | (9) |
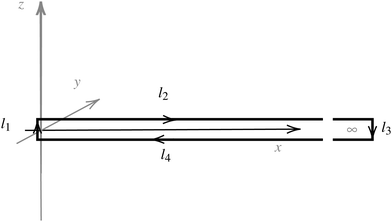 | ||
| Fig. 1 An illustration of the integration path giving a relation between the magnetic shielding tensor (σzz) along the path and the magnetically induced ring-current inside the closed loop (Iinside). | ||
The ring-current profile in the x direction (p(x)) can be analogously obtained by calculating the ring current passing through rectangular domains whose edge is stepwisely shifted along the x axis. Alternatively, the strength of the current density inside the rectangular domain can also be obtained by integrating the appropriate elements of the magnetic shielding tensor along the edges of the rectangle. The integration domains along the sides of the rectangle are defined by the corners at r0 = (x,0,−∞), r1 = (x,0,∞), r2 = (∞,0,−∞), and r3 = (∞,0,∞). However, three of the contributions vanish since the induced magnetic field dies out at long distances from the molecule. The only remaining contribution is given by
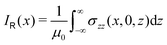 | (10) |
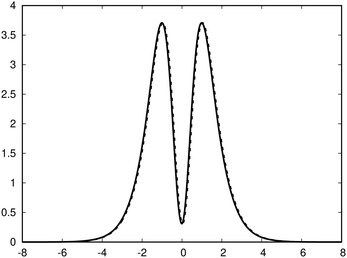
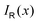 with respect to x. The profiles obtained using eqn (10) and (9) or by differentiating the integrated current density passing through the rectangular surface are identical.44 However, the one deduced from the shielding tensor has the correct sign in the whole range, whereas the one obtained from the current density changes sign on the other side of the ring-current vortex, because the returning ring current has the opposite sign due to charge conservation.
with respect to x. The profiles obtained using eqn (10) and (9) or by differentiating the integrated current density passing through the rectangular surface are identical.44 However, the one deduced from the shielding tensor has the correct sign in the whole range, whereas the one obtained from the current density changes sign on the other side of the ring-current vortex, because the returning ring current has the opposite sign due to charge conservation.
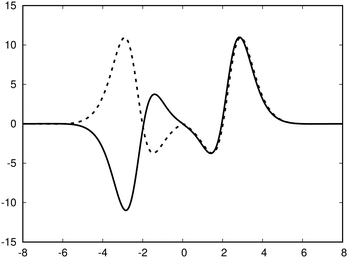 | ||
| Fig. 3 The profile (in nA T−1 bohr−1) of the ring current p(x) of benzene along the x axis calculated from the magnetic shielding tensor using eqn (10) and (9) is shown with the dashed line. The ring-current profile deduced from the current density is shown with the solid line. The dashed curve is slightly shifted to avoid that they are on top of each other. | ||
A relation between NICSzz values at z0 and the ring current can be obtained by differentiating eqn (8) with respect to z
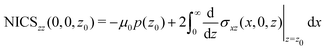 | (11) |
Conclusions and outlook
We have shown that the strength of magnetically induced ring currents can be deduced from the zz component of the magnetic shielding tensor calculated in discrete points along the z axis. The approach has been demonstrated by calculating the ring-current strength of a few aromatic, antiaromatic and nonaromatic molecular rings. The theory is formally exact and the calculated ring-current strengths agree within numerical precision with values that were obtained by integrating the current-density flux circling around the molecular ring. The mean average error (MAE) is 0.0087nA·T−1 when using a spacing of 1a0.The accumulated profile of the total ring current in the z direction can be calculated in discrete points (z0) by integrating σxz(x) in the interval x ∈ [0,∞] at z0 and σzz(z) in the interval z ∈ [−z0,z0] along the z axis. The accumulated radial ring-current profile along for example the x axis can be calculated in discrete points (x0) along the x axis by integrating σzz(z) at x = x0 in the interval z ∈ [−∞,∞]. The ring-current profiles are obtained by differentiating the accumulated ring-current profiles.
We also show that the popular NICSzz(0) value has one contribution from the first derivative of the ring-current strength with respect to the z direction and the second one is a non-local contribution consisting of an integral over the first derivative in the z direction of the appropriate off-diagonal element of the magnetic shielding tensor calculated in the ring plane. The NICSzz(1) value is analogously given by the first derivative of the ring-current strength with respect to the z direction and the non-local contribution is calculated 1 Å from the ring plane. Calculating magnetically induced current densities using NICS values on a three-dimensional grid is probably not feasible,14,45 whereas current-density strengths can be obtained from the magnetic shielding tensor calculated in discrete points. In our GIMIC method, we use the expression for magnetic shielding densities when we calculate magnetically induced current densities.19,21,39 NICS values and magnetic shielding tensors in discrete points can be obtained from magnetically induced current densities by integrating the Biot–Savart expression.46–50
For molecular rings with lower symmetry, the exact ring-current strength can be obtained by integrating along the stagnation line i.e., the center of the global ring-current vortex instead of following the z axis. Then, the induced magnetic field along the integration path is no longer restricted by the symmetry implying that also off-diagonal tensor elements such as σxz and σyz become non-zero and contribute to the ring-current strength.
The proposed methods to calculate ring-current strengths and ring-current profiles are easily employed in combination with electronic structure programs that provide nuclear magnetic resonance (NMR) shielding tensors. The present method should therefore contribute to settling the discussion about the choice of NICS points to assess molecular aromaticity. The ring-current strengths of three-dimensional molecules can be determined using our approach, when the external magnetic field is oriented in an appropriate direction for the system under consideration and the induced magnetic field is calculated along a closed path such that the studied ring current is enclosed by it. Depending on the direction of the external magnetic field and the path of the line integration, all elements of the magnetic shielding tensor may contribute to the ring-current strength. Calculating strengths of the current density inside carefully chosen integration paths may provide useful information about the current-density flux in complicated molecules.
The Ampère–Maxwell integration scheme combined with stagnation graph analysis can ultimately be used for calculating in an automatizable way the current strength of all vortices occurring in a molecule. Then, the line integral of the elements of the magnetic shielding tensor has to be evaluated along stagnation lines delimited by branching points. Some of us are currently working with their collaborators on the implementation of such a procedure.
Author contributions
R. B. conceived the idea to integrate the induced magnetic field along the stagnation lines of the current density. D. S. realized how to calculate ring-current profiles and ring-current strengths from magnetic shielding tensors. R. B. and D. S. developed the theory. M. D., R. N., and R. V. developed the computational methodology and performed the calculations. All authors discussed the results and contributed to the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Academy of Finland through project numbers 314821 and 340583, the Finnish Cultural Foundation, the Swedish Cultural Foundation in Finland and by the DFG (German Research Foundation) in the Priority Program SPP1807 “Control of LD in molecular chemistry”, BE4632/2-2. We acknowledge computational resources from the Finnish Grid and Cloud Infrastructure (persistent identifier urn:nbn:fi:research-infras-2016072533) and the CSC – IT Center for Science, Finland. R. R. V. thanks the Academy of Finland (340582) and is also thankful to the Russian Scientific Foundation (18-19-00268-P).Notes and references
- L. Pauling, J. Chem. Phys., 1936, 4, 673–677 CrossRef CAS.
- K. Lonsdale, Proc. R. Soc. (London) A, 1937, 159, 149–161 CAS.
- F. London, J. Phys. Radium, 1937, 8, 397–409 CrossRef CAS.
- J. Pople, Mol. Phys., 1958, 1, 175–180 CrossRef CAS.
- R. McWeeny, Mol. Phys., 1958, 1, 311–321 CrossRef CAS.
- P. Lazzeretti, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 36, 1–88 CrossRef CAS.
- J. A. N. F. Gomes and R. B. Mallion, Chem. Rev., 2001, 101, 1349–1384 CrossRef CAS PubMed.
- C. Kumar, H. Fliegl and D. Sundholm, J. Phys. Chem. A, 2017, 121, 7282–7289 CrossRef CAS PubMed.
- P. von Ragué Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef PubMed.
- J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 1999, 1, 3429–3435 RSC.
- J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 2000, 2, 2145–2151 RSC.
- Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. von Ragué Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS PubMed.
- H. Fallah-Bagher-Shaidaei, C. S. Wannere, C. Corminboeuf, R. Puchta and P. von Ragué Schleyer, Org. Lett., 2006, 8, 863–866 CrossRef CAS PubMed.
- S. Klod and E. Kleinpeter, J. Chem. Soc., Perkin Trans. 2, 2001, 1893–1898 CAS.
- G. Merino, T. Heine and G. Seifert, Chem. – Eur. J., 2004, 10, 4367–4371 CrossRef CAS PubMed.
- T. Heine, R. Islas and G. Merino, J. Comput. Chem., 2007, 28, 302–309 CrossRef CAS PubMed.
- R. Gershoni-Poranne and A. Stanger, Chem. – Eur. J., 2014, 20, 5673–5688 CrossRef CAS PubMed.
- M. Orozco-Ic, M. Dimitrova, J. Barroso, D. Sundholm and G. Merino, J. Phys. Chem. A, 2021, 125, 5753–5764 CrossRef CAS PubMed.
- J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963 CrossRef PubMed.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518 RSC.
- D. Sundholm, H. Fliegl and R. J. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 639–678 CAS.
- H. Fliegl, R. Valiev, F. Pichierri and D. Sundholm, in Chemical Modelling, Theoretical studies as a tool for understanding the aromatic character of porphyrinoid compounds, 2018, ch. 1, vol. 14, pp. 1–42 Search PubMed.
- M. Dimitrova and D. Sundholm, in Aromaticity: Modern Computational Methods and Applications, ed. I. F. López, Elsevier, 2021, ch. 5, pp. 155–194 DOI:10.1016/C2019-0-04193-3, http://arxiv.org/abs/2105.04902.
- D. Sundholm and H. Fliegl, in Handbook of Porphyrin Science, Vol 46, ed. K. M. Kadish, K. M. Smith and R. Guilard, World Scientific, 2022 Search PubMed.
- J. Jusélius and D. Sundholm, J. Org. Chem., 2000, 65, 5233–5237 CrossRef PubMed.
- J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 2001, 3, 2433–2437 RSC.
- A. C. Tsipis, Phys. Chem. Chem. Phys., 2009, 11, 8244–8261 RSC.
- G. Monaco and R. Zanasi, J. Phys. Chem. A, 2014, 118, 1673–1683 CrossRef CAS PubMed.
- A. Stanger, J. Phys. Chem. A, 2019, 123, 3922–3927 CrossRef CAS PubMed.
- M. Jirásek, H. L. Anderson and M. D. Peeks, Acc. Chem. Res., 2021, 54, 3241–3251 CrossRef PubMed.
- G. Monaco, R. Zanasi, S. Pelloni and P. Lazzeretti, J. Chem. Theory Comput., 2010, 6, 3343–3351 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodynski and J. M. Yu, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed.
- K. Reiter, F. Weigend, L. N. Wirz, M. Dimitrova and D. Sundholm, J. Phys. Chem. C, 2019, 123, 15354–15365 CrossRef CAS.
- GIMIC, version 2.0, a current density program, can be freely downloaded from https://github.com/qmcurrents/gimic, 2019.
- Handbook of Mathematical Functions, ed. M. Abramowitz and I. A. Stegun, Dover, 1965 Search PubMed.
- G. Boole, A Treatise on the Calculus of Finite Differences, Dover, New York, 2003 Search PubMed.
- R. R. Valiev, I. Benkyi, Y. V. Konyshev, H. Fliegl and D. Sundholm, J. Phys. Chem. A, 2018, 122, 4756–4767 CrossRef CAS PubMed.
- S. Lehtola, M. Dimitrova, H. Fliegl and D. Sundholm, J. Chem. Theory Comput., 2021, 17, 1457–1468 CrossRef CAS PubMed.
- H. Fliegl, D. Sundholm, S. Taubert, J. Jusélius and W. Klopper, J. Phys. Chem. A, 2009, 113, 8668–8676 CrossRef CAS PubMed.
- S. Van Damme, G. Acke, R. W. A. Havenith and P. Bultinck, Phys. Chem. Chem. Phys., 2016, 18, 11746–11755 RSC.
- R. M. Stevens, R. M. Pitzer and W. N. Lipscomb, J. Chem. Phys., 1963, 38, 550–560 CrossRef CAS.
- C. J. Jameson and A. D. Buckingham, J. Phys. Chem., 1979, 83, 3366–3371 CrossRef CAS.
- G. Acke, S. Van Damme, R. W. A. Havenith and P. Bultinck, Phys. Chem. Chem. Phys., 2019, 21, 3145–3153 RSC.
- R. K. Jinger, H. Fliegl, R. Bast, M. Dimitrova, S. Lehtola and D. Sundholm, J. Phys. Chem. A, 2021, 125, 1778–1786 CrossRef CAS PubMed.
- H. Fliegl, M. Dimitrova, R. J. F. Berger and D. Sundholm, Chemistry, 2021, 3, 1005–1021 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The Cartesian coordinates of the optimized molecular structures are reported. See DOI: 10.1039/d1cp05061c |
| This journal is © the Owner Societies 2022 |