Assessment of DFT approaches in noble gas clathrate-like clusters: stability and thermodynamics

Abstract

We have assessed the performance and accuracy of different wavefunction-based electronic structure methods, such as DFMP2 and domain-based local pair-natural orbital (DLPNO-CCSD(T)), as well as a variety of density functional theory (DFT) approaches on He@(H₂O)_N cage systems. We have selected representative clathrate-like structures corresponding to the building blocks present in each of the sI, sII and sH natural gas clathrate hydrates, and we have carefully studied the interaction between a He atom with each of their individual cages. We reported well-converged DFMP2 and DLPNO-CCSD(T) reference data, together with interaction and cohesive energies of four different density functionals (two GGA, revPBE and PW86PBE, and two hybrids, B3LYP and PBE0), including diverse dispersion correction schemes (D3(0), D3(BJ), D4 and XDM) for both He-filled and empty clathrate-like cages. After the analysis of the results, we came to the conclusion that the PW86PBE functional, with both XDM and D4 corrections, and the PBE0-D4 functional present reasonably adequate approaches to describe the guest–host noncovalent interactions that take place in such He clathrate hydrates. Taking into account that the He@sII is the only helium clathrate that scientists have been able to synthesize recently, we have performed a thermodynamic study on the individual 5¹² and 5¹²6⁴ cages present in the sII crystal. We determined the change in enthalpy, ΔH, and in Gibbs free energy, ΔG, at various temperatures and pressures, and we found out that in the range of experimental conditions the reactions associated with the encapsulation of the He atom inside the cages are exothermic and spontaneous. Finally, we highlighted the importance of an accurate description of the interaction in He@water mixtures, as a crucial component in construction of reliable data-driven models.

---

Gas hydrates or clathrates are nonstoichiometric crystalline structures in which a firm host skeleton of hydrogen bonded water molecules forms cage-like structures that encapsulate guest molecules,¹ mostly apolar or weakly polarized, such as noble gases, H₂, CO₂, CH₄, etc. These ice-like solid compounds naturally form (or can be formed) under certain conditions of pressure and temperature (P–T), usually high pressure and low temperature, within a gas/water mixture.² Generally, the stability of these compounds comes from van der Waals (vdW) interactions between the guest and the surrounding water host network and the hydrogen bond interactions between water molecules. Therefore, the type of clathrate structure which is thermodynamically favored depends on the P–T conditions and the guest species (nature, size, abundance, etc).³

Clathrate research has become a field of great interest for both theoreticians and experimentalists, as a consequence of their promising applications.^4–7 On the one hand, natural gas hydrates are considered one of the recent valuable sources of energy due to its high content of methane gas which can be exploited and used in different energy applications, and on the other hand, gas hydrates can also be synthesized in the laboratory for different purposes, such as CO₂ sequestration and storage, gas separation, water desalination, gas storage and transport, etc.^8–12

These compounds are naturally present in permafrost regions of Earth (such as Antarctica and Greenland) and in ocean sediments and are also expected to be in astrophysical environments such as Titan's atmosphere, Mars polar caps and icy comets.^13,14 Although many types of clathrate hydrate structures are in principle plausible, only a limited number of them occur in nature: the cubic structures sI and sII and the hexagonal structure sH.¹⁵ All three classes consist of a hydrogen-bonded water framework composed by different building blocks (see Fig. 1). The sI structure (the most abundant gas hydrate structure on the Earth) comprises 46 water molecules forming two pentagonal dodecahedra small cages (5¹²) and six, ellipsoidal-shaped, tetracaidecahedral large cages (5¹²6²) by sharing vertices between 5¹² blocks without direct face sharing. The sII unit cell is composed of 136 water molecules located in sixteen small cages (5¹²) and eight hexakaidecahedral large cages (5¹²6⁴) by sharing faces between small cavities. Finally, the sH unit cell is made up of 34 water molecules arranged in three small cavities (5¹²), two irregular dodecahedron medium cavities (4³5⁶6³) and one icosahedron large cage (5¹²6⁸). The occupancy of each structure depends on the number of cages and each cage could accommodate one or more guest molecules,²e.g. sI can allocate small guest molecules, sII larger guest molecules and sH both small and large guests. In the absence of guest molecules, the cages network remains unstable, however some recent experiments by Falenty et al.¹⁶ and del Rosso et al.¹⁷ have successfully obtained ice XVI by emptying a type sII clathrate hydrate and ice XVII by emptying a hydrogen filled ice, respectively.

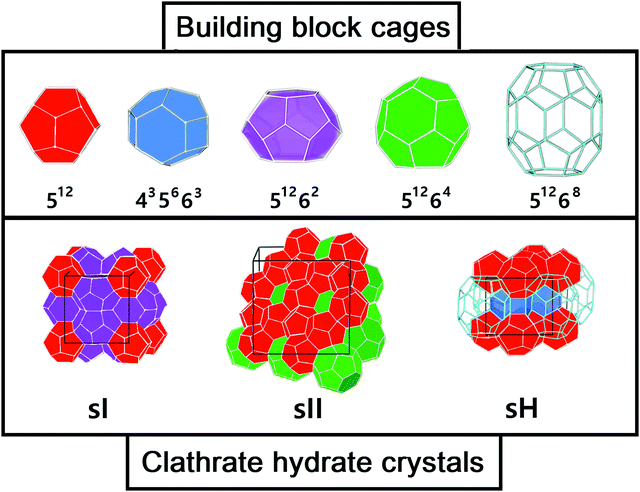Fig. 1 Three most common types of clathrate hydrates: building cages (upper panel) and crystals (lower panel).

Many research groups have investigated the stability and the role of host–guest interactions in clathrate hydrates with different guest molecules.^18–23 However, we are still far away from fully understand these systems and answer questions like, how can we control their stability? How can we have power over their structural evolution/phase behaviors? How can we exploit their storage capacity? Once we can explain all these factors, we will be able, among other things, to efficiently use clathrates for industrial purposes. Noble gas hydrates, and specifically helium clathrates, are perhaps one of the systems with less information available.^24–35 Although helium atoms and water molecules are the most frequent mono- and triatomic entities, respectively, in the universe, their interactions are weak and therefore, compounds are difficult to form. Nevertheless, it was possible to obtain the first helium clathrate hydrate in 2018 by filling ice XVI with helium atoms.³⁶ The simplicity of this noble gas atom and its low chemical reactivity, makes it a perfect target and since there is a lack of reference computations on helium clathrates, this fact motivates us to further investigate these systems.

In the recent years, computer simulations have become a powerful tool, allowing to model molecular systems and processes. Computer power and technology have rapidly improved, numerous new computational techniques have been developed, that contribute to a significant increase in the capability and ability of computational approaches. The most recent developments have been revolutionised by the emergence of data science, machine-learning, and high-throughput approaches, promising a new framework to efficiently evaluate the properties of molecular systems.^37–41 In this sense, different methodologies in electronic structure theory,^35,42–45 as well as in molecular dynamics^46–49 and Monte Carlo^50–53 simulations have been developed, implemented and tested in order to understand energetic and thermodynamic stability, as well as storage capacity of clathrates hydrates. Regarding the description of the underlying guest–host molecular interactions, several computational approaches are nowadays available, ranging from the most accurate wavefunction(WF)-based methods to the computationally more viable density-functional theory (DFT) ones.^38,54–61 Following our previous efforts in the field, in this study we report well-converged reference data from wavefunction-based electronic structure methods, that serve to systematically evaluate the performance of conventional and modern density functional approaches. In general, the dispersion-corrected density functional methods prevail the conventional functionals,⁶² however for certain type of vdW systems, like gas clathrate hydrates, may not be the case and their assessment is still necessary. Thus, the extra effort involved in checking DFT approximations can provide valuable information on their reliability and a comprehensive guidance for choosing functionals in future studies. From such elaborate calibration calculations appropriate computational schemes/protocols are recommended in order to determine the most adequate functional/s in describing noncovalent guest–host interactions for such He@water systems. Moreover, as the stability of a system can be understood by following the variation of the entropy during the thermodynamic process, we also investigate such changes, through optimization and frequency calculations, at a range of temperature and pressure values comparable to the experimental conditions.³⁶ In this way we infer on the feasibility of the He atom encapsulation in the sII cages, and discuss on specific thermodynamic conditions for the laboratory formation of such He@water clathrates.

1. Computational details

1.1 Cages’ configurations

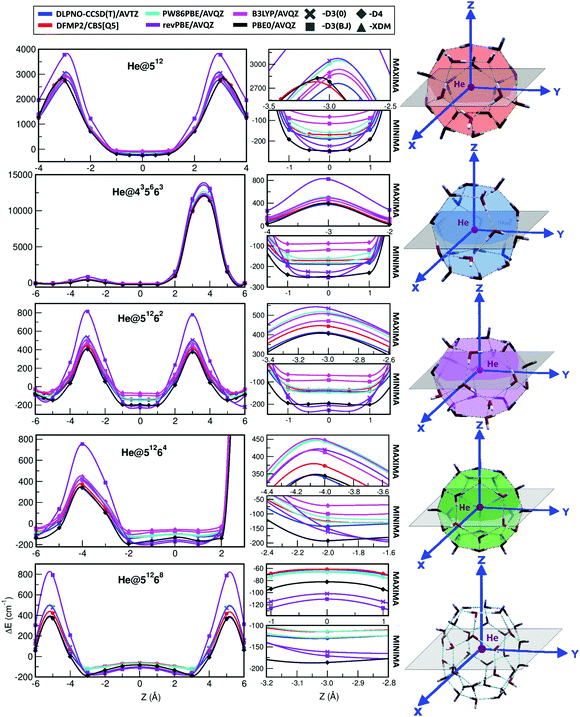
The target systems in this work are each of the building blocks of increased cage size present in the three most common clathrate hydrates (sI, sII and sH), namely, the 5¹², 4³5⁶6³, 5¹²6², 5¹²6⁴ and 5¹²6⁸ clathrate-like structures. We have analyzed both the empty (see Fig. 1) and He-filled structures (see Fig. 2). As mentioned above, the 5¹² cage is present in the three clathrate hydrates, whereas the 5¹²6², 5¹²6⁴ and 5¹²6⁸ cages belong to the sI, sII and sH complexes, respectively. The sH clathrate contains also the 4³5⁶6³ cage. The average cage diameter as a function of the cages width is shown in Fig. 2. In the case of the small cages, with 20 water molecules, similar values of 7.3 and 7.4 Grindeq issue SI were found for the 4³5⁶6³ and 5¹² systems, respectively. In turn, there is a small gap with respect to the next size cavity with 24 water molecules (5¹²6²), where the average diameter is 8.8 Grindeq issue SI, closely followed by the 5¹²6⁴ cage (28 water molecules) with 9.0 Grindeq issue SI and ending with the higher order clathrate-like cluster in this study, 5¹²6⁸ (36 water molecules), with a diameter of 9.4 Grindeq issue SI.

Fig. 2 He@(H₂O)_N systems, with N = 20 24, 28 and 36, considered in this study.

The geometries of each cage were extracted from the 3D sI, sII and sH crystalline frameworks, as they have been determined in ref. 63, using the DENEB software package.⁶⁴ The positions of the oxygen atoms have been obtained from X-ray diffraction experiments, while the proton coordinates have been choosen to satisfy the ice rules, to have the lowest potential energy configuration, and a net zero dipole moment. As it can be seen in Fig. 2 we show such specific sets of proton configurations. The origin of each coordinate system is placed at the center of mass of the corresponding empty cage hydrostructure, with the Z-axis serving as the reference direction.

1.2 Electronic structure calculations: energies and structures

We have obtained reference total and interaction energies from different wavefunction-based methods, such as domain-based local pair-natural orbital approach, DLPNO-CCSD(T), and density fitting Møller–Plesset perturbation theory, DFMP2, as implemented in the Orca⁶⁵ and Molpro⁶⁶ packages of codes, respectively. The computational efficiency and performance of such linear scaling approaches have been previously reported^35,67,68 from extensive comparisons with their conventional analogs in small size water-containg systems. Thus, the augmented correlation consistent basis sets,⁶⁹ AVXZ (X = T for DLPNO calculations and X = Q, 5 for the DFMP2 ones), were used, together with the required auxiliary basis sets for density fitting of the Fock, exchange and other two-electron integrals (jkfit, mp2fit) in the DFMP2 calculations, whereas the correlation fitting aug-cc-pVTZ/C basis sets were employed in the DLPNO calculations for the resolution of the identity (RI). Further, the tight threshold for both SCF and PNO settings was specified to achieve better converged wave-functions and to reduce numerical noise, respectively.

The counterpoise correction (CP) was applied to the energies obtained to reduce the basis set superposition error (BSSE) effect in the present calculations. It was calculated as the difference between the uncorrected interaction energy and the BSSE,⁷⁰, where , E′ stands for the monomer (He or cage) energies calculated with the dimer (He–cage) basis set, while E represents the energies of the monomers and dimer calculated with the monomer and dimer basis sets, respectively. Furthermore, we have also computed the cohesive energies per water molecule for each N empty water system (N = 20, 24, 28 and 36), as the difference between the cluster energy and the energies of the geometry-relaxed water monomers, .

Since such water-containing systems suffer from rather large BSSE effects, that increase as the number of water molecules increases, a complete basis set (CBS) extrapolation scheme has been employed to obtain accurate well-converged results in the DFMP2 interaction energy calculations. As the CP correction has a large influence on the interactions energies the most adequate equation for our calculations was the two-step scheme by Lee et al.,⁷¹ for the interaction energies , with δ_X = E^CP_X − E_X, ε_X = E^CP_X + E_X, where E^CP is the CP-corrected energy and E represents the uncorrected one, with X = 4 and 5.

Looking for a computational affordable method to calculate energies in larger systems up to crystalline hydrate frameworks, we have also assessed the performance of different DFT functionals. Specifically, we have consider those functionals which showed a better behavior in previous studies of clathrate-like systems,^{35,43,45,58,61,72} namely the PW86PBE,^73,74 revPBE,⁷⁵ B3LYP⁷⁶ and PBE0⁷⁷ functionals, together with dispersion corrections, such as the original zero-damping function, D3(0),⁷⁸ as well as the most popular Becke–Johnson damping function, D3(BJ),⁷⁹ the most recent developed, D4,^80,81 and the exchange-hole dipole moment (XDM) model.⁸² All the DFT calculations were performed using Gaussian⁸³ and Orca⁶⁵ (in the case of the revPBE and B3LYP functionals) packages with the additional dispersion corrections computed by the DFT-D3,⁸⁴ DFT-D4⁸⁵ and POSTG^86,87 programs. The AVQZ basis sets were employed and the ultrafine grid was specified for the numerical integration.

1.3 Thermodynamics of He encapsulation: enthalpy variation calculations

The feasibility of He atom encapsulation in the sII clathrate hydrate cages is analysed in terms of enthalpy and Gibbs free energy variations. These two quantities are practical and important thermodynamic properties, that provide valuable information about the course of a formation/dissociation reaction. Thus, optimizations followed by frequency calculations were performed at the PBE0-D4/AVTZ level for the He@sII cages. The He@5¹² and He@5¹²6⁴ minimum energy structures were determined by optimizing the He atom position inside a fixed cage. The enthalpy variation, ΔH, and the change in Gibbs free energy, ΔG, for the formation of the He@5¹² and He@5¹²6⁴ complexes are calculated as the difference in enthalpy/Gibbs free energy between the enclathrated He system and the sum of the enthalpy/Gibbs free energy of the empty cage and He atom,

ΔH/G = H/G_He@cage − [H/G_He + H/G_cage] (1)

where H(T) =E + ZPE − ε(T) and G(T) = H−T × S, with E the total electronic energies, ZPE represents the zero-point vibrational energy corrections, ε(T) the thermal corrections for the filled and empty cage systems, while S stands for their calculated entropies. The ΔG of the encapsulated He@5¹² and He@5¹²6⁴ systems at different pressure values is also investigated.

2 Results and discussion

In this study we generated benchmark datasets of different configurations at the repulsive, near-equilibrium, and asymptotic/long-range regions of the full potential energy surface of He clathrate-like systems. On the one hand, the CCSD(T)/CBS method is widely considered as the “gold-standard” in quantum chemistry due to its high accuracy. However, the key limitation of this method is its rapid increase in computational cost with system size. This is where an important variety of computational techniques, known as linear scaling methods, come into play as they provide a linear computational cost scale with the size of the system,⁵⁴ what allows not only the increase of the calculation speed, but also the possibility to study larger systems. In this context, domain-based local pair natural orbitals (DLPNO) in combination with CCSD(T) is a linear scaling technique that approximates the CCSD(T) standard. It arises as a perfect alternative, since it recovers 99.9% of the CCSD(T) correlation energy and significantly reduces the computational cost.^56,88 On the other hand, Møller–Plesset Perturbation Theory (MP2) is a cheap ab initio method, which doesn't produce results as accurate as the coupled cluster (CC) ones, but offers less computational cost. It may be made even more efficient by means of the Density-Fitting (DF) approximation, another linear scaling counterpart, resulting in a quite robust and accurate method.⁸⁹ In fact, this technique reduces the computational cost as well as the required memory considerably, while maintaining reliable accuracies for practical chemical applications of MP2 quality.⁵⁷ Thus, as CC calculations are not affordable in the case of our systems, we will consider here, both the DLPNO-CCSD(T) and DFMP2 computations as the reference ones.

Since the performance of methods and basis sets or functionals in near-equilibrium geometries may not be representative of the behavior in the whole potential surface, we thus considered both minimum and non-minimum configurations. Our purpose is to assess the accuracy and performance of various conventional and modern WF and DFT/D approaches in describing the guest–host interactions acting on the He-filled clathrate-like cages. In this vein, we adopted a previously proposed validation protocol,⁴³ following some general evaluation criteria, and in Fig. 3 we present a schematic description of each step of the procedure summarized below:

Fig. 3 Criteria taken into account during the validation procedure.

1. As a first step the performance of each approach, in comparison to reference data, is extracted from single point calculations at optimized geometries.

2. Interaction/cohesive energies are calculated and compared to reference data in selected non-minimum configurations in order to visualize a variety of potential energy curves.

3. The computed energies should converge from above to the reference values. If more than two functionals fulfill the above criteria, then the one with the lowest mean absolute error and less computational cost should be chosen.

On the basis of such criteria, we critically evaluate the performance of different DFT-D approaches and conclude which one is the most suitable to describe the non-covalent guest–host molecular interactions in the He@clathrate-like systems.

2.1 Benchmarking He@cage interactions vs cage size

2.1.1 Equilibrium configurations: interaction and cohesive energies. Total energies were first computed for all empty and filled cage systems shown in Fig. 1 and 2, by performing ab initio WF-based DLPNO-CCSD(T)/AVTZ and DFMP2/CBS[Q5] calculations at their near equilibrium configurations. Counterpoise correction was applied in order to account for the BSSE correction, while in the DFMP2 interaction energies, well-converged results are also obtained from CBS calculations. Firstly, the resulting interaction energies corresponding to the He-filled structures in their minimum (Z = 0 Grindeq issue SI for He@5¹², He@4³5⁶6³ and He@5¹²6², Z = −2 Grindeq issue SI for He@5¹²6⁴ and Z = 3 Grindeq issue SI for He@5¹²6⁸) are listed in Table S1 (ESI†). In the case of the empty 5¹² cohesive energies have been previously reported at MP2-F12, MP2/CBS⁵⁶ and explicitly correlated local CCSD(T) levels of theory,^90,91 while for all empty sI, sII and sH clathrate-like cavities such energy values have been obtained from DFMP2/CBS[Q5] calculations,⁵⁸ as summarized in Table S1 (ESI†). As one can see in the Table S1 (ESI†), the difference between these two methods approximately ranges from 15 to 20 cm⁻¹ for the He-filled cages, what supposes an error of 9–12%. In the case of the He@5¹²6² that difference is just 7 cm⁻¹ (with an error of 5%). As for the empty cages, in spite of the fact that the difference between both reference methods is higher (102–110 cm⁻¹), the error is approximately 3% and even 2.2% in the case of the 5¹²6⁸ cage.

In turn, DFT-based approaches, namely PW86PBE, revPBE, B3LYP and PBE0 functionals, considering the D3(0), D3BJ, D4 and XDM dispersion corrections schemes are also employed. The calculated energies are also given in Table S1 (ESI†) and in Fig. 4 we compare graphically for each of the individual He-filled and empty cages the difference in energy between the DFT calculations (solid bars) and the reference DLPNO-CCSD(T) and DFMP2 (dashed lines) values. Regarding the DFT results, the first feature which stands out is the need to use dispersion corrections, since the energies resulting from the calculations with the pure functionals are considerably overestimated, both in the He-filled and empty structures (see also Fig. 4). Therefore, from now on we will just refer to those results including dispersion corrections. If we take into consideration the interaction energy values of the He-filled structures, we observe that the PW86PBE functional is the one which provides closer results to the reference values. By taking a closer look to these results, we see that this functional with the XDM dispersion generates interaction energies which are closer to the DLPNO-CCSD(T) ones, whereas the same functional with the D4 dispersion produces values closer to the DFMP2 values. On the contrary, the revPBE and PBE0 functionals underestimate the energy, being this character more pronounced in the case of PBE0, whereas the B3LYP functional overestimates the energy, specially when considering the D4 dispersion correction.

Fig. 4 Interaction and cohesive (per water molecule) energies (in cm⁻¹) for the individual He-filled and empty cages, respectively, obtained from the indicated DFT-D (solid bars) and DLPNO-CCSD(T)/DFMP2 (dashed lines) calculations. In the case of He@5¹²6⁸ the DFMP2 calculations were carried out with AVQZ basis sets. Numerical results are listed in Table S1 (ESI†).

Although there are only few data available concerning noble gas hydrates, some previous research have reported interaction energies for this complexes. In this way, Kumar and Sathyamurthy⁹² obtained an interaction energy of −0.31 kcal mol⁻¹ (−108.4 cm⁻¹) at MP2/6-31G** level for the He@5¹² cage system, whereas Kaur and Ramachandran³³ calculated an energy of −0.75 kcal mol⁻¹ (−262.3 cm⁻¹) at B97-D/cc-pVTZ for the same system. Finally, Mondal and Chattaraj²⁷ reported energies of −0.62 kcal mol⁻¹ (−216.9 cm⁻¹) and −0.35 kcal mol⁻¹ (−122.4 cm⁻¹) for the He@5¹² and He@5¹²6⁸ cages, respectively, from B3LYP/6-31G(d) calculations. As we can see, there is no agreement neither between these results nor with our reference values. It may be a consequence of the configuration studied, the level of calculation or the consideration of dispersion correction schemes.

In order to check the tendency of the same DFT functionals in the absence of the He atom, now we focus our attention on the cohesive energy per water molecule results for the empty cages. Surprisingly, the B3LYP-D4 functional is the one which provides closer results to the reference data, in contrast with the He-filled cages, where this functional significantly overestimates the energy. Opposite to the rest of pure functionals, the PBE0 results without dispersion corrections are in good agreement with the DFMP2 reference ones. Nevertheless, when adding the D4 dispersion the energy values are overestimated. The same behavior is observed in the B3LYP-D3(BJ) functional, although to a lesser extent. The PW86PBE-XDM/D4 values are slightly underestimated, whereas the revPBE-D3(0)/-D3(BJ) results considerably overestimate the energy. Thus, as we can see the performance of the different functionals tested here is appreciably conditioned by the presence/absence of the He atom inside the cages, that sometimes results in completely contrary behaviors, as it is the case of the B3LYP functional. This analysis may be clearer seen in Fig. 4.

2.1.2 Non-equilibrium configurations: interaction energies. Once we have analysed the performance of the DFT/DFT-D functionals in the equilibrium geometries, the next step to further evaluate the accuracy of these functionals consists in examining their behavior in non-minimum configurations, so that entire potential energy curves are considered. To this aim, we compute interaction energies at a variety of configurations corresponding to the He atom moving along the Z-axis. The resulting curves are displayed in Fig. 5.

Fig. 5 Interaction energy curves obtained from the indicated DFT-D functionals when moving the He atom along the Z-axis and compared with the reference DLPNO-CCSD(T)/AVTZ and DFMP2/CBS[Q5] (DFMP2/AVQZ in the case of He@5¹²6⁸) reference values.

One can see certain differences in the potential curves, corresponding to their well-depths, as well as in the repulsive part of them close to potential barriers. The He@5¹² and He@5¹²6²/He@5¹²6⁸ curves are symmetric to the Z-axis direction, with barriers corresponding to He atom at the center of a pentagonal or hexagonal face, respectively. Those corresponding to the He@4³5⁶6³ and He@5¹²6⁴ systems are asymmetric influenced by the anisotropy of the cage in the +Z and −Z directions. In the 4³5⁶6³ cage, the barriers correspond to the He atom at the center of a tetrahedral face along the +Z direction and at the center of a hexagonal face in the −Z direction, while for the He@5¹²6⁴ the barriers coincide with the He atom getting close to a water molecule shared by three pentagonal faces in the +Z direction and the He atom at the center of a hexagonal face along the −Z direction.

In general, all the curves show similar tendencies, but as expected, there are noticeable energetic differences between them. Starting with the reference curves, the difference between DLPNO-CCSD(T) and DFMP2/CBS methods accounts for 15–20 cm⁻¹ in the minima and 30–70 cm⁻¹ in the maxima. Continuing with the DFT-D functionals, the revPBE-D3(BJ) stands out as a consequence of the huge energy difference found in the maxima with respect to the DLPNO-CCSD(T) and DFMP2/CBS energies for all the systems under study. However, in the minima the energy is underestimated, although the difference is not that significant and the calculated values are even close to the PBE0-D4 ones. The same functional with the D3(0) dispersion correction improves the results in the maxima, taking values similar to the PW86PBE-D4 ones in most of the systems, while presenting similar values to those obtained with the D3(BJ) scheme in the minima. The B3LYP functional with both D3(BJ) and D4 dispersion schemes overestimates the interaction energy along the whole curve, as we expected from the previous analysis in Table S1 (ESI†). As regards the PBE0-D4 functional, it shows a curve surprisingly close to the DLPNO-CCSD(T) one, except in the minima of the curve, where the energy is underestimated, getting values even similar to those from the revPBE calculations, as commented before. Curiously, in those systems containing 20 water molecules (He@5¹² and He@4³5⁶6³) the PBE0-D4 curve is closer to the DFMP2/CBS one, although it presents the same behaviour just described. Finally, the PW86PBE functional is the one which presents the greatest agreement with respect to the DFMP2/CBS and DLPNO-CCSD(T) reference values in the minima region, taking values in between these two approaches when using the XDM dispersion correction and values hardly higher than the DFMP2/CBS ones when using the D4 dispersion correction. Nonetheless, this concordance is slightly lost in the maxima curve region.

Considering that the PBE0-D4 and PW86PBE-XDM/D4 functionals are the ones which show a better performance and following the validation protocol described in Fig. 3, we decided to further check their accuracy with respect to the reference data in terms of error analysis. In this way, in Fig. S1 (ESI†) we display a graphical representation of the individual root-mean-square (RMS) and percentage errors of each of the PBE0-D4 and the PW86PBE-XDM functionals, calculated as , with E_REF corresponding to the DLPNO-CCSD(T)/AVTZ energies at the reference structures along the Z-axis for each He@cage system (see Fig. 2 and 5). In general terms, one can draw the following conclusions. On one hand, we see that both RMS and % error are smaller for the PW86PBE-XDM in the near-equilibrium regions, in contrast to the repulsive region, where these values are notably higher and even surpass the PBE0-D4 ones, and on the other hand, we observe that the variations produced in the PBE0-D4 errors along the Z-axis configurations are more linear than in the PW86PBE-XDM case, where the calculated differences are considerable. Taking all this information into consideration, we highlight the performance of two functionals: PBE0-D4 and PW86PBE-XDM. The first one implies a heavier calculation, but represents reasonably well most configurations inside the cages, especially those close to the potential barriers, and presents an error which is approximately regular during the whole curve. The PW86PBE-XDM is a significantly faster calculation, which provides a much better description of the near equilibrium geometries, but whose accuracy is lost in the repulsive regions. Therefore, depending on the objective pursued, the size of the system under study and the computational resources available, one will be more interested in selecting one functional or another.

2.2 Thermochemistry: stability of the He@sII cages

Up to day, the only helium clathrate that has been synthesized in the laboratory is the He@sII³⁶ structure, and its small and large cage filling has been studied as a function of pressure and temperature. It has been shown that for temperature and pressure values between 80–120 K and 50–150 MPa, respectively, He atoms occupied both cages.³⁶ Such experimental findings provide good testing grounds for computational quantum chemistry methods, thus in this section we aim to assess the He@sII cages stability, through thermochemical calculations. To this purpose, we performed optimization and frequency calculations at the PBE0-D4/AVTZ level of theory, given the reliability found for this DFT functional approach in both He@clathrate-like cages and ice-like channels.³⁵ In this way, we determined the change in enthalpy, ΔH, and the change in Gibbs free energy, ΔG, for the He + 5¹²/5¹²6⁴ → He@5¹²/He@5¹²6⁴ formation reaction at a wide range of temperature (T) and pressure (P) values, ranging from 50–298 K and 1–1500 atm, respectively, in order to cover the experimentally explored regime.³⁶

The corresponding results are plotted in Fig. 6, where the range of experimental T/P conditions is highlighted in a colored dashed box. On the one hand, in the upper panel one can observe that for both He@cage systems, the enthalpy variation has negative values for all the temperatures studied, indicating that the reactions involving the encapsulation of a He atom inside any of the sII clathrate-like cages are exothermic. However, for the He@5¹² cage the higher the temperature, the higher ΔH, in contrast to the He@5¹²6⁴ system where this tendency is negative, and in addition, the effect of the temperature is more pronounced (higher slope). On the other hand, in the lower panels of the figure, ΔG takes positive or negative values depending mostly on the pressure value. Thus, at P = 10 atm, for example, the reaction is spontaneous (ΔG < 0) up to approximately 83 and 53 K in the case of He@5¹² and He@5¹²6⁴, respectively, while for higher temperature values the encapsulation reaction needs to be driven by an external source of energy.

Fig. 6 ΔH (upper panel) and ΔG (lower panels) as a function of temperature at various pressures for the He@5¹² (circles) and He@5¹²6⁴ (triangles) systems in their minimum energy configurations. Color (magenta) dashed boxes indicate the T–P range of experimental conditions.

The most outstanding characteristic in these plots is that at high pressures of 500, 1000 and 1500 atm, which correspond to the experimentally reported values,³⁶ ΔG is negative for the whole range of temperatures studied by the experiment for both He@cage systems. This means that the He@sII cages formation reaction is thermodynamically favoured, and therefore, it is capable of proceeding by itself until it is finished. This behavior reinforces the idea that this kind of inclusion complexes are formed at high pressures. Finally, another difference found between the small and large He@sII cavities is the fact that for the He@5¹² cage one can observe two tendencies in the distribution of Gibbs free energies variation: one in the range of 1–100 atm, where the slope of the lines is positive, so ΔG increases as temperature is increasing, and the second one from 500–1500 atm with a negative slope, and thus, ΔG takes lower values as temperature increases. Nevertheless, for He@5¹²6⁴ only positive tendencies are observed in the pressure values studied, in spite of the fact that the slope's increase is gradually smaller.

The present results for enthalpy and free Gibbs energy variations are compared with previous reported data on such systems.^27,33 For example, earlier B3LYP/6-31G(d) calculations for the He@5¹² and He@5¹²6⁸ cages have reported²⁷ ΔH of −0.56 kcal mol⁻¹ and −0.21 kcal mol⁻¹, respectively, while our values are −0.43 and −0.92 kcal mol⁻¹ at T = 298 K. Further, more recent B97-D/cc-pVTZ computations³³ have estimated ΔH and ΔG values at 180 K and 1 atm for the He@5¹² cage of −0.97 and 2.18 kcal mol⁻¹ at 180 K and 1 atm compared to our predictions of −0.55 and 1.54 kcal mol⁻¹, respectively. Although the obtained values in a range of temperature and pressure values are distinct, the overall behavior for both ΔH and ΔG is similar, with the the enthalpy variation for the encapsulation of the He being greater for 5¹² than for larger He@5¹²6⁴ one.

3 Summary and conclusions

In this work, we have assessed the performance of different DFT functionals, such as GGAs (revPBE and PW86PBE) and hybrids (B3LYP, PBE0), including various dispersion correction schemes (D3(0), D3(BJ), D4 and XDM), in comparison with reference data obtained from well-converged wavefunction-based calculations (DLPNO-CCSD(T) and DFMP2). The cages structures under study, He@(H₂O)_N (N = 20, 24, 28, 36), correspond to the building blocks present in the three most common clathrate hydrates: sI, sII and sH. We have computed interaction and cohesive energies of all He-filled and empty clathrate-like systems, respectively, in minimum and non-minimum energy configurations in order to ensure an overall description of the He–water and water–water interactions. We have adopted a general protocol scheme to examine the validity of promising DFT approaches against the reference data. First of all, we have analysed the energy results of the equilibrium geometries, finding differences in the performance of the DFT functionals in presence/absence of the He atom. Thus, the B3LYP-D4 functional is the one which provides closer results to the reference values in the case of the empty cages, whereas the same functional significantly overestimates the energy in the He-filled cages, being the PW86PBE-XDM/D4 the one which better performs in that case. In general, different tendencies are distinguished when taking into consideration or not the He atom. Second, we have assessed the performance of the DFT functionals in non-minimum configurations. Thus, we have observed that the functionals revPBE and B3LYP are inadequate to describe the guest–host interactions which take place in these systems, whereas the PBE0 results are in good agreement with the reference ones, finding that the interaction energy curves of PBE0-D4 and DLPNO-CCSD(T) almost overlap in those configurations close to the potential barriers. Nevertheless, this functional presents some difficulties to describe the interactions in the minima of the curves, where the energy is underestimated. Finally, the PW86PBE functional also shows a well-balanced performance, presenting the greatest agreement with respect to the DFMP2 and DLPNO-CCSD(T) reference values in the minima. As regards the maxima, the difference with respect to the reference is more noticeable, but it is still small. Both the D4 and XDM dispersion corrections behave correctly, finding that the XDM results are in between the DFMP2 and DLPNO-CCSD(T) ones, whereas the D4 results are slightly higher than the DFMP2 ones. Taking all this information into account, our analysis came to the conclusion that the functionals which better perform for the description of the He@(H₂O)_N interactions are the PW86PBE-XDM/D4 and PBE0-D4.

We have also performed a thermodynamic study in order to evaluate the stability of each of the cavities which shape the sII clathrate hydrate, that is, the He@(H₂O)_N (N = 20, 28) systems. The change in enthalpy, ΔH, and the change in Gibbs free energy, ΔG, at various temperatures and pressures is calculated and compared with the experimental conditions (80–120 K and 50–150 MPa). The encapsulation process of the He atom inside the individual 5¹² and 5¹²6⁴ sII cages is predicted to be exothermic and spontaneous in the range of T/P experimental conditions. It would be interesting to perform the same thermodynamic study in the bulk He@sII in order to observe if there is any significant difference with respect to the study of the individual cages as a consequence of, for example, periodicity, inter-cage effects… or, on the contrary, these results are sufficiently representative and may be taken as a reference to have a realistic idea of the type of reactions occurring in the periodic crystal structure.

These outcomes reveal less demanding methods which are adequate to describe the He–water interactions in isolated clathrate hydrates cages, as well as to study thermodynamically the kind of reactions involved in the enclathration process. Such systematic accuracy cross-check studies of modern computational approaches are of high relevance in developing predictive data-driven models, in a general automated (machine-learned) fashion, for such noncovalent interactions. They may also be useful to further investigate the sI, sII and sH periodic crystals, or filled-ice water networks, as well as more recently discovered ones, such as the C₀, C₁, etc. structures, so as to examine, among other contributions, multiple cage occupancy, and lattice effects.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank Dr Daniel Arismendi-Arrieta for numerous useful discussions on clathrate hydrates, and Raúl Rodríguez-Segundo for assistance with DENEB-Atelgraphics software. The authors thank to Centro de Cálculo del IFF, SGAI (CSIC) and CESGA for allocation of computer time. This work has been supported by MINECO grant No. FIS2017-83157-P, MICINN grant No, PID2020-114654GB-I00, Comunidad de Madrid grant No. IND2018/TIC-9467, and COST Action CA18212(MD-GAS).

References

1. B. Journaux, K. Kalousová, C. Sotin, G. Tobie, S. Vance, J. Saur, O. Bollengier, L. Noack, T. Rückriemen-Bez, T. Van Hoolst, K. M. Soderlund and J. M. Brown, Space Sci. Rev., 2020, 216, 7.
2. A. Hassanpouryouzband, E. Joonaki, M. Vasheghani Farahani, S. Takeya, C. Ruppel, J. Yang, N. J. English, J. M. Schicks, K. Edlmann, H. Mehrabian, Z. M. Aman and B. Tohidi, Chem. Soc. Rev., 2020, 49, 5225–5309.
3. A. Bouquet, O. Mousis, C. R. Glein, G. Danger and J. H. Waite, Astrophys. J., 2019, 885, 14.
4. C. A. Koh and E. D. Sloan, AIChE J., 2007, 53, 1636–1643.
5. P. S. R. Prasad and B. S. Kiran, Sci. Rep., 2018, 8, 1–10.
6. D. Guo, H. Wang, Y. Shen and Q. An, RSC Adv., 2020, 10, 14753–14760.
7. S. M. Daghash, P. Servio and A. D. Rey, Chem. Eng. Sci., 2020, 227, 115948.
8. G. J. MacDonald, Annu. Rev. Energy, 1990, 15, 53–83.
9. I. Chatti, A. Delahaye, L. Fournaison and J.-P. Petitet, Energy Convers. Manage., 2005, 46, 1333–1343.
10. H. Dashti, L. Z. Yew and X. Lou, J. Nat. Gas Sci. Eng., 2015, 23, 195–207.
11. Z. Yin and P. Linga, Chin. J. Chem. Eng., 2019, 27, 2026–2036.
12. S. F. Cannone, A. Lanzini and M. Santarelli, Energies, 2021, 14, 387.
13. E. Gloesener, O. Karatekin and V. Dehant, Icarus, 2021, 353, 114099.
14. H. D. Nagashima, T. Miyagi, K. Yasuda and R. Ohmura, Fluid Phase Equilib., 2020, 517, 112610.
15. H. Tanaka, T. Yagasaki and M. Matsumoto, J. Chem. Phys., 2018, 149, 074502.
16. A. Falenty, T. C. Hansen and W. F. Kuhs, Nature, 2014, 516, 231–233.
17. L. del Rosso, M. Celli and L. Ulivi, Nat. Commun., 2016, 7, 1–7.
18. E. D. Sloan, Nature, 2003, 426, 353–359.
19. P. K. Chattaraj, S. Bandaru and S. Mondal, J. Phys. Chem. A, 2011, 115, 187–193.
20. S. Alavi and J. A. Ripmeester, Mol. Simul., 2017, 43, 808–820.
21. M. H. Waage, T. J. H. Vlugt and S. Kjelstrup, J. Phys. Chem. B, 2017, 121, 7336–7350.
22. J. Ghosh, R. R. J. Methikkalam, R. G. Bhuin, G. Ragupathy, N. Choudhary, R. Kumar and T. Pradeep, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 1526–1531.
23. A. Kumar, Y. Gao, X. C. Zeng and C. L. Cheung, Nanoscale, 2021, 13, 7447–7470.
24. Y. A. Dyadin, E. G. Larionov, A. Y. Manakov, F. V. Zhurko, E. Y. Aladko, T. V. Mikina and V. Y. Komarov, Mendeleev Commun., 1999, 9, 209–210.
25. Y. A. Dyadin, E. Y. Aladko, A. Y. Manakov, F. V. Zhurko, T. V. Mikina, V. Y. Komarov and E. V. Grachev, J. Struct. Chem., 1999, 40, 790–795.
26. J. S. Loveday and R. J. Nelmes, Phys. Chem. Chem. Phys., 2008, 10, 913–1068.
27. S. Mondal and P. K. Chattaraj, Phys. Chem. Chem. Phys., 2014, 16, 17943–17954.
28. R. V. Belosludov, Y. Y. Bozhko, O. S. Subbotin, V. R. Belosludov, H. Mizuseki, Y. Kawazoe and V. M. Fomin, J. Phys. Chem. C, 2014, 118, 2587–2593.
29. X. Yu, J. Zhu, S. Du, H. Xu, S. C. Vogel, J. Han, T. C. Germann, J. Zhang, C. Jin, J. S. Francisco and Y. Zhao, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 10456–10461.
30. P. Teeratchanan and A. Hermann, J. Chem. Phys., 2015, 143, 154507.
31. A. Vítek, D. J. Arismendi-Arrieta, R. Rodríguez-Cantano, R. Prosmiti, P. Villarreal, R. Kalus and G. Delgado-Barrio, Phys. Chem. Chem. Phys., 2015, 17, 8792–8801.
32. D. J. Arismendi-Arrieta, A. Vítek and R. Prosmiti, J. Phys. Chem. C, 2016, 120, 26093–26102.
33. S. P. Kaur and C. N. Ramachandran, Mol. Phys., 2018, 116, 54–63.
34. S. Takeya and A. Hachikubo, J. Chem. Phys., 2019, 20, 2518–2524.
35. R. Yanes-Rodríguez, D. J. Arismendi-Arrieta and R. Prosmiti, J. Chem. Inf. Model., 2020, 60, 3043–3056.
36. F. W. Kuhs, T. C. Hansen and A. Falenty, J. Phys. Chem. Lett., 2018, 9, 3194–3198.
37. F. Noé, A. Tkatchenko, K.-R. Müller and C. Clementi, Annu. Rev. Phys. Chem., 2020, 71, 361–390.
38. Y. S. Al-Hamdani, P. R. Nagy, A. Zen, D. Barton, M. Kállay, J. G. Brandenburg and A. Tkatchenko, Nat. Commun., 2021, 12, 3927.
39. M. Ceriotti, C. Clementi and O. Anatole von Lilienfeld, J. Chem. Phys., 2021, 154, 160401.
40. J. Westermayr, M. Gastegger, K. T. Schütt and R. J. Maurer, J. Chem. Phys., 2021, 154, 230903.
41. M. Ceriotti, C. Clementi and O. Anatole von Lilienfeld, Chem. Rev., 2021, 121, 9719–9721.
42. N. Giricheva, A. Ischenko, V. Yusupov, V. Bagratashvili and G. Girichev, J. Mol. Struct., 2017, 1132, 157–166.
43. D. J. Arismendi-Arrieta, Ã. Valdés and R. Prosmiti, Chem. – Eur. J., 2018, 24, 9353–9363.
44. Q. Lu, X. He, W. Hu, X. Chen and J. Liu, J. Phys. Chem. C, 2019, 123, 12052–12061.
45. A. Cabrera-Ramírez, D. J. Arismendi-Arrieta, A. Valdés and R. Prosmiti, ChemPhysChem, 2020, 21, 2618–2628.
46. N. Plattner, T. Bandi, T. D. Doll, D. L. Freeman and M. Meuwly, Mol. Phys., 2008, 106, 1675–1684.
47. M. M. Conde and C. Vega, J. Chem. Phys., 2010, 133, 064507.
48. T. Yagasaki, M. Matsumoto, Y. Andoh, S. Okazaki and H. Tanaka, J. Phys. Chem. B, 2014, 118, 1900–1906.
49. M. Rossi, J. Chem. Phys., 2021, 154, 170902.
50. A. Demurov, R. Radhakrishnan and B. L. Trout, J. Chem. Phys., 2002, 116, 702.
51. K. Katsumasa, K. Koga and H. Tanaka, J. Chem. Phys., 2007, 127, 044509.
52. L. Hakim, K. Koga and H. Tanaka, Phys. Rev. Lett., 2010, 104, 115701.
53. A. Patt, J.-M. Simon, S. Picaud and J. M. Salazar, J. Phys. Chem. C, 2018, 122, 18432–18444.
54. R. Zalesny, M. G. Papadopoulos, P. G. Mezey and J. Leszczynski, Linear-Scaling techniques in computational chemistry and Physics: Methods and applications, Springer, Netherlands, 2011.
55. G. J. O. Beran, Chem. Rev., 2016, 116, 5567–5613.
56. C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109.
57. P. Baudin, P. Ettenhuber, S. Reine, K. Kristensen and T. KjÃęrgaard, J. Chem. Phys., 2016, 144, 054102.
58. I. León-Merino, R. Rodríguez-Segundo, D. J. Arismendi-Arrieta and R. Prosmiti, J. Phys. Chem. A, 2018, 122, 1479–1487.
59. M. Kodrycka and K. Patkowski, J. Chem. Phys., 2019, 151, 070901.
60. Y. S. Al-Hamdani and A. Tkatchenko, J. Chem. Phys., 2019, 150, 010901.
61. A. Cabrera-Ramírez, D. J. Arismendi-Arrieta, Ã. Valdés and R. Prosmiti, ChemPhysChem, 2021, 22, 359–369.
62. A. J. A. Price, K. R. Bryenton and E. R. Johnson, J. Chem. Phys., 2021, 154, 230902.
63. F. Takeuchi, M. Hiratsuka, R. Ohmura, S. Alavi, A. Sum and K. Yasuoka, J. Chem. Phys., 2013, 138, 124504.
64. DENEB 1.30 beta: the Nanotechnology Software by Atelgraphics, 2020, https://www.atelgraphics.com.
65. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327.
66. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. M. Schützet al., MOLPRO, A Package of Ab Initio Programs. See http://www.molpro.net.
67. E. Semidalas and J. M. L. Martin, J. Chem. Theory Comput., 2020, 16, 7507–7524.
68. J. Chen, B. Chan, Y. Shao and J. Ho, Phys. Chem. Chem. Phys., 2020, 22, 3855–3866.
69. R. A. Kendall, T. H. Dunning Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–806.
70. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
71. E. C. Lee, D. Kim, P. Jurecka, P. Tarakeshwar, P. Hobza and K. S. Kim, J. Phys. Chem. A, 2007, 111, 3446–3457.
72. A. Cabrera-Ramírez, R. Yanes-Rodríguez and R. Prosmiti, J. Chem. Phys., 2021, 154, 044301.
73. J. P. Perdew and W. Yue, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8800.
74. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
75. Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890.
76. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
77. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
78. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
79. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
80. E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112.
81. E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122.
82. A. D. Becke, J. Chem. Phys., 2007, 127, 154108.
83. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria and M. A. Robbet al.Gaussian16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
84. Universität-Bonn, A dispersion correction for density functionals, Hartree–Fock and semi-empirical quantum chemical methods, https://www.chemie.uni-bonn.de/pctc/mulliken-center/software/dft-d3/dft-d3.
85. Universität-Bonn, D4 - A Generally Applicable Atomic-Charge Dependent London Dispersion Correction, https://www.chemie.uni-bonn.de/pctc/mulliken-center/software/dftd4.
86. A. Otero-de-la Roza and E. R. Johnson, J. Chem. Phys., 2013, 138, 204109.
87. F. O. Kannemann and A. D. Becke, J. Chem. Theory Comput., 2010, 6, 1081–1088.
88. Fast & accurate-computational-chemistry-tools (FAccTs), The Fastest Way to Accurate Quantum Chemical Energies, https://www.faccts.de/dlpno/.
89. R. M. Parrish, DF-MP2: DENSITY-FITTED 2ND-ORDER MØLLER–PLESSET PERTURBATION THEORY, https://psicode.org/psi4manual/master/dfmp2.html.
90. D. Manna, M. K. Kesharwani, N. Sylvetsky and J. M. L. Martin, J. Chem. Theory Comput., 2017, 13, 3136–3152.
91. G. Schmitz and C. Hättig, J. Chem. Theory Comput., 2017, 13, 2623–2633.
92. P. Kumar and N. Sathyamurthy, J. Phys. Chem., 2011, 115, 14276–14281.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04935f

---