Open Access Article
Open Access ArticleStudy and quantification of the enantiodiscrimination power of four polymeric chiral LLCs using NAD 2D-NMR†
Philippe
Berdagué
 a,
Boris
Gouilleux
a,
Boris
Gouilleux
 a,
Markus
Noll
b,
Stefan
Immel
a,
Markus
Noll
b,
Stefan
Immel
 b,
Michael
Reggelin
b,
Michael
Reggelin
 *b and
Philippe
Lesot
*b and
Philippe
Lesot
 *ac
*ac
aUniversité Paris-Saclay, UFR d’Orsay, RMN en Milieu Orienté, ICMMO, UMR CNRS 8182, Bât. 410, 15 rue du Doyen Georges Poitou, F-91405 Orsay cedex, France. E-mail: philippe.lesot@universite-paris-saclay.fr
bClemens-Schöpf-Institut für Organische Chemie und Biochemie Technische Universität Darmstadt, Alarich-Weiss-Strasse 4, 64287 Darmstadt, Germany. E-mail: re@chemie.tu-darmstadt.de
cCentre National de la Recherche Scientifique (CNRS), 3 rue Michel Ange, F-75016 Paris, France
First published on 21st February 2022
Abstract
Identifying and understanding the role of key molecular factors involved in the orientation/discrimination phenomena of analytes in polymer-based chiral liquid crystals (CLCs) are essential tasks for optimizing computational predictions (molecular dynamics simulation) of the existing orienting systems, as well as designing novel helically chiral polymers as new enantiodiscriminating aligning media. From this perspective, we propose to quantify and compare the enantiodiscrimination power of four homochiral polymer-based lyotropic liquid crystals (LLCs) toward a given chiral solute using their 2H residual quadrupolar couplings (2H-RQCs) measured by anisotropic natural abundance deuterium 2D-NMR (ANAD 2D-NMR). Two families of chiral polymers are investigated in this study: (i) poly-peptide polymers (PBLG and PCBLL), and (ii) polyacetylene polymers (PDA and L-MSP, a new system never published so far). As model solute, we investigate the case of camphor, an interesting rigid bicyclic chiral molecule possessing ten 2H-RQCs (10 inequivalent monodeurated isotopomers per enantiomer). In order to analyse the orientational behaviour of each enantiomer in a single oriented sample, while simplifying the identification of the (D/L)-isomer signals on spectra, a D-isomer enriched scalemic mixture (ee(D) = 30%) was used. Orientational data of camphor in each mesophase were calculated for the first time using the computer program ConArch+, modified to accept 2H-RQCs as anisotropic data input. Differences in enantiodiscriminations provided by the four aligning systems are examined and discussed in terms of structural and chemical features between polymers. The new L-MSP mesophase described in this work exhibits very promising enantiodiscrimination capacities.
1. Introduction
All data highlighting the factors/parameters involved in the molecular orientation processes and/or the chiral discrimination mechanisms (noted in short CDMs) in polymer-based lyotropic liquid crystals (LLCs) are key for three reasons: (i) to understand the molecular shape recognition phenomena in helical systems (polypeptide or other types of polymers) and their contribution to the global phenomenon;1–8 (ii) to optimize the computer simulation of the solute orientational behavior, and the prediction of their anisotropic observables (by molecular dynamics, for example)9–14 with the final aim of determining the absolute configuration of chiral molecules;15,16 and (iii) to structurally design novel helically chiral polymers as new efficient enantio-discriminating aligning media.17–22Collecting these data experimentally by all possible anisotropic 1D/2D-NMR methods, in order to assess/quantify their respective roles/effects on the enantiodiscrimination properties, therefore deserves special attention.22,24
In a recent work, we have qualitatively examined the enantiodiscriminating abilities of a polyacetylene-based chiral polymer (PLA) compared with the historical polypeptide-based polymer (PBLG), by screening a large collection of mono- (or per-)deuterated chiral analytes, covering several aspects of enantiomorphism.21 The 2H-NMR data based analysis pointed out that the enantiodiscriminating abilities (EDAs) of PLA were globally more efficient than those of PBLG, especially for chiral secondary alcohols (see the analysis presented in the ESI† (SI-I)), but also for an apolar solute such as 3-methylhexane, a very challenging chiral molecule.
A simple evaluation of EDAs of deuterated enantiomers (at a given site, as a stereogenic center) can be achieved by determining the local “differential ordering effect” (DOE factor) calculated as ΔΔνQ(2H) over their mean values:24,25
 | (1) |
This DOE(2H) factor can be considered as a local quantification of the orientational deviation for a given site in the R/S isomers with the situation that would be observed in an achiral mesophase where no discrimination is possible.25 As seen in Section SI (ESI†), in the case of a series of secondary chiral alcohols, it can be correlated with various molecular parameters such as the molecular shape anisotropy regarding the difference of the persistent volume substituents around the asymmetric carbon.26–28
This local analysis can be extended to a more global evaluation by comparing the average molecular orientation of each enantiomer via their alignment tensors. This approach provides a more insightful and reliable comparison of EDAs. In practice, this description is achieved by calculating the molecular Saupe matrix of each enantiomer, {Sαβ}R,S, derived from three types of NMR interactions:22,23 (i) the residual chemical shift anisotropies (RCSAs);29–32 (ii) the residual dipolar couplings (RDCs);33–38 and (iii) the residual quadrupolar couplings (RQCs) of nuclei with spin quantum number I > ½ as deuterium (I = 1).39,40 These matrices can be then compared by calculating the generalized 9D β angle (eqn (2)), or its cosine value (GCB value).41,42
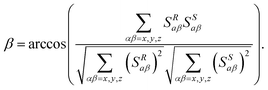 | (2) |
In this article, we exploited the analytical potential of 2H-RQCs extracted from the Anisotropic Natural Abundance Deuterium 2D-NMR (ANAD 2D-NMR) spectra22,23,43 to quantify the EDAs of two important families of enantiodiscriminating helical polymers: (i) two polyacetylene-based LLCs: (D)-valine-based polyacetylene, PDA (poly-1),21,44 and L-serine-based polyacetylene, L-MSP (poly-2), reported for the first time in this work (synthesis described below and in the ESI†), and (ii) two polypeptide-based LLCs: poly-γ-benzyl-L-glutamate, PBLG (poly-3),33–35,45 and poly-ε-carbobenzyloxy-L-lysine, PCBLL (poly-4) (see Fig. 1).46
The choice of these two polymer families (see Fig. 1a) is motivated by their common global characteristics such as their rod-like shape (persistence length ≫ persistence diameter), the helical structure of their scaffold and the complex conformational dynamics of their side chains. On the other hand, they are chemically different and possess notable structural differences such as the flexibility of their helical backbones or the position of their stereogenic centers (side chain versus backbone). In all cases, the complex array of analyte–polymer interactions for a given solute, and the chemically very different side chains (steric factors, electronic profiles, and positioning of functional groups relative to the helix) produce highly versatile orientational and discriminative “responses” to electrostatic contributions, to shape anisotropy and conformational behaviour of the solute. In practice, the subtle balances between all molecular factors involved makes it difficult to qualitatively or empirically establish an “overall” superiority of a given chiral polymer over another (polypeptide versus polyacetylene). However, given the current set of analytes, the polyacetylenes could appear to be superior in enantiodiscriminating capability.21,44
Generally, all studies dedicated to the EDA are based on the analysis of (1H–1H)-RDCs and/or (13C–1H)-RDCs of each isomer in two distinct ordered samples to avoid the peak overlaps met with a mixture of two enantiomers. Given the fact that 2H-RQCs are about a factor of ten larger than (13C–1H)-RDCs, it becomes possible to analyze both enantiomers of a chiral analyte in the same oriented sample. In this work, a scalemic mixture (ee(D) = 30%) is used to simplify the identification of the (D/L)-isomer signals in the anisotropic NMR spectra. This strategy is advantageous for two reasons: (i) a single oriented NMR sample and a single set of NMR experiments is prepared and performed, respectively, and (ii) the orientational behavior of the enantiomers can be compared under strictly identical experimental conditions.
As a model analyte, we focus our attention on a small chiral bicyclic molecule, (D)-(1R,4R)-(+)-camphor and (L)-(1S,4S)-(−)-camphor (denoted as R-(5) and S-(5), respectively), NMR-spectroscopically well characterized,47,48 for which the detection of ten pairs of monodeuterated enantiomeric isotopomers is expected (see Fig. 1b). In order to compare the EDAs of four chiral mesophases, the differences of intrafamily (e.g. polypeptide/polypeptide) and interfamily (e.g. polypeptide/polyacetylene), enantiomeric orientational behavior of camphor is examined and discussed.
Moreover, we also highlight the promising enantiodiscrimination capability of the new L-MSP orienting system in comparison to the three other chiral LLCs.
2. Theoretical considerations, NMR approach, and computational tool
Specificities of ANAD 2D-NMR
Despite the low receptivity of deuterons at natural abundance (∼1.5 × 10−2% with respect to 1H), measuring 2H-RQCs on isotopically normal analytes is analytically relevant.22,43 First, the 2H-RQCs are ten times more sensitive to an anisotropic environment as compared to (13C–1H)-RDCs or even more so with 13C-RCSAs.43 Second, the 2H spectral enantiodiscrimination in CLCs is easily revealed because two 2H quadrupolar doublets (2H-QDs) are observed with δaniso,S ≈ δaniso,R, with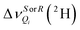 equal to22,43
equal to22,43 | (3) |
From the local order parameters,  , of various (noncolinear) internuclear C–Di directions (rC–Di), we can derive the Saupe matrix elements, SS
, of various (noncolinear) internuclear C–Di directions (rC–Di), we can derive the Saupe matrix elements, SS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) or
or![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Rαβ, expressed in an initial molecular axis system, IAS, (a, b, c)S
Rαβ, expressed in an initial molecular axis system, IAS, (a, b, c)S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) or
or![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R according to eqn (4):22,43
R according to eqn (4):22,43
 | (4) |
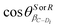 , are the director cosines of vectors, rC–Di, in the IAS.
, are the director cosines of vectors, rC–Di, in the IAS.
From an analytical point of view, any deuterons present at natural abundance can be detected with a reasonable amount (<50 mg) of chiral solute (with MW about 300 g mol−1). The use of 2H cryogenic NMR probes is a valuable aid but is not necessary for low molecular weight compounds.49 When the spectral analysis of enantiomers occurs in a scalemic mixture the preparation of two distinct samples can be avoided and the identification of the two enantiomers in QUOSY-type 2D experiments is unproblematic.22,43 Moreover, this guarantees an easy assignment of the absolute configuration for all 2H-QDs observed, based on the difference of their respective peak intensities. Also, due to the dilute nature of NAD spin systems, the determination of 2H-RQC values for diastereotopic protons in methylene groups are not affected by second order effects as in the case of (13C–1H)-RDCs (1DCH couplings) for which strong 1H–1H coupling effects can hamper their accurate determination.50 However, even if the measurement of 2H-RQCs in CH2 groups is direct and accurate, the determination of their signs requests the analysis of associated 1H-coupled 13C signals whose structure is sometimes complex when both enantiomers are present in the sample. An adapted protocol to determine their signs, when a scalemic mixture is used, is discussed below.
Data analysis by ConArch+
So far, the recent exploitation of 2H-RQCs has been performed using the MSpin-RQC program,51,52 a variant of MSpin, initially able to manage RDCs or RCSAs as input data.30,53 In this work, another computational approach delivering orientational data of a solute has been explored, the ConArch+ (Configurational Architect) software package.54,55Like MSpin, the ConArch+ program computes the Saupe order parameters, Sαβ, (via an algorithm based on the principle of singular value decomposition (SVD)) in order to minimize the difference between the experimental values (2H-RQCExptl.) and the back-calculated values (2H-RQCCalc.) from the order matrix for a given geometry. A schematic description of the operating principle of the ConArch+ program using 2H-RQC data is presented in Fig. S4 (ESI†).
Although not used in the current investigation, the main difference between ConArch+ and MSpin is the distance geometry module of the former.56 The determination of the alignment or the Saupe tensor from RDCs or RQCs does not differ substantially in both programs. The decisive strength of ConArch+ is that it is able to let structures evolve under the influence of the NMR data. This means that ConArch+ does not rely on structural comparisons between precalculated structures (from DFT, for example) and measured data; it generates structures from the data.
Therefore, using a good data set, ConArch+ is able to determine correct relative configurations from an input structure of arbitrary configuration. This is possible because “wrong” configurations can change during a molecular dynamics simulation in 4D space with a pseudo-force field restraining only observables from NMR data and distance ranges from the constitution.54–59
In the course of the investigation it turned out that it is not necessary to compute the 2H quadrupolar coupling constants, KDi, (see eqn (3)) for each site. Instead, three selected values depending on the type of carbon hybridization were used for the computations, namely KDi (Csp3–D) = 170.0, KDi (Csp2–D) = 185.0 and KDi (Csp–D) = 210.0 kHz. DFT seems to overestimate the electric field gradients (EFGs) at the deuterium sites, so the computed EFGs are too large, but this is compensated by a downscaling of the corresponding alignment tensor. In total, there seems to be no or very little difference between the RQCs using the computed EFGs or the “default” quadrupolar coupling constants for the different hybridization modes (sp3, sp2, and sp) of carbon atoms. Finally, the agreement between the values of ΔνExpt.Q and ΔνCalc.Q is evaluated by the well-known Cornilescu quality factor, Q,60 or the root mean square deviation (RMSD) parameter (see eqn (S3) and (S4) in Section SII, ESI†).
3. Results and discussion
NAD specificities of camphor
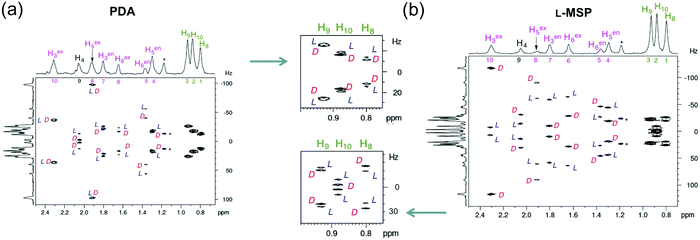
Camphor (5) possesses two stereogenic centers of defined absolute configuration leading to ten non-equivalent hydrogenated (deuterated) sites and including eight diastereotopic positions associated with the three prochiral methylene groups and one pair of diastereotopic methyl groups. The remaining two sites are the methine proton at position 4 and the methyl group at position 1.For a scalemic (or a racemic) mixture of 5 (see Tables in the ESI†), the maximum number of theoretically expected 2H-QDs to be observed on an ANAD 2D-NMR map is 20 when all non-equivalent positions in the enantiomers are spectrally differentiated by the chiral oriented phase.
Two typical examples of tilted/symmetrized ANAD 2D spectra (Q-resolved type) of 5 recorded in PDA and L-MSP (Texp = 15 hours) are presented in Fig. 2a and b;22,43,61 spectra obtained in the PBLG and PCBLL mesophases are given in Fig. S9 and S10 (ESI†). Whatever the mesophase used, the NAD signals of polymer and organic co-solvent (chloroform) do not interfere with the NAD signals of 5. Additionally, for each mesophase, the pairs of enantioisotopomers are spectrally discriminated, except for the site H3ex in the PDA phase where two identical 2H-RQCs are measured (see Fig. 2a). Due to the modulated peak intensities associated with the ee(D), the identification of NAD signals belonging to the major (D) and the minor enantiomer (L) is direct and unambiguous. All 2H-QDs experimentally measured were exploited for the determination of orientational data.
Analysis of methylene groups
Although the measurement of the 2H-RQC magnitude on ANAD tilted 2D-NMR spectra can be read directly on maps, the determination of their absolute signs remains unknown.22 Determination of the sign of 2H-RQCs relative to the heteronuclear (13C–2H)-RDCs, is possible using 2H Q.E.COSY 2D experiments,62 but for sensitivity reasons, this approach is difficult to achieve experimentally when applied to non-isotopically enriched molecules.63 Another possibility could be to explore all possible combinations of signs for each inequivalent site, using a screening-protocol computational approach.52 Currently, the experimental approach used in this work consists in exploiting additional 13C data (1TCH) extracted from the analysis of simple proton-coupled 1D experiments (inverse gate/single pulse) with the help of heteronuclear (1TCH/2)- or (1TCH/4)-resolved heteronuclear 2D spectra (see Fig. S7 and S8, ESI†).22 The reason for using a phase-sensitive (1TCH/4)-resolved sequence is to simplify the signal multiplicity in the F1 dimension by avoiding long-range 13C–1H couplings, and thus ease the determination of 1TCH values. The combined analysis of 2H-RQC and one-bond (13C–1H)-RDC data extracted from 2H–{1H} and 13C spectra, respectively, is possible because the order parameter SCH and SCD (for a given site) can be assumed to be equal within variations of about 5%. Hence the ΔνQ(CD)/1D(CH) ratio is independent of any order parameter, and is approximately equal to (for each enantiomer):64 | (5) |
Depending on the 2H quadrupolar coupling constant, qCD, and the inter-atomic distance C–H, a value of −11.5 is a good compromise to get an estimate of the magnitude of 1DCH (1DEstim.CH). Comparison of 1DEstim.CH and 1DExptl.CH values (even approximatively evaluated) allows for a determination of the sign of 2H-RQCs. In the case of a scalemic mixture of enantiomers, the correlation between 2H-RQCs and 1DCH (1DCH = [1TCH − 1JCH]/2) for both CH and CH3 groups is generally trivial. In contrast, the situation is generally more complex for CH2 groups due to the inequivalence of diastereotopic positions, endo/exo, (leading to two pairs of 2H-QDs centered on two 2H chemical shifts), while enantiomers can be discriminated by the 13C-RCSA difference in the 13C spectra. In this case, we have to correlate the 2H-RQC data for each of the diastereotopic positions (endo or exo) with the (13C–1H)-RDC data for each enantio-isotopomer (L or D).
Fig. 3 depicts the schematic principle applied to correlate the 2H-RQC and (13C–1H)-RDC spectral patterns (and associated data) in the complex case of the methylene group at C5 to determine the sign of 2H-RQCs, in a scalemic mixture. Here the spectral 2H and 13C situations shown correspond to the case of the methylene group 5 of 5 dissolved in L-MSP, but other situations are encountered with the inversion of 13C resonances of minor and major enantiomers in the F2 dimension and/or 13C–1H dipolar or 2H quadrupolar splitting in the F1 dimension (see the ESI†). The same correlation approach was applied for the analysis of the two methylenes located at positions 3 and 6 of 5 (see Fig. S16 and S18, ESI†) in L-MSP, but also in the three other CLCs. Thus, the coherence between experimental RQC and RDC data enables the determination of the sign of the 2H-RQCs.
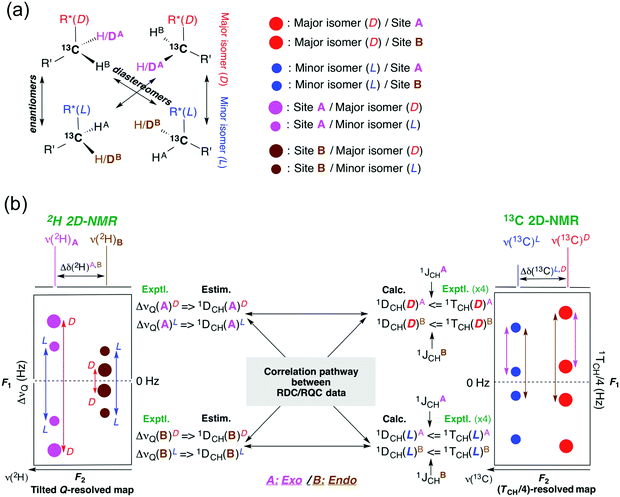 | ||
| Fig. 3 (a) Stereochemical relationships existing between the four isotopomers associated with a methylene group in a chiral molecule (here a scalemic mixture where the major enantiomer is D). The color code (minor/major isomers and diastereotopic sites A/B) shown is used in Fig. 4b. (b) Schematic description of the principle leading to correlation of 2H-RQC and one-bond (13C-1H)-RDC data in order to determine of the sign of 2H-RQCs for two diastereotopic directions (exo and endo) of a CH2 group. Correlation is done by combining 2H-RQC data extracted from NAD tilted Q-resolved 2D experiments (left) and (13C–1H)-RDCs from 13C (1TCH/4)-resolved 2D experiments (right). The situation shown here corresponds to the methylene group 5 of 5 in L-MSP. | ||
The consistency of the two (L/D)-isomer datasets with respect to the exo/endo positions in CH2 groups as well as for CH and CH3 groups, leading to the sign of any 2H-RQC can be scrutinized in Tables S5, S7, S9 and S11 (ESI†). Moreover, the small Q-factors (Q < 0.07) obtained with all the mesophases definitively validate the determined signs by correlation of the 2H-RQCs.
Analysis of results in four chiral mesophases
All experimental and back-calculated 2H-RQC data (ΔνExptl.Q and ΔνCalc.Q) as well as all pertinent spectral (13C/2H) data for (R)-5 and (S)-5 oriented in mesophases poly-1 to poly-4 are listed in Tables S5/6, S7/8, S9/10 and S10/11 (ESI†), respectively, while the key order-based molecular data, as the generalized degree of order (GDO) or eigenvalues of the Saupe tensor, for instance, associated with each isomer are summarized in Table 1. Whatever the CLC, the small Q values (from 0.02 to 0.06) calculated for each enantiomer indicate an excellent agreement between experimental and back-calculated values. Associated correlation graphs (ΔνExptl.Qvs. ΔνCalc.Q) as well as column bar plots showing comparisons between ΔνExptl.Q and ΔνCalc.Q values for each enantiomer in the four CLCs are presented in the ESI.†| Parameters | PDA (poly-1) | L-MSP (poly-2) | PBLG (poly-3) | PCBLL (poly-4) |
|---|---|---|---|---|
| a Factor of quality, Q, according to Cornilescu's definition for the best-fit (SVD) (see text and SI and SII, ESI). b RMSD: standard root mean square deviation (see the text and SI and SII, ESI). c GDO: generalized degree of order. d Value of generalized 9D-angle β between the L- and D-enantiomeric Saupe matrices for the best-fit (see eqn (2)). e GCB: “Cosine of generalized 9D-angle β”. | ||||
| Configuration of the repeating unit | R/(D) | S/(L) | S/(L) | S/(L) |
| Polymer abs. conf. | M | M | M | M |
| Solute abs. conf. | R,R/(D) | S,S/(L) | R,R/(D) | S,S/(L) | R,R/(D) | S,S/(L) | R,R/(D) | S,S/(L) |
|---|---|---|---|---|---|---|---|---|
| Q factora | 0.0656 | 0.0417 | 0.0606 | 0.0603 | 0.0171 | 0.0173 | 0.0194 | 0.0241 |
| RMSD (Hz)b | 5.0 | 3.5 | 6.4 | 4.8 | 7.7 | 7.7 | 2.7 | 2.5 |
| Eigenvalues of {Sαβ} Sx′x′, Sy′y′, Sz′z′ (×10−4) | +3.75 | +3.48 | −0.64 | −1.86 | −20.08 | −20.80 | +0.81 | +0.98 |
| +4.35 | +5.35 | −9.19 | −6.19 | −27.87 | −27.10 | +11.90 | +10.77 | |
| −8.10 | −8.83 | +9.83 | +8.05 | +47.96 | +47.90 | −12.71 | −11.74 | |
GDO (×10−3)c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 42 |
0.81 | 0.89 | 1.10 | 0.84 | 4.82 | 4.80 | 1.42 | 1.30 |
| Axial comp. (×10−3)42 | −0.81 | −0.88 | +0.98 | +0.81 | +4.80 | +4.79 | −1.27 | −1.17 |
| Rhombic comp. (×10−3)42 | −0.04 | −0.12 | +0.57 | +0.29 | +0.52 | +0.42 | −0.74 | −0.65 |
| Rhombicity par. (×10−1)42 | 0.50 | 1.41 | 5.80 | 3.58 | 1.08 | 0.88 | 5.82 | 5.56 |
| Asymmetric par. (×10−1)42 | 0.74 | 2.12 | 8.70 | 5.37 | 1.62 | 1.31 | 8.73 | 8.33 |
β angle [L,D]d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 42 |
8.4° | 78.0° | 4.3° | 61.5° | ||||
GCB [L,D]e![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 42 |
0.9893 | 0.2078 | 0.9972 | 0.4767 | ||||
In terms of orientational behavior, the analysis of GDO values calculated in the four CLCs clearly shows that 5 is much more strongly oriented in PBLG (GDO(poly-3) ≈ 4.8 × 10−3) than in the PDA, L-MSP and PCBLL mesophases for which the GDO values vary from 0.8 to 1.5 × 10−3, thus confirming the range of 2H-RQCs measured in each mesophase (up to 1100 Hz in PBLG, and up to 250 Hz in the other CLCs). With regard to the chemical structure of the PBLG sidechain, this result is quite surprising. Indeed, the latter does not seem favorable to promote strong analyte–polymer interactions compared to the other polymers which exhibit one hydrogen-bond donor site (see Fig. 1a). In fact, the high GDO value of 5 in the PBLG mesophase is probably related to a better packing effect of PBLG fibers (inducing a stronger solute orientation) due to (i) a higher rigidity of the helical backbone of PBLG (stabilized by internal H-bonds in the peptide chain) that does not exist for polyacetylenic polymers; and (ii) a weaker flexibility of the (short) side chains of PBLG (only six rotors) compared to the sidechain of PCBLL, PDA and L-MSP polymers that explore larger 3D volumes during their conformational dynamics, thus reducing the degree of order of the polymer.
In terms of the molecular enantiodiscrimination process, the comparison of β angles or GCB values (see Table 1) provides a quantitative description of the differences of enantiomer orientation in the four lyotropic CLCs. These differences can also be visualized with graphical representations of R/S-tensors using 3D surfaces as depicted in Fig. 4. Thus, the analysis of GCB values shows that the eigenvectors of the diagonalized Saupe matrix (PAS) of (D) and (L)-5 are relatively close in PDA and PBLG mesophases, while they are strongly different in the L-MSP and PCBLL mesophases. Thus, in terms of differentiation, the newly reported aligning system, a polyarylacetylene with modified serine sidechains (L-MSP) provides the best EDAs as highlighted by the value of the intertensor angle β respectively its GCB (Table 1). Although limited to a single example, it may be stated that L-MSP is a promising chiral system for the analysis of chiral rigid solutes of average polarity exhibiting hydrogen-bond acceptors (e.g. camphor).
The comparison of enantiomer discrimination abilities between the four CLCs leads also to interesting insights into the mechanisms of enantiodiscrimination occurring in the chiral environments. First, values of GDO versus GCB calculated for L-MSP and PBLG selectors demonstrate no clear correlations between the degree of order and the EDAs, even if high degrees of order are generally favorable to separate the quadrupolar doublets associated with each enantiomer (i.e. increasing the |ΔΔνQ(2H)|).
Furthermore, the absence of a global trend in GCB between polypeptide and polyacetylene based polymers suggests that both (i) the location of the stereogenic center (within the helix or in the side chain), and (ii) the dynamics of the helical scaffold (less flexible in the case of polypeptides) are not of major importance. Then, the lower GCB obtained with L-MSP versus PDA might be explained by a highly sterically hindered stereogenic center in the first one, but this remains a working hypothesis at this stage.
In summary, it can be stated that from such an intra- and interfamily comparison, there is no major factor that governs the CDMs, but rather multiple molecular parameters acting in a synergistic way. This highlights the complexity of CDMs and how small functional changes in the polymer structure can affect the whole analyte's orientational behavior. Under these conditions, the design of new enantiodiscriminating polymer structures associated with a given organic solvent remains a challenging but exciting task. Accumulation of comparative experimental data paves the way to a global understanding of this complex phenomenon.
4. Conclusion and prospects
With the aim of gaining new and deeper insights into the mechanism of enantiodifferentiation caused by lyotropic CLCs, we have exploited the analytical potential of ANAD 2D-NMR to investigate and quantify the enantiodiscrimination power of two families of chiral helical polymers in oriented phases: (i) the “historical” polypeptide-based polymers (PBLG and PCBLL) abundantly used in many analytical applications;22,23 and (ii) the new CLC systems based on polyarylacetylenes bearing amino acid derived lateral groups such as PDA or PLA recently reported,21,44 and L-MSP described in this work for the first time.In contrast to many investigations reported so far, using 1H/13C-RDCs or 13C-RCSAs for evaluating the enantiodiscriminating power of new mesophases from two separated samples, one per enantiomer,17,44,65–67 the use of 2H-RQCs allows the simultaneous analysis of each enantiomer dissolved in a single oriented sample preferentially when a scalemic mixture is studied. This new approach, exploiting the approximately ten times larger 2H-RQCs as compared to the 1H/13C-RDCs, circumvents possible small variations of the mesophase properties that cannot be excluded when two samples are prepared.
Inter- and intra-family comparisons of results show that the L-MSP and PCBLL mesophases possess higher enantiodiscrimination power (toward the enantiomers of camphor), irrespective of the position of the chiral centers with respect to the helical backbone of the chiral polymers (backbone or side chains). This result clearly indicates that although the electronic/structural characteristics of a chiral solute strongly influences the propensity for the enantiomers to be discriminated, this phenomenon also depends on the characteristics of the chiral polymer used in combination with the organic co-solvent.
The outcomes and insights obtained from this study clearly highlight the complex interplay between the solute and the polymer. The high dimensionality of these interactions at the same time makes the design of global chiral descriptors able to reliably model all recognition phenomenon, and then the prediction of the NMR results, very difficult.
This new study demonstrates that it is mandatory to understand the fine intermolecular interactions between enantiomers and the chiral selectors in the case of a series of analogous chiral molecules. With regard to the results obtained with camphor, it should be pertinent, for instance, to examine the case of isoborneol (1S-endo)-1,7,7-trimethyl-bicyclo[2.2.1]heptan-2-ol), that possesses a molecular structure very close to that of camphor while the hydroxyl group is susceptible to hydrogen bonding with LLC as PBLG.
Moreover, the NMR studies of transitory polymer–analyte complexes would be beneficial to in the further understanding of CDMs. NMR methods, such as Saturation Transfer Difference (STD) NMR,68 which provide insights into the spatial proximity of the analyte and the polymer side chains at the atomic level (epitope mapping), could be used to screen potential differences in the binding process between enantiomers toward the polymer side chain. Such an approach is currently in progress with promising preliminary results.
Finally, polymer–polymer interactions could also play an important role in the recognition process, which is certainly worth investigating.
5. Experimental section
Helically chiral polymers used
The degree of polymerization (DP) of polymers poly-1, poly-2, poly-3 and poly-4 is equal to 750, 750, 768 and 778 respectively.Synthesis of PDA (poly-1)
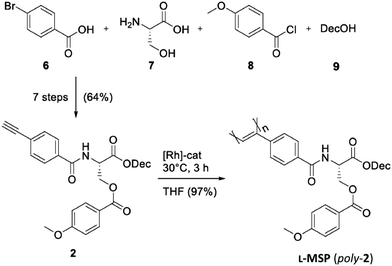
Description of the synthesis of PDA can be found in ref. 21 and 44.Synthesis of L-MSP (poly-2)
The synthesis of monomer 2 (L-MSP) was achieved in seven steps with an overall yield of 64% starting from 4-bromobenzoic acid 6, L-serine 7, p-anisoyl chloride 8 and n-decanol 9 (Scheme 1; for a more detailed description see the ESI†). The L-MSP monomer (2) was subsequently polymerized using a ternary triphenylvinyl rhodium-based initiator, originally introduced by Misumi and Masuda.69 As detailed in the ESI† the polymerization of 9 g of L-MSP 2 with a monomer/initiator ratio of 750![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 yielded poly-2, quantitatively. The polymer showed a very low dispersity and its helical chirality in chloroform was confirmed by CD spectroscopy (ESI†). We found that poly-2 forms a lyotropic liquid crystalline phase above a critical concentration of 8–9% (w/w) in CDCl3 solutions. Thus, this new alignment medium generates anisotropic phases at significantly lower concentrations compared to the already established valine-derived poly(phenylacetylene) PLA (poly-1); ccrit = 15 wt%).21,70–72
1 yielded poly-2, quantitatively. The polymer showed a very low dispersity and its helical chirality in chloroform was confirmed by CD spectroscopy (ESI†). We found that poly-2 forms a lyotropic liquid crystalline phase above a critical concentration of 8–9% (w/w) in CDCl3 solutions. Thus, this new alignment medium generates anisotropic phases at significantly lower concentrations compared to the already established valine-derived poly(phenylacetylene) PLA (poly-1); ccrit = 15 wt%).21,70–72
PBLG and PCBLL
These polymers were not synthesized but purchased from Sigma-Aldrich company. They were used without any further purification of the materials.Oriented sample preparation
Analyte 5 (C10H16O; MW = 152.2 g mol−1). The scalemic mixture of 5 was prepared with an ee(D) of 30% by mixing approximately 26 mg (0.17 mmol) of the D-isomer with 14 mg (0.09 mmol) of the L-enantiomer. Polymer-based LLC samples (poly-1, poly-2, poly-3, and poly-4) were prepared as 19% (w/w) solutions in an appropriate solvent CHCl3. The exact compositions, ratio and ee(%) of samples are given in Table S2 (ESI†).Oriented samples (fire-sealed, high-precision 5 mm NMR tubes) were homogenized by centrifugation (up and down at about 600 rpm during about 10 s). FWHM < 3–5 Hz is required to maximize the signal-to-noise ratio, SNR. Note here that attempts to measure 2H-RQCs of 5 with PCBLL dissolved in chlorinated organic solvents (CHCl3 and CH2Cl2) were not successful.
ANAD 2D-NMR
Anisotropic NAD QUOSY 2D spectra (Q-resolved Fz 2D experiments) were recorded at 14.1 T (92.1 MHz for 2H) on a Bruker Avance II spectrometer equipped with a 5 mm o.d. selective cryogenic 2H probe (see details in the ESI†). All 2H–1H scalar and dipolar couplings were removed by the WALTZ-16 composite pulse decoupling (CPD) sequence. The recycling delay and the number of points of the 2D matrix (t2, t1) and scans per t1 increment of Q-resolved Fz 2D experiments were optimized to record spectra within 20–23 hours. Adapted exponential filtering (LB1,2 = 1.5 Hz) and zero-filling to 4k(t2) × 4k(t1) were applied prior to the two-dimensional Fourier transform. The resulting 2D maps were finally tilted clockwise and then symmetrized.Isotropic and anisotropic 13C NMR
Isotropic and anisotropic 13C 1D/2D spectra were obtained @ 9.4 T (100.3 MHz for 13C) using a Bruker Avance I (5 mm QXO NMR probe). Analysis and assignment of 13C resonances were made using classical approaches (COSY, HSCQ, and HMBC) in combination with data from the literature.47,48 Evaluation of scalar couplings, 1JCH, and total spin–spin couplings, 1TCH, of 5 were obtained by the analysis of 1H coupled 13C spectra and (TCH/4)-resolved experiments (see the ESI†).All NMR 1D/2D spectra (NAD and 13C) were recorded at 300 K and controlled with a stability of ± 0.1 K.
Computational methodology
The molecular geometry of (D)-(−)-camphor was DFT optimized at the B3LYP/6-311+G(d,p) level of theory, using the solvent chloroform as a polarizable continuum model (PCM). All RQCs were back-calculated for this structure using the same frame of reference for tensor comparisons.Conflicts of interest
The authors declare no competing financial interest and have given approval to the final version of the manuscript.Acknowledgements
P. L. acknowledges the CNRS for its recurrent funding of fundamental research and the Université Paris-Saclay (previously Université Paris-Sud) for its support, as well as Ms Fofana Djeneba for her participation in this project in the frame of her first year of her Master student's internship. M. R. thanks the DFG (Re 1007/9-1) and CAPES (418729698) for financial support.References
- E. Alvira, J. Breton and J. Plata, Chiral discrimination – A model for the interaction between a helicoidal system and an amino-acid molecule, Chem. Phys., 1991, 155, 7–18 CrossRef CAS.
- P. Lesot, M. Sarfati and J. Courtieu, Natural abundance deuterium NMR spectroscopy in polypeptide liquid crystals as a new and incisive means for enantiodifferentiation of chiral hydrocarbons, Chem. – Eur. J., 2003, 9, 1724–1745 CrossRef CAS PubMed.
- N. Nandi, Role of secondary level chiral structure in the process of molecular recognition of ligand: Study of model helical peptide, J. Phys. Chem. B, 2004, 108, 789–797 CrossRef CAS.
- K. Okoshi, K. Sakajiri, J. Kumaki and E. Yashima, Well-defined lyotropic liquid crystalline properties of rigid-rod helical polyacetylenes, Macromolecules, 2005, 38, 4061–4064 CrossRef CAS.
- K. Okoshi, K. Nagai, T. Kajitani, S. I. Sakurai and E. Yashima, Anomalous stiff backbones of helical poly(phenyl isocyanide) derivatives, Macromolecules, 2008, 41, 7752–7754 CrossRef CAS.
- P. Berdagué, E. Herbert-Puchetta, V. Jha, A. Panossian, A. F. Leroux and P. Lesot, Multi-nuclear NMR of axially chiral biaryls in polypeptide orienting solvents: Spectral discriminations and enantiorecognition mechanisms, New J. Chem., 2015, 39, 9504–9571 RSC.
- J. Shen and Y. Okamoto, Efficient separation of enantiomers using stereoregular chiral polymers, Chem. Rev., 2016, 116, 1094–1138 CrossRef CAS PubMed.
- F. Freire, E. Quiñoá and R. Riguera, Supramolecular assemblies from poly(phenylacetylene)s, Chem. Rev., 2016, 116, 1242–1271 CrossRef CAS PubMed.
- J. Helfrich, R. Hentschke and U. M. Apel, Molecular-dynamics simulation study of poly(gamma-benzyl-L-glutamate) in dimethylformamide, Macromolecules, 1994, 2, 472–482 CrossRef.
- A. O. Frank, J. C. Freudenberger, A. K. Shaytan, H. Kessler and B. Luy, Direct prediction of residual dipolar couplings of small molecules in a stretched gel by stochastic molecular dynamics simulations, Magn. Reson. Chem., 2015, 53, 213–217 CrossRef CAS PubMed.
- M. E. Di Pietro, U. Sternberg and B. Luy, Molecular dynamics with orientational tensorial constraints: A new approach to probe the torsional angle distributions of small rotationally flexible molecules, J. Phys. Chem. B, 2019, 123, 8480–8491 CrossRef CAS PubMed.
- E. Sager, P. Tzvetkova, A. D. Gossert, P. Piechon and B. Luy, Determination of configuration and conformation of reserpine derivative with seven stereogenic centers using molecular dynamics with RDC-derived tensorial constraints, Chem. – Eur. J., 2020, 26, 14435–14444 CrossRef CAS PubMed.
- A. Ibanez de Opakua, F. Klama, I. E. Ndukwe, G. E. Martin, T. Williamson and M. Zweckstetter, Determination of complex small-molecule structures using molecular alignment simulation, Angew. Chem., Int. Ed., 2020, 59, 6172–6176 CrossRef CAS PubMed.
- A. Ibanez de Opakua and M. Zweckstetter, Extending the applicability of P3D for structure, Magn. Reson., 2021, 2, 105–116 CrossRef.
- R. Berger, J. Courtieu, R. R. Gil, C. Griesinger, M. Köck, P. Lesot, B. Luy, D. Merlet, A. Navarro-Vazquez, M. Reggelin, U. M. Reinscheid, C.-M. Thiele and M. Zweckstetter, Is the determination of absolute configuration possible by using residual dipolar douplings from chiral-non-racemic alignment media? – A critical assessment, Angew. Chem., Int. Ed., 2012, 51, 2–5 CrossRef.
- L. Ziani, P. Lesot, A. Meddour and J. Courtieu, Empirical determination of the absolute configuration of small chiral molecules using natural abundance 2H NMR in chiral liquid crystals, Chem. Commun., 2007, 45, 4737–4739 RSC.
- S. Hansmann, T. Larem and C.-M. Thiele, Enantiodifferentiating properties of the alignment media PELG and PBLG, Eur. J. Org. Chem., 2016, 1324–1329 CrossRef CAS.
- S. Jeziorowski and C.-M. Thiele, Poly-γ-S-perillyl-L-glutamate and poly-γ-S-perillyl-D-glutamate: Diastereomeric alignment media used for the investigation of the alignment process, Chem. – Eur. J., 2018, 24, 15631–15637 CrossRef CAS PubMed.
- B. Nieto-Ortega, R. Rodriguez, S. Medina, E. Quinoa, R. Riguera, J. Casado, F. Freire and F. J. Ramirez, J. Phys. Chem. Lett., 2018, 9, 2266–2270 CrossRef CAS PubMed.
- G.-W. Li, H. Liu, F. Qiu, X.-J. Wang and X.-X. Lei, Residual dipolar douplings in structure determination of natural products, Nat. Prod. Bioprospect., 2018, 8(S.I.), 279–295 CrossRef CAS PubMed.
- P. Lesot, P. Berdagué, A. Meddour, A. Kreiter, M. Noll and M. Reggelin, 2H and 13C NMR-based enantiodetection using polyacetylene versus polypeptide aligning media: Versatile and complementary tools for chemists, ChemPlusChem, 2019, 84, 144–153 CrossRef CAS PubMed.
- P. Lesot, C. Aroulanda, P. Berdagué, A. Meddour, D. Merlet, J. Farjon, N. Giraud and O. Lafon, Multinuclear NMR in polypeptide liquid crystals: Three fertile decades of methodological developments and analytical challenges, Prog. Nucl. Magn. Reson. Spectrosc., 2020, 116, 85–154 CrossRef CAS PubMed.
- C. Aroulanda and P. Lesot, Molecular enantiodiscrimination by NMR spectroscopy in chiral oriented systems: Concept, tools and applications, Chirality, 2022, 34, 1–63 CrossRef.
- A. Meddour, D. Atkinson, A. Loewenstein and J. Courtieu, Enantiomeric analysis of homologous series of secondary alcohols by deuterium NMR spectroscopy in a chiral nematic liquid crystal: Influence of molecular geometry on chiral discrimination, Chem. – Eur. J., 1998, 4, 1142–1147 CrossRef CAS.
- J. Courtieu, C. Aroulanda, P. Lesot, A. Meddour and D. Merlet, Evolution of the Saupe order parameters of enantiomers from a non-chiral to a chiral liquid crystal solvent: An original light on the absolute configuration problem, Liq. Cryst., 2010, 7, 903–912 CrossRef.
- P. Lesot, Z. Serhan, C. Aroulanda and I. Billault, Analytical contribution of NAD 2D-NMR spectroscopy in polypeptide mesophases to the investigation of triglycerides, Magn. Reson. Chem., 2012, 50, S2–S12 CrossRef CAS PubMed.
- C. Aroulanda, D. Merlet, J. Courtieu and P. Lesot, NMR experimental evidence of the differentiation of enantiotopic directions in Cs and C2v molecules using partially oriented, chiral media, J. Am. Chem. Soc., 2001, 123, 12059–12066 CrossRef CAS PubMed.
- P. Lesot, C. Aroulanda, H. Zimmermann and Z. Luz, Enantiotopic discrimination in the NMR spectrum of prochiral solutes in chiral liquid crystals, Chem. Soc. Rev., 2015, 44, 230–275 RSC.
- B. Luy, Distinction of enantiomers by NMR spectroscopy using chiral orienting media, J. Indian Inst. Sci., 2010, 90, 119–132 CAS.
- F. Hallwass, S. Schmidt, H. Sun, A. Mazur, A. G. Kummerlöwe, B. Luy, C. Griesinger and U. M. Reinscheid, Residual chemical shift anisotropy (RCSA): A tool for the analysis of the configuration of small molecules, Angew. Chem., Int. Ed., 2011, 50, 9487–9490 CrossRef CAS PubMed.
- N. Nath, M. Schmidt, R. R. Gil, R. T. Willamson, G. E. Martin, A. Navarro-Vazquez, C. Griensinger and Y. Liu, Determination of relative configuration from residual chemical shift anisotropy, J. Am. Chem. Soc., 2016, 138, 9548–9556 CrossRef CAS PubMed.
- N. Nath, J. C. Fuentes-Monteverde, D. Pech-Puch, J. Rodriguez, C. Jimenez, M. Noll, A. Kreiter, M. Reggelin, A. Navarro-Vazquez and C. Griesinger, Relative configuration of micrograms of natural compounds using proton residual chemical shift anisotropy, Nat. Commun., 2020, 11(4372), 9 Search PubMed.
- P. Lesot, Y. Gounelle, D. Merlet, A. Loewenstein and J. Courtieu, Measurement and analysis of the molecular ordering tensors of two enantiomers oriented in a polypeptide liquid crystalline system, J. Phys. Chem. A., 1995, 99, 14871–14875 CrossRef CAS.
- P. Lesot, M. Merlet, J. Courtieu, J. W. Emsley, T. T. Rantala and J. Jokisaari, Calculation of the molecular ordering parameters of (±)-3-butyn-2-ol dissolved in an organic Solution of poly(γ-benzyl-L-glutamate), J. Phys. Chem. A, 1997, 101, 5719–5724 CrossRef CAS.
- C.-M. Thiele, Use of RDCs in rigid organic compounds and some practical considerations concerning alignment media, Concepts Magn. Reson. A., 2007, 30, 65–80 CrossRef.
- G. Kummerlöwe and B. Luy, Residual dipolar couplings as a tool in determining the structure of organic molecules, TrAC, Trends Anal. Chem., 2009, 28, 483–493 CrossRef.
- G. Kummerlöwe and B. Luy, Residual dipolar couplings for the configurational and conformational analysis of organic molecules, in Annu. Rep. NMR Spectrosc., ed. G. A. Webb, 2009, vol. 68, pp. 193–230 Search PubMed.
- B. Böttcher and C.-M. Thiele, Determining the stereochemistry of molecules from residual dipolar couplings (RDCs), in eMagRes, John Wiley & Sons, Ltd, 2012, pp. 169–180 Search PubMed.
- C. Aroulanda, P. Lesot, D. Merlet and J. Courtieu, Structural ambiguities in bridged ring systems resolved using natural abundance deuterium NMR in chiral liquid crystals, J. Phys. Chem. A, 2003, 107, 10911–10918 CrossRef CAS.
- C. Aroulanda, O. Lafon and P. Lesot, Enantiodiscrimination of flexible cyclic solutes using deuterium NMR spectroscopy in polypeptide chiral mesophases: Investigation of cis-decalin and THF, J. Phys. Chem. B, 2009, 113, 10628–10640 CrossRef CAS PubMed.
- J. Sass, F. Cordier, A. Hoffmann, M. Rogowski, A. Cousin, J. G. Omichinski, H. Löwen and S. Grzesiek, Purple membrane induced alignment of biological macromolecules in the magnetic field, J. Am. Chem. Soc., 1999, 121, 2047–2055 CrossRef CAS.
- F. Kramer, M. V. Deshmukh, H. Kessler and S. J. Glaser, Residual dipolar coupling constants: An elementary derivation of key equations, Concepts Magn. Reson., Part A, 2004, 21, 10–21 CrossRef.
- P. Lesot and J. Courtieu, Natural abundance deuterium NMR spectroscopy: Developments and analytical applications in liquids, liquid crystals and solid phase, Prog. Nucl. Magn. Reson. Spectrosc., 2009, 55, 128–159 CrossRef CAS.
- A. Krupp, M. Noll and M. Reggelin, Valine derived poly(acetylenes) as versatile chiral lyotropic liquid crystalline alignment media for RDC-based structure elucidations, Magn. Reson. Chem., 2020, 59, 577–586 CrossRef PubMed.
- J.-P. Bayle, J. Courtieu, E. Gabetty, A. Loewenstein and J.-M. Péchiné, Enantiomeric analysis in a polypeptide lyotropic liquid-crystal through proton decoupled deuterium NMR, New J. Chem., 1992, 16, 837–838 CAS.
- C. Aroulanda, M. Sarfati, J. Courtieu and P. Lesot, Investigation of enantioselectivity of three polypeptide liquid-crystalline solvents using NMR spectroscopy, Enantiomer, 2001, 6, 281–287 CAS.
- G. B. Crull, A. R. Garber, J. W. Kennington, C. M. Prosser, P. W. Stone, J. W. Fant and J. H. Dawson, Carbon-13 NMR spectra of nineteen (1R)-(+)-camphor derivatives, Magn. Reson. Chem., 1986, 24, 737–739 CrossRef CAS.
- C. R. Kaiser, R. Ritter and E. A. Basso, Proton Resonance Spectra and Substituent-induced Chemical Shifts of 3-Halocamphors, Magn. Reson. Chem., 1994, 32, 503–508 CrossRef CAS.
- H. Kovacs, D. Moskau and M. Spraul, Cryogenically cooled probes—A leap in NMR technology, Prog. Nucl. Magn. Reson. Spectrosc., 2005, 46, 131–155 CrossRef CAS.
- N. Marcó, P. Nolis, R. R. Gil and T. Parella, 2JHH-resolved HSQC: exclusive determination of geminal proton-proton, J. Magn. Reson., 2017, 282, 18–26 CrossRef PubMed.
- A. Navarro-Vázquez, P. Berdagué and P. Lesot, Integrated computational protocol for analyzing quadrupolar splittings from natural abundance deuterium NMR spectra in (chiral) oriented media, ChemPhysChem, 2017, 18, 1252–1266 CrossRef PubMed.
- P. Lesot, R. R. Gil, P. Berdagué and A. Navarro-Vázquez, Residual quadrupolar couplings: Crossing the current frontiers in the relative configuration analysis of natural products, J. Nat. Prod., 2000, 83, 3141–3148 CrossRef PubMed.
- A. Navarro-Vázquez, MSpin-RDC. A program for the use of residual dipolar couplings for structure elucidation of small molecules, Magn. Reson. Chem., 2012, 50, S73–S79 CrossRef PubMed.
- S. Immel, M. Köck and M. Reggelin, Configurational analysis by residual dipolar coupling driven floating chirality distance geometry calculations, Chem. – Eur. J., 2018, 24, 13918–13930 CrossRef CAS PubMed.
- The source code (free of charge for academic institutions) of the ConArch+ program can be obtained on website: https://www.chemie.tu-darmstadt.de/reggelin/.
- S. Immel and M. Reggelin, Configurational, analysis by residual dipolar couplings: A critical assessment of diastereomeric differentiabilities, Chirality, 2019, 31, 384–400 CrossRef CAS PubMed.
- M. Köck, M. Reggelin and S. Immel, The advanced floating chirality distance geometry approach—How anisotropic NMR parameters can support the determination of the relative configuration of natural products, Mar. Drugs, 2020, 18, 330–352 CrossRef PubMed.
- M. Reggelin and S. Immel, Configurational analysis by residual dipolar couplings: Critical assessment of “structural noise” from thermal vibrations, Angew. Chem., Int. Ed., 2021, 60, 3412–3416 CrossRef CAS PubMed.
- M. Köck, M. Reggelin and S. Immel, Model-free approach for the configurational analysis of marine natural products, Mar. Drugs, 2021, 19, 283–298 CrossRef PubMed.
- G. Cornilescu and A. Bax, Measurement of proton, nitrogen, and carbonyl chemical shielding anisotropies in a protein dissolved in a dilute liquid-crystalline phase, J. Am. Chem. Soc., 2000, 122, 10143–10154 CrossRef CAS.
- O. Lafon, P. Lesot, D. Merlet and J. Courtieu, Modified z-gradient filtering as a mean to obtain phased deuterium autocorrelation 2D NMR spectra in oriented solvents, J. Magn. Reson., 2004, 171, 135–142 CrossRef CAS PubMed.
- P. Tzvetkova and B. Luy, Q.E.COSY: Determining sign and size of small deuterium residual quadrupolar couplings using an extended E.COSY principle, Magn. Reson. Chem., 2016, 54, 35–357 CrossRef PubMed.
- P. Lesot and O. Lafon, Experimental detection of achiral and chiral naturally abundant 13C-2H isotopomers by 2D-NMR in liquids and chiral oriented solvents, Anal. Chem., 2012, 84, 4569–4573 CrossRef CAS PubMed.
- J. W. Emsley, P. Lesot and D. Merlet, The orientational order and conformational distributions of the two enantiomers in a racemic mixture of a chiral, flexible molecule dissolved in a chiral nematic liquid crystalline solvent, Phys. Chem. Chem. Phys., 2004, 6, 522–530 RSC.
- F. Hallwass, R. R. Teles, E. Hellemann, C. Griesinger, R. R. Gil and A. Navarro-Vázquez, Measurement of residual chemical shift anisotropies in compressed polymethylmethacrylate gels. Automatic compensation of gel isotropic shift contribution, Magn. Reson. Chem., 2018, 56, 321–328 CrossRef CAS PubMed.
- S. Jeziorowski and C.-M. Thiele, Poly-γ-p-biphenylmethyl-glutamate as enantiodifferentiating alignment medium for NMR spectroscopy with temperature-tunable properties, Chem. –Eur. J., 2018, 24, 15631–15637 CrossRef CAS PubMed.
- M. Hirschmann, M. Schwab and C.-M. Thiele, Molecular weights: The key of lyotropic liquid crystalline of poly-β-benzyl-L-aspartate, Macromolecules, 2019, 52, 6025–6034 CrossRef CAS.
- M. Mayer and B. Meyer, Characterization of ligand binding by saturation transfer difference NMR spectroscopy, Angew. Chem., Int. Ed., 1999, 38, 1784–1788 CrossRef CAS PubMed.
- Y. Misumi and T. Masuda, Living polymerization of phenylacetylene by novel rhodium catalysts. Quantitative initiation and introduction of functional groups at the initiating chain end, Macromolecules, 1998, 31, 7572–7573 CrossRef CAS.
- N.-C. Meyer, A. Krupp, V. Schmidts, C.-M. Thiele and M. Reggelin, Polyacetylenes as enantiodifferentiating alignment media, Angew. Chem., Int. Ed., 2012, 51, 8334–8338 CrossRef CAS PubMed.
- N. Nath, N. J. C. Fuentes-Monteverde, D. Pech-Puch, J. Rodriguez, C. Jimenez, M. Noll, A. Kreiter, A. M. Reggelin, A. Navarro-Vazque and C. Griesinger, Relative configuration of micrograms of natural compounds using proton residual chemical shift anisotropy, Nat. Commun., 2020, 11, 4372–4381 CrossRef CAS PubMed.
- A. Krupp, M. Noll and M. Reggelin, Valine derived poly(acetylenes) as versatile chiral lyotropic liquid crystalline alignment media for RDC-based structure elucidations, Magn. Reson. Chem., 2021, 59, 577–586 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Some theoretical reminders and principles; synthesis and multi-technique analysis of the L-MSP polymer; oriented sample preparation; extra isotropic and oriented 2D-NMR spectra; analysis of anisotropic data. See DOI: 10.1039/d1cp04915a |
| This journal is © the Owner Societies 2022 |