Multipole-moment effects in ion–molecule reactions at low temperatures: part II – charge–quadrupole-interaction-induced suppression of the He⁺ + N₂ reaction at collision energies below k_B·10 K

Abstract

We report on an experimental and theoretical investigation of the He⁺ + N₂ reaction at collision energies in the range between 0 and k_B·10 K. The reaction is studied within the orbit of a highly excited Rydberg electron after merging a beam of He Rydberg atoms (He(n), n is the principal quantum number), with a supersonic beam of ground-state N₂ molecules using a surface-electrode Rydberg–Stark decelerator and deflector. The collision energy E_coll is varied by changing the velocity of the He(n) atoms for a fixed velocity of the N₂ beam and the relative yields of the ionic reaction products N⁺ and N₂⁺ are monitored in a time-of-flight mass spectrometer. We observe a reduction of the total reaction-product yield of ∼30% as E_coll is reduced from ≈k_B·10 K to zero. An adiabatic capture model is used to calculate the rotational-state-dependent interaction potentials experienced by the N₂ molecules in the electric field of the He⁺ ion and the corresponding collision-energy-dependent capture rate coefficients. The total collision-energy-dependent capture rate coefficient is then determined by summing over the contributions of the N₂ rotational states populated at the 7.0 K rotational temperature of the supersonic beam. The measured and calculated rate coefficients are in good agreement, which enables us to attribute the observed reduction of the reaction rate at low collision energies to the negative quadrupole moment, Q_zz, of the N₂ molecules. The effect of the sign of the quadrupole moment is illustrated by calculations of the rotational-state-dependent capture rate coefficients for ion–molecule reactions involving N₂ (negative Q_zz value) and H₂ (positive Q_zz value) for |J, M〉 rotational states with J ≤ 5 (M is the quantum number associated with the projection of the rotational angular momentum vector J⃑ on the collision axis). With decreasing value of |M|, J⃑ gradually aligns perpendicularly to the collision axis, leading to increasingly repulsive (attractive) interaction potentials for diatomic molecules with positive (negative) Q_zz values and to reaction rate coefficients that decrease (increase) with decreasing collision energies.

---

1 Introduction

Experimental studies of ion–molecule reactions at low temperatures and low-collision energies are difficult because ions are easily heated up by stray electric fields and space-charge effects. Experiments combining cold ions in ion-traps and Coulomb crystals with cold molecules in slow beams are promising approaches to reach very low temperatures and collision energies in studies of ion–molecule reactions^1–3 but have not yet been broadly applied. Measurements of reaction rates down to ≈10 K are possible in ion guides and traps^4–7 and in uniform supersonic flows^8–10 but hardly any measurements have been performed below 10 K. It is, however, below 10 K that the effects of the electrostatic interactions between the charge of the ion and the multipole moments of the molecule become dominant and are expected to strongly affect the reaction rates.^11–16

This article is the second in a series of three articles exploring the effects of molecular electric multipole moments on the rates of ion–molecule reactions at low energies. The first and third articles in this series present studies of the reactions of He⁺ with ammonia (NH₃ and ND₃)¹⁷ (referred to as Article I below) and methane (CH₄ and CD₄)¹⁸ and focus on the role of the interaction between the charge of the ion and the electric dipole and octupole moments of the neutral molecule, respectively. In the present article, the effect of the charge–quadrupole interaction is investigated with the example of the He⁺ + N₂ reaction, for which we have measured the collision-energy dependence of the reaction rate coefficient in the range of collision energies between 0 and k_B·10 K at a resolution of about k_B·250 mK near E_coll = 0.

These reactions are all fast and strongly exothermic.^19,20 Consequently, their rates can be described by capture theories.^{11,12,21–25} At high temperatures (beyond 300 K) and collision energies, the capture rates can be approximated by the Langevin rate constant (in SI units)

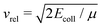where σ is the reaction cross-section, is the asymptotic relative velocity, α′ is the polarisability volume of the neutral molecule, Ze is the charge of the ion, μ is the reduced mass of the reactants and ε₀ is the permittivity of vacuum.

The effect of the electric dipole moment of the neutral molecule on ion–molecule reactions is to increase the capture rates compared to the Langevin rates at low collision energies or temperatures.^8,10,17,26 The rate enhancements predicted theoretically depend strongly on the degree of sophistication of the treatment of the orientation of the molecular permanent dipole moment during the collision.²² Calculations assuming full orientation are the simplest but greatly overestimate the rate enhancements at low temperatures or collision energies. The explicit consideration of the rotational-state-dependent orientation of the molecules in the field of the ion via the Stark effect in the realm of adiabatic capture models^{11–14,26–29} typically leads to much less pronounced enhancements, except at the lowest collision energies or temperatures (typically below 1 K)^17,26 and for rotational states that are subject to a linear negative Stark shift at low fields.¹⁷ It is only very recently that the first experimental studies of the rates of reactions between ions and polar molecules have been reported at collision energies below ≈k_B·10 K, revealing the details of the rotational-state-specific rate enhancements at low collision energies for the reactions of He⁺ with CH₃F,²⁶ NH₃ and ND₃.¹⁷

The Stark effect does not only shift the rotational level energies of polar molecules but also affects the energy levels of nonpolar molecules via charge–induced-dipole, charge–quadrupole and charge–octupole interactions. The charge–induced-dipole interaction leads to an attractive long-range interaction potential scaling with the separation R between the ion and the polarisable molecule as R⁻⁴. The effect of this interaction is included in the Langevin model and leads to the well-known expression for the rate constant given by eqn (1). The effect of the charge–quadrupole interaction is insensitive to the orientation of the neutral molecule but depends on the alignment of its angular momentum vector along the collision axis, as demonstrated by Dashevskaya et al.^15,16

In Article I, we have presented a general formalism, based on the earlier theoretical treatments of capture reactions by Clary and coworkers^11,24,27 and Troe and coworkers,^{12,15,16,25,30,31} to calculate collision-energy- and temperature-dependent capture rate coefficients for reactions between ions and neutral molecules with permanent dipole, quadrupole, octupole, etc. moments, in terms of the multipole coefficients Q_λ characterising the molecular charge distribution. In the present work, we apply this formalism to the charge–quadrupole interaction (λ = 2) between ions and diatomic molecules to interpret the reduction of the rate of the He⁺ + N₂ reaction observed at low collision energies. The electric quadrupole moment of N₂ can be described by a traceless, diagonal rank-2 tensor with elements Q_zz = −2Q_xx = −2Q_yy, and a negative value of Q_zz (= −1.394 D Å).³² We present calculations of rotational-state-dependent rate coefficients k_JM(E_coll) for the low-lying |JM〉 rotational states of N₂ with J ≤ 5 and highlight their dependence on the magnetic quantum number M, which is the projection of the total angular momentum of the molecule, , onto the quantisation axis defined by the electric field of the ion, i.e., the collision axis. These calculations demonstrate that the observed reduction of the product-ion yield at low collision energies originates from the negative Q_zz value of N₂. In order to illustrate the effect of the sign of Q_zz on the rotational-state-specific k_JM(E_coll) rate coefficients, we also present calculations for ion–molecule capture reaction involving H₂, which has a positive quadrupole moment = +0.638 D Å,¹⁶ and for which an overall increase of the rate constant was predicted^15,16 and observed^33,34 at E_coll ≤ k_B·1 K. Our results are consistent with previous theoretical calculations of the dependence of the capture rate coefficients of the reactions between ions and homonuclear diatomic molecules on the sign of the qQ_zz product (q is the ionic charge).^15,16,30,31

The He⁺ + N₂ reaction is an example of a charge-transfer reaction and is one of the most studied ion–molecule reactions.^9,20,35–43 It is known to proceed by a near-resonance pathway⁴⁴ involving the v = 3 and 4 vibrational levels of the C ²Σ_u⁺ state of N₂⁺ and vibrationally excited levels of other electronic states.⁴² The reaction plays an important role in astrochemistry and in the atmospheric chemistry of the Earth^45,46 and Titan.⁴⁷ Molecular nitrogen is relatively abundant in dense interstellar clouds, with fractional abundances with respect to H₂ estimated to be in the (4–6) × 10⁻⁶ range.⁴⁸ In dense interstellar clouds, the He⁺ + N₂ reaction is responsible for the liberation of N⁺, which is involved in the synthesis of NH₃.⁴⁹ The reaction has been studied experimentally in the 1960s and 1970s at room temperature and above using a broad range of experimental techniques – e.g., flowing-afterglow (FA),^36–38 drift-tube (DT),⁵⁰ ion-cyclotron-resonance (ICR),^51–53 selected ion flow-drift tube (SIFT),⁴¹ slow flow drift tube (SFDT),⁵⁴ and photoionisation mass spectrometry (PI-MS).³⁵ The He⁺ + N₂ reaction has two product channels,

He⁺ + N₂ → He + N + N⁺ (2)

→ He + N₂⁺, (3)

producing N⁺ and N atoms by dissociative charge transfer [reaction (2)] and N₂⁺ ions by charge transfer [reaction (3)]. In the 1980s, the reaction was studied at temperatures as low as ∼8 K in a uniform supersonic flow (CRESU) apparatus.^9,10 By making the range of temperatures below 10 K accessible to the investigations of ion–molecule reactions, these CRESU studies represented a breakthrough. They have remained unsurpassed until the present work and terminated a period of intense experimental research activity.

Representative results on these reactions obtained in this early period are summarised in Table 1. The total reaction rate constant was measured to be in the (1.0–1.6) × 10⁻¹⁵ m³ s⁻¹ range,²⁰ slightly lower than the Langevin rate of 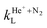= 1.637 × 10⁻¹⁵ m³ s⁻¹. Overall, these measurements did not reveal any significant dependence on the temperature or collision energy, as expected for a fast, Langevin-type reaction. In particular, no effects resulting from the charge–quadrupole interaction were detected nor discussed. The N⁺ : N₂⁺ product-ion branching ratio was determined to be 0.60^[±11%] : 0.40^[±11%], with a slight but consistent bias favouring the N⁺ product ion and substantial differences between individual measurements.

Table 1 Previous results on the He⁺ + N₂ reaction obtained with different experimental methods. See ref. 20 for a summary of all results prior to 1986

Exp. method	N^+ : N2^+ product ratio	k (m^3 s^−1)	T (K)
SIFT^41	0.6 : 0.4	1.6(3) × 10^−15	300
FA^55	0.6 : 0.4	1.2(4) × 10^−15	300
FA^37	0.7 : 0.3	1.2(4) × 10^−15	300–600
DT^50	0.55 : 0.45	1.0(3) × 10^−15	300–1200
ICR^51,52	0.66 : 0.34	1.20(10) × 10^−15	300
PI-MS^35	0.52 : 0.48	1.5 × 10^−15	300
CRESU^9		1.25 × 10^−15	300
CRESU^9		1.3 × 10^−15	28
CRESU^9		1.3 × 10^−15	20
CRESU^9		1.2 × 10^−15	8
This work	0.50 : 0.50	(0.9–1.2) × 10^−15	0–12

---

The differences in the observed N⁺:N₂⁺ product ratios are not fully understood yet. Fluorescence studies of the He⁺ + N₂ reaction system^39,43 have demonstrated that the B, C and other electronic states of N₂⁺ are populated by charge transfer. Charge transfer to the D′ state was estimated to be 30% of that to the C state.⁴³ Luminescence measurements in an ICR apparatus have demonstrated that charge transfer to the B state represents only ∼2% of the near-resonant charge transfer to the C state.⁴² Measurements of the product ratios of the He⁺ + ¹⁵N₂ reaction at thermal energies have revealed strong isotopic effects.^40,56

The complex decay dynamics of N₂⁺ molecules excited in the energy region of the C state by charge-transfer reactions or photoexcitation has been recently discussed by Ayari et al., who have determined the radiative and predissociation lifetimes of the vibrational levels of the C state on the basis of a full set of potential energy curves obtained in high-level ab initio calculations.⁵⁷ The potential energy curves for the ground state of N₂ and of the ground and several electronically excited states of N₂⁺, reproduced from ref. 57, are presented in Fig. 1. The ionisation energy of He [E_I(He) = 24.58738881(3) eV or 198310.66632(20) cm⁻¹],⁵⁸ marked by a horizontal red line, lies above the first, N (⁴S_3/2) + N⁺ (³P₀), dissociative ionisation limit of N₂ [L1 = 24.2883(10) eV or 195 899(8) cm⁻¹, obtained by adding the adiabatic ionisation energy of N₂⁵⁹ and the dissociation energy of N₂⁺];⁶⁰ see short horizontal black line in the inset. Any rovibronic state of N₂⁺ with an energy below E_I(He) can be produced by charge transfer from He⁺ in combination with the emission of He and N₂⁺ products of the corresponding kinetic energy. E_I(He) lies 5.6 meV and 250.3 meV above the C ²Σ_u⁺(v = 4 and 3) ionisation thresholds⁶¹ of N₂, respectively. These states are also located above the dissociative-ionisation threshold of N₂ and can further predissociate in N (⁴S_3/2) and N⁺ (³P_J) fragments.³⁹

The N⁺ product ions formed in the He⁺ + N₂ reaction are attributed to charge transfer to the predissociative v = 3 and 4 levels of the C state of N₂⁺, whereas the N₂⁺ ions result from charge transfer to longer-lived excited states of N₂⁺. These states are either metastable and survive until the N₂⁺ ions are detected or decay radiatively to low-lying rovibronic states of N₂⁺ located energetically below the N⁺ + N dissociation threshold. The predissociation of the C ²Σ_u⁺(v = 3, 4) states most likely takes place through interactions with the 1 ⁴Π_u state.^39,57,63,64 The radiative and predissociation lifetimes of the first seven vibrational states of the C ²Σ_u⁺ have been measured in ref. 65. The predissociation lifetimes of the v = 3 and 4 levels were found to be 4.2 ± 0.2 and 5.3 ± 0.3 ns, respectively. The radiative decay to the X ²Σ_g⁺(v′′) state is governed by Franck–Condon factors, which favour Δv = v − v′′ = −6 transitions.⁶⁶ The radiative lifetimes were measured to be τ^{rad,(C,v= 1,2)} ≈ 78 ns,⁶⁵ and determined theoretically by Ayari et al.⁵⁷ to be about 60 ns for the C (v = 0–2) states. From these results, we conclude that charge transfer to the C (v = 0–2) states exclusively leads to the formation of N₂⁺ and that the branching ratios for the formation of N₂⁺ (η_N2⁺ = I(N₂⁺)/[I(N₂⁺) + I(N⁺)]) decrease to about 34% for the C (v = 3) level and to about 1% for the C (v = 4) level. The branching ratios for other states of N₂⁺ produced by charge transfer from He⁺ are not known, nor is the exact nature of these states.

The bias in favour of the N⁺ product ions in previous FA, SIFT, and IRC measurements (Table 1), has been attributed to collision-induced dissociation of the metastable N₂⁺ reaction products.⁴² This collisional dissociation results from the relatively high pressures of the background He and N₂ gas in these experiments (e.g., 0.5–1 torr in the FA and SIFT experiments) and the long reaction-observation times in the ms-range. This interpretation was supported by studies of the pressure dependence of the N⁺/N₂⁺ product ratio in ICR experiments,^42,44,53,56 which demonstrated that the N⁺ product yield increases with increasing pressure and that the lowest N⁺/N₂⁺ ratio (∼1.13, i.e., 0.53 : 0.47) is observed at the lowest pressure of ∼0.2 × 10⁻⁴ torr. Our experiments are carried out at low gas densities and under conditions where no secondary collisions are observed and therefore offer the possibility of establishing the low-temperature, low-pressure limit of the product branching ratios.

Table 2 Properties of the N₂ and H₂ molecules required to model the capture rate coefficients of the He⁺ + N₂ and D₂⁺ + H₂ reactions, taken from ref. 31 and 73

	B 0 (cm^−1)	Q zz (D Å)	Δα′ (a0^3)	α′ (a0^3)	μ (u)	k L (m^3 s^−1)
He^+ + N2	1.990	−1.036	4.697	11.54	3.502	1.637 × 10^−15
D2^+ + H2	59.3398	0.474	2.120	5.437	1.341	1.816 × 10^−15

---

2 Experimental procedure

The experimental setup and procedure have been described in detail in Article I¹⁷ and we present here only the aspects that are specific to the study of the He⁺ + N₂ reaction. Two short-pulse home-built valves (pulse duration ∼20 μs) are used to produce supersonic beams of He and N₂. The N₂ valve is heated to 330 ± 1 K, resulting in a mean forward velocity of 880 m s⁻¹ and a rotational temperature of less than 10 K for the N₂ sample. The helium valve is vertically displaced from the N₂ valve and tilted at a 5° angle with respect to the vertical. A pulsed electric discharge at the He valve opening is used to populate the (1s)(2s) ³S₁ state of helium (referred to as He* below). After passing through two skimmers, the He* beam is excited in the presence of an electric field to the (n, k, m) = (30, 21, 0) low-field-seeking Rydberg–Stark state. The Rydberg-helium [He(n)] beam is then deflected using a curved 50-electrode surface Rydberg–Stark decelerator^26,67 and merged with the N₂ beam. The He valve was cooled and temperature stabilised to 66.0 ± 0.1 K, resulting in an initial mean forward velocity of the beam of 860 m s⁻¹. By applying the appropriate potentials to the deflector electrodes, the velocity of the Rydberg He beam can be set to any value in the range 720–1100 m s⁻¹ and a relative-velocity distribution corresponding to a temperature of 250 mK.

The distribution of the N₂ molecules in the supersonic beam over the rotational levels of the X ²Σ_g⁺(v = 0) ground state was measured by monitoring the yield of N₂⁺ ions generated by (2 + 1) resonance-enhanced-ionisation spectroscopy of the a′′ ¹Σ_g⁺ (v′ = 0, J′)–X(v = 0, J′′) transition of N₂, following the procedure described in ref. 68. The distribution was found to be well described by a rotational temperature of 7.0 ± 1.0 K (see further discussion in Section 5.1 and inset of Fig. 3(b) below).

After the He(n) and the N₂ beams are merged, they enter a reaction zone inside a time-of-flight mass spectrometer (TOFMS) where the reaction product ions are extracted by a pulsed electric field and accelerated towards a microchannel-plate (MCP) detector (see Fig. 1 of Article I for details). The duration of the reaction-observation window is set to be Δt_r = 7 μs using a sequence of two electric-field pulses separated by Δt_r. The first pulse of the sequence serves the purpose of sweeping out all ions produced before the reaction-observation window. The second pulse extracts the ions generated during the temporal observation window. The electric-field strength of the pulses is not high enough to field ionise the initially prepared He(n) atoms. Nevertheless He⁺ ions are detected because some of the initially populated Rydberg states undergo transitions to higher-lying Rydberg states that can be field ionised, as discussed in more detail in ref. 69.

Fig. 1 Potential-energy curves for the X ¹Σ_g⁺ ground state of N₂ from ref. 62, and for selected low-lying electronic states of N₂⁺ (taken with permission from ref. 57). Also shown are the ionisation energy of He (E_I(He)) and N₂ (E_I(N₂)), the first dissociation limit (L1) of N₂⁺, and the relevant vibrational levels in the C ²Σ_u⁺ state of N₂⁺. See text for details.

Typical ion time-of-flight mass spectra used to determine the N⁺ and N₂⁺ product yields are presented in Fig. 2. They were obtained by averaging over 500 experimental cycles after setting the Rydberg helium velocity to v_Ryd = 1040 m s⁻¹. When the He(n)-Rydberg-excitation laser is turned on (black trace), a strong He⁺ signal is observed at ∼1.6 μs, followed by an almost constant background signal originating from the slow ionisation of the He(n) molecules by blackbody radiation and tunnel ionisation. In addition, two peaks, corresponding to the N⁺ and N₂⁺ product ions are clearly distinguishable at 2.84 μs and 3.98 μs, respectively. Small amounts of OH⁺ and H₂O⁺ ions produced by Penning-ionisation reactions between He* and H₂O are also detected. The kinetic energy of the N⁺ and N₂⁺ molecules generated by the reactions are sufficiently low (see inset of Fig. 1) so that hardly any product ions leave the ion-extraction volume during the reaction-observation window.

Fig. 2 Ion-time-of-flight mass spectra used to determine the yield of N⁺ and N₂⁺ products of the He⁺ + N₂ reaction. Black trace: Spectrum obtained following reactions of the He⁺ ion core of He(n) Rydberg states with N₂ molecules in the merged beams at a collision energy of k_B·5.4 K after a reaction time Δt_r of 7 μs. Blue trace: Spectrum consisting of the background signal generated from reactions of metastable He atoms and H₂O and N₂ molecules in the vacuum chamber. The areas shaded in pale green indicate the regions over which the N⁺ and N₂⁺ products were integrated. See text for details.

When the Rydberg-excitation laser is not turned on (blue trace), the N⁺ and N₂⁺ product ions are suppressed, indicating that they are produced by the He⁺ + N₂ reaction. The He(n) ionisation background signal also disappears but the OH⁺ and H₂O⁺ ion signals remain. This observation proves that these ions are produced from Penning-ionisation reactions of He* with background water in the vacuum chamber.

To determine the relative yields of the N⁺ and N₂⁺ product ions, we integrate the TOF spectra over the corresponding TOF ranges, indicated by the areas shaded in pale green in Fig. 2. The integration is performed after subtraction of the background signals from Penning-ionisation processes and from the slow ionisation of He(n) Rydberg atoms by blackbody-radiation and tunnel ionisation. The collision-energy dependence of the rate coefficients is then obtained by monitoring the total product-ion yield as a function of the velocity v_Ryd of the He(n) beam. By varying v_Ryd between 720 m s⁻¹ and 1100 m s⁻¹ for a fixed value of the N₂-beam velocity, we probe the collision-energy range between 0 and ∼k_B·10 K.

The experiments are carried out under conditions where the density of N₂ molecules by far exceeds that of the He(n) atoms, so that the product formation follows pseudo-first-order kinetics. Only a very small fraction (typically ≃1%) of the He(n) reacts to form product ions during the 7 μs-long reaction observation-window. Consequently, the product-ion signals directly reflect the relative rate coefficients.

3 Experimental results

3.1 Branching ratios

The relative strength of the N⁺ and N₂⁺ ion signals [I(N⁺) and I(N₂⁺)] is determined by integrating the ion signals in time-of-flight mass spectra such as those displayed in Fig. 2 over the corresponding time-of-flight ranges. The ratio of product-ion signal I(N⁺)/I(N₂⁺) was determined to be 1.00(10) and was found not to depend on the collision energy in the range below k_B·10 K. The observed I(N⁺)/I(N₂⁺) ratio of 1.00(10) corresponds to a branching ratio of 0.50(5) for the two product channels (eqn (2) and (3)). This value is lower than the I(N⁺)/I(N₂⁺) ratio of about 1.5 observed in most earlier studies (see Table 1). In these studies, the reactions were observed under conditions where part of the N⁺ yield resulted from the dissociation of metastable N₂⁺ product ions caused by secondary collisions with N₂ molecules and He atoms in the background gas, as discussed in, e.g., ref. 39, 42, 53 and 56.

These observations indicate that, at low collision energies, about half of the N₂⁺ ions generated in the reaction between He⁺ and N₂ predissociates on a timescale shorter than 1 μs and that the remaining half is formed in longer-lived N₂⁺ states, either in metastable states or in states that radiatively decay to states located below the lowest dissociation threshold of N₂⁺. Two recent studies have examined the predissociation of the different vibrational levels of the C state of N₂⁺.^57,70 As explained in the introduction, only v ≤ 4 levels of the C state can be produced at low collision energies and, of these levels, only the v = 3 and 4 levels are located above the lowest dissociation limit of N₂⁺ (see inset of Fig. 1). The predissociation lifetimes of the v = 3 and 4 levels were reported to be 28.7 ns (7.19 ns) and 0.585 ns (2.46 ns) in ref. 57 (ref. 70), respectively. In ref. 57, the radiative lifetime of these levels were reported to be 56.04 and 55.03 ns, respectively. Consequently, 99%, 66% and 0% of the N₂⁺ ions initially generated in the C-state v = 4, 3 and ≤2 levels, respectively, should be detected as N⁺ ions in our experiment and, correspondingly, 1%, 34% and 100% should be detected as N₂⁺ ions. The fraction of the reactions that initially lead to N₂⁺ ions in the C state is not known. Assuming that the almost resonant charge transfer to the C (v = 4) level dominates over the charge transfer to the C (v ≠ 4) levels and that it is the main source of N⁺ ions would lead to the conclusion that about 50% of the charge-transfer processes populate rovibrational levels of other electronic states of N₂⁺ that do not predissociate within 1 μs, either because their predissociation lifetimes are longer than 1 μs or because they are longer than their radiative lifetimes.

3.2 Collision-energy dependence of the reaction rate coefficient

Fig. 3(a) displays the sum of the integrated N⁺ and N₂⁺ ion signals (green circles) measured for different mean velocities (v_Ryd) of the Rydberg helium beam in the 720–1100 m s⁻¹ range. The error bars are obtained from the statistical analysis of 5 consecutive measurements, each consisting of an average of 500 experimental cycles. The integration windows used to monitor the product ions are indicated in green in Fig. 2. The velocity spread around the mean velocity of the N₂ beam (v_N2) in the reaction zone is Δv_N2 ≃ ±10 m s⁻¹. The opening of the valve generating the N₂ supersonic beam was adjusted for each experimentally selected value of v_Ryd to ensure that the Rydberg atoms always interact with N₂ molecules of the same velocity class. The product-ion signals were corrected for (i) the change of He(n) density resulting from the higher acceleration or deceleration from the initial beam velocity, and (ii) the changing overlap between the packet of He(n) Rydberg atoms and the N₂ beam, as discussed in Article I. The data presented in Fig. 3(a) reveal that the product-ion signal gradually decreases as v_Ryd approaches the velocity v_N2 of the N₂ beam, which is indicated by the dash-dotted vertical line. The signal reduction is symmetric with respect to v_N2 within the error bars.

Fig. 3 (a) Sum of the integrated N⁺ and N₂⁺ reaction product ion signals of the He⁺ + N₂ reaction (green dots with error bars), for a range of velocities v_Ryd of the He(n) Rydberg-atom beam obtained for a Δt_r = 7 μs-long reaction-observation window. (b) Sum of the integrated N⁺ and N₂⁺ product-ion signals (green dots) measured as a function of the collision energy. The horizontal error bars indicate the range of collision energies probed experimentally at each selected value of E_coll. The purple circles represent the weighted sum of the calculated rotational-state-specific reaction rate coefficients for a rotational temperature T_rot = 7.0 K of the N₂ sample. The solid black curve corresponds to a convolution of the calculated rate coefficient with a Gaussian line-shape function describing the experimental collision-energy resolution. The dashed black horizontal line gives the value of the Langevin rate coefficient k_L. The inset gives the occupation probabilities of the N₂ rotational levels at 7.0 K. See text for details.

The sum of the N⁺ and N₂⁺ product-ion signals, I = I(N⁺) + I(N₂⁺), after correction for the detection bias favouring product yields measured at higher He(n)-beam velocities, is depicted as a function of the collision energy as full green circles in Fig. 3(b). The vertical error bars represent one standard deviation of the five measurements performed at each relative velocity and the horizontal bars correspond to the range of collision energies probed in each case according to eqn (4):

which describes the collision-energy resolution of the experiments for ΔE_res = k_B·250 mK.²⁶ The purple dots in Fig. 3(b) are weighted sums of the calculated rotational-state-dependent capture rate coefficients for a rotational temperature T_rot of 7.0 K. The inset in Fig. 3(b) displays the rotational population distribution of the N₂ molecules at this temperature (7.0 K) which reflects the 2 : 1 ortho-to-para ratio of the nuclear-spin-statistical factors, i.e., 2/3 of the N₂ molecules are in states with J = 0, 2, 4… (ortho N₂) and 1/3 are in states with J = 1, 3, 5… (para N₂).

The data presented in Fig. 3 indicate that the reaction rate coefficient decreases by 30% as the collision energy E_coll decreases from k_B·10 K to zero. The opposite behaviour, i.e., an enhancement of the reaction rate coefficient with decreasing collision energy, was observed in the charge–quadrupole capture reaction of H₂⁺ with H₂ forming H₃⁺ and H.^33,71 This difference can be explained by the different sign of the quadrupole tensor element Q_zz of N₂ and H₂, as explained in the next section.

4 The charge–quadrupole interaction and the effect of the sign of the Q_zz quadrupole tensor element on the rotational-state-specific capture rate coefficients

The calculations presented in this section follow an adiabatic channel model initially formulated in ref. 11 and 12 for the description of the ion–molecule capture. They disregard the effects of quantum-Langevin scattering near zero collision energy⁷² and of the Coriolis coupling of adiabatic reaction channels involving rotational states of the neutral molecule of different M values, where M is the quantum number associated with the projection of the rotational angular momentum J⃑ of the neutral molecule onto the collision axis. These effects were shown to be significant only at very low collision energies (below k_B·10 mK) in ref. 15 and 16 and are expected to be negligible at the energy resolution of k_B·250 mK of the experiments presented in the previous section.

In the absence of a permanent dipole moment of the neutral molecule, the lowest member of the multipole-moment interaction series between an ion and a neutral molecule is the charge–quadrupole interaction. The simplest molecules without a permanent dipole moment but with a quadrupole moment are homonuclear diatomic molecules (we consider here H₂ and ¹⁴N₂). The quadrupole moment tensor, Q, with elements Q_ij∈{x,y,z}, describes a distribution of partial charges in the molecular centre-of-mass reference frame. It is a rank-two tensor, usually written as a traceless matrix with only diagonal elements (Q_xx, Q_yy and Q_zz). For symmetric-top and linear molecules, Q_xx = Q_yy, and the Q_zz component of the quadrupole-moment tensor is sufficient to describe the quadrupolar charge distribution.

Classically, the interaction between an ion of charge q and a homonuclear neutral molecule with Q_zz component of the quadrupole tensor in the molecular reference frame, can be written as:^15,31

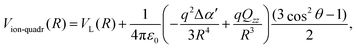where and θ is the angle between the collision axis and the internuclear axis of the diatomic molecule (see Fig. 5 below). The Langevin interaction potential, V_L(R), is given by:where and μ are the magnitude of the orbital angular momentum and the reduced mass of the collision, respectively. The second term in eqn (6) is the isotropic component of the charge–induced-dipole interaction, which scales as ∝R⁻⁴ and depends on the average polarisability volume of the molecule, . The second and third terms in eqn (5) describe the anisotropic components of the interaction between the ion and the molecule as a function of the angle θ. The second term in eqn (5) describes the contribution to the charge–induced-dipole interaction of the polarisability anisotropy , and the third term describes the electrostatic interaction between the charge of the ion and the quadrupolar charge distribution of the molecule, which is proportional to qQ_zz/R³. The values of the relevant physical quantities in the ground electronic state of N₂ and H₂ from ref. 31 and 73 are listed in Table 2.

The quadrupole moment leads to Stark shifts of the molecular rotational level energies in the electric field of the ion. These Stark shifts can be calculated with perturbation theory in the realm of the perturbed-rotor approximation (see, e.g., ref. 15, 30 and 31). Alternatively, one can obtain the exact value of the Stark shifts ΔE_JM(R) of the rotational levels |JM〉 by diagonalizing the Hamiltonian:

Ĥ(R) = Ĥ_rot + Ĥ_Stark(R), (7)

for a range of values of the ion–molecule separation R. The rotational Hamiltonian Ĥ_rot of N₂ and H₂ in their ground vibronic state is a diagonal matrix with matrix elements corresponding to the zero-field rotational energies, hcB₀J(J + 1), where B₀ is the rotational constant of the vibrational ground state in cm⁻¹. For diatomic molecules in electronic states of Σ symmetry, the Stark effect can be described in the |JM〉 rigid-rotor wavefunction basis. In this basis, the Stark Hamiltonian has matrix elements given by:The ion–quadrupole interaction mixes rotational states according to the selection rule ΔJ = 0, ±1, ±2 (0 ↛ 0, 1) and ΔM = 0. States with J = 0 have no quadrupole moment to first order, but acquire one through mixing with the J = 2 states.¹⁵ The strength of this mixing decreases with increasing value of rotational constant B₀.^15,30

We consider the total charge–quadrupole interaction potential for a molecule in a state which correlates adiabatically to the |JM〉 state in zero electric field as:^12,24

V^(JM)_int(R) = V_L(R) + ΔE_JM(R). (9)

This interaction potential can then be used to calculate the collision-energy-dependent rate coefficients, k_JM(E_coll), as described in Article I.¹⁷

The calculated interaction potentials between He⁺ and N₂ molecules in rotational states with J ≤ 5 are presented in Fig. 4. They were obtained by diagonalizing the Hamiltonian in eqn (7) in a basis with J ≤ 16 for values of the ion–molecule separation R in the 0.1–60 Å range, in steps of 0.05 Å, and using the data presented in Table 2. The black and coloured lines in Fig. 3 represent the Langevin interaction potential V_L and the rotational-state-specific interaction potential V^(JM)_int(R) for the He⁺ + N₂ reaction, respectively. In each case the full and dashed lines represent the potential obtained for [small script l] = 0 and 11, respectively. The charge–quadrupole interaction significantly modifies the interaction potentials associated with all |J, M〉 states and the effect becomes stronger with increasing J value. The interaction potential for the |0, 0〉 state is slightly more attractive than V_L because of the field-induced mixing with the |2, 0〉 level. Consequently, the [small script l] = 11 centrifugal energy barrier (V^{[small script l]=11,max}_L) in the interaction potential is lowered from k_B·1.46 K for a pure Langevin potential to k_B·1.01 K. For J ≥ 1, the effect of the charge–quadrupole interaction depends on the value of M. The interaction potentials V^(J,M=0)_int(R) for M = 0 are more attractive than both V_L and V^(0,0)_int(R) [see Fig. 4(g)] and the effect is strongest for J = 1 and decreases with increasing J value.

Fig. 4 Comparison of the calculated interaction potentials between He⁺ and N₂(J, M) for J ≤ 5 (coloured lines, as indicated in the different panels) with the Langevin potential (black lines). The potentials for [small script l] = 0 and 11 are indicated by full and dashed lines, respectively. Panels (a)–(f) present the results for |J, M〉 states with J ranging from 0 (a) to 5 (f). Panels (g) and (h) compare the potentials of the M = 0 and |M| = J states, respectively.

In contrast, the interaction potentials of the states with the maximum value of |M| (i.e., |M| = J) are more repulsive than V_L, even for [small script l] = 0 head-on collisions, resulting in a potential energy barrier with maxima highlighted by the short coloured horizontal bars in Fig. 4(b–f). The heights of the potential energy barriers increase with the value of J, from V^(1,1), max_int/k_B = 0.250 K for the |1, 1〉 state to V^(5,5), max_int/k_B = 4.894 K for the |5, 5〉 state [see Fig. 4(h)]. For molecules in these states, the reaction is suppressed for collision energies E_coll < V^{(J,|M|=J),max}_int. For states with M values between these two limiting situations (0 < |M| < J), the interaction potentials V^(J,M)_int(R) are in general more attractive than V_L but less attractive than V^(J,0)_int(R).

The results obtained for the V^(J,M)_int(R) interaction potentials in the case of the He⁺ + N₂ reaction and displayed in Fig. 4 can be qualitatively understood in terms of electrostatic arguments based on an angular-momentum vector model of the rotation of the diatomic molecule (see Fig. 5). In homonuclear diatomic molecules, a positive (negative) value of the Q_zz quadrupole tensor element corresponds to a partial-charge distribution with a partial charge of −2|δ| (+2|δ|) near the molecular centre of mass, and equal, positive (negative) partial charges of + |δ| (−|δ|) near the two ends of the molecule. The negative Q_zz value of N₂ arises from the excess negative charges from the electron lone pairs on the N atoms. In H₂, Q_zz is positive because the excess negative charge is located near the molecule geometric centre, where the electron density from the sigma bond is maximal.

Fig. 5 Schematic charge–quadrupole interaction between He⁺ and N₂ in |JM〉 rotational states with M = J (a) and M = 0 (b).

In the angular-momentum vector model (see, e.g., Section 1.4 of the book by Zare⁷⁴), the rotational angular-momentum vector J⃑ of the diatomic molecule precesses around the quantisation axis (which is the collision axis) at an angle given by . The internuclear axis of a diatomic molecule lies in a plane perpendicular to J⃑. In M = J states, α is minimal and J⃑ points along the collision axis. Consequently, the molecular rotation takes place in a plane perpendicular to the collision axis, so that the N₂ molecule approaches the ion in a “helicoptering” motion [see Fig. 5(a)]. This configuration exposes the region of positive charge to the He⁺ ion so that the electrostatic interaction is overall repulsive, which explains the increase in the height of the potential barrier compared to the pure Langevin potential. In M = 0 states, J⃑ points in a direction perpendicular to the collision axis, so that the N₂ rotational motion can be described as a “cartwheeling” motion in the collision plane [see Fig. 5(b)]. In this configuration, the regions of excess negative charges are exposed to the He⁺ ion and the electrostatic interaction is attractive.

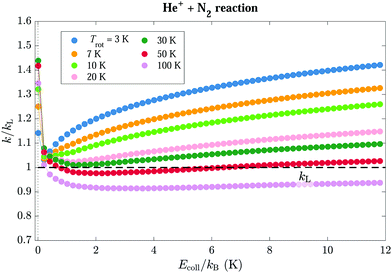
The rotational-state-specific modifications of the interaction potentials caused by the charge–quadrupole interaction has a significant effect on the capture rate coefficients. The state-specific capture rate coefficients for the He⁺ + N₂(J, M) reaction for rotational levels with J ≤ 5 are displayed in colour in Fig. 6(a)–(f) after normalisation to the Langevin rate constant k_L represented by the horizontal black lines. The calculations of capture rate coefficients were performed for collision energies in the k_B·(0.01–12.01) K range, in steps of 0.2 K, following the procedure described in Article I.¹⁷

Fig. 6 Calculated rotational-state-dependent reaction rate coefficients for the reaction between He⁺ and N₂. Panels (a)–(f) present the results for |J, M〉 states with J ranging from 0 (a) to 5 (f). Panels (g) and (h) compare the rate coefficients of the M = 0 and |M| = J states, respectively. Panel (i) gives the rate coefficients averaged over all M values for J = 0–2.

The rotational states can be classified in four types according to the dependence of the capture rate coefficients on the collision energy. (i) The first group of states contains only the |0, 0〉 state. Its rate coefficient is approximately equal to k_L at the lowest energies, and increases with increasing E_coll, reaching a value of 1.51 k_L at E_coll/k_B = 12 K. This effect is caused by the mixing between the |0, 0〉 and |2, 0〉 states in the electric field of the ion. (ii) The second group consists of (J, M ≈ 0) states, which exhibit reaction rate coefficients that are overall higher than k_L. The rate coefficients are relatively collision-energy-independent for collision energies E_coll/k_B ≳ 2 K, but sharply increase at collision energies below k_B·1 K. This effect is most pronounced for the (1, 0) state, which reaches a rate constant of 4.1k_L at E_coll/k_B = 0.01 K, and gradually decreases with increasing J value, as can be seen in Fig. 6(g), which compares the rate coefficients of all M = 0 states. (iii) The third group of states comprises the states (J, |M| ≈ J) which have vanishing rate coefficients for collision energies E_coll ≤ V^(J,M),max_int. For these states, the rate coefficients increase with increasing E_coll beyond E_coll = V^(J,M),max_int [panel (h)]. (iv) The last group of states includes states of relatively high values of J and intermediate values of |M|, such as the |5, ±3〉 and |4, ±3〉 states, for which the interaction potentials do not strongly deviate from the pure Langevin potential, indicating that the role of the charge–quadrupole interaction is minor. These states are characterised by capture rate coefficients that are very close to k_L and are almost independent of E_coll. At high collision energies the rate coefficients of all states converge to the value of k_L (see, e.g., left panel of Fig. 9 below for J = 0, 1).

To highlight the effect of the sign of Q_zz on the rate coefficients, calculations for the D₂⁺ + H₂ ion–molecule reaction were performed following the same procedure as for the He⁺ + N₂ reaction [the He⁺ + H₂ reaction is a slow reaction that does not follow Langevin behaviour, see, e.g., ref. 75. We therefore replaced He⁺ by D₂⁺ because of their almost equal mass]. H₂ has a positive quadrupole moment of Q_zz = 0.638 D Å ³¹ and a rotational constant of B₀(H₂) = 59.3398 cm⁻¹,⁷³ more than an order of magnitude larger than B₀(N₂). The relevant interaction potentials are presented in Fig. 7 and the rotational-state-specific reaction rate coefficients are depicted in Fig. 8.

Fig. 7 (a)–(f) Comparison of the calculated interaction potentials between D₂⁺ and H₂(J, M) for J ≤ 5 (coloured lines, as indicated in the different panels) with the Langevin potential. The potentials for [small script l] = 0 and 11 are indicated by full and dashed lines, respectively. Panels (a)–(f) present the results for |J, M〉 states with J ranging from 0 (a) to 5 (f). Panels (g) and (h) compare the potentials of the M = 0 and |M| = J states, respectively.

Fig. 8 Calculated rotational-state-dependent reaction rate coefficients for the D₂⁺ + H₂ reaction. Panels (a)–(f) present the results for |J, M〉 states with J ranging from 0 (a) to 5 (f). Panels (g) and (h) compare the rate coefficients of the M = 0 and |M| = J states, respectively. Panel (i) gives the rate coefficients averaged over all M values for J = 0–2.

Because of the positive value of Q_zz in the case of H₂, the states with M = 0 (|M| = J) are now the states that experience a repulsive (attractive) electrostatic interaction, as can be immediately understood from the considerations based on the vector model (see Fig. 5). An approach in the helicoptering (|M| = J) configuration indeed now exposes the negative partial charge near the molecule geometric centre and an approach in the cartwheeling configuration exposes to the ion the positive partial charges at the ends of the molecule. Attractive and repulsive contributions to the interaction potential result, respectively. Consequently, the behaviour of the states in categories (ii) and (iii) is exchanged when N₂ is replaced by H₂. In contrast to the situation encountered in N₂, however, the height of the potential energy barrier for M = 0 states, V^(J,0),max_int, decreases with increasing J. This difference is the result of the larger rotational constant in H₂, which increases the energetic separation between adjacent J levels and reduces the state mixing caused by the charge–quadrupole interaction. For the same reason, the interaction potentials involving |M| = J states become more attractive for increasing J value. The deviation of the V^(0,0)_int(R) potential from V_L in H₂ is also strongly reduced compared to the situation encountered in N₂ because the larger rotational constant in H₂ leads to a much reduced mixing between the |0, 0〉 and |2, 0〉 states.

The rotational-state-dependent capture rate constants for the D₂⁺ + H₂ reaction displayed in Fig. 8 reflect these considerations. Because the |0, 0〉 state hardly gets mixed with the |2, 0〉 state, its rate coefficient is almost E_coll – independent and does not significantly deviate from k_L [Fig. 8(a)]. It weakly increases with increasing E_coll and reaches a value of 1.02k_L at E_coll/k_B = 12 K. The rate-coefficient enhancement of the |M| = J states at the lowest collision energies increases with the J value [see panel Fig. 8(h)], reaching a value of 3.49k_L for the (5,5) state at 0.01 K. This effect can be understood in terms of the reduced precession angle α and the resulting energetically more favourable configuration for H₂ [see Fig. 5(a)].

The rate coefficients associated with M = 0 states of H₂ [Fig. 8(g)] increase faster with increasing E_coll than those associated with |M| = J states of N₂, because for these states the potential-energy barriers are smaller in H₂ than in N₂ [compare Fig. 8(g) with Fig. 6(h)]. A second important difference between the reactions of He⁺ with N₂ and D₂⁺ with H₂ concerns the behaviour of the J-dependent capture rate coefficients after averaging over the M states, as depicted for J = 0, 1, and 2 in Fig. 6(i) for N₂ and in Fig. 8(i) for H₂. At the lowest collision energies, the rate coefficients for the J = 1 and 2 states are highest but they rapidly decrease as the collision energy increases and then start growing again. In the case of N₂, the rate coefficients become larger than k_L and reach a maximum at collision energies in the range between k_B·50 K and k_B·100 K, before decreasing again towards k_L at high collision energies, see left panel of Fig. 9. In the case of H₂, the rates do not significantly increase beyond k_L and remain constant at collision energies beyond k_B·10 K, see Fig. 8(i) and right panel of Fig. 9.

Fig. 9 Calculated reaction rate coefficients for the |0, 0〉, |1, 0〉, and |1, |M| = 1 〉 states in the He⁺ + N₂ (a) and D₂⁺ + H₂ (b) reactions, in the high collision-energy regime. The curves labelled “J = 1” are averages over all M levels.

The collision-energy dependence up to k_B·10⁶ K of the rate coefficients involving the J = 0 and 1 rotational levels of N₂ and H₂ are compared in Fig. 9. These levels are the ground states of the two nuclear-spin isomers and have nuclear-spin statistical factors of 1 (J = 0, para) and 3 (J = 1, ortho) in H₂, and 6 (J = 0, ortho) and 3 (J = 1, para) in N₂. The main difference in behaviour concerns the J = 1 levels and originates from the opposite sign of the quadrupole tensor element Q_zz, as discussed above. The charge–quadrupole interaction is attractive for M = 0 in N₂ and for |M| = 1 in H₂, which leads to an enhancement of the rate coefficients compared to k_L at the lowest collision energies. In contrast, the interaction is repulsive for |M| = 1 in N₂ and M = 0 in H₂, which leads to the complete suppression of the reaction rates. The second difference originates from the mixing of rotational levels induced by the field of the ion, which induces a red Stark shift of the lowest rotational levels (J = 0, 1) with M = 0 in N₂ and |M| = 1 in H₂ and an increase of the rate coefficients compared to k_L. In N₂, this effect is twice stronger than in H₂ because the rotational levels are much more closely spaced.

States with |M| > 0 and M = 0 have degeneracy factors of 2 and 1, respectively, and J ≥ 1, M = 0 (|M| = 1) states have attractive (repulsive) potentials in H₂ and repulsive (attractive) potentials in N₂. Consequently, the overall dependence of the rate coefficients on the collision energy after averaging over the M sublevels is different. In H₂, the k^J=1 capture rate coefficient only slightly decreases with decreasing energy, reaching a minimum of approximately 0.95k_L at E_coll/k_B = 1.55 K [see inset of Fig. 8(i)] before increasing again to a value of 1.6k_L at 10 mK. In N₂, the decrease of the rate coefficient below k_B·10 K is more pronounced and amounts to about 30%. This behaviour reflects the fact that rate coefficients of the M = ±1 states become zero when the collision energy drops below the barrier in the interaction potential. It is only at extremely low collision energies, below k_B·50 mK, that the effect of the rate coefficient of the M = 0 state becomes dominant again, causing the M-averaged rate coefficient to rise again and reach a value of 1.35k_L at k_B·10 mK.

5 Discussion

5.1 Comparison with experimental results

In the case of the ion–molecule reactions involving H₂ and D₂, the validity of the adiabatic capture model had already been verified prior to this work by comparing the results of the calculations of Dashevskaya et al.¹⁶ with experimental results.^33,71

For comparison with the experimental data reported in Section 3 for the He⁺ + N₂ reaction, the rotational-state-specific and collision-energy-dependent rate coefficients must be averaged to account for the finite energy resolution of the measurements and for the fact that several rotational states of N₂ are populated in the supersonic expansion. In the range of collision energies probed experimentally (E_coll/k_B between 0 and 12 K), the averaged capture rate coefficients depend strongly on the rotational temperature T_rot of the N₂ sample in the supersonic beam. This dependence is illustrated in Fig. 10 which displays the collision-energy-dependent rate coefficients k(E_coll) after averaging over the rotational-state-population distribution according to

In eqn (10), g_ns,JM represents the nuclear-spin statistical factor, i.e., 6 for rotational levels with even J value (ortho N₂) and 3 for rotational levels with odd J value (para N₂), E_0,o/p is the rotational energy of the ground state of ortho (0) or para (2hcB₀) N₂, and Q_rot is the molecular rotational partition function constructed so that ortho and para N₂ represent 2/3 and 1/3 of the total population, respectively.

Fig. 10 Calculated reaction rate coefficients for the He⁺ + N₂ averaged over all |J,M〉 states for the indicated rotational temperatures. The dashed horizontal line corresponds to the Langevin rate, k_L.

At the rotational temperature of 7.0 K, the average rate coefficient k(E_coll) decreases by more than 30% from a value of about 1.5 k_L at E_coll/k_B = 12 K to ≈k_L at E_coll/k_B ≈ 0.2 K before growing again at the lowest collision energies, as explained in the previous section. At higher rotational temperatures (T_rot ≥ 20 K), k(E_coll) becomes much less dependent on the collision energy and its value gradually decreases in the collision-energy range investigated experimentally.

At the rotational temperature of 7.0 ± 1.0 K determined experimentally (see Section 2), only the J = 0, 1, and 2 levels of N₂ are significantly populated [see inset of Fig. 3(b)]. A comparison of the calculated rate coefficients presented in Fig. 10 with the experimental data in Fig. 3(b) shows qualitative agreement for rotational temperatures below 10 K. The sharp rise of the calculated rate coefficients near zero collision energies is indeed not observable experimentally because of the limited collision-energy resolution. A quantitative analysis requires averaging over the distribution of collision energies given by eqn (4). The dependence of k(E_coll) on T_rot is large. Optimizing the value of T_rot to best reproduce the experimentally observed rate coefficients led to the same value for T_rot (7.0 ± 1.0 K) as obtained by 2 + 1 REMPI spectroscopy (see Section 2). The result of the quantitative analysis are presented with the experimental data in Fig. 3(b). The violet circles in Fig. 3(b) are weighted sums of the calculated rotational-state-dependent reaction rate coefficients (see Section 4), for a rotational temperature of T_rot = 7.0 K, which was found to best describe the experimental data. The inset displays the corresponding rotational population distribution of N₂, including nuclear-spin-statistics effects. The solid black line depicts the Gaussian convolution of the calculated weighed sum of the rotational-state-dependent rate coefficients taking into account the experimental energy resolution, as described in ref. 26. This curve reproduces the experimental data well. Given that the analysis does not contain any adjustable parameter other than T_rot and the collision-energy resolution at the lowest collision energies [ΔE_res in eqn (4)], we conclude that the adiabatic capture model presented in Section 4 is adequate to describe the capture rate coefficient at low collision energies, where the charge–quadrupole interaction plays an important role.

Rowe et al.⁹ have measured the thermal rate constant of the He⁺ + N₂ reaction at temperatures of 8, 20 and 28 K in uniform supersonic flows (CRESU technique). To compare with these experimental results, thermal capture rate constants were determined from the collision-energy-dependent rotational-state-specific rate coefficients presented in Section 4 using eqn (20) and (21) of Article I.¹⁷ The comparison is presented in Fig. 11, which depicts the experimental results of ref. 9 as violet squares with error bars and the calculated thermal rate constants as black open circles and full line. The calculated capture rates are larger than the measured reaction rates, which suggests that not all capture processes lead to a reaction. If one assumes that the discrepancy between the calculated and measured reaction rate constants originates from a less-than-unity reaction probability upon close encounter of the reactants and that the reaction probability is independent of the collision energy, the reaction probability can be estimated by scaling down the calculated thermal capture rate constants until they match the experimental data (see orange open circles and full line). This procedure suggests that the reaction probability is 0.65(20). Unfortunately, the experimental error bars are too large for any conclusion to be drawn concerning the predicted temperature dependence of the thermal rate constant.

Fig. 11 Comparison of the calculated thermal capture rate constant for the He⁺ + N₂ reaction (black line and open circles) with the Langevin rate (dashed horizontal red line) and the thermal rate constants measured by Rowe et al.⁹ at temperatures of 8, 20 and 28 K using the CRESU technique (violet squares with error bars). The orange open circles and line represent the calculated rate constants scaled by a factor of 0.625.

5.2 Comparison with earlier calculations

Troe and coworkers have reported detailed calculations of the capture rate coefficients of ion–molecule reactions involving molecules having an electric quadrupole moment.^15,16,30,31 These calculations introduced and tested several approximations in the treatment of the interaction potentials and served as reference to validate our results. In contrast to the present calculations, the calculations of Dashevskaya et al.^15,16,31 also considered the effects of quantum scattering and of the Coriolis interaction, which mixes rotational levels of the neutral molecule of different M values. These effects were found to lead to (i) an increase of the k^J=0 capture rate coefficients to a value of 2k_L at very low collision energies (below k_B·0.3 mK for the He⁺ + N₂ reaction), regardless of the sign of the qQ_zz product, and (ii) a suppression of the divergence of the k^J=1 capture rate coefficients at very low temperatures, such that the k^{J=1, He++N₂} (k^{J=1, Ar++H₂}) rate coefficient averaged over all M states stabilises to a finite value at the lowest collision energies ∼k_B·10 nK, i.e., to ∼11k_L (∼5.6k_L). As explained in ref. 15, these effects only become significant at extremely low collision energies, and they are not detectable at the collision energy resolution of ∼k_B·250 mK of our experiments (see Section 2) and were therefore ignored in our calculations.

The calculated capture rate coefficients presented in the previous section are consistent with the calculations of Dashevskaya et al.,¹⁵ in which the perturbed-rotor (PR) approximation was used to calculate the Stark shifts of the rotational levels of the neutral molecule. In the case of the capture of H₂ by an ion, the PR approximation accurately describes the Stark shifts of the |1, 0〉 and |1, 1〉 rotational levels and the k^H₂(1,0) and k^H₂(1,1) capture rate coefficients. A small difference between the PR approximation and the exact calculation is observed for the |1, 0〉 level. In the PR approximation, the k^H₂(0,0) rate coefficient is predicted to be exactly equal to k_L over the temperature range considered, whereas the exact treatment through diagonalisation of the Stark Hamiltonian leads to a small (about 2%) increase of k^H₂(0,0) as E_coll increases up to k_B·12 K [see inset of Fig. 8(a)]. For reactions involving N₂, the k^N₂(0,0) and k^N₂(1,0) rate coefficients are accurately predicted using the perturbed-rotor approximation, but deviations from the rate coefficients calculated with the exact method are apparent for the (1, 1) state, with (E_coll/k_B = 12 K) ≈ 0.5(E_coll/k_B = 12 K).

6 Conclusions

We have presented the first experimental measurements of the N⁺ and N₂⁺ product yields of the He⁺ + N₂ reaction for a range of collision energies between 0 and k_B·10 K. The reaction was studied within the orbit of the helium Rydberg electron. The product-ions ratio was determined to be N⁺ : N₂⁺ ≈ 0.50(5) : 0.50(5), whereas most previous studies had shown a consistent bias towards the generation of N⁺, with N⁺ : N₂⁺ ≈ 0.60 : 0.40.^{37,41,50–52,55} We attribute the higher fraction of N₂⁺ ions observed in our experiments to the absence of collisional dissociation in the supersonic beams during the short reaction-observation time of 7 μs. The dissociation of metastable N₂⁺ molecules into an N⁺ ion and an N atom induced by secondary collisions has been observed in earlier experiments carried out in the presence of higher background gas densities.^42,53,56

A ≈30% decrease of the reaction yield was observed when the collision energy was decreased from k_B·10 K to 0. To explain this observation, calculations of the rotational-state-specific capture rate coefficients were performed using a statistical adiabatic-channel model inspired by earlier works^11,12 and explicitly calculating the Stark shifts of the rotational levels of the neutral molecule in the field of the ion. The excellent agreement obtained between the calculated and observed energy dependence of the rate coefficients [see Fig. 3(b)] indicates that the treatment of the charge–quadrupole interaction through diagonalisation of the Stark Hamiltonian in the realm of the adiabatic channel model leads to reliable interaction potentials and capture rate coefficients in the range of collision energies investigated experimentally. The comparison of experimental and theoretical results for the He⁺ + N₂ reaction and with results obtained on ion–molecule reactions involving H₂ molecules enabled the first clear observation and quantification of the role of the sign of the quadrupole moment of the neutral molecule in the capture rate coefficients of ion–molecule reactions. At low collision energies, the capture rate coefficients of ion–molecule reactions characterised by a positive (negative) qQ_zz product were found to increase (decrease) with decreasing collision energy.

For low J values and intermediate collision energies, i.e., in the range beyond k_B·10 K (see Fig. 9), quadrupolar molecules with a small rotational constant, such as N₂, were found to have rate coefficients that are larger than the Langevin rate constant k_L, whereas molecules with a large rotational constant, such as H₂, have capture rate coefficients that are much closer to k_L. This behaviour can be explained by the fact that in quadrupolar molecules with small rotational constants the Stark shifts originating from the interaction between the electric quadrupole and the field of the ion are stronger than in molecules with large rotational constants. The nonlinear Stark shifts become significant at much lower fields and are on the average negative, which effectively reduces the heights of the centrifugal barriers compared to the pure Langevin case and increases the rate coefficients. The calculations also indicate that the deviations from Langevin capture behaviour rapidly decrease with increasing collision energy and rotational excitation of the neutral molecule.

The comparison of calculated thermal capture rate coefficients for the He⁺ + N₂ reactions with thermal reaction rate constants measured in uniform supersonic flow⁹ suggests that the probability of reaction upon close encounter of He⁺ and N₂ is less than unity, probably in the range 0.63 ± 0.20.

Calculations of the rotational-state-specific and collision-energy-dependent rate coefficients of ion–molecule reactions involving H₂ and N₂ revealed a large sensitivity on the absolute value of the magnetic rotational quantum number M of the neutral molecule. Moreover, changing the sign of the quadrupole was found to exchange the role played by rotational states with M = 0 and |M| = J. This behaviour was explained qualitatively by simple electrostatic considerations based on the angular-momentum vector model (see Fig. 5).

The calculations reveal that a rich behaviour could be explored in experiments using neutral-molecule samples prepared in states with aligned rotational angular momentum. In the future, efforts should also be invested to further improve the collision-energy resolution of the experiments, with the prospect of observing the effects of quantum scattering and Coriolis coupling predicted in ref. 15 and 16. These effects decrease rapidly with increasing reduced mass of the collision system. In this respect, the H₂⁺ + H₂ reaction (μ ≈ 1 u) offers advantages over the He⁺ + N₂ reaction (μ ≈ 3.5 u) and work on the H₂⁺ + H₂ reaction is currently under way in our laboratory.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Joel Jenny for his contributions to the data acquisition, Katharina Höveler and Johannes Deiglmayr for fruitful discussions, Josef A. Agner and Hansjürg Schmutz for technical assistance, and Majdi Hochlaf and Laurent Nahon for making the potential-energy functions of N₂⁺ depicted in Fig. 1 available in digital form. This work is supported financially by the Swiss National Science Foundation (Grant No. 200020B-200478) and by the European Research Council through the ERC advanced grant (Grant No. 743121) under the European Union's Horizon 2020 research and innovation programme.

References

1. S. Willitsch, Chemistry with Controlled Ions, Advances in Chemical Physics, ed. S. A. Rice and A. R. Dinner, 2017, vol. 162, pp. 307–340.
2. B. R. Heazlewood and T. P. Softley, Nat. Rev. Chem., 2021, 5, 125–140.
3. L. Ploenes, P. Straňák, H. Gao, J. Küpper and S. Willitsch, Mol. Phys., 2021, 119, e1965234.
4. I. Savić, S. Schlemmer and D. Gerlich, Astrophys. J., 2005, 621, 1163–1170.
5. D. Gerlich, The study of cold collisions using ion guides and traps, in Low Temperatures and Cold Molecules, ed. I. M. W. Smith, Imperial College Press, London, 2008, ch. 3, pp. 121–174.
6. R. Wester, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 154001.
7. C. Markus, O. Asvany, T. Salomon, P. Schmid, S. Brünken, F. Lipparini, J. Gauss and S. Schlemmer, Phys. Rev. Lett., 2020, 124, 233401.
8. J. B. Marquette, B. R. Rowe, G. Dupeyrat, G. Poissant and C. Rebrion, Chem. Phys. Lett., 1985, 122, 431–435.
9. B. R. Rowe, J. B. Marquette, G. Dupeyrat and E. E. Ferguson, Chem. Phys. Lett., 1985, 113, 403–406.
10. B. Rowe, A. Canosa and V. L. Page, Int. J. Mass Spectrom. Ion Processes, 1995, 149, 573–596.
11. D. C. Clary, Mol. Phys., 1985, 54, 605–618.
12. J. Troe, Chem. Phys., 1987, 87, 2773–2780.
13. M. Auzinsh, E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2013, 139, 084311.
14. M. Auzinsh, E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2013, 139, 144315.
15. E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2005, 122, 184311.
16. E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2016, 145, 244315.
17. V. Zhelyazkova, F. B. V. Martins, J. A. Agner, H. Schmutz and F. Merkt, Phys. Chem. Chem. Phys., 2021, 23, 21606–21622.
18. V. Zhelyazkova, F. B. V. Martins and F. Merkt, submitted for publication.
19. D. Albritton, At. Data Nucl. Data Tables, 1978, 22, 1–89.
20. V. G. Anicich and W. T. Huntress, Astrophys. J. Suppl. Ser., 1986, 62, 553–672.
21. Kinetics of Ion-Molecule Reactions, ed. P. Ausloos, Plenum Press, New York, 1978.
22. Gas Phase Ion Chemistry, ed. M. T. Bowers, Academic Press, New York, 1979, vol. 1 and 2.
23. State-selected and state-to-state ion-molecule reaction dynamics: Part 1. Experiment and Part 2. Theory, ed. C.-Y. Ng and M. Baer, John Wiley & Sons, Inc., New York, 1992.
24. D. C. Clary, Annu. Rev. Phys. Chem., 1990, 41, 61–90.
25. J. Troe, J. Chem. Phys., 1996, 105, 6249–6262.
26. V. Zhelyazkova, F. B. V. Martins, J. A. Agner, H. Schmutz and F. Merkt, Phys. Rev. Lett., 2020, 125, 263401.
27. T. Stoecklin, D. C. Clary and A. Palma, J. Chem. Soc., Faraday Trans., 1992, 88, 901–908.
28. M. T. Bell, A. D. Gingell, J. M. Oldham, T. P. Softley and S. Willitsch, Faraday Discuss., 2009, 142, 73–91.
29. A. Kilaj, H. Gao, D. Rösch, U. Rivero, J. Küpper and S. Willitsch, Nat. Commun., 2018, 9, 2096.
30. S. C. Smith and J. Troe, J. Chem. Phys., 1992, 97, 5451–5464.
31. E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2004, 120, 9989–9997.
32. C. Graham, D. A. Imrie and R. E. Raab, Mol. Phys., 1998, 93, 49–56.
33. P. Allmendinger, J. Deiglmayr, K. Höveler, O. Schullian and F. Merkt, J. Chem. Phys., 2016, 145, 244316.
34. K. Höveler, J. Deiglmayr, J. A. Agner, H. Schmutz and F. Merkt, Phys. Chem. Chem. Phys., 2021, 23, 2676–2685.
35. P. Warneck, J. Chem. Phys., 1967, 47, 4279–4281.
36. D. B. Dunkin, F. C. Fehsenfeld, A. L. Schmeltekopf and E. E. Ferguson, J. Chem. Phys., 1968, 49, 1365–1371.
37. A. L. Schmeltekopf, E. E. Ferguson and F. C. Fehsenfeld, J. Chem. Phys., 1968, 48, 2966–2973.
38. W. Lindinger, F. C. Fehsenfeld, A. L. Schmeltekopf and E. E. Ferguson, J. Geophys. Res., 1974, 79, 4753–4756.
39. T. R. Govers, F. C. Fehsenfeld, D. L. Albritton, P. G. Fournier and J. Fournier, Chem. Phys. Lett., 1974, 26, 134.
40. T. Govers, C. van de Runstraat and F. de Heer, Chem. Phys., 1975, 9, 285–299.
41. N. G. Adams and D. Smith, J. Phys. B: At. Mol. Phys., 1976, 9, 1439–1451.
42. T. R. Govers, M. Gérard, G. Mauclaire and R. Marx, Chem. Phys., 1977, 23, 411–427.
43. H. Sekiya, M. Tsuji and Y. Nishimura, J. Chem. Phys., 1987, 87, 325–330.
44. P. R. Kemper and M. T. Bowers, J. Chem. Phys., 1973, 59, 4915.
45. W. B. Maier, Planet. Space Sci., 1968, 16, 477–493.
46. S. J. Bauer, J. Geophys. Res., 1966, 71, 1508–1511.
47. O. Dutuit, N. Carrasco, R. Thissen, V. Vuitton, C. Alcaraz, P. Pernot, N. Balucani, P. Casavecchia, A. Canosa, S. L. Picard, J.-C. Loison, Z. Herman, J. Zabka, D. Ascenzi, P. Tosi, P. Franceschi, S. D. Price and P. Lavvas, Astrophys. J. Suppl. Ser., 2013, 204, 20.
48. M. Womack, L. M. Ziurys and S. Wyckoff, Astrophys. J., 1992, 393, 188.
49. D. Smith, Chem. Rev., 1992, 92, 1473–1485.
50. J. Heimerl, R. Johnsen and M. A. Biondi, J. Chem. Phys., 1969, 51, 5041–5048.
51. V. G. Anicich, J. B. Laudenslager, W. T. Huntress and J. H. Futrell, J. Chem. Phys., 1977, 67, 4340–4350.
52. J. B. Laudenslager, W. T. Huntress and M. T. Bowers, J. Chem. Phys., 1974, 61, 4600–4617.
53. R. Marx, G. Mauclaire and S. Fenistein, Chem. Phys. Lett., 1975, 33, 357–361.
54. W. Lindinger, E. Alge, H. Störi, R. Varney, H. Helm, P. Holzmann and M. Pahl, Int. J. Mass Spectrom. Ion Phys., 1979, 30, 251–261.
55. A. L. Farragher, Trans. Faraday Soc., 1970, 66, 1411.
56. P. R. Kemper and M. T. Bowers, Chem. Phys. Lett., 1975, 36, 183.
57. T. Ayari, M. Desouter-Lecomte, R. Linguerri, G. A. Garcia, L. Nahon, A. B. Houria, H. Ghalila, R. B. Said and M. Hochlaf, Adv. Phys.: X, 2020, 5, 1831955.
58. A. Kramida, Y. Ralchenko, J. Reader and N. A. Team, NIST Atomic Spectra Database (ver. 5.8), available: https://physics.nist.gov/asd, National Institute of Standards and Technology, Gaithersburg, MD, 2021.
59. R. Seiler, U. Hollenstein, G. M. Greetham and F. Merkt, Chem. Phys. Lett., 2001, 350, 189.
60. X. Tang, Y. Hou, C. Y. Ng and B. Ruscic, J. Chem. Phys., 2005, 123, 074330.
61. F. Merkt and P. M. Guyon, J. Chem. Phys., 1993, 99, 3400–3410.
62. X. Li and J. Paldus, J. Chem. Phys., 2008, 129, 054104.
63. C. A. van de Runstraat, F. J. de Heer and T. R. Govers, Chem. Phys., 1974, 3, 431–450.
64. J. C. Lorquet and M. Desouter, Chem. Phys. Lett., 1972, 16, 136.
65. P. Erman, Phys. Scr., 1976, 14, 51–54.
66. A. Lofthus and P. H. Krupenie, J. Phys. Chem. Ref. Data, 1977, 6, 113–307.
67. P. Allmendinger, J. Deiglmayr, J. A. Agner, H. Schmutz and F. Merkt, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 043403.
68. S. R. Mackenzie, F. Merkt, E. J. Halse and T. P. Softley, Mol. Phys., 1995, 86, 1283–1297.
69. F. B. V. Martins, V. Zhelyazkova, Ch. Seiler and F. Merkt, New J. Phys., 2021, 23, 095011.
70. B. Paulus, J. F. Pérez-Torres and C. Stemmle, Phys. Rev. A, 2016, 94, 053423.
71. K. Höveler, J. Deiglmayr and F. Merkt, Mol. Phys., 2021, 119, e1954708.
72. E. Vogt and G. H. Wannier, Phys. Rev., 1954, 95, 1190–1198.
73. K. P. Huber and G. Herzberg, Molecular spectra and molecular structure; Volume IV – Constants of diatomic molecules, Van Nostrand Reinhold Company, New York, 1979.
74. R. N. Zare, Angular Momentum, John Wiley & Sons, New York, 1988.
75. M. M. Schauer, S. R. Jefferts, S. E. Barlow and G. H. Dunn, J. Chem. Phys., 1989, 91, 4593–4596.

---