Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Variational quantum eigensolver simulations with the multireference unitary coupled cluster ansatz: a case study of the C2v quasi-reaction pathway of beryllium insertion into a H2 molecule†
Kenji
Sugisaki
 *abc,
Takumi
Kato‡
d,
Yuichiro
Minato
d,
Koji
Okuwaki
e and
Yuji
Mochizuki
*abc,
Takumi
Kato‡
d,
Yuichiro
Minato
d,
Koji
Okuwaki
e and
Yuji
Mochizuki
 ef
ef
aDepartment of Chemistry, Graduate School of Science, Osaka City University, 3-3-138 Sugimoto, Sumiyoshi-ku, Osaka 558-8585, Japan. E-mail: sugisaki@osaka-cu.ac.jp
bJST PRESTO, 4-1-8 Honcho, Kawaguchi, Saitama 332-0012, Japan
cCentre for Quantum Engineering, Research and Education (CQuERE), TCG Centres for Research and Education in Science and Technology (TCG CREST), 16th Floor, Omega, BIPL Building, Blocks EP & GP, Sector V, Salt Lake, Kolkata, 700091, India
dBlueqat Inc., 2-24-12 Shibuya, Shibuya-ku, Tokyo 150-6139, Japan
eDepartment of Chemistry, Faculty of Science, Rikkyo University, 3-34-1 Nishi-ikebukuro, Toshima-ku, Tokyo 171-8501, Japan
fInstitute of Industrial Science, The University of Tokyo, 4-6-1 Komaba, Meguro-ku, Tokyo 153-8505, Japan
First published on 15th March 2022
Abstract
Variational quantum eigensolver (VQE)-based quantum chemical calculations have been extensively studied as a computational model using noisy intermediate-scale quantum devices. The VQE uses a parametrized quantum circuit defined through an “ansatz” to generate approximated wave functions, and the appropriate choice of an ansatz is the most important step. Because most chemistry problems focus on the energy difference between two electronic states or structures, calculating the total energies in different molecular structures with the same accuracy is essential to correctly understand chemistry and chemical processes. In this context, the development of ansatzes that are capable of describing electronic structures of strongly correlated systems accurately is an important task. Here we applied a conventional unitary coupled cluster (UCC) and a newly developed multireference unitary coupled cluster with partially generalized singles and doubles (MR-UCCpGSD) ansatzes to the quasi-reaction pathway of Be insertion into H2, LiH molecule under covalent bond dissociation, and a rectangular tetra-hydrogen cluster known as a P4 cluster; these are representative systems in which the static electron correlation effect is prominent. Our numerical simulations revealed that the UCCSD ansatz exhibits extremely slow convergence behaviour around the point where an avoided crossing occurs in the Be + H2 → BeH2 reaction pathway, resulting in a large discrepancy of the simulated VQE energy from the full-configuration interaction (full-CI) value. By contrast, the MR-UCCpGSD ansatz can give more reliable results with respect to total energy and the overlap with the full-CI solution, insisting the importance of multiconfigurational treatments in the calculations of strongly correlated systems. The MR-UCCpGSD ansatz allows us to compute the energy with the same accuracy regardless of the strength of multiconfigurational character, which is an essential property to discuss energy differences of various molecular systems.
1. Introduction
Quantum computers have emerged as one of the most disruptive technologies in current science. Computational costs on classical computers with certain problems like prime factorization and group isomorphism grow exponentially against the problem size, but it can be solved in polynomial time by using quantum computers.1,2 Among the diverse topics in quantum computing and quantum information processing, sophisticated quantum chemical calculations of atoms and molecules are one of the most intensively studied realms as the near future applications of quantum computers. In 2005, Aspuru-Guzik and co-workers proposed a quantum algorithm for full-configuration interaction (CI) calculation that gives variationally the best possible wave function within the space spanned by the basis set being used, by utilizing a quantum phase estimation (QPE) algorithm.3 The QPE-based full-CI is very powerful and exponential speedup against its classical counterpart is guaranteed, but the quantum circuit for the QPE-based full-CI is so deep that it is quite difficult to obtain meaningful results unless quantum error correction code is implemented and fault-tolerant quantum computing is realized. Note that experimental demonstrations of quantum error correction have been reported recently,4–6 but the number of available logical qubits is still too small for practical purposes.A quantum–classical hybrid algorithm known as a variational quantum eigensolver (VQE) was proposed in 20147,8 as the alternative computational model in the noisy intermediate-scale quantum (NISQ)9 era. The VQE uses a quantum processing unit (QPU) for the preparation of approximated wave function by utilizing parameterized quantum circuits and evaluation of energy expectation values, and a classical processing unit (CPU) for the variational optimizations. The parametrized quantum circuit is defined by an empirical “ansatz”, and thus the ansatz used in the computation determines the accuracy of the wave function and energy. Intuition-oriented ansatzes of chemists such as unitary coupled cluster (UCC) ansatz,10–12 and adaptive derivative-assembled pseudo-Trotter ansatz (ADAPT),13 qubit coupled cluster,14 and more heuristic ansatzes called “hardware-efficient” ones15 have been well investigated. Development of new ansatzes16–25 is one of the mainstream of the VQE study, and other developments such as qubit reductions by utilizing natural orbitals,26,27 extension of ansatzes for larger systems,28–31 introduction of error mitigation techniques,32–34 spatial and spin symmetry adaptations,35–38 reduction of the number of qubit measurements,39–42 applications for electronically excited states,32,43–46 and proof-of-principle demonstration on quantum devices47–51 have also been documented. Recent reviews in this field can be found elsewhere.52–56
From the viewpoint of chemistry, we emphasize that most problems in chemistry focus on the energy differences between two or larger numbers of electronic states or geometries, rather than the total energies themselves. To understand the chemistry and chemical processes correctly and to make quantum computers useful in the investigations of real-world chemistry problems, calculating various electronic structures and molecular systems with the same accuracy is essential. Most theoretical studies on VQE-based energy calculations focus on the simple potential energy curves by stretching covalent bonds or changing bonding angles, or simple concerted chemical reactions. It is interesting whether VQE is able to correctly describe more complex chemical reactions; for example, the reactant and product have different electronic configurations, and an avoided crossing between the ground and excited states is involved in the reaction pathway. If an avoided crossing is present in the reaction process, the wave function around the crossing point cannot be well approximated by a single Slater determinant like Hartree–Fock (HF) and by a single configuration state function. In such systems both dynamic and static (or non-dynamic) electron correlation effects are prominent, and non-variational single-reference (SR) molecular orbital theories such as the second-order Møller–Plesset (MP2) and a coupled cluster with singles and doubles (CCSD) become less reliable.57–59 Multireference (MR) treatment is more feasible for the study of such strongly correlated systems.
In this work, we mainly focus on a beryllium atom insertion reaction into H2 to generate a BeH2 molecule illustrated in Fig. 1 as the representative example of the chemical reactions in which S0–S1 avoided crossing is involved, to study how the performance of the VQE changes for weakly and strongly correlated regimes and to examine the MR ansatz for strongly correlated systems. This reaction pathway has been precisely investigated as the model system of MR electronic structure treatments.60–67 As clearly seen in Fig. 1, this reaction pathway contains avoided crossing at R(Be⋯H2) ∼ 2.75 Bohr, and it is a good testing ground for the sophisticated quantum chemical calculations using the VQE. This reaction pathway was studied by Metcalf and co-workers by means of the VQE using a double unitary coupled cluster (DUCC) ansatz, which effectively downfold correlation effects into the reduced-size orbital space.25 They reported a DUCC ansatz with 6 orbitals that provides substantial improvement of the bare Hamiltonian in the active space. Evangelista studied this reaction pathway using various SR-CC methods including traditional CCSD, UCCSD, variational CCSD and extended CCSD in the context of classical computing, finding that these SR-CC approaches break down near the MR region.67 It should also be noted that this system is illustrative in teaching physical chemistry including molecular orbital theory and valence bond descriptions. We examined numerical simulations of the VQE along the quasi-reaction pathway in C2v symmetry by using a traditional UCCSD ansatz and a multireference unitary coupled cluster with partially generalized singles and doubles (MR-UCCpGSD) ansatz, focusing on the accuracy of wave functions and energies, and convergence behaviour of the variational optimization in the VQE. We also applied the MR-UCCpGSD ansatz to the LiH molecule under bond dissociation (R(Li–H) = 3.0 and 4.0 Å), and a rectangular tetra-hydrogen atom cluster known as a P4 model,68 which also exhibits strong multiconfigurational characters.
2. Theory
Here, we briefly review the theoretical methods for quantum chemical calculations using the VQE. The schematic view of the VQE-based quantum chemical calculations is provided in Fig. 2. The VQE consists of two parts, namely, computations on a QPU and those on a CPU. The QPU repeatedly executes the preparation of an approximated wave function using a parametrized quantum circuit and following qubit measurements to calculate an energy expectation value. Information of the energy expectation value is transferred to the CPU, and the CPU carries out variational optimization of the parameters and convergence check. If the variational calculation did not converge, a set of information of the revised parameters are returned to the QPU, and the QPU executes the evaluation of the energy expectation value using the new parameters. These procedures are iterated until convergence.In order to execute the VQE, the wave function is mapped onto qubits and the second quantized Hamiltonian in eqn (1) is transformed into the qubit Hamiltonian in eqn (2) that is described by a linear combination of Pauli strings in eqn (3), by applying fermion–qubit transformations.3,69–73
 | (1) |
 | (2) |
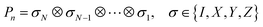 | (3) |
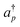 and ap in eqn (1) are the creation and annihilation operators, respectively, acting on the p-th spin orbital. hpq and hpqrs are one- and two-electron molecular orbital integrals, respectively. Throughout this paper we use indices i, j, and k for occupied; a, b, and c for unoccupied; and p, q, r, and s for general spin orbitals. We used u and v for the indices for general molecular orbitals. Pauli strings Pn are shown in eqn (2) and the number of qubits used for wave function storage N in eqn (3) depends on the fermion–qubit transformation method being adopted. In this study we used a Jordan–Wigner transformation (JWT),3 in which each qubit possesses an occupation number of a particular spin orbital; the qubit is in the |1〉 state if the spin orbital is occupied, otherwise |0〉. N equals the number of spin orbitals included in the active space.
and ap in eqn (1) are the creation and annihilation operators, respectively, acting on the p-th spin orbital. hpq and hpqrs are one- and two-electron molecular orbital integrals, respectively. Throughout this paper we use indices i, j, and k for occupied; a, b, and c for unoccupied; and p, q, r, and s for general spin orbitals. We used u and v for the indices for general molecular orbitals. Pauli strings Pn are shown in eqn (2) and the number of qubits used for wave function storage N in eqn (3) depends on the fermion–qubit transformation method being adopted. In this study we used a Jordan–Wigner transformation (JWT),3 in which each qubit possesses an occupation number of a particular spin orbital; the qubit is in the |1〉 state if the spin orbital is occupied, otherwise |0〉. N equals the number of spin orbitals included in the active space.
An approximate wave function is generated on the QPU by using a parametrized quantum circuit defined through an ansatz, and thus selection of an appropriate ansatz is the most important process. Ansatzes used in VQE-based quantum chemical calculations can be roughly classified into two categories; chemistry inspired and hardware efficient.56 The most famous chemistry inspired ansatz is the UCC ansatz defined as in eqn (4) and (5).10
 | (4) |
 | (5) |
In eqn (4),  is the reference wave function and the HF wave function |ΨHF〉 is usually used. T defined in eqn (5) is the operator describing electron excitations from the occupied orbitals to the virtual orbitals in the reference wave function. Compared with the traditional CC method, the UCC wave function takes into account electron de-excitations from the unoccupied to occupied orbitals (T†) and electron excitations T. The UCC energy can be computed variationally, although the number of UCC applications in classical computing is very limited.67,74–76 One of the reasons is that the Baker–Campbell–Hausdorff (BCH) expansion of the similarly transformed Hamiltonian
is the reference wave function and the HF wave function |ΨHF〉 is usually used. T defined in eqn (5) is the operator describing electron excitations from the occupied orbitals to the virtual orbitals in the reference wave function. Compared with the traditional CC method, the UCC wave function takes into account electron de-excitations from the unoccupied to occupied orbitals (T†) and electron excitations T. The UCC energy can be computed variationally, although the number of UCC applications in classical computing is very limited.67,74–76 One of the reasons is that the Baker–Campbell–Hausdorff (BCH) expansion of the similarly transformed Hamiltonian  does not terminate and therefore truncation of the expansion is necessary. By contrast, preparation of the UCC wave function on a quantum computer is straightforward, because
does not terminate and therefore truncation of the expansion is necessary. By contrast, preparation of the UCC wave function on a quantum computer is straightforward, because  is a unitary operator. Since the CCSD(T)77 (single and double excitation operators are considered, and effects of connected triples are taken into account through many body perturbation theory) method is regarded as the “gold standard” in quantum chemistry, the UCCSD can be a practical tool for reliable quantum chemical calculations on quantum computers. However, it is well known that the approximation of CCSD becomes worse when the static electron correlation effect is significant and wave function cannot be well approximated at the HF level. As a result, traditional CCSD cannot describe the potential curve associated with covalent bond dissociation correctly where static correlation is crucial and it sometimes gives the energy substantially lower than the full-CI value.58,59 By contrast, UCCSD is solved variationally and thus an upper bound condition is always satisfied. However, as Evangelista reported, the UCCSD energy largely deviates from the full-CI value around the transition structure of Be + H2 → BeH2 reaction due to slow convergence behaviour of the BCH expansion.67 Following the ab initio molecular orbital theory for classical computers, we expect that MR extension of the UCCSD ansatz is promising for the description of strongly correlated systems.
is a unitary operator. Since the CCSD(T)77 (single and double excitation operators are considered, and effects of connected triples are taken into account through many body perturbation theory) method is regarded as the “gold standard” in quantum chemistry, the UCCSD can be a practical tool for reliable quantum chemical calculations on quantum computers. However, it is well known that the approximation of CCSD becomes worse when the static electron correlation effect is significant and wave function cannot be well approximated at the HF level. As a result, traditional CCSD cannot describe the potential curve associated with covalent bond dissociation correctly where static correlation is crucial and it sometimes gives the energy substantially lower than the full-CI value.58,59 By contrast, UCCSD is solved variationally and thus an upper bound condition is always satisfied. However, as Evangelista reported, the UCCSD energy largely deviates from the full-CI value around the transition structure of Be + H2 → BeH2 reaction due to slow convergence behaviour of the BCH expansion.67 Following the ab initio molecular orbital theory for classical computers, we expect that MR extension of the UCCSD ansatz is promising for the description of strongly correlated systems.
So far, VQE with the multiconfigurational wave functions based on the UCC with generalized singles and doubles (UCCGSD) and the k-UpCCGSD ansatzes have been proposed.17,23,24 The UCCGSD ansatz takes into account occupied → occupied (e.g.,  ) and unoccupied → unoccupied (
) and unoccupied → unoccupied ( ) excitations, in addition to occupied → unoccupied (
) excitations, in addition to occupied → unoccupied (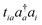 ) excitations included in the conventional UCCSD ansatz.17 In the k-UpCCGSD ansatz, fully generalized singles (
) excitations included in the conventional UCCSD ansatz.17 In the k-UpCCGSD ansatz, fully generalized singles ( ) and generalized pair-double excitations (
) and generalized pair-double excitations (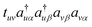 ) are considered, and the cluster operator is applied k times to the reference wave function, with each k having variationally independent amplitudes.17,24 Here, we examine the most straightforward extension of the UCC ansatz to the MR regime by using the MR-UCCpGSD ansatz as the modification of the reported MR ansatzes. In the MR-UCCpGSD the reference wave function |Ψ0〉 is not a single determinant but a multiconfigurational (MC) wave function such as complete active space self-consistent-field (CASSCF) wave functions,78,79 as defined in eqn (6) and (7).
) are considered, and the cluster operator is applied k times to the reference wave function, with each k having variationally independent amplitudes.17,24 Here, we examine the most straightforward extension of the UCC ansatz to the MR regime by using the MR-UCCpGSD ansatz as the modification of the reported MR ansatzes. In the MR-UCCpGSD the reference wave function |Ψ0〉 is not a single determinant but a multiconfigurational (MC) wave function such as complete active space self-consistent-field (CASSCF) wave functions,78,79 as defined in eqn (6) and (7).
 | (6) |
 | (7) |
Here,  is the Slater determinant included in |ΨMC〉. As the excitation operator T we take into account all possible symmetry-adapted single and double excitation operators from each reference Slater determinant |ΦI〉, as in eqn (8).
is the Slater determinant included in |ΨMC〉. As the excitation operator T we take into account all possible symmetry-adapted single and double excitation operators from each reference Slater determinant |ΦI〉, as in eqn (8).
 | (8) |
Here, the summations run over the spin orbitals those i and j are occupied and a and b are unoccupied in  . For example, in this study we used the CASSCF(2e,2o) wave function as the |ΨMC〉 in a BeH2 system, which consists of two Slater determinants: |2220000000〉 and |2202000000〉. Here, 2 and 0 specify the occupation number of molecular orbitals. In this case we consider one- and two-electron excitation operators and their complex conjugates from these two determinants. Therefore, in the MR-UCCpGSD calculations up to four-electron excitation operators from the HF configuration are involved. In our formulation of the MR-UCCpGSD, the occupied → occupied and the unoccupied → unoccupied excitations outside of the active space are not included, because these terms have zero contributions to the reference wave function as the connected terms
. For example, in this study we used the CASSCF(2e,2o) wave function as the |ΨMC〉 in a BeH2 system, which consists of two Slater determinants: |2220000000〉 and |2202000000〉. Here, 2 and 0 specify the occupation number of molecular orbitals. In this case we consider one- and two-electron excitation operators and their complex conjugates from these two determinants. Therefore, in the MR-UCCpGSD calculations up to four-electron excitation operators from the HF configuration are involved. In our formulation of the MR-UCCpGSD, the occupied → occupied and the unoccupied → unoccupied excitations outside of the active space are not included, because these terms have zero contributions to the reference wave function as the connected terms  . They can have nonzero contributions as the disconnected terms such as
. They can have nonzero contributions as the disconnected terms such as  and
and 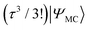 , but we assume that such contributions are small. Similar to the UCCGSD ansatz, the cluster operator is applied only once. Thus, the number of variables in MR-UCCpGSD is smaller than that of UCCGSD. In this context we used the term “partially generalized” for the name of ansatz. As easily expected, the same excitation operator can be derived from different reference determinants. In this case we merge the operators and treat them as one excitation operator. In the traditional state-specific MRCC calculations on classical computers, (i) optimization of excitation amplitudes tia and tijab and (ii) diagonalization of an effective operator to optimize |ΨMC〉 are iterated until converge.64–66 In our MR-UCCpGSD ansatz, by contrast, the abovementioned step (ii) is not included. Instead, excitation/de-excitation operators within the active space (HOMO–LUMO two-electron excitation/de-excitation operator in the case of a BeH2 system with CASSCF(2e,2o) reference) are included in the cluster operators to describe relaxation of the CI coefficients in |ΨMC〉.
, but we assume that such contributions are small. Similar to the UCCGSD ansatz, the cluster operator is applied only once. Thus, the number of variables in MR-UCCpGSD is smaller than that of UCCGSD. In this context we used the term “partially generalized” for the name of ansatz. As easily expected, the same excitation operator can be derived from different reference determinants. In this case we merge the operators and treat them as one excitation operator. In the traditional state-specific MRCC calculations on classical computers, (i) optimization of excitation amplitudes tia and tijab and (ii) diagonalization of an effective operator to optimize |ΨMC〉 are iterated until converge.64–66 In our MR-UCCpGSD ansatz, by contrast, the abovementioned step (ii) is not included. Instead, excitation/de-excitation operators within the active space (HOMO–LUMO two-electron excitation/de-excitation operator in the case of a BeH2 system with CASSCF(2e,2o) reference) are included in the cluster operators to describe relaxation of the CI coefficients in |ΨMC〉.
It should be noted that the same excited function can be generated from different cluster operators in the MR-UCCpGSD ansatz. For example, |2200200000〉 can be generated by the operation  and
and  . In our implementation of the MR-UCCpGSD ansatz, different cluster amplitudes are assigned for these excitations. However, by comparison with the MRCI wave function, only one CI coefficient per excited function is determined from the variational principle, and thus redundancy of the cluster operators is present. The existence of such variational parameter redundancy can retard variational optimization, but to our knowledge, this aspect has not been well discussed in the preceding work.24 It should also be noted that this parameter redundancy problem has a connection with the barren plateau problem80 often discussed in the VQE with hardware-efficient ansatzes. Removal of the linearly dependent variables is important to accelerate the VQE convergence, which is left as a future study.
. In our implementation of the MR-UCCpGSD ansatz, different cluster amplitudes are assigned for these excitations. However, by comparison with the MRCI wave function, only one CI coefficient per excited function is determined from the variational principle, and thus redundancy of the cluster operators is present. The existence of such variational parameter redundancy can retard variational optimization, but to our knowledge, this aspect has not been well discussed in the preceding work.24 It should also be noted that this parameter redundancy problem has a connection with the barren plateau problem80 often discussed in the VQE with hardware-efficient ansatzes. Removal of the linearly dependent variables is important to accelerate the VQE convergence, which is left as a future study.
Once an energy expectation value is computed on the QPU, the CPU executes variational optimization of the parameters. The variables are excitation amplitudes tia and tijab in eqn (5) and (8) for the UCCSD and MR-UCCpGSD ansatzes, respectively. Variational optimizations are often carried out by using gradient-free algorithms such as Nelder–Mead, Powell, and constrained optimization by linear approximation (COBYLA) methods.
As naturally expected, variational optimization in VQE cycles converges faster if the initial estimates of the parameters are closer to the optimal values. In the UCCSD ansatz, an approach to use the MP2 amplitudes is given in eqn (9) as the initial amplitudes were proposed.81
 | (9) |
In the MP2 framework one electron excitation amplitudes tia are zero due to Brillouin's theorem.82 However, if we consider the second order wave function in the perturbation theory, we can derive eqn (10),83 which can be used as the initial estimate of tia amplitudes.
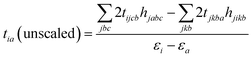 | (10) |
Note that in the presence of non-dynamic electron correlation, the reorganization from the HF description should be substantial through sizable contributions from single excitations.84,85 We expect that nonzero tia initial amplitudes can accelerate the convergence of the VQE, especially when static electron correlation is prominent. Using a partial renormalization with size-consistency, the scaled amplitudes in eqn (11) can also be derived86 and tested in this study.
 | (11) |
Importantly, only the spatial symmetry-adapted excitation operators have nonzero amplitudes by adopting the initial amplitude estimation methods described here. Excitation operators giving zero initial amplitudes have no contribution to the ground state wave function when they appear in the connected terms. Thus, application of perturbation theory-based initial amplitude estimation is useful not only to find good initial estimates of variables but also to automatically select excitation operators that give a nonzero contribution to the ground state wave function. For the MR-UCCpGSD calculations, we extended the initial amplitude estimation technique described above to the MR regime as follows. Assume that the reference wave function is described by a linear combination of Slater determinants as in eqn (7). The initial amplitudes for MR-UCCpGSD can be computed by a linear combination of the product of the CI expansion coefficient cI and the MP2 amplitudes computed by using each Slater determinant as in eqn (12), for two electron excitation amplitudes, for example.
 | (12) |
Calculations of the amplitudes tijab(ΦI) using eqn (9)–(11) require orbital energies. We used the CASSCF canonical orbital energies for the 1 1A1 ground state for the initial amplitude estimations. The UCCSD and MR-UCCpGSD energies using initial (unoptimized) amplitudes are lower than the energy of reference wave functions (see Table S1 in the ESI† for details). It should be emphasized that the ability to use perturbation theory to estimate good initial amplitudes with a low computational cost described here is one of the major advantages of the UCCSD and the MR-UCCpGSD ansatzes.
Because molecules exhibit different molecular properties at different spin multiplicities, spin symmetry-adapted treatment is very important in quantum chemical calculations. Spin symmetry adaptation can be accomplished by considering the spin symmetry-adapted excitation operators for the singlet defined in eqn (13).
 | (13) |
In the UCCSD and MR-UCCpGSD ansatzes the spin symmetry adaptation can be done by using the same excitation amplitudes for the spin α → α and β → β excitations, as in eqn (14).
 | (14) |
For two-electron excitation operators, we assumed the spin independence of the amplitudes in the Goldstone diagram82 to ensure the wave function being spin symmetry-adapted.
3. Computational conditions
In this study, we calculated ten geometries along the sampling path for the C2v potential energy surface of Be + H2 → BeH2 reaction pathway, by following the previous study by Purvis and co-workers.61 The Cartesian coordinates of H atoms are listed in Table 1. Here, the Be atom is located at the origin of the coordinates (0.0, 0.0, 0.0). We used the same basis set as the study by Purvis and co-workers,61 which is comprised of (10s 3p)/[3s 1p] for Be and (4s)/[2s] for H. The exponents and contraction coefficients for the basis set is given in Section S1 of the ESI.† The wave function is mapped onto 20 qubits by using this basis set. For the LiH molecule with R(Li–H) = 1.0, 2.0, 3.0, and 4.0 Å, we employed the STO-3G basis set and performed 12 qubit simulations. The geometry of the P4 cluster is illustrated in Fig. 3. The P4 cluster consists of two parallel hydrogen molecules with nuclei in a rectangular arrangement. Its geometry is characterized by intra- and inter-molecular H–H distances a and α, respectively. In this study we used a fixed value a = 2.0 Bohr with different α values (α = 1.8, 1.9, 1.99, 2.01, 2.1, and 2.2 Bohr). We used the 6-31G basis set for the study of the P4 cluster, which needs 16 qubits for the VQE.| Point | X | Y | Z |
|---|---|---|---|
| A | 0.0 | ±2.540 | 0.00 |
| B | 0.0 | ±2.080 | 1.00 |
| C | 0.0 | ±1.620 | 2.00 |
| D | 0.0 | ±1.390 | 2.50 |
| E | 0.0 | ±1.275 | 2.75 |
| F | 0.0 | ±1.160 | 3.00 |
| G | 0.0 | ±0.930 | 3.50 |
| H | 0.0 | ±0.700 | 4.00 |
| I | 0.0 | ±0.700 | 6.00 |
| J | 0.0 | ±0.700 | 20.00 |
For the numerical simulations of the VQE-based UCCSD and MR-UCCpGSD calculations, we developed a python program by utilizing OpenFermion87 and Cirq88 libraries. We used a quantum state vector simulator to calculate the energy expectation value, which calculates the expectation value of operator A using the state vector directly, 〈A〉 = 〈Ψ|A|Ψ〉, rather than a statistical sampling of the measurement outcome. This corresponds to the infinite number of repetitive measurements. Needless to say, in the real quantum devices only a finite number of measurements are available, but we are interested in the accuracy and the validity of the ansatz, and hence a quantum state vector simulator is more suitable for this purpose. The quantum circuits for the UCCSD and MR-UCCpGSD ansatzes are constructed by adopting the first order Trotter decomposition with the Trotter slice number n = 1. It is known that the Trotterized UCC ansatz depends on the term ordering of cluster operators.89 In this work we adopted a magnitude ordering, in which excitation operators are ordered by the absolute value of initial amplitudes. Magnitude ordering is known to exhibit a smaller Trotter error than lexicographical ordering.90 We also evaluated the effect of Trotter term ordering by randomly shuffling the terms for UCCSD/STO-3G simulations of the BeH2 system at point E, obtaining that the standard deviation is less than 1 kcal mol−1 for ten simulations (see Table S3 in the ESI†). The HF calculations and computations of one- and two-electron atomic orbital integrals were performed by using the GAMESS-US program package.91 One- and two-electron molecular orbital integrals were prepared by using our own AO → MO integral transformation program. All the numerical simulations were executed on Linux workstations with Intel Xeon Gold 6134 processors.
4. Results and discussion
4.1. Dependence of the optimization algorithm and initial cluster amplitudes in a LiH molecule
Selection of the appropriate optimization algorithm for variational optimization of parameters and using a good initial estimate of variables are important to rapidly achieve the variational minima. We carried out preliminary VQE-UCCSD/STO-3G simulations of a LiH molecule with R(Li–H) = 1.0, 2.0, 3.0, and 4.0 Å using Nelder–Mead, Powell, and COBYLA algorithms for the parameter optimizations, with three types of different initial tia amplitudes (tia = 0, tia(unscaled) using eqn (10), and tia(scaled) using eqn (11)). The results of the quantum circuit simulations at the geometry R(Li–H) = 3.0 Å are plotted in Fig. 4, and those of other geometries are given in Fig. S1–S3 in the ESI.† Our simulations revealed that Nelder–Mead is sometimes trapped to a local minimum and gives rise to a larger deviation in energy from the full-CI value when we adopted tia = 0 or tia(unscaled) as the initial estimate. By employing COBYLA and Powell algorithms the optimization converged to the same energy regardless of the choice of initial tia amplitudes. COBYLA exhibits slightly faster convergence than Powell. Thus, we adopted the COBYLA algorithm and tia(scaled) for the following VQE-UCCSD and MR-UCCpGSD simulations. The initial tia amplitude dependences were also examined in the BeH2 system at points A, D, E, F, and I. The results are summarized in Fig. S4 in the ESI.† | ||
| Fig. 4 The VQE-UCCSD simulation results of the LiH molecule with R(Li–H) = 3.0 Å. Top: The energy difference from the full-CI value. Bottom: The square overlap with the full-CI wave function. | ||
4.2. UCCSD simulations of the BeH2 system
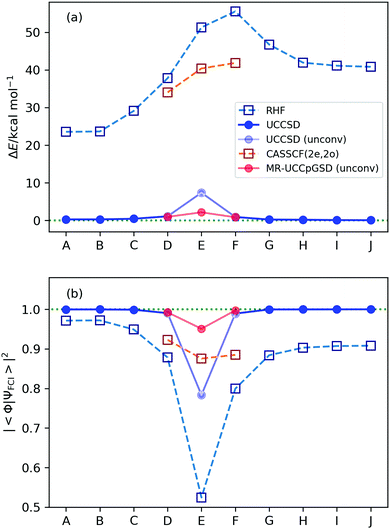
The deviations of the energy expectation values calculated at the RHF, CASSCF(2e, 2o), UCCSD, and MR-UCCpGSD methods from the full-CI one is illustrated in Fig. 5a, and the square overlap between the approximated and the full-CI wave functions is plotted in Fig. 5b. The values of the HF, CASSCF, UCCSD, MR-UCCpGSD, and full-CI energies are summarized in Table S4 in the ESI.† We also confirmed that the HF and full-CI energies computed in this work coincides with the values reported by Purvis and co-workers.61 Note that we set the number of maximum iterations in the variational optimization to be 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, but the UCCSD simulations did not converge after 10
000, but the UCCSD simulations did not converge after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations for points D, E, and F (these points are plotted using faded blue in Fig. 5). As clearly seen in Fig. 5, the UCCSD ansatz gives the energy close to the full-CI one for all points except for point E. The point E corresponds to the transition structure of the reaction pathway under study, and it is closest to the point where the avoided crossing occurs. The square overlap between the HF and the full-CI wave functions are calculated to be 0.524, and thus the HF wave function is not a good approximation for the electronic ground state. We also checked the stability of the HF wave function92 at points D, E, and F, observing the triplet instabilities at these points, and singlet instability at point E (see Section S7 in the ESI† for details). The deviation of the simulated VQE energy using the UCCSD ansatz from the full-CI one is 0.263 and 0.056 kcal mol−1 for points A and J, respectively, and that of point E with unconverged simulation after 10
000 iterations for points D, E, and F (these points are plotted using faded blue in Fig. 5). As clearly seen in Fig. 5, the UCCSD ansatz gives the energy close to the full-CI one for all points except for point E. The point E corresponds to the transition structure of the reaction pathway under study, and it is closest to the point where the avoided crossing occurs. The square overlap between the HF and the full-CI wave functions are calculated to be 0.524, and thus the HF wave function is not a good approximation for the electronic ground state. We also checked the stability of the HF wave function92 at points D, E, and F, observing the triplet instabilities at these points, and singlet instability at point E (see Section S7 in the ESI† for details). The deviation of the simulated VQE energy using the UCCSD ansatz from the full-CI one is 0.263 and 0.056 kcal mol−1 for points A and J, respectively, and that of point E with unconverged simulation after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations is 7.360 kcal mol−1. The VQE-UCCSD simulation overestimates the reaction energy barrier of about 7.0 kcal mol−1 from the full-CI if the variational optimization is terminated at 10
000 iterations is 7.360 kcal mol−1. The VQE-UCCSD simulation overestimates the reaction energy barrier of about 7.0 kcal mol−1 from the full-CI if the variational optimization is terminated at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations. This is the result of unconverged simulations, and therefore this value is the upper limit of the overestimation. The magnitude of the overestimation can be reduced by applying more iterations. However, the numerical simulation takes 18 days in our computer environment, and raising the maximum number of iterations seems to be impractical. Note that estimating the computational time of the VQE with real quantum devices is not straightforward, because decoherence time, available basis quantum gates, qubit connectivity, and time for single quantum gates, etc., are device dependent, and the accuracy of the VQE energy depends not only on the ansatz but also error rates, the number of repetitions for expectation value evaluation, and so on.
000 iterations. This is the result of unconverged simulations, and therefore this value is the upper limit of the overestimation. The magnitude of the overestimation can be reduced by applying more iterations. However, the numerical simulation takes 18 days in our computer environment, and raising the maximum number of iterations seems to be impractical. Note that estimating the computational time of the VQE with real quantum devices is not straightforward, because decoherence time, available basis quantum gates, qubit connectivity, and time for single quantum gates, etc., are device dependent, and the accuracy of the VQE energy depends not only on the ansatz but also error rates, the number of repetitions for expectation value evaluation, and so on.
Convergence behaviour of the VQE-UCCSD simulations at point E are plotted in Fig. 6, and those of other points is summarized in Fig. S5 in the ESI.† To estimate the number of iterations required to achieve convergence, we attempted to fit the energy difference plot in the range between 1000 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations with an exponential function, obtaining ΔE = 123.68x−0.303 with R2 = 0.9827 (see Fig. S6 in the ESI†). Needless to say, there is no theoretical background for the energy change in the optimizations to be in the form of an exponential function. However, if we assume that the VQE optimization proceeds along the exponential function, we need about 8
000 iterations with an exponential function, obtaining ΔE = 123.68x−0.303 with R2 = 0.9827 (see Fig. S6 in the ESI†). Needless to say, there is no theoretical background for the energy change in the optimizations to be in the form of an exponential function. However, if we assume that the VQE optimization proceeds along the exponential function, we need about 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations to achieve 1.0 kcal mol−1 of deviation from the full-CI value. It should also be noted that the square overlap between the UCCSD and the full-CI wave functions is at most 0.783 even after 10
000 iterations to achieve 1.0 kcal mol−1 of deviation from the full-CI value. It should also be noted that the square overlap between the UCCSD and the full-CI wave functions is at most 0.783 even after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations at point E. These results clearly exemplify the fact that convergence of the UCCSD ansatz is very slow if the square overlap between the reference and full-CI wave functions is small. One of the major reasons for this extreme slow convergence behaviour is that the number of excitation operators with sizable excitation amplitudes are large at point E, due to the poorness of the HF approximation and significant contributions from the T1 terms. The wave function of strongly correlated systems are highly entangled, and thus acquiring optimal parameters becomes a more difficult task. This aspect can be supported by the traditional CCSD, CCSD(T), quadratic configuration interaction with singles and doubles (QCISD),93 and Brueckner doubles (BD)94 calculations (see Section S9 in the ESI†). It should also be noted that in the VQE-DUCC study by Metcalf and co-workers, point E showed a larger deviation from the full-CI energy (27 mHartree) compared with other points (12–17 mHartree).25 This fact also exemplifies the complexity of the electronic structure at point E. Another possible reason is that the initial amplitudes evaluated using eqn (9)–(11) are not so good for strongly correlated electronic structures because of the slow convergence of perturbation expansion.
000 iterations at point E. These results clearly exemplify the fact that convergence of the UCCSD ansatz is very slow if the square overlap between the reference and full-CI wave functions is small. One of the major reasons for this extreme slow convergence behaviour is that the number of excitation operators with sizable excitation amplitudes are large at point E, due to the poorness of the HF approximation and significant contributions from the T1 terms. The wave function of strongly correlated systems are highly entangled, and thus acquiring optimal parameters becomes a more difficult task. This aspect can be supported by the traditional CCSD, CCSD(T), quadratic configuration interaction with singles and doubles (QCISD),93 and Brueckner doubles (BD)94 calculations (see Section S9 in the ESI†). It should also be noted that in the VQE-DUCC study by Metcalf and co-workers, point E showed a larger deviation from the full-CI energy (27 mHartree) compared with other points (12–17 mHartree).25 This fact also exemplifies the complexity of the electronic structure at point E. Another possible reason is that the initial amplitudes evaluated using eqn (9)–(11) are not so good for strongly correlated electronic structures because of the slow convergence of perturbation expansion.
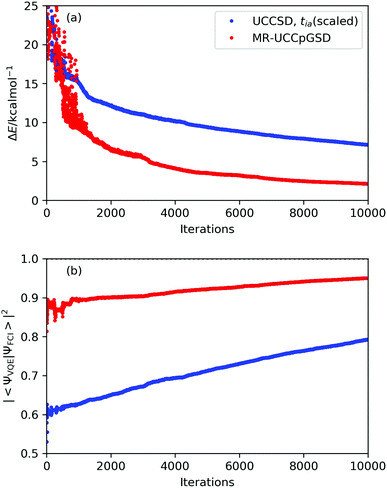 | ||
| Fig. 6 Convergence behaviour of the VQE-UCCSD and MR-UCCpGSD simulations at point E. (a) The energy difference from the full-CI and (b) the square overlap with the full-CI wave function. | ||
To investigate the convergence behaviour in more detail, we examined the UCCSD simulations at point E by using the STO-3G basis set. The number of variables is reduced from 151 to 44 by employing the STO-3G basis set, and thus VQE optimization converges faster. The UCCSD/STO-3G simulation converged after 3329 iterations, giving ΔEUCCSD–full-CI = 2.866 kcal mol−1 and |〈ΨUCCSD|Ψfull-CI〉|2 = 0.963. From this result the UCCSD seems to give accurate energy if a sufficient number of iterations are possible. We also checked the reference orbital dependence on the convergence behaviour by using the optimized orbital of the CASSCF(2e,2o)/STO-3G as the SR-UCCSD simulations. After 3496 iterations, we obtained that ΔEUCCSD–full-CI = 2.864 kcal mol−1 and |〈ΨUCCSD|Ψfull-CI〉|2 = 0.962, confirming that reference orbital dependence is very small. Nevertheless, it is natural to assume that the number of iterations required for convergence depends on the choice of reference orbitals. In this context, orbital optimized VQE techniques19,20 are promising candidates to accelerate the convergence behaviour. In addition, we performed the k-UpCCGSD/STO-3G simulations with k = 1, 2, and 3 at point E for comparison. The simulations did not converge after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations for k = 3. The energies obtained from the unconverged 3-UpCCGSD simulations are ΔE = 10.231 and 6.907 kcal mol−1 for the HF and CASSCF reference orbitals, respectively. The 3-UpCCGSD energies are slightly larger than the UCCSD ones, but we cannot exclude the possibility that 3-UpCCGSD can have a lower energy than UCCSD and MR-UCCpGSD, by improving the initial amplitudes or by taking more iterations (see Section S10 in the ESI† for details).
000 iterations for k = 3. The energies obtained from the unconverged 3-UpCCGSD simulations are ΔE = 10.231 and 6.907 kcal mol−1 for the HF and CASSCF reference orbitals, respectively. The 3-UpCCGSD energies are slightly larger than the UCCSD ones, but we cannot exclude the possibility that 3-UpCCGSD can have a lower energy than UCCSD and MR-UCCpGSD, by improving the initial amplitudes or by taking more iterations (see Section S10 in the ESI† for details).
4.3. MR-UCCpGSD simulations of the BeH2 system
Because the conventional SR-UCCSD converges very slowly for the calculations of strongly correlated systems, adopting the MR framework is a natural choice for the alternative. One of the authors proposed a theoretical method to generate the multiconfigurational wave functions on quantum computers by utilizing the diradical characters y computed from the broken-symmetry spin-unrestricted Hartree–Fock (BS-UHF) wave functions.95 First, we computed the energy expectation values and square overlaps with the full-CI wave functions of the two-configurational wave functions constructed by following the approach described in ref. 95. The results are summarized in Table 2. The BS-UHF computations converged to the closed-shell RHF wave function at points A, B, I, and J.| Point | y | ΔE2c–full-CI/kcal mol−1 | |〈Ψ2c|Ψfull-CI〉|2 |
|---|---|---|---|
| C | 0.0008 | 28.536 | 0.952 |
| D | 0.2991 | 35.591 | 0.933 |
| E | 0.7851 | 43.553 | 0.905 |
| F | 0.6125 | 48.498 | 0.886 |
| G | 0.0373 | 42.417 | 0.903 |
| H | 0.0007 | 40.998 | 0.906 |
Noticeably, the two-configurational wave function constructed by using the diradical character y has a larger square overlap with the full-CI wave function compared with the unconverged UCCSD wave function after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations at point E due to the extremely slow convergence behaviour of the UCCSD ansatz, although the energy difference between the two-configurational wave function and the full-CI is notably large due to the lack of the dynamic electron correlation effect. One of the anticipated applications of the VQE is the preparation of approximate wave functions for the input of the QPE-based full-CI.96 The QPE utilizes a projective measurement to obtain the full-CI energy, and therefore using the wave function having a large overlap with the full-CI is very important.3 In this context, the conventional SR-UCCSD is less appropriate than the two-configurational wave functions constructed using the diradical characters for the initial wave functions of the QPE,95 unless this slow convergence problem is resolved. We attempted to carry out VQE simulations with the MR-UCCpGSD ansatz for the points D, E, and F, which have large diradical characters. However, using the two-configurational wave functions directly as the reference wave functions in the MR-UCCpGSD simulations is not plausible, because the two-configurational wave functions constructed by utilizing the diradical character y are not spatial symmetry adapted, and therefore the number of excitation operators with nonzero contributions to the electronic ground state will increase. Instead, we performed the CASSCF(2e,2o) calculations and use the CASSCF wave function as the reference in the MR-UCCpGSD calculations. Note that the computational cost for CASSCF increases exponentially against the size of active space, and thus the reference CASSCF calculation itself becomes a bottleneck in the MR-UCCpGSD calculations for large systems. The application of the spatial symmetry recovery technique97 to the natural orbitals of the BS-UHF wave function is a plausible solution.
000 iterations at point E due to the extremely slow convergence behaviour of the UCCSD ansatz, although the energy difference between the two-configurational wave function and the full-CI is notably large due to the lack of the dynamic electron correlation effect. One of the anticipated applications of the VQE is the preparation of approximate wave functions for the input of the QPE-based full-CI.96 The QPE utilizes a projective measurement to obtain the full-CI energy, and therefore using the wave function having a large overlap with the full-CI is very important.3 In this context, the conventional SR-UCCSD is less appropriate than the two-configurational wave functions constructed using the diradical characters for the initial wave functions of the QPE,95 unless this slow convergence problem is resolved. We attempted to carry out VQE simulations with the MR-UCCpGSD ansatz for the points D, E, and F, which have large diradical characters. However, using the two-configurational wave functions directly as the reference wave functions in the MR-UCCpGSD simulations is not plausible, because the two-configurational wave functions constructed by utilizing the diradical character y are not spatial symmetry adapted, and therefore the number of excitation operators with nonzero contributions to the electronic ground state will increase. Instead, we performed the CASSCF(2e,2o) calculations and use the CASSCF wave function as the reference in the MR-UCCpGSD calculations. Note that the computational cost for CASSCF increases exponentially against the size of active space, and thus the reference CASSCF calculation itself becomes a bottleneck in the MR-UCCpGSD calculations for large systems. The application of the spatial symmetry recovery technique97 to the natural orbitals of the BS-UHF wave function is a plausible solution.
The MR-UCCpGSD results are also plotted in Fig. 5, and the convergence behaviour of the UCCSD and MR-UCCpGSD calculations at point E are depicted in Fig. 6. The energy expectation value at point E drastically improved by adopting the MR approach. The MR-UCCpGSD calculation did not converge even after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations, but the deviation from the full-CI energy is calculated to be 2.143 kcal mol−1 and 〈ΨMR-UCCpGSD|Ψfull-CI〉|2 = 0.950, which is greatly improved by the SR-UCCSD results. By fitting the plot of energy difference with an exponential function, we obtained ΔE = 1289.2x−0.693 with R2 = 0.9932 (see Fig. S6 in the ESI†). From this, we expect that about 30
000 iterations, but the deviation from the full-CI energy is calculated to be 2.143 kcal mol−1 and 〈ΨMR-UCCpGSD|Ψfull-CI〉|2 = 0.950, which is greatly improved by the SR-UCCSD results. By fitting the plot of energy difference with an exponential function, we obtained ΔE = 1289.2x−0.693 with R2 = 0.9932 (see Fig. S6 in the ESI†). From this, we expect that about 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations are needed to achieve the energy deviation from the full-CI within 1 kcal mol−1. This value should be compared with ca. 8
000 iterations are needed to achieve the energy deviation from the full-CI within 1 kcal mol−1. This value should be compared with ca. 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations in the conventional SR-UCCSD. However, 30
000 iterations in the conventional SR-UCCSD. However, 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations are still too many for practical use. The MR-UCCpGSD simulations took more time (33 days) compared with the SR-UCCSD simulations (18 days), because the MR-UCCpGSD ansatz includes a larger number of variables, and the parametrized quantum circuit is deeper. Note that our numerical simulations were performed without parallelization, and therefore the simulation can be accelerated by high performance computing with parallelization.
000 iterations are still too many for practical use. The MR-UCCpGSD simulations took more time (33 days) compared with the SR-UCCSD simulations (18 days), because the MR-UCCpGSD ansatz includes a larger number of variables, and the parametrized quantum circuit is deeper. Note that our numerical simulations were performed without parallelization, and therefore the simulation can be accelerated by high performance computing with parallelization.
The current simulations are based on gradient-free optimization, and gradient-based optimization may accelerate the convergence. We tested the gradient-based optimizations in the UCCSD/STO-3G and MR-UCCpGSD/STO-3G calculations at point E using the BFGS algorithm in conjunction with the gradient estimation based on the 2-point finite difference method. By adopting the BFGS algorithm the optimization converged a smaller number of iterations (35 and 63 iterations for UCCSD and MR-UCCpGSD, respectively) giving ΔE(VQE–full-CI) = 2.579 and 1.647 kcal mol−1 for UCCSD and MR-UCCpGSD, respectively. However, we need a larger number of function evaluations (3566 and 9512 for UCCSD and MR-UCCpGSD) than COBYLA (3329 and 4917) to achieve convergence. We emphasize that implementation of methods that can reduce the number of function evaluations or application of more sophisticated optimization algorithms such as an approach to calculate analytical gradients by adopting a parameter shift rule98 or DIIS-based algorithm99 is essential for the practical use of the VQE for quantum chemical calculations. Another possible approach to improve the convergence behaviour is adopting the sequential optimization approaches. Nevertheless, it should be emphasized that the MR-UCCpGSD ansatz shows faster convergence behaviour compared with UCCSD at strongly correlated systems and it can give a more reliable wave function. Multiconfigurational treatment is quite powerful to study the strongly correlated systems on quantum computers.
4.4. LiH molecule and P4 cluster
In order to further investigate the performance of the MR-UCCpGSD ansatz, we executed VQE simulations of the LiH molecule with R(Li–H) = 3.0 and 4.0 Å, and a rectangular P4 cluster using UCCSD and MR-UCCpGSD ansatzes. Note that the BS-UHF calculations converged to the RHF solution in the LiH molecule with R(Li–H) = 1.0 and 2.0 Å, indicating that the ground state wave function is well approximated at the RHF level. The P4 cluster becomes strongly correlated systems when the intermolecular distance α approaches a.The results are summarized in Table 3. In all the geometries being studied, the MR-UCCpGSD ansatz needs more iterations than the UCCSD ansatz, but the deviations of the computed energies from the full-CI values are smaller for MR-UCCpGSD ansatz. Importantly, the UCCSD gives large ΔE values at the geometries with a large diradical character, y, although the MR-UCCpGSD gives ΔE < 0.13 kcal mol−1 and an almost constant error for all the points being studied. These results exemplify that the MR-UCCpGSD ansatz is capable of describing the electronic structures of intermediate and strongly correlated systems with the same accuracy, which is essential to correctly understand chemical phenomena from quantum chemical calculations.
| System | Geometry | y(PUHF) | ΔE(VQE–full-CI)/kcal mol−1 | |〈ΨVQE|Ψfull-CI〉|2 | Number of function evaluations | |||
|---|---|---|---|---|---|---|---|---|
| UCCSD | MR-UCCpGSD | UCCSD | MR-UCCpGSD | UCCSD | MR-UCCpGSD | |||
| LiH | R(Li–H) = 3.0 Å | 0.5015 | 0.111 | 0.024 | 0.9987 | 0.9996 | 1013 | 1060 |
| LiH | R(Li–H) = 4.0 Å | 0.8334 | 0.156 | 0.022 | 0.9985 | 0.9996 | 680 | 957 |
| P4 cluster | α = 1.80 Bohr | 0.3895 | 0.537 | 0.125 | 0.9990 | 0.9999 | 2247 | 4814 |
| P4 cluster | α = 1.90 Bohr | 0.6850 | 1.259 | 0.105 | 0.9965 | 0.9999 | 2361 | 3234 |
| P4 cluster | α = 1.99 Bohr | 0.9692 | 2.685 | 0.122 | 0.9921 | 0.9998 | 2847 | 3558 |
| P4 cluster | α = 2.01 Bohr | 0.9696 | 2.668 | 0.117 | 0.9922 | 0.9999 | 2680 | 3330 |
| P4 cluster | α = 2.10 Bohr | 0.7148 | 1.242 | 0.113 | 0.9965 | 0.9999 | 2427 | 3053 |
| P4 cluster | α = 2.20 Bohr | 0.4860 | 0.560 | 0.093 | 0.9989 | 0.9999 | 2051 | 3134 |
5. Summary
In this work, we carried out numerical simulations of the VQE for the quasi-reaction pathway in the C2v symmetry of Be atom insertion into a H2 molecule, LiH molecule and P4 cluster, focusing on the accuracy of the wave function at the geometry nearby an avoided crossing point and applicability of the UCCSD and MR-UCCpGSD ansatzes to strongly correlated systems. The conventional SR-UCCSD shows extremely slow convergence behaviour in the quasi-transition structure in the Be + H2 → BeH2 reaction pathway, which makes us difficult to acquire optimal parameters and relevant energies. The simulated VQE energy of the BeH2 system at point E obtained using the UCCSD ansatz after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations is 7.360 kcal mol−1 higher than the full-CI value, and the square overlap with the full-CI wave function is at most 0.783. This square overlap value is smaller than that calculated by using the two-configurational wave function constructed by using the diradical character y. Unless this slow convergence problem is resolved, the UCCSD ansatz is not a proper choice for the study of strongly correlated systems, even for the purpose of preparing the initial wave function for the QPE-based full-CI.
000 iterations is 7.360 kcal mol−1 higher than the full-CI value, and the square overlap with the full-CI wave function is at most 0.783. This square overlap value is smaller than that calculated by using the two-configurational wave function constructed by using the diradical character y. Unless this slow convergence problem is resolved, the UCCSD ansatz is not a proper choice for the study of strongly correlated systems, even for the purpose of preparing the initial wave function for the QPE-based full-CI.
By contrast, the MR-UCCpGSD ansatz gives an energy much closer to the full-CI one at the geometry nearby the avoided crossing, exemplifying that the MR treatment is more feasible for the accurate descriptions of the electronic structures of strongly correlated systems. The reaction energy barrier computed using the MR-UCCpGSD ansatz is still overestimated, but significant improvement of the transition energy is observed by applying the MR approach. Importantly, in the calculations of the LiH molecule and P4 cluster, the deviation of the UCCSD energies from the full-CI values depends on the diradical character y and hence multiconfigurational character. By contrast, the MR-UCCpGSD ansatz gives similar ΔE(VQE–full-CI) values regardless of the magnitude of open shell electronic configurations. This feature is very important for the application of the VQE to various chemical systems and for correctly understanding the chemical phenomena from the quantum chemical point of view.
The reaction pathway of Be atom insertion into a H2 molecule being investigated is a representative system, in which both dynamic and static electron correlation effects are prominent. However, investigating other strongly correlated systems is nevertheless very important to further disclose the characteristics of the UCCSD and the MR-UCCpGSD ansatzes in more detail. There are many molecular systems whose dynamic and static electron correlation effects play significant roles, such as the electronic ground state of ozone,100 the out-of-plane transition state of the cis–trans isomerization reaction of diazene,101 zigzag edges of graphene nanoribbons,102,103 and so on. Molecules having such complicated electronic structures are the systems in which sophisticated quantum chemical calculations are truly desirable, and thus the importance of MR treatments cannot be overemphasized. Applications of the MR-UCCpGSD ansatz for other strongly correlated systems are ongoing and will be discussed in the forthcoming paper.
Author contributions
K. Sugisaki, Y. Minato and Y. Mochizuki planned and conducted the project. K. Sugisaki, K. Okuwaki and Y. Mochizuki carried out the quantum chemical calculations. K. Sugisaki and T. Kato developed the quantum circuit simulation programs and performed numerical simulations. K. Sugisaki and Y. Mochizuki wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by JSPS KAKENHI Scientific Research C (Grant No. 18K03465 and 21K03407). K. S. acknowledges the support from the JST PRESTO project “Quantum Software” (JPMJPR1914). K. S. thanks Prof. D. Mukherjee, Prof. B. P. Das, and Dr V. S. Prasannaa for helpful discussions.References
- P. W. Shor, Algorithms for quantum computation: discrete logarithms and factoring, in Proc. 35th Ann. Symp. on the Foundations of Computer Science, ed. S. Goldwasser, IEEE Computer Society Press, Los Alamitos, California, 1994, pp. 124–134 Search PubMed.
- K. K. H. Cheung and M. Mosca, Decomposing finite Abelian groups, Quantum Inf. Comput., 2001, 1(3), 26–32 Search PubMed.
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Simulated quantum computation of molecular energies, Science, 2005, 309, 1704–1707 CrossRef CAS PubMed.
- C. Ryan-Anderson, J. G. Bohnet, K. Lee, D. Gresh, A. Hankin, J. P. Gaebler, D. Francois, A. Chernoguzov, D. Lucchetti, N. C. Brown, T. M. Gatterman, S. K. Halit, K. Gilmore, J. A. Gerber, B. Neyenhuis, D. Hayes and R. P. Stutz, Realization of real-time fault-tolerant quantum error correction, Phys. Rev. X, 2021, 11, 041058 CAS.
- S. Krinner, N. Lacroix, A. Remm, A. Di Paolo, E. Genois, C. Leroux, C. Hellings, S. Lazar, F. Swiadek, J. Herrmann, G. J. Norris, C. K. Andersen, M. Müller, A. Blais, C. Eichler and A. Wallraff, Realizing repeated quantum error correction in a distance-three surface code, 2021, arXiv:2112.03708 DOI:10.48550/arXiv.2112.03708.
- Y. Zhao, Y. Ye, H.-L. Huang, Y. Zhang, D. Wu, H. Guan, Q. Zhu, Z. Wei, T. He, S. Cao, F. Chen, T.-H. Chung, H. Deng, D. Fan, M. Gong, C. Guo, S. Guo, L. Han, N. Li, S. Li, Y. Li, F. Liang, J. Lin, H. Qian, H. Rong, H. Su, L. Sun, S. Wang, Y. Wu, Y. Xu, C. Ying, J. Yu, C. Zha, K. Zhang, Y.-H. Huo, C.-Y. Lu, C.-Z. Peng, X. Zhu and J.-W. Pan, Realization of an error-correcting surface code with superconducting qubits, 2021, arXiv:2112.13505 DOI:10.48550/arXiv.2112.13505.
- M.-H. Yung, J. Casanova, A. Mezzacapo, J. McClean, L. Lamata, A. Aspuru-Guzik and E. Solano, From transistor to trapped-ion computers for quantum chemistry, Sci. Rep., 2014, 4, 3589 CrossRef PubMed.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O’Brien, A variational eigenvalue solver on a photonic quantum processor, Nat. Commun., 2014, 5, 4213 CrossRef CAS PubMed.
- J. Preskill, Quantum computing in the NISQ era and beyond, Quantum, 2018, 2, 79 CrossRef.
- A. G. Taube and R. J. Bartlett, New perspectives on unitary coupled-cluster theory, Int. J. Quantum Chem., 2006, 106, 3393–3401 CrossRef CAS.
- F. A. Evangelista, G. K.-L. Chan and G. E. Scuseria, Exact parametrization of fermionic wave functions via unitary coupled cluster theory, J. Chem. Phys., 2019, 151, 244112 CrossRef PubMed.
- A. Anand, P. Schleich, S. Alperin-Lea, P. W. K. Jensen, S. Sim, M. Díaz-Tinoco, J. S. Kottmann, M. Degroote, A. F. Izmaylov and A. Aspuru-Guzik, A quantum computing view on unitary coupled cluster theory, Chem. Soc. Rev., 2022, 51, 1659–1684 RSC.
- H. R. Grimsley, S. E. Economou, E. Barnes and N. J. Mayhall, An adaptive variational algorithm for exact molecular simulations on a quantum computer, Nat. Commun., 2019, 10, 3007 CrossRef PubMed.
- I. G. Ryabinkin, T.-C. Yen, S. N. Genin and A. F. Izmaylov, Qubit coupled cluster method: A systematic approach to quantum chemistry on a quantum computer, J. Chem. Theory Comput., 2018, 14, 6317–6326 CrossRef CAS PubMed.
- A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow and J. M. Gambetta, Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets, Nature, 2017, 549, 242–246 CrossRef CAS PubMed.
- P. K. Barkoutsos, J. F. Gonthier, I. Sokolov, N. Moll, G. Salis, A. Fuhrer, M. Ganzhorn, D. J. Egger, M. Troyer, A. Mezzacapo, S. Filipp and I. Tavernelli, Quantum algorithms for electronic structure calculations: Particle–hole Hamiltonian and optimized wave-function expansions, Phys. Rev. A, 2018, 98, 022322 CrossRef CAS.
- J. Lee, W. J. Huggins, M. Head-Gordon and K. B. Whaley, Generalized unitary coupled cluster wave functions for quantum computation, J. Chem. Theory Comput., 2019, 15, 311–324 CrossRef CAS PubMed.
- P.-L. Dallaire-Demers, J. Romero, L. Veis, S. Sim and A. Aspuru-Guzik, Low-depth circuit ansatz for preparing correlated fermionic states on a quantum computer, Quantum Sci. Technol., 2019, 4, 045005 CrossRef.
- W. Mizukami, K. Mitarai, Y. O. Nakagawa, T. Yamamoto, T. Yan and Y. Ohnishi, Orbital optimized unitary coupled cluster theory for quantum computer, Phys. Rev. Res., 2020, 2, 033421 CrossRef CAS.
- I. O. Sokolov, P. K. Barkoutsos, P. J. Ollitrault, D. Greenberg, J. Rice, M. Pistoia and I. Tavernelli, Quantum orbital-optimized unitary coupled cluster method in the strongly correlated regime: Can quantum algorithms outperform their classical equivalents?, J. Chem. Phys., 2020, 152, 124107 CrossRef CAS PubMed.
- Y. Matsuzawa and Y. Kurashige, Jastrow-type decomposition in quantum chemistry for low-depth quantum circuits, J. Chem. Theory Comput., 2020, 16, 944–952 CrossRef CAS PubMed.
- I. G. Ryabinkin, R. A. Lang, S. N. Genin and A. F. Izmaylov, Iterative qubit coupled cluster approach with efficient screening of generators, J. Chem. Theory Comput., 2020, 16, 1055–1063 CrossRef CAS PubMed.
- N. H. Stair, R. Huang and F. A. Evangelista, A multireference quantum Krylov algorithm for strongly correlated electrons, J. Chem. Theory Comput., 2020, 16, 2236–2245 CrossRef CAS PubMed.
- G. Greene-Diniz and D. M. Ramo, Generalized unitary coupled cluster excitations for multireference molecular states optimized by the variational quantum eigensolver, Int. J. Quantum Chem., 2021, 121, e26352 CrossRef CAS.
- M. Metcalf, N. P. Bauman, K. Kowalski and W. A. de Jong, Resource-efficient chemistry on quantum computers with the variational quantum eigensolver and the double unitary coupled-cluster approach, J. Chem. Theory Comput., 2020, 16, 6165–6175 CrossRef CAS PubMed.
- Y. Mochizuki, K. Okuwaki, T. Kato and Y. Minato, Reduction of orbital space for molecular orbital calculations with quantum computation simulator for educations, chemRxiv, Preprint DOI:10.26434/chemrxiv.9863810.v1.
- P. Verma, L. Huntington, M. P. Coons, Y. Kawashima, T. Yamazaki and A. Zaribafiyan, Scaling up electronic structure calculations on quantum computers: The frozen natural orbital based method of increments, J. Chem. Phys., 2021, 155, 034110 CrossRef CAS PubMed.
- N. C. Rubin, A hybrid classical/quantum approach for large-scale studies of quantum systems with density matrix embedding theory, 2016, arXiv:1610.06910 DOI:10.48550/arXiv.1610.06910.
- T. Yamazaki, S. Matsuura, A. Narimani, A. Saidmuradov and A. Zaribafiyan, Towards the practical application of near-term quantum computers in quantum chemistry simulations: A problem decomposition approach, 2018, arXiv:1806.01305 DOI:10.48550/arXiv.1806.01305.
- T. Takeshita, N. C. Rubin, Z. Jiang, E. Lee, R. Babbush and J. R. McClean, Increasing the representation accuracy of quantum simulations of chemistry without extra quantum resources, Phys. Rev. X, 2020, 10, 011004 CAS.
- K. Fujii, K. Mizuta, H. Ueda, K. Mitarai, W. Mizukami and Y. O. Nakagawa, Deep variational quantum eigensolver: a divide-and-conquer method for solving a larger problem with smaller size quantum computers, PRX Quantum, 2022, 3, 010346 CrossRef.
- J. R. McClean, M. E. Kimchi-Schwartz, J. Carter and W. A. de Jong, Hybrid quantum–classical hierarchy for mitigation of decoherence and determination of excited states, Phys. Rev. A, 2017, 95, 042308 CrossRef.
- S. Endo, S. C. Benjamin and Y. Li, Practical quantum error mitigation for near-future applications, Phys. Rev. X, 2018, 8, 031027 CAS.
- R. Sagastizabal, X. Bonet-Monroig, M. Singh, M. A. Rol, C. C. Bultink, X. Fu, C. H. Price, V. P. Ostroukh, N. Muthusubramanian, A. Bruno, M. Beekman, N. Haider, T. E. O’Brien and L. DiCarlo, Experimental error mitigation via symmetry verification in a variational quantum eigensolver, Phys. Rev. A, 2019, 100, 010302 CrossRef CAS.
- I. G. Ryabinkin and S. N. Genin, Symmetry adaptation in quantum chemistry calculations on a quantum computer, 2018, arXiv:1812.09812 DOI:10.48550/arXiv.1812.09812.
- T. Tsuchimochi, Y. Mori and S. L. Ten-no, Spin projection for quantum computation: A low-depth approach to strong correlation, Phys. Rev. Res., 2020, 2, 043142 CrossRef CAS.
- B. T. Gard, L. Zhu, G. S. Barron, N. J. Mayhall, S. E. Economou and E. Barnes, Efficient symmetry-preserving state preparation circuits for the variational quantum eigensolver algorithm, npj Quantum Inf., 2020, 6, 10 CrossRef.
- K. Setia, R. Chen, J. E. Rice, A. Mezzacapo, M. Pistoia and J. D. Whitfield, Reducing qubit requirements for quantum simulations using molecular point group symmetries, J. Chem. Theory Comput., 2020, 16, 6091–6097 CrossRef CAS PubMed.
- A. F. Izmaylov, T.-C. Yen and I. G. Ryabinkin, Revising the measurement process in the variational quantum eigensolver: is it possible to reduce the number of separately measured operators?, Chem. Sci., 2019, 10, 3746–3755 RSC.
- P. Gokhale, O. Angiuli, Y. Ding, K. Gui, T. Tomesh, M. Suchara, M. Martonosi and F. T. Chong, O(N3) measurement cost for variational quantum eigensolver on molecular Hamiltonians, IEEE Trans. Quantum Eng., 2020, 1, 1–24 Search PubMed.
- A. Zhao, A. Tranter, W. M. Kirby, S. F. Ung, A. Miyake and P. J. Love, Measurement reduction in variational quantum algorithms, Phys. Rev. A, 2020, 101, 062322 CrossRef CAS.
- V. Verteletskyi, T.-C. Yen and A. F. Izmaylov, Measurement optimization in the variational quantum eigensolver using a minimum clique cover, J. Chem. Phys., 2020, 152, 124114 CrossRef CAS PubMed.
- K. M. Nakanishi, K. Mitarai and K. Fujii, Subspace-search variational quantum eigensolver for excited states, Phys. Rev. Res., 2019, 1, 033062 CrossRef CAS.
- O. Higgott, D. Wang and S. Brierley, Variational quantum computation of excited states, Quantum, 2019, 3, 156 CrossRef.
- R. M. Parrish, E. G. Hohenstein, P. L. McMahon and T. J. Martínez, Quantum computation of electronic transitions using a variational quantum eigensolver, Phys. Rev. Lett., 2019, 122, 230401 CrossRef CAS PubMed.
- P. J. Ollitrault, A. Kandala, C.-F. Chen, P. K. Barkoutsos, A. Mezzacapo, M. Pistoia, S. Sheldon, S. Woerner, J. M. Gambetta and I. Tavernelli, Quantum equation of motion for computing molecular excitation energies on a noisy quantum processor, Phys. Rev. Res., 2020, 2, 043140 CrossRef CAS.
- P. J. J. O’Malley, R. Babbush, I. D. Kivlichan, J. Romero, J. R. McClean, R. Barends, J. Kelly, P. Roushan, A. Tranter, N. Ding, B. Campbell, Y. Chen, Z. Chen, B. Ciaro, A. Dunsworth, A. G. Fowler, E. Jeffrey, E. Lucero, A. Megrant, J. Y. Mutus, M. Neeley, C. Neill, C. Quintana, D. Sank, A. Vainsencher, J. Wenner, T. C. White, P. V. Coveney, P. J. Love, H. Neven, A. Aspuru-Guzik and J. M. Martinis, Scalable quantum simulation of molecular energies, Phys. Rev. X, 2016, 6, 031007 Search PubMed.
- C. Hempel, C. Maier, J. Romero, J. McClean, T. Monz, H. Shen, P. Jurcevic, B. P. Lanyon, P. Love, R. Babbush, A. Aspuru-Guzik, R. Blatt and C. F. Roos, Quantum chemistry calculations on a trapped-ion quantum simulator, Phys. Rev. X, 2018, 8, 031022 CAS.
- F. Arute, et al., Hartree–Fock on a superconducting qubit quantum computer, Science, 2020, 369, 1084–1089 CrossRef CAS PubMed.
- J. E. Rice, T. P. Gujarati, M. Motta, T. Y. Takeshita, E. Lee, J. A. Latone and J. M. Garcia, Quantum computation of dominant products in lithium-sulfur batteries, J. Chem. Phys., 2021, 154, 134115 CrossRef CAS PubMed.
- Q. Gao, H. Nakamura, T. P. Gujarati, G. O. Jones, J. E. Rice, S. P. Wood, M. Pistoia, J. M. Garcia and N. Yamamoto, Computational investigations of the lithium superoxide dimer rearrangement on noisy quantum devices, J. Phys. Chem. A, 2021, 125, 1827–1836 CrossRef CAS PubMed.
- Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, B. Peropadre, N. P. D. Sawaya, S. Sim, L. Veis and A. Aspuru-Guzik, Quantum chemistry in the age of quantum computing, Chem. Rev., 2019, 119, 10856–10915 CrossRef CAS PubMed.
- S. McArdle, S. Endo, A. Aspuru-Guzik, S. C. Benjamin and X. Yuan, Quantum computational chemistry, Rev. Mod. Phys., 2020, 92, 015003 CrossRef CAS.
- B. Bauer, S. Bravyi, M. Motta and G. K.-L. Chan, Quantum algorithms for quantum chemistry and quantum materials science, Chem. Rev., 2020, 120, 12685–12717 CrossRef CAS PubMed.
- Y. Li, J. Hu, X.-M. Zhang, Z. Song and M.-H. Yung, Variational quantum simulation for quantum chemistry, Adv. Theory Simul., 2019, 2, 1800182 CrossRef CAS.
- D. A. Fedorov, B. Peng, N. Govind and Y. Alexeev, VQE method: A short survey and recent developments, 2021, arXiv:2103.08505 DOI:10.48550/arXiv.2103.08505.
- H. B. Schlegel, Potential energy curves using unrestricted Møller–Plesset perturbation theory with spin annihilation, J. Chem. Phys., 1986, 84, 4530–4534 CrossRef CAS.
- W. D. Laidig, P. Saxe and R. J. Bartlett, The description of N2 and F2 potential energy surfaces using multireference coupled cluster theory, J. Chem. Phys., 1987, 86, 887–907 CrossRef CAS.
- I. W. Bulik, T. M. Henderson and G. E. Scuseria, Can single-reference coupled cluster theory describe static correlation?, J. Chem. Theory Comput., 2015, 11, 3171–3179 CrossRef CAS PubMed.
- G. D. Purvis III and R. J. Bartlett, A full coupled-cluster singles and doubles model: The inclusion of disconnected triples, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef.
- G. D. Purvis III, R. Shepard, F. B. Brown and R. J. Bartlett, C 2v insertion pathway for BeH2: A test problem for the coupled-cluster single and double excitation model, Int. J. Quantum Chem., 1983, 23, 835–845 CrossRef.
- D. O’Neal, H. Taylor and J. Simons, Potential surface walking and reaction paths for C2v Be + H2 ← BeH2 → Be + 2H (1A1), J. Phys. Chem., 1984, 88, 1510–1513 CrossRef.
- H. Nakano, Quasidegenerate perturbation theory with multiconfigurational self-consistent field reference functions, J. Chem. Phys., 1993, 99, 7983–7992 CrossRef CAS.
- U. S. Mahapatra, B. Datta and D. Mukherjee, A size-consistent state-specific multireference coupled cluster theory: Formal developments and molecular applications, J. Chem. Phys., 1999, 110, 6171–6188 CrossRef CAS.
- U. S. Mahapatra, B. Datta and D. Mukherjee, Molecular applications of a size-consistent state-specific multireference perturbation theory with relaxed model-space coefficients, J. Phys. Chem. A, 1999, 103, 1822–1830 CrossRef CAS PubMed.
- D. Pahari, S. Chattopadhyay, S. Das, D. Mukherjee and U. S. Mahapatra, Size-consistent state-specific multi-reference methods: a survey of some recent developments, in Theory and Applications of Computational Chemistry: The First Forty Years, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, ch. 22, pp. 581–633 Search PubMed.
- F. A. Evangelista, Alternative single-reference coupled cluster approaches for multireference problems: The simpler, the better, J. Chem. Phys., 2011, 134, 224102 CrossRef PubMed.
- J. Puldus, P. Piecuch, L. Pylypow and B. Jeziorski, Application of Hilbert-space coupled cluster theory to simple (H2)2 model systems: Planar models, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 47, 2738–2782 CrossRef PubMed.
- G. Ortiz, J. E. Gubernatis, E. Knill and R. Laflamme, Quantum algorithms for fermionic simulations, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 64, 022319 CrossRef; G. Ortiz, J. E. Gubernatis, E. Knill and R. Laflamme, Erratum: Quantum algorithms for fermionic simulations, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 65, 029902 CrossRef.
- J. T. Seeley, M. J. Richard and P. J. Love, The Bravyi–Kitaev transformation for quantum computation of electronic structure, J. Chem. Phys., 2012, 137, 224109 CrossRef PubMed.
- S. Bravyi, J. M. Gambetta, A. Mezzacapo and K. Temme, Tapering off qubits to simulate fermionic Hamiltonians, 2017, arXiv:1701.08213 DOI:10.48550/arXiv.1701.08213.
- K. Setia and J. D. Whitfield, Bravyi–Kitaev superfast simulation of electronic structure on a quantum computer, J. Chem. Phys., 2018, 148, 164104 CrossRef PubMed.
- M. Steudtner and S. Wehner, Quantum codes for quantum simulation of fermions on a square lattice of qubits, Phys. Rev. A, 2019, 99, 022308 CrossRef CAS.
- C. Sur, R. K. Chaudhuri, B. K. Sahoo, B. P. Das and D. Mukherjee, Relativistic unitary coupled cluster theory and applications, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 065001 CrossRef.
- B. Cooper and P. J. Knowles, Benchmark studies of variational, unitary and extended coupled cluster methods, J. Chem. Phys., 2010, 133, 234102 CrossRef PubMed.
- M. Hodecker and A. Dreuw, Unitary coupled cluster ground- and excited-state molecular properties, J. Chem. Phys., 2020, 153, 084112 CrossRef CAS PubMed.
- K. Raghavachari, G. W. Trucks, J. A. People and M. Head-Gordon, A fifth-order perturbation comparison of electron correlation theories, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- B. O. Roos, P. Linse, P. E. M. Siegbahn and M. R. A. Blomberg, A simple method for the evaluation of the second-order-perturbation energy from external double-excitations with a CASSCF reference wavefunction, Chem. Phys., 1982, 66, 197–207 CrossRef CAS.
- K. Andersson, P.-Å. Malmqvist and B. O. Roos, Second-order perturbation theory with a complete active space self-consistent field reference function, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- J. R. McClean, S. Boixo, V. N. Smelyanskiy, R. Babbush and H. Neven, Barren plateaus in quantum neural network training landscapes, Nat. Commun., 2018, 9, 4812 CrossRef PubMed.
- J. Romero, R. Babbush, J. R. McClean, C. Hempel, P. J. Love and A. Aspuru-Guzik, Strategies for quantum computing molecular energies using the unitary coupled cluster ansatz, Quantum Sci. Technol., 2018, 4, 014008 CrossRef.
- A. Szabo and N. S. Ostlund, Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory, Dover Publications, Inc., New York, 1996 Search PubMed.
- Y. Mochizuki and K. Tanaka, Modification for spin-adapted version of configuration interaction singles with perturbative doubles, Chem. Phys. Lett., 2007, 443, 389–397 CrossRef CAS.
- T. J. Lee and P. R. Taylor, A diagnostic for determining the quality of single-reference electron correlation methods, Int. J. Quantum Chem., 1989, 36, 199–207 CrossRef.
- T. J. Lee, A. P. Rendell and P. R. Taylor, Comparison of the quadratic configuration interaction and coupled-cluster approaches to electron correlation including the effect of triple excitations, J. Phys. Chem., 1990, 94, 5463–5468 CrossRef CAS.
- Y. Mochizuki, A size-extensive modification of super-CI for orbital relaxation, Chem. Phys. Lett., 2005, 410, 165–171 CrossRef CAS.
- J. R. McClean, N. C. Rubin, K. J. Sung, I. D. Kivlichan, X. Bonet-Monroig, Y. Cao, C. Dai, E. Schuyler Fried, C. Gidney, B. Gimby, P. Gokhale, T. Häner, T. Hardikar, V. Havlíček, O. Higgott, C. Huang, J. Izaac, Z. Jiang, X. Liu, S. McArdle, M. Neeley, T. O’Brien, B. O’Gorman, I. Ozfidan, M. D. Radin, J. Romero, N. P. D. Sawaya, B. Senjean, K. Setia, S. Sim, D. S. Steiger, M. Steudtner, Q. Sun, W. Sun, D. Wang, F. Zhang and R. Babbush, OpenFermion: the electronic structure package for quantum computers, Quantum Sci. Technol., 2020, 5, 034014 CrossRef.
- Quantum AI team and collaborators. (March 5, 2021). quantumlib/Cirq: Cirq, Version v0.10.0. Zenodo DOI:10.5281/zenodo.4586899.
- H. R. Grimsley, D. Claudino, S. E. Economou, E. Barnes and N. J. Mayhall, Is the Trotterized UCCSD ansatz chemically well-defined?, J. Chem. Theory Comput., 2020, 16, 1–6 CrossRef CAS PubMed.
- A. Tranter, P. J. Love, F. Mintert and P. V. Coveney, A comparison of the Bravyi–Kitaev and Jordan–Wigner transformations for the quantum simulation of quantum chemistry, J. Chem. Theory Comput., 2018, 14, 5617–5630 CrossRef CAS PubMed.
- G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Włoch, P. Xu, F. Zahariev and M. S. Gordon, Recent developments in the general atomic and molecular electronic structure system, J. Chem. Phys., 2020, 152, 154102 CrossRef CAS PubMed.
- T. Yamada and S. Hirata, Singlet and triplet instability theorems, J. Chem. Phys., 2015, 143, 114112 CrossRef PubMed.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, Quadratic configuration interaction. A general technique for determining electron correlation energies, J. Chem. Phys., 1987, 87, 5968–5975 CrossRef CAS.
- N. C. Handy, J. A. Pople, M. Head-Gordon, K. Raghavachari and G. W. Trucks, Size-consistent Brueckner theory limited to double substitutions, Chem. Phys. Lett., 1989, 164, 185–192 CrossRef CAS.
- K. Sugisaki, S. Nakazawa, K. Toyota, K. Sato, D. Shiomi and T. Takui, Quantum chemistry on quantum computers: A method for preparation of multiconfigurational wave functions on quantum computers without performing post-Hartree–Fock calculations, ACS Cent. Sci., 2019, 5, 167–175 CrossRef CAS PubMed.
- D. Halder, S. V. Prasannaa, V. Agarawal and R. Maitra, Digital quantum simulation of strong correlation effects with iterative quantum phase estimation over the variational quantum eigensolver algorithm: H4 on a circle as a case study, 2021, arXiv:2110.02864 DOI:10.48550/arXiv.2110.02864.
- M. Ozaki, On the recovery of spatial symmetry by spin projection of unrestricted Hartree–Fock wave functions, Prog. Theor. Phys., 1980, 63, 84–90 CrossRef.
- K. Mitarai, M. Negoro, M. Kitagawa and K. Fujii, Quantum circuit learning, Phys. Rev. A, 2018, 98, 032309 CrossRef CAS.
- R. M. Parrish, J. T. Iosue, A. Ozaeta and P. L. McMahon, A Jacobi diagonalization and Anderson acceleration algorithm for variational quantum algorithm parameter optimization, 2019, arXiv:1904.03206 DOI:10.48550/arXiv.1904.03206.
- A. Kalemos and A. Mavridis, Electronic structure and bonding of ozone, J. Chem. Phys., 2008, 129, 054312 CrossRef PubMed.
- M. Biczysko, L. A. Poveda and A. J. C. Varandas, Accurate MRCI study of ground-state N2H2 potential energy surface, Chem. Phys. Lett., 2006, 424, 46–53 CrossRef CAS.
- F. Plasser, H. Pašalić, M. H. Gerzabek, F. Libisch, R. Reiter, J. Burgdörfer, T. Müller, R. Shepard and H. Lischka, The multiradical character of one- and two-dimensional graphene nanoribbons, Angew. Chem., Int. Ed., 2013, 52, 2581–2584 CrossRef CAS PubMed.
- W. Mizukami, Y. Kurashige and T. Yanai, More π electrons make a difference: Emergence of many radicals on graphene nanoribbons studied by ab initio DMRG theory, J. Chem. Theory Comput., 2013, 9, 401–407 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: the Gaussian basis set used for the BeH2 system; the UCCSD and MR-UCCpGSD energies and wave functions with initial amplitudes; Trotter term ordering dependence; VQE-UCCSD simulations of LiH; initial amplitude dependence on the UCCSD wave functions; RHF, CASSCF, UCCSD, MR-UCCpGSD, and full-CI energies of BeH2; singlet and triplet instabilities; convergence behaviour of the VQE-UCCSD simulations of BeH2; fitting the energy difference plots; CCSD, CCSD(T), BD, and QCISD calculations; and k-UpCCGSD simulations. See DOI: 10.1039/d1cp04318h |
| ‡ Present address: NTT DATA Corporation, Toyosu Center Bldg. Annex, 3–9, Toyosu 3–chome, Koto–ku, Tokyo 135-8671, Japan. |
| This journal is © the Owner Societies 2022 |