J-Driven dynamic nuclear polarization for sensitizing high field solution state NMR†
Received
13th September 2021
, Accepted 5th January 2022
First published on 7th January 2022
Abstract
Dynamic nuclear polarization (DNP) is widely used to enhance solid state nuclear magnetic resonance (NMR) sensitivity. Its efficiency as a generic signal-enhancing approach for liquid state NMR, however, decays rapidly with magnetic field B0, unless mediated by scalar interactions arising only in exceptional cases. This has prevented a more widespread use of DNP in structural and dynamical solution NMR analyses. This study introduces a potential solution to this problem, relying on biradicals with exchange couplings Jex of the order of the electron Larmor frequency ωE. Numerical and analytical calculations show that in such Jex ≈ ±ωE cases a phenomenon akin to that occurring in chemically induced DNP (CIDNP) happens, leading to different relaxation rates for the biradical singlet and triplet states which are hyperfine-coupled to the nuclear α or β states. Microwave irradiation can then generate a transient nuclear polarization build-up with high efficiency, at all magnetic fields that are relevant in contemporary NMR, and for all rotational diffusion correlation times that occur in small- and medium-sized molecules in conventional solvents.
1. Introduction
Higher NMR sensitivity could bring transformative breakthroughs to analytical, pharmaceutical and biophysical chemistry. NMR sensitivity can be enhanced by higher external magnetic fields B0, but this is a slow, expensive approach. An alternative arises if electron magnetization is transferred, from a stable radical, to the nuclei to be detected. By irradiating electrons with microwaves a their Larmor frequency, ωE, the so-called Dynamic Nuclear Polarization (DNP) effect can then enhance NMR sensitivity up to the ratio between the gyromagnetic constants of the electron and the nucleus: γE/γN. Based on the irradiation of a stable organic monoradical, such effect can enhance the Boltzmann equilibrium nuclear magnetization by factors of hundredfold, thereby transforming the analytical potential of NMR. Predicted by Overhauser in 19531 and thereafter confirmed by Carver and Slichter,2 DNP has revolutionized solid state NMR;3–6 it has also made inroads into in vivo spectroscopy, based on rapid melting approaches.7,8 DNP, however, has not yet impacted what is arguably the widest of NMR realms – high-field solution-state studies. This longstanding problem arises from an Overhauser DNP efficiency, that in liquids depends on the electron-nuclear cross-relaxation rate σE,N:| |  | (1) |
The typical rotational correlation time τc of a radical/nucleus dipolar-coupled spin pair is τc ≈ 0.1–1 ns, while typical electron and nuclear Larmor frequencies in mid- to high-field scenarios are ωE ≥ 200 GHz and ωN ≥ 300 MHz. This leads to (ωE ± ωN)2τC2 ≫ 1; i.e., negligible cross-relaxation rates in eqn (1) for most cases of practical analytical interest, and Overhauser DNP efficiencies that decrease quadratically with B0. Consequently – and unless aided by the contact couplings that can arise for certain radicals and solutes9–13 – typical 1H DNP enhancements drop from a maximum of ≈330× when B0 ≤ 0.4 T, to ≈1.001× at the ≥7 T fields were contemporary NMR is done.11,14–17 We recently discussed a way to bypass this bottleneck, proposing a cross-correlated (CC) DNP strategy involving biradicals as polarization sources.18 CCDNP, however, required significant coincidences between nuclear/electron spin interaction tensors, and long-term stability in the nuclear-electron geometry; for optimal conditions, it then provided steady-state NMR enhancements that approached ≈10–20×. This study reports a further investigation into the physics of a three-spin biradical/nuclear system, revealing a new polarization transfer possibility. Unlike CCDNP, the mechanism that is here introduced: (i) does not put stringent conditions on multiple independent coupling tensors; (ii) can lead to nuclear polarization enhancements of ≈100–200× for B0 ranging from ≤1 T to ≥20 T and for rotational correlation times in the 0.1–1 ns range; and (iii) does not result from a steady state arising upon electron saturation, but rather from transient phenomena. At the centre of this proposal are two electrons interacting through an exchange coupling Jex in the order of ωE, a chemically tuneable condition that can be fulfilled by many biradicals known to have exchange couplings in the 0 ≤ Jex ≤ 1 THz range.19–21 Under such conditions we found that moderate microwave fields can lead to the DNP enhancement improvements shown in Fig. 1. The present study demonstrates and explains the basis of this J-driven (J-DNP) mechanism based on Liouville space numerical simulations, and on analytical calculations using Redfield's relaxation theory.22–26 The latter serve to highlight similarities between the roles that the electronic singlet and triplet states play in polarizing nuclei in J-DNP, and those played by singlet and triplet states arising in chemically-induced DNP (CIDNP) experiments.27–30
 |
| | Fig. 1 On the left: Comparison between the maximal enhancements delivered by the Overhauser and by J-driven DNP, as function of B0. On the right: Models of the biradical/nuclear system assumed for simulating J-DNP (A) and of the monoradical/nuclear system used for Overhauser DNP (B). The only nucleus in the system (a proton) was assumed in the “solvent” molecule; the red arrows represent dipolar interactions between the electron(s) placed in the centre of the radical and the proton in this “solvent”. No other protons/nuclei were assumed. The J-DNP simulation was performed using a biradical/proton dipolar-coupled triad (A) with a τc = 500 ps rotational correlation time, a Jex = +(ωE + ωN) at each field strength, and other parameters as given in Table 1. The Overhauser DNP simulation was performed for a monoradical/proton dipolar-coupled pair (B) with τc = 157 ps (typical of trityl31) and other parameter as given in Table 1 – but with one of the electrons in the table absent. The enhancement in the J-DNP was calculated after 20 ms of microwave irradiation; the Overhauser DNP enhancements were calculated vs. field at the steady state (Overhauser enhancements slightly larger than those predicted in the Fig. 1 were observed in water solutions at 1.4 T and 3.4 T;32,33 this likely arises due to translational diffusion effects, which were not consider in this work). | |
2. Spin system and theoretical methodology
The system examined in this work was a biradical interacting with a proton exclusively through dipolar (aka anisotropic hyperfine) couplings. Hyperfine couplings were assumed between both electrons and the proton, the inter-particle distances were assumed fixed. These distances between the two unpaired spin-1/2 electrons (belonging to the radical) and the spin-1/2 proton (belonging to the solvent) were 8.6 Å and 11.1 Å respectively (see Table 1 for the actual proton and electron Cartesian coordinates). Scalar electron-nuclear couplings were set to zero. The J-DNP mechanism described in this study was assumed driven by a rotational dynamics, modulating the relaxation of the three-spin system with a rotational correlation time, τc, as shown in Fig. 1. The two electrons were assumed to have identical g-tensors, assumed anisotropic for the sake of realism (even if the ESI† 6, shows that neither nuclear shielding anisotropy nor g-anisotropy are required for the J-DNP enhancement). The most important variable in the system is the isotropic inter-electron exchange coupling Jex, which was modelled on the basis of trityl-based symmetric biradicals for which such couplings have been observed.19,20 These parameters were used to create the spin Hamiltonian, and to calculate the evolution subject to microwave irradiation and relaxation as per Redfield's theory22,25 (see ESI† 1, for additional discussion of these radicals, including their estimated solution-state T1s and T2s34,35).
Table 1 Biradical/proton parameters used in the simulations shown in Fig. 1–5. B0, Jex and τc were set as described in the figures; all other coupling parameters relied on the inter-spin distances
| Parameter |
Value |
|
Simulations used identical Zeeman interaction tensors, that were made axially symmetric along the main molecular axis (corresponding the linker connecting the two trityls).
|
|
1H chemical shift tensor, ppm |
[5 10 20] |
|
g-tensora for electrons 1 and 2, Bohr magneton |
[2.0032 2.0032 2.0026] |
|
1H coordinates, [x y z], Å |
[−3 0.5 1.3] |
| Electron 1 coordinates, [x y z], Å |
[0 0 −9.37] |
| Electron 2 coordinates, [x y z], Å |
[0 0 9.37] |
| Scalar relaxation modulation depth, GHz |
3 |
| Scalar relaxation modulation time, ps |
1 |
| Microwave nutation frequency, ωμw, MHz |
1 |
| Temperature, K |
298 |
The bulk of this study focuses on a Jex ≫ ωΔe scenario, where ωΔe = ωe1 − ωe2 is the difference between the Larmor frequency of the two electrons. In such cases the electron Zeeman eigenstates |αe1βe2〉 and |βe1αe2〉 are no longer eigenfunctions of the spin Hamiltonian; the relevant Hamiltonian was therefore treated in the singlet/triplet electron basis set {Ŝ(e1,e2)0,![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (e1,e2)0,
(e1,e2)0,![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (e1,e2)±1}. As shown in ESI† 2, this leads to a microwave rotating frame Hamiltonian:
(e1,e2)±1}. As shown in ESI† 2, this leads to a microwave rotating frame Hamiltonian:
| | | Ĥrot = ĤS0T0 + ĤT+1T−1 + Ĥμw | (2) |
where
ĤS0T0 is a Hamiltonian acting in the
Ŝ0![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0
0 sub-space,
ĤT+1T−1 acts in the
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) +1
+1![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) −1
−1 sub-space, and
Ĥμw is the microwave operator (see ESI
† 2, for further definitions). With this Hamiltonian, Liouville-space time domain calculations were performed based on the equation of motion:
| |  | (3) |
where
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif)
(
t) is the state vector of the system, and

is the Liouvillian containing the rotating frame Hamiltonian superoperator plus the relaxation superoperator

accounting for the stochastic rotation of all anisotropies. The latter was computed according to the Bloch–Redfield–Wangsness relaxation theory
22,36 both by analytical
24 and numerical
25,26 means, including all possible longitudinal, transverse and cross-correlated pathways. Since the spin system was considered at room temperature, Di-Bari–Levitt thermalization was used.
37 Considering that the exchange coupling has the same order of magnitude as the electron Larmor frequency, these calculations incorporated into the relaxation superoperator a scalar relaxation of the first kind.
38 This did not have an effect on the DNP enhancement, since in the
ωΔe → 0 case in question, the exchange coupling,

, commutes with the Zeeman interaction,
Ê1Z+ Ê2Z. Time evolution
Ô(
t) of multiple spin state populations was calculated by taking their scalar products with the state vector
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif)
(
t) at each time.
3. Features of J-DNP
Fig. 2 shows how the isotropic exchange coupling modulates the maximum nuclear enhancement achievable by J-DNP upon on-resonance irradiation at the electron Larmor frequency of the biradicals, as a function of magnetic field B0. These numerically simulated plots39 predict that, for every field strength, there are two Jex = ±(ωE + ωN) values for which microwave irradiation leads to a nuclear enhancement close to the maximum γE/2γN achievable value.
 |
| | Fig. 2 Simulated DNP enhancement achieved within 20 ms of microwave irradiation as a function of Jex and B0. The plots arise from time domain simulations using the parameters in Table 1, a biradical/proton dipolar-coupled triad τc = 500 ps, and an on-resonance irradiation at the electron Larmor frequency of the biradicals. In this and other graphs shown below, DNP enhancements denote the achieved nuclear polarization, normalized by its Boltzmann counterpart at the same temperature and field. | |
Unlike Overhauser DNP and CCDNP enhancements,18 where nuclear polarization enhancements are observed at the steady state, the nuclear polarization enhancements shown in Fig. 2 and arising at the Jex = ±(ωE + ωN) conditions, are transient phenomena. This is illustrated in Fig. 3, which shows the enhancement's time-dependence for different rotational correlation times and magnetic fields, for spin systems with an optimally chosen Jex = +(ωE + ωN) coupling. These graphs show a nuclear polarization that rapidly builds up and then decays into steady states which, at the usual NMR fields used in analytical/biophysical studies, are essentially the Boltzmann equilibrium nuclear magnetization. However, in all cases, substantial transient enhancements are observed after 10–50 ms of continuous microwave irradiation, with precise timings and maximal values that depend on B0 and on the correlation time τc of the biradical/proton triad. In fact, notice that these transient enhancements improve slightly with both higher B0s and slower τcs of the biradical/proton triad. Additional differences between the behaviours of Overhauser and J-DNP are discussed in Fig. S3 of ESI† 1, which compares expectations from a two-spin proton/electron system (Overhauser DNP), and the changes arising when a second electron is added to form a three-spin proton/biradical system, where the two electrons interact with Jex = +(ωE + ωN). Upon introducing such second electron, weak steady-state nuclear polarization values similar to those arising in Overhauser DNP are reached – but on the way to those steady states, there are strong transient enhancements of the nuclear polarization.
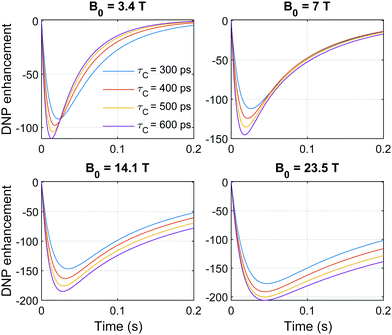 |
| | Fig. 3 Time domain simulations showing the evolution of the DNP enhancement observed under continuous microwave irradiation of the electrons, for an array of B0 and of τc values of the biradical/proton dipolar-coupled triad. For all fields Jex was set to +(ωE + ωN); other simulation parameters were as given in Table 1. | |
4. The physics of J-DNP
The physics that drives the J-DNP effects summarized in Fig. 2 and 3, is reminiscent of the cross-correlations arising in the CIDNP mechanism. According to the radical pair theory,28,29,40 nuclear magnetization enhancement in CIDNP proceeds from three processes: (i) singlet/triplet interconversion within a spin-correlated biradical; (ii) a modulation of the rate of this interconversion by hyperfine couplings (i.e., different fates of the electron states depending on whether the nuclear spin state is α or β); and (iii) a rapid nuclear spin relaxation of the unreacted triplet biradical, acting as a nuclear spin state filter. In the J-DNP case, the biradical is not (photo)chemically produced and does not recombine after a transient action; still, the singlet–triplet behaviour vis-à-vis the nuclear spin once again becomes relevant. In the J-DNP case, it is microwaves (rather than a laser) that drive the system away from the thermal equilibrium. As in CIDNP, it is essential that the nucleus is differentially hyperfine-coupled to the two electrons for the J-DNP enhancement to occur (the effect disappears otherwise, see ESI† 6). It is then the different relaxation characteristics of the two-electron singlet/triplet states when facing the nuclear α or β states, that build up the nuclear polarization. Fig. 4a–d further clarify this, by showing the time dependencies of the three-spin population operators Ôα/β,41,42 computed from direct-product of two-electron triplet/singlet states with a nuclear spin state in Zeeman basis, that can be in either the α or β state. These states are represented as ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1,α/β,
±1,α/β,![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0,α/β and Ŝ0,α/β (see ESI† 3, for the expressions of these Ôα/β as Cartesian operators). Fig. 4e shows the states arising from the difference between Ôα and Ôβ, defined as:
0,α/β and Ŝ0,α/β (see ESI† 3, for the expressions of these Ôα/β as Cartesian operators). Fig. 4e shows the states arising from the difference between Ôα and Ôβ, defined as:| |  | (4) |
where Ô(e1e2) denotes the two-electron singlet and triplet, and ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z is the longitudinal nuclear magnetization. Fig. 4f shows the overall
Z is the longitudinal nuclear magnetization. Fig. 4f shows the overall ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z amplitude calculated upon summing the amplitudes of Ŝ0
Z amplitude calculated upon summing the amplitudes of Ŝ0![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z,
Z, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0
0![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z and
Z and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1
±1![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z, normalized to the equilibrium nuclear magnetization.
Z, normalized to the equilibrium nuclear magnetization.
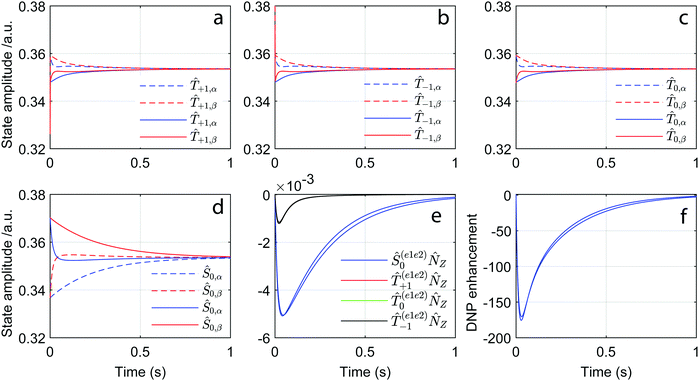 |
| | Fig. 4 Time evolution of the three-spin population operators: ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1,α/β, ±1,α/β, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0,α/β and Ŝ0,α/β (a–d), and of the 0,α/β and Ŝ0,α/β (a–d), and of the ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) ZŜ0, ZŜ0, ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z Z![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1 and ±1 and ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z Z![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0 states (e) arising from the difference between the various Ôα and Ôβ. Time evolution of the overall longitudinal nuclear magnetization 0 states (e) arising from the difference between the various Ôα and Ôβ. Time evolution of the overall longitudinal nuclear magnetization ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z (f), showing the sum of all Z (f), showing the sum of all ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z-related contributions, normalized by the thermal nuclear magnetization under the same conditions. Plots (a–d) are normalized to a total electron spin population of one, as defined in ESI† 3. Jex = +(ωE + ωN) was used for the dashed lines calculations, and Jex = −(ωE + ωN) was used for the continuous lines. In (e), the red and green traces are barely seen as they fall underneath an overlapping black trace. The slightly different curves in (f) reflect Jex = ±(ωE + ωN) conditions, respectively. For all these calculations B0 = 14.08 T, τc = 500 ps for the biradical/proton dipolar-coupled triad; all other parameters as given in Table 1. Z-related contributions, normalized by the thermal nuclear magnetization under the same conditions. Plots (a–d) are normalized to a total electron spin population of one, as defined in ESI† 3. Jex = +(ωE + ωN) was used for the dashed lines calculations, and Jex = −(ωE + ωN) was used for the continuous lines. In (e), the red and green traces are barely seen as they fall underneath an overlapping black trace. The slightly different curves in (f) reflect Jex = ±(ωE + ωN) conditions, respectively. For all these calculations B0 = 14.08 T, τc = 500 ps for the biradical/proton dipolar-coupled triad; all other parameters as given in Table 1. | |
 |
| | Fig. 5 Numerically computed (Redfield theory) self-relaxation rates of the three-spin population operators as a function of Jex and B0. Rates of Ŝ0,β, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0,β and 0,β and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1,β are on the left, and rates of Ŝ0,α, ±1,β are on the left, and rates of Ŝ0,α, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0,α and 0,α and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1,α are on the right. Calculations relied on the parameters of Table 1 and on τc = 500 ps for the biradical/proton dipolar-coupled triad. ±1,α are on the right. Calculations relied on the parameters of Table 1 and on τc = 500 ps for the biradical/proton dipolar-coupled triad. | |
At time zero, the system is at thermal equilibrium, and negligible differences arise between the populations of the α and β nuclear states – even if singlet and triplet electron state populations differ. When the microwave irradiation is turned on, the electron spin is taken out of the thermal equilibrium and electron saturation sets in, the triplet states are mixed, and their populations start to converge to similar amplitudes (Fig. 4a–c). However, at the Jex = ±(ωE + ωN) condition, the rates at which electron states settle into this new equilibrium are different for α and β nuclear components: when Jex = +(ωE + ωN) the α component of the triplets (Fig. 4, blue dashed line) reaches the steady state faster than the β component (red dashed line), while the β component of the singlet (red dashed line) reaches steady state faster than the α component of the singlet (blue dashed line).43 The opposite α/β behaviour arises when Jex = −(ωE + ωN). Still, because different initial conditions exist when Jex = ±(ωE + ωN), both situations lead to similar transient nuclear polarization build-ups, as shown in Fig. 4e. Consequently, due to the different self-relaxation rates of the α and β nuclear components of the triplet and singlet electron states, a sizable nuclear polarization ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z builds up. As can be appreciated in Fig. 4f, this polarization is only weakly dependent on the sign of Jex. Also note that, as eventually all electron/nuclear states reach the same populations, this J-DNP build up is transient: no nuclear polarization gains are predicted when the steady-state conditions examined in conventional Overhauser DNP analyses, are considered.
Z builds up. As can be appreciated in Fig. 4f, this polarization is only weakly dependent on the sign of Jex. Also note that, as eventually all electron/nuclear states reach the same populations, this J-DNP build up is transient: no nuclear polarization gains are predicted when the steady-state conditions examined in conventional Overhauser DNP analyses, are considered.
The plots shown in Fig. 4 were computed assuming continuous microwave irradiation. To avoid the decay of the enhancement – dominated by the nuclear T1 decay draining the ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) ZŜ0 state – microwaves could be turned off when nuclear magnetization has reached a maximum; the electron population operators would then relax back to thermal equilibrium, and the build-up could be “pumped” again by repeated irradiation. However, in an actual J-DNP enhancement experiment, the polarizing proton would not be covalently bound; rather, it would be randomly diffusing at rates of ca. 1 μm ms−1.31 The interaction with the polarizing biradical would thus be short-lived, and the proton pool would get repeatedly polarized by different transient encounters with different biradicals; a certain “pulsing” of the effect will therefore occur spontaneously.13,44,45
ZŜ0 state – microwaves could be turned off when nuclear magnetization has reached a maximum; the electron population operators would then relax back to thermal equilibrium, and the build-up could be “pumped” again by repeated irradiation. However, in an actual J-DNP enhancement experiment, the polarizing proton would not be covalently bound; rather, it would be randomly diffusing at rates of ca. 1 μm ms−1.31 The interaction with the polarizing biradical would thus be short-lived, and the proton pool would get repeatedly polarized by different transient encounters with different biradicals; a certain “pulsing” of the effect will therefore occur spontaneously.13,44,45
5. Analysis of the self-relaxation rates driving J-DNP
Fig. 5 examines another facet of J-DNP, by showing how the self-relaxation rates of the ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1,α/β,
±1,α/β,![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0,α/β and Ŝ0,α/β population operators driving the population decays of the various nuclear spin states, change over a range of magnetic fields B0 and exchange couplings Jex. Notice the marked differentials arising whenever Jex matches ±(ωE + ωN), between the self-relaxation rates of various Ôα and Ôβ operators. It is these differential decays that drive the enhancements shown in Fig. 1–4.
0,α/β and Ŝ0,α/β population operators driving the population decays of the various nuclear spin states, change over a range of magnetic fields B0 and exchange couplings Jex. Notice the marked differentials arising whenever Jex matches ±(ωE + ωN), between the self-relaxation rates of various Ôα and Ôβ operators. It is these differential decays that drive the enhancements shown in Fig. 1–4.
The numerical trends in Fig. 5 can be explained by considering the analytical expressions for the relaxation rates of singlet and the triplet states, as derived from Redfield's relaxation theory.24,36 As long as this theoretical model is valid (which for the present scenario we estimate at τc ≤ 2 ns), these rates will be given by sums of terms involving products of second-rank norms squared and/or other quadratic products,46 times spectral density functions. For the Ŝ0,α/β operators these rates can be summarized as:
| |  | (5) |
and
| |  | (6) |
For the ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) +1,α/β operators, the self-relaxation rates are:
+1,α/β operators, the self-relaxation rates are:
| |  | (7) |
and
| |  | (8) |
For the
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0,α/β
0,α/β operators, the self-relaxation rates are:
| |  | (9) |
and
| |  | (10) |
and for
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) −1,α/β
−1,α/β operators, the self-relaxation rates:
| |  | (11) |
and
| |  | (12) |
where Δ
G =
G1 –
G2 and ΔHF = HFC
1–HFC
2 are anisotropies associated to the differences between the two
g- and electron/nuclear hyperfine coupling tensors, respectively; CSA is the chemical shift anisotropy tensor; and, as is usual in spin relaxation theory,
22,23 all rates contain combinations of second-rank norms squared
ΔA2 for all the aforementioned tensors
A,
46 and second-rank scalar products

of tensors
A and
B. The “…” in
eqn (5)–(12) denote terms that contribute equally to
Ôα and
Ôβ and thus are not relevant for the
J-DNP effect; full analytical expressions for all the self-relaxation rates in eqn
(5)–(12) are given in ESI
† 4, and the definitions of second-rank norm squared and of scalar product are given in ESI
† 5.
As mentioned for the Overhauser DNP, at high B0 fields, the contribution of terms J(ωE) ≈ 0, to the rates in eqn (5)–(12), can be disregarded. Exceptions, however, will arise when a spectral density's ω-argument is ωN, or when it can be made zero by Jex – such spectral density functions will no longer be negligible and the terms cannot be disregarded. Eqn (5)–(12) reveal many of such potential terms; as a result of them, large differences will arise between the self-relaxation rates of the Ôα and Ôβ population operators under Jex ≈ ±ωE conditions, leading to the transient generation of non-zero ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) ZŜ0,
ZŜ0, ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z
Z![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1 states, as shown in Fig. 4. This can be most easily appreciated for the Ŝ0,α and Ŝ0,β relaxation rates: the latter will be dominated by the J(Jex + ωE + ωN) term if Jex = +(ωE + ωN), and the former by the J(Jex − ωE − ωN) if Jex = −(ωE + ωN). In either case, such Jex condition will result in large differences between −R[Ôα] and −R[Ôβ], due to the cancellation of ωE by Jex. Similar differences can be observed in Fig. 5 also for
±1 states, as shown in Fig. 4. This can be most easily appreciated for the Ŝ0,α and Ŝ0,β relaxation rates: the latter will be dominated by the J(Jex + ωE + ωN) term if Jex = +(ωE + ωN), and the former by the J(Jex − ωE − ωN) if Jex = −(ωE + ωN). In either case, such Jex condition will result in large differences between −R[Ôα] and −R[Ôβ], due to the cancellation of ωE by Jex. Similar differences can be observed in Fig. 5 also for ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1,α and
±1,α and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1,β; ESI† 4 provides additional information about these self-relaxation rates. Note as well that, even though the absolute values of these rates decrease with B0 and τc, their differences actually remain present (Fig. S4 and S5, ESI†). This helps to understand the increased efficiencies that J-DNP enhancements exhibit as a function of B0 and τc, leading to the sizable transient longitudinal nuclear magnetizations shown in Fig. 1–4.
±1,β; ESI† 4 provides additional information about these self-relaxation rates. Note as well that, even though the absolute values of these rates decrease with B0 and τc, their differences actually remain present (Fig. S4 and S5, ESI†). This helps to understand the increased efficiencies that J-DNP enhancements exhibit as a function of B0 and τc, leading to the sizable transient longitudinal nuclear magnetizations shown in Fig. 1–4.
It is also instructive to consider the maximum enhancement expected from the differences between the −R[Ôα] and the −R[Ôβ] relaxation rates. Assuming for simplicity that one of the states relaxes infinitely fast while the other has no relaxation, an assumption of complete microwave-driven electron saturation will lead to a nuclear polarization reaching a 0.5 value – i.e., the NMR signal would be enhanced by |γE/2γN|. The data in Fig. 1–4 show ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z enhanced to a significant fraction of this “back-of-the-envelop” upper bound.
Z enhanced to a significant fraction of this “back-of-the-envelop” upper bound.
6. Conclusions and outlook
The present study introduced a new proposal for enhancing signals in solution state NMR, that could provide substantial sensitivity gains for a wide range of magnetic fields and rotational correlation times. The J-DNP mechanism underlying this proposal uses biradicals, it is transient, and it emerges in the hitherto unexplored Jex = ±(ωE + ωN) regimes. This requires exchange couplings in the order of the electron Larmor frequencies; i.e., ranging between ≈200–700 GHz for NMR measurements in 7–23.5 T fields. Such Jex values are not out of the ordinary: radical monomers connected by conjugated linkers having inter-electron exchange couplings in this order, have been reported in the literature.19–21 Under such conditions, both numerical and analytical simulations provide coinciding predictions of significant NMR polarization build-ups. These enhancements require irradiation times lasting a fraction of a second and, if implemented at the right electron Larmor frequency, they can proceed efficiently with microwave nutation fields ≤1 MHz (see ESI† 1 for additional details). ESI† 6 demonstrates that similar enhancements are reached with zero g- and shielding tensor anisotropies; the enhancements are also preserved if the two electrons have different but isotropic g-tensors. Much like the radical pair mechanism of CIDNP, the mechanism of J-DNP requires different hyperfine coupling to the two electrons; this drives nuclear state dependent electron relaxation which disappears if the nucleus is symmetrically placed between the two electrons. The enhancement is also quenched if the two electrons have different anisotropic g-tensors, as the resulting Δg-driven electron relaxation would then, at high magnetic fields, overtake the weaker differential relaxation mechanism arising from distinct intermolecular nuclear hyperfine couplings to the two electrons. Likewise, the enhancement goes to zero if the nucleus remains too distant from the biradical: for instance, a proton placed 20 Å away from the biradical may require over 1 s to achieve significant polarization gains – a time by which the DNP effect will lose against competing relaxation pathways.
Despite its encouraging conclusions, the present study also made a number of strong assumptions. It assumes that the non-Redfield relaxation terms in monoradicals resembled those acting in biradicals (ESI† 1); it remains to be seen how realistic this assumption is. Another major approximation was assuming a fixed electron/electron/nuclear geometry over the course of the DNP process: as the latter requires 10–100 ms and molecules in regular liquids diffuse tens of microns over such times, this fixed molecular geometry assumption is clearly unrealistic. On the other hand, a similar fixed-geometry assumption is successfully used and leads to realistic predictions in Overhauser DNP, where it works by virtue of DNP's independence on maintaining specific cross-correlations (a requirement present in our previous CCDNP proposal). Likewise, we hypothesize that the different −R[Ôα/β] rates required for J-DNP will be preserved regardless of the transient contact that a specific nucleus makes with an ensemble of biradicals over the course of its spin polarization process. Experiments are in progress to evaluate the correctness of these assumptions.
Author contributions
LF and MGC discovered the J-DNP effect and, jointly with IK, provided a theoretical description of its mechanism. IK has written Spinach kernel code and the symbolic processing engine. MGC wrote the simulation scripts to perform analytical and numerical simulations, and derived the analytical expressions of the relaxation rates. All authors discussed and wrote the paper.
Conflicts of interest
The authors declare no competing interests.
Acknowledgements
This project was funded by the Weizmann-UK Joint Research Programme, the Israel Science Foundation (ISF 965/18), the Perlman Family Foundation, and the US National Science Foundation (grants numbers CHE-1808660, DMR-1644779). MGC acknowledges Weizmann's Faculty of Chemistry for a Dean Fellowship. LF holds the Bertha and Isadore Gudelsky Professorial Chair and Heads the Clore Institute for High-Field Magnetic Resonance Imaging and Spectroscopy, whose support is acknowledged.
References
- A. W. Overhauser, Polarization of nuclei in metals., Phys. Rev., 1953, 92, 411 CrossRef CAS.
- T. R. Carver and C. P. Slichter, Experimental verification of the Overhauser nuclear polarization effect., Phys. Rev., 1956, 102, 975 CrossRef CAS.
- K.-N. Hu, H.-h. Yu, T. M. Swager and R. G. Griffin, J. Am. Chem. Soc., 2004, 126, 10844 CrossRef CAS PubMed.
- V. S. Bajaja, M. K. Hornstein, K. E. Kreischer, J. R. Sirigiri, P. P. Woskov, M. L. Mak-Jurkauskas, J. Herzfeld, R. J. Temkin and R. G. Griffin, 250 GHz CW gyrotron oscillator for dynamic nuclear polarization in biological solid state NMR., J. Magn. Reson., 2007, 189, 251 CrossRef PubMed.
- V. S. Bajaj, C. T. Farrar, M. K. Hornstein, I. Mastovsky, J. Vieregg, J. Bryant, B. Eléna, K. E. Kreischer, R. J. Temkin and R. G. Griffin, Dynamic nuclear polarization at 9 T using a novel 250 GHz gyrotron microwave source., J. Magn. Reson., 2011, 213, 404 CrossRef CAS PubMed.
- K. N. Hu, G. T. Debelouchina, A. A. Smith and R. G. Griffin, Quantum mechanical theory of dynamic nuclear polarization in solid dielectrics., J. Chem. Phys., 2011, 134, 125105 CrossRef PubMed.
- J. H. Ardenkjær-Larsen, B. Fridlund, A. Gram, G. Hansson, L. Hansson, M. H. Lerche, R. Servin, M. Thaning and K. Golman, Increase in signal-to-noise ratio of >10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times in liquid-state NMR, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10158 CrossRef PubMed.
000 times in liquid-state NMR, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10158 CrossRef PubMed.
- K. Golman, M. Lerche, R. Pehrson and J. H. Ardenkjaer-Larsen, Metabolic imaging by hyperpolarized 13C magnetic resonance imaging for in vivo tumor diagnosis., Cancer Res., 2006, 66, 10855 CrossRef CAS PubMed.
- N. M. Loening, M. Rosay, V. Weis and R. G. Griffin, Solution-state dynamic nuclear polarization at high magnetic field., J. Am. Chem. Soc., 2002, 124, 8808 CrossRef CAS PubMed.
- G. Liu, M. Levien, N. Karschin, G. Parigi, C. Luchinat and M. Bennati, One-thousand-fold enhancement of high field liquid nuclear magnetic resonance signals at room temperature., Nat. Chem., 2017, 9, 676 CrossRef CAS PubMed.
- T. Dubroca, S. Wi, J. van Tol, L. Frydman and S. Hill, Large volume liquid state scalar Overhauser dynamic nuclear polarization at high magnetic field., Phys. Chem. Chem. Phys., 2019, 21, 21200 RSC.
- G. Parigi, E. Ravera, M. Bennati and C. Luchinat, Understanding Overhauser Dynamic Nuclear Polarisation through NMR relaxometry., Mol. Phys., 2019, 117, 888 CrossRef CAS.
- M. Levien, M. Hiller, I. Tkach, M. Bennati and T. Orlando, Nitroxide Derivatives for Dynamic Nuclear Polarization in Liquids: The Role of Rotational Diffusion., J. Phys. Chem. Lett., 2020, 11, 1629 CrossRef CAS PubMed.
-
K. H. Hausser and D. Stehlik, Dynamic nuclear polarization in liquids, in Advances in Magnetic and Optical Resonance, Elsevier, 1968, p. 79.
- C. G. Riesinger, M. Bennati, H. M. Vieth, C. Luchinat, G. Parigi, P. Höfer, F. Engelke, S. J. Glaser, V. Denysenkov and T. F. Prisner, Dynamic nuclear polarization at high magnetic fields in liquids, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 64, 4 CrossRef PubMed.
- T. Prisner, V. Denysenkov and D. Sezer, Liquid state DNP at high magnetic fields: Instrumentation, experimental results and atomistic modelling by molecular dynamics simulations., J. Magn. Reson., 2016, 264, 68 CrossRef CAS PubMed.
- E. Ravera, C. Luchinat and G. Parigi, Basic facts and perspectives of Overhauser DNP NMR., J. Magn. Reson., 2016, 264, 78 CrossRef CAS PubMed.
- M. G. Concilio, M. Soundararajan, L. Frydman and I. Kuprov, High-field solution state DNP using cross-correlations., J. Magn. Reson., 2021, 326, 106940 CrossRef CAS PubMed.
- G. W. Reginsson, N. C. Kunjir, S. T. Sigurdsson and O. Schiemann, Trityl radicals: spin labels for nanometer-distance measurements., Chem. – Eur. J., 2012, 18, 13580 CrossRef CAS PubMed.
- J. J. Jassoy, A. Meyer, S. Spicher, C. Wuebben and O. Schiemann, Synthesis of Nanometer Sized Bis- and Tris-trityl Model Compounds with Different Extent of Spin-Spin Coupling., Molecules, 2018, 23, 682 CrossRef PubMed.
- N. Fleck, T. Hett, J. Brode, A. Meyer, S. Richert and O. Schiemann, C-C Cross-Coupling Reactions of Trityl Radicals: Spin Density Delocalization, Exchange Coupling, and a Spin Label., J. Org. Chem., 2019, 84, 3293 CrossRef CAS PubMed.
-
A. Redfield, The theory of relaxation processes, in Advances in Magnetic and Optical Resonance, Elsevier, 1965, p. 1.
- M. Goldman, Formal theory of spin-lattice relaxation., J. Magn. Reson., 2001, 149, 160 CrossRef CAS PubMed.
- I. Kuprov, N. Wagner-Rundell and P. Hore, Bloch-Redfield-Wangsness theory engine implementation using symbolic processing software., J. Magn. Reson., 2007, 184, 196 CrossRef CAS PubMed.
- I. Kuprov, Diagonalization-free implementation of spin relaxation theory for large spin systems., J. Magn. Reson., 2011, 209, 31 CrossRef CAS PubMed.
- D. Goodwin and I. Kuprov, Auxiliary matrix formalism for interaction representation transformations, optimal control, and spin relaxation theories., J. Chem. Phys., 2015, 143, 084113 CrossRef CAS PubMed.
- J. Bargon, H. Fischer and U. Johnsen, Kernresonanz-Emissionslinien während rascher Radikalreaktionen, Z. Naturforsch., A: Phys., Phys. Chem., Kosmophys., 1967, 22, 1551 CAS.
- R. Kaptein and L. J. Oosterhoff, Chemically induced dynamic nuclear polarization II: (Relation with anomalous ESR spectra)., Chem. Phys. Lett., 1969, 4, 195 CrossRef CAS.
- G. L. Closs, Mechanism explaining nuclear spin polarizations in radical combination reactions., J. Am. Chem. Soc., 1971, 93, 1546 CrossRef CAS.
- S. Santabarbara, I. Kuprov, W. V. Fairclough, S. Purton, P. J. Hore, P. Heathcote and M. C. W. Evans, Bidirectional electron transfer in photosystem I: determination of two distances between P700+ and A1- in spin-correlated radical pairs, Biochemistry, 2005, 44, 2119 CrossRef CAS PubMed.
- J. H. Ardenkjær-Larsen, I. Laursen, I. Leunbach, G. Ehnholm, L.-G. Wistrand, J. S. Petersson and K. Golman, EPR and DNP properties of certain novel single electron contrast agents intended for oximetric imaging., J. Magn. Reson., 1998, 133, 1 CrossRef PubMed.
- R. A. Wind and J. H. Ardenkjaer-Larsen, 1H DNP at 1.4 T of water doped with a triarylmethyl-based radical., J. Magn. Reson., 1999, 141, 347 CrossRef CAS PubMed.
- P. Höfer, G. Parigi, C. Luchinat, P. Carl, G. Guthausen, M. Reese, T. Carlomagno, C. Griesinger and M. Bennati, Field dependent dynamic nuclear polarization with radicals in aqueous solution., J. Am. Chem. Soc., 2008, 130, 3254 CrossRef PubMed.
- L. Yong, J. Harbridge, R. W. Quine, G. A. Rinard, S. S. Eaton, G. R. Eaton, C. Mailer, E. Barth and H. J. Halpern, Electron spin relaxation of triarylmethyl radicals in fluid solution., J. Magn. Reson., 2001, 152, 156 CrossRef CAS PubMed.
- R. Owenius, G. R. Eaton and S. S. Eaton, Frequency (250 MHz to 9.2 GHz) and viscosity dependence of electron spin relaxation of triarylmethyl radicals at room temperature., J. Magn. Reson., 2005, 172, 168 CrossRef CAS PubMed.
- R. K. Wangsness and F. Bloch, The dynamical theory of nuclear induction., Phys. Rev., 1953, 89, 728 CrossRef CAS.
- M. H. Levitt and L. Di Bari, Steady state in magnetic resonance pulse experiments., Phys. Rev. Lett., 1992, 69, 3124 CrossRef PubMed.
- I. Kuprov, D. M. Hodgson, J. Kloesges, C. I. Pearson, B. Odell and T. D. W. Claridge, Anomalous Nuclear Overhauser Effects in Carbon-Substituted Aziridines: Scalar Cross-Relaxation of the First Kind, Angew. Chem., Int. Ed., 2015, 54, 3697 CrossRef CAS PubMed.
- H. Hogben, M. Krzystyniak, G. Charnock, P. Hore and I. Kuprov, Spinach – a software library for simulation of spin dynamics in large spin systems., J. Magn. Reson., 2011, 208, 179 CrossRef CAS PubMed.
- P. J. Hore and R. W. Broadhurst, Photo-CIDNP of biopolymers., Prog. NMR Spectrosc., 1993, 25, 345 CrossRef CAS.
- S. Vega, Fictitious spin 1/2 operator formalism for multiple quantum NMR., J. Chem. Phys., 1978, 68, 5518 CrossRef CAS.
-
R. R. Ernst, G. Bodenhausen and A. Wokaun, Principles of Nuclear Magnetic Resonance in One and Two Dimensions, Clarendon Press, Oxford, 1987, p. 610 Search PubMed.
- I. Kuprov, T. D. Craggs, S. E. Jackson and P. J. Hore, Spin relaxation effects in photochemically induced dynamic nuclear polarization spectroscopy of nuclei with strongly anisotropic hyperfine couplings., J. Am. Chem. Soc., 2007, 129, 9004 CrossRef CAS PubMed.
- W. Müller-Warmuth, R. Vilhjalmsson, P. A. M. Gerlof, J. Smith and J. Trommel, Intermolecular interactions of benzene and carbon tetrachloride with selected free radicals in solution as studied by 13C and 1H dynamic nuclear polarization., Mol. Phys., 1976, 31, 1055 CrossRef.
- M. Levien, M. Reinhard, M. Hiller, I. Tkach, M. Bennati and T. Orlando, Spin density localization and accessibility of organic radicals affect liquid-state DNP efficiency., Phys. Chem. Chem. Phys., 2021, 23, 4480 RSC.
- J. Blicharski, Nuclear magnetic relaxation by anisotropy of the chemical shift., Z. Naturforsch., A: Phys., Phys. Chem., Kosmophys., 1972, 27, 1456 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04186j |
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Ilya
Kuprov
*a,
Ilya
Kuprov
 b and
Lucio
Frydman
b and
Lucio
Frydman
 *ac
*ac


![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (e1,e2)0,
(e1,e2)0,![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (e1,e2)±1}. As shown in ESI† 2, this leads to a microwave rotating frame Hamiltonian:
(e1,e2)±1}. As shown in ESI† 2, this leads to a microwave rotating frame Hamiltonian:![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0 sub-space, ĤT+1T−1 acts in the
0 sub-space, ĤT+1T−1 acts in the ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) +1
+1![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) −1 sub-space, and Ĥμw is the microwave operator (see ESI† 2, for further definitions). With this Hamiltonian, Liouville-space time domain calculations were performed based on the equation of motion:
−1 sub-space, and Ĥμw is the microwave operator (see ESI† 2, for further definitions). With this Hamiltonian, Liouville-space time domain calculations were performed based on the equation of motion:
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t) is the state vector of the system, and
(t) is the state vector of the system, and  is the Liouvillian containing the rotating frame Hamiltonian superoperator plus the relaxation superoperator
is the Liouvillian containing the rotating frame Hamiltonian superoperator plus the relaxation superoperator  accounting for the stochastic rotation of all anisotropies. The latter was computed according to the Bloch–Redfield–Wangsness relaxation theory22,36 both by analytical24 and numerical25,26 means, including all possible longitudinal, transverse and cross-correlated pathways. Since the spin system was considered at room temperature, Di-Bari–Levitt thermalization was used.37 Considering that the exchange coupling has the same order of magnitude as the electron Larmor frequency, these calculations incorporated into the relaxation superoperator a scalar relaxation of the first kind.38 This did not have an effect on the DNP enhancement, since in the ωΔe → 0 case in question, the exchange coupling,
accounting for the stochastic rotation of all anisotropies. The latter was computed according to the Bloch–Redfield–Wangsness relaxation theory22,36 both by analytical24 and numerical25,26 means, including all possible longitudinal, transverse and cross-correlated pathways. Since the spin system was considered at room temperature, Di-Bari–Levitt thermalization was used.37 Considering that the exchange coupling has the same order of magnitude as the electron Larmor frequency, these calculations incorporated into the relaxation superoperator a scalar relaxation of the first kind.38 This did not have an effect on the DNP enhancement, since in the ωΔe → 0 case in question, the exchange coupling,  , commutes with the Zeeman interaction, Ê1Z+ Ê2Z. Time evolution Ô(t) of multiple spin state populations was calculated by taking their scalar products with the state vector
, commutes with the Zeeman interaction, Ê1Z+ Ê2Z. Time evolution Ô(t) of multiple spin state populations was calculated by taking their scalar products with the state vector ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t) at each time.
(t) at each time.


![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1,α/β,
±1,α/β,![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0,α/β and Ŝ0,α/β (see ESI† 3, for the expressions of these Ôα/β as Cartesian operators). Fig. 4e shows the states arising from the difference between Ôα and Ôβ, defined as:
0,α/β and Ŝ0,α/β (see ESI† 3, for the expressions of these Ôα/β as Cartesian operators). Fig. 4e shows the states arising from the difference between Ôα and Ôβ, defined as:
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z is the longitudinal nuclear magnetization. Fig. 4f shows the overall
Z is the longitudinal nuclear magnetization. Fig. 4f shows the overall ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z amplitude calculated upon summing the amplitudes of Ŝ0
Z amplitude calculated upon summing the amplitudes of Ŝ0![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z,
Z, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0
0![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z and
Z and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1
±1![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z, normalized to the equilibrium nuclear magnetization.
Z, normalized to the equilibrium nuclear magnetization.

![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1,α/β,
±1,α/β, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0,α/β and Ŝ0,α/β (a–d), and of the
0,α/β and Ŝ0,α/β (a–d), and of the ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) ZŜ0,
ZŜ0, ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z
Z![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1 and
±1 and ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z
Z![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0 states (e) arising from the difference between the various Ôα and Ôβ. Time evolution of the overall longitudinal nuclear magnetization
0 states (e) arising from the difference between the various Ôα and Ôβ. Time evolution of the overall longitudinal nuclear magnetization ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z (f), showing the sum of all
Z (f), showing the sum of all ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z-related contributions, normalized by the thermal nuclear magnetization under the same conditions. Plots (a–d) are normalized to a total electron spin population of one, as defined in ESI† 3. Jex = +(ωE + ωN) was used for the dashed lines calculations, and Jex = −(ωE + ωN) was used for the continuous lines. In (e), the red and green traces are barely seen as they fall underneath an overlapping black trace. The slightly different curves in (f) reflect Jex = ±(ωE + ωN) conditions, respectively. For all these calculations B0 = 14.08 T, τc = 500 ps for the biradical/proton dipolar-coupled triad; all other parameters as given in Table 1.
Z-related contributions, normalized by the thermal nuclear magnetization under the same conditions. Plots (a–d) are normalized to a total electron spin population of one, as defined in ESI† 3. Jex = +(ωE + ωN) was used for the dashed lines calculations, and Jex = −(ωE + ωN) was used for the continuous lines. In (e), the red and green traces are barely seen as they fall underneath an overlapping black trace. The slightly different curves in (f) reflect Jex = ±(ωE + ωN) conditions, respectively. For all these calculations B0 = 14.08 T, τc = 500 ps for the biradical/proton dipolar-coupled triad; all other parameters as given in Table 1.
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0,β and
0,β and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1,β are on the left, and rates of Ŝ0,α,
±1,β are on the left, and rates of Ŝ0,α, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0,α and
0,α and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1,α are on the right. Calculations relied on the parameters of Table 1 and on τc = 500 ps for the biradical/proton dipolar-coupled triad.
±1,α are on the right. Calculations relied on the parameters of Table 1 and on τc = 500 ps for the biradical/proton dipolar-coupled triad.![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z builds up. As can be appreciated in Fig. 4f, this polarization is only weakly dependent on the sign of Jex. Also note that, as eventually all electron/nuclear states reach the same populations, this J-DNP build up is transient: no nuclear polarization gains are predicted when the steady-state conditions examined in conventional Overhauser DNP analyses, are considered.
Z builds up. As can be appreciated in Fig. 4f, this polarization is only weakly dependent on the sign of Jex. Also note that, as eventually all electron/nuclear states reach the same populations, this J-DNP build up is transient: no nuclear polarization gains are predicted when the steady-state conditions examined in conventional Overhauser DNP analyses, are considered.![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) ZŜ0 state – microwaves could be turned off when nuclear magnetization has reached a maximum; the electron population operators would then relax back to thermal equilibrium, and the build-up could be “pumped” again by repeated irradiation. However, in an actual J-DNP enhancement experiment, the polarizing proton would not be covalently bound; rather, it would be randomly diffusing at rates of ca. 1 μm ms−1.31 The interaction with the polarizing biradical would thus be short-lived, and the proton pool would get repeatedly polarized by different transient encounters with different biradicals; a certain “pulsing” of the effect will therefore occur spontaneously.13,44,45
ZŜ0 state – microwaves could be turned off when nuclear magnetization has reached a maximum; the electron population operators would then relax back to thermal equilibrium, and the build-up could be “pumped” again by repeated irradiation. However, in an actual J-DNP enhancement experiment, the polarizing proton would not be covalently bound; rather, it would be randomly diffusing at rates of ca. 1 μm ms−1.31 The interaction with the polarizing biradical would thus be short-lived, and the proton pool would get repeatedly polarized by different transient encounters with different biradicals; a certain “pulsing” of the effect will therefore occur spontaneously.13,44,45![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1,α/β,
±1,α/β,![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0,α/β and Ŝ0,α/β population operators driving the population decays of the various nuclear spin states, change over a range of magnetic fields B0 and exchange couplings Jex. Notice the marked differentials arising whenever Jex matches ±(ωE + ωN), between the self-relaxation rates of various Ôα and Ôβ operators. It is these differential decays that drive the enhancements shown in Fig. 1–4.
0,α/β and Ŝ0,α/β population operators driving the population decays of the various nuclear spin states, change over a range of magnetic fields B0 and exchange couplings Jex. Notice the marked differentials arising whenever Jex matches ±(ωE + ωN), between the self-relaxation rates of various Ôα and Ôβ operators. It is these differential decays that drive the enhancements shown in Fig. 1–4.


![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) +1,α/β operators, the self-relaxation rates are:
+1,α/β operators, the self-relaxation rates are:

![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 0,α/β operators, the self-relaxation rates are:
0,α/β operators, the self-relaxation rates are:

![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) −1,α/β operators, the self-relaxation rates:
−1,α/β operators, the self-relaxation rates:

 of tensors A and B. The “…” in eqn (5)–(12) denote terms that contribute equally to Ôα and Ôβ and thus are not relevant for the J-DNP effect; full analytical expressions for all the self-relaxation rates in eqn (5)–(12) are given in ESI† 4, and the definitions of second-rank norm squared and of scalar product are given in ESI† 5.
of tensors A and B. The “…” in eqn (5)–(12) denote terms that contribute equally to Ôα and Ôβ and thus are not relevant for the J-DNP effect; full analytical expressions for all the self-relaxation rates in eqn (5)–(12) are given in ESI† 4, and the definitions of second-rank norm squared and of scalar product are given in ESI† 5.
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) ZŜ0,
ZŜ0, ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z
Z![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1 states, as shown in Fig. 4. This can be most easily appreciated for the Ŝ0,α and Ŝ0,β relaxation rates: the latter will be dominated by the J(Jex + ωE + ωN) term if Jex = +(ωE + ωN), and the former by the J(Jex − ωE − ωN) if Jex = −(ωE + ωN). In either case, such Jex condition will result in large differences between −R[Ôα] and −R[Ôβ], due to the cancellation of ωE by Jex. Similar differences can be observed in Fig. 5 also for
±1 states, as shown in Fig. 4. This can be most easily appreciated for the Ŝ0,α and Ŝ0,β relaxation rates: the latter will be dominated by the J(Jex + ωE + ωN) term if Jex = +(ωE + ωN), and the former by the J(Jex − ωE − ωN) if Jex = −(ωE + ωN). In either case, such Jex condition will result in large differences between −R[Ôα] and −R[Ôβ], due to the cancellation of ωE by Jex. Similar differences can be observed in Fig. 5 also for ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1,α and
±1,α and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ±1,β; ESI† 4 provides additional information about these self-relaxation rates. Note as well that, even though the absolute values of these rates decrease with B0 and τc, their differences actually remain present (Fig. S4 and S5, ESI†). This helps to understand the increased efficiencies that J-DNP enhancements exhibit as a function of B0 and τc, leading to the sizable transient longitudinal nuclear magnetizations shown in Fig. 1–4.
±1,β; ESI† 4 provides additional information about these self-relaxation rates. Note as well that, even though the absolute values of these rates decrease with B0 and τc, their differences actually remain present (Fig. S4 and S5, ESI†). This helps to understand the increased efficiencies that J-DNP enhancements exhibit as a function of B0 and τc, leading to the sizable transient longitudinal nuclear magnetizations shown in Fig. 1–4.![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Z enhanced to a significant fraction of this “back-of-the-envelop” upper bound.
Z enhanced to a significant fraction of this “back-of-the-envelop” upper bound.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times in liquid-state NMR, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10158 CrossRef PubMed.
000 times in liquid-state NMR, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10158 CrossRef PubMed.