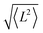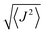Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetic properties of coordination clusters with {Mn4} and {Co4} antiferromagnetic cores†
Simona
Achilli
 *ab,
Claire
Besson
*ab,
Claire
Besson
 c,
Xu
He
c,
Xu
He
 d,
Pablo
Ordejón
d,
Pablo
Ordejón
 d,
Carola
Meyer
d,
Carola
Meyer
 e and
Zeila
Zanolli
e and
Zeila
Zanolli
 bdf
bdf
aDipartimento di Fisica “Aldo Pontremoli”, Universitá degli Studi di Milano, Via Celoria 16, Milan, Italy. E-mail: simona.achilli@unimi.it
bEuropean Theoretical Spectroscopy Facilities,
cDepartment of Chemistry, The George Washington University, Washington, DC 20052, USA
dCatalan Institute of Nanoscience and Nanotechnology - ICN2 (CSIC and BIST), Campus UAB, Bellaterra, 08193 Barcelona, Spain
eDepartment of Physics, Universität Osnabrück, 49076 Osnabrück, Germany
fChemistry Department, Debye Institute for Nanomaterials Science, Condensed Matter and Interfaces, Utrecht University, PO Box 80 000, 3508 TA Utrecht, The Netherlands
First published on 18th January 2022
Abstract
We present a joint experimental and theoretical characterization of the magnetic properties of coordination clusters with an antiferromagnetic core of four magnetic ions. Two different compounds are analyzed, with Co and Mn ions in the core. While both molecules are antiferromagnetic, they display different sensitivities to external magnetic field, according to the different atomic magnetic moments and strength of the intra-molecular magnetic couplings. In particular, the dependence of the magnetization versus field of the two molecules switches with temperature: at low temperature the magnetization is smaller in {Mn4} than in Co4, while the opposite happens at high temperature. Through a detailed analysis of the electronic and magnetic properties of the two compounds we identify a stronger magnetic interaction between the magnetic ions in {Mn4} with respect to {Co4}. Moreover {Co4} displays not negligible spin–orbit related effects that could affect the spin lifetime in future antiferromagnetic spintronic applications. We highlight the necessity to account for these spin–orbit effects together with electronic correlation effects for a reliable description of these compounds.
1 Introduction
Molecular magnets constitute an excellent platform for molecular spintronics and quantum information storage and processing as their properties can be controlled at the nano/micro-scale during fabrication.1–3 Coordination clusters formed by an inner magnetic core and a surrounding shell of organic ligands can be synthesized to control both the magnetic interactions between the ions within the molecule and the coupling between magnetic core and environment,4 while practically reducing to nothing the influence of intermolecular interactions on the magnetic properties. Single-molecule magnets are particularly attractive for spin-dependent quantum transport applications5 as the spin retains its orientation in the absence of an external magnetic field and applications can leverage on the technology developed for functionalization with nanoparticles.6,7In recent years, research has concentrated on molecular magnets with large overall spin generated by ferromagnetic coupling between magnetic centers.8–10 On the other hand, the incorporation of molecular antiferromagnets in spintronic devices11,12 is still a new area of research. Recent proposals are only theoretical, and concern molecular AFM crystals13 or systems that can hardly be realized experimentally.14 The expected advantages of antiferromagnetic coordination clusters are the same as for antiferromagnetic spintronic devices, i.e. robustness against perturbation due to magnetic fields, absence of stray fields, and capability to generate ultrafast dynamics and large magnetotransport effects.15 Antiferromagnetic molecules can be used to functionalize other organic systems, as carbon nanotubes, with the advantage that the current flowing through the tube does not alter the magnetic properties of the molecules16,17 and the low spin–orbit coupling allows long spin-flip lengths and spin lifetimes.
The application of molecular magnets in spintronics and quantum technologies would benefit from molecular design aimed at identifying the most suitable combinations of magnetic ions and organic ligands to ensure long spin coherence times, efficient spin injections and tunable transitions between spin states.18–20 Property-tuning efforts are usually concentrated on modifications of the ligands surrounding a given metal core. This approach, however, has some limitations for integrating the molecule in a device: the ligands are also the place where the interaction with the environment takes place. Changing the ligands can have unwanted and unpredictable effects on the electronic properties of the device-molecule interface, in addition to changes of the magnetic properties of the core. We propose here a reverse approach: the ligand system is kept identical, and the magnetic properties are modified by changing the metal atoms.
We selected the architecture of a M4O4 cubane structure based on the family of {Mn4} antiferromagnets with the general formula [(RCO2)4Mn4L2] (R = CF3, CH3, Ph, H2L = 2,6-bis(1-(2-hydroxyphenyl)iminoethyl)pyridine) previously reported by Kampert et al.21 The presence of four metal centers offers a rich landscape of electronic and magnetic levels for spintronic applications. Through a joint experimental and theoretical characterization we compare the {Mn4} acetate complex with its newly prepared cobalt analogue.
Many M4O4 cubane complexes are reported in the literature, for M = Co and Mn. However, their magnetic properties have been investigated only in four cases22–25 showing a switching or an enhancement of the magnetic coupling by changing the inner core. In [M4(dpd-H)4(OAc)3(OH2)1]+ and [M4(dpd-H)4(OAc)2 {N(CN)2}2] (dpd-H2 = di-2-pyridylketone in gem-diol form), the overall magnetic coupling shifts from antiferromagnetic for manganese(II) centers to ferromagnetic for cobalt(II).22,23 In [M4(cit)4]8− (cit = citrate) and [M4(nic)4(OMe)4] (nic = nicotinate) the coupling is antiferromagnetic for both ions, but the coupling is larger for manganese in the former case24 and for cobalt in the latter.25 Additionally, while MnII centers are adequately described by the spin magnetic moment (spin-only model), CoII centers in octahedral or pseudo-octahedral environments are characterized by significant orbital moments, leading to spin–orbit coupling (SOC) effects that are expected to significantly affect more complex devices.
Our theoretical analysis, performed through a first-principles approach and a Heisenberg model Hamiltonian explains the marked experimental differences between the two compounds, opening the door to using in silico work to design complexes with targeted magnetic properties.
2 Methods
2.1 Theory
Theoretical calculations were performed in the Density Functional Theory (DFT) framework, using a pseudopotential description of the core electrons and atomic orbital basis set, as implemented in the SIESTA code.26,27 We adopted the local density approximation (LDA)28,29 for the exchange–correlation energy functional. A Hubbard correction for Mn and Co was included to account for the strong Coulomb interaction of localized d electrons. We use U = 6 eV for Mn and U = 4 eV for Co, according to the literature.21,30 To evaluate the role of spin–orbit coupling, which is relevant in Co, we also performed calculations including spin–orbit correction using the formalism of ref. 31, as implemented in SIESTA.32 The current version of the SIESTA code does not allow to simultaneously include Hubbard and spin–orbit corrections, thus the two effects are treated separately. The structure was relaxed with a tolerance on the forces on the atoms equal to 0.03 eV Å−1. In the LDA+U calculations the finesse of the real-space grid (mesh-cutoff) was set to 400 Ry and the smearing of the electronic occupation (electronic temperature) to 100 K. In order to increase the accuracy in the convergence, SOC calculations where performed with 600 Ry mesh cutoff and 1 K electronic temperature. The structural relaxation has been refined with SOC, starting from the LDA+U equilibrium geometry. The exchange coupling parameters Ji,j were obtained by considering the lowest energy spin configurations of the Mn and Co centers and solving a system of equations (Heisenberg model) in the DFT energies with four Ji,j parameters. The geometry of the various spin configurations was kept fixed to the ground state one in order to exclusively account for the effect of the spin-flip on the total energy of the molecules.33 Further, we exploited the model Heisenberg Hamiltonian , where
, where 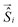 is the spin vector of atom i and Ji,j is the matrix of the exchange parameters, to fit experimental temperature and field-dependent magnetization data, as allowed by the implementation in the PHI code.34 In the following we label J1 = J1,4 = J2,3, J2 = J1,3 = J2,4, J3 = J1,2, J4 = J3,4, with the Mi atoms numbered as indicated on Fig. 1.
is the spin vector of atom i and Ji,j is the matrix of the exchange parameters, to fit experimental temperature and field-dependent magnetization data, as allowed by the implementation in the PHI code.34 In the following we label J1 = J1,4 = J2,3, J2 = J1,3 = J2,4, J3 = J1,2, J4 = J3,4, with the Mi atoms numbered as indicated on Fig. 1.
 | ||
| Fig. 1 Molecular structure of the {M4} complex. (a) Side view. Blue: Mn, Co or Zn atoms; red: O; green: N; gray: C, white: H. (b) Top view of the lower half of the molecule. (c) Top view of the upper half of the molecule. Relaxed coordinates are available in ESI.† | ||
2.2 Experiment
The complexes [M4L2(OAc)4] (M = Mn, Co, Zn, {M4} for short), where H2L = 2,6-bis-(1-(2-hydroxyphenyl)iminoethyl)pyridine, HOAc = acetic acid, and M = MnII, CoII or ZnII) were synthesized by one pot reaction of 2-aminophenol, diacetylpyridine and manganese, cobalt or zincacetate, as described by Kampert et al. for the manganese complex,21 with some modifications for the cobalt and zinc analogues. Full details of the synthesis methods are given in the ESI.† The two new molecular complexes were characterized via single crystal diffraction conducted on a SuperNova (Agilent Technologies) diffractometer using Mo K radiation at 120 K. The crystals were mounted on a Hampton cryoloop with Paratone-N oil to prevent solvent loss. Thermogravimetric analysis was performed using a Mettler-Toledo TGA/SDTA 851e instrument with a heating rate of 10 K min−1. Cyclic voltammograms were recorded in dry and deaerated acetonitrile solutions containing tetrabutylammonium perchlorate (0.1 M) as electrolyte and 3 mM of the analyte, using a SP-150 potentiostat (BioLogic Science Instruments) controlled by the EC-Lab software and a standard three-electrodes setup including a glassy carbon working electrode (diameter 3 mm), a platinum wire counter electrode and an Ag/AgNO3 (0.1 M) reference electrode. Ferrocene was used as an internal standard. Magnetometry was performed on a Quantum Design MPMS-5XL SQUID magnetometer. The crystalline samples were crushed and placed under vacuum for 16 h before the complete removal of solvate molecules was checked by TGA. The resulting powders were compacted and immobilised into PTFE capsules. All data were corrected for the contribution of the sample holder (PTFE capsule). Measurements on {Zn4} were used to determine the diamagnetic susceptibility of this complex χdia(Zn4) = −5.3 × 10−9 m3 mol−1. The diamagnetic contribution in {Co4} and Mn4 was then calculated from this value and Pascal's constants35 for the Zn2+, Co2+ and Mn2+ ions, yielding χdia(Co4) = −5.1 × 109 m3 mol−1 and χdia(Mn4) = −5.2 × 10−9 m−3 mol−1, and subtracted from the experimental susceptibility data.3 Theoretical and experimental analysis
3.1 Synthesis and redox properties
The {M4} are stable towards oxidation in the solid state as well as in solution, despite the sensitivity of the {Co4} precursors to oxidation by O2 during synthesis. This observation is confirmed by the cyclic voltammetry of the complex (Fig. 2, purple dotted line), which displays two quasi-reversible (ΔE = 120 mV) one-electron oxidation waves at 0.30 and 0.80 V vs. Fc+/Fc which can be assigned as {CoII4} → {CoII3CoIII} → {CoII2CoIII2}. As expected, the redox couples in the manganese complexes are shifted to lower potentials and show the large peak-to-peak characteristic of MnII(HS) → MnIII(LS) processes (Fig. 2, yellow solid line). Finally, the zinc derivative shows irreversible ligand-centered oxidation processes above 0.5 V vs. Fc+/Fc (Fig. 2, gray dashed line).3.2 Molecular structure
The structure of the cobalt and zinc complexes was determined by single crystal X-ray diffraction to be analogue to that of the previously published manganese complex:21 the complexes consist of a cubic M4O4 core with two sets of two different ligand groups, for a total of 118 atoms (Fig. 1). The metallic core is a quasi-tetrahedron composed of two 7-coordinated ions (M1, M2) with pentagonal bipyramidal coordination and two 6-coordinated ions (M3, M4) with pseudo-octahedral symmetry.The metal ions with the same coordination number are almost equivalent, as they overall face a quasi-identical chemical environment. The molecular cluster has an approximately C2 symmetry and can be described as two identical structures on different planes that are rotated of 90° one respect to the other (Fig. 1), taking the rotation axis along z. Seven-coordinated M1 and M2 lie on different planes, each being connected in-plane to a pentadentate pyridine–diimine–diphenoxide type ligand (L2−), completed by the oxygen of a bridging acetate and a κ3 phenoxide oxygen from the other L2− ligand. The coordination sphere of M3, M4 is a pseudo octahedron of six oxygen atoms provided by a bidentate acetate ligand, the other oxygen of the two bridging acetate and two phenoxide oxygen from the L2− ligand (relaxed coordinates available in ESI†).
The inner cage of the three molecules is composed by four transition metal ions with different atomic valence configurations, 3d5 for Mn(II), 3d7 for Co(II) and 3d10 for zinc(II). The latter complex is therefore diamagnetic; it was used experimentally to determine the diamagnetic contribution to the susceptibility of the complexes and will not be discussed further. Both Mn(II) and Co(II) ions display high spin configurations, i.e. S = 5/2 for Mn and S = 3/2 for Co.
Despite the similarity between the structures of the manganese and cobalt complexes, experimental evidence and DFT calculations show small differences in bond lengths in the inner core. In agreement with the larger atomic radius of Mn with respect to Co, the {Mn4} central cage is slightly larger than the {Co4} one, due to larger M–O and M–N bond-lengths. Details of the structure are reported in Table 1.
| d (Å) | M1–M2 | M3–M4 | M1–M3a | M2–OB,1b | M4–OA,2b |
|---|---|---|---|---|---|
| a The two values correspond to the equivalent pairs of atoms. b Range given for all equivalent distances in the complex. | |||||
| {Mn4} | |||||
| DFT | 3.35 | 3.45 | 3.64/3.65 | 2.20–2.30 | 2.15–2.22 |
| XRD | 3.62 | 3.47 | 3.50/3.55 | 2.27–2.31 | 2.21–2.22 |
| {Co4} | |||||
| DFT | 3.26 | 3.21 | 3.42/3.44 | 2.15–2.21 | 2.07–2.11 |
| XRD | 3.39 | 3.19 | 3.15/3.16 | 2.17–2.29 | 2.11–2.19 |
3.3 Behavior in magnetic field
In order to quantify the strength of the magnetic interaction within the molecule and the response to an external magnetic field we performed SQUID magnetometry experiments (Fig. 3). A singlet ground state is observed in both complexes, indicating the presence of antiferromagnetic coupling between the magnetic ions in the molecule. The molecular moment μmol as a function of magnetic field (H = 0–5 T) and temperature (T = 20–300 K) was fitted to a mean field model (Curie–Weiss law, eqn (1)), yielding Néel temperatures of TN = 23 K for {Mn4} and TN = 12 K for {Co4}: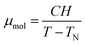 | (1) |
 | ||
| Fig. 3 SQUID magnetometry data of {Mn4} (orange) and {Co4} (purple) at T = 3.6 K (open symbols) and T = 50 K (filled symbols). | ||
Those values, as well as the larger slope of the molecular moment at low field/low temperature observed for {Co4} in comparison to {Mn4}, suggests that the antiferromagnetic coupling between the metal atoms in {Co4} is smaller than in {Mn4}.
Notably, the behavior is reversed at high temperature with a larger magnetic moment for {Mn4} than for {Co4}, which is in agreement with the higher spin moment of the Mn centers.
The Curie constant C obtained for the {Mn4} complex (3.0 × 10−3μB K Oe−1) is in good agreement with a spin-only model (3.1 × 10−3μB K Oe−1 for g = 2 and S = 5/2). Such a model is not adequate for octahedral cobalt(II) complexes, with their 4T1g ground term, and effective orbital momentum L = 1.36 Indeed, the Curie constant of {Co4} (2.4 × 10−3μB K Oe−1) obtained from the Curie–Weiss fit deviates significantly from the one calculated by the spin-only model (1.3 × 10−3μB K Oe−1).
The measured magnetic susceptibility is reported in ESI,† together with the theoretical one obtained from spin dynamics calculations. The agreement between theory and experiment is fairly good in the LDA+U approximation (see the discussion in Section 3.6).
3.4 Magnetic and electronic properties
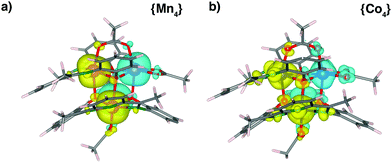
In order to characterize the magnetic configuration of the inner cage and to ascertain the role of spin–orbit coupling in {Co4} we performed DFT calculations which show that the ground state is characterized by an antiferromagnetic coupling between non-equivalent metal ions (M1/M3 and M2/M4), and a ferromagnetic one between the equivalent pairs (M1/M2 and M3/M4) giving rise to a up-up-down-down (uudd) configuration, referring to the relative alignment of the spins of the four metal ions. The magnetic moments of Co, Mn, N and O in the two molecular complexes, deduced from the Mulliken charge population, are reported in Table 2. Due to the chemical interaction with the ligands the magnetic moment of the metal atoms in the molecular complexes is reduced with respect to the isolated ions (∼4% in {Mn4}, ∼10% {Co4}). Accordingly, the induced magnetization of the ligands is smaller for {Mn4} than for {Co4}, as can be appreciated also through the small differences in the spatial distribution of the spin density (ρup − ρdown on the oxygen atoms, Fig. 4). In {Mn4} the magnetic moment of OA and OB is negligible. In {Co4} the bridging phenoxy oxygens have opposite magnetization: OB2 and OB3 are magnetized up while OB1 and OB4 are magnetized down. Out of the eight acetate oxygens OA, only two (OA+) display a small positive magnetic moment while the other six (OA−) have a larger (in modulus) negative magnetic moment (mean value reported in Table 2). The average magnetization of the N atoms is comparable to the average contribution of OA but with opposite sign. As a consequence, despite the presence of local magnetic moments, the total spin of both molecules is STOT = 0 confirming their antiferromagnetic character. Nevertheless, the major spread of the magnetic moment observed in {Co4} is an indication of a possible large magnetic interaction of this molecule with other systems when the complex is used for functionalization.| (μB) | M1,2 | M3,4 | N | OA+ | OA− | OB2,3 | OB1,4 |
|---|---|---|---|---|---|---|---|
| {Mn4} | 4.82 | −4.89 | 0.01 | 0.01 | −0.01 | 0.00 | 0.00 |
| {Co4} | 2.71 | −2.73 | 0.05 | 0.03 | −0.04 | 0.02 | −0.02 |
In Fig. 5 the DOS of the two molecules projected on different atoms of the complex (PDOS), is reported. The PDOS of Mn ions is characterized by the prevalence a single spin population, due to the almost complete filling of the spin-up 3d electrons. In Co, instead, majority and minority spins are present, according to the more-than-half filling of the 3d orbitals. The oxygen atoms display a different PDOS depending on the group they are attached to. In particular the states of the bridging oxygen atoms OB partially overlap with the states of the magnetic ions, with larger extent for the seven-coordinated ones (M1,2) in the majority-spin component and with the six-coordinated ones (M3,4) in the minority spin component. This overlap, which appears to be slightly more intense in {Mn4}, is responsible for the coupling between magnetic ions via superexchange interaction mechanism.37
 | ||
| Fig. 5 Density of states projected on the magnetic ions and different oxygen atoms (OA and OB) in the two molecular complexes. The average PDOS per atom type is reported. | ||
For both complexes, the OA atoms are characterized by majority spin states in the [−3, −1] eV energy range and minority states centered around −2.5 eV, with a moderate overlap with the metal atoms in both cases. We can therefore conclude that they contribute to the magnetic coupling between metal centers with a similar strength.
The hybridization with states of the ligands is also responsible for the charge transfer from the magnetic ions to the nearby atoms. In the molecular complexes, Mn and Co atoms display a number of electrons smaller than the valence of the isolated atom, as reported in Table 3 in term of the net atomic charge, i.e. they donate electron charge. This reduction of charge is larger for the two metal ions bound to the pyridine–diimine group (M1,2) with respect to the 6-coordinated magnetic atoms in the same molecule (M3,4). Moreover, the percentage of lost charge is larger in {Mn4} (∼25%) than in {Co4} (∼22%), according to the larger hybridization with the surrounding coordination groups. The oxygen atoms act as electron acceptors in both molecules. The maximum charge transfer is toward the bridging oxygens that acquire 0.60 and 0.68 electrons (mean values) in {Mn4} and {Co4}, respectively. For OA atoms the absolute values of the acquired charge (∼0.4e) are similar in the two complexes. N atoms participate to charge transfer towards the ligands by donating electrons, with a slightly larger fraction in {Mn4} (∼0.29e) than in {Co4} (∼0.21e). On the basis of the results reported by Kampert et al.21 the charge withdrawn from the [M4O4] core (by the ligands) is inversely proportional to the strength of the magnetic interaction within the complex. For both complexes, the analysis of Mulliken charges predicts that the [M4O4] core acts as a donor, with 2.45 and 3.43 electrons donated in the Mn and Co case, respectively. Therefore, we expect that a stronger antiferromagnetic coupling in {Mn4} than in {Co4}, supporting the experimental findings.
| Δq (e) | M1,2 | M3,4 | N | OA | OB |
|---|---|---|---|---|---|
| {Mn4} | +1.10 | +1.32 | +0.29 | −0.39 | −0.60 |
| {Co4} | +1.49 | +1.63 | +0.21 | −0.44 | −0.68 |
3.5 Role of spin orbit coupling
In the previous paragraphs we have analyzed the results obtained with the LDA+U approximation, necessary to account for the electronic correlation of localized 3d orbitals, but limited in the SIESTA code to a collinear-spin description of magnetism. This approximation is valid for the Mn(II) ions, as the high-spin d5 electronic configuration does not have a net orbital momentum. In Co(II) centers, instead, the d7 configuration leads to an orbital momentum L = 3 for an isolated ion. While the orbital momentum is quenched in low symmetry environments, including pentagonal bipyramidal, it is not in a perfect octahedron, where L = 1. As two of the metal centers in {Co4} display a pseudo-octahedral geometry, SOC is expected to have a significant effect on the magnetic properties of this complex.In order to investigate the role of SOC in the complexes, we have performed DFT calculations including SOC for both molecules at U = 0 using the fully relativistic pseudopotential formalism31 implemented in SIESTA.32 The magnetization direction has been set along the z axis for {Mn4}. Indeed we verified that for this molecule the magnetic anisotropy related to spinflip along five independent directions is at most ∼100 μeV per molecule. For {Co4}, which is expected to display strong spin–orbit effects, we have explored 30 different direction of the magnetization. The easy axis for {Co4} is rotated with respect to the z direction with a polar angle 150° and azimuthal angle 45°. The maximum magnetic anisotropy for spinflip amounts to 12 meV per molecule. The results reported below are relative to {Co4} with the spin along the easy axis.
In Tables 4 and 5 the computed S, L, and their sum (J) are reported for both molecular complexes. In both cases, the atomic spin is slightly reduced with respect to the LDA+U calculation. The four metal ions in {Co4} display an orbital moment which is smaller than the value expected for the isolated ion, but significantly larger than the manganese analogue. The quenching is stronger for the two ions in the pentagonal bipyramidal coordination, for which  . For the 6-coordinated pseudo-octahedral Co ions L is not negligible (∼0.4) and contributes to an overall value of
. For the 6-coordinated pseudo-octahedral Co ions L is not negligible (∼0.4) and contributes to an overall value of  .
.
3.6 Exchange coupling
In order to ascertain the strength of the (anti)ferromagnetic coupling in the two complexes we computed the exchange coupling parameters (Ji) from first-principles total energies by considering the five lowest-energy spin configurations of the molecules (uudd, udud, uddu, uddd, uuuu) as explained in Section 2.1. The calculated exchange parameters, obtained in the LDA+U approximation, are reported in Table 6, where positive and negative values correspond to ferromagnetic (FM) or antiferromagnetic (AFM) coupling.| LDA+U (meV) | J 1 | J 2 | J 3 | J 4 |
|---|---|---|---|---|
| {Mn4} | −0.2 | −0.9 | −0.2 | 0.9 |
| {Co4} | −1.8 | −0.19 | 0.8 | −0.6 |
The calculated Ji are of the same order of magnitude of those extracted from experimental susceptibility (see ESI†), and are in fair agreement with those reported in ref. 21 for a three-J model. Both J1 and J2 are negative, confirming the antiferromagnetic coupling between not equivalent atoms. One of the other two parameters describing the coupling between equivalent atoms (J3 or J4) is positive (FM), in agreement with the data extracted from the experiments. The overall exchange interaction, estimated as the average of the Js (−3.7 meV for {Co4} and −1.4 for {Mn4}), is AFM for both molecular complexes.
The strongest Ji (J1 in {Co4}, J2 in {Mn4}) corresponds to the interaction between the two pairs of not-equivalent ions and it is related to the energy difference between the AFM ground state and the high spin FM state (S = 12 for {Co4} and S = 20 for {Mn4}) which is larger for {Co4}. The FM interaction between equivalent ions (intra-pair) is, instead, smaller for {Co4}. The latter governs the transition to low-spin FM states (for example uddd) which influences the behavior of the magnetization at low fields and low temperatures, hence explaining the observed switching with temperature of the magnetization curves M(B) of the two molecules (Fig. 3). To further explore this behavior, we have exploited a model Heisenberg Hamiltonian with J parameters and g-factor fitted from the experimental low-field susceptibility (ESI†) and used them to calculate M(B) at two different temperatures. We find that the observed (Fig. 3) switch of M(B) with temperature is an effect of the more marked AFM character of {Mn4} giving rise to a positive curvature of M(B) at low field/low T. At high field/high T, instead, the most relevant factor is the larger saturation value of the magnetization in {Mn4} compared to {Co4}. By increasing the range of the magnetic field beyond the experimental one, a crossing of the two theoretical curves is observed due to the combination of these two aspects (ESI†).
The inclusion of SOC in the calculation leads to Js with a sign that reflects the uudd magnetic order of the ground state, i.e. AFM (FM) coupling between M1/M4 and M2/M3 non-equivalent (M1/M2 and M3/M4 equivalent) ions (see Table S2 in ESI†). Nevertheless, the exchange parameters obtained with SOC are too large compared to those extracted from the experiments,21 suggesting that the electronic correlation can not be neglected for a reliable estimate of the strength of the magnetic interactions. A complete description of the magnetic properties of the clusters requires treating spin–orbit coupling and Hubbard-U correction on the same footing. However, the usual formulation of the Hamiltonian for exchange interaction only depends on the spin quantum number. This is accurate when the orbital moment are negligible with respect to the spin moment. We verified this is the case (Table 4) and use the LDA+U approximation to predict the exchange coupling parameters.
For a deeper insight of the exchange interaction, we have computed the exchange parameters also with the Liechtenstein–Katsnelson–Antropov–Gubanov (LKAG) formula38 implemented in the TB2J package,39 which treats the local spin rotation of the numerical atomic orbitals for the magnetic atoms as a perturbation.
The Ji, evaluated with this approach present the same overall trend as those computed from total energies (Table 6), for both LDA+U and SOC case, and are reported in the ESI† (Table S3).
The different predictions of the various approximations (LDA+U or SOC) are a consequence of the complexity of the magnetic potential energy landscape of these molecular complexes. A small perturbation (geometry, electron correlation, spin alignment) can drive the results out of equilibrium and towards a different local minimum. Despite these difficulties, all the computed Ji parameters predict the experimentally observed uudd ground state, regardless of the approach (total energies or perturbative) and inclusion of correlations or SOC. This has been verified by feeding the computed Ji in the Heisenberg Hamiltonian and computing the various spin configurations (Fig. S3, ESI†).
Finally, we used all the computed Ji parameters as input for spin dynamics simulations40–42 to predict the magnetic susceptibility, finding a good agreement with experiment in the LDA+U case (ESI†). The results obtained without U correction are, instead, in striking contradiction with experiments, confirming the importance of taking into account electron correlation in the transition metal sites.
4 Conclusions
Through a joint experimental and theoretical analysis we have characterized the properties of two coordination complexes, {Mn4} and {Co4}, that display the same chemical structure but different inner magnetic core formed by Mn and Co atoms, respectively. The theoretical analysis was performed under different approximations (LDA+U, SOC) and methods (first-principles, model Hamiltonians, perturbation theory).The experimental data and the theoretical calculations show that by changing the magnetic core, the robustness of the AFM configuration in an external magnetic field is changed, being stronger in {Mn4} than in {Co4}. The reason for this behavior can be found in the different interaction of the magnetic atoms with the surrounding ligands, which determines a different strength of the magnetic interaction within the molecule. This result confirms the possibility to tune the magnetic properties of the molecule through the chemical synthesis by acting on the magnetic inner core. Nevertheless, a general rule explaining the relationship between the choice of the magnetic atoms and the magnetic coupling in the molecule can not be established because the ligands, which are molecule-specific, also play a role. We also verified that the different magnetic properties of the two chemical species lead to a different spatial extension of the magnetic moment and electronic charge density on the ligands, which could influences the interaction with foreign systems and affects the efficiency of the two compounds when employed for magnetic functionalization.
We find and explain an unusual switch with temperature of the dependence of the magnetic moment from the applied magnetic field M(B) for the two molecules. We relate it to two competing effects: the stronger AFM coupling in {Mn4} and the large value of magnetization in {Mn4} which dominate at low and high temperature, respectively.
The calculations clarify the role of spin–orbit effects: negligible in {Mn4} and relevant in {Co4}, showing that SOC has to be considered for a reliable theoretical description of the magnetic moments of the latter. In perspective of future exploitation of these compounds in spintronics the SOC effects found in {Co4} should be taken into account as possible source of spin decoherence.
Our study of the exchange coupling parameters and spin dynamics demonstrate that it is necessary to explicitly include electron correlations (for instance, via a Hubbard U parameter) to properly recover these properties. The complete description of the molecular complexes can only be performed in a framework in which electronic correlation and SOC are treated on the same footing.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Natalya Izarova for acquisition of the crystallographic data, Brigitte Jansen for acquisition of the TGA data and Christina Houben for acquisition of some of the SQUID data. The Authors acknowledge EU H2020 project NFFA (Grant No. 654360) under Transnational Access Activity ID-753. Computational resources in MareNostrum4 at the Barcelona Supercomputing Center were provided by the Red Española de Supercomputacion (Grants FI-2019-2-0038 and FI-2020-1-0022) and PRACE (grant OptoSpin, project id. 2020225411). ZZ acknowledges financial support by the Ramon y Cajal program RYC-2016-19344 (MINECO/AEI/FSE, UE) and the Netherlands Sector Plan program 2019-2023. PO, HX and ZZ thank the support by the EU H2020-NMBP-TO-IND-2018 project “INTERSECT” (Grant No. 814487), the EC H2020-INFRAEDI-2018-2020 MaX “Materials Design at the Exascale” CoE (Grant No. 824143), Grant PGC2018-096955-B-C43 funded by MCIN/AEI/10.13039/501100011033 (Spain) and “ERDF A way of making Europe” (European Union), the “Centro de Excelencia Severo Ochoa” Grant SEV-2017-0706 funded by MCIN/AEI/ 10.13039/501100011033 (Spain) and Generalitat de Catalunya (CERCA program and Grant 2017SGR1506). CM acknowledges funding by Niedersächsisches Vorab, Akz. 11-76251-14-3/15(ZN3141).Notes and references
- M. Ganzhorn and W. Wernsdorfer, Molecular Magnets, Springer, Berlin, Heidelberg, 2014 Search PubMed.
- E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104 CrossRef.
- M. Gobbi, M. A. Novak and E. Del Barco, J. Appl. Phys., 2019, 125, 240401 CrossRef.
- D. Maniaki, E. Pilichos and S. P. Perlepes, Front. Chem., 2018, 6, 461 CrossRef CAS PubMed.
- L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186 CrossRef CAS PubMed.
- Z. Zanolli, R. Leghrib, A. Felten, J.-J. Pireaux, E. Llobet and J.-C. Charlier, ACS Nano, 2011, 5, 4592–4599 CrossRef CAS PubMed.
- Z. Zanolli and J.-C. Charlier, ACS Nano, 2012, 6, 10786–10791 CrossRef CAS PubMed.
- H. Oshio and M. Nakano, Chem. – Eur. J., 2005, 11, 5178–5185 CrossRef CAS PubMed.
- S. Brooker and J. A. Kitchen, Dalton Trans., 2009, 7331–7340 RSC.
- K. S. Pedersen, J. Bendix and R. Clerac, Chem. Commun., 2014, 50, 4396–4415 RSC.
- T. Jungwirth, X. Marti and P. Wadley, Nat. Nanotechnol., 2016, 11, 231–241 CrossRef CAS PubMed.
- M. Bragato, S. Achilli, F. Cargnoni, D. Ceresoli, R. Martinazzo, R. Soave and M. I. Trioni, Materials, 2018, 11, 2030 CrossRef PubMed.
- N. Makoto, H. Satoru, K. Hiroaki, Y. Yuki, M. Yukitoshi and S. Hitoshi, Nat. Commun., 2019, 10, 4305 CrossRef PubMed.
- X.-X. Fu, F. Wei, Y. Niu and C.-K. Wang, Phys. E, 2021, 131, 114737 CrossRef CAS.
- V. Baltz, A. Manchon, M. Tsoi, T. Moriyama, T. Ono and Y. Tserkovnyak, Rev. Mod. Phys., 2018, 90, 015005 CrossRef CAS.
- R. Frielinghaus, C. Besson, L. Houben, A.-K. Saelhoff, C. M. Schneidera and C. Meyer, RCS Adv., 2015, 5, 84119 CAS.
- C. Besson, P. Stegmann, M. Schnee, Z. Zanolli, S. Achilli, N. Wittemeier, A. Vierck, R. Frielinghaus, P. Kögerler, J. Maultzsch, P. Ordejón, C. M. Schneider, A. Hucht, J. König and C. Meyer, 2021, arXiv:2107.07723.
- A. Ardavan, O. Rival, J. J. L. Morton, S. J. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2007, 98, 057201 CrossRef PubMed.
- Y. Yu, C. Li, B. Yin, J.-L. Li, Y.-H. Huang, Z.-Y. Wen and Z.-Y. Jiang, J. Chem. Phys., 2013, 139, 054305 CrossRef PubMed.
- B. Yin, J. Li, H. Bai, Z. Wen, Z. Jiang and Y. Huang, Phys. Chem. Chem. Phys., 2012, 14, 1121–1130 RSC.
- E. Kampert, F. F. B. J. Janssen, D. W. Boukhvalov, J. C. Russcher, J. M. M. Smits, R. de Gelder, B. de Bruin, P. C. M. Christianen, U. Zeitler, M. I. Katsnelson, J. C. Maan and A. E. Rowan, Inorg. Chem., 2009, 48, 11903–11908 CrossRef CAS PubMed.
- M.-L. Tong, S.-L. Zheng, J.-X. Shi, Y.-X. Tong, H. K. Lee and X.-M. Chen, J. Chem. Soc., Dalton Trans., 2002, 1727–1734 RSC.
- G. S. Papaefstathiou, A. Escuer, F. A. Mautner, C. Raptopoulou, A. Terzis, S. P. Perlepes and R. Vicente, Eur. J. Inorg. Chem., 2005, 879–893 CrossRef CAS.
- T. A. Hudson, K. J. Berry, B. Moubaraki, K. S. Murray and R. Robson, Inorg. Chem., 2006, 45, 3549–3556 CrossRef CAS PubMed.
- C.-B. Tian, H.-B. Zhang, Y. Peng, Y.-E. Xie, P. Lin, Z.-H. Li and S.-W. Du, Eur. J. Inorg. Chem., 2012, 4029–4035 CrossRef CAS.
- J. M. Soler, E. Artacho, J. D. Gale, A. Garca, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef CAS.
- A. García, N. Papior, A. Akhtar, E. Artacho, V. Blum, E. Bosoni, P. Brandimarte, M. Brandbyge, J. I. Cerdá1, F. Corsetti, R. Cuadrado, V. Dikan, J. Ferrer, J. Gale, P. García-Fernández, V. Garcá-Suárez, S. García, G. Huhs, S. Illera, R. Korytár, P. Koval, I. Lebedeva, L. Lin, P. López-Tarifa, S. G. Mayo, S. Mohr, P. Ordejón, A. Postnikov, Y. Pouillon, M. Pruneda, R. Robles, D. Sánchez-Portal, J. M. Soler, R. Ullah, V. Wen-zhe Yu and J. Junquera, J. Chem. Phys., 2020, 152, 204108 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev. B, 1965, 140, A1133 CrossRef.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566 CrossRef CAS.
- A. M. Ritzmann, M. Pavone, A. B. Muñoz García, J. A. Keith and E. A. Carter, J. Mater. Chem. A, 2014, 2, 8060–8074 RSC.
- R. Cuadrado and J. I. Cerdá, J. Phys. Condens. Matter, 2012, 24, 086005 CrossRef CAS PubMed.
- R. Cuadrado, R. Robles, A. García, M. Pruneda, P. Ordejón, J. Ferrer and J. I. Cerdá, Phys. Rev. B, 2021, 104, 195104 CrossRef CAS.
- Z. Zanolli, C. Niu, G. Bihlmayer, Y. Mokrousov, P. Mavropoulos, M. J. Verstraete and S. Blügel, Phys. Rev. B, 2018, 98, 155404 CrossRef CAS.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, Phys. Rev. Lett., 2013, 34, 1164 CAS.
- G. A. Bain and J. F. B. Berry, J. Chem. Ed., 2008, 85, 532–536 CrossRef CAS.
- F. Lloret, M. Julve, J. Cano, R. Ruiz-García and E. Pardo, Inorg. Chim. Acta, 2008, 361, 3432–3445 CrossRef CAS.
- J.-P. Launay and M. Verdaguer, Electrons in molecules, Oxford University Press, 2014 Search PubMed.
- A. I. Liechtenstein, M. I. Katsnelson, V. P. Antropov and V. A. Gubanov, J. Magn. Magn. Mater., 1987, 67, 65–74 CrossRef CAS.
- X. He, N. Helbig, M. J. Verstraete and E. Bousquet, Comput. Phys. Commun., 2021, 264, 107938 CrossRef CAS.
- L. Landau and E. Lifshitz, Perspectives in Theoretical Physics, Elsevier, 1992, pp. 51–65 Search PubMed.
- T. L. Gilbert, IEEE Trans. Magn., 2004, 40, 3443–3449 CrossRef CAS.
- X. Gonze, B. Amadon, G. Antonius, F. Arnardi, L. Baguet, J.-M. Beuken, J. Bieder, F. Bottin, J. Bouchet and E. Bousquet, et al. , Comput. Phys. Commun., 2020, 248, 107042 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Full experimental details, Heisenberg fit of the SQUID data. Spin dynamics calculation. Relaxed structures. See DOI: 10.1039/d1cp03904k |
| This journal is © the Owner Societies 2022 |