Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Diffusion Monte Carlo evaluation of disiloxane linearisation barrier†
Adie Tri
Hanindriyo
 *a,
Amit Kumar Singh
Yadav
*a,
Amit Kumar Singh
Yadav
 b,
Tom
Ichibha
b,
Tom
Ichibha
 c,
Ryo
Maezono
c,
Ryo
Maezono
 d,
Kousuke
Nakano
d,
Kousuke
Nakano
 de and
Kenta
Hongo
de and
Kenta
Hongo
 *f
*f
aSchool of Materials Science, JAIST, Asahidai 1-1, Nomi, Ishikawa, 923-1292, Japan. E-mail: adietri@icloud.com
bDepartment of Electrical Engineering, Indian Institute of Technology Gandhinagar, Palaj 382355, Gujarat, India
cMaterials Science and Technology Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA
dSchool of Information Science, JAIST, Asahidai 1-1, Nomi, Ishikawa, 923-1292, Japan
eScuola Internazionale Superiore di Studi Avanzati (SISSA), via Bonomea, 265-34136 Trieste, Italy
fResearch Center for Advanced Computing Infrastructure, JAIST, Asahidai 1-1, Nomi, Ishikawa 923-1292, Japan. E-mail: kenta_hongo@mac.com
First published on 11th January 2022
Abstract
The disiloxane molecule is a prime example of silicate compounds containing the Si–O–Si bridge. The molecule is of significant interest within the field of quantum chemistry, owing to the difficulty in theoretically predicting its properties. Herein, the linearisation barrier of disiloxane is investigated using a fixed-node diffusion Monte Carlo (FNDMC) approach, which is one of the most reliable ab initio methods in accounting for the electronic correlation. Calculations utilizing the density functional theory (DFT) and the coupled cluster method with single and double substitutions, including noniterative triples (CCSD(T)) are carried out alongside FNDMC for comparison. It is concluded that FNDMC successfully predicts the disiloxane linearisation barrier and does not depend on the completeness of the basis-set as much as DFT or CCSD(T), thus establishing its suitability.
1 Introduction
The simplest molecule containing the Si–O–Si bond is disiloxane or Si2H6O. Also called disilyl ether, its structure is a single Si–O–Si bond terminated by three H atoms at each end (H3Si–O–SiH3). There have been numerous studies investigating the Si–O–Si bond,1–5 particularly owing to its importance in the modelling of silica compounds, which are the most abundant constituent of the Earth's crust. Most importantly, silica compounds range in function from glasses to quartz crystals, both of which comprise large sectors in industry.6–8 In some studies, disiloxane has been used as a sealant and as a component in cosmetics,9 or as a prototype region of a zeolite or clay substrate for applications ranging from catalysis to prebiotic synthesis.10Experimental evaluations of the Si–O–Si bond indicated an anharmonic bending potential with a low linearisation barrier, which makes it quite difficult to attain sufficient accuracy in such measurements.11,12 Despite the significant volume of previous studies dedicated to the Si–O–Si bond,10,13–19 the properties of Si–O–Si bond obtained in most of these studies are not consistent with each other. In ab initio studies, in particular, multiple calculation methods resulted in different values for the bond angle and length,18,20,21 as well as the linearisation energy13,14,17 and Si–O–Si potential energy surface,10,18 among other factors. These properties and the bond geometry itself were shown to be sensitive to the choice of basis-set and level of theory (the former more than the latter) according to at least one previous study.17
To narrow down the possibilities, it would be ideal to employ the most reliable methods at our disposal. Quantum Monte Carlo (QMC), one of the most reliable many-body calculation methods, is expected to provide a reliable result.22 We used the fixed-node diffusion Monte Carlo (FNDMC) method,22 which has been widely and successfully applied to several molecular systems.23–30 Although FNDMC results are also affected by the choice of basis-set,27,31 we note that the basis-set dependency is considerably different from that for a self-consistent-field (SCF)-based method, such as the density functional theory (DFT) and molecular orbital (MO) methods. In SCF-based approaches, the choice of the basis-set affects both the amplitude and the nodal positions of the corresponding many-body wavefunctions (although the methods do not explicitly employ a many-body wavefunction condition). With FNDMC, by contrast, the choice only affects the nodal positions. The amplitude can be automatically adjusted such that its shape approaches that of the exact solution as closely as possible under a restriction with fixed nodal positions.22,32 Its typical example is the description of electron–nucleus cusps.33 Even without explicit inclusion of the singular electron–electron cusp analytical form in the wavefunction, numerical evolution driven by FNDMC will still produce an appropriate singular cusp amplitudes on electron–electron interaction.22,32 (However, practically speaking, such poor description of the wavefunction frequently causes singularity of the local energy due to electron–nucleus cusps and numerical instability within the algorithm. This is easily remedied by introducing cusp correction proposed by Ma et al.33). The self-healing property of the amplitude works to considerably reduce the basis-set dependency: the bias arisen from using an incomplete basis-set is generally significantly lower than SCF-based methods.17 This bias in FNDMC is dependent on the fixed nodal positions (the nodal surface), which can be characterised by the total energy due to the fixed-node variational principle.22 This principle allows for the comparison of qualities of nodal surfaces based on the comparison of the total energies; the lower the total energy, the higher the quality of the nodal surface. In turn, a higher nodal surface quality means the closer it is to the true ground state nodal surface, which translates to a more reliable FNDMC calculation result.
In this study, we apply single determinant FNDMC to investigate the basis-set dependence of the linearisation energy of a disiloxane molecule in comparison with other methods including DFT and CCSD(T), as well as empirical measurements from earlier studies.11,12,34 The FNDMC depends on the basis-set implicitly through its fixed nodal surface provided by the Slater determinant whose orbitals are expanded in terms of the basis-set, whereas DFT and CCSD(T) strongly depend on the choice of basis-set. The cc-pVxZ35–37 and cc-pCVxZ38 basis-sets (x = D, T, Q), which are usually applied to account for electron correlation, are examined in the present study and then applied to all the ab initio and semi empirical calculations to investigate the basis-set dependency of linearisation energy evaluation.
2 Model and methodology
Our target property is simply a linearisation barrier of disiloxane Si2H6O between “linear” and “nonlinear” (bent) structures. As can be seen from Fig. 1, the linear structure possesses an eclipsed D3h symmetry16 and the nonlinear structure is a bent conformation of the C2v symmetry.39 For the two fixed structures, the barrier, ΔEbarrier, is defined as the energy difference between the linear and nonlinear structures.The accuracy of computed ΔEbarrier values can be calibrated by referring to experimentally observed ΔEbarrier values. To compare our computational results with the experimental results, however, we note that the experimental ΔEbarrier involves the zero-point energy (ZPE) contribution, whereas our computational ΔEbarrier value considers only the electronic contribution. The ZPE contributions can also be evaluated at each level of theory, although their accuracy depends on methods adopted and the basis-set. To investigate the basis-set dependence of ΔEbarrier, we simply consider the electronic ΔEbarrier. Thus, the experimental ΔEbarrier values are corrected by adopting a theoretical estimate from the work of Koput.15 We address this issue in more detail later.
In the present study, the energies of the two structures Elinear and Enonlinear are computed through various combinations of (1) ab initio and semi empirical methods and (2) basis-sets.
(1) Calculation methods applied are DFT with B3LYP exchange–correlation functional (DFT-B3LYP),40 CCSD(T),41 and FNDMC22 with trial wavefunctions generated from DFT-B3LYP. Within the framework of DFT, DFT-B3LYP is a standard method for covalent systems. Within the correlated methods, CCSD(T) is known to be the “gold standard” in quantum chemistry. A variety of methods and basis-sets are chosen in line with the previous results17 indicating dependence of the Si–O–Si bond description on such choice. FNDMC is known to be comparable with CCSD(T); however, for the first time, we apply FNDMC to an evaluation of ΔEbarrier. In order to account for relativistic effects, some calculations at the CCSD(T) level have been performed using the Douglas–Kroll–Hess (DKH) second-order Hamiltonian. We compare these results with regular CCSD(T) calculations to gauge the significance of relativistic effects on disiloxane. To our knowledge, this is the first such investigation of relativistic effects for the disiloxane molecule.
(2) Our basis-sets are a family of Pople triple zeta basis-set from 6-311G, as well as polarisation function added 6-311G** and 6-311G(3df), and accounting for diffuse functions as well in 6-311+G, 6-311+G**, and 6-311+G(3df) sets.42,43 Also studied is the family of Dunning's correlation-consistent basis-set (cc-pVxZ; x = D, T, Q)35–37 and their core-valence correlated variants (cc-pCVxZ; x = D, T, Q).38 The cc-pVxZ and cc-pCVxZ basis-sets were originally developed for correlated methods such as CCSD(T), but have been found to be appropriate even for DFT-B3LYP and FNDMC in properly reproducing the dynamic electron correlation.35 In particular, the polarisation functions included implicitly in cc-pVxZ are essential for properly describing the Si–O–Si bond. To describe the correlation effects more precisely, the present study considers the dynamic correlation between core and valence electrons by applying the cc-pCVxZ basis-set, which can reproduce the core-valence correlation by minimising the difference in the correlation energies between all-electron and valence-only (using pseudopotentials) calculations.44 In order to compare with state-of-the-art approaches in quantum chemistry, CCSD(T) calculations are performed using even more robust basis-sets, including the quintuple zeta sets (cc-pV5Z and cc-pCV5Z), as well as their aug-cc-pVxZ and aug-cc-pCVxZ counterparts, which possess added diffuse functions. The cc-pV(x + d) basis-sets are also used, which possess additional d functions, to better describe Si atoms.35,37,45 In order to extrapolate to the complete basis-set (CBS) limit, both quadruple and quintuple zeta sets are included. Extrapolation to the CBS limit are performed using the scheme of Halkier et al.,46 with extrapolation coefficients from the optimisation of Truhlar.47
In the present study we obtain the linear and nonlinear structures of disiloxane using the second-order Møller–Plesset perturbation theory (MP2)48 with the cc-pVQZ basis-set (MP2/cc-pVQZ level), and previous studies conducted at the MP2/cc-pVQZ level of theory16,20 have established a reliable favourability toward a nonlinear structure and provide good agreement for the Si–O–Si angle in accordance with experimental results.39 Modelling of the Si–O–Si angle in particular has been heavily emphasised in previous theoretical studies for both disiloxane17 and pyrosilisic acid.18,19 While geometry optimization by CCSD(T) is desirable, the computational cost associated is unfortunately much higher, especially for the more robust basis-set used in this work. For example, the cc-pVQZ basis-set for disiloxane translates to over 350 basis functions. With 20 degrees of freedom in the disiloxane molecule, optimization with CCSD(T) involved steep computational costs, and optimization at the MP2/cc-pVQZ level is chosen instead. A comparison between the MP2 and CCSD(T) geometry optimization with the cc-pVTZ basis-set is shown in the ESI.† With a difference of 0.5 degrees for the Si–O–Si angle between the two calculation methods at the cc-pVTZ level, and a linearization barrier difference of less than 0.001 kcal mol−1 calculated for both geometries at MP2 and CCSD(T) level, geometry optimization at the MP2 level of theory does not seem to significantly impact the linearization barrier calculated at the CCSD(T) level. The two optimised structures at the MP2/cc-pVQZ level of theory are used in this work to calculate all ΔEbarrier values, i.e., common to all levels of theory, where the linear structure has a Si–O–Si angle of 180° and the nonlinear structure has an optimised Si–O–Si angle of 146.8° comparable with the experimental value of 144.1°.39 The other structural parameters are given in the ESI,† and are also in good agreement with experiments.
The present study adopted no pseudopotential calculations, but rather all-electron calculations with a total of 42 electrons for a single disiloxane molecule. This molecular system is not so large that the CCSD(T) calculation within the frozen core approximation is feasible, despite the computational cost of CCSD(T) scaling as N7, where N is the number of electrons in the system. By contrast, the DFT cost scales with N3 (or less) and is therefore unimportant. Similar to DFT, the FNDMC cost scales as N3, although the prefactor of FNDMC is much larger than that of DFT. This is because a vast number of random sampling points are required to obtain a sufficiently small error bar (sub-chemical accuracy of ∼0.1 kcal mol−1) to calibrate a small ΔEbarrier (∼0.5 kcal mol−1). Recent parallel computers, however, enable us to apply FNDMC to evaluate such a tiny ΔEbarrier, because its algorithm is intrinsically parallel.
In our FNDMC calculations, we adopted Slater–Jastrow type wavefunctions as their fixed-node trial wavefunctions.49 Molecular orbitals entering the single Slater determinants were generated by DFT-B3LYP with various types of basis-set. The Jastrow factor consists of one-, two-, and three-body terms50 including 88 variational parameters in total. These parameters are optimised through a variance minimisation scheme,51 and only the two-body term holds the electron–electron cusp condition.52 The electron–nucleus cusp condition, which is a short-range one-body correlation effect, is satisfied by the cusp correction scheme applied to the Gaussian basis-set33 instead of imposing the cusp condition on the one-body term. Note that the Jastrow factor does not change the (fixed) nodal surfaces and is responsible for the numerical stability in FNDMC. However, the quality of the nodal surfaces determines the accuracy of the FNDMC energies in terms of the fixed-node variational principles.53 Accordingly, the FNDMC accuracy depends implicitly on the basis-set adopted, which is used to expand the molecular orbitals entering the Slater determinant. In addition to the fixed-node error, another source of bias in actual FNDMC calculations arises from the short-time approximation with finite (small) timesteps.54 To remove this bias, it is common to use multiple timesteps to make the linear regression and obtain calculation results for δt → 0. This regression is an approximation of the theoretical δt = 0 result. The present study considers both linear and quadratic extrapolations. It is commonly understood that the size of the error bar from FNDMC calculations scale inversely proportional with the square root of the number of samples in the calculations.22 In order to halve the error bar, for example, the computational cost is increased fourfold. This results in an effective limit on the size of the error bar due to feasible computational cost of FNDMC calculations.
The software package Gaussian0955 was used to conduct the MP2 (geometry optimisation), DFT-B3LYP, and CCSD(T) calculations, whereas the CASINO56 code was used to perform FNDMC calculations. An electron–nucleus cusp correction scheme33 for Gaussian orbitals was utilised in the all-electron FNDMC calculation in CASINO. Most of the basis-sets utilised in this work are available in the Gaussian09 software package. Basis-sets of the cc-pCVxZ, cc-pV(x + d)Z and aug-cc-pCVxZ families are obtained from the online Basis-Set Exchange library.57–59 In FNDMC for both structures, the number of target population was 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520, and the number of steps in the imaginary-time evolution was set to 2000 and 500
520, and the number of steps in the imaginary-time evolution was set to 2000 and 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for equilibrated and accumulated phases, respectively. In addition, we carried out FNDMC calculations with different timesteps of 0.01, 0.005, and 0.001 a.u.−1 to remove the short-time bias (see ESI† for more details).
000 for equilibrated and accumulated phases, respectively. In addition, we carried out FNDMC calculations with different timesteps of 0.01, 0.005, and 0.001 a.u.−1 to remove the short-time bias (see ESI† for more details).
3 Results and discussion
3.1 Geometry and ZPE contribution
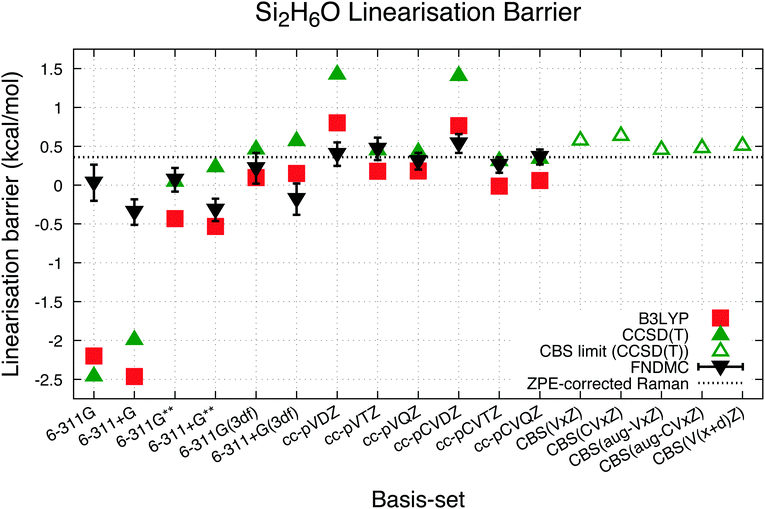
Several studies have been conducted on the geometry of the disiloxane molecule, although most ab initio methods tested did not manage to replicate the available experimental results. Rather than the Si–O bond length, the Si–O–Si bond angle and linearisation barrier have been found to be greatly dependent on the choice of basis-set used to represent the wavefunction.17 This study focuses on the linearisation barrier of disiloxane, taking the same optimised geometries for all calculations, partly owing to the difficulty to optimise the geometries by FNDMC.‡The bending potential energy of the disiloxane molecule is a shallow one, as shown in Fig. 2. In comparison with the water molecule for example, which has a relatively harmonic bending potential curve with a potential difference of 1.0 kcal mol−1 at deviation of H–O–H bending angle of around 8°,71 the disiloxane molecule bending potential curve is anharmonic, with a potential difference of 1.0 kcal mol−1 at deviation of Si–O–Si bending angle of around 15° to 20° less than the optimal, and a small linearisation barrier of less than 0.5 kcal mol−1. Although the linearisation barriers shown in Fig. 2 differ depending on the calculation method and basis-set used, all potential curves share these similar properties with one another.
The computational and experimental linearisation barriers of disiloxane, ΔEbarrier, are listed in Table 1 and plotted in Fig. 3. It has been commonly observed experimentally that the nonlinear (bent) structure of disiloxane is energetically more favourable than a linear structure, which translates to a positive linearisation barrier. All three experimental results seem to agree on this point, and the work of Aronson et al.34 in particular reports a higher linearisation barrier (at 1.1 to 1.4 kcal mol−1) than the other two results,11,12 which report a barrier of approximately 0.3 kcal mol−1.
| Basis-set | Δε0 [kcal mol−1] | ||
|---|---|---|---|
| DFT-B3LYP | CCSD(T) | FNDMC | |
| 6-311G | −2.20 | −2.45 | −0.12 ± 0.27 |
| 6-311+G | −2.46 | −1.98 | −0.35 ± 0.16 |
| 6-311G** | −0.43 | 0.06 | 0.07 ± 0.15 |
| 6-311+G** | −0.53 | 0.24 | −0.32 ± 0.14 |
| 6-311G(3df) | 0.10 | 0.47 | 0.45 ± 0.24 |
| 6-311+G(3df) | 0.15 | 0.58 | −0.42 ± 0.23 |
| cc-pVDZ | 0.80 | 1.44 | 0.40 ± 0.15 |
| cc-pVTZ | 0.18 | 0.46 | 0.47 ± 0.14 |
| cc-pVQZ | 0.18 | 0.44 | 0.26 ± 0.10 |
| cc-pV5Z | — | 0.49 | — |
| cc-pCVDZ | 0.76 | 1.42 | 0.54 ± 0.12 |
| cc-pCVTZ | −0.01 | 0.32 | 0.31 ± 0.11 |
| cc-pCVQZ | 0.06 | 0.35 | 0.36 ± 0.10 |
| cc-pCV5Z | — | 0.48 | — |
| aug-cc-pVQZ | — | 0.50 | — |
| aug-cc-pV5Z | — | 0.48 | — |
| aug-cc-pCVQZ | — | 0.46 | — |
| aug-cc-pCV5Z | — | 0.47 | — |
| cc-pV(Q + d)Z | — | 0.45 | — |
| cc-pV(5 + d)Z | — | 0.48 | — |
The experimental work of Durig, Flanagan, and Kalasinsky obtained Raman (10–3500 cm−1) and infrared spectra of gaseous (4000–30 cm−1) and solid (4000–450 cm−1) disiloxane and deuterated disiloxane.11 Most significantly, their assessment of the Raman (10–200 cm−1) spectra produced potential energy functions which results in a disiloxane linearisation barrier of 112 ± 5 cm−1 (0.32(1) kcal mol−1), while the analysis of Koput and Wierzbicki of the low frequency Raman spectra (10–200 cm−1) produced a similar value of 103.9 ± 2.6 cm−1 (0.297(7) kcal mol−1).12 These results were reported more recently than the first and achieve good consilience with the DFT predictions from the highest quality basis-set.17 Therefore, it is reasonable to infer that a linearisation barrier of approximately 0.3 kcal mol−1 is a reliable value for the disiloxane molecule.
It needs to be stressed, however, that the experimentally measured linearisation barrier may not be comparable to the ground state values calculated from the first principles. The ground state energy obtained through ab initio calculations are physically unobtainable experimentally because of the ZPE, i.e. the difference between the ground state and the lowest energy vibrational state. Even at absolute zero temperature, the lowest energy level achievable is a vibrational state ε1 instead of the electronic ground state ε0:
| Δε1 = Δε0 + ΔZPE | (1) |
The preceding theoretical study by Koput15 estimates a ΔZPE value of −20 cm−1 ≈ −0.06 kcal mol−1, which in line with eqn (1) should result in a higher ground state linearisation barrier than the experimentally measured result. The study considered separately the large amplitude motion (Si–O–Si bending, which is the imaginary frequency mode in linear disiloxane) and the small amplitude vibrations, leading to a more refined estimation of the zero-point vibrational energy. By constructing the harmonic force constants at the MP2 level of theory using D/T basis-set, the energy levels of the small amplitude vibrations of the disiloxane molecule were estimated. The upper bound of the contribution was estimated at 20 cm−1 from Si–O–Si bending angles of 180° to 150°. Therefore, this work treats the ground state linearisation barrier of 0.36 kcal mol−1 as a reasonably accurate “exact” linearisation barrier for a point of comparison with ab initio calculations. This value is referred to as “ZPE-corrected Raman” in Table 1 and based on a dotted line in the figures herein, as a point of comparison. ZPE correction has not been considered in ab initio comparisons or based on experimental results, which have cited 0.3 kcal mol−1 as the point of comparison.17
3.2 DFT-B3LYP results
The results for DFT-B3LYP in this study, particularly the results for the quadruple zeta basis-set cc-pVQZ and cc-pCVQZ, seem to indicate that previous agreement between the B3LYP results and experimental data17 is due to coincidence instead of convergence toward the complete basis-set limit. Indeed, for the largest basis-set used in this study, the linearisation barrier calculated by B3LYP is at best approximately 0.1 kcal mol−1 smaller than the ZPE-corrected measurement. It does not seem that the B3LYP exchange–correlation functional provides adequate accounting of the electron correlation for properly describing a disiloxane molecule.3.3 CCSD(T) results
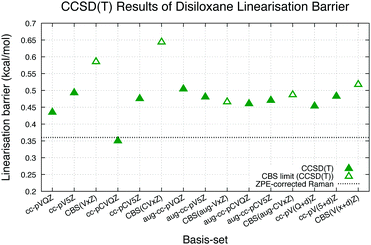
CCSD(T) calculations were conducted with the same geometries and basis-sets as the B3LYP calculations. The results of these calculations are shown in Table 1. The trends of the linearization barrier agree almost perfectly with B3LYP calculations, with a universal shift in the energetic favourability toward the nonlinear conformer denoted by the larger linearisation barriers. We achieve good agreement with another CCSD(T) calculation in an earlier study17 reporting a linearisation barrier of 0.48 kcal mol−1 using the cc-pVTZ basis-set. These results show that accounting for the electron correlation is indeed necessary to properly model the Si–O–Si bond in disiloxane, and supports the conclusion of earlier studies citing cc-pVTZ and CCSD(T) as the minimum reliable level of description for the disiloxane molecule.16,17Calculations with more state-of-the-art basis-sets have also been performed on the disiloxane linearisation barrier. Quintuple zeta basis-set cc-pV5Z and cc-pCV5Z are used, as well as quadruple and quintuple zeta sets for diffusion function augmented aug-gcc-pVxZ family of basis-set. Extra d functions present in the cc-pV(x + d)Z family of basis-set are also taken into account. Extrapolations to the CBS limit are performed according to the scheme in eqn (2):
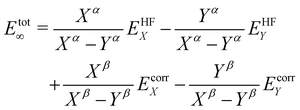 | (2) |
The trends of CCSD(T) results seem to converge to linearisation barrier values around 0.1–0.3 kcal mol−1 higher than the ZPE-corrected Raman results of 0.36 kcal mol−1, with the extrapolated CBS limit for various basis-set families showing linearisation barriers of 0.45–0.65 kcal mol−1. CCSD(T) calculation shows then that previous works underestimated the linearisation barrier of disiloxane, though it must be noted that the calculations are performed with MP2/cc-pVQZ geometries owing to the high computational cost of CCSD(T) geometry optimisations with equivalent basis-sets.
Comparison is also made to measure the significance of relativistic effects between the non-relativistic and scalar relativistic Hamiltonian at the CCSD(T) level. The basis-sets used are of the cc-pVxZ and cc-pCVxZ families (x = D, T, Q). These results are shown in Table 2. At the higher level basis-sets, inclusion of relativistic effects seem to contribute strengthening of the linearization barrier in the order of 0.05–0.1 kcal mol−1. As relativistic effects serve to energetically stabilize the s- and p-orbitals,72,73 it follows that the lone pair repulsion at the oxygen atom is strengthened due to radially contracted p orbitals, leading to an energetic stabilization of the non-linear structure. While usually considered negligible, these effects prove somewhat significant in the context of the disiloxane linearization barrier (0.36 kcal mol−1).
| Basis-set | Δε0 [kcal mol−1] | |
|---|---|---|
| ΔEnon-relativisticbarrier | ΔEscalar relativisticbarrier | |
| cc-pVDZ | 1.44 | 1.24 |
| cc-pVTZ | 0.46 | 0.50 |
| cc-pVQZ | 0.44 | 0.50 |
| cc-pCVDZ | 1.42 | 1.23 |
| cc-pCVTZ | 0.32 | 0.42 |
| cc-pCVQZ | 0.35 | 0.46 |
3.4 FNDMC results
The linearisation barrier calculated by FNDMC is also shown in Table 1 and Fig. 3. These values from FNDMC converge to a value close to the ZPE-corrected Raman benchmark adopted in this study of 0.36 kcal mol−1 for the largest basis-sets. Also observed is the relative independence of the linearisation barrier calculated from the basis-set used to form the initial trial wavefunction using DFT-B3LYP relative to the other two calculation methods. The influence of the different basis-sets on the end result of the FNDMC calculations directly translates into how they affect the trial wavefunction nodal surfaces. The amplitudes of the trial wavefunction, meanwhile, do not affect the end result at (τ → ∞), which, in turn, limits the dependence of the end result on the basis-sets used to form the trial wavefunction. Pople basis-sets in particular affects the FNDMC calculations relative to the correlation consistent basis-sets, with relatively lower linearisation barriers and particularly for basis-sets with diffuse functions (6-311+G, 6-311+G**, and 6-311+G(3df)) even energetically favouring linear structures of disiloxane. This dependence is clearly visible in Fig. 3, though the magnitude is lesser than DFT-B3LYP and CCSD(T).As mentioned previously, the fixed-node variational principle allows for characterization of nodal surface quality by way of comparing the absolute values of total energies. These absolute values are shown in Table 4, sorted in accord with the quality of the nodal surface (from low quality, high total energy, to high quality, low total energy). It can be observed that the cc-pCVTZ produces a nodal surface of slightly better quality than cc-pVQZ, indicating that the electron correlation between the core and valence electrons can be a significant factor for improvement beyond the triple zeta level of atomic orbital description.
| Basis-set | Δε0 [kcal mol−1] | ||
|---|---|---|---|
| ΔEHFbarrier | ΔEcorrbarrier | ΔEbarrier | |
| cc-pVQZ | −0.00 | 0.44 | 0.44 |
| cc-pV5Z | −0.02 | 0.52 | 0.49 |
| CBS(VxZ) | 0.59 | ||
| cc-pCVQZ | −0.05 | 0.40 | 0.35 |
| cc-pCV5Z | −0.04 | 0.51 | 0.48 |
| CBS(CVxZ) | 0.65 | ||
| aug-cc-pVQZ | 0.01 | 0.50 | 0.51 |
| aug-cc-pV5Z | −0.03 | 0.51 | 0.48 |
| CBS(aug-VxZ) | 0.47 | ||
| aug-cc-pCVQZ | −0.03 | 0.49 | 0.46 |
| aug-cc-pCV5Z | −0.04 | 0.51 | 0.47 |
| CBS(aug-CVxZ) | 0.49 | ||
| cc-pV(Q + d)Z | −0.05 | 0.50 | 0.45 |
| cc-pV(5 + d)Z | −0.03 | 0.52 | 0.48 |
| CBS(V(x + d)Z) | 0.52 | ||
| Basis-set | E total [Hartree] | |
|---|---|---|
| Nonlinear | Linear | |
| cc-pVDZ | −657.7994(2) | −657.7988(2) |
| cc-pCVDZ | −657.8062(1) | −657.8053(1) |
| cc-pVTZ | −657.8270(2) | −657.8263(2) |
| cc-pVQZ | −657.8366(1) | −657.8362(1) |
| cc-pCVTZ | −657.8376(1) | −657.8371(1) |
| cc-pCVQZ | −657.8437(1) | −657.8431(1) |
3.5 Effects of basis-sets
Disiloxane linearisation barrier dependence on the basis-set was observed for all cases. In agreement with previous studies,17 this dependence is more significant than the methodologies used in the ab initio calculations, particularly considering the double zeta-level basis-sets cc-pVDZ and cc-pCVDZ. Triple zeta basis-sets seem to offer the minimum level of description to reliably predict the linearisation barrier, whereas quadruple zeta basis-sets result in an extremely good prediction, especially for the CCSD(T) and FNDMC calculations. Fig. 3 clearly shows very similar trends for each calculation method with a substantial dependence on the basis-set indicated, particularly towards the smaller sets. Convergence of the disiloxane linearisation barrier is generally observed for all three calculation methods, albeit not necessarily converging to the same value.Previous theoretical studies suggest that this converging trend is attributed to the increasing addition of polarisation functions17 within the basis-sets used. Adding polarisation functions serves to better reproduce dynamical correlations in the system. This is in line with previous theoretical works with semi-empirical methods implying that calculations without electron correlation favour the linear structure, thereby resulting in negative values of linearisation barrier. This is also reflected in preceding geometry optimisation calculations without polarisation functions, resulting in Si–O–Si angles close to 170°.13,14 Therefore, it is expected that both cc-pVxZ and cc-pCVxZ basis-sets should converge to a reliable predicted linearisation barrier value because polarisation functions are systematically included with an increasing description of the atomic orbitals.
FNDMC is overall less dependent on the basis-set used compared to both B3LYP and CCSD(T). Although previous studies have recommended treating disiloxane with the cc-pVTZ basis-set at a minimum, cc-pVDZ is shown to generate a sufficiently high quality nodal surface for use in DMC calculations, giving a linearisation barrier in good agreement with the experimental values. Even for the smallest basis-sets tested in this study, FNDMC shows relatively more accurate values of the linearisation barrier, and therefore less dependence on the basis-set used to form the trial wavefunction per the initial expectations.
Comparing the FNDMC results to the CCSD(T) ones using more robust basis-sets show that in general there are improvements that can be significant to the nodal surface by employing these more robust basis-sets, as CCSD(T) results at the CBS limit clearly show more energetic preference toward the nonlinear structure of disiloxane. The effects of using these more robust basis-sets to the nodal surface may be intriguing to explore, in order to find basis-sets more suited for FNDMC application in disiloxane.
3.6 Effects of methodologies
Previous expectations on the trend in methodologies are derived from previous studies,13,74 particularly the study by Koput in 1990,13 in which the inclusion of the electron correlation proved vital to predicting the energetic favourability of the nonlinear structure of disiloxane because the SCF calculation produced a near-linear structure of disiloxane. This and other studies74 gave rise to the general expectation that the inclusion of the electron correlation is important to properly model the structure of disiloxane. As previously mentioned, it can be observed that the B3LYP exchange–correlation functional is insufficient to properly recover the electron correlation and thereby predict the disiloxane linearisation barrier. Our CCSD(T) calculation results shown in Table 3 reinforce the significance of accounting for electron correlation, as most of the energy difference between the nonlinear and linear structures of disiloxane come from electron correlation. Increasingly accounting for correlation, therefore, leads to calculation results favouring the nonlinear structure, and thus resulting in a higher linearisation barrier.FNDMC has the added advantage of being able to reliably predict the energetics of disiloxane with smaller basis-sets. While improvements to the nodal surface is clearly possible by accounting for electron correlation, the difference in scalability between CCSD(T) and FNDMC means that this advantage only grows more significant when considering larger systems. With better scalability for application in high performance computing (HPC) systems and the availability of pseudopotentials, FNDMC is a promising alternative method to CCSD(T) for describing the Si–O–Si bonds, particularly for larger systems.
4 Conclusion
The Si2H6O linearisation barrier was calculated using three separate methods, DFT-B3LYP, CCSD(T), and FNDMC, with six different basis-set choices in line with expectations derived from previous theoretical studies on disiloxane. The disiloxane molecule was optimized for both the non-linear and linear structures at the MP2/cc-pVQZ level. Geometry optimization at the MP2 level of theory does not seem to significantly impact the linearization barrier calculated at the CCSD(T) level, with differences of linearization barrier at less than 0.001 kcal mol−1 with the cc-pVTZ basis-set. Similar with previous studies, we observed that the systematic inclusion of polarisation functions, along with an increasing level of description for atomic orbitals, eventually result in a reliable prediction of the disiloxane linearisation barrier. All calculation methods eventually produced converged values with increasing level of basis-sets for the linearisation barrier, with 0.1 kcal mol−1 for DFT-B3LYP and 0.45–0.65 kcal mol−1 for CCSD(T), respectively. Inclusion of relativistic effects by scalar relativistic calculations slightly increases the linearization barrier by 0.05–0.1 kcal mol−1 due to the increased lone pair repulsion from the contracted p-orbitals. The agreement between the experimental measurements and the DFT-B3LYP results at 0.3 kcal mol−1 are shown to be likely accidental. ZPE-corrected experimental measurements are in good agreement with FNDMC results, with the ground state linearisation barrier taken at 0.36 kcal mol−1. The CCSD(T) results using state-of-the-art basis-sets, however, show that the linearisation barrier might be underestimated in these results. FNDMC is shown to be least dependent on the choice of basis-set among the three calculation methods applied, in line with initial expectations owing to the nature of FNDMC.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The computations in this work have been performed using the facilities of Research Center for Advanced Computing Infrastructure at JAIST. T. I. acknowledges support by the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division and support from Grant-in-Aid for JSPS Research Fellow (18J12653). R. M. is grateful for financial supports from MEXT-KAKENHI (JP16KK0097, JP19H04692, and JP21K03400), FLAGSHIP2020 (project no. hp190169 and hp190167 at K-computer), the Air Force Office of Scientific Research (AFOSR-AOARD/FA2386-17-1-4049; FA2386-19-1-4015), and JSPS Bilateral Joint Projects (with India DST). K. H. is grateful for financial support from the HPCI System Research Project (Project ID: hp210019, hp210131, and jh210045), MEXT-KAKENHI (JP16H06439, JP17K17762, JP19K05029, JP19H05169, and JP21K03400), and the Air Force Office of Scientific Research (Award Numbers: FA2386-20-1-4036). K. N. acknowledges a support from the JSPS Overseas Research Fellowships, that from Grant-in-Aid for Early-Career Scientists (Grant Number JP21K17752), and that from Grant-in-Aid for Scientific Research(C) (Grant Number JP21K03400).Notes and references
- E. Dupree and R. F. Pettifer, Nature, 1984, 308, 523–525 CrossRef CAS.
- U. Selvaray, K. J. Rao, C. N. R. Rao, J. Klinowski and J. M. Thomas, Chem. Phys. Lett., 1985, 114, 24–27 CrossRef CAS.
- R. F. Pettifer, E. Dupree, I. Farnan and U. Sternberg, J. Non-Cryst. Solids, 1988, 106, 408–412 CrossRef CAS.
- F. Mauri, A. Pasquarello, B. G. Pfrommer, Y. G. Yoon and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, R4786 CrossRef CAS.
- W. J. Malfait, W. E. Halter and R. Verel, Chem. Geol., 2008, 256, 269–277 CrossRef CAS.
- M. F. M. Santos, E. Fujiwara, E. A. Schenkel, J. Enzweiler and C. K. Suzuki, Int. J. Miner. Process., 2015, 135, 65–70 CrossRef CAS.
- K. I. Vatalis, G. Charalambides and N. P. Benetis, Procedia Economics and Finance, 2015, 24, 734–742 CrossRef.
- E. C. Peres, J. C. Slaviero, A. M. Cunha, A. H. Bandegharaei and G. L. Dotto, J. Environ. Chem. Eng., 2018, 6, 649–659 CrossRef CAS.
- K. M. Ryan, A. D. Drumm, C. E. Martin, A. K. Krumpfer and J. W. Krumpfer, Reactive and Functional Polymers Volume One, Springer, 2020, pp. 301–328 Search PubMed.
- B. T. Luke, J. Phys. Chem., 1993, 97, 7505–7510 CrossRef CAS.
- J. R. Durig, M. J. Flanagan and V. F. Kalasinsky, J. Chem. Phys., 1977, 66, 2775 CrossRef CAS.
- J. Koput, J. Mol. Spec., 1983, 99, 116–132 CrossRef CAS.
- J. Koput, J. Chem. Phys., 1990, 148, 299–308 CAS.
- G. I. Csonka and J. Réffy, Chem. Phys. Lett., 1994, 229, 191–197 CrossRef CAS.
- J. Koput, J. Phys. Chem., 1995, 99, 15874–15880 CrossRef CAS.
- C. Carteret, A. Labrosse and X. Assfeld, Spectrochim. Acta, Part A, 2007, 67, 1421–1429 CrossRef CAS PubMed.
- A. R. A. Derzi, A. Gregušová, K. Runge and R. J. Bartlett, Int. J. Quantum Chem., 2008, 108, 2088–2096 CrossRef.
- F. Noritake and K. Kawamura, J. Comput. Chem. Jpn., 2015, 14, 124–130 CrossRef CAS.
- F. Noritake, J. Comput. Chem. Jpn.-Int. Ed., 2019, 5, 2018-0016 Search PubMed.
- J. B. Nicholas and M. Feyereisen, J. Chem. Phys., 1995, 103, 8031 CrossRef CAS.
- X. Yuan and A. N. Cormack, J. Non-Cryst. Solids, 2003, 319, 31–43 CrossRef CAS.
- W. M. C. Foulkes, L. Mitas, R. J. Needs and G. Rajagopal, Rev. Mod. Phys., 2001, 73, 33 CrossRef CAS.
- K. Hongo, M. A. Watson, R. S. Sánchez-Carrera, T. Iitaka and A. Aspuru-Guzik, J. Phys. Chem. Lett., 2010, 1, 1789–1794 CrossRef CAS.
- M. A. Watson, K. Hongo, T. Iitaka and A. Aspuru-Guzik, A Benchmark Quantum Monte Carlo Study of Molecular Crystal Polymorphism: A Challenging Case for Density-Functional Theory, 2012, ch. 10, pp. 101–117 Search PubMed.
- K. Hongo, N. T. Cuong and R. Maezono, J. Chem. Theory Comput., 2013, 9, 1081–1086 CrossRef CAS PubMed.
- K. Hongo, T. Iitaka, M. Watson, A. Aspuru-Guzik and R. Maezono, J. Chem. Theory Comput., 2015, 11, 907–917 CrossRef CAS PubMed.
- J. Koseki, R. Maezono, M. Tachikawa, M. D. Towler and R. J. Needs, J. Chem. Phys., 2008, 129, 085103 CrossRef PubMed.
- K. Hongo and R. Maezono, J. Chem. Theory Comput., 2017, 13, 5217–5230 CrossRef CAS PubMed.
- H. Takagishi, T. Matsuda, T. Shimoda, R. Maezono and K. Hongo, J. Phys. Chem. A, 2019, 123, 8726–8733 CrossRef CAS PubMed.
- T. Ichibha, Z. Hou, K. Hongo and R. Maezono, Sci. Rep., 2017, 7, 2011 CrossRef PubMed.
- K. Nakano, R. Maezono and S. Sorella, J. Chem. Theory Comput., 2019, 15, 4044–4055 CrossRef CAS PubMed.
- R. Maezono, J. Comput. Theor. Nanosci., 2009, 6, 2474–2482 CrossRef CAS.
- A. Ma, M. D. Towler, N. D. Drummond and R. J. Needs, J. Chem. Phys., 2005, 122, 224322 CrossRef CAS PubMed.
- J. R. Aronson, R. C. Lord and D. W. Robinson, J. Chem. Phys., 1960, 33, 1004 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef.
- R. A. Kendall and T. H. Dunning Jr., J. Chem. Phys., 1992, 96, 6796 CrossRef CAS.
- D. E. Woon and T. H. Dunning Jr., J. Chem. Phys., 1993, 98, 1358 CrossRef CAS.
- K. A. Peterson and T. H. Dunning Jr., J. Chem. Phys., 2002, 117, 10548 CrossRef CAS.
- A. Almenningen, O. Bastiansen, V. Ewing, K. Hedberg and M. Traetteberg, Acta Chem. Scand., 1963, 17, 2455–2460 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS.
- H. J. Monkhorst, Int. J. Quantum Chem., 1977, 12, 421–432 CrossRef.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef CAS.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639 CrossRef CAS.
- D. E. Woon and T. H. Dunning Jr., J. Chem. Phys., 1995, 103, 4572 CrossRef CAS.
- T. H. Dunning Jr., K. A. Peterson and A. K. Wilson, J. Chem. Phys., 2001, 114, 9244–9253 CrossRef.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252 CrossRef CAS.
- D. G. Truhlar, Chem. Phys. Lett., 1998, 294, 45–48 CrossRef CAS.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef.
- R. Jastrow, Phys. Rev., 1955, 98, 1479–1484 CrossRef.
- N. D. Drummond, M. D. Towler and R. J. Needs, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 235119 CrossRef.
- N. D. Drummond and R. J. Needs, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085124 CrossRef.
- T. Kato, Commun. Pure Appl. Math., 1957, 10, 151–177 CrossRef.
- P. J. Reynolds and D. M. Ceperley, J. Chem. Phys., 1982, 77, 5593 CrossRef CAS.
- C. J. Umrigar, M. P. Nightingale and K. J. Runge, J. Chem. Phys., 1993, 99, 2865 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- R. J. Needs, M. D. Towler, N. D. Drummond and P. L. Ríos, J. Phys.: Condens. Matter, 2010, 22, 023201 CrossRef CAS PubMed.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814 CrossRef CAS PubMed.
- D. Feller, J. Comput. Chem., 1996, 17, 1571–1586 CrossRef CAS.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS PubMed.
- R. Assaraf and M. Caffarel, J. Chem. Phys., 2003, 119, 10536–10552 CrossRef CAS.
- R. Assaraf and M. Caffarel, J. Chem. Phys., 2000, 113, 4028–4034 CrossRef CAS.
- P. L. Ríos and G. J. Conduit, Phys. Rev. E, 2019, 99, 063312 CrossRef PubMed.
- J. Tiihonen, R. C. Clay and J. T. Krogel, J. Chem. Phys., 2021, 154, 204111 CrossRef CAS PubMed.
- A. Badinski and R. J. Needs, Phys. Rev. E, 2007, 76, 036707 CrossRef CAS PubMed.
- A. Badinski and R. J. Needs, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 035134 CrossRef.
- C. Filippi and C. J. Umrigar, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, R16291–R16294 CrossRef CAS.
- C. Attaccalite and S. Sorella, Phys. Rev. Lett., 2008, 100, 114501 CrossRef PubMed.
- S. Sorella and L. Capriotti, J. Chem. Phys., 2010, 133, 234111 CrossRef PubMed.
- C. Filippi, R. Assaraf and S. Moroni, J. Chem. Phys., 2016, 144, 194105 CrossRef PubMed.
- R. Assaraf, S. Moroni and C. Filippi, J. Chem. Theory Comput., 2017, 13, 5273–5281 CrossRef CAS PubMed.
- M. R. Milovanović, J. M. Živković, D. B. Ninković, I. M. Stanković and S. D. Zarić, Phys. Chem. Chem. Phys., 2020, 22, 4138 RSC.
- K. S. Pitzer, Acc. Chem. Res., 1979, 12, 271–276 CrossRef CAS.
- W. Liu, Natl. Sci. Rev., 2016, 3, 204–221 CrossRef.
- S. Shambayati, S. L. Schreiber, J. F. Blake, S. G. Wierschke and W. L. Jorgensen, J. Am. Chem. Soc., 1990, 112, 697–703 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp01471d |
| ‡ Geometry optimisation by FNDMC is a long-standing issue due to the existence of the systematic bias mainly depending on the fixed-nodes quality60 and the infinite variance problem.61,62 Although the continuous efforts are overcoming the problems,60–70 the methods are still in development level and its application is practically accompanied by many difficulties. |
| This journal is © the Owner Societies 2022 |