Solid-state stability of Z′ < 1 and Z′ = 2 polymorphs of N,N,N′,N′-tetrabenzylethylenediamine: a combined experimental and theoretical study

Abstract

The synthesis and structural analysis by means of single crystal X-ray diffraction (SC-XRD) and DFT calculations, of two additional new polymorphs of the flexible organic molecule N,N,N′,N′-tetrabenzylethylenediamine (L) which is used as first sphere ligand in outer sphere adducts are reported. Slow crystallization of L in the solution-state yields two polymorphs (L_α-phase and L_β-phase) with Z′ = 0.5, while fast crystallization by rapid cooling from solution and directly from melt, allows a third, less stable polymorph with Z′ = 2 (L_γ-phase). The latter structure can be seen as a low-density metastable phase obtained by trapping L molecules after they reached high mobility by thermal treatment (i.e., high energy state). The three L polymorphs have been also studied using quantum mechanical (QM) calculations specific for the solid state by comparing the sublimation energy for each polymorph, and by comparing the experimental X-ray structures against the optimized structures from DFT, showing that L_β-phase is the most stable and L_γ-phase is the least stable phase. The high Z′ structure can be considered as a “crystal on the way” of a more stable form. These results provide insights about crystallization mechanisms and polymorphism in organic crystals. The potential use of conformational polymorphs of flexible ligands to prepare second sphere adducts with marked polymorphism is commented.

---

Introduction

Polymorphism,¹ the ability of a compound to exist in more than one crystalline form, is of crucial importance because polymorphs can offer a unique opportunity to study the structure–property relationships of the same compound.^2,3 Studies concerning polymorphism are vital for any solid material, in particular in the pharmaceutical industry, whether single-component or multi-component (i.e., co-crystals) as two different structures of the same organic molecule can have very different physico-chemical properties.⁴

The number of polymorphs that a substance can form is very important as it allows to gain insights in their solid-state interconversions and to understand in some cases early crystallization processes.⁵ While most polymorphic systems show two polymorphs, those crystallizing in three or more polymorphs are less common.⁶ Flexible molecules that can adopt conformations that imply low-energy conformational changes can lead to different orientations of the functional groups, and therefore give different intermolecular interactions responsible for the final crystallizing aggregates which are often metastable.

An important aspect in crystal engineering concerns the fact that some crystals contain more than one molecule in the asymmetric unit (i.e., Z′ > 1).⁷ The reason why Z′ > 1 occurs is still not well understood. Low symmetry and flexible molecules prone to difficult packing and highly directional hydrogen bonding could explain the occurrence of crystal structures with high Z′ values.⁸ Moreover, Z′ > 1 crystal structures are directly related with polymorphism and with the crystallization conditions that allow to explore as many as possible molecular conformations with different lattice energies before nucleating and crystallizing in a solid form.^9–11 Therefore, studies providing additional examples of structures with more than one molecule in the asymmetric unit are indeed needed for its better understanding.

Derivative ligands of N,N,N′,N′-tetrabenzylethylenediamine (L) have been used to great effect for the synthesis and solid-state reactivity of metal organic materials by using second sphere interactions.¹² However, to the best of our knowledge, polymorphic studies of bidentate ligand L have not been reported despite its use in the preparation of metal organic materials by means of coordination chemistry. Interestingly, a flexible ligand such as L with strong polymorphic behaviour can induce polymorphism in coordination complexes (i.e., metal organic frameworks (MOFs)¹¹ and other metal–organic complexes),¹³ due to the inherent structural versatility.

The aim of the current work is to study the polymorphic behaviour of the benzylethylenediamine derivative L using various crystallization methods and the solvent effect. Because the ligand has several torsional angles among the pendant benzyl groups and the flexible central alkyl chain, it can yield different polymorphs. The rationale for choosing this molecule is because derivatives of L ligands, either by changing the length^12,14 and the nature¹⁵ of the central backbone or by functionalizing the external aromatic rings¹⁶ are being used to synthesize metal organic materials applying second sphere interactions.¹³ It has been observed that few outer sphere structures have been obtained showing polymorphic behavior.^14,15 Furthermore, our interest in the polymorphism of L is also because it can give us insights on the solid-state reactivity of the second sphere adducts (i.e., dehydrochlorination reactions) which may depend on the intrinsic polymorphic behavior of the organic part of the metal–organic materials.

Here, we report on the structural properties of three polymorphs of the N,N,N′,N′-tetrabenzylethylenediamine ligand (L) (Scheme 1) which has been recently used in the synthesis of outer sphere adducts.^13,14 The different polymorphs are obtained by varying the crystallization conditions. Two of the polymorphs have half molecule of L in the asymmetric unit (Z′) and are obtained via slow crystallization methods upon evaporation. While the third one, is obtained by fast crystallization from solution or melt and contains two independent molecules of L in the asymmetric unit (Z′ = 2). The thermodynamic stability among the three polymorphs showed that the least stable corresponds to a metastable phase with Z′ = 2 (i.e., the less dense structure). This has been demonstrated by experimental results and corroborated using density functional theory (DFT) calculations specific for solid-state systems. Interestingly the metastable phase can be obtained upon heating followed by cooling of one of the polymorphs with Z′ = 0.5 (stable phase). This could be considered as a high energy phase (mesophase) of the crystal structure before reaching melting and fits with the theory that Z′ > 1 is just one of the many options that organic molecules (i.e., L) can take during the crystallization process (or just before it melts). Our point of view on whether a ligand with high tendency to form polymorphs might also induce polymorphism in second sphere adducts is given.

Scheme 1 Ligand (L) reported in this work showing the three polymorphs L_α-phase, L_β-phase (top) and L_γ-phase (bottom) which are obtained by slow, fast crystallization conditions and directly from melt.

Results and discussion

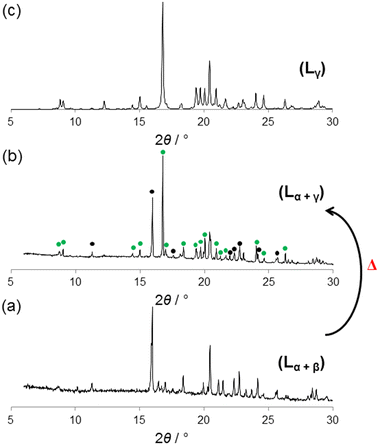
The list of ethylenediamine derivative ligands that are flexible and potential candidates to form conformers is vast. For instance N,N,N′,N′-tetrabenzylpropydiamine, N,N,N′,N′-tetrabenzylbutyldiamine, N,N,N′,N′-tetra-p-methoxybenzyl-ethylenediamine, (R,R)-N,N′-dibenzyl-1,2-diaminocyclohexane, N,N,N′,N′-p-methyl-tetrabenzyl-ethylenediamine or N,N,N′,N′-p-trifluoromethyl-tetrabenzyl-ethylenediamine, are bidentate ligands with potential formation of polymorphs. For the focus of this work the ligand N,N,N′,N′-tetrabenzyl-ethylenediamine (L) was selected because it has the shortest central backbone chain –N–CH₂–CH₂–N– that forms second sphere adducts undergoing dehydrochlorination reactions.¹⁴

Ligand L was synthesized according to literature.¹⁷ The obtained product was recrystallized using various crystallization conditions giving three polymorphs which are described hereafter. Recrystallization by evaporation of the as synthesized L was carried out at ambient conditions using a variety of different solvents such as methanol, ethanol, acetone, THF and DMF. In all the cases, block-shape colorless single crystals suitable for single crystal X-ray (SC-XRD) analysis were obtained (Scheme 1). Crystallographic analysis¹⁸ revealed that the unit cell and space group are the same as those already reported. Herein, the reported phase is labelled as (L_α-phase).¹⁹L_α-phase crystallizes in the low symmetry triclinic system in the P1̄ space group. The asymmetric unit contains half L molecule. As shown in Fig. 1, C–H⋯π interactions and π⋯π stacking are the main driving forces for the stabilization of the structures. Interestingly, powder X-ray diffraction (powder XRD) analysis of the bulk material clearly showed that additional peaks to L_α-phase were observed, thus indicating that a new extra phase was obtained (Fig. S1†). Therefore, we named the new phase L_β-phase. In most cases from the crystallization experiments, the yield of L_α-phase was higher than that of L_β-phase.

Fig. 1 Crystal structure of the L_α-phase. Short C–H⋯π contacts are depicted by black dashed lines. Colour code: carbon, orange; nitrogen, blue and hydrogen, white.

Crystal structure description of L_α-phase

As seen in Fig. 1, in L_α-phase the two methylene groups belonging to the phenyl rings in one molecule form C–H⋯π interactions with the neighbouring molecules, forming a chain along the b-axis (d_C–H⋯π = 3.668(4) Å, angle ∠d_C–H⋯π = 139°) (Fig. 1). No other significant weak interactions are observed. As mentioned,¹⁴ the angles N1–C2–C3 (113°) and N1–C9–C10 (114°) differ significantly from the regular tetrahedral value of (109.5°) due to the steric hindrance brought by the vicinity of benzene rings.

Crystal structure description of L_β-phase

Even though all the single crystals look similar (i.e., colorless blocks), a careful screening using optical microscopy and SC-XRD allowed the identification of a crystal with a different unit cell (Table 1), thus corroborating the powder XRD results. X-ray crystallography revealed that the new crystal (i.e., L_β-phase) also crystallizes in the triclinic system (P1̄) and contains half molecule in the asymmetric unit.

Table 1 Crystal data and refinement summary for three L phases: L_α-phase, L_β-phase and L_γ-phase

	L α-phase ^14	L β-phase	L γ-phase
Temperature	293 K	296 K	293 K
Crystal system	Triclinic	Triclinic	Monoclinic
Space group	P1̄	P1̄	C2/c
a (Å)	5.872(1)	6.356(4)	39.090(1)
b (Å)	10.202(3)	9.042(6)	12.916(1)
c (Å)	10.629(3)	11.117(7)	20.068(1)
α (°)	97.62(1)	76.99(1)	90
β (°)	101.62(1)	86.68(1)	93.66(1)
γ (°)	93.95(1)	79.28(1)	90
V (Å^3)	615.2(3)	611.5(7)	10111.8(7)
D x (g cm^−3)	1.135	1.142	1.105
μ (mm^−1)	0.07	0.07	0.49
F (000)		226	3616
R int	0.03	0.02	0.03
Total reflections	3224	2690	17 079
Unique reflections	2166	2033	9184
Observed refs. (I > 2σ(I))	1283	1418	6046
Refined parameters	146	145	578
R f/wRf	0.05/0.18	0.05/0.13	0.07/0.20
All data Rf/wRf		0.10/0.15	0.09/0.23
GoF	1.06	1.08	1.05

---

In the crystal structure of the L_β-phase, one methylene group takes part in the C–H⋯π electrostatic interaction's network (d_C–H⋯π = 3.630(3) Å, angle ∠d_C–H⋯π = 138°) giving rise to a chain expanding approximately along the crystallographic b-axis (Fig. 2). In L_β-phase the deviation from the standard 109.5° is less pronounced for the N1–C1–C2 (112°) and N1–C8–C9 (114°). The overall structures of L_α-phase and L_β-phase are nearly identical, which might be an important aspect explaining their co-existence in the same crystallization batch (i.e., concomitant polymorphs). The simulated powder XRD of L_α-phase and L_β-phase are markedly different (see ESI†).

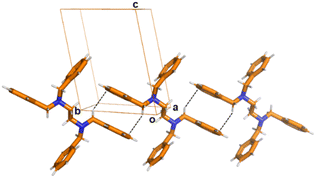Fig. 2 Crystal structure of L_β-phase. Short C–H⋯π contacts are depicted by black dashed lines. Colour code as in Fig. 1.

On the view of the polymorphic behaviour of L, we thought to explore different crystallization methods. According to literature reports,^7d crystal structures with Z′ > 1 can be obtained by rapid crystallization as most Z′ > 1 structures are considered kinetic (i.e., metastable) products. Therefore, we explored crystallization of L by fast cooling methods prone to give kinetic products. Rapid crystallization from a supersaturated methanol solution of L at high temperature (i.e., nearly methanol boiling point (65 °C)) yielded a new phase (L_γ-phase) with a completely different habit (i.e., long needles) as shown in Scheme 1. Despite the fast crystallization, the single crystals obtained were of good quality for SC-XRD analysis. Interestingly, when the solution containing the crystallized long needles were left standing at room temperature, the crystals dissolved within minutes, thus indicating that they belong to a metastable phase. Then, we turned out to explore if the L_γ-phase can be obtained from the melt which has been also claimed to have high chances to give structures with Z′ > 1.²⁰ Melting L followed by rapid cooling (quenching) at room temperature gave long colourless needles suitable for SC-XRD. X-ray crystallography showed that the new phase corresponds to L_γ-phase with remarkably different unit cell parameters compared to L_α-phase and L_β-phase (Table 1). Crucially, in the bulk sample there is no presence of L_α-phase and L_β-phase, and therefore crystallization from the melt allows a selective way to obtain this polymorph.

Crystal structure description of L_γ-phase

The L_γ-phase crystallizes in the monoclinic system in the C2/c space group. Notably, there are two independent molecules in the asymmetric unit with different conformations, herein labelled as conformers L_A and L_B, respectively (Fig. 3). That means that Z′ = 2. The unit cell of L_γ-phase is quite different compared to those of L_α-phase and L_β-phase. We note that the unit cell volume of L_γ-phase is 10 112 ų while that of L_α-phase and L_β-phase are 615 ų and 611 ų respectively (Table 1). This is a remarkable change in unit cell volume showing that interactions in the high temperature phase, prevails over packing in the thermodynamic structure.

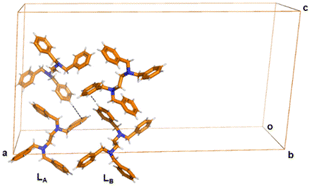Fig. 3 Crystal structure of L_γ-phase. Short C–H⋯π contacts are depicted by black dashed lines. The two independent molecules in the asymmetric unit are labelled L_A and L_B. The intermolecular interactions are clearly different from the L_α-phase and L_β-phase. Colour code as in Fig. 1.

The three-dimensional arrangement involves a different set of C–H⋯π interactions between L_A and L_B, independent molecules, by means of C21–H21⋯π interactions (d_C–H⋯π 3.751(6) Å, angle ∠d_C–H⋯π = 176°). We note that the C–H⋯π interaction is different from the C–H⋯π interaction mode in L_α-phase and L_β-phase, in which the hydrogen bonding donor comes from the benzene ring instead of methylene group (Fig. 3).

A comparison among three phases is also made in terms of the density and overall packing efficiency. The density of phase γ (1.105 g cm⁻³) is lower than those of phases α (1.135 g cm⁻³) and β (1.142 g cm⁻³). The packing efficiencies are 70.5% for α, 71.1% for β and 69.6% for γ, respectively. The greater density of β correlates with its greater packing efficiency when compared to that of α and γ.

The IR spectra of three polymorphs of L were quite similar, as seen in Fig. S2.† The most distinguishable differences in the IR spectra of the L_α-phase, L_β-phase and L_γ-phase are in the C–H bending of benzene rings (782 cm⁻¹ for L_γ-phase, 780 cm⁻¹ for phase L_α-phase/L_β-phase), indicating the different molecular environments of CH and CH₂ groups could be involved in the formation of different short contacts. This is consistent with the crystal structures studies of polymorphs L_α-phase, L_β-phase and L_γ-phase. Table 1 shows the crystallographic details of the three L polymorphs described herein.

Analysis of isolated L molecules shows that the conformations in L_α-phase and L_β-phase are very similar (see Fig. 4a), while the two conformations observed in L_γ-phase (L_A and L_B) are significantly different from the L_α-phase and L_β-phase (Fig. 4b). Moreover, the conformational energy of L_γ-phase is higher than that of L_α-phase and L_β-phase, so that L molecules need to be trapped into higher conformational energy levels to arrange into the L_γ-phase crystalline structure (i.e., in this case thermal treatment).

Fig. 4 (a) Overlapped L molecules in the conformation found in L_α-phase and L_β-phase. In the case of L_α-phase the colour code is yellow for all atoms. Hydrogens are omitted for clarity. (b) Overlapped L molecules in the conformation found in L_α-phase and L_γ-phase phases. In the case of L_α-phase molecule the color code is yellow for all atoms. Hydrogens are omitted for clarity. (c) Overlap of four independent molecules of L (red: L_α-phase, green: L_β-phase, and for L_γ-phase, yellow: L_A, blue: L_B).

Thermodynamic stabilities of L_α-phase, L_β-phase and L_γ-phase

To gain insights on the relative thermodynamic stabilities of the three L polymorphs, powder XRD experiments upon heating were carried out. The starting material is a mixture of L_α-phase and L_β-phase due to their concomitant crystallization (see Fig. 5a).²¹ The sample was heated²² from room temperature to 90 °C and annealed for 1 h and measured by in situ powder XRD. As shown in Fig. S3,† the phase transition from L_α-phase to the L_γ-phase did not occur until ca. 80 °C. At 80 °C, with the L_β-phase disappearing, and the intensity of L_γ-phase, particularly the peak at 2θ = 16°, is significant (Fig. 5b). Upon annealing at 90 °C for 6 h the L_γ-phase is the predominant one although the transformation is not completed.²³ However, there is no doubt that upon heating the phase that forms is the L_γ-phase (Fig. 5).

Fig. 5 (a) Starting mixture containing both L_α-phase and L_β-phase. (b) Experimental XRPD obtained after heating the as synthesized L. The product is a mixture of L_γ-phase (green circle) and L_α-phase (black circle). (c) Simulated XRPD pattern corresponding to L_γ-phase.

DSC was also used to monitor the thermal behavior of L. For both a freshly crystallized sample containing a mixture of phases α and β (Fig. S4†) and phase γ (Fig. S5†) there is no phase transition below 90 °C, even at a heating rate of 1 °C min⁻¹. This is apparently inconsistent with the powder XRD data but it should be noted that the two experiments followed different protocols. In Fig. S4,† the small exothermic peak at 92.4 °C is associated with the transformation of α and β to γ (with β possibly transforming through α as an intermediate). The larger endothermic peak at 94.7 °C is due to the melting of the γ phase. This was confirmed by heating a fresh sample to just below 94 °C which was then subjected to an ex situ powder XRD experiment. The powder XRD pattern of the product (Fig. S6a†), shows that the solid is the γ phase due to the good match among both diffractograms (Fig. S6b†).

DFT structural analysis

To gain insights on the relative stabilities among the three polymorphs described, we have carried out DFT calculations specific for the solid state. Complementary information in the field of solid-state chemistry can be obtained by theoretical methods and in particular QM calculations specific for solid phases. Herein, DFT approaches have been used. The GGA–PBE Perdew–Burke–Ernzerhof (PBE)²⁴ exchange–correlation functional has employed both for gas and solid phase (i.e., under periodical conditions) calculations. For the sake of consistency and to maintain reasonable computational costs, all calculations were carried out using the DMOL³ software.²⁵

In all the calculations, we used the experimental X-ray determined unit cells while relaxing atomic coordinates of all atoms. The same approach has been used for similar systems²⁶ and for other organic crystalline phases.²⁷ A numerical double-ζ quality basis set [including polarization functions on all atoms, i.e., double-ζ numerical with polarization (DNP)], roughly comparable with the usual 6-31G** Gaussian basis, was adopted. The inclusion of explicit van der Waals terms in the calculations has been chosen because of their importance when describing inter-particle interactions.²⁸

DFT results show that L_γ-phase is the less stable polymorph. In fact, the estimated sublimation energy (E*) (i.e., the energy required to extract a single molecule from the corresponding crystal structure) for L_γ-phase is about 10 kcal mol⁻¹ lower with respect to that of L_α-phase and L_β-phase. This agrees with the experimental data reported and, with the fast crystallisation conditions required for the formation of the L_γ-phase (i.e., the trapping of a metastable phase). The DFT calculations also show that L_β-phase is only ca. 1.5 kcal mol⁻¹ more stable with respect to L_α-phase. We note that the short contacts are closer in the L_β-phase than in the L_γ-phase, suggesting a higher stability.

Comparison among experimental and DFT optimized structures (i.e., alpha, beta and gamma structures)

Because the changes among the various described phases are small, we decided to have a closer look at the optimized L_α-phase, L_β-phase and L_γ-phase structures and compare them with the X-ray experimental structures to see any significant changes that might help to understand the observed polymorphism, in particular their relative stabilities.

Importantly, in the L_α-phase the C–H⋯π interaction between a methyl group from the benzene ring that yields the chain along the b-axis shown in Fig. 1 is still maintained with shorter distances with respect to the room temperature data (experimental). The optimized C–H⋯π distance is d_C–H⋯π = 3.650 Å and angle ∠d_C–H⋯π = 139°. As expected for a low temperature data, several other weak interactions are present such as the one including the second methylene group belonging to the phenyl rings is also observed with the following geometries d_C–H⋯π = 3.617 Å and angle ∠d_C–H⋯π = 151°. Additionally, the two central methylene groups in the ethylenic backbone interact with neighbouring aromatic rings via repulsive interactions by means of C–H⋯H contacts (d_C–H⋯H = 3.365 Å, angle ∠d_C–H⋯H = 154° and d_C–H⋯H = 3.395 Å, angle ∠d_C–H⋯H = 160°). For this polymorph, no major changes are observed in the optimized structure compared to the experimental data.

The L_β-phase polymorph is very similar to the alpha phase (i.e., differing in only 1.5 kcal mol⁻¹ in the sublimation energy calculated in both phases) (Fig. 6), and the main interaction used to describe the room temperature structure between the methylene group from the aromatic ring and adjacent benzene ring shown in Fig. 2 is d_C–H⋯π = 3.808 Å with angle ∠d_C–H⋯π = 142°. The L_β-phase also shows a second CH₂ from the benzene ring interacting with an adjacent aromatic ring. This second contact is stronger with distance d_C–H⋯π = 3.543 Å and angle ∠d_C–H⋯π = 136°. Interestingly, in this case the beta polymorph does not present the repulsive C–H⋯H contacts involving the ethylenic backbone, which corroborates the slightly higher stability seen in this phase with respect to the alpha phase. No big structural differences are observed between the experimental and optimized structure in the L_β-phase.

Fig. 6 Plot showing the relative sublimation energies (E*) calculated using DFT for L_α-phase, L_β-phase and L_γ-phase. The lower E* denotes that the gamma phase is the less stable polymorph.

In the L_γ-phase, the short interactions are described for the independent L_A and L_B molecules in the asymmetric unit. In the optimized structure the main interaction, which is among two aromatic rings via C–H⋯π used for the description of the structure at room temperature (Fig. 3), shows a shorter C–H(L_B)⋯C(L_A) distance d_C–H⋯π = 3.692 Å, ∠d_C–H⋯π = 175° which is expected for the low temperature (DFT) data. In the independent L_A molecule, only one CH₂ from a benzene group shows attractive C–H⋯π contacts (d_C–H⋯π = 3.690 Å, ∠d_C–H⋯π = 140°) with the other three methylene groups left without interactions. The two central ethylenic CH₂ groups interact via repulsive C–H⋯H contacts with adjacent L molecules (d_C–H⋯H 3.007 Å, ∠d_C–H⋯H 119° and d_C–H⋯H 3.087 Å, ∠d_C–H⋯H 121°). In the other independent L_B molecule, the four CH₂ groups belonging to the aromatic ring show different interactions. One of the CH₂ group is interacting via attractive C–H⋯π contacts (d_C–H⋯π = 3.723 Å, ∠d_C–H⋯π = 140°), stabilizing the structure. However, two CH₂ groups interact via repulsive interactions (d_C–H⋯H 3.125 Å, ∠d_C–H⋯H 129° and d_C–H⋯H 3.112 Å, ∠d_C–H⋯H 124°) and one methylene group is not showing any short contact. The two CH₂ groups in the ethylenic backbone do not show interactions. Also in this case, no major structural differences are observed in the experimental X-ray data compared to the optimized DFT structures in the L_γ-phase.

According to the above-described weak interactions, the more stable structure among the very similar alpha and beta phases, is the beta phase, the one showing less repulsive interactions. This stability shows a good correlation with the idea that Z′ with lower values are regarded thermodynamic structures. In fact, in the alpha and beta phases Z′ = 0.5. The gamma phase with Z′ = 2 is the less stable polymorph as confirmed by the presence of more repulsive interactions compared to L_α-phase and L_β-phase. This is also explained by the presence of the two L conformers in the asymmetric unit as more intermolecular interactions can be established. Thus, the DFT optimized structures show a good agreement with the experimental data and with the computed sublimation energies used to determine the relative thermodynamic stabilities among polymorphs. The following polymorphic stability order L_β-phase > L_α-phase > L_γ-phase is therefore confirmed by the DFT calculations (Fig. 6).

Kinetic trapping of L with Z′ = 2 by fast crystallization: a snapshot in the crystallization process towards Z′ < 2

Crystal structures with Z′ > 1 have been reported to be considered as “crystals on the way”, as “fossil relics of the fastest growing crystal nucleus” or as different “snapshot pictures at different stages of crystallization”. Desiraju and co-workers²⁹ stated that Z′ > 1 can be just one of the many options that organic molecules can take during the crystallization process. Generally, packing problems will tend to lead towards structures having Z′ > 1 due to awkward molecular geometries and flexible conformations. From our experimental data, upon heating and fast cooling, the L_α-phase and L_β-phase transforms into the L_γ-phase which is metastable (i.e., lower E* from DFT calculations). The extra thermal energy given to the solid implies that due to higher atomic mobility the conformation in L changes (i.e., ligand L contains eleven torsion angles) giving the arrangement of two L conformers (L_A and L_B) in the crystalline state which can be trapped as a metastable phase. If the solid melts or becomes a mesophasic state, upon fast cooling it will crystallize as the L_γ-phase. Therefore, the L_γ-phase can be considered as the metastable structure. In our opinion, the L_γ-phase corresponds to a snapshot that captures a picture of a crystallization event where a high energy phase (i.e., metastable phase) with Z′ = 2 is trapped in the crystalline state by means of fast crystallization events that do not allow L to reach the most thermodynamically stable conformation. The combination of flexible (ethylenic backbone) and rigid groups (benzene rings) in ligand L is contributing to the observed polymorphism described in this work.

L polymorphism and second sphere coordination adducts

From the combined X-ray and DFT work reported herein, we have observed that the difference in the sublimation energies (E*) among the three polymorphs is within 10 kcal mol⁻¹ (Fig. 6). It is important to notice that such energies are the typical energies associated with intramolecular torsions.³⁰ Although much weaker, van der Waals and dispersive interactions present in the three polymorphs reported are in the order of 0.5–1.0 kcal mol⁻¹. The computed difference in E* among L_α-phase, and L_β-phase is quite small (1.5 kcal mol⁻¹) but in the order of magnitude mentioned above. Higher energy is needed to form the L_γ-phase, which is the polymorph formed because more significant changes in the torsional angles are observed, that gives two L conformers in the asymmetric unit. Thus, the intrinsic flexibility of L is giving different conformers (L_A and L_B) in the form of polymorphs. In particular, the less stable phase can be obtained selectively as a kinetic form from the melt by fast crystallization.

The polymorphic behaviour of L studied in this work is relevant because gives insights about structural variability that can be exploited also in hybrid metal organic materials self-assembled using non-covalent second sphere interactions.³¹ Since organic ligands, in this case L, are used as first sphere ligands in combination with transition metals, the polymorphic behaviour of L can thus induce polymorphism (i.e., can be translated) to the second sphere adduct formed by the combination of metal anions and protonated ligands. In a second sphere adduct, the organic component can drive the formation of an outer sphere polymorph rather than the metal ion. In this regard, it was demonstrated that in the solid-state by mechanochemical means the second sphere adduct [LH]⁺·[FeCl₄]⁻, (where L is N,N,N′,N′-tetrabenzyl-trans-1,2-diaminocyclohexane) formed selectively one polymorph that crystallized in the polar space group Pna2₁ displaying NLO properties.

Although in this work only one ligand (L) has been studied, our aim is to monitor the polymorphic behaviour of L derivatives, to explore if a marked polymorphic behaviour of a given ligand (i.e., L derivative) can form a high number of polymorphs with high Z′ when such ligand is employed as first sphere ligand in outer sphere adducts. Despite the long history of second sphere interactions, polymorphism on hybrid metal–organic materials has not been explored much (i.e., compared to polymorphism of organic molecules and pharmaceuticals). Therefore, the reported results not only are of interest for the L itself, but also because other polymorphs can be formed using L and metals in outer sphere adducts.

Conclusions

In conclusion, we have reported structural aspects of three polymorphs of the flexible bidentate ligand L (L_α-phase, L_β-phase and L_γ-phase) that differ in the geometry and number of molecules in the asymmetric unit. Polymorphs L_β-phase and L_γ-phase are reported for the first time. Slow crystallization yields two polymorphs with Z′ = 0.5, while fast crystallization directly from melt allows a third polymorph with Z′ = 2. Our interpretation is that the polymorph with Z′ = 2 is a metastable structure that can form only by fast crystallisation and is observed experimentally by powder XRD upon heating, and by fast cooling the more stable structures with Z′ = 0.5 are formed. Theoretical QM calculations specific for solid-state systems have demonstrated that the structure with Z′ = 2 is the less stable among the three polymorphs, thus corroborating the theory that the polymorph with Z′ = 2 is a metastable structure which is kinetically trapped by fast crystallization events. As coined by Steed³² that high Z′ structure are “crystals on the way” of a more stable form, our results reported herein just confirm that statement. It is our opinion that a ligand which forms various polymers might be used to form also polymorphic second sphere adducts by using non-covalent electrostatic interactions. Research in this direction is being carried in our labs to explore crystallization conditions that can trap crystalline structures with high Z′ numbers in L derivatives and in second coordination spheres self-assembled using L derivatives and transition metal ions.

Experimental

All chemicals were obtained from commercial sources and used without further purification. Powder XRD were recorded at room temperature on a D8 Bruker diffractometer, with Cu-K_α1 radiation (λ = 1.54056 Å) and a step size of 0.01°, step time of 0.2 s. High temperature powder XRD experiments were performed in reflection (Bragg–Brentano) geometry using a Bruker D8 powder diffractometer with CuK_α1 radiation. An Anton Paar HTK 1200 furnace was used in the variable-temperature study. The temperatures are accurate to ±2 °C. Samples (about 100 mg) were placed in a sample holder and smoothed with a glass slide. Data were collected in the range 5° < 2θ < 30° with a step size of 0.02°. Differential scanning calorimetry (DSC) was performed using a TA Instrument Q100 differential scanning calorimeter. Small amounts (5–10 mg) of sample were weighed and sealed in DSC pans and placed in the sample chamber of the calorimeter. Heating/cooling rates were tuned during the DSC experiment, 20 °C min⁻¹ in the range of 20–80 °C and 110–20 °C, and 1 °C min⁻¹ in the range of 80 to 110 °C.

Single crystal X-ray diffraction for L_β-phase was carried out using a Bruker D8 QUEST X-ray single crystal diffractometer. An Agilent SuperNova Dual Atlas diffractometer was used for phase L_γ-phase. Crystal structures were solved and refined using SHELXS and SHELXL.^33,34 Non-hydrogen atoms were refined with anisotropic displacement parameters. Hydrogen atoms were inserted in idealized positions, and a riding model was used with U_iso set at 1.2 times the value of U_eq for the atom to which they are bonded. Crystallographic data for phases L_β-phase and L_γ-phase have been deposited with the Cambridge Crystallographic Data Center (CCDC) under reference numbers 2109973 and 2108276, respectively.

Author contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This research was supported by National Science Foundation of China (No. 21571090), and Liaoning BaiQianWan Talents Program, and Project of Education Department of Liaoning Province of China (LJKZ0102). A. F. acknowledges MIUR for FFARB “Fondo finanziamento delle attività base di ricerca” and CINECA for computational resources.

References

1. (a) J. Bernstein, Polymorphism in Molecular Crystals, OUP, Oxford, 2002; (b) S. L. Price, Acc. Chem. Res., 2009, 42, 117; (c) J.-P. Brog, C.-L. Chanez, A. Crochet and K. M. Fromm, RSC Adv., 2013, 3, 16905–16931; (d) A. J. Cruz-Cabeza and J. Bernstein, Chem. Rev., 2014, 114, 2170; (e) A. J. Cruz-Cabeza, S. M. Reutzel-Edens and J. Bernstein, Chem. Soc. Rev., 2015, 44, 8619; (f) A. J. Cruz-Cabeza, N. Feeder and R. J. Davey, Commun. Chem., 2020, 3, 142–146.
2. (a) B. M. Kariuki, C. L. Bauer, K. D. M. Harris and S. J. Teat, Angew. Chem., Int. Ed., 2000, 39, 4485–4487; (b) M. Xu and K. D. M. Harris, J. Phys. Chem. B, 2007, 111, 8705–8707.
3. (a) P. Sanphui, B. Sarma and A. Nangia, J. Pharm. Sci., 2011, 6, 2287–2299; (b) Y. Zhou, F. Guo, C. E. Hughes, D. L. Browne, T. R. Paskett and K. D. M. Harris, Cryst. Growth Des., 2015, 15, 2901–2907.
4. (a) S. Aitipamuka, P. S. Chow and R. B. H. Tan, CrystEngComm, 2014, 16, 3451–3465; (b) K. Xu, X. Xiong, L. Guo, L. Wang, S. Li, P. Tang, J. Yan, S. Wu and H. Li, J. Pharm. Sci., 2015, 104, 4123; (c) N. K. Duggirala, M. L. Perry, O. Almarsson and M. J. Zarowotko, Chem. Commun., 2016, 52, 640; (d) S. A. Ross, D. A. Lamprou and D. Douromis, Chem. Commun., 2016, 52, 8772; (e) H. Kulla, S. Greiser, S. Benemann, K. Rademann and F. Emmerling, Cryst. Growth Des., 2017, 17, 1190; (f) R. Kaur, S. Cherukuvada, P. B. Managutti and T. N. G. Row, CrystEngComm, 2016, 18, 3191–3203; (g) P. Bora, B. Saikia and B. Sarma, Chem. – Eur. J., 2020, 26, 699–710; (h) S. Aitipamula and L. P. Shan, CrystEngComm, 2022, 24, 560–570.
5. (a) C. E. Hughes and K. D. M. Harris, J. Phys. Chem. A, 2008, 112, 6808–6810; (b) C. E. Hughes and K. D. M. Harris, Chem. Commun., 2010, 46, 4982–4984; (c) P. C. Vioglio, G. Mollica, M. Juramy, C. E. Hughes, P. A. Williamos, F. Ziarelli, S. Viel, P. Thurreau and K. D. M. Harris, Angew. Chem., Int. Ed., 2018, 57, 6619–6623.
6. (a) L. Yu, G. A. Stephenson, C. A. Mitchell, C. A. Bunnell, C. A. Snorek, J. J. Bowyer, T. B. Borchardt, J. G. Stowell and S. R. Byrn, J. Am. Chem. Soc., 2000, 122, 585; (b) C. A. Mitchell, L. Yu and M. D. Ward, J. Am. Chem. Soc., 2001, 123, 10830; (c) S. Chen, I. Guzei and L. Yu, J. Am. Chem. Soc., 2005, 127, 9881; (d) P. A. Williams, C. E. Hughes, G. K. Lim, B. M. Kariuki and K. D. M. Harris, Cryst. Growth Des., 2012, 12, 3104–3113; (e) S. Ahn, F. Guo, B. M. Kariuki and K. D. M. Harris, J. Am. Chem. Soc., 2006, 128, 8441–8452.
7. (a) N. J. Babu and A. Nangia, Cryst. Growth Des., 2006, 6, 1995–1999; (b) M. Rafilovich and J. Bernstein, J. Am. Chem. Soc., 2006, 128, 12185–12191; (c) S. Mahapatra, T. S. Thakur, S. Joseph, S. Varughese and G. R. Desiraju, Cryst. Growth Des., 2010, 10, 3191–3202; (d) E. M. Brás, M. S. C. Henrique, J. A. Paixao and R. Fausto, Cryst. Growth Des., 2018, 18, 4167–4173; (e) J. B. Nanubolu, Cryst. Growth Des., 2021, 21, 133–148; (f) N. Caimac, E. Melnic, D. Chisca and M. S. Fonari, CrystEngComm, 2021, 23, 3099–3108.
8. J. W. Steed, CrystEngComm, 2003, 5, 169–179.
9. K. M. Steed and J. W. Steed, Chem. Rev., 2015, 115, 2895–2933.
10. G. R. Desiraju, CrystEngComm, 2007, 9, 91–92.
11. C. S. Hawes, N. F. Chilton, B. Moubaraki, G. P. Knowles, A. L. Chaffee, K. S. Murray, S. R. Batten and D. R. Turner, Dalton Trans., 2015, 44, 17494–17507.
12. F. Guo, X. Wang, H.-Y. Guan, H.-B. Yu, L. Li, S.-S. Chen, A. Famulari and J. Martí-Rujas, Cryst. Growth Des., 2015, 15, 2842–2852.
13. (a) F. Guo and J. Martí-Rujas, Dalton Trans., 2016, 45, 13648–13662; (b) F. Guo and J. Martí-Rujas, Dalton Trans., 2021, 51, 11665–11680.
14. H. Y. Guan, Z. Wang, A. Famulari, X. Wang, F. Guo and J. Martí-Rujas, Inorg. Chem., 2014, 53, 7438.
15. H. B. Yu, H. T. Li, P. Zhang, A. Famulari, F. Guo, I. Bargigia and J. Martí-Rujas, CrystEngComm, 2016, 18, 2408–2412.
16. F. Guo, Z. Wang, J.-J. Zhang, A. Famulari, H.-T. Li and J. Martí-Rujas, Dalton Trans., 2017, 46, 9466–9471.
17. Z. Pan, M. Zhang, D. Yuan and P. Ma, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2005, 61, o185–o186.
18. SC-XRD structure analysis was carried out at room temperature.
19. FAYHAP is the CCDC code for the L_α-phase described in ref. 14.
20. B. Sarma, S. Roy and A. Nangia, Chem. Commun., 2006, 4918–4920.
21. J. Bernstein, R. J. Davey and J.-O. Henck, Angew. Chem., Int. Ed., 1999, 38, 3440–3461.
22. Heating conditions: at 50 °C, 60 °C, 70 °C, 80 °C, 85 °C and 90 °C respectively.
23. Complete transformation has been obtained upon melting in DSC. See ESI.†.
24. (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865; (b) J. P. Perdew, K. Burke and M. E. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396–1396.
25. B. J. Delley, Chem. Phys., 2000, 113, 7756.
26. (a) H. Yu, L. Li, J. Gao, J. Tong, W. Zheng, M. Cametti, A. Famulari, S. V. Meille, F. Guo and J. Martí-Rujas, Dalton Trans., 2015, 44, 15960–15965; (b) F. Guo, M.-Q. Zhang, A. Famulari and J. Martí-Rujas, CrystEngComm, 2013, 15, 6237–6243.
27. (a) A. Famulari, G. Raos, A. Baggioli, M. Casalegno, R. Po and S. V. Meille, J. Phys. Chem. B, 2012, 116, 14504–14509; (b) T. Nicolini, A. Famulari, T. Gatti, J. Martí-Rujas, F. V. Monteleone, E. V. Canesi, C. Botta, E. Parisini, S. V. Meille and C. Bertarelli, J. Phys. Chem. Lett., 2014, 5, 2171–2176.
28. (a) S. Grimme, J. Chem. Phys., 2006, 124, 34108–34134; (b) A. Baggioli, S. Meille, G. Raos, R. Po, M. Brinkmann and A. Famulari, Int. J. Quantum Chem., 2013, 113, 2154–2162; (c) A. Baggioli, C. Cavallotti and A. Famulari, Phys. Chem. Chem. Phys., 2016, 18, 29616–29628; (d) L. Catalano, D. P. Karothu, S. Schramm, E. Ahmed, R. Rezgui, T. J. Barber, A. Famulari and P. Naumov, Angew. Chem., Int. Ed., 2018, 57, 17254–17258; (e) S. Torresi, A. Famulari and J. Martí-Rujas, J. Am. Chem. Soc., 2020, 142, 9537–9543; (f) J. Marti-Rujas, S. Ma and A. Famulari, Inorg. Chem., 2022, 61, 10863–10871.
29. S. Mahapatra, T. S. Thakur, S. Joseph, S. Varughese and G. R. Desiraju, Cryst. Growth Des., 2010, 10, 3191–3202.
30. A. Nangia, Acc. Chem. Res., 2008, 41, 595–604.
31. J. F. Stoddart, Z. Liu, S. T. Schneebeli and J. F. Stoddart, Chimia, 2014, 68, 315–320.
32. J. W. Steed, CrystEngComm, 2003, 5, 169.
33. G. M. Sheldrick, SHELXTL reference manual, Siemens analytical X-ray systems, Inc., Madison, WI, 1996.
34. G. M. Sheldrick, A short history of SHELX, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.

---

Footnote

† Electronic supplementary information (ESI) available: Further details on the synthesis and crystallographic information. CCDC 2109973 and 2108276. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2ce01174c

---