Open Access Article
Open Access ArticleHidden ordered structure in the archetypical Fe(pyrazine)[Pt(CN)4] spin-crossover porous coordination compound†
Ángel
Fernández-Blanco
ab,
Lorenzo A.
Mariano
b,
Lucía
Piñeiro-López
c,
José Antonio
Real
 d,
Jose Sanchez
Costa
d,
Jose Sanchez
Costa
 c,
Roberta
Poloni
c,
Roberta
Poloni
 *b and
J. Alberto
Rodríguez-Velamazán
*b and
J. Alberto
Rodríguez-Velamazán
 *a
*a
aInstitut Laue Langevin, 71 Avenue des Martyrs, CS 20156-38042, Grenoble, France. E-mail: velamazan@ill.eu
bUniv. Grenoble Alpes, SIMaP, Grenoble-INP, CNRS, F-38042, Grenoble, France. E-mail: roberta.poloni@grenoble-inp.fr
cIMDEA Nanociencia, Faraday 9, Ciudad Universitaria de Cantoblanco, 28049, Madrid, Spain
dDepartamento de Química Inorgánica, Insituto de Ciencia Molecular (ICMol), Universidad de Valencia, 46980, Paterna, Spain
First published on 12th August 2022
Abstract
Despite the fact that Fe(pyrazine)[MII(CN)4] (where MII is a metal in an open square-planar configuration, namely Pt, Pd, and Ni) is one of the most thoroughly studied families of spin-crossover compounds, its actual structure has remained imprecisely known up to now. Using neutron diffraction and density-functional theory calculations, we demonstrate that the pyrazine rings, instead of being disordered in two orthogonal positions in the low-spin phase, adopt an ordered arrangement with the rings alternately oriented in these two positions. This finding has a direct implication on the most characteristic property of these systems, the spin-crossover transition, which is notably affected by this arrangement. This is because the energy difference between both spin states depends on the pyrazine configuration and the ordering of the rings changes the balance of entropy contributions to the entropy-driven spin-crossover phenomenon.
1 Introduction
Coordination chemistry has experienced a remarkable surge in the last few years largely due to the burgeoning of metal–organic frameworks (MOFs), a topic where the structure–property correlation plays a crucial role. Evidently, X-ray diffraction is an essential tool in this research field, but it has some limitations that may be overcome with other techniques. In this line, neutron diffraction is a powerful complement, in particular for cases where hydrogen positioning is important, since it gives information that can be essential, as we illustrate in this work.A new field opened for spin-crossover (SCO) materials1 when bistability provided by the SCO phenomenon was combined with porosity in a porous coordination polymer (PCP) or a MOF.2 This combination opened a vast playground of possibilities for applications in fields like gas capture3 or chemical sensing,4 since SCO can both modulate the interaction with a guest molecule and be modulated by the interaction with an adsorbed molecule.5–9 An archetypical example of this class of compounds is the family Fe(pyrazine)[MII(CN)4] (where MII is a metal in an open square-planar configuration, namely Pt, Pd, and Ni).10,11 Based on classical Hofmann clathrate compounds,12 these three-dimensional frameworks present, together with the mentioned combination of porosity and SCO,13,14 an extremely rich display of functional properties. These include, for example, chemo-15–17 and photo-switching,18–20 molecular rotation correlated with the change of spin state,21 and pressure-tunable bistability.22 Inspired by this approach, many other examples have followed, aiming at enhancing the porosity,23 the cooperativity and loading capacity,24 and the interplay between the host–guest function and the SCO.25 The structure of Fe(pyrazine)[MII(CN)4] adopts a general topology consisting of 2D {Fe[MII(CN)4]}∞ layers, with the pyrazine ligands occupying the apical positions of Fe octahedra and connecting the layers along the perpendicular direction (Fig. 1). Three possible configurations can be contemplated for the orientation of the pyrazine rings in a layer (Fig. 1): the molecules in a parallel configuration, in a perpendicular configuration in two positions 90° from each other, and orientationally disordered in these two positions (disordered configuration). It is generally assumed that the pyrazine rings are orientationally disordered, with this disorder being dynamic in the high-spin (HS) state and nearly static in the low spin (LS) state.21 Initially, the tetragonal space group P4/m, which implies a disordered configuration due to the 4-fold axis passing through the N atoms of the pyrazine, was proposed from structural determination based on PXRD data.10 Later, single-crystal X-ray diffraction studies allowed the assignation of the P4/mmm space group (also implying a disordered configuration),13,15–17,26 which has been thoroughly assumed in subsequent studies for these compounds in both spin states in the absence of host molecules. Interestingly, Southon et al.13 pointed to a parallel configuration upon incorporation of two water molecules per unit cell. They found a twinned structure with the orthorhombic space group Pmmm, with the pyrazines parallel within each twin, but with a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 occupation of both possible orthogonal orientations. In the same work, the authors reported also an intermediate partially dehydrated phase, with one water molecule in the cavities presenting a perpendicular configuration of the pyrazine rings characterized by the appearance of superstructure peaks. The disordered configuration was nevertheless retained for the apohost.
50 occupation of both possible orthogonal orientations. In the same work, the authors reported also an intermediate partially dehydrated phase, with one water molecule in the cavities presenting a perpendicular configuration of the pyrazine rings characterized by the appearance of superstructure peaks. The disordered configuration was nevertheless retained for the apohost.
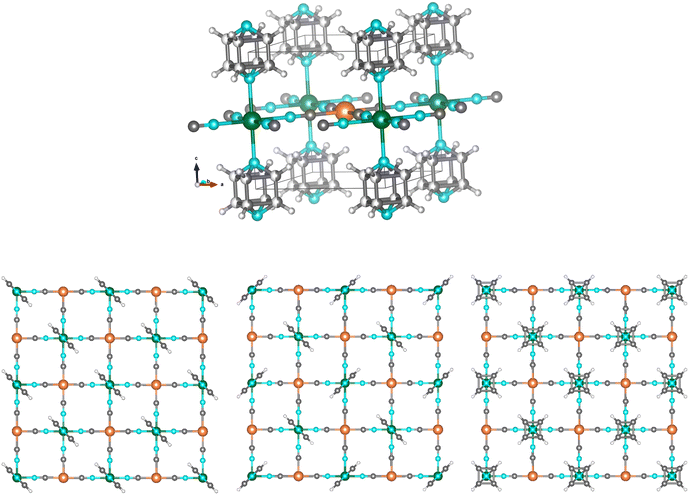 | ||
| Fig. 1 (Top) Scheme of the crystal structure of Fe(pyrazine)[MII(CN)4] with the pyrazine rings in a disordered configuration: Fe (green), MII (orange), N (light blue), C (dark grey), H (light grey). The unit cell is represented by the black lines. (Bottom) Representations of the three possible configurations of the pyrazine bridges: in a parallel configuration, in a perpendicular configuration and in a disordered configuration. Details of the structural parameters used for depicting these structures are given in the ESI.† | ||
In this work, we use neutron diffraction to demonstrate that the pyrazine rings adopt the perpendicular configuration in the LS state in the guest-free Fe(pyrazine)[PtII(CN)4] compound, contrary to what has been generally assumed before. This observation is fully confirmed by density-functional theory calculations performed on the two configurations. Finally, the consequences of the pyrazine ordering on the spin crossover transition temperature are discussed based on the effect on the computed energy and entropy contributions. These findings have important implications because the number of studies dedicated to this family is huge owing to the vast panoply of remarkable properties these compounds present.
2 Results and discussion
2.1 Neutron diffraction
The structure of the generally accepted disordered configuration is described in the P4/mmm tetragonal space group with cell parameters a = b = 7.33(3) Å and c = 6.94(2) Å for the low-spin state.15 The perpendicular configuration implies instead a structural transformation to a tetragonal supercell with a′′ = a − b, b′′ = a + b, and c′′ = c, giving a′′ = b′′ ≈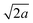 and c′′ ≈ c.13 This transformation may therefore involve the emergence of superstructure diffraction peaks. However, when working with X-rays, these peaks are weak and can be overlooked, particularly in powder diffraction. Additionally, these superstructure reflections can be diffuse, because the orientation of the rings may be uncorrelated between layers along c.13 The contrast provided by neutrons for light atoms (like hydrogen in the pyrazine molecule) allows distinguishing between the possible configurations of the rings, particularly if hydrogen is replaced by the more coherent scatterer deuterium (Fig. 2). We note that the parallel configuration, with the same cell parameters as the disordered configuration but with the space group Pmmm,15 is also clearly distinguishable when using neutron diffraction on the deuterated compound (Fig. 2).
and c′′ ≈ c.13 This transformation may therefore involve the emergence of superstructure diffraction peaks. However, when working with X-rays, these peaks are weak and can be overlooked, particularly in powder diffraction. Additionally, these superstructure reflections can be diffuse, because the orientation of the rings may be uncorrelated between layers along c.13 The contrast provided by neutrons for light atoms (like hydrogen in the pyrazine molecule) allows distinguishing between the possible configurations of the rings, particularly if hydrogen is replaced by the more coherent scatterer deuterium (Fig. 2). We note that the parallel configuration, with the same cell parameters as the disordered configuration but with the space group Pmmm,15 is also clearly distinguishable when using neutron diffraction on the deuterated compound (Fig. 2).
 | ||
| Fig. 2 Simulated powder diffraction patterns (wavelength 1.54 Å) of Fe(pyrazine)[Pt(CN)4] in the low-spin state with the pyrazine rings in the disordered configuration (red lines), and in the ordered perpendicular (black lines) and parallel (blue lines) configurations: (top) X-rays and hydrogenated pyrazine; (middle) neutrons and hydrogenated pyrazine; (bottom) neutrons and deuterated pyrazine. Details of the parameters used in the simulation are given in the ESI.† | ||
Dehydrated microcrystalline Fe(pyrazine)[PtII(CN)4] and its d4 pyrazine homologue Fe(d4-pyrazine)[PtII(CN)4] were prepared as described elsewhere.10,15–17 Neutron diffraction experiments were performed on powder samples of ca. 0.25 g using the D20 instrument27 at Institut Laue-Langevin, Grenoble, France, equipped with a cryo-furnace and using a wavelength of 1.54 Å coming from a germanium monochromator. Rietveld refinements and calculations of the structures were performed using the FullProf suite of programs28,29 and the tools from the Bilbao Crystallographic Server.30
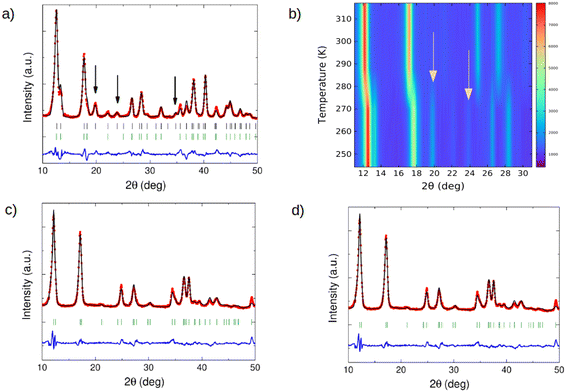
The neutron diffraction results are shown in Fig. 3 and Table 1. Fig. 3a shows the neutron diffraction pattern of Fe(d4-pyrazine)[MII(CN)4] at 100 K (low-spin state). At 2θ = 19.5, 23.7 and 34.7 degrees, the superstructure reflections appearing due to the pyrazine ordering in the perpendicular configuration can be clearly observed. The experimental pattern agrees well with a model with the pyrazine rings in the perpendicular configuration, described in the supercell defined above, with the tetragonal space group P4/mbm13 presenting a 4-fold axis passing through the Pt atom. We note that the real symmetry is probably lower, but the tetragonal pseudosymmetry avoids overparametrization. The fit is slightly improved if some disorder is allowed between both perpendicular positions of the pyrazine – with a refined value of 17.4(3)%. This is consistent with some degree of orientational disorder and with defects in the correlation of the layers along c.
| Compound | Fe(d4-pyrazine)[Pt(CN)4] | Fe(pyrazine)[Pt(CN)4] | ||
|---|---|---|---|---|
| T (K) | 100 | 320 | 130 | 320 |
| Spin state | Low-spin | High-spin | Low-spin | High-spin |
| Space group | P4/mbm | P4/mmm | P4/mbm | P4/mmm |
| a, b (Å) | 10.1568(4) | 7.4285(8) | 10.1576(5) | 7.4299(3) |
| c (Å) | 6.7632(5) | 7.2316(7) | 6.7668(4) | 7.2369(5) |
| d (Fe–N(C)) (Å) | 1.903(5) | 2.1599(3) | 1.941(5) | 2.1583(2) |
| d (Fe–N(pz)) (Å) | 1.983(7) | 2.2273(3) | 1.978(7) | 2.2291(3) |
| R Bragg | 5.69 | 7.70 | 5.03 | 8.81 |
The ordering in the perpendicular configuration of the pyrazine bridges is concomitant with the spin transition. The recorded diffraction patterns upon cooling from 320 K to 245 K (Fig. 3b) show the appearance of the superstructure reflections at the same temperature (ca. 285 K) of the abrupt change in the whole pattern occurring at the transition. The perpendicular configuration is the most stable at low temperatures (see below) and in fact, it has been observed in similar compounds not displaying spin-crossover.31 However, in the present case, it occurs concurrently with the abrupt structural changes produced at the spin transition. It deserves to be noted that the perpendicular configuration is also the one found compatible with the experimental results and calculations when certain types (and quantities) of molecules are adsorbed.13,32 In the high-spin state, the diffractogram does not show any signal of superstructure reflections and can be satisfactorily fitted with the disordered model with the space group P4/mmm (Fig. 3c). It is worthy to note that the ordering of the pyrazine molecules in the low-spin state is not an effect of the deuteration. Indeed, although less visible than those in the deuterated compound, the diffraction patterns measured for the hydrogenated compound in the low-spin state (Fig. 3d) also show evidence of pyrazine ordering (see the superstructure reflections at 2θ = 34.6 degrees).
2.2 Pyrazine interaction
In order to understand the greater stability of the perpendicular configuration, we have performed DFT calculations using the Quantum ESPRESSO package.33,34 The PBE+D2 functional35,36 was used to compute the binding energy of three different pyrazine dimers that represent the possible configurations present in the system: i) perpendicular, ii) top-on and iii) side-to-side dimers for the parallel arrangement (see inset in Fig. 4). See computational details in the ESI† for more details.Taking the positions and structures of the pyrazine rings from the corresponding relaxed compound as the starting point, one of the monomers was moved along the axis that connects the centers of mass of the two molecules until a local minimum was reached. The potential energy curves obtained for the three configurations are presented in Fig. 4. The three minima were found at center-to-center distances (Rcenters) between pyrazines of 4.8 Å, 3.8 Å, and 6.4 Å for the perpendicular, top-on, and side-to-side dimers, respectively. We note that the distance between complexed pyrazines in the framework is 7.1 Å, which is significantly larger than any of the Rcenters values and falls almost at the end of the potential energy curves (see circles on the curves in Fig. 4). An attractive interaction is predicted nonetheless for every configuration at Rcenters = 7.1 Å, being Eint = −11.1 meV and Eint = −6.7 meV for the perpendicular and side-to-side configurations, respectively, and negligible (Eint = −0.2 meV) for the top-on dimer. By adding up the side-to-side and top-on energy contributions, we obtain a lower value than the interaction predicted for the perpendicular configuration. This simple dimer model therefore suggests a perpendicular configuration of pyrazines for molecules located at the same distance found in the clathrate.
We note the unusual shape of the potential energy curve of the side-to-side configuration where two different regions can be found: a stabilization region between 6.1 Å and 7.6 Å and a destabilization region for Rcenters > 7.6 Å. The first corresponds to d(H–H) between 2.1 and 3.4 Å which correlates with the typical formation distances of a H–H bond.37,38 This weak bond with a dispersive nature exhibits energies of the order of 0.017 eV, comparable to the maximum stabilization of 0.020 eV predicted at the equilibrium position in Fig. 4. For Rcenters > 7.6 Å, the H–H distance is too large for a typical H–H bond and the electrostatic repulsion between the pyrazines may dominate. Finally, this analysis is consistent with the (PBE+D2) computed total energy difference between the parallel and perpendicular configurations in the supercell which gives a more stable perpendicular case by 35 meV per pyrazine.
2.3 Influence of the pyrazine arrangement on the spin transition
The configuration of the pyrazine rings has important consequences for the most characteristic feature of this material: the spin-crossover transition.It is not unusual to observe order–disorder processes coupled to SCO.39,40 In most cases, it is related to counterions or solvent molecules present in the structure,41,42 and more rarely to ligands.43,44 An order–disorder process can affect the spin transition in several ways, including the temperature of the transition and its abruptness (and hysteresis), and this has been taken into account in theoretical models of the spin transition.45 When coupling exists between the spin-active part of the system and the moieties susceptible of undergoing order–disorder, the presence of order–disorder processes tends to increase the abruptness of the transition, as has been observed in different examples.46–48 The wide hysteresis observed in Fe(pyrazine)[Pt(CN)4] may be therefore related to the order–disorder process undergone by the pyrazine rings.
Particularly relevant is how the pyrazine arrangement significantly affects the transition temperature. The spin transition temperature, T1/2, from LS to HS is defined as the temperature at which the thermodynamic equilibrium between the two phases is reached, i.e. when the Gibbs free energy is zero. The transition temperature is then given by T1/2 = ΔHHS–LS/ΔSHS–LS, with ΔHHS–LS (ΔSHS–LS) being the enthalpy (entropy) difference between both spin states. The experimental values for these quantities are ΔHexp = 25 kJ mol−1 and ΔSexp = 84 J mol−1 K−1 (giving T1/2 = 297 K).11 Both the energy and entropy differences depend on the configuration of the pyrazine rings, and therefore the transition temperature would be substantially modified if the pyrazine arrangement was different. The different terms contributing to ΔHHS–LS and ΔSHS–LS, and thus to T1/2, are written in eqn (1)
 | (1) |
The enthalpy difference, ΔHHS–LS, contains two terms, the adiabatic energy difference, ΔEad, and the vibrational contribution, ΔEvib. The entropy variation, ΔSHS–LS, contains the vibrational contribution, ΔSvib, a rotational term, ΔSrot, which accounts for the degrees of freedom associated with the rotational motion of the pyrazine rings,21 and an electronic contribution, ΔSel, which takes into account the different spin multiplicities between the two spin states. In the case of a LS–HS transition in Fe(II) complexes between a LS state with S = 0 and a HS state with S = 2, ΔSel = 13.38 J mol−1 K−1. This term, which represents ca. 16% of the entropy variation at the transition, is independent from the arrangement of the pyrazine rings.
ΔSrot is instead significantly affected by the pyrazine configuration. In 2012, a study of the dynamics of this system by some of us demonstrated, by means of quasielastic neutron scattering – a technique particularly adapted to probe the movement of hydrogen atoms – that the pyrazine rings are rotating in HS, while in LS, the movement is virtually deactivated.21 The rotational term ΔSrot was thereby calculated to amount to 7.95 J mol−1 K−1 (ref. 21) (ca. 9.4% of the total entropy gain at the transition) assuming a LS state with the pyrazine rings disordered in two perpendicular positions. Because the pyrazine molecules are ordered in LS, as demonstrated in the present neutron diffraction study, the number of accessible positions is divided by two, and so does the entropy. This leads to a change in ΔSrot of at least a factor of two (under the approximation of a harmonic oscillator around its equilibrium position, which is the case with less entropy, and therefore less favorable to produce big differences when applying a factor of two to it). A difference of this magnitude in ΔSrot between the LS-ordered case and the LS-disordered one implies a decrease of ca. 10% of the total experimental entropy obtained for the title compound.
We performed DFT calculations to compute how the pyrazine configuration affects the other terms such as Ead, Evib and Svib. For this, we computed the total energy and normal modes for the compound with the pyrazine rings in perpendicular and parallel configurations in both the HS and LS states. We take the average of the perpendicular and parallel cases as an approximation for the disordered case (see the full set of values in Table S2 in the ESI†). The expression for the vibrational contributions Evib and Svib can be derived within the statistical thermodynamic theory from the partition function of a harmonic oscillator. For a given normal mode vibrational spectrum {νi}, the vibrational contributions are:
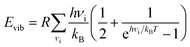 | (2) |
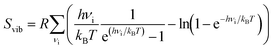 | (3) |
The DFT results show a difference of 0.83 J mol−1 K−1 in ΔSvib (ca. 1% of the total experimental entropy gain at the transition) between a LS-ordered case and a fully disordered scenario. The LS-ordered case consists of the difference between a disordered HS state and an ordered LS state with a perpendicular arrangement. The fully disordered case consists of disordered configurations both in the HS and LS states. Regarding ΔEvib, a negligible difference of 0.02 kJ mol−1 (less than 0.1% of the total enthalpy variation at the transition) is computed.
Finally, the adiabatic energy difference, ΔEad, is computed as the total energy difference between the two spin states each taken at their corresponding geometry. We note that the calculation of adiabatic energy differences in transition metal complexes presents a significant challenge for modern electronic structure methods.49–53 Within DFT, different exchange and correlation functionals including semilocal, meta-GGAs, and global hybrids have been tested in this respect and variations by up to 3 eV can be found depending on the specific choice of the functional and the chosen molecular complex.54 Here, to evaluate ΔEad, we use the non-self consistent Hubbard U-corrected density approach scheme which employs linear response U55 values computed separately for high spin and low spin (see the ESI† for more details). Recently, this method has been shown to provide accurate results of spin splitting energies for a series of Fe(II) molecules and periodic compounds when compared with higher level calculations and experimentally extracted results.53 The adiabatic energy difference computed with this method is 36.64 kJ mol−1 when both spin states are disordered and 36.91 kJ mol−1 when the LS state is in the perpendicular arrangement. This gives, as expected, a marginal energy difference of 0.27 kJ mol−1 between the two pyrazine configurations.
Adding together all the contributions (see eqn (1)), we obtain that the change in the configuration of pyrazine moieties in the LS state from an ordered perpendicular arrangement to a disordered case implies a decrease of 0.29 kJ mol−1 in ΔH and of 8.78 J mol−1 K−1 in ΔS at the spin transition, which translates in a variation of T1/2 of the order of 30 K. Thus, if the configuration of the pyrazine rings in the LS state was disordered and not ordered, the transition temperature would have been ca. 30 K higher, mostly due to the change in rotational entropy.
3 Conclusion
Herein, we have demonstrated, by means of neutron diffraction experiments, that the pyrazine rings in Fe(pyrazine)[Pt(CN)4] adopt an ordered arrangement in the low-spin state with the rings alternately oriented in two positions perpendicular to each other. Our DFT calculations have shown that this configuration stems from the interaction between the pyrazine molecules and have allowed us to estimate the effect of this arrangement at the spin transition temperature. The implications of the actual configuration of the pyrazine moieties in the energy and entropy balance between the high-spin and low-spin states are substantial, and thus the spin transition temperature is significantly dependent on this configuration. The fact that Fe(pyrazine)[MII(CN)4] (MII = Pt, Pd, Ni) are prototypical examples of the growing class of porous spin-crossover compounds, with a relevant potential for applications, and the great number of studies concerning this family and many other compounds based on it, underlines the significance of accurate structural knowledge, which may be of crucial importance for the understanding of the properties of such materials.Data availability
ILL beamtime allocation experiment numbers 5-22-795 (https://doi.ill.fr/10.5291/ILL-DATA.5-22-795) and DIR-274 (https://doi.ill.fr/10.5291/ILL-DATA.DIR-214).Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the ILL for the PhD contract of A. F. B. and for the beamtime allocation under experiment numbers 5-22-795 and DIR-274. J. S. C. acknowledges funds from the MICINN through the National Research Project (PID2019-111479GB-100) and the Ramon y Cajal Research Program (RYC-2014-16866). IMDEA Nanociencia acknowledges support from the Severo Ochoa Program for Centres of Excellence in R&D (MICINN, Grant CEX2020-001039-S). J. A. R. thanks Grant PID2019-106147GB-I00 funded by MCIN/AEI. Calculations were performed using resources granted by GENCI under the CINES and TGCC grant numbers A0020907211 and A0110907211. Additionally, the froggy and Dahu platform of the CIMENT infrastructure, which is supported by the Rhone-Alpes region (GRANT CPER07 13 CIRA) and the Equip@Meso project, was employed for the calculations.References
- P. Gütlich and H. A. Goodwin, Spin-Crossover in Transition Metal Compounds, in Topics in Current Chemistry, Springer, Berlin, 2004, vol. I–III Search PubMed.
- J. A. Real, E. Andrés, M. C. Muñoz, M. Julve, T. Granier, A. Bousseksou and F. Varret, Science, 1995, 268, 265–267 CrossRef CAS PubMed.
- D. A. Reed, B. K. Keitz, J. Oktawiec, J. A. Mason, T. Runčevski, D. J. Xiao, L. E. Darago, V. C. Valentina, S. Bordiga and J. R. Long, Nature, 2017, 550, 1476–4687 CrossRef PubMed.
- G. J. Halder, C. J. Kepert, B. Moubaraki, K. S. Murray and J. D. Cashion, Science, 2002, 298, 1762–1765 CrossRef CAS PubMed.
- X. Bao, H. J. Shepherd, L. Salmon, G. Molnár, M.-L. Tong and A. Bousseksou, Angew. Chem., Int. Ed., 2013, 52, 1198–1202 CrossRef CAS PubMed.
- R. Ohtani and S. Hayami, Chem. – Eur. J., 2017, 23, 2236–2248 CrossRef CAS PubMed.
- Z.-P. Ni, J.-L. Liu, M. N. Hoque, W. Liu, J.-Y. Li, Y.-C. Chen and M.-L. Tong, Coord. Chem. Rev., 2017, 335, 28–43 CrossRef CAS.
- E. Resines-Urien, E. Burzurí, E. Fernandez-Bartolome, M. A. García García-Tuñón, P. de la Presa, R. Poloni, S. J. Teat and J. S. Costa, Chem. Sci., 2019, 10, 6612–6616 RSC.
- A. Develioglu, E. Resines-Urien, R. Poloni, L. Martín-Pérez, J. S. Costa and E. Burzurí, Adv. Sci., 2021, 8, 2102619 CrossRef CAS PubMed.
- V. Niel, J. M. Martínez-Agudo, M. C. Muñoz, A. B. Gaspar and J. A. Real, Inorg. Chem., 2001, 40, 3838–3839 CrossRef CAS PubMed.
- T. Tayagaki, A. Galet, G. Molnár, M. C. Muñoz, A. Zwick, K. Tanaka, J. A. Real and A. Bousseksou, J. Phys. Chem. B, 2005, 109, 14859–14867 CrossRef CAS PubMed.
- K. A. Hofmann, F. Küspert and Z. Anorg, Chem, 1897, 15, 204–207 CAS.
- P. D. Southon, L. Liu, E. A. Fellows, D. J. Price, G. J. Halder, K. W. Chapman, B. Moubaraki, K. S. Murray, J.-F. Létard and C. J. Kepert, J. Am. Chem. Soc., 2009, 131, 10998–11009 CrossRef CAS PubMed.
- M. C. Muñoz and J. A. Real, Coord. Chem. Rev., 2011, 255, 2068–2093 CrossRef.
- M. Ohba, K. Yoneda, G. Agustí, M. C. Muñoz, A. Gaspar, J. A. Real, M. Yamasaki, H. Ando, Y. Nakao, S. Sakaki and S. Kitagawa, Angew. Chem., Int. Ed., 2009, 48, 4767–4771 CrossRef CAS PubMed.
- G. Agustí, R. Ohtani, K. Yoneda, A. B. Gaspar, M. Ohba, J. F. Sánchez-Royo, M. C. Muñoz, S. Kitagawa and J. A. Real, Angew. Chem., Int. Ed., 2009, 48, 8944–8947 CrossRef PubMed.
- R. Ohtani, K. Yoneda, S. Furukawa, N. Horike, S. Kitagawa, A. B. Gaspar, M. C. Muñoz, J. A. Real and M. Ohba, J. Am. Chem. Soc., 2011, 133, 8600–8605 CrossRef CAS PubMed.
- S. Bonhommeau, G. Molnár, A. Galet, A. Zwick, J. A. R. Real, J. J. McGarvey and A. Bousseksou, Angew. Chem., Int. Ed., 2005, 44, 4069–4073 CrossRef CAS PubMed.
- S. Cobo, D. Ostrovskii, S. Bonhommeau, L. Vendier, G. Molnár, L. Salmon, K. Tanaka and A. Bousseksou, J. Am. Chem. Soc., 2008, 130, 9019–9024 CrossRef CAS PubMed.
- M. Castro, O. Roubeau, L. Piñeiro López, J. A. Real and J. A. Rodríguez-Velamazán, J. Phys. Chem. C, 2015, 119, 17334–17343 CrossRef CAS.
- J. A. Rodríguez-Velamazán, M. A. González, J. A. Real, M. Castro, M. C. Muñoz, A. B. Gaspar, R. Ohtani, M. Ohba, K. Yoneda, Y. Hijikata, N. Yanai, M. Mizuno, H. Ando and S. Kitagawa, J. Am. Chem. Soc., 2012, 134, 5083–5089 CrossRef PubMed.
- A. Galet, A. B. Gaspar, M. C. Muñoz, G. V. Bukin, G. Levchenko and J. A. Real, Adv. Mater., 2005, 17, 2949–2953 CrossRef CAS.
- C. Bartual-Murgui, N. A. Ortega-Villar, H. J. Shepherd, M. C. Muñoz, L. Salmon, G. Molnár, A. Bousseksou and J. A. Real, J. Mater. Chem., 2011, 21, 7217–7222 RSC.
- L. Piñeiro López, M. Seredyuk, M. C. Muñoz and J. A. Real, Chem. Commun., 2014, 50, 1833–1835 RSC.
- M. Meneses-Sánchez, R. Turo-Cortés, C. Bartual-Murgui, I. da Silva, M. C. Muñoz and J. A. Real, Inorg. Chem., 2021, 60, 11866–11877 CrossRef PubMed.
- S. Cobo, D. Ostrovskii, S. Bonhommeau, L. Vendier, G. Molnár, L. Salmon, K. Tanaka and A. Bousseksou, J. Am. Chem. Soc., 2008, 130, 9019–9024 CrossRef CAS PubMed.
- T. C. Hansen, P. F. Henry, H. E. Fischer, J. Torregrossa and P. Convert, Meas. Sci. Technol., 2008, 19, 034001 CrossRef.
- J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69 CrossRef.
- https://www.ill.eu/sites/fullprof/ .
- M. I. Aroyo, J. M. Perez-Mato, C. Capillas, E. Kroumova, S. Ivantchev, G. Madariaga, A. Kirov and H. Wondratschek, Z. Kristallogr. - Cryst. Mater., 2006, 221, 15–27 CrossRef CAS.
- J. Rodríguez-Hernández, A. Lemus-Santana, J. Ortiz-López, S. Jiménez-Sandoval and E. Reguera, J. Solid State Chem., 2010, 183, 105–113 CrossRef.
- A. Fernández-Blanco, L. Piñeiro López, M. Jiménez-Ruiz, S. Rols, J. A. Real, J. A. Rodríguez-Velamazán and R. Poloni, J. Phys. Chem. C, 2022, 126, 8090–8099 CrossRef.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- P. Giannozzi, O. Baseggio, P. Bonfá, D. Brunato, R. Car, I. Carnimeo, C. Carvazzoni, S. de Gironcoli, P. Delugas, F. F. Ruffino, A. Ferreti, N. Mazari, I. Timrov, A. Urru and S. Baroni, J. Chem. Phys., 2020, 152, 154105 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- S. J. Grabowski, Hydrogen Bonding- New Insights, Springer, Amsterdam, 2006 Search PubMed.
- D. J. Wolstenholme and T. S. Cameron, J. Phys. Chem. A, 2006, 110, 8970–8978 CrossRef CAS PubMed.
- S. Pillet, J. Appl. Phys., 2021, 129, 181101 CrossRef CAS.
- A. Kashiro, K. Some, Y. Kobayashi and T. Ishida, Inorg. Chem., 2019, 58, 7672–7676 CrossRef PubMed.
- C.-F. Sheu, S. Pillet, Y.-C. Lin, S.-M. Chen, I.-J. Hsu, C. Lecomte and Y. Wang, Inorg. Chem., 2008, 47, 10866–10874 CrossRef CAS PubMed.
- H. J. Shepherd, G. Tonge, L. E. Hatcher, M. J. Bryant, J. V. Knichal, P. R. Raithby, M. A. Halcrow, R. Kulmaczewski, K. J. Gagnon and S. J. Teat, Magnetochemistry, 2016, 2, 9 CrossRef.
- T. M. Ross, B. Moubaraki, K. S. Wallwork, S. R. Batten and K. S. Murray, Dalton Trans., 2011, 40, 10147–10155 RSC.
- D. Rosario-Amorin, P. Dechambenoit, A. Bentaleb, M. Rouzières, C. Mathonière and R. Clérac, J. Am. Chem. Soc., 2018, 140, 98–101 CrossRef CAS PubMed.
- D. Chernyshov, N. Klinduhov, K. W. Törnroos, M. Hostettler, B. Vangdal and H.-B. Bürgi, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 014406 CrossRef.
- R. Kulmaczewski, E. Trzop, E. Collet, S. Vela and M. A. Halcrow, J. Mater. Chem. C, 2020, 8, 8420–8429 RSC.
- G. S. Matouzenko, A. Bousseksou, S. A. Borshch, M. Perrin, S. Zein, L. Salmon, G. Molnar and S. Lecocq, Inorg. Chem., 2004, 43, 227–236 CrossRef CAS PubMed.
- G. A. Craig, J. S. Costa, O. Roubeau, S. J. Teat and G. Aromí, Chem. – Eur. J., 2011, 17, 3120–3127 CrossRef CAS PubMed.
- M. Radoń, Phys. Chem. Chem. Phys., 2019, 21, 4854–4870 RSC.
- L. M. L. Daku, A. Vargas, A. Hauser, A. Fouqueau and M. E. Casida, ChemPhysChem, 2005, 6, 1393–1410 CrossRef CAS PubMed.
- K. Pierloot, Int. J. Quantum Chem., 2011, 111, 3291–3301 CrossRef CAS.
- A. Droghetti, D. Alfè and S. Sanvito, J. Chem. Phys., 2012, 137, 124303 CrossRef CAS PubMed.
- L. A. Mariano, B. Vlaisavljevich and R. Poloni, J. Chem. Theory Comput., 2021, 17, 2807–2816 CrossRef CAS PubMed.
- L. A. Mariano, B. Vlaisavljevich and R. Poloni, J. Chem. Theory Comput., 2020, 16, 6755–6762 CrossRef CAS PubMed.
- M. Cococcioni and S. De Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ce00895e |
| This journal is © The Royal Society of Chemistry 2022 |