Epitaxies of Ca-sulfates on calcite (CaCO₃) I. Gypsum {010} on the calcite {10.4} form: epi-twins of gypsum induced by the calcite substrate

Abstract

3D-epitaxy of the {010} pinacoid of deposited gypsum (CaSO₄·2H₂O) on the substrate {10.4} calcite rhombohedron is described, in order to give a theoretical background to the replacement of calcite with gypsum both in the laboratory and by weathering in nature. 2D-lattice coincidences are geometrically obtained from the matching of periodic bond chains (PBCs) running within the elementary slices facing towards the substrate/deposit interfaces. The epitaxy in the third dimension, perpendicular to the interfaces, has been verified as well, to establish if ad/absorption occurs (anomalous mixed crystals) at the calcite/gypsum contact. This research represents the reticular part of a wider program extended to the epi-interaction among the gypsum/calcite, gypsum/bassanite (CaSO₄·1/2H₂O) and gypsum/anhydrite (CaSO₄) couples.

---

1. Introduction

In recent papers, Ruiz-Agudo et al.^1,2 investigated the crystallographic control in the replacement of calcite with the three main calcium sulfates: gypsum (CaSO₄·2H₂O), bassanite (CaSO₄·1/2H₂O) and anhydrite (CaSO₄). By 2D-X ray diffraction, they found that all these sulfates can epitaxially grow on the fresh cleavage surfaces {10.4} of calcite, CaCO₃. At that time, they described the geometry of the epitaxies as follows:

i) Gypsum {010}/calcite {10.4}. The [001] direction of gypsum {010} is parallel to the [4̄41] direction of calcite {10.4}, i.e. to the cleavage rhombohedron edge, the misfit between the length of the two vectors being ∼1.0%.^3–5 Moreover, another good fit (0.9%) was found between the vectors (3 × [01̄0] + 2 × [4̄12]) = 17.019 Å in calcite and 3 × [100] = 16.860 Å in gypsum. However, the angular misfit between the matching vectors reaches ∼6° which, in our opinion, is not in favor of a good 2D-coincidence cell (2D-CC hereinafter) between the two structures.

ii) Bassanite {010}/calcite {10.4}. Only [001] = 6.336 Å of bassanite is parallel to the [4̄41] = 6.425 Å of calcite, the linear misfit between these vectors being 1.45%. No other match was found and then 2D-coincidence lattices, in our opinion, cannot exist in this case.

iii) Anhydrite {100}/calcite {10.4}. Vector [001] = 6.245 Å of anhydrite is parallel to [4̄41] = 6.425 Å of calcite, the misfit between them being 2.8%. Another good match (4.3%) was found between the vector (3 × [01̄0] + 2 × [4̄12]) = 17.019 Å in calcite and (2 × [001] + 5 × [011]) = 17.764 Å in anhydrite. However, the angular misfit between the matching vectors reaches ∼12°, which does not satisfy the constraints at all for a good epitaxy to be set up.

Finally, concerning the epitaxial conditions, the quoted authors correctly noted that in all three investigated phases the Ca–SO₄ chains run parallel to the common [001] direction, and that in the {10.4} calcite faces the symmetry equivalent <4̄41> PBCs are formed by Ca–CO₃ chains. Accordingly, they concluded that the epi-growth of Ca-sulfates on calcite crystals is controlled by the very similar Ca–Ca spacing (in Å) along the <4̄41> directions in calcite (6.425) and the [001] direction in gypsum (6.491), bassanite (6.336) and anhydrite (6.245). We would like it to be clear, from now on, that we are not here to judge the connection between this long standing^1–5 experimental work, largely in the majority, and its theoretical–crystallographic interpretation, strongly in the minority. The combination of these two aspects, along with the complexity of the subject of calcite/replacing sulfates, requires a long-lasting effort and a set of integrating formations in the wide field of crystal growth.

Starting from the quoted experiments and having considered that searching for 2D-epitaxy among low symmetry crystal structures is not always an easy goal to achieve, we aimed at investigating all compatible 2D super-lattices among the {10.4} form of calcite and the gypsum {010}, bassanite {010}, and anhydrite {100} forms. In the present work, we will focus our attention to the possible epitaxies between the cleavage {10.4}_C of the calcite form (substrate), and the main gypsum {010}_G form (deposit). To do this, we have to start from their surface profiles, as obtained through strictly adopting the Hartman–Perdok method of the periodic bond chains (PBCs).⁶ Concerning new experiments, we planned a precise investigation on the growth patterns, especially with optical microscopy and AFM, arising from the {10.4} calcite/Ca-sulfate (gypsum, bassanite and anhydrite) interfaces.

2. Experimental and theoretical aspects of the {10.4} surfaces of calcite

The unit cell (in Å) of the rhombohedral calcite (S.G. R3̄c) reads: a₀ = b₀ = 4.9896; c₀ =17.06, α = β = 90°, and γ = 120°.⁸ The rectangular 2D-cell on a (10.4) face can be written as: [010] = 4.9896 and 1/3 × [421̄] = 8.103. This cleavage rhombohedron is limited by a set of symmetry-equivalent vectors, all generated by the ruling vector 1/3 × [4̄41] = 12.85, which runs parallel to the edge of the (10.4) face. Recently,⁷ we outlined that (10.4) shows a sharp pseudohexagonal symmetry. In fact, a large supercell, anticlockwise presented in Fig. 1(right side), can be drawn. It is made of three supercells; each of them has multiplicity (2×) and is described by vectors and angles in between them, which are: [020] = 9.979, 1/3 × [4̄11] = 9.516, and δ = 121.62°; −1/3 × [4̄51] = 9.516, −[020] = 9.979, and δ = 121.62°; −1/3 × [4̄11] = 9.516, 1/3 × [451̄] = 9.516, and ρ = 116.75°. The pseudo-hexagonal supercell with multiplicity (6×) occupies an area of 242.58 Ų. The rectangular 2D-cell on the (10.4) face is drawn in Fig. 1(upper left side), while an example of a 2D-supercell is drawn as well in Fig. 1(lower left side).

Fig. 1 The pseudo-hexagonality of the cleaved {10.4} form of calcite_. A (6×) supercell (right side), made of three (2×) supercells (left, lower side), is shown. The smallest 2D-cell of {10.4} is also drawn (upper left).

It is well known that the {10.4} calcite rhombohedron is a flat (F) form that can grow through the layer-by-layer mechanism (2D-nucleation, or spiral, or both).⁷ As a matter of fact, four periodic bond chains (PBCs) run within the slice d_10.4 = 3.034 Å thick. Two of them develop along the equivalent <4̄41> and <481̄> directions, through the glide plane “c”: they build the main edges of the six rhombohedral faces. The other two run along the <421̄> and <010> directions. We take this opportunity here to remind you that we calculated as well the hierarchy of the strength (ECE, the end chain energy) of the corresponding PBCs i.e., the energy released (ECE, erg per ion × 10¹⁰) when an ion enters, in a crystallographic position, at one end of each semi-infinite chain: 0.391, 0.359 and 0.333 for the PBCs <4̄41>, <421̄> and <010>, respectively.^8,9

The structure of the <4̄41> PBCs, the strongest ones in the crystal, can be described as a succession of positive (Ca²⁺) and negative (CO₃²⁻) ions with their centers of mass alternating along a common row with a repeat period of 1/3 × [4̄41] = 12.85 Å. This PBC does not show any dipole moment, neither orthogonal nor parallel to its development axis; thanks to this property and to the interconnections with the two other kinds of PBC running within the d_10.4 slice, there is only one way to choose the surface profile of this rhombohedron. Thus, this profile does not need to be reconstructed, since no atom can be found on the ideal planes separating two adjacent and consecutive d_10.4 slices. In other words, slices of thickness d_10.4 are self-consistent.

Finally, it might be interesting to consider another feature of the d_10.4 slice: its compactness. Ten years ago, more or less, we calculated the slice energy, i.e., the interaction energy among the atoms contained in this slice, and found that E^10.4_slice = 0.222 erg per ion × 10⁻¹⁰, corresponding to nothing less than ∼94% of the calcite crystallization energy.¹⁰ This property, along with the number of PBCs contained in the slice, confirms once again the historical flat character of the {10.4} form. Accordingly, it can grow either by spiral or 2D-mechanism (or both).¹¹ The shape of growth (or dissolution) patterns (spirals and/or 2D nuclei) is theoretically limited¹⁰ by the dominant steps <4̄41>, followed by <421̄> and <010>.

3. The growth layers on the {010} pinacoid of gypsum

The frame we adopted^12,13 to represent the crystal morphology (in Å) of monoclinic gypsum single crystals and twins is always that by De Jong and Bouman,¹³i.e., a₀ = 5.63, b₀ = 15.201, c₀ = 6.23, β = 113.80° and space group C2/c. Alternative reference frames do not constitute a problem for the results of the present work and thus they would not be considered here. The gypsum crystal structure, projected along the [001] zone axis, is shown in Fig. 2.

Fig. 2 Gypsum structure projected along the [001] direction. (a) The [001]_a PBC allows the surface profile with d^a₀₂₀ of the {010} F-form to be drawn; the development of the [001]_a PBC showing the strong Ca–O(SO₄²⁻) bonds between the polar [001] chains. (b) The [001]_b PBC originates the surface profile with d^b₀₂₀; the development of the [001]_b PBC showing the hydrogen bonds: O_w–H⋯O(SO₄²⁻) between the polar [001] chains. In the middle of each figure the enlarged view of the idealized ellipses containing the [001] PBC is shown. The alternative d₀₂₀ surface profiles are noteworthy, since their terminations at 1/2 × d₀₁₀, or d₀₁₀, and 1/4 × d₀₁₀, or 3/4 × d₀₁₀, have been outlined along with the role played by water molecules. The black spheres indicate Ca-atoms, small-white spheres indicate oxygen atoms, while the smallest-white spheres represent water hydrogens. Finally, the ionic SO₄²⁻ groups have been drawn with yellow tetrahedra. Redrawn from Massaro et al.¹²

From the constraints inherent to the PBC method, two PBCs can be found along the strongest bond chains, [001]_a and [001]_b. The first one, shown in Fig. 2a, is contained within a slice of thickness d^a₀₂₀ and is limited by two outermost layers only populated by water molecules. The second one (Fig. 2b) builds the slice d^b₀₂₀ that has the same thickness as d^a₀₂₀, but is terminated by Ca²⁺ and SO₄²⁻ ions. As found by Simon and Bienfait,^14,15 the [100] PBCs connect the [001] PBCs within the d₀₂₀ slices, thus determining the flat character of the {010} form. Accordingly, it can grow through a layer-by-layer mechanism. The distribution of bonds within both slices building these layers is such that the electrical dipole moment components, orthogonal to the 010 plane, are symmetry related: thus, their surface profiles are non-polar and do not need to be reconstructed. Then, the different surface profiles show the corresponding specific surface energy values: γ_(010)a = 432 erg cm⁻² for the slice d^a₀₂₀ and γ_(010)b = 965 erg cm⁻² for the slice d^b₀₂₀, respectively. The difference between the γ values is so striking that only the d^a₀₂₀ slice should surely belong to the profile of the equilibrium shape of the crystal.^12,16,17 It is neither superfluous nor academic to spend a few words to explain our choice of outlining the difference between the terminations of d^a₀₂₀ and d^b₀₂₀ slices; as a matter of fact, it is the first time that somebody distinguishes the different interfaces that {010}_G can offer to different surrounding growth media. This is of particular importance when the external phase of gypsum is a crystal (like calcite) with which an adsorbed epitaxy could occur: hence, the experiments proving the correctness of the Hartman–Perdok approach have been validated by our recent discovery. Actually, it has been proved in our lab, both experimentally and theoretically, that mono-layered growth spirals could spread on the {010} form of gypsum (Fig. 3). Gypsum spiral layers with a thickness of 1/4 × d₀₁₀ and 3/4 × d₀₁₀ have been very seldom measured by AFM during the growth of the {010} form of gypsum in pure aqueous solution; these steps could be generated by partial screw dislocations outcropping on the {010} surface.¹⁸

Fig. 3 A comparison between the thicknesses of the layers which can appear on the surfaces (blue color) of (10.4)_C and (orange color) (010)_G. It can be clearly seen that five elementary periods of (10.4)_C, 5 × d_10.4 = 15.215 Å, are equal in height to the single period of (010)_G, d₀₁₀ = 15.15 Å, with a linear misfit of −0.43%.

As we did for calcite, we calculated for gypsum as well the ECE values for the main PBCs we found within its {010} form: 0.422, 0.409 and 0.370 (erg per ion × 10¹⁰), for the <001>, <100> and <101> PBCs, respectively.

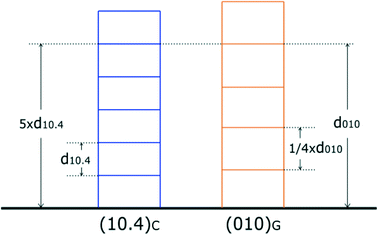
In this regard, it is of strategic value to take into account the comparison between the growth layer thicknesses of the substrate and deposit. Both forms, {10.4}_C and {010}_G, have a strong F character and hence can grow layer by layer (2D-mechanism, spiral growth, or both). As shown in Fig. 3, one could observe that during the chemical process (growth–dissolution–growth…), layers of gypsum of partial or entire thickness d₀₁₀ can be incorporated in the calcite crystal, since the quasi-perfect coincidence between the thickness of calcite (5 × d_10.4 = 15.215 Å) and that of gypsum (d₀₁₀ = 15.15 Å) is easily reached when the thickness of dissolving calcite is equal to that of obtained gypsum. In other words, anomalous mixed crystals¹⁹ can be perfectly obtained at this interface. At the risk of repeating ourselves, the primary condition that regulates the heterogeneous (10.4)_C/(010)_G epitaxy is the peculiar coincidence^20,21 among the most compact elementary layers of the two crystal phases, as outlined in Fig. 3.

It almost seems to be done on purpose: the perfect agreement (absorption) between the cleavage surface of the rhombohedral CaCO₃ and the basic pinacoid of the monoclinic CaSO₄·2H₂O allows an exchange of 2D layers of cleaving calcite (acidic rain, for instance) with 2D layers of gypsum to be made (entering the calcite substrate as an altering deposit). The 2D coincidence lattices that we will examine later on (Table 1), occurring at the (10.4)_C/(010)_G interface, witness only for the 2D ad-sorption of gypsum on calcite cleaved surface. However, the simultaneous occurrence of adsorption and absorption at the same interface is the proof of the intimate chemical–reticular connection of the same weathering event, which naturally occurs and is reproducible in the laboratory.

Table 1 2D lattice-coincidences between {10.4}_C and the deposit {010}_G. Only rankings of 1a and 1b are here represented because both have their [101]_G sides parallel to the main [481̄] and [4̄41] equivalent sides of the cleaved {10.4}_C substrate. Obliquity indicates the angular misfit between the corresponding vectors of the substrate and deposit

Ranking	{10.4}C lattice vectors (Å)	{010}G lattice vectors (Å)	Maximum linear and area misfit (Δ%)	Total obliquity (°)	Notes
	−1/3 × [481̄] = 12.85	2 × [101] = 12.987	+1.66
	1/3 × [41̄1̄] = 9.516	[10 1̄] = 9.941	+4.46
1a	121.292 (3×)	128.339 (4×)	+5.81	1.12°	Coherent linear misfits
	1/3 × [4̄41] = 12.85	2 × [101] = 12.987	+1.07
	−5 × [010] = 24.948	−[104] = 23.223	−7.43
1b	202.153 (5×)	192.486 (6×)	−5.02	0.47°	[104]G//[010]C
					Opposite linear misfits

---

Towards the end of this paragraph, we needed to use terms such as: adsorption, absorption and anomalous mixed crystals, to describe the mutual crystallographic relations in the epi-couple (10.4)_C/(010)_G. We intend here to point out that these terms do not belong to the specific pair we just illustrated, but are usually used every time an interface is generated between two crystalline species. In this case:

i) Adsorption occurs when the m layers of the depositing phase (dep) m × d^dep_h′k′l′ remain unrelated to that which functions as a substrate (sub) n × d^sub_hkl, owing to the incommensurability of the elementary layers of the two phases, m × d^dep_h′k′l′ ≠ n × d^sub_hkl. A screw dislocation, outcropping at the interface, can quite randomly generate a partial mixed layer of substrate/deposit, but it will only be able to do so in its area of pertinence. For the remaining surface, the two structures will continue to operate independently. Usually, single deposited twins can be generated.

ii) Absorption occurs, in contrast, when the depositing phase m × d^dep_h′k′l′ is strictly related to the substrate n × d^sub_hkl, since the following relation is satisfied: m × d^dep_h′k′l′ = n × d^sub_hkl. Here, n and m are the layers of one structure fit into the other perfectly: a mixed crystal generates and a screw dislocation interesting the two substances, mutually overwhelms them, everywhere. As a consequence, interlaced spirals revealing periodic polysynthetic twins (PPTs) and/or polytypes are obtained.

iii) As concerns the “anomalous mixed crystals”, it is that particular phenomenon whereby the absorption occurs only for one or more growth sectors of the same mixed crystal. It is not accidental that, in fact, the epitaxy between the two crystal phases (A and B) occurs only for several forms of A on other forms of B.

Some spectacular and didactic laboratory examples of the three items described above have been recently illustrated and published.¹⁹

4. 2D-coincidence lattices between gypsum {010} and calcite {10.4}

Booth et al.,²² first observed a spectacular parallel alignment of gypsum single crystals nucleated and grown on the cleavage (10.4) face of calcite and outlined that the dominant face in contact with calcite is the (010)_G. From the analysis of the 3D structures of calcite and gypsum, they also found that both structures reveal parallel rows of cations and anions. The cation–cation spacing in each case is 4.99 Å, suggesting that the overgrowth of the 010 gypsum planes on top of the calcite cleavage plane is favorable in that rows of anions and cations can “match up” (epitaxial overgrowth). As mentioned in the Introduction, Ruiz-Agudo et al.^1,2 improved the as-mentioned results and found a probable 2D-epitaxy, starting from the observation that the [001] direction of gypsum {010} is parallel to the [4̄41] edge of the calcite cleavage rhombohedron {10.4}, the misfit between the length of the two vectors being ∼1.0%. More recently,²⁰ such findings were confirmed since single crystals and twins of gypsum were observed in the [001] direction aligned to both the equivalent [4̄41] and [481̄] edges ruling the cleavage rhombohedron.

Starting from these findings and our considerations on calcite and gypsum PBCs, we are led to overturn the criteria for determining the coincidences in three dimensions for the two crystals A (deposit) and B (substrate) making an epitaxy:

i) First of all, one has to decide if A can absorb into B, even partially;

ii) Secondly, one has to investigate if at the contact interface, the PBCs of A can match with the PBCs of B, in order to state the physical–chemical conditions of the A/B epitaxy;

iii) Finally, one has to find if 2D-coincidence lattices can be obtained at the same A/B interface. These three items form the basis of the Hartman–Perdok theory,⁶ in which the geometry and energy have been intimately connected.

A supplementary consideration should be made, when absorption occurs, as shown in Fig. 3: one has to face two different contact interfaces, according to whether the epi-contact occurs with the gypsum termination at 1/4 or 3/4 × d₀₁₀, for instance. In such cases, only the calculation of the specific adhesion energy can solve correctly the problem; but this will be the purpose of a forthcoming paper.

Once the surface profiles of the calcite and gypsum slices (in contact with the vacuum) have been determined, we have to search for the 2D-coincidence cells that could arise when the respective lattice planes are superimposed. In Tables 1 and 2, all the coincidences we found are summarized. The main sides [4̄41] and [481̄] of cleaved calcite (substrate) are drawn in yellow colour; 2D-cells belonging to gypsum crystals (deposit–parent) are blue; the 2D-coincidence cells necessarily obtained on the substrate through the reflection due to the glide c plane inherent to the calcite {10.4} form have been drawn in red colour; the unavoidable and resulting “twinned forms” have been located in the upper part of each figure.

Table 2 2D lattice-coincidences between {10.4}_C and the deposit {010}_G. Only rankings of 2a and 2b have been here represented because both have their [001]_G sides parallel to the main [481̄] sides of the cleaved {10.4}_C substrate

Ranking	{10.4}C lattice vectors (Å)	{010}G lattice vectors (Å)	Maximum linear and area misfit (Δ%)	Total obliquity (°)	Notes
	1/3 × [481̄] = 12.85	−2 × [001] = 12.46	−3.16
	1/3 × [812̄] = 16.95	3 × [100] = 16.89	−0.35
2a	202.15 (5×)	192.55 (6×)	−4.99	1.86°	Coherent linear misfits
	1/3 × [481̄] = 12.85	2 × [001] = 12.46	−3.13
	1/3 × [47̄1̄] = 17.021	3 × [100] = 16.89	−7.75
2b	202.153 (5×)	192.55 (6×)	−4.99	4.08°	[101]G//1/3 × [421̄]C
					Coherent linear misfits

---

Before going into detail on the forthcoming tables and figures, we would like to explain to the readers the reasons why we restricted once more our 2D-LC choice with the term “obliquity”; in other words this is the shortening of the concept “angular misfit calculated within every 2D-LC, that means the angular misfit measured between the corresponding vectors of the substrate and deposit”. We adopted a maximum of 3–4° of the obliquity value, for the sake of practice: first, because a higher obliquity propagates the linear misfits between 2D-LCs; second, because the calculation of the interfacial adhesion energy becomes meaningless when 2D-LCs rapidly diverge. This second reason is strictly correlated to the first one, especially when the 2D-LC linear misfits are “coherent” and not “opposite”. It is therefore clear why we wanted to add the further restriction of “maximum area misfit” and of the coherence or linear opposition of leading vectors.

4.1. A comparison among the 2D-coincidence lattices (2D-CC)

At first glance, what is most impressive is that from the most important lattice coincidences (Tables 1 and 2), only the [101] and [001] directions of gypsum should be assumed parallel to the leading directions of calcite, whereas the [100] is not. Other minor gypsum directions are reported in Table S1 (ESI†) and ref. 21.

For [101]_G//[481̄]_C or [4̄41]_C: (i) the smallest 2D-CC (ranking 1a) has multiplicity (3×) with respect to calcite and (4×) with respect to gypsum; moreover, its obliquity is negligible (1.12°). Their linear misfits are coherent and the corresponding percent area misfit (Δ_area% = 5.81) reaches a sensible limit of the epitaxy constraints. Thus, one should consider this supercell for the epitaxy, but we cannot recommend it for future calculation of the (10.4)_C/(010)_G specific interfacial energy. (ii) A better choice is the 2D-CC: (ranking 1b). Multiplicity is (5×) and (6×) with respect to calcite and gypsum, respectively; the obliquity is very low (<1°) and the area misfit is near 5%.

For [001]_G//[481̄]_C, cases 2a and 2b simply describe that the same gypsum embryo can nucleate on cleaved calcite with its [001] side parallel to the same [481̄] direction of calcite, but with its other [100] side differently oriented. The resulting twinned individuals generated by the glide plane c are thus different. Perhaps this is the time to draw attention to a new fact: here we are not dealing with twins who are grown in a free space, as they should nucleate in a bulky solution. Here, we consider a well-defined crystalline substrate (calcite {10.4}) that imposes the epitaxy rules to another crystal (gypsum {010}). Gypsum can be formed following the as-found 2D-CC rules but, once the nuclei are formed, they propagate on the free calcite surface, meeting only in a predefined way and hence giving rise to “unexpected contact or penetration twins”. Classic gypsum twin laws have already been deeply explored and are known all over the world.^15,20,23,24

Once our cases (1a and 1b and 2a and 2b) have been selected, based on the gypsum orientation with respect to its substrate and on the minimum area of their 2D-CC (Table 1, 1a and b), we have to investigate how the calcite substrate influences the topological distribution of gypsum twins generated on it. Cases 1a and 2a give rise to “anonymous twins” where the angles among the directions shown in Fig. 4a and 5a are not of particular interest.

Fig. 4 Drawings in (a) and (b) correspond to items 1a and 1b, respectively, in Table 1. In both cases, the [101]_G direction of the nucleating {010} embryo is parallel to the main sides of the substrate, the cleaved {10.4} rhombohedron of calcite. (a) It is worth noting that the calcite/gypsum angle of 104° practically coincides with the theoretical one (101.84°) made by the equivalent [4̄41] and [481̄] edges of cleaved {10.4} calcite. (b) The angle between the two symmetry-equivalent [101]_G directions is 80.31°.

Fig. 5 Drawings in (a) and (b) correspond to items 2a and 2b, respectively, in Table 2. In these cases, the [001]_G direction of the nucleating {010} embryo is parallel to the main sides of the substrate, as in the cases just illustrated. It is worth noting again that the red individuals are necessarily obtained from the blue ones (parent) through the symmetry c operation (glide mirror plane) inherent to the calcite substrate.

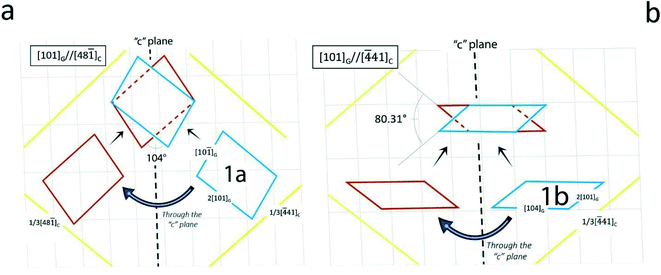
However, the drawings in Fig. 4b and 5b are worthy of the utmost attention: in Fig. 6 the spreading of the parent gypsum embryo on calcite and its c-symmetry related twinned one can produce either a contact or a penetration twin. In both cases, the [104] gypsum direction becomes the “twin axis” for this new kind of 2D epi-twin of gypsum {010} on calcite {10.4}.

Fig. 6 It is nothing else than an improved version of Fig. 4b. Parent and twinned gypsum individuals met on the common substrate giving rise either to a contact or a penetration twin. The twin axis is the [104] direction of gypsum and superposes to the important [010] PBC of calcite. It is a new 2D-twin, imposed by the substrate, and does not correspond to an important twin law of the free gypsum crystal. In fact, the calculated angle reaches 2ε = 80.31°.

Moreover, the most surprising case of the twin can be expressed in Fig. 7(bottom right). Let's imagine that a 2D gypsum nucleus was made with the two sides [100]_G and [101]_G, which is perfectly legitimate: a perfect twin is reproduced, like those obtained from free floating solutions. And so, we could prove that also the 2D-epitaxy the can generate 3D-gypsum twin laws, in addition to those obtained in large numbers²⁴ through our 2D-CC and recently listed in the ESI† of innovative works in nature.^20,21

Fig. 7 The last example in Table 2 represents an unexpected epi-twin. From the epi-embryo 2b, contact and penetration twins are generated with a common [101]_G twin axis which is parallel to the important PBC [421̄] of calcite {10.4} (upper right). The angle (104°) calculated and drawn in this figure is nothing else than the measured one (105.2°) in the historical penetration twin of gypsum having [101]_G as the twin axis.

5. Conclusions

We started from investigations on the crystallographic control in the replacement of calcite with the three main calcium sulphates: gypsum, bassanite and anhydrite.^1–5 Knowing that 2D-X ray diffraction is a useful but not always complete and adequate system for this kind of study, we restricted our research to the interaction between calcite and gypsum with the aim at giving a quantitative answer to the question: what happens on the energetic plane and therefore the reticular plane at the interfaces lying between the easily cleaved {10.4} calcite and the most important form of gypsum, i.e., the layered {010} pinacoid? To be up to the challenge, we preferred to start from scratch, using both the acquired results^1–5 and the interesting experimental insights developed in our previous studies.^20,21

First, we stated if the adsorption/absorption mechanism could be set up at the epi-interface between the substrate and deposit: this was the necessary but not sufficient constraint to be respected in order to continue our research. Secondly, we analyzed the interfaces by strictly applying the Hartman–Perdok method;⁶ accordingly, the energetics of the PBCs contained in the elementary slices d_10.4 (calcite) along with d₀₄₀ and d₀₂₀ (gypsum) have been associated to their crystallographic directions within these slices. This was the only way to establish a bi-univocal correspondence between the physical-chemistry of the interfaces and their 2D-coincidence cells, having kept in mind that the gypsum [u0w] PBCs with major strength “must” be aligned along the main PBCs of the substrate: <4̄ 41>, [421] and [010] of {10.4} calcite. Thus, the 2D-CCs obtained from the superposition of suitable gypsum and calcite lattices have been listed following the order of increasing areas of their common 2D-supercells. In this way, we were able to distinguish whether the unavoidable c twinned structures at the interface were only generated by gypsum/calcite epitaxy or had a more universal character (if any), such as those long identified as contact or penetration free twins. All this has nothing to do with the generation of authentic twins that we still have to build, starting from the nuclei calculated in Tables 1 and 2 and which will be the subject of a future study. In the same way, we will deepen the as-obtained results,^20,21 using the adhesion energy calculation as a new discriminant tool to examine whether epitaxy of gypsum on calcite will occur. Furthermore, bassanite will be the new subject of an accurate Hartman–Perdok analysis that, to the best of our knowledge, has never been used, while anhydrite has already been the subject of our careful study.²⁵

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The present study has been partly funded by the project PRIN 2017 (2017L83S77) of the Italian Ministry for Education, University and Research (MIUR).

References

1. E. Ruiz-Agudo, C. V. Putnis, J. Hövelmann, P. Álvarez-Loret, A. Ibañes-Velasco and A. Putnis, Geochim. Cosmochim. Acta, 2015, 156, 75–93.
2. E. Ruiz-Agudo, P. Álvarez-Loret, A. Ibañes-Velasco and M. Ortega-Huertas, Cryst. Growth Des., 2016, 16, 4950–4959.
3. J. D. Rodriguez-Blanco, A. Jiménez and M. Prieto, Cryst. Growth Des., 2007, 7, 2756–2763.
4. E. Ruiz-Agudo, P. Álvarez-Loret, C. V. Putnis, A. B. Rodriguez-Navarro and A. Putnis, CrystEngComm, 2013, 15, 9968–9979.
5. E. Ruiz-Agudo, K. Kudlacz, C. V. Putnis, A. Putnis and C. Rodriguez-Navarro, Environ. Sci. Technol., 2013, 47, 11342–11349.
6. P. Hartman, in Crystal Growth: An Introduction, ed. P. Hartman, North-Holland, Amsterdam, 1973, pp. 367–402.
7. D. Aquilano, M. Bruno and L. Pastero, Cryst. Growth Des., 2020, 20, 2497–2507.
8. D. Aquilano, M. Calleri, E. Natoli, M. Rubbo and G. Sgualdino, Mater. Chem. Phys., 2000, 66, 159–163.
9. W. M. M. Heijnen, Neues Jahrb. Mineral., Monatsh., 1985, 8, 357–362.
10. F. R. Massaro, L. Pastero, M. Rubbo and D. Aquilano, J. Cryst. Growth, 2008, 310, 706–715.
11. H. H. Teng, P. M. Dove, C. A. Orme and J. J. de Yoreo, Science, 1998, 282, 724–727.
12. F. R. Massaro, M. Rubbo and D. Aquilano, Cryst. Growth Des., 2010, 10, 2870–2878.
13. W. F. de Jong and J. Bouman, Z. Kristallogr., 1938, 100, 275–276.
14. B. Simon and M. Bienfait, Acta Crystallogr., 1965, 19, 750–756.
15. B. Simon, Contribution à l'étude de la formation des macles de croissance, PhD, Université Aix-Marseille, 1968.
16. F. R. Massaro, M. Rubbo and D. Aquilano, Cryst. Growth Des., 2011, 11, 1607–1614.
17. J. Criado-Reyes, L. Pastero, M. Bruno, J. M. García-Ruiz, D. Aquilano and F. Otálora, Cryst. Growth Des., 2020, 20, 1526–1530.
18. L. Pastero, private communication.
19. D. Aquilano and L. Pastero, Cryst. Res. Technol., 2013, 48, 819–839.
20. L. Pastero, R. Giustetto and D. Aquilano, CrystEngComm, 2017, 19, 3649–3659.
21. R. Giustetto, L. Pastero and D. Aquilano, J. Build. Eng., 2020, 32, 101794.
22. J. Booth, Q. Hong, R. G. Compton, K. Prout and R. M. Payne, J. Colloid Interface Sci., 1997, 192, 207–214.
23. M. Rubbo, M. Bruno, F. R. Massaro and D. Aquilano, Cryst. Growth Des., 2012, 12, 264–270.
24. M. Rubbo, M. Bruno, F. R. Massaro and D. Aquilano, Cryst. Growth Des., 2012, 12, 3018–3024.
25. D. Aquilano, M. Rubbo, M. Catti, A. Pavese and P. Ugliengo, J. Cryst. Growth, 1992, 125, 519–532.

---

Footnote

† Electronic supplementary information (ESI) available: Table S1 and other 2D coincidences between substrate {10.4}_C and deposit {010}_G. See DOI: https://doi.org/10.1039/d2ce00508e

---