The pressure–temperature phase diagram of tetramorphic pyrazinamide

Abstract

The phase behaviour of drug molecules is important for the control over the desired polymorph in drug formulations, whether it is to ensure better stability or better solubility. In the case of pyrazinamide, a drug against tuberculosis, stability studies have been complicated due to the very slow transition kinetics observed in DSC measurements. Using vapour pressure measurements, in which the reluctance of phase transformation is in fact an advantage, all solid–solid phase transformation temperatures have been determined. This method has been key to map the phase behaviour of pyrazinamide. The use of high-pressure measurements with synchrotron X-ray diffraction has allowed the construction of the pressure–temperature phase diagram of the four solid phases of pyrazinamide and the liquid phase. The α form was found to be the stable form at room temperature. One striking feature of pyrazinamide is that one polymorph, the δ form, has a very large thermal expansion and extreme compressibility not found in the other three forms. This gives rise to curved solid–solid transition equilibria in the pressure–temperature phase diagram, which is not commonly observed in the pressure range of 0 to 1 GPa. Using the phase diagram, polymorph β could be obtained in its stable temperature domain.

---

1 Introduction

Understanding of the solid-state behaviour of drug molecules is important for the development of reliable oral drugs and, even if pharmaceutical research nowadays tends to favour biological strategies, a major effort is also taking place to find small organic molecules that can be used as oral drugs similar to remdesivir to help cure Covid-19 before it develops into a severe case.¹

The solid-state behaviour of pyrazinamide (PZA) has received a lot of attention, because of its four known solid phases, α, β, γ, and δ, and the fact that it has not been clear whether form α or form δ is the most stable form at room temperature.^2–12 Moreover, the phase transitions between these phases exhibit large hysteresis, making it difficult to interpret the thermodynamics behind the transition behaviour.^4,9,10,13 A consensus exists in the literature that form γ is the high-temperature form and that form α is stable at lower temperatures, probably down to room temperature, while form δ is most likely stable below room temperature.^2,9,10 It is not clear whether the β form possesses a stable domain, but it has not been considered likely.^9,10 Recently, the melting point of form α has been reported and the equilibrium temperature between α and γ has been established as low as 392 K (Table 1),² however, except for the melting temperature of γ at 462 K, which has been known for some time,^9,10 none of the other phase equilibrium temperatures between the four solid phases or between the solid phases and the liquid have been reported.

Table 1 Essential data from the alpha–gamma–liquid phase diagram of pyrazinamide (123.11 g mol⁻¹)^a

Property	Value	Unit
a The data from this table originates from ref. 2. b Estimated error, nonetheless dP/dTα→L must be larger than dP/dTγ→L (see ref. 2).
T γ→L	462.0 ± 0.5	K
ΔHγ→L	240.6 ± 1.0	J g^−1
dP/dTγ→L	3.5 ± 0.3	MPa K^−1
T α→L	457 ± 1	K
ΔHα→L	253 ± 4	J g^−1
dP/dTα→L	4.0 ± 1^b	MPa K^−1
T α→γ	392 ± 1	K
ΔHα→γ	13.2 ± 0.6	J g^−1
dP/dTα→γ	−2.7 ± 0.9	MPa K^−1

---

Considering the large hysteresis in transition temperatures for pyrazinamide samples studied by DSC (differential scanning calorimetry),^2,9,10 the high sublimation pressure of pyrazinamide^14–17 can be used to obtain information about which phase is the most stable at a given temperature, provided that the solid phase does not transform into another phase. The latter condition appears to be met for pyrazinamide because of the large hysteresis in the system, so this disadvantage in the DSC becomes an advantage for the sublimation pressure measurements.

In the current paper, the phase behaviour of all four phases will be studied and a pressure–temperature phase diagram will be proposed involving all equilibria between all known phases in the system: α, β, γ, δ, the liquid, and the vapour phase. The analysis is based on vapour pressure measurements, but also uses studies of the thermal expansion of the different phases and of compression under pressure obtained from laboratory and synchrotron X-ray diffraction, respectively. In Table 1, previously published data on the phase behaviour of forms α and γ in relation to each other and the liquid can be found.²

The vapor (V) pressures of forms α and γ reported previously are mentioned here as they will be used in the phase diagram calculations:²

α → V : ln P = −94 945(1024)/RT + 32.3(4) (1)

γ → V : ln P = −92 192(2024)/RT + 31.5(7) (2)

where P is the pressure in pascal and T is the temperature in kelvin. R is the gas constant 8.3145 J mol⁻¹ K⁻¹. The values between parentheses are the standard deviations given with the rank of the preceding digit.

Similarly, the specific volumes of forms α and γ have been published previously leading to the following equations:²

v_α = 0.6624(7) + 6.8(6) × 10⁻⁵ T + 8.44(1.06) × 10⁻⁸ T² (3)

v_γ = 0.6520(7) + 4.8(5) × 10⁻⁵ T + 1.22(9) × 10⁻⁷ T² (4)

with the volume v in cm³ g⁻¹ and the temperature in kelvin.

2 Materials and methods

2.1. Pyrazinamide

Pyrazinamide was purchased from Sigma-Aldrich (France) and its purity was ≥97.5% (GC) before recrystallisation. The commercial form was determined to be polymorph α by X-ray diffraction. Single crystals of α were obtained by sublimation.² The γ form was obtained by heating the commercial sample above the α–γ transition temperature (see introduction). δ was obtained by cooling crystallization from 1,4-dioxane⁵ and β by cooling crystallization from chloroform. The procedure was as follows: solutions of pyrazinamide ranging in concentration from 5.8 to 8.3 mg g⁻¹ were prepared in chloroform. The solutions were heated up to 328 K and once clear allowed to cool down at different cooling rates (1 to 4.5 K min⁻¹) until crystallisation using a Crystalline apparatus (Technobis, NL). Once the phase diagram had been established form β has also been obtained by crystallisation from acetonitrile at 252 K; solutions were prepared at room temperature and filtered and subsequently set at 252 K for crystallisation. The crystals were separated from the solution by filtration at 252 K. Powder X-ray diffraction (PXRD) and DSC were used to verify the obtained polymorphs (see Fig. S1a† for the patterns of the used samples). For further details see also the thesis of K. Li.¹⁸

2.2. Vapor pressure measurement

Vapor pressure measurements have been carried out isothermally in the temperature range of 293.15–383.15 K with a DVS Vacuum apparatus from Surface Measurement Systems, London, U.K., using a Knudsen cell whose orifice had a diameter of 440 μm and using benzoic acid (purity >99%) vapour pressure as a standard.

2.3. Differential scanning calorimetry

The thermal behaviour of pyrazinamide was studied with a DSC 214 from Netzsch, which uses an inert atmosphere of nitrogen gas. The melting points and enthalpies of mercury (T_fus = 234.28 K), indium (T_fus = 429.75 K), tin (T_fus = 505.05 K), bismuth (T_fus = 544.15 K) and zinc (T_fus = 692.65 K) have been used to calibrate the DSC. Heating rates from 1 K min⁻¹ up to 10 K min⁻¹ have been used. The amount of material was in the order of 4–10 mg, which was weighed in with a microbalance with a precision of 0.01 mg.

2.4. High-resolution powder X-ray diffraction

High-resolution powder X-ray diffraction (PXRD) was used to determine the specific volumes of the β and δ forms as a function of the temperature. Powdered specimens were placed in capillaries of 0.5 mm diameter. The measurements were carried out with a vertically mounted INEL cylindrical position sensitive detector (CPS-120) and by using the Debye–Scherrer geometry. A monochromatic Cu-Kα₁ radiation (1.54056 Å) source applying an asymmetrically focusing incident-beam curved germanium monochromator was used and diffraction intensities were registered over a 2θ range from 3.0° to 112° with a step size of 0.029°. The temperature was controlled by a liquid nitrogen 700 series Cryostream Cooler (Oxford Cryosystems). The PXRD patterns were refined by FullProf software to calculate the lattice parameters and the specific volumes.^19,20

2.5. Synchrotron powder X-ray diffraction

The specific volumes of α, β, γ, and δ as a function of pressure have been obtained at a number of temperatures from PXRD data measured on the high-pressure diffraction beamline PSICHE at the synchrotron SOLEIL (Gif sur Yvette, France) which used a focused monochromatic mode and a CdTe2M Dectris pixel detector. High pressure was controlled with a membrane driven diamond anvil cell with an upper pressure limit of 2 GPa. Silicon oil was used as the pressure transmitting medium. NaCl was used as an internal reference for the pressure. The wavelength used for the experiments was 0.4859 Å. Pawley fits and Rietveld refinements were carried out using TOPAS-Academic V4.1 software in combination with DASH and Mercury of the CCDC.

2.6. Calculation of the isobaric thermal expansion and the isothermal compression tensors

The principal isobaric thermal expansion and isothermal compression tensors of the four polymorphs of pyrazinamide have been calculated with the PASCal program. The computational details have been presented in the literature.²¹

3 Results

3.1. Vapour pressures of forms β and δ

The vapour pressure data obtained for forms β and δ have been compiled in Table S1 in the ESI.† Fits of the data were obtained using a linearized exponential expression. For forms β and δ this has resulted in:

β → V : ln P = −101 858(1896)/RT + 35.2(8) (5)

δ → V : ln P = −100 592(727)/RT + 34.6(6) (6)

where P is the pressure in pascal and T is the temperature in kelvin. R is the gas constant 8.3145 J mol⁻¹ K⁻¹. The absolute values of the numerators in eqn (5) and (6) represent the enthalpies of sublimation (ΔH_sub) in units of RT.

3.2. Transition enthalpies of the observed transitions involving phases β and δ

The transitions observed in the DSC of form δ have been compiled in Table S2 in the ESI† (and Fig. S1c and d). Considering that form δ could be obtained as a pure polymorph and that the final melting transition could be confirmed as that of form γ (through its melting temperature), the enthalpy of transformation between δ and γ can be determined with relative certainty as it constitutes the entire solid–solid transition enthalpy between the initial form loaded in the capsule and the final form (liquid). The average enthalpy, ΔH_δ→γ, has been found to be 16.5 ± 1.1 J g⁻¹. As phase purity at the time of observation (partial conversions on heating into other forms, particularly α) is not guaranteed, the lower observed values in the data series in Table S2† may be considered underestimates which are pulling down the average, so the real enthalpy may be closer to 18 J g⁻¹, i.e. the maximum values observed for the δ to γ transition.

The δ to α transition is harder to interpret (Fig. S1c and d†), because several transitions may occur at the same time and therefore the identity of the final state of the sample cannot be established with certainty. In the DSC measurements, an enthalpy difference, ΔH_δ→α, of 5.7 ± 0.4 J g⁻¹ is found, but the low error is more a sign of the few data points than of a high precision. Taking the data from Table 1 on the enthalpy of the α to γ transition, ΔH_α→γ, of 13.2 J g⁻¹ and the difference between δ and γ discussed above, the enthalpy difference between α and δ should be between 3.3 and 4.8 J g⁻¹. Thus, the value of 5.7 J g⁻¹ obtained from integrating the observed DSC peak is most likely too high, probably due to partial transformation from δ into γ.

The DSC observations of form β (Fig. S1e†) are possibly even more complicated as demonstrated by the X-ray diffraction data of β as a function of the temperature in Fig. S1b in the ESI,† where both α and δ are observed on heating β. In the DSC curves, often a double peak is observed with an onset at around 370 K. The second peak cannot always be separated and has an onset at about 390 K, when separation is possible. Considering that melting of these β samples invariably occurs at the melting point of form γ (see Table S3†), it can again be surmised that, neglecting the heat capacity, all solid–solid transformations from the initial β form up to the melting point together must reflect the enthalpy difference between β and γ, ΔH_β→γ. Taking the average of the total enthalpy for the solid–solid transitions, 17.9 ± 2.3 J g⁻¹ is found. Taking only the enthalpies obtained using single crystals of β, as the phase purity of the powder cannot be guaranteed, leads to 19.1 ± 2.6 J g⁻¹. Because the double peak observed for the solid–solid transitions involving β cannot be properly separated, the enthalpy difference between α and γ of 13.2 J g⁻¹ can be used leading to an enthalpy difference between α and β, ΔH_β→α, of 4.7–5.9 J g⁻¹. This also suggests that the enthalpy difference between β and δ, ΔH_β→δ, is in the order of −0.1 to 2.6 J g⁻¹ with β in all likelihood possessing a higher enthalpy content than form δ.

3.3. Specific volumes of the four solid phases of pyrazinamide as a function of temperature

The refinement results of all diffraction experiments as a function of the temperature have been provided in Tables S4 to S7† for forms α, β, γ, and δ respectively and the specific volumes are presented in Fig. 1. Moreover, those of forms α and γ have already been published previously (see eqn (3) and (4) in the introduction). Using the data from Table S5† for the β form, one finds the following expression for its specific volume as a function of the temperature (125–320 K):

v_β = 0.6537(6) + 1.074(23) × 10⁻⁴ T, (7)

and using the data from Table S7,† the specific volume of form δ can be described as follows:

v_δ = 0.6519(9) + 5.6(8) × 10⁻⁵ T + 1.44(16) × 10⁻⁷ T². (8)

In both cases, the volume is given in cm³ g⁻¹ and the temperature in kelvin.

Fig. 1 The specific volumes of forms α (red circles), β (green triangles), γ (black squares), and δ (blue diamonds) as a function of temperature under ordinary pressure.

As can be seen in Fig. 1, where the specific volumes of all four solid phases are presented, form γ has the smallest specific volume and thus the highest density, form α has the largest specific volume and δ has the largest thermal expansion (see also Table S15†).

3.4. Specific volumes of the four phases as a function of pressure at several temperatures

In Table S8 in the ESI† the unit-cell parameters and the unit-cell volumes of the α form have been compiled as a function of pressure for four different temperatures including room temperature (295 K). The unit-cell volumes of β can be found in Table S9† for three different temperatures. Those of γ have been compiled in Table S10 for four temperatures and those of δ can be found in Table S11† for three temperatures. The resulting graphs of the specific volume as a function of the pressure for the different temperatures are presented in Fig. S2–S5 in the ESI† for forms α, β, γ, and δ, respectively. In Fig. 2, the specific volumes of the four forms are presented as a function of pressure at room temperature. It can be seen that the lowest specific volume under pressure at room temperature is now observed for form δ, whereas under ordinary pressure, the data in Fig. 1, form γ possesses the lowest specific volume. Although the data for γ have not been measured all the way down to zero pressure (Fig. 2), it can be calculated that the two curves for γ and δ intersect each other at around 60 MPa. The scatter over the specific volume of β is caused by several issues: the sample did not contain pure phase β, but it was mixed with γ giving rise to various extra peaks to fit and making it a challenge to correctly assign the shifting peaks and interpret their displacements. Moreover, there may have been preferred orientation, making indexing challenging at times.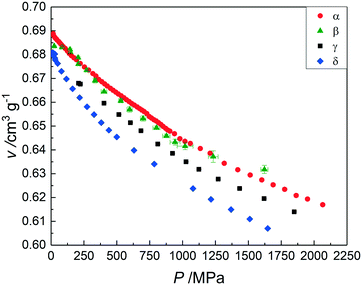

Fig. 2 The specific volumes of forms α (red circles), β (green triangles), γ (black squares), and δ (blue diamonds) as a function of pressure at room temperature.

3.5. Analysis of the isobaric thermal expansion

The isobaric thermal expansion tensors of the four polymorphs have been calculated using PASCal²¹ and the results are presented in Tables S12 to S15 in the ESI† for forms α, β, γ, and δ respectively, whereas a graphic presentation of the tensors can be found in Fig. S10.† Finally, in Fig. S6 to S9,† the relative change of the principal axes is presented, in which uniaxial negative thermal expansion can be observed for α and β, whereas γ and δ both possess a hard direction that does not change (or shows minimal contraction) on heating.

3.6. Isothermal compression

The isothermal compression tensor, also obtained with PASCal²¹ has led to tensors of which the details are presented in Tables S16 to S19 in the ESI.† A graphic depiction of the compression tensor for each of the polymorphs can be found in Fig. S15,† whereas more graphic information, the relative change of the principal axes of the tensors and the change of the tensor coefficient K as a function of pressure, can be found for each polymorph in Fig. S11 to S14.† For the four forms compression is ‘positive’ in all directions. For α, K₃ appears even to increase with pressure as can be seen in Fig. S11 in the ESI.† The hard directions observed in the thermal expansion do exhibit less compression, however.

3.7. Thermal expansion and compression in relation to the crystal structures

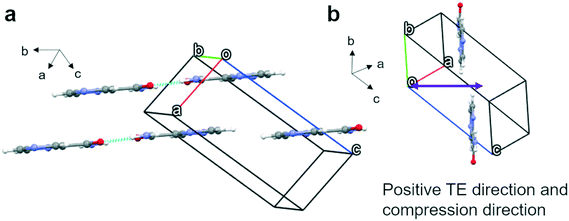
Polymorph α crystallizes in the P2₁/n space group with four molecules in the unit cell (Fig. 3) and only one molecule in the asymmetric unit. These four molecules form four equivalent 2D bands with neighbouring molecules outside the unit cell through strong N–H⋯O and N–H⋯N hydrogen bonds. Parallel 2D bands are linked through pi–pi stacking and they make a 43° angle with a second set of bands (Fig. 3b). The two sets of angled bands are linked together through weak hydrogen bonds involving C–H⋯N in the aromatic rings. The maximum expansion (TE) and compression direction (see Fig. S10a and S15a† respectively), which coincide, have been indicated in Fig. 3a and are more or less parallel to the a axis. The negative thermal expansion (NTE) direction, parallel to the b axis, is indicated in Fig. 3b and coincides with limited compression with increasing pressure. It can be concluded that the expansion and compression are related to the angles between the two planes formed by the two sets of 2D bands; i.e. expansion in the a axis direction leads to compression in the b axis direction (see Fig. 3b).

Fig. 3 Packing in form α and the maximum expansion and compression direction (purple arrow in panel a). NTE, black arrow, is indicated in panel b. Panel c shows the bands of hydrogen bonded molecules parallel to the diagonals of the a and b axes as shown in panel b. The unit-cell axes have been indicated by a, b, and c.

Polymorph β possesses a P2₁/c space group with four molecules per unit cell (Fig. 4) and one molecule in the asymmetric unit. The four molecules form four “classic” dimers through two strong N–H⋯O hydrogen bonds with molecules outside the unit cell graph set R²₂(8). However, a C¹₁(4) chain along the c-axis of slightly longer hydrogen bonds with the same groups links these dimers together. Along the c-axis a corrugated chain of dimers exists; however, due to the angles of the dimers these corrugated chains are interconnected through their C¹₁(4) interactions in the direction of the b-axis forming a dimer-wide slab along the bc plane with the thickness of the a-axis. In the direction of the a-axis, these slabs are interconnected through weaker hydrogen bonds C–H⋯N in the aromatic ring. The maximum positive and negative expansion directions and compression direction are indicated in Fig. 4. The maximum thermal expansion and compression possess different directions, however, overall, the thermal expansion and the compression tensors remain very similar as can be seen in Fig. S10 and S15,† respectively. The positive thermal expansion is linked to the complex way that the corrugated bands in the direction of the c-axis are interconnected in the direction of the b-axis, apparently providing sufficient room for expansion along the b-axis. The compression (Fig. 4b) may be related to a mix between a displacement of the complex hydrogen network in the slabs and the weaker interactions between the slabs, while the negative thermal expansion is most likely a slight contraction due to the expansion along the b-axis and an expansion along the inverted compression direction a⃑ − c⃑.

Fig. 4 Unit cell of form β with (a) the maximum thermal expansion (red arrow) and (b) the compression (blue arrow) and the negative thermal expansion (NTE, black arrow) directions. Many other hydrogen bonds are present that do not link the molecules within the unit cell; a figure with an overview can be found in the ESI† Fig. S17.

Polymorph γ crystallizes in the non-centrosymmetric space group Pc with two molecules in the unit cell and one in the asymmetric unit. The molecules form linear chains through strong N–H⋯N hydrogen bonds with graph set C¹₁(6). The two molecules in the unit cell are connected by a slightly longer hydrogen bond between N–H⋯O of their amide moieties. In addition, they possess a weak hydrogen bond C–H⋯N between their respective pyrazine rings. The planes through the rings of the two molecules in the unit cell form an angle between each other of 47.6°. Due to this angle the molecules form corrugated sheets parallel to the ac plane of the unit cell. These different sheets are interconnected through multiple weak hydrogen bonds involving the C–H and N from the pyrazine rings and the O of the amide moiety. The maximum expansion and compression directions are along the b axis as shown in Fig. 5, which is the overall direction of the complex network of multiple weaker hydrogen bond interactions involving the C–H in the rings.

Fig. 5 Unit cell of form γ and the maximum thermal expansion and compression directions (purple arrow).

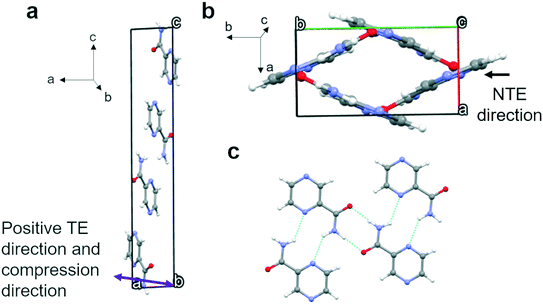
Polymorph δ crystallizes in the triclinic system with the space group P1̄ with two molecules per unit cell and one in the asymmetric unit. A cyclic dimer, graph set R²₂(8), exists in form δ through the strong hydrogen bonds N–H⋯O of the amide moiety. Slightly longer hydrogen bonds exist between the oxygen and N–H of another pyrazinamide molecule, creating quite flat 2D bands of dimers as shown from the side in Fig. 6a. These 2D bands are reinforced by weaker hydrogen bonds between the C–H and the N in the respective pyrazine rings. The bands are parallel to the b-axis and are approximately found on the (101) plane. These slabs of dimers that are bound through strong hydrogen bonds form extended sheets through weaker hydrogen bonds, C–H⋯N, in the pyrazine rings of different slabs that lie in the same plane. These sheets are extremely flat. Short contacts involving mainly aromatic interactions (pi–pi interactions) keep the different sheets together in the a⃑ + c⃑ direction. The maximum expansion and compression directions are roughly perpendicular to the slabs/layers as indicated in Fig. 6b. As can be seen in Fig. S10d and S15d and also in Tables S15 and S19,† these layers are in fact extremely sensitive to compression and expansion.

Fig. 6 (a) Unit cell of form δ and (b) the maximum thermal expansion and compression directions (purple arrow).

4 Discussion

4.1. The equilibrium temperatures between the four solids and their melting points

One of the major issues in determining the phase behaviour of pyrazinamide is the hysteresis of the metastable phases at increased temperature at constant pressure; for example, the transitions of form δ into α or γ are not recorded before 385 and 400 K, respectively (see Table S2 in the ESI†).¹⁰ Using the vapour pressures, these equilibrium temperatures can be estimated by calculating the temperature and pressure of intersection of the different vapour pressure curves and the results are given in Table 2. The low and high temperature phases of a given equilibrium temperature can be deduced from the lowest sublimation pressure for each phase at each side of the equilibrium temperature.

Table 2 Equilibrium temperatures, pressures, and enthalpy differences (T/K; P/Pa; ΔH/J g⁻¹) between pyrazinamide phases obtained by vapour pressure and DSC^a,b

LT↓\HT→	δ	α	γ	L
a The phase on the left is the low temperature phase (LT), while the phase on top is the high temperature (HT) phase for each equilibrium. b Stable equilibria are indicated in italic bold.
β	254; 2 × 10 ^−6 ; 1	290; 8 × 10^−4; 5	314; 2 × 10^−2; 18	414; 275; 260
δ	—	299; 3 × 10 ^−3 ; 3	326; 8 × 10^−2; 17	423; 403; 258
α		—	399; 41; 13.2	456; 1459; 253
γ			—	462.0; 1816; 240.6

---

Because the sublimation curve for the γ form is known (eqn (2)) and the melting quantities of γ are known too (Table 1), an estimate for the vapour pressure of the liquid phase can be obtained:

L → V : ln P = −62 571/RT + 23.8 (9)

With this expression, the melting points of the different solids can be estimated, where necessary (Table 2).

The results obtained with the vapour pressure are not perfect, as the intersection temperatures suffer a high uncertainty due to the fact that the vapour pressure equations have similar slopes; a slight shift of those lines can have large effects on the calculated transition temperature. Therefore, temperatures listed in Table 2 may not fully coincide with the equilibrium temperatures, but they are certainly the best estimates, as long as better data are not available. Preference will be given to directly measured quantities if available.

With Table 2, the temperature domains for the stability of the different forms can be determined. It is known that the γ form has the highest melting temperature at 462 K and thus γ is the high temperature polymorph. The highest equilibrium temperature involving γ and another solid is that with α at 399 K (although direct experiments indicate that this temperature is 392 K) (see also Table 1).² The subsequent highest equilibrium temperature involving α is that with δ at 299 K and thus below this temperature δ is the most stable form. Moreover, the β–δ equilibrium temperature can be observed at 254 K, indicating that below this temperature β is the most stable form.

In particular the β–δ and the δ–α equilibrium temperatures will need to be considered with care. Unfortunately, in the lowest temperature region where vapour pressure data of α and δ have been obtained (Table S1†), α is still the most stable form, but it is also clear that the vapour pressure values are very close around room temperature and that it is therefore very likely that the equilibrium temperature between α and δ is located between 0 and 30 °C; their vapor pressures and thus their Gibbs free energies are virtually the same in this temperature domain.

The equilibrium temperature between β and δ contains considerably more uncertainty due to the necessary extrapolations of the vapour pressure expressions to obtain this temperature, however, the fact that the vapour pressure of δ approaches that of β indicates that the β form appears to possess a stable domain at low temperature, something that had not been expected previously.^9,10 Moreover, the proximity of the respective transitions of δ and β with the other phases, not more than 10 degrees apart, indicates that their Gibbs free energies are not far apart. To verify the stability of β at low temperatures, crystallisation experiments in acetonitrile have been carried out at 252 K, which is below the predicted phase equilibrium temperature between β and δ. The β form crystallised with possibly a small δ impurity (peak at 16.415° 2θ, see ESI† Fig. S16).

The fact that all polymorphs of pyrazinamide possess a stable temperature domain, as can be concluded from the vapor pressure data, is corroborated by the enthalpies that have been obtained by DSC (Table 2). While the enthalpy between β and δ is about +1 J g⁻¹ and for δ to α about +3 J g⁻¹, the enthalpy difference between α and γ was measured to be +13.2 J g⁻¹ and the melting of γ involves +240.6 J g⁻¹. This series clearly indicates that all transitions with increasing temperature are endothermic, which is necessary for fully enantiotropic systems. The enthalpy data in Table 2 are rounded values based on the averages discussed in section 3.2.

An energy plot as a function of the temperature based on the results discussed above can be found in Fig. 7.

Fig. 7 An energy-temperature diagram for the four solid phases and the liquid of pyrazinamide valid at solid-vapor equilibrium (liquid–vapor in the case of the melt). The temperatures are based on the vapour pressure results. The transition temperature between δ and α may therefore not be accurate and could be as low as 273 K; other values will shift accordingly in order to maintain the relative stability ranking.

4.2. Slopes in the pressure–temperature phase diagram based on the Clapeyron equation

Having established the equilibrium temperatures in the previous section and using the enthalpies obtained by DSC and the specific volumes as a function of the temperature, the slopes of the equilibria in the pressure–temperature phase diagrams can be calculated using the Clapeyron equation:where P is the pressure, T is the temperature, and ΔS, Δv, and ΔH, respectively, are the entropy, volume, and enthalpy differences between the two phases in equilibrium. Using the values in Table 2 and eqn (3), (4), (7), and (8), the entropy difference, ΔS, the volume difference, Δv, and the slope dP/dT have been calculated (the volume of the liquid as a function of the temperature has been estimated with eqn (15) in ref. 2). The results are presented in Table 3.

Table 3 Entropy differences, specific volume differences and slopes (ΔS/J g⁻¹ K⁻¹; Δv/cm³ g⁻¹; dP/dT/MPa K⁻¹) for the phase equilibria between pyrazinamide phases^a,b

HT→\LT↓	δ	α	γ	L
a The phase on the left is the low temperature phase (LT), while the phase on top is the high temperature (HT) phase for each equilibrium. b Stable equilibria are indicated in italic bold.
β	0.0062; −0.0054; −1.15	0.0233; 0.0044; 5.26	0.0570; −0.0082; −6.94	0.578; 0.097; 5.94
δ	—	0.0171; 0.0087; 1.97	0.0508; −0.0049; −10.3	0.572; 0.104; 5.50
α		—	0.0337; −0.0124; −2.72	0.554; 0.133; 4.17
γ			—	0.521; 0.148; 3.53

---

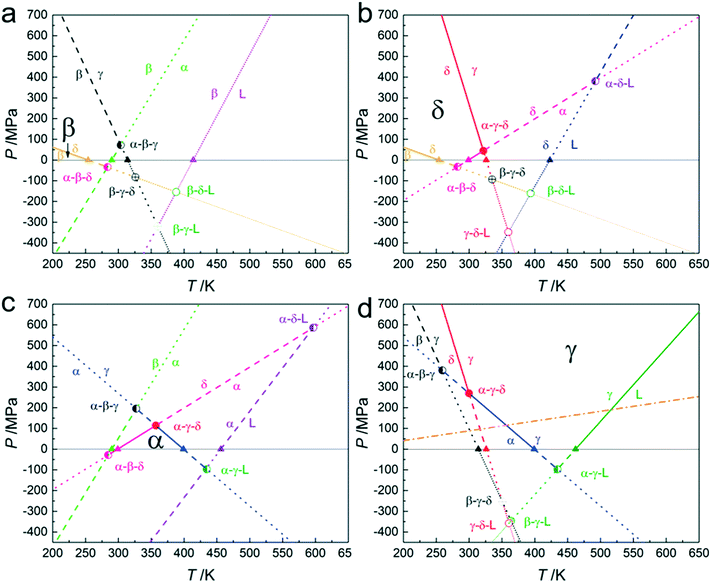
4.3. Pressure–temperature stability domains for each of the solid phases

Using the temperatures obtained by the vapour pressure measurements and listed in Table 2 in combination with the slopes that have been listed in Table 3, the stability domains of each solid phase and their stability relation with the other phases are presented in separate phase diagrams in Fig. 8. For each of the solid phases, these diagrams demonstrate their stability domains and under these approximate conditions the phase becomes metastable relative to one of the other condensed phases. It means for example that form β existing under a pressure of 300 MPa at room temperature can transform into form δ or form γ, but not into form α. This can be concluded from the fact that stable β at low temperature, when it is brought to 300 MPa at room temperature, will have passed the β–δ equilibrium and at higher pressure and temperature the β–γ equilibrium, but not the β–α equilibrium. It can also be seen that δ and γ are the main high-pressure forms, with δ taking the low temperature domain and γ the high-temperature domain, whereas the stability domains of forms α and β are limited to low pressure. From this point of view, it is even almost surprising to see that form α happens to be the best polymorph for formulation (considered from a physical stability point of view) as it is only stable in a temperature range between roughly 0 and 110 °C and for pressures up to 100 MPa.

Fig. 8 The phase equilibria for each solid phase of pyrazinamide and their pressure–temperature stability domain: (a) form β, (b) form δ, (c) form α, and (d) form γ. Solid lines: stable phase equilibria, triangles: triple points representing an equilibrium with the vapour phase, circles: triple points representing an equilibrium between three condensed phases with solid circles representing stable equilibria, half solid circles metastable equilibria and open circles even lower Gibbs energy rankings. The orange dash-dotted line indicates the approximate pressure and temperature conditions under which the difference in specific volume between forms γ and δ equals zero (see also text).

4.4. The compression of δ and its consequences for the pressure–temperature phase diagram

There is one issue with the proposed phase diagrams in Fig. 8 and that is that the dP/dT slopes have been determined with data obtained under ordinary conditions, i.e., without any applied pressure. It is also clear from the current measurements under pressure that form δ exhibits a large thermal expansion and a large compressibility, to such an extent that under pressure, the specific volume of the δ form becomes smaller than that of form γ. In other words, the specific volume inequality between the two polymorphs (Δ_δ→γv) changes in sign from negative to positive, which would imply a change from a negative slope to a positive one for the δ–γ phase equilibrium under pressure. Moreover, it would lead to a minimum temperature in the equilibrium curve and at higher temperatures two pressures will represent the equilibrium with δ being the low-pressure form at lower pressures and at higher pressures δ being the high-pressure form, while the γ form will be stable at intermediate pressures.

The full consequences in relation to phase theory are not entirely clear. The change in the sign means that for a given pressure and temperature Δv equals zero, indicated by the orange dash-dot line in Fig. 8d. Below this line γ possesses the highest density, and above this line, δ possesses the highest density. It appears therefore that δ is the ultimate high-pressure form in the system. Nonetheless, the orange dash-dot line is not the phase equilibrium, which will be lying higher as next to the volume difference, also the enthalpy difference is of importance. At the point where the δ–γ phase equilibrium intersects the orange dash-dot line, the slope of the equilibrium is expected to be infinity (see eqn (10)) and then bend back to a positive finite slope.

In the case of gases and liquids, Δv = 0 implies that both phases are the same and therefore that also ΔS = 0. This in turn implies a critical point, as the two phases have become indistinguishable. In the present case, there is no trace of a phase transition, neither in the δ form nor in the γ form. Both phases have a clear own identity based on different space groups and unit-cell dimensions. It can therefore not be stated that the two phases are one and the same and due to their different molecular configurations, the energetic and entropic states must be different too. This would imply that for these two intersecting densities in the solid state, with two distinct crystallographic phases, no critical point exists.

As the situation is caused by the extreme compressibility of the δ form, the effect on its Gibbs energy surface may have the form of a ripple perpendicular to the pressure axis, which in the current situation with four phases, happens to intersect with the Gibbs energy surface of the γ form, causing the extremely curved phase equilibrium. At the same time, the compressibility of δ must also have an effect on the equilibrium curves of δ–α and β–δ. δ has already a smaller volume with respect to α and thus Δ_δ→αv > 0, which remains the case when δ is compressed. Due to the faster compression of δ over α however, Δ_δ→αv will increase and thus the slope of the equilibrium curve will be more curved and decrease, lowering the position of the triple point α–δ–L. A similar effect is expected for the β–δ equilibrium for which the inequality Δ_β→δv < 0 is expected to become more negative and thus the equilibrium will be curved towards lower negative slopes. It should be clear however that in both cases the sign of the volume inequality remains the same, so the expected behaviour, obtained by extrapolation, remains the same, from a topological point of view.

4.5. The pressure–temperature phase diagram of tetramorphic pyrazinamide

The phase behaviour of pyrazinamide has long been a difficult issue, in particular because of the strong hysteresis in the phase transitions to more stable phases. It is clear that by measuring the vapour pressure a better understanding about the phase behaviour of pyrazinamide can be obtained resulting in the phase diagram in Fig. 9. Nonetheless, uncertainties in the transition temperatures between β and δ and δ and α still exist as they have not been directly measured. It is however very likely that the equilibrium temperature of the α–δ phase equilibrium is found between 0 and 25 °C considering the current vapour pressure data.

Fig. 9 The pressure–temperature phase diagram of pyrazinamide and its five condensed phases. The extreme compressibility of the δ form results in the curvature of the red line (δ–γ equilibrium). The uncertainty over the position of the δ–α equilibrium (0–25 °C or 273–298 K) has been used to achieve consistency within this phase diagram. Solid lines are stable phase equilibria and dashed lines are metastable.

In fact, it is likely that the α–δ phase equilibrium is found at about 0 °C. Considering Fig. 9 with the calculated α–δ phase equilibrium (Tables 2 and 3) leads to an intersection with the α–γ phase equilibrium (blue line) somewhat above 350 K. However, taking into account that this is a supposed α–δ–γ triple point, the δ–γ phase equilibrium must intersect here too, whereas the latter equilibrium (red line) actually has a negative slope at 0 MPa and does not approach the intersection between α–δ and α–γ. Nonetheless, the observation that the δ–γ phase equilibrium must be curved solves part of this problem, bringing its intersection with the α–γ phase equilibrium closer to the α–δ and α–γ intersection. Using the uncertainty in the α–δ equilibrium temperature and shifting this equilibrium down to 0 °C allows for a consistent phase diagram of the stable phases with a properly defined α–δ–γ triple point at around 340 K and 150 MPa (Fig. 9). In this adjustment only the α–δ transition temperature at 0 MPa was changed, but other adjustments to the slopes of the α–δ and δ–γ phase equilibria may also be necessary. The slope of the α–γ equilibrium was obtained by measurement and its uncertainty is considered smaller than that of the other two equilibria.

5 Conclusions

A pressure–temperature phase diagram, Fig. 9, has been obtained for the four polymorphs of pyrazinamide consistent with the data presented in this paper, although some uncertainties remain about the precise phase equilibrium temperatures at lower temperature. The diagram immediately resulted in the achievement of almost pure form β as it could be crystallised in the temperature domain where it is stable.

Another result that can be derived from the current phase diagram is that the observation by Tan et al.⁸ that form β is obtained by putting form γ under pressure is probably a misinterpretation of their Raman data, as the γ form gets stabilized with respect to β under pressure. If anything, transformation of γ into δ is much more likely under pressure, if γ changes at all.

Comparing the volumetric thermal expansion of the polymorphs, it can be observed that form δ possesses a larger thermal expansion than the other polymorphs. This result is most likely due to its layered structure in accordance with observations by Saraswatula et al.²² Form δ also exhibits the largest compression most likely due to the weakly interacting layers. Interestingly, forms α and β, which both exhibit negative thermal expansion to some level, are only stable at low pressures.

The most stable form at room temperature appears to be form α on a par with form δ. At room temperature both solids must have the same solubility, as their vapour pressure is virtually the same. Preference should probably be given to developing α as it will be the most stable form at temperatures above room temperature, where the risk of phase transformation is larger than at temperatures below room temperature, where δ will be more stable. Considering the studies carried out under pressure, tabletting will not affect a phase change of the formulated form, as no phase transformation has been observed under pressure.

The extreme curvature in the δ–γ equilibrium curve (see curved partially dashed red line in Fig. 9) leading to a minimum in the temperature for the curve represents a challenge for the topological approach to establish phase diagrams using only ordinary pressure data and the Clapeyron equation (eqn (10)). From a large number of experiments, it is clear that most solid–solid equilibria are straight lines,^23,24 so the current finding appears to be a rare case. In addition, it is already clear from the ordinary pressure measurements that the thermal expansion of δ was much larger than that of the other forms, which may therefore function as an indication that also under the influence of pressure large changes can occur.

Funding

This work was supported by the Region Normandie (PhD scholarship), an Erasmus grant for three months for research in the Grup de Caracterització de Materials in Barcelona, synchrotron Soleil (beamline Psiché) proposal 20180552, Spanish AEI/MCIN through Project PID2020-112975GB-I00, and AGAUR DGU Project No. 2017SGR-42.

Author contributions

Kangli Li: investigation, formal analysis, writing – original draft, funding acquisition; Gabin Gbabode, formal analysis, supervision, writing – original draft and review, funding acquisition; Marine Vergé-Depré: investigation; Benoit Robert: investigation, formal analysis, supervision; Maria Barrio: investigation, formal analysis, supervision, writing – review; Jean-Paul Itié: methodology, resources; Josep-Lluis Tamarit: supervision, funding acquisition, writing – review; Ivo B. Rietveld: conceptualization, funding acquisition, supervision, formal analysis, writing – original draft and review & editing.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors thank R. Céolin for discussions about phase theory. K. Li thanks the Region Normandie for a PhD scholarship and the ERASMUS organization for a travel grant for three months of research in Barcelona.

References

1. B. Halford, Chem. Eng. News, 2021, 24, 28–31.
2. K. Li, G. Gbabode, M. Barrio, J.-L. Tamarit, M. Vergé-Depré, B. Robert and I. B. Rietveld, Int. J. Pharm., 2020, 580, 119230.
3. M. M. H. Smets, G. Baaklini, A. Tijink, L. Sweers, C. H. F. Vossen, C. Brandel, H. Meekes, H. M. Cuppen and G. Coquerel, Cryst. Growth Des., 2018, 18, 1109–1116.
4. G. Baaklini, V. Dupray and G. Coquerel, Int. J. Pharm., 2015, 479, 163–170.
5. M. W. Hermanto, A. Yeoh, B. Soh, P. S. Chow and R. B. H. Tan, Org. Process Res. Dev., 2015, 19, 1987–1996.
6. Y.-H. Luo, Q.-L. Liu, L.-Y. Yang, W. Wang, Y. Ling and B.-W. Sun, Res. Chem. Intermed., 2015, 41, 7059–7072.
7. N. Wahlberg, P. Ciochon, V. Petricek and A. O. Madsen, Cryst. Growth Des., 2013, 14, 381–388.
8. X. Tan, K. Wang, S. Li, H. Yuan, T. Yan, J. Liu, K. Yang, B. Liu, G. Zou and B. Zou, J. Phys. Chem. B, 2012, 116, 14441–14450.
9. S. Cherukuvada, R. Thakuria and A. Nangia, Cryst. Growth Des., 2010, 10, 3931–3941.
10. R. A. E. Castro, T. M. R. Maria, A. O. L. Evora, J. C. Feiteira, M. R. Silva, A. M. Beja, J. Canotilho and M. E. S. Eusebio, Cryst. Growth Des., 2010, 10, 274–282.
11. A. Borba, M. Albrecht, A. Gomez-Zavaglia, M. A. Suhm and R. Fausto, J. Phys. Chem. A, 2010, 114, 151–161.
12. Y. Takaki, Y. Sasada and T. Watanabe, Acta Crystallogr., 1960, 13, 693–702.
13. S. Gad, Int. J. Pharm. Pharm. Sci., 2015, 7, 581_584.
14. H. Negoro, Takamine Kenkyusho Nenpo, 1959, 11, 66–75.
15. H. Negoro, T. Miki and S. Ueda, Yakugaku Zasshi, 1960, 80, 665–669.
16. M. D. M. C. Ribeiro da Silva, M. S. Miranda, C. M. V. Vaz, M. A. R. Matos and W. E. Acree, J. Chem. Thermodyn., 2005, 37, 49–53.
17. S. Blokhina, A. Sharapova, M. Ol'khovich, T. Volkova and G. Perlovich, J. Therm. Anal. Calorim., 2015, 120, 1053–1060.
18. K. Li, The interactions between pyrazinamide and urea derivatives and their role in the stabilization of the γ form of pyrazinamide, PhD Research thesis, University of Rouen Normandie, 2021.
19. J. Rodriguez-Carvajal, T. Roisnel and J. Gonzales-Platas, Full-Prof suite version 2005, Laboratoire Léon Brillouin, CEA-CNRS, CEN Saclay, France, 2005.
20. J. Rodriguez-Carvajal, Phys. B, 1993, 192, 55–69.
21. M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329.
22. V. G. Saraswatula, S. Bhattacharya and B. K. Saha, New J. Chem., 2015, 39, 3345–3348.
23. I. Gana, M. Barrio, B. Do, J.-L. Tamarit, R. Céolin and I. B. Rietveld, Int. J. Pharm., 2013, 456, 480–488.
24. S. Toscani, R. Céolin, L. Ter Minassian, M. Barrio, N. Veglio, J.-L. Tamarit, D. Louër and I. B. Rietveld, Int. J. Pharm., 2016, 497, 96–105.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ce00484d

‡ Current address: Zhejiang Shaoxing Institute of Tianjin University, 312 300, Shaoxing, Zhejiang, China.

---