Crystal growth and structure of a high temperature polymorph of Sr₂TiO₄ with tetrahedral Ti-coordination, and transition to the Ruddlesden–Popper tetragonal phase

Abstract

Single crystals of transition metal oxides forming the Ruddlesden–Popper series are necessary for complete studies of their often exciting physical properties. In the strontium titanate family, crystal growth of all compounds apart from SrTiO₃ has been elusive so far. We have successfully grown crystals of the high-temperature polymorph of Sr₂TiO₄, by using a floating-zone melt growth followed by a rapid cooling procedure. We report the crystal structure of the new modification, which is isostructural to the orthorhombic Sr₂VO₄ and Sr₂CrO₄. This structure hosts an uncommon layered sub-lattice of TiO₄ tetrahedra and transforms into the tetragonal low-temperature polymorph via a complex reconstructive transition. The transformation mechanism between the two phases was studied and explains the reasons for the unsuccessful growth of tetragonal Sr₂TiO₄. The orthorhombic Sr₂TiO₄ is an insulator, with a band gap of 3.9 eV. It has a large (≈40) dielectric constant, but despite its polar structure does not show any signatures of a ferroelectric order.

---

1 Introduction

Transition-metal oxides which crystallize in the Ruddlesden–Popper (RP) series A_n+1B_nO_3n+1 (A = alkaline or rare earth, B = transition metal element) are characterized by a periodic stacking of perovskite-like blocks (ABO₃)_n and rock-salt layers (AO). These compounds often exhibit exciting properties, which can be tuned by controlling the arrangement of the perovskite blocks. In the case of Sr_n+1Ti_nO_3n+1 series, the end compound SrTiO₃ (corresponding to n = ∞) is one of the most intriguing and studied perovskite materials: its insulating ground state can be switched to conducting and even superconducting upon doping, pressure or strain, and its peculiar quantum paraelectric state can be driven to ferroelectricity.¹ The other end member, Sr₂TiO₄ with n = 1, which can be viewed as the 2D limit of the series, is isostructural with the high temperature superconductor (La,Sr)₂CuO₄, the unconventional superconductor Sr₂RuO₄ and the spin–orbital ordered compounds Sr₂IrO₄ and Sr₂VO₄. Long known for its thermoelectric properties,² it has been recently brought to the fore also for its photocatalytic performance.³ Moreover, Sr₂TiO₄ can serve as a platform for exploring the 2D electron liquid on the SrTiO₃ perovskite interfaces.⁴

While SrTiO₃ is widely studied, the growth process can be controlled to a high degree of perfection⁵ and crystals are even commercially available, the other members of the series are much less known and poorly investigated, mainly because of the difficulties to prepare high quality samples. Epitaxial thin films of the first members (n < 5) have been successfully grown and the dielectric constant was measured as a function of n,⁶ but bulk crystals of these compounds have never been reported.

According to the SrO–TiO₂ phase diagram assessed by Cocco & Massazza sixty years ago,⁷ only SrTiO₃ and Sr₂TiO₄ are in equilibrium with a high-temperature (>1800 °C) melt, but the latter melts incongruently and undergoes a destructive structural transition upon cooling, frustrating any attempts to grow crystals. There are no studies of this phase transition and the structure of the high temperature phase is unknown, except for an unindexed powder pattern given by Dryś & Trzebiatowski.⁸

We have stabilized the high-temperature phase of Sr₂TiO₄ in a bulk single crystal form by quenching of the floating molten zone, and we have investigated its crystal structure. In this modification titanium atoms occupy sites with tetrahedral oxygen coordination, which is rather unusual among the titanates and might be potentially interesting for applications, as other oxides with tetrahedral coordination of titanium are already known for their photocatalytic activity.⁹ In this article, we report the crystal structure of the new high-temperature polymorph. We present the studies of its stability with X-ray diffraction, differential thermal analysis and Raman spectroscopy, we discuss the mechanism driving the transition and report the dielectric constant and the optical gap of this new compound.

2 Experimental

2.1 Sample preparation

Crystals of Sr₂TiO₄ were grown from the melt by the floating zone method. Two polycrystalline rods (the “feed” and the “seed”) were prepared from stoichiometric amounts of SrCO₃ (99.99% Cerac) and TiO₂ (99.99%, Alpha Aesar), calcined at 1200 °C for 12 hours, ground, pressed into a pellet and annealed for 12 hours at 1100 °C. After verifying that the only phase present was Sr₂TiO₄, the powder was pressed in a rubber tube with 7 mm diameter at 300 MPa in ethanol, then sintered at 1400 °C in flowing O₂ gas. Straight, dense and homogenous precursor rods were obtained (see Fig. 1(a)). They were mounted in a two-mirror furnace (Image Furnace by Cyberstar®), equipped with two either 1000 W or 2000 W halogen lamps. The feed rod was suspended on a Pt wire and rotated at 12 rpm, the seed rod was mounted on a fixed Al₂O₃ holder and counterrotated at 12 rpm. The travelling velocity was 1–1.5 mm h⁻¹. The molten zone could be observed with a camera (Fig. 1(b)) and the crystal grew with visible facets. After 5–10 hours of growth, the lamps were turned off abruptly and at the same time the seed rod was pulled downwards at the fastest velocity of 90 mm min⁻¹. Given the estimated temperature gradient at the liquid–solid interface of ∼30–40 °C mm⁻¹, this corresponds to a cooling rate faster than 300 °C min⁻¹.

Fig. 1 Growth of single crystals of the high-temperature phase of Sr₂TiO₄. a) The feed and seed rod after quenching. b) A picture of the molten zone with a facet forming on the left side of the grown crystal. c) Closer view of the top-end of the crystallized rod. d) Single crystals after polishing.

2.2 X-ray diffraction

Single crystal diffraction data were collected on a Rigaku Supernova diffractometer equipped with an ATLAS CCD camera using Mo Kα radiation at T = 100 K. The structure was solved by SHELXT¹⁰ and the refinement was carried away in SHELXL¹¹ using full-matrix least square method on F².

The Laue diffraction was measured in back-reflection, using tungsten radiation and a two-dimensional gas detector (MultiWire®Laboratories). The powder diffraction at room temperature was measured with a PANalytical Aeris diffractometer equipped with a PIXcel 1D Medipix detector and a Cu X-ray tube operating at 40 kV and 7.5 mA in the range of 15 to 130° (2θ).

High temperature diffraction patterns were collected with a PANalytical X'Pert PRO diffractometer equipped with a conventional X-ray tube (Co Kα radiation, 40 kV, 30 mA, line focus) and a multichannel detector X'Celerator with an anti-scatter shield. Scans were collected in a 2θ range of 15 to 70° (step of 0.0334° and 50 s counting per step yielding a scan of ca. 11 minutes). Samples were heated in the high temperature chamber (HTK 16, Anton Paar). For each experiment a small amount of powder was placed on the Pt sample holder, which served as the heating element at the same time. Two experiments were performed. In one, the X-ray pattern was measured at different temperatures between 25 and 800 °C, with the heating ramp of 5 °C min⁻¹ (the temperature was kept constant during each measurement). In the second experiment the sample was heated rapidly (60 °C min⁻¹) to 550 °C and repeated scans were collected during five hours.

The diffraction patterns were analysed using the Profex/BGMN software.¹² For the refinement of the lattice parameters at elevated temperature the specimen displacement and the zero shift of the detector were fixed at zero value, which resulted in the refinement in which the lattice parameter of platinum at all temperatures was very close to the reported values.¹³

2.3 Differential thermal analysis

DTA measurements were performed in a Setaram TAG-24 thermal analyser using Al₂O₃ as reference in flowing synthetic air (O₂ 21%, Ar balance). Powder samples of ca 50 mg were put in a Al₂O₃ crucible without a lid and heated at a rate of 5 °C min⁻¹.

2.4 Spectroscopy

Raman spectroscopy down to 50 K was performed on the Horiba LabRAM HR Evolution spectrometer with an excitation wavelength of 532 nm and the resolution of 0.5 cm⁻¹. The polished (100)-oriented single crystal samples were glued onto the copper plate of a He flow cryostat with silver paint. The actual temperature of the sample was estimated from the intensity ratio between the Stokes and anti-Stokes lines using the Reffit software.¹⁴

The static dielectric constant was determined from the complex impedance of a parallel plate capacitor with an Agilent E4980A LCR meter over a range of 100 Hz to 1 MHz using excitation fields between 1 and 7 V cm⁻¹. Gold electrodes were evaporated on both sides of the polished sample with a thickness of 750 μm and contacted with silver paint.

The complex dielectric constant was also measured on polished samples mounted on Cu cones in a range from 4000 to 40 000 cm⁻¹ with a J. A. Woollam variable angle spectroscopic ellipsometer.

3 Results and discussion

3.1 Crystal growth

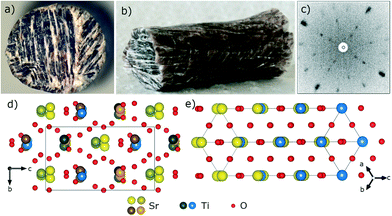
The as-grown top-end of the crystallized rod is shown in Fig. 1(c). Due to the vertical temperature profile of the mirror furnace and the need to quench the crystals from high temperature (the phase transition to the low temperature polymorph is supposed to take place at ∼1550 °C), the length of the crystallized rod is limited to ∼8–10 mm. The part of the rod which contains the high-temperature phase is transparent, with yellow to purple hue. It can be cut with a wire saw and polished to obtain flat slabs of a thickness of 500–900 μm. The very fast cooling rate, the mechanical cut and polishing induce several cracks in the crystals, and individual crack-free grains are obtained with an area of ∼1 mm² (Fig. 1(d)).

The Laue pattern measured on the top part of the crystalline rod in the growth direction is shown in Fig. 2(b): a slightly distorted six-fold pattern indicates a pseudo-hexagonal axis along the growth direction.

Fig. 2 X-ray diffraction of the orthorhombic Sr₂TiO₄. a) Unwarped single crystal data for the 0kl reflections. b) The Laue diffraction collected in the growth direction. c) Refinement of the powder diffraction data collected at room temperature.

A small quantity of the crystals was ground into powder for further characterization. The X-ray powder diffraction pattern (Fig. 2(c)) agrees very well in the range between 30 and 60° (2θ, Cu) with the 10 most prominent diffraction lines proposed by Dryś et al. for the high-temperature structural modification of Sr₂TiO₄.⁸

3.2 Crystal structure

Crystallographic data are reported in Table 1. Unwarped single crystal data are shown in Fig. 2(a).

Table 1 Crystallographic data and structure refinement for high-temperature phase of Sr₂TiO₄

a The structure is non-centrosymmetric achiral, the inversion domains are related by a pure rotation.
Empirical formula	O4Sr2Ti
Formula weight	287.14
Temperature/K	100.0(1)
Crystal system, space group	Orthorhombic, Pna21
a, b, c (Å)	14.2901(5), 5.87288(18), 10.0872(3)
α, β, γ (°)	90, 90, 90
Volume (Å^3)	846.56(5)
Z	8
ρ calc (g cm^−3)	4.506
μ (mm^−1)	26.829
F(000)	1040.0
Crystal size (mm^3)	0.306 × 0.151 × 0.115
Radiation	Mo Kα (λ = 0.71073 Å)
2θ range for data collection (°)	5.702 to 57.338
Index ranges	−18 ≤ h ≤ 18, −7 ≤ k ≤ 7, −12 ≤ l ≤ 12
Reflections collected	12 336
Independent reflections	1989 [Rint = 0.0545, Rσ = 0.0355]
Data/restraints/parameters	1989/1/128
Goodness-of-fit on F^2	1.080
Final R indexes [I ≥ 2σ(I)]	R 1 = 0.0287, wR2 = 0.0659
Final R indexes [all data]	R 1 = 0.0308, wR2 = 0.0671
Largest diff. peak/hole (e Å^−3)	0.84/−0.94
Flack parameter^a	0.492(15)

---

High-temperature Sr₂TiO₄ crystallizes with the orthorhombic symmetry and is isostructural with the orthorhombic forms of Sr₂VO₄ and Sr₂CrO₄.†

These compounds belong to the β-K₂SO₄ structure type, which itself can be described as a distortion of the hexagonal α-K₂SO₄. In the orthorhombic Sr₂TiO₄, the 6₃ screw axis, which runs along the a direction in the hexagonal archetype, is lost due to a slight deformation of the unit cell. The ratio between the b and c lattice parameters is no longer , as would be expected for a hexagonal lattice described by a centered orthorhombic cell, see Fig. 3(d).

Fig. 3 Crystal structure of the high-temperature modification of Sr₂TiO₄. a) Projection along the c-axis with visible alternation of cationic and anionic planes. b) Pseudohexagonal symmetry along the a-axis. c) Projection along the b-axis. The structure contains two symmetrically non-equivalent Ti- and four non-equivalent Sr-atoms. d) Schematic view of two possible descriptions of the hexagonal lattice.

Nevertheless, the pseudohexagonal symmetry along a is conserved to some extent, because the c-parameter 10.0872 Å is rather close to . Both the Laue pattern in Fig. 2(b) and the unwarped single crystal data in Fig. 2(a) collected along the a-axis show this pseudohexagonal symmetry, which is also visible in the arrangement of the atoms in the crystal structure, see Fig. 3(b).

Perpendicular to the b axis, there are planes formed only by oxygen atoms, alternating with planes containing cations and oxygen atoms, as can be seen in Fig. 3 (upper panels).

Compared to the α-K₂SO₄ structural type, the unit cell of the orthorhombic Sr₂TiO₄ is doubled along the a axis and the two subcells along a are slightly misaligned, so that the cationic/anionic planes are “pleated”, and the titanium atoms are not all symmetrically equivalent anymore, (Fig. 3, left panels).

It is important to note that in these structures the transition metal occupies the tetrahedral cavities, which is a very rare case among the titanates, the other example being only Ba₂TiO₄. Sr₂TiO₄ is, however, not isostructural with Ba₂TiO₄, in which the structure is closer to the hexagonal archetype, less distorted, the cationic/anionic planes are less pleated, but the unit cell is tripled along the pseudohexagonal axis.

Two types of symmetrically independent TiO₄⁻⁴ tetrahedra are present (central Ti atoms drawn blue and green in Fig. 3), which are considerably distorted. These distortions can be evaluated quantitatively, based on the continuous symmetry measures approach.¹⁵ The S-values and bond valences,^16,17 of few relevant structures are listed in Table 2.

Table 2 S-Parameter and bond valence sum of the coordination tetrahedra for several related structures

	α-K2SO4	α-Ba2TiO4-1	α-Ba2TiO4-2	α-Ba2TiO4-3	β-Ba2TiO4
Valence	6.41	4.14	3.96	3.95	4.09
S(Td)	0.006	0.091	0.190	0.066	0.068

---

	Sr2TiO4-1	Sr2TiO4-2	Sr2CrO4-1	Sr2CrO4-2	Sr2VO4-1	Sr2VO4-2
Valence	4.09	3.95	3.98	3.62	4.49	3.77
S(Td)	0.279	1.14	0.201	1.184	0.790	1.692

---

The continuous symmetry measure represents the smallest deformation of the polyhedron necessary to obtain the required symmetry. It is independent on size, allowing a comparison of tetrahedra with different central atoms. The tetrahedron in the α-K₂SO₄, which can serve as an approximation for the hypothetical hexagonal superstructure, is very regular, with the S(T_d) value of 0.006 and with a rather dense structure, manifested by the higher valence of the sulphur than usual. When the structure loses the hexagonal symmetry, the S(T_d) value is first increased by one order of magnitude in the Ba₂TiO₄ structures, then by another order of magnitude as barium is substituted by smaller strontium. Two symmetrically non-equivalent tetrahedra in the strontium compounds are very distinct, with different bond valence and a different degree of distortion. The tetrahedra geometries are very similar in the chromium and the vanadium compound, but while in the Sr₂TiO₄ the valence of titanium is close to 4, in the Sr₂CrO₄ it is slightly lower and in the Sr₂VO₄ it is slightly higher, as can be expected from their preferred valence of 3 and 5, respectively.

It should be noted that single crystals of the structural prototype Sr₂CrO₄ have been grown by melting in a Pt crucible by Wilhelmi in 1966.¹⁸ Single crystals of the Sr₂VO₄, which is a magnetic spin dimer system,¹⁹ have been grown recently by the optical floating zone method, substituted by up to 20% of Ti.²⁰

3.3 Raman spectroscopy

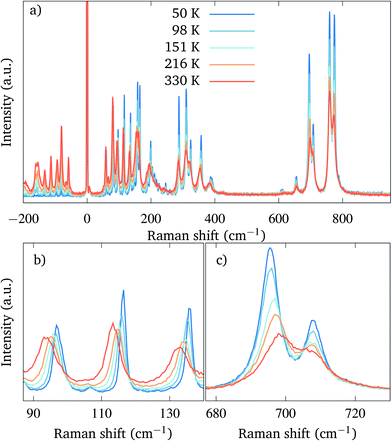
Raman spectroscopy was performed on the polished crystals of the orthorhombic Sr₂TiO₄. The spectra measured at different temperatures are plotted in Fig. 4. The lowest temperature we were able to reach due to the absorption of the laser by our material was 50 K.

Fig. 4 Temperature evolution of the Raman spectra of the high-temperature phase of Sr₂TiO₄. a) The spectra in the whole recorded range. b) Softening of lower-energy modes with increasing temperature. c) Hardening of the mode at 695 cm⁻¹.

The spectra contain a large number of overlapping peaks, as can be expected from the rather low symmetry and the large unit cell,‡ in contrast to the tetragonal modification, in which only four modes are active.²²

Upon cooling down from room temperature, we do not observe any structural transition and the orthorhombic phase remains stable down to 50 K. (Fig. 4(a)). With a decreasing temperature, the Raman peaks become narrower and better separated, and we observe an overall increase of the intensity and a general hardening of the modes. Interestingly, however, the hardening of the modes with cooling is not uniform and one particular mode even follows the opposite trend (Fig. 4(b) and (c)).

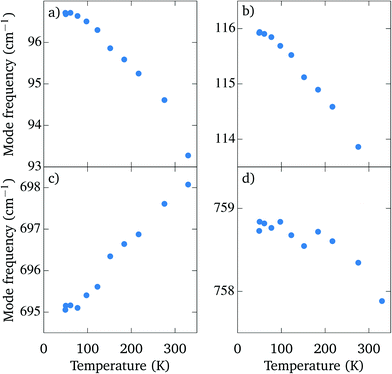
In Fig. 5 the frequencies of selected modes with high intensity are plotted as a function of the temperature. The hardening is strongest for the mode at 93 cm⁻¹ (Fig. 5(a)), whose frequency increases by 3.5 cm⁻¹ upon cooling. On the other hand, there is a mode at 695 cm⁻¹ (Fig. 5(c)) which softens by 3 cm⁻¹ when the crystals are cooled down to 50 K. A similar positive temperature dependence of the modes was described in the tetragonal modification of Sr₂TiO₄, where it was attributed to an anharmonic contribution to the potential well.²² Lastly, there is also a mode of high intensity at 758 cm⁻¹ (Fig. 5(d)), whose frequency changes by less than 1 cm⁻¹ when the temperature is lowered.

Fig. 5 Temperature evolution of selected Raman modes of the high-temperature phase of Sr₂TiO₄.

We did not find any report of Raman spectroscopy performed on the orthorhombic Sr₂VO₄ and Sr₂CrO₄. For this reason we prepared a ceramic sample of Sr₂CrO₄ which contained impurities of Sr₃Cr₂O₈ (6.2 wt%) and SrO (3.1 wt%). The Raman microscope made it possible to focus on a single Sr₂CrO₄ grain of ca. 8 μm diameter. The recorded room temperature spectrum (not shown here) resembles the one of the isostructural titanate, with frequencies of most of the modes shifted to lower values with respect to the titanate.

3.4 Differential thermal analysis

Differential thermal analysis was performed on the powder sample of the tetragonal RP Sr₂TiO₄, which was later used for preparation of the seed rods. The data can be seen in Fig. 6(a). They show an endothermic peak upon heating with an onset at 1578 ± 2 °C and a visible hysteresis, as the exothermic peak upon cooling has an onset at 1530 ± 5 °C. These peaks correspond to the phase transition between the low-temperature tetragonal and high-temperature orthorhombic phase, which was estimated to occur by different authors at 1600 °C (ref. 8) and 1525 ± 20 °C.⁷ Although no other transitions are visible in Fig. 6(a), traces of Sr₃Ti₂O₇ can be identified in the diffractogram collected on the powder sample after performing the DTA. This is in agreement with the phase diagrams in ref. 7 and 8 which suggest a peritectoid decomposition of Sr₃Ti₂O₇ into Sr₂TiO₄ and SrTiO₃ at ≈1600 °C.

Fig. 6 Differential thermal analysis of Sr₂TiO₄. a) The starting powder was tetragonal low temperature phase. b) The starting powder was the high-temperature orthorhombic phase.

If the orthorhombic phase, which is metastable at room temperature, is annealed at 5 °C min⁻¹, another peak appears in the DTA data, with an onset at 720 °C upon warming up, see Fig. 6(b). This peak is not present on cooldown and represents the exothermic transition to the stable tetragonal phase, which is irreversible.

3.5 High-temperature powder diffraction experiments

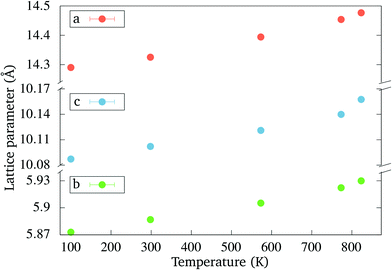
Powder diffraction was measured at several temperatures up to 800 °C. The transition occurred earlier than during the DTA experiment and at 650 °C the orthorhombic phase has completely transformed. This discrepancy is due to a different heating profile in the diffraction experiment, as compared with the DTA run. The phase transition temperature is strongly affected by kinetic factors, which results in a delay of the transition onset in the DTA experiment.

The evolution of the lattice parameters of the orthorhombic phase with temperature is plotted in Fig. 7 up to 550 °C. The lattice parameters of the tetragonal phase (not shown here) are generally in good agreement with those reported by Kawamura et al.²³

Fig. 7 Evolution of the lattice parameters of the orthorhombic phase with temperature. The errorbars are smaller than the point size. The measurement at 100 K is refined from the single crystal diffraction.

With the disappearance of the reflections from the orthorhombic phase, new lines become visible in the diffraction patterns, which are not ascribable to any known titanate. In order to verify whether these reflections belong to an intermediate phase, a small amount of the orthorhombic phase powder was annealed at 550 °C for one hour with a fast heating ramp of 20 °C min⁻¹. The sample was taken out directly of the hot furnace after one hour and was left to cool in air. In the XRD pattern of this sample (Fig. 8(a)) 7 peaks of the intermediate phase can be seen, labelled with a symbol “I”. Another powder sample of the orthorhombic phase was annealed at 850 °C for seven hours. After the long treatment all of the intermediate phase lines disappeared and in the powder pattern only the tetragonal phase is present, thus confirming that the peaks don't belong to an impurity/decomposition phase.

Fig. 8 Room temperature X-ray diffraction. a) Powder diffraction of the sample quenched after 1 hour annealing at 550 °C and of a sample annealed for 7 hours at 850 °C. The diffraction lines of the intermediate phase labelled with “I” disappear after the transformation completes. b) A 2θ scan of pristine {h00} oriented single crystal of the orthorhombic phase before annealing (red) and after annealing at different conditions. Red labels mark the reflections of the orthorhombic phase, blue labels the tetragonal phase. The reflection at 40° (2θ) belongs to the intermediate phase.

In Table 3 all diffraction lines identified as the intermediate phase are listed, in order of their intensity. The reflections could be indexed by a monoclinic cell with a space group P2, the lattice parameters of 7.3567, 3.4588, 11.780 Å and the unit cell angles of 90, 91.6271 and 90°.

Table 3 Interplanar distances of the diffraction lines belonging to the intermediate phase

Angle (° 2θ, Cu)	d (Å)	Intensity
32.19	2.778	High
46.18	1.964	Medium
25.11	3.544	Medium
39.7	2.268	Low
67.4	1.388	Low
28.16	3.166	Low
22.59	3.933	Low
25.74	3.458	Low
49.9	1.826	Low

---

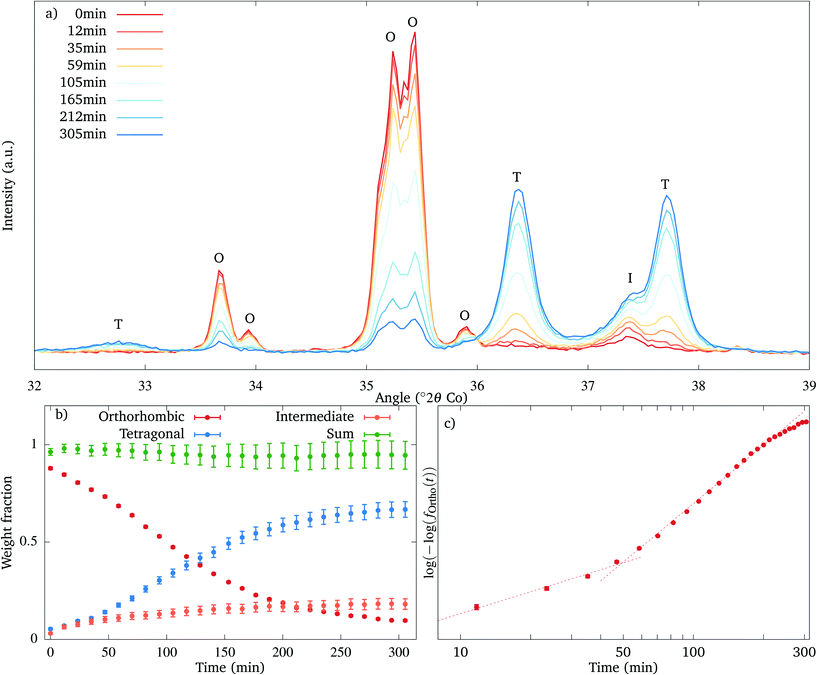
The decomposition of the orthorhombic phase and the appearance of the intermediate and the tetragonal phase have been tracked by isothermal powder XRD as function of time, at 550 °C. Selected diffraction patterns are shown in Fig. 9(a). As the lines of the orthorhombic phase disappear, together with the tetragonal phase several peaks of the intermediate phase appear, the one with the highest intensity located at 37.3° (2θ) (using Co Kα radiation). The tetragonal phase appears directly from the beginning of the annealing as a very broad doublet. The transformation is not yet complete after 5 hours, since the reflections of the orthorhombic phase are still present.

Fig. 9 Powder X-ray diffraction of the metastable orthorhombic phase at 550 °C. a) Evolution of the diffraction pattern with the annealing time. Labels O, T and I stand for the orthorhombic, tetragonal and intermediate reflections, respectively. b) The evolution of the weight fraction of the Sr₂TiO₄ polymorphs during the annealing at a constant temperature. c) Avrami plot of the volume fraction of the orthorhombic phase.

The quantitative analysis was performed using the Profex/BGMN software. In order to ensure a good thermal contact between the sample and its holder, a very small amount of sample was used. As a consequence, the relative intensities of the reflections might be affected, thus preventing us from reliably refining the atomic positions. The R-factor of the fit was largely improved if the preferential orientation of the powder sample was modelled by a spherical harmonic of 6th–10th order.²⁴ Lastly, the amount of the intermediate phase could not be determined precisely because of the unknown structure, but (assuming that the reference intensity ratio of the intermediate phase will be similar to that of the tetragonal phase) it was approximated by the ratio:

where I_I and I_T are the integral intensities of the most intensive peaks and S_I and S_T are the scale factors of the intermediate and the tetragonal phase, respectively. Each scale factor was then normalized with respect to the sum of the scale factors of all phases at 25 °C to obtain the weight fractions of each of the polymorphs.

The resulting distribution diagram is plotted in Fig. 9(b). The decomposition of the orthorhombic and formation of the tetragonal phase follow approximately a sigmoid curve, while the relative amount of the intermediate phase grows very slowly, resembling a steady state. The transformation is not yet complete after 5 hours, with 10% of the material being still present in the orthorhombic form. As the amount of the intermediate phase grows and more reflections of the intermediate phase appear, the R-factors of the refinement increase steadily.

According to the JMAK theory,^25,26 a transition between two phases which proceeds via nucleation and growth follows an exponential dependence:

f(t) = 1 − exp(−K·tⁿ),

where f(t) is the volume fraction transformed as a function of annealing time. The exponent n reflects the nucleation mechanism and the growth dimensionality and can be determined from the slope of the so-called Avrami plot of ln(−ln(1 − f(t))) vs. ln(t). In Fig. 9(c) this dependence is plotted directly for the volume fraction of the orthorhombic phase, since (1 − f(t)) equals the untransformed volume fraction. Such a plot will describe the first step of the transformation, from the orthorhombic to the intermediate phase. It clearly shows a non-linear dependence with at least two different regimes with slopes of 0.5 and 1.2, respectively. The second stage of the transformation cannot be described by the Avrami kinetics, since the volume of the initial (i.e. intermediate) phase is not constant. It is worth noting that the change of slope, which means a change of the regime of the transformation, occurs at the time when the volume fraction of the intermediate phase seems to reach a steady value in Fig. 9(b). Even if our experimental data do not allow to establish the transformation mechanism, we can state that the structural phase transition is not direct and is driven by the formation of the monoclinic intermediate phase.

3.6 Orientation relationship

If the grown crystal of the orthorhombic phase is pulled out of the hot zone slowly at 1 mm h⁻¹, instead of quenching, the phase transition proceeds and polycrystalline rods are obtained with a very regular structure. In these rods dark brown macroscopic plates alternate with polycrystalline layers, as can be seen in Fig. 10(a) and (b). These plates run at an oblique angle to the growth direction, can be very easily cleaved, they produce a tetragonal Laue diffraction pattern (Fig. 10(c)) and their XRD pattern only consists of sharp 00l reflections. This suggests an orientational relationship between the orthorhombic and tetragonal phase during the transition.

Fig. 10 Grown rod after the phase transition to tetragonal Sr₂TiO₄ took place. a) View along the growth direction. b) View of the rod perpendicular to the growth direction. The rod breaks into brown plates which run at an oblique angle with respect to the growth direction. c) Laue reflection pattern of one of the brown single crystalline plates of tetragonal Sr₂TiO₄. d) Orthorhombic structure viewed along the growth direction, which is along the pseudohexagonal a-axis. e) Tetragonal structure viewed along the [227] direction shows a pseudohexagonal pattern and alternation of the anionic and cationic planes.

To confirm the presence of the orientational relationship, we have annealed several polished single crystal pieces of orthorhombic phase of <0.5 mm² area with known {h00} orientation at different temperatures and time delays: 800 °C for 5 minutes up to 1000 °C during 6 hours. After the annealing, the crystals lost their transparency and were weakly diffracting, not allowing to collect single-crystal diffraction data. The θ–2θ scans could be measured, however, and the results are visible in Fig. 8(b). The peak at 2θ = 40.0° coincides with the diffraction line of the intermediate phase (up to the shift due to the sample displacement), which was observed in the powder samples. This reflection disappears gradually as the annealing temperature is increased. The tetragonal phase which is formed is strongly (11l) oriented, with 112, 114, 116 and 1110 lines visible and the 114 reflection being especially strong. Except for the 11l lines only those reflections are visible, which have very high nominal intensity: the most intensive doublet of 110 and 103 reflections and the 123 reflection, which is the fourth strongest.

An insight into this intriguing orientation relationship can be gained by visualizing the crystal structure of the low temperature–tetragonal–polymorph. In the projection along the [227] direction in Fig. 10(e) a pseudohexagonal arrangement of atoms can be seen, similar to the pseudohexagonal structure of the orthorhombic phase in the [100] direction (Fig. 10(d)).

An important feature of both structures is the alternation of cationic and anionic planes parallel to the hexagonal direction, with the interplanar distance being 2.7482 Å in the tetragonal and 2.9364 Å in the orthorhombic phase. If this planar structure is to be conserved, one can expect the c axis of the tetragonal phase to lie in the plane defined by the a and c axes of the orthorhombic phase, (as is the orientation of the axes drawn in Fig. 10(d) and (e)), or rotated by ±60° along the hexagonal axis.

During the transition between the orthorhombic and tetragonal phase a considerable reconstruction occurs in the titanium first coordination sphere, resulting in a change between the tetrahedral and octahedral arrangement of oxygens, which cannot be described by a simple symmetry breaking. In addition, the transition is connected to a rather high change in volume per formula unit, with the high temperature phase having 11% lower density. This explains why growing the RP Sr₂TiO₄ is usually challenging. Our experiments show, however, that it might, at least in theory, be possible to obtain single crystalline tetragonal phase, since the two structures are related.

3.7 Dielectric properties

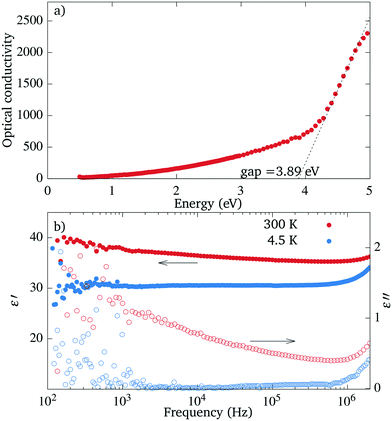
The value of the optical gap measured with ellipsometry is approximately 3.9 eV, see Fig. 11(a). This value is comparable to the value of 3.2 eV reported for SrTiO₃ (ref. 27) and the values of 3.9 and >4 eV reported for the in-plane and out-of-plane electron momentum in Sr₂TiO₄.²⁸ The optical conductivity shows a broad tail reaching from the gap well into the visible range, as could be expected from the light coloration of the sample.

Fig. 11 Dielectric properties of the orthorhombic Sr₂TiO₄. a) Optical conductivity measured by ellipsometry. b) The dependence of the dielectric constant on frequency, measured at different temperatures.

At room temperatures the samples are leaky dielectrics and the impedance spectra show a dependence of capacitance on the frequency (see Fig. 11(b)). They can be modelled by an equivalent circuit consisting of a constant phase element and a parallel resistor.²⁹ The dispersion depends on temperature and is significantly weaker already at 250 K. At 4.2 K, the parallel resistor is not necessary to model the circuit and the capacitance dependence on the frequency is flat. This behaviour could be caused by partially mobile charges which become trapped on defects or interfaces.³⁰ The upturn at higher frequency comes from the inductance of the measurement apparatus.

The static dielectric constant measured along the [100] direction at 4.2 K has a value of 30 ± 10. At room temperature, the value rises to 40 ± 10, which might be overestimated, however, due to the charge trapping. This value is close to the dielectric constant ε₃₃ of 44 ± 4 and the ε₁₁ of 42 ± 2.5 measured on the epitaxial (001)-oriented layers of RP Sr₂TiO₄,^6,31

Tetragonal Sr₂TiO₄ is a member of the Ruddlesden–Popper series, of which several members can become ferroelectric at certain conditions. Since the orthorhombic Sr₂TiO₄ crystallizes in a polar group, we tested few crystals for signs of ferroelectricity. There was no sign of ferroelectric switching in the dependence of capacitance on voltage, neither at room temperature nor at 4.2 K, no polarization was present, and no piezoelectric response could be measured. Hence, the dependence of the dielectric constant on the temperature is most likely caused by the charge trapping and not by a ferroelectric transition.

4 Conclusions

When the single crystal growth of the Ruddlesden–Popper Sr₂TiO₄ from melt is attempted, an orthorhombic structure forms first, which undergoes a two-step transformation to the low-T tetragonal phase via a monoclinic phase at 1530 °C. During this transition a dramatic reconstruction takes place between tetrahedral and octahedral Ti coordination, connected to a large 11% change in volume. An orientational relationship between the two modifications is observed, identified through a common sixfold rotational symmetry element as [100]_O∥[227]_T and [001]_O∥[1̄1̄6]_T.

We have stabilized the orthorhombic modification of the Sr₂TiO₄ by rapid cooling of the crystal during the floating zone growth, which produces bulk single crystals suitable for further characterization. We have solved the crystal structure of the new polymorph and discovered an uncommon tetrahedral Ti coordination. The new material is an insulator with a band gap of 3.9 eV and the static dielectric constant of 40 at room temperature. The Raman spectra contain a large number of peaks and reveal a quartic anharmonic contribution to the potential well.

Author contributions

D. P.: conceptualization, investigation, formal analysis, writing of the original draft, writing-review and editing. C. B.: investigation, formal analysis, writing-review and editing. E. G.: conceptualization, supervision, writing-review and editing. M. H.: investigation, writing-review and editing. J. T.: investigation, writing-review and editing. P. B.: investigation, writing-review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the assistance provided by the Research Infrastructure NanoEnviCz, supported by the Ministry of Education, Youth and Sports of the Czech Republic under Project No. LM2018124.

We would like to thank Radovan Černý for guidance and useful discussions.

Notes and references

1. C. Collignon, X. Lin, C. W. Rischau, B. Fauqué and K. Behnia, Annu. Rev. Condens. Matter Phys., 2019, 10, 25–44.
2. Y. Wang, K. H. Lee, H. Ohta and K. Koumoto, J. Appl. Phys., 2009, 105, 103701.
3. X. Sun, Y. Mi, F. Jiao and X. Xu, ACS Catal., 2018, 8, 3209–3221.
4. Y. F. Nie, D. D. Sante, S. Chatterjee, P. D. King, M. Uchida, S. Ciuchi, D. G. Schlom and K. M. Shen, Phys. Rev. Lett., 2015, 115, 1–5.
5. C. Guguschev, D. J. Kok, U. Juda, R. Uecker, S. Sintonen, Z. Galazka and M. Bickermann, J. Cryst. Growth, 2017, 468, 305–310.
6. J. H. Haeni, C. D. Theis, D. G. Schlom, W. Tian, X. Q. Pan, H. Chang, I. Takeuchi and X. D. Xiang, Appl. Phys. Lett., 2001, 78, 3292–3294.
7. A. Cocco and F. Massazza, Ann. Chim., 1963, 53, 883–893.
8. M. Dryś and W. Trzebiatowski, Rocz. Chem., 1957, 31, 489–496.
9. G. Li, N. M. Dimitrijevic, L. Chen, J. M. Nichols, T. Rajh and K. A. Gray, J. Am. Chem. Soc., 2008, 130, 5402–5403.
10. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
11. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
12. N. Doebelin and R. Kleeberg, J. Appl. Crystallogr., 2015, 48, 1573–1580.
13. J. W. Arblaster, Platinum Met. Rev., 1997, 41, 12–21.
14. A. B. Kuzmenko, Rev. Sci. Instrum., 2005, 76, 083108.
15. M. Pinsky and D. Avnir, Inorg. Chem., 1998, 37, 5575–5582.
16. I. D. Brown and D. Altermatt, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 244–247.
17. O. C. Gagné and F. C. Hawthorne, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 562–578.
18. K. Wilhelmi, Arkiv för Kemi, 1966, 26, 157–165.
19. J. Deisenhofer, S. Schaile, J. Teyssier, Z. Wang, M. Hemmida, H.-A. K. von Nidda, R. M. Eremina, M. V. Eremin, R. Viennois, E. Giannini, D. van der Marel and A. Loidl, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 214417.
20. K. Funahashi, T. Higashide, T. Ueno, K. Tasaki, Y. Tahara, M. Adachi, T. Saiki, T. Kajita and T. Katsufuji, Phys. Rev. B, 2018, 98, 184422.
21. E. Kroumova, M. Aroyo, J. Perez-Mato, A. Kirov, C. Capillas, S. Ivantchev and H. Wondratschek, Phase Transitions, 2003, 76, 155–170.
22. R. Viennois, E. Giannini, M. Koza and J. L. Sauvajol, J. Phys.: Conf. Ser., 2007, 92, 1–5.
23. K. Kawamura, M. Yashima, K. Fujii, K. Omoto, K. Hibino, S. Yamada, J. R. Hester, M. Avdeev, P. Miao, S. Torii and T. Kamiyama, Inorg. Chem., 2015, 54, 3896–3904.
24. M. Järvinen, European Powder Diffraction 5, 1998, pp. 184–199.
25. W. A. Johnson and R. F. Mehl, Trans. Am. Inst. Min. Metall. Eng., 1939, 135, 416–442.
26. M. Avrami, J. Chem. Phys., 1940, 8, 212–224.
27. K. van Benthem, C. Elsässer and R. H. French, J. Appl. Phys., 2001, 90, 6156–6164.
28. J. Matsuno, Y. Okimoto, M. Kawasaki and Y. Tokura, Phys. Rev. Lett., 2005, 95, 176404.
29. F. D. Morrison, D. J. Jung and J. F. Scott, J. Appl. Phys., 2007, 101, 094112.
30. A. K. Jonscher, Dielectric Relaxation in Solids, Chelsea Dielectrics Press, London, 1983.
31. N. D. Orloff, W. Tian, C. J. Fennie, C. H. Lee, D. Gu, J. Mateu, X. X. Xi, K. M. Rabe, D. G. Schlom, I. Takeuchi and J. C. Booth, Appl. Phys. Lett., 2009, 94, 042908.

---

Footnotes

† The crystallographic data have been deposited with the ICSD (deposition number 2158480).

‡ There are in total 14 different crystallographic sites, each of them situated on the Wyckoff position a. Using the Symmetry Adapted Modes tool²¹ accessible on the Bilbao crystallographic server, 165 Raman active modes are predicted; 41A₁ + 42A₂ + 41B₁ + 41B₂.

---