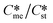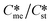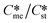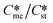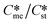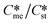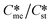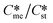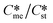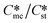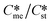Open Access Article
Open Access ArticleThe role of the pre-exponential factor in determining the kinetic selection of polymorphs during solution crystallization of organic compounds
Vivek
Verma
 a and
Benjamin K.
Hodnett
a and
Benjamin K.
Hodnett
 *b
*b
aDepartment of Chemical Engineering, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
bSynthesis and Solid State Pharmaceutical Centre, Department of Chemical Sciences, Bernal Institute, University of Limerick, V94 T9PX, Ireland. E-mail: kieran.hodnett@ul.ie
First published on 25th March 2022
Abstract
Generally, pairs of polymorphs can be characterized by their ratios of equilibrium solubilities 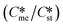 and interfacial energies (γst/γme) for a given temperature and solvent. We refer to this point as the solubility-interfacial energy characteristic point (characteristic point for short) of a polymorphic pair. The equations of the classical nucleation theory have been used to determine the influence of supersaturation, the absolute size of the interfacial energies and the ratio of the pre-exponential factors for pairs of polymorphs to predict the experimental conditions in which metastable or stable polymorphs crystallize first. Domain diagrams for polymorph pairs based on the equilibrium solubility ratios
and interfacial energies (γst/γme) for a given temperature and solvent. We refer to this point as the solubility-interfacial energy characteristic point (characteristic point for short) of a polymorphic pair. The equations of the classical nucleation theory have been used to determine the influence of supersaturation, the absolute size of the interfacial energies and the ratio of the pre-exponential factors for pairs of polymorphs to predict the experimental conditions in which metastable or stable polymorphs crystallize first. Domain diagrams for polymorph pairs based on the equilibrium solubility ratios 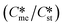 and the ratio of interfacial energies (γst/γme) have been developed. Separate zones are identified where the metastable and stable polymorphs are favoured kinetically; generally higher supersaturation kinetically favour the metastable form. This contribution investigates the circumstances where large values for the pre-exponential factor, particularly for the metastable polymorph, in the classical nucleation theory description of nucleation can expand the zone where the metastable zone is kinetically favoured. The results indicate that the pre-exponential factor has a strong influence in expanding the kinetically metastable zone when the interfacial energies of the metastable and stable polymorphic are low (less than 3.5 mJ m−2) but has little or no effect when these values are high (greater than 5.5 mJ m−2). This work also identifies the circumstances where a metastable polymorph with a higher interfacial energy than the stable polymorph will crystallize first.
and the ratio of interfacial energies (γst/γme) have been developed. Separate zones are identified where the metastable and stable polymorphs are favoured kinetically; generally higher supersaturation kinetically favour the metastable form. This contribution investigates the circumstances where large values for the pre-exponential factor, particularly for the metastable polymorph, in the classical nucleation theory description of nucleation can expand the zone where the metastable zone is kinetically favoured. The results indicate that the pre-exponential factor has a strong influence in expanding the kinetically metastable zone when the interfacial energies of the metastable and stable polymorphic are low (less than 3.5 mJ m−2) but has little or no effect when these values are high (greater than 5.5 mJ m−2). This work also identifies the circumstances where a metastable polymorph with a higher interfacial energy than the stable polymorph will crystallize first.
Introduction
This paper follows on from ref. 1 which looked at the 95% probability that the thermodynamic solubility ratio between pairs of polymorphs is less than 2 fold.2–4 There are exceptions to this observation, for example in the case of ritonavir, where a 4–5 fold difference in solubilities has been reported for selected solvents.5 In parallel with this work Nyman and Day6 and, independently, Cruz-Cabeza, Reutzel-Edens and Bernstein7 demonstrated that the free energy and lattice energy differences between pairs of polymorph rarely exceed 5 kJ mol−1 with differences extending to 10 kJ mol−1 for pairs of conformational polymorphs.Ref. 1 took as its starting point the calculation of critical free energies of nucleation for pairs of polymorphs using the classical nucleation theory:8
Where
 | (1) |
 approaches 2 then the value of the supersaturation with respect to the metastable form (Sme) is typically half the supersaturation with respect to the stable form (Sst).1 This has profound effects on the value of
approaches 2 then the value of the supersaturation with respect to the metastable form (Sme) is typically half the supersaturation with respect to the stable form (Sst).1 This has profound effects on the value of 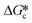 for each of the pairs of polymorphs. Generally, for
for each of the pairs of polymorphs. Generally, for  values above 2 it is easy to find circumstances where
values above 2 it is easy to find circumstances where  is less than
is less than 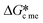 . This work also illustrated that
. This work also illustrated that  can is less than
can is less than  at low supersaturations (but still supersaturated with respect to both polymorphs) and when the ratio of γst/γme is low. This approach explains the numerous literature reports which specify that high supersaturation favour the formation of the metastable polymorph and low supersaturations favour the stable form, where in each case the system was supersaturated with respect to both polymorphs.9–22 These results were interpreted in the light of the single nucleation event hypothesis whereby one particle of a particular polymorph forms and is propagated throughout the solution via a secondary nucleation mechanism.23–28 Ultimately, that work led to the development of a series of domain diagrams by identifying for any selected value of supersaturation the combinations of
at low supersaturations (but still supersaturated with respect to both polymorphs) and when the ratio of γst/γme is low. This approach explains the numerous literature reports which specify that high supersaturation favour the formation of the metastable polymorph and low supersaturations favour the stable form, where in each case the system was supersaturated with respect to both polymorphs.9–22 These results were interpreted in the light of the single nucleation event hypothesis whereby one particle of a particular polymorph forms and is propagated throughout the solution via a secondary nucleation mechanism.23–28 Ultimately, that work led to the development of a series of domain diagrams by identifying for any selected value of supersaturation the combinations of  and γst/γme at which
and γst/γme at which  equals
equals  .1
.1
A limitation of the work in ref. 1 was that it was based on the determination of critical free energies of nucleation, rather than the full classical nucleation equation which determines nucleation rates namely:
 | (2) |
Eqn (2) comprises two parts, namely the exponential term, which basically ranges from 0 to 1 and a pre-exponential term which can take on any value. There is a good deal of literature regarding the nature of the pre-exponential factor.29–35 According to Li et al.31 reducing the interfacial energy or enhancing supersaturation does not increase the nucleation rate as effectively as reducing the kinetic barrier. Dimensional analysis of eqn (2) would indicate that A and J should have the same units. For J this is usually expressed as the number of nuclei of a size greater than the critical nucleus size generated per unit volume and per unit time (no. of stable nuclei per m3 s−1). On this basis, A may be defined as the total number of nuclei (or clusters) of any size generated per unit volume and per unit time (no. of pre-critical and stable nuclei per m3 s−1). The exponential factor is the fraction of these pre-critical nuclei which can advance to the critical size.
There is a limited amount of literature data which records interfacial energies and pre-exponential factors for various crystallizations of organic compounds. Table 1 presents the influence of solvent on these parameters for tolbutamide,36 salicylic acid,37 and risperidone38 which clearly show a solvent effect in determining the values of the pre-exponential factors and interfacial energies. Two studies on curcumin39 and 3-nitrophenol40 demonstrate the effects of impurities on the pre-exponential factors and interfacial energies and finally there are 4 studies which show how these factors change for polymorph pairs, namely eflucimibe,11D-mannitol,12 mefenamic acid,41 and famotidine.13
| Compound | Polymorphic form | Solvent | Pre-exponential factor A (m−3 s−1) | Interfacial energy γ (mJ m−2) | Ref. |
|---|---|---|---|---|---|
| a DMA: dimethyl acetamide; DMC: demethoxy curcumin; BDMC: bisdemethoxy curcumin. b These are B values. | |||||
| Tolbutamide | Form IL | Acetonitrile | 15.6 | 1.25 | 36 |
| Ethylacetate | 23.3 | 1.90 | |||
| n-Propanol | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 210 210 |
3.99 | |||
| Toluene | 220 | 3.46 | |||
| Salicylic acid | Chloroform | 57 | 0.71 | 37 | |
| Ethyl acetate | 148 | 1.82 | |||
| Acetonitrile | 289 | 2.40 | |||
| Acetone | 8645 | 3.81 | |||
| Methanol | 586 | 4.13 | |||
| Acetic acid | 175 | 5.50 | |||
| Risperidone | Cumene | 348 | 1.72 | 38 | |
| Toluene | 181 | 1.70 | |||
| Acetone | 161 | 1.77 | |||
| Ethyl acetate | 71 | 1.58 | |||
| Methanol | 134 | 2.18 | |||
| 1-Propanol | 129 | 2.25 | |||
| 1-Butanol | 61 | 2.04 | |||
| Curcumin | 2-Propanol | 659 | 4.45 | 39 | |
| 2-Propanol with 0.1 mM DMCa | 113 | 4.70 | |||
| 2-Propanol with 0.1 nM BDMCa | 165 | 5.01 | |||
| 3-Nitrophenol | Toluene | 4.8 × 108 | 5.1 ± 1.3b | 40 | |
| Toluene with 0.25 mol% 3-aminobenzoic acid | 1.3 × 105 | 3.7 ± 1.0b | |||
| Eflucimibe | Form B metastable | Ethanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n-heptane (7 n-heptane (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) 3) |
118 | 4.23 | 11 |
| Form A stable | 14 | 5.17 | |||
| D-Mannitol | Form δ metastable | Water | 610 | 1.78 | 12 |
| Form β stable | 3000 | 3.23 | |||
| Mefenamic acid | Form II metastable | 40% DMAa–60% water | 1324 | 2.92 | 41 |
| Form I stable | 70% DMAa–30% water | 160 | 2.86 | ||
| Famotidine | Form B metastable | Water | 109 | 14.36 | 13 |
| Form A stable | 1.25 × 104 | 9.16 | |||
Perusals of the data in Table 1 indicated that ratio of pre-exponential factors for the various crystallizations encountered rarely exceed 103. This range of ratios cover the effect of solvent (rows 1–3, Table 1), the effects of impurities (rows 4 and 5) and the effect of polymorph selection (rows 6–8). The single exception is in the case of famotidine (row 9) where the ratio Ame/Ast is just less than 105. This work reports that the interfacial energy is 14.36 mJ m−2 for the metastable form of famotidine and 9.16 mJ m−2 for the stable polymorph. This case will be discussed further below but as a working hypothesis we will proceed on the assumption that the 103 ratio is attainable and should be considered as a reasonable upper ratio limit for this study.
Methods
The present study seeks to explore further the role of the pre-exponential factor in eqn (2) in determining the kinetic outcome (namely the first polymorph in a pair which will crystallise). The work does not explore the role of polymorphic transformations neither in the solid state nor through a solution mediated process. Clearly, there is a temporal aspect to polymorphism and if the metastable polymorph crystallizes first it will transform into the stable form on a timescale which can vary from milliseconds to years. The approach taken here has been to seek the conditions whereby the nucleation rate for the metastable polymorph (Jme) is equal to the nucleation rate of the stable polymorph (Jst) eqn (3). Throughout these calculations the pre-exponential term of the stable polymorph (Ast) was set at 1 and the value of Ame required to achieve Jme = Jst was calculated.| Jme = Jst | (3) |
 | (4) |
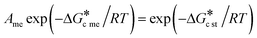 | (5) |
For this work a range of scenarios was explored principally for  ratios between 1.2 and 4.0; the range of interfacial energies (γst and γme) was 2–11 mJ m−2 and the range of supersaturations with respect to the stable form (Sst) was 3–8. Generally, the results are presented below as values of Ame needed to satisfy eqn (5), namely the conditions in which the nucleation rate of the metastable (Jme) and stable polymorphs (Jst) are equal.
ratios between 1.2 and 4.0; the range of interfacial energies (γst and γme) was 2–11 mJ m−2 and the range of supersaturations with respect to the stable form (Sst) was 3–8. Generally, the results are presented below as values of Ame needed to satisfy eqn (5), namely the conditions in which the nucleation rate of the metastable (Jme) and stable polymorphs (Jst) are equal.
Results
Tables 2–4 present the values of Ame needed to satisfy eqn (5) in circumstances where the interfacial energies for each pair of polymorphs is set at low values (2–2.7 mJ m−2) for Table 2, set at intermediate values (4–5.5 mJ m−2) for Table 3 and set at high values (8–11 mJ m−2) for Table 4. The range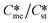 explored as 1.2 to 4.0 with set values of supersaturation with respect to the stable polymorph (Sst) of 3.5 and 5.5. In these tables' circumstances where γst = γme, γst > γme and γst < γme were explored.
explored as 1.2 to 4.0 with set values of supersaturation with respect to the stable polymorph (Sst) of 3.5 and 5.5. In these tables' circumstances where γst = γme, γst > γme and γst < γme were explored.
| S st | γ st | γ me | Min. Ame at = 1.2 | Min. Ame at = 1.5 | Min. Ame at = 2.2 | Min. Ame at = 3 | Min. Ame at = 4 |
|---|---|---|---|---|---|---|---|
| S me = 4.58 | S me = 3.67 | S me = 2.5 | S me = 1.83 | S me = 1.38 | |||
| n/a not applicable because Sme < 1. | |||||||
| 5.5 | 2.7 | 2.0 | 0.90 | 0.94 | 1.1 | 1.6 | 9.4 |
| 5.5 | 2.7 | 2.7 | 1.05 | 1.16 | 1.7 | 4.3 | 3.4 × 102 |
| 5.5 | 2.0 | 2.7 | 1.20 | 1.32 | 1.9 | 4.9 | 3.8 × 102 |
| S st | γ st | γ me | Min. Ame at = 1.2 | Min. Ame at = 1.5 | Min. Ame at = 2.2 | Min. Ame at = 3 | Min. Ame at = 4 |
|---|---|---|---|---|---|---|---|
| S me = 4.58 | S me = 3.67 | S me = 2.5 | S me = 1.83 | S me = 1.38 | |||
| n/a not applicable because Sme < 1. | |||||||
| 5.5 | 5.5 | 4.0 | 0.40 | 0.55 | 1.9 | 45 | 7.0 × 105 |
| 5.5 | 5.5 | 5.5 | 1.6 | 3.6 | 1.0 × 102 | 2.2 × 105 | >1010 |
| 5.5 | 4.0 | 5.5 | 4.7 | 10.7 | 3.0 × 102 | 7.0 × 105 | >1010 |
| S st | γ st | γ me | Min. Ame at = 1.2 | Min. Ame at = 1.5 | Min. Ame at = 2.2 | Min. Ame at = 3 | Min. Ame at = 4 |
|---|---|---|---|---|---|---|---|
| S me = 4.58 | S me = 3.67 | S me = 2.5 | S me = 1.83 | S me = 1.38 | |||
| n/a not applicable because Sme < 1. | |||||||
| 5.5 | 11.0 | 8.0 | 6.4 × 10−4 | 8 × 10−3 | 1.6 × 102 | >1010 | >1010 |
| 5.5 | 11.0 | 11.0 | 3.7 × 101 | 3 × 104 | >1010 | >1010 | >1010 |
| 5.5 | 8.0 | 11.0 | 2.3 × 105 | >1010 | >1010 | >1010 | >1010 |
When the interfacial energies for the metastable and stable form are both low the metastable form seems to be kinetically attainable at Sst = 5.5 for all values  explored. No values of Ame/Ast greater than 103 are ever required to arrive at equal nucleation rates for the metastable and stable polymorphs, even in circumstances where γst < γme. A very similar results pertains when Sst = 3.5, except we can identify very high values of Ame/Ast required to attain equal nucleation rates when the value of
explored. No values of Ame/Ast greater than 103 are ever required to arrive at equal nucleation rates for the metastable and stable polymorphs, even in circumstances where γst < γme. A very similar results pertains when Sst = 3.5, except we can identify very high values of Ame/Ast required to attain equal nucleation rates when the value of  is 3 and above. In this table the value of Sme calculated as
is 3 and above. In this table the value of Sme calculated as 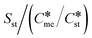 is presented for each entry to illustrate the extent to which the supersaturation with respect to the metastable polymorph reduced dramatically as the ratio
is presented for each entry to illustrate the extent to which the supersaturation with respect to the metastable polymorph reduced dramatically as the ratio  increases.
increases.
When the interfacial energies for the pair of polymorphs take on intermediate values (4–5.5 mJ m−2) very large values of Ame/Ast are required when Sst = 3.5 to satisfy eqn (5) for all values of  at and above 2.2. However, at Sst = 5.5 more reasonably achievable values of Ame/Ast (<103) are required at
at and above 2.2. However, at Sst = 5.5 more reasonably achievable values of Ame/Ast (<103) are required at  = 2.2 and 3. This trend is again consistent with our earlier observation that the metastable form becomes more kinetically favoured as the applied supersaturation increases.1
= 2.2 and 3. This trend is again consistent with our earlier observation that the metastable form becomes more kinetically favoured as the applied supersaturation increases.1
When the highest interfacial energies (8.0–11.0 mJ m−2) very large values of Ame/Ast are required when Sst = 3.5 and 5.5 to satisfy eqn (5) for all values of  above 2.2.
above 2.2.
As γ increases through the ranges 2.0–2.7, 4.0–5.5 and 8.0–11.0 mJ m−2 the minimum value of Ame needed to generate identical nucleation rates of the metastable and stable polymorphs, i.e. Jme = Jst with Ast = 1 increases very significantly. For Tables 2–4 the reader should be aware that the values are those calculate to Jme = Jst, namely the value at which both polymorphs would be expected to appear concomitantly. To attain “clean” metastable polymorphs which would be expected if a characteristic point were placed firmly within the metastable zone would require significantly higher values of Ame/Ast.
As reported previously1 higher supersaturations favour the metastable polymorph so that smaller values of Ame are generally required at Sst = 5.5 than the corresponding values at Sst = 3.5.
The results presented in Tables 2–4 are further confirmed when the range of interfacial energies is allowed to vary in the range γme = γst ± 3 mJ m−2 (Table 5). Unreasonably high values of Ame (greater than 103) are required for Jme to become equal to Jst at Sst equal to 3.5 and 5.5 and where γst is set at 11.0 kJ m−2.
| γ st | γ me | S st | Min. Ame at = 2.2 | S st | Min. Ameat = 2.2 |
|---|---|---|---|---|---|
| 2.7 | 0.35 | 3.5 | 0.7 | 5.5 | 0.8 |
| 0.7 | 0.7 | 0.8 | |||
| 1.7 | 1.4 | 1.0 | |||
| 2.7 | 13 | 1.7 | |||
| 3.7 | 1.4 × 103 | 5.5 | |||
| 4.7 | 4.1 × 106 | 41 | |||
| 5.7 | >1010 | 8.9 × 102 | |||
| 5.5 | 2.5 | 3.5 | 0.4 | 5.5 | 0.3 |
| 3.5 | 23.5 | 0.95 | |||
| 4.5 | 3.3 × 104 | 5.3 | |||
| 5.5 | >1010 | 1.0 × 102 | |||
| 6.5 | >1010 | 5.4 × 103 | |||
| 7.5 | >1010 | 1.4 × 106 | |||
| 8.5 | >1010 | >1010 | |||
| 11.0 | 6.0 | 3.5 | 4.8 × 102 | 5.5 | 2 × 10−3 |
| 7.0 | >1010 | 0.3 | |||
| 8.0 | >1010 | 1.7 × 102 | |||
| 9.0 | >1010 | 6.2 × 105 | |||
| 10.0 | >1010 | >1010 | |||
| 11.0 | >1010 | >1010 | |||
| 12.0 | >1010 | >1010 |
When γst is set at 5.5 kJ m−2 and Sst is equal to 3.5, reasonable values of Ame (103 or less) according to Table 1 are only attainable in circumstances where γme < γst. For the same set of circumstances where Sst = 5.5 a reasonably attainable value of Ame can only be achieved when γme = γst.
When γst is set at 2.7 kJ m−2 and Sst is equal to 3.5 and 5.5 reasonable values of Ame (103 or less) according to Table 5 are attainable in most circumstances except where γme ≥ (γst + 2) mJ m−2.
Taken together Tables 2–5 demonstrate that as γst increases we need higher and higher values of Ame to make Jme = Jst, i.e., Ame is less effective at expanding the metastable zone at high values of γme, and accordingly γst. In addition, Table 5 demonstrates that when γst is less than γme, Jme becomes equal to Jst only in circumstances where very high ratios of Ame/Ast are possible.
Of particular interest to this paper is to add the influence of Ame/Ast to the domain diagram presented as Fig. 7 of ref. 1 where ratios of equilibrium solubilities  were plotted against the ratio of interfacial energies (γst/γme) for a range of Sst values. The outcome was a series of supersaturation lines in the range Sst = 2–8 representing the combinations of
were plotted against the ratio of interfacial energies (γst/γme) for a range of Sst values. The outcome was a series of supersaturation lines in the range Sst = 2–8 representing the combinations of 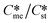 and γst/γme for which the critical free energies of nucleation are equal for pairs of polymorphs. For the purposes of the domain diagrams, each pair of polymorphs is characterized by the ratio of equilibrium solubilities
and γst/γme for which the critical free energies of nucleation are equal for pairs of polymorphs. For the purposes of the domain diagrams, each pair of polymorphs is characterized by the ratio of equilibrium solubilities  and the ratio of interfacial energies (γst/γme). Together these ratios are referred to as the characteristic point for a pair of polymorphs and will vary depending on temperature and solvent choice. Where the characteristic point lies below the domain line for a particular supersaturation, the metastable polymorph is favoured kinetically, namely it will be the first polymorph to appear. If the characteristic point lies above the domain line the stable form will be favoured kinetically.
and the ratio of interfacial energies (γst/γme). Together these ratios are referred to as the characteristic point for a pair of polymorphs and will vary depending on temperature and solvent choice. Where the characteristic point lies below the domain line for a particular supersaturation, the metastable polymorph is favoured kinetically, namely it will be the first polymorph to appear. If the characteristic point lies above the domain line the stable form will be favoured kinetically.
The assumption in ref. 1 was that Ame = Ast = 1 that the critical free energy of nucleation alone determined the nucleation rates, i.e. if  then Jst = Jme. In Fig. 1–3 below domain diagrams are constructed which include ratios of Ame/Ast in the range 1–1000. Briefly when the nucleation rate of each of the pair of polymorphs are equal as expressed in eqn (4) and (5) the value of Ast is set at 1 and the value of Ame varied from 1–1000.
then Jst = Jme. In Fig. 1–3 below domain diagrams are constructed which include ratios of Ame/Ast in the range 1–1000. Briefly when the nucleation rate of each of the pair of polymorphs are equal as expressed in eqn (4) and (5) the value of Ast is set at 1 and the value of Ame varied from 1–1000.
 | ||
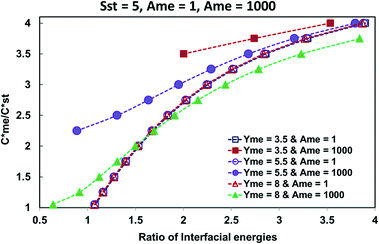
| Fig. 3 The influence the ratio of Ame/Ast for supersaturations in the range Sst = 3–8 on the expansion of the metastable zone when γme = 5.5 mJ m−2. | ||
Expanding eqn (5) leads to eqn (6):
Ame![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−16πNaγme3vm2/3k2T2ln2SmeRT) = exp(−16πNaγst3vm2/3k2T2ln2SstRT) exp(−16πNaγme3vm2/3k2T2ln2SmeRT) = exp(−16πNaγst3vm2/3k2T2ln2SstRT) | (6) |
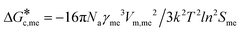 and
and 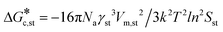
Substituting the values of Na = 6.023 × 1023 mol−1, vm,me = vm,st = 4 × 10−28 m3 per molecule, K = 1.38 × 10−23 m2 kg s−2 K−1, T = 293 K, R = 8.3142 J mol−1 K−1, Sst = 3, 5, and 8, γme = 3.5, 5.5, and 8 mJ m−2, Ame = 1, 10, 100, and 1000, and Sme as defined earlier will help to determine the value of γst. These calculations allow us to plot  against the ratio of interfacial energies (γst/γme) for a range of selected supersaturation (Sst) and to assess the influence of Ame on the location of the domain line provided that the term Sme does not fall below 1 at which point the solution would be undersaturated with respect to the metastable polymorph.
against the ratio of interfacial energies (γst/γme) for a range of selected supersaturation (Sst) and to assess the influence of Ame on the location of the domain line provided that the term Sme does not fall below 1 at which point the solution would be undersaturated with respect to the metastable polymorph.
An assumption of this work is that  is always greater than
is always greater than 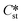 (essentially the working definition of the metastable and stable phases). The extent of the domain along the y-axis is determined by the applied supersaturation (Sst) and where
(essentially the working definition of the metastable and stable phases). The extent of the domain along the y-axis is determined by the applied supersaturation (Sst) and where 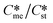 = Sst. So then Sst is set at 5 the maximum value of
= Sst. So then Sst is set at 5 the maximum value of  is also 5 at which point the value of Sme is equal to 1. The purpose of the domain diagram is to determine the zones where the metastable and stable forms are favoured kinetically, i.e. the forms which appear initially when both are supersaturated. Hence, the absolute maximum value of interest to this work is where
is also 5 at which point the value of Sme is equal to 1. The purpose of the domain diagram is to determine the zones where the metastable and stable forms are favoured kinetically, i.e. the forms which appear initially when both are supersaturated. Hence, the absolute maximum value of interest to this work is where  = Ssti.e. where the value of Sme is 1 and so cannot crystallize. Hence, the extent of the combined domains along the y-axis is 1 <
= Ssti.e. where the value of Sme is 1 and so cannot crystallize. Hence, the extent of the combined domains along the y-axis is 1 < 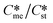 = Sst. Along the x-axis the ratio of γst/γme cannot be less than zero. Equally, it would be unrealistic to set the upper limit of γst/γme at greater than 4.
= Sst. Along the x-axis the ratio of γst/γme cannot be less than zero. Equally, it would be unrealistic to set the upper limit of γst/γme at greater than 4.
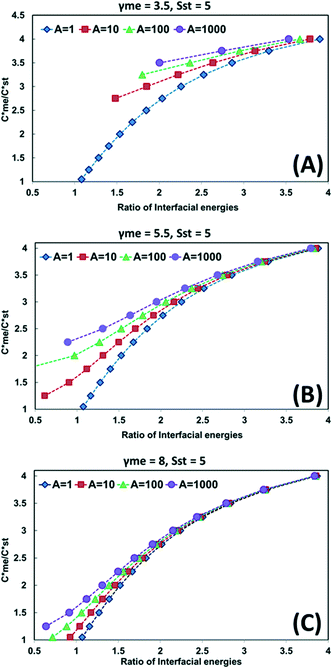
Fig. 1A–C illustrates the situation where the domain diagram is presented for the range  in the range 1–4. With the value of the interfacial energy for the metastable polymorph (γme) set at 3.5, 5.5 and 8.0 mJ m−2, the required value of the interfacial energy of the stable polymorph (γst) required to satisfy eqn (5) is calculated and expressed as the ratio of interfacial energies (γst/γme). One domain line in each of Fig. 1A–C represent the situation where Ame = Ast = 1. The other lines represent the situations where Ame = 10, 100 or 1000. The examples shown in Fig. 1A–C set the supersaturation with respect to the stable polymorph (Sst) at 5.
in the range 1–4. With the value of the interfacial energy for the metastable polymorph (γme) set at 3.5, 5.5 and 8.0 mJ m−2, the required value of the interfacial energy of the stable polymorph (γst) required to satisfy eqn (5) is calculated and expressed as the ratio of interfacial energies (γst/γme). One domain line in each of Fig. 1A–C represent the situation where Ame = Ast = 1. The other lines represent the situations where Ame = 10, 100 or 1000. The examples shown in Fig. 1A–C set the supersaturation with respect to the stable polymorph (Sst) at 5.
Fig. 1A illustrates that for low values of interfacial energies (γme = 3.5 mJ m−2) the domain within which the metastable form is kinetically favoured increases very significantly as the value of Ame increased over the range 1–1000. In fact at the highest Ame value applied (Ame = 1000) the kinetically favoured metastable zone nearly covers the entire domain. In such circumstances, the combination of low interfacial energies with high Ame/Ast ratios does allow the for 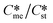 ratios in excess of 2. According to ref. 1 just 5% of polymorph pairs fall into this category.
ratios in excess of 2. According to ref. 1 just 5% of polymorph pairs fall into this category.
Fig. 1B and C illustrate the situation where the value of the interfacial energy of the metastable form increases to 5.5 and 8 mJ m−2, respectively while allowing Ame/Ast to vary from 1 to 1000. For the higher values of interfacial energies the value of Ame needed to expand the kinetically favoured metastable zone increases significantly. At γme equal to 5.5 mJ m−2 there is a modest expansion of the kinetically favoured zone for the highest value of Ame modelled whereas for γme equal to 8.0 mJ m−2 the expansion of the kinetically favoured zone for the metastable polymorph is very small. The expansion of the kinetically favoured metastable zone in these diagrams is entirely consistent with data in Tables 2–5 which demonstrate the need for higher values of Ame/Ast as the interfacial energies applied increase.
Overall, the pre-exponential factor plays a dominant role in determining the relative sizes of the kinetically favoured zones in the domain diagrams then the interfacial energies are low but have a diminishing to negligible effect as the interfacial energies increase.
Fig. 2 summarises this situation further: here the original domain line is reproduced. This line is almost coincident when γme is in the range 3.5–8 mJ m−2, Sst = 5 and Ame = Ast = 1. The corresponding domain lines for γme equal to 3.5, 5.5 and 8 mJ m−2 with Ame = 1000 are combined in this figure and clearly show that the expansion of the metastable favoured kinetic zone depends strongly on the absolute value of γme applied and by association with eqn (6), the absolute value of γst. The expansion of the metastable zone is most pronounced at low values of γme.
In all circumstances where γst < γme the only possible circumstances where the metastable form is favoured kinetically is if Ame ≫ Ast. In Fig. 2 this situation is illustrated for γst/γme in the range 0.5–1. Above γst/γme = 1 a zone emerges where the metastable form is favoured kinetically. When γst/γme < 1 the stable phase only is favoured kinetically when Ame = Ast = 1. The metastable form starts to be favoured kinetically when Ame becomes greater than Ast by a significant amount. The metastable zone is hardly attainable according to Fig. 2 when γme is equal to 11 mJ m−2, but becomes readily attainable for γme values of 3.5 and 5.5 mJ m−2. For example, the characteristic point for a pair of polymorphs where γst/γme = 0.8 and  is equal to 2 falls in the stable zone when Ame = 1 but is in the metastable zone when Ame = 103 where γme is equal to 3.5 or 5.5 mJ m−2. This is the situation outline in Table 1 for famotidine.13 In that case the reported value of γst = 9.16 mJ m−2 and γme = 14.36 mJ m−2, i.e. γst/γme = 0.64. The reported ratio of
is equal to 2 falls in the stable zone when Ame = 1 but is in the metastable zone when Ame = 103 where γme is equal to 3.5 or 5.5 mJ m−2. This is the situation outline in Table 1 for famotidine.13 In that case the reported value of γst = 9.16 mJ m−2 and γme = 14.36 mJ m−2, i.e. γst/γme = 0.64. The reported ratio of  is less than 1.3. In these circumstances we would predict that the metastable form becomes kinetically attainable provided that the ratio of Ame/Ast is high. The reported ratio is 109/1.25 × 104 = 105. Both polymorphs can be attained; the kinetically favoured metastable form and the stable form which can be formed through a solution mediated transformation into the stable form.
is less than 1.3. In these circumstances we would predict that the metastable form becomes kinetically attainable provided that the ratio of Ame/Ast is high. The reported ratio is 109/1.25 × 104 = 105. Both polymorphs can be attained; the kinetically favoured metastable form and the stable form which can be formed through a solution mediated transformation into the stable form.
Fig. 3 presented the influence of applied supersaturation. Three values of Sst are considered, namely, 3, 5 and 8 and the value of γme is set at 5.5 mJ m−2. The original domain lines where Ame = Ast = 1 are presented for each supersaturation. Superimposed are the corresponding domain lines when Ame = 103 is applied at each supersaturation. At all supersaturations applied there was a significant expansion of the zone where the metastable form of the polymorph pair was kinetically favoured. The extend of the expansion was greater at interfacial energies γme less than 5.5 mJ m−2 and less for higher values of γme.
Conclusions
Looking then at the overall conclusions of the influence of the pre-exponential factor in determining the relative sizes of the kinetically favoured metastable and stable zones for a polymorph pair, we can conclude that low values of interfacial energies lead to very significant expansion of the kinetically favoured zone for the metastable polymorph; the extent of the expansion depends on the ratio of Ame/Ast. The higher interfacial energies explored in this work lead to small and sometimes insignificant expansion of the kinetic metastable zone. The general conclusion of ref. 1 still stands, namely that for a given polymorph pair, higher supersaturations kinetically favour the metastable form although the extent of the expansion is similar for all supersaturation explored in the range Sst = 3–8. The observation that above 2 are rarely encountered for polymorph pairs still stands although the kinetically favoured metastable zone does expand when the ratio of Ame/Ast increases. The attainment of
above 2 are rarely encountered for polymorph pairs still stands although the kinetically favoured metastable zone does expand when the ratio of Ame/Ast increases. The attainment of 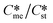 above 2 in a limited number of polymorph pairs may well be possible in circumstances where Ame/Ast is large. This work has also expanded the application of the domain diagrams and explains how metastable polymorphs are kinetically favoured in circumstances where γme > γst, namely through the occurrence of very high Ame/Ast values.
above 2 in a limited number of polymorph pairs may well be possible in circumstances where Ame/Ast is large. This work has also expanded the application of the domain diagrams and explains how metastable polymorphs are kinetically favoured in circumstances where γme > γst, namely through the occurrence of very high Ame/Ast values.
Conflicts of interest
There is no conflict to declare.Acknowledgements
Results incorporated in this standard have received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 101026339. KH thank the Science Foundation Ireland (SFI) for support (award Grant Numbers 12/RC/2275_P2).References
- V. Verma and B. K. Hodnett, CrystEngComm, 2018, 20(37), 5551 RSC.
- Y. A. Abramov, Org. Process Res. Dev., 2013, 17(3), 472 CrossRef CAS.
- Y. A. Abramov, J. Phys. Chem. A, 2011, 115(45), 12809 CrossRef CAS PubMed.
- Y. A. Abramov and K. Pencheva, in Chemical Engineering in the Pharmaceutical Industry, ed. D. J. A. Ende, Wiley, 2019, ch. 22, pp. 405–518, DOI:10.1002/9781119600800.
- J. Bauer, S. Spanton, R. Henry, J. Quick, W. Dziki, W. Porter and J. Morris, Pharm. Res., 2001, 18(6), 859 CrossRef CAS PubMed.
- J. Nyman and G. M. Day, CrystEngComm, 2015, 17(28), 5154 RSC.
- A. J. Cruz-Cabeza, S. M. Reutzel-Edens and J. Bernstein, Chem. Soc. Rev., 2015, 44(23), 8619 RSC.
- I. Stranski and D. Totomanow, Z. Phys. Chem., 1933, 163, 399 CrossRef.
- J. V. Parambil, S. K. Poornachary, S. J. Hinder, R. B. H. Tan and J. Y. Y. Heng, CrystEngComm, 2015, 17(33), 6384 RSC.
- J. V. Parambil, S. K. Poornachary, R. B. H. Tan and J. Y. Y. Heng, CrystEngComm, 2014, 16(23), 4927 RSC.
- S. Teychené and B. Biscans, Cryst. Growth Des., 2008, 8(4), 1133 CrossRef.
- W. Su, H. Hao, B. Glennon and M. Barrett, Cryst. Growth Des., 2013, 13(12), 5179 CrossRef CAS.
- J. Lu, X.-J. Wang, X. Yang and C.-B. Ching, Cryst. Growth Des., 2007, 7(9), 1590 CrossRef CAS.
- C. P. M. Roelands, S. Jiang, M. Kitamura, J. H. ter Horst, H. J. M. Kramer and P. J. Jansens, Cryst. Growth Des., 2006, 6(4), 955 CrossRef CAS.
- M. Mirmehrabi, S. Rohani, K. S. K. Murthy and B. Radatus, Cryst. Growth Des., 2006, 6(1), 141 CrossRef CAS.
- S. Jiang, J. H. ter Horst and P. J. Jansens, Cryst. Growth Des., 2008, 8(1), 37 CrossRef CAS.
- M. Kitamura, T. Hara and M. Takimoto-Kamimura, Cryst. Growth Des., 2006, 6(8), 1945 CrossRef CAS.
- P. Zhang, C. Zhang, R. Zhao, Y. Wan, Z. Yang, R. He, Q. Chen, T. Li and B. Ren, J. Chem. Eng. Data, 2018, 63(6), 2046 CrossRef CAS.
- C. P. M. Roelands, J. H. ter Horst, H. J. M. Kramer and P. J. Jansens, J. Cryst. Growth, 2005, 275(1), e1389 CrossRef CAS.
- L. Li, S. Zhao, Z. Xin and S. Zhou, J. Cryst. Growth, 2020, 538, 125610 CrossRef CAS.
- Y. Cao, S. Du, X. Ke, S. Xu, Y. Lan, T. Zhang, W. Tang, J. Wang and J. Gong, Org. Process Res. Dev., 2020, 24(7), 1233 CrossRef CAS.
- J. Ouyang, J. Chen, I. Rosbottom, W. Chen, M. Guo and J. Y. Y. Heng, CrystEngComm, 2021, 23(4), 813 RSC.
- S. S. Kadam, H. J. M. Kramer and J. H. ter Horst, Cryst. Growth Des., 2011, 11(4), 1271 CrossRef CAS.
- S. A. Kulkarni, S. S. Kadam, H. Meekes, A. I. Stankiewicz and J. H. ter Horst, Cryst. Growth Des., 2013, 13(6), 2435 CrossRef CAS.
- A. Maher, B. K. Hodnett, N. Coughlan, M. O'Brien and D. M. Croker, Org. Process Res. Dev., 2018, 22(3), 306 CrossRef CAS.
- E. Verdurand, C. Bebon, D. Colson, J. P. Klein, A. F. Blandin and J. M. Bossoutrot, J. Cryst. Growth, 2005, 275(1), e1363 CrossRef CAS.
- B. de Souza, G. Cogoni, R. Tyrrell and P. J. Frawley, Cryst. Growth Des., 2016, 16(6), 3443 CrossRef CAS.
- R. R. E. Steendam, L. Keshavarz, M. A. R. Blijlevens, B. de Souza, D. M. Croker and P. J. Frawley, Cryst. Growth Des., 2018, 18(9), 5547 CrossRef CAS.
- D. Erdemir, A. Y. Lee and A. S. Myerson, Acc. Chem. Res., 2009, 42(5), 621 CrossRef CAS PubMed.
- J. W. Mullin, Crystallization, Elsevier, 2001 Search PubMed.
- Q. Li and Y.-S. Jun, Commun. Chem., 2018, 1(1), 56 CrossRef.
- C. Brandel and J. H. ter Horst, Faraday Discuss., 2015, 179(0), 199 RSC.
- R. J. Davey, S. L. M. Schroeder and J. H. ter Horst, Angew. Chem., Int. Ed., 2013, 52(8), 2166 CrossRef CAS PubMed.
- D. Kashchiev, Nucleation, Elsevier, 2000 Search PubMed.
- J. H. ter Horst and D. Kashchiev, J. Chem. Phys., 2003, 119(4), 2241 CrossRef CAS.
- J. Zeglinski, M. Kuhs, D. Khamar, A. C. Hegarty, R. K. Devi and Å. C. Rasmuson, Chem. – Eur. J., 2018, 24(19), 4916 CrossRef CAS PubMed.
- D. Mealey, D. M. Croker and Å. C. Rasmuson, CrystEngComm, 2015, 17(21), 3961 RSC.
- D. Mealey, J. Zeglinski, D. Khamar and Å. C. Rasmuson, Faraday Discuss., 2015, 179(0), 309 RSC.
- C. Heffernan, M. Ukrainczyk, J. Zeglinski, B. K. Hodnett and Å. C. Rasmuson, Cryst. Growth Des., 2018, 18(8), 4715 CrossRef CAS.
- C. A. Pons Siepermann and A. S. Myerson, Cryst. Growth Des., 2018, 18(6), 3584 CrossRef CAS.
- K. Bodnár, S. P. Hudson and Å. C. Rasmuson, Cryst. Growth Des., 2019, 19(2), 591 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |