Controlling desolvation through polymer-assisted grinding

Abstract

We demonstrate the ability to controllably desolvate a crystal-solvate system in a step-wise fashion through polymer-assisted grinding by varying the type and proportion of polymer agent used. A plausible mechanistic explanation is proposed based on a combination of experimental evidence and computational analysis. Specifically, Raman spectroscopy, total scattering pair distribution function analysis and computed reaction energies suggest that the desolvation process is associated with preferred interactions between the solvent molecules and specific polymers. This approach could potentially be extended to any type of material, including heat-sensitive materials, where classical desolvation by thermal processes is not possible, and provides an additional route for formulation processing.

---

Introduction

Desolvation involves removing solvent molecules from a substrate, an active site, or from within a structure. It can occur during the processing of food¹ or pharmaceuticals,² organic synthesis,³ and activation of porous compounds.^4,5 As with solvate formation, desolvation is also an important lever for controlling the physicochemical properties, stability, and reactivity of a specific solid product. The primary method for inducing desolvation is through heating. Examples of uncontrolled desolvation as a consequence of combining heat and process-induced stresses have been reported.^6,7 For example, Raijada et al.⁸ explored the combination of heating and the addition of a polymer through hot melt extrusion for investigating the dehydration of nitrofurantoin monohydrate. Interestingly, the released water remained in the molten polymer during heating and had a plasticizing effect on the drug–polymer mixture.⁹

Mechanochemistry^10–13 is well established in providing suitable conditions for obtaining different solid forms of the same molecule or molecular system.^13–16 However, its application specifically for desolvation processes is not yet widely studied. To the best of our knowledge, only one study¹⁷ has reported the conversion of discrete complexes to corresponding coordination networks by mechanochemical dehydration using liquid-assisted grinding (LAG). Mechanochemical dehydration was observed to be more effective than heating or immersion in bulk solvents. Work by Strobridge et al.¹⁸ suggests that the efficiency of hydration and dehydration processes through LAG can be adjusted by modification of water activity, e.g. by the addition of small amounts of liquid during LAG reactions. Meanwhile, Hasa et al.¹⁹ have recently reported that polymer-assisted grinding (POLAG) is efficient for the dehydration of carbamazepine dihydrate.²⁰

Herein, we demonstrate the possibility to control the solvate stoichiometry of an organic system through POLAG-based mechanochemical desolvation. We suggest that the driving force to remove solvent molecules from the solvate by POLAG involves different affinities between the selected polymer and solvent molecules.²¹ If we consider the POLAG process to be an equilibrium between desolvation ↔ solvation, then the energy of binding of the solvent molecule with a specific site of the polymer chain would be crucial for moving such equilibrium towards desolvation. In other words, the thermodynamic driving force of the reverse process (solvate formation) during mechanochemical desolvation would decrease if the solvent molecules are already stabilized within a polymeric network. Therefore, adjusting the polymer chemistry and amount used should enable the regulation of the desolvation rate in the solid state.

Results and discussion

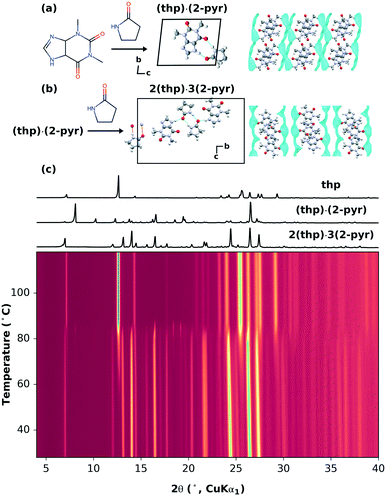
A recent mechanochemical solvate screen using theophylline (thp) and 2-pyrrolidinone (2-pyr), a solvent with negligible vapor pressure,²² resulted in two different stoichiometric solvates: theophylline-2-pyrrolidinone monosolvate (thp)·(2-pyr) and sesquisolvate 2(thp)·3(2-pyr).²² Either solvate could be obtained through both mechanochemical synthesis and cooling crystallization, and were stable at room temperature. As shown in Fig. 1(a and b), the hydrogen bonding motifs found in the two solvates are different. In (thp)·(2-pyr), heterodimers are formed between thp and 2-pyrvia two N–H⋯O hydrogen bonds. In 2(thp)·3(2-pyr), 2-pyr molecules form homodimers, one of which additionally interacts with two thp molecules via single N–H⋯O hydrogen bonds.

Fig. 1 (a) Molecular structures of thp and 2-pyr and the crystal structure of (thp)·(2-pyr). (b) Crystal structure of 2(thp)·3(2-pyr). The packing of thp molecules is highlighted on the far right, with the locations of 2-pyr molecules represented by a turquoise hypersurface. (c) The variable-temperature XRPD patterns of 2(thp)·3(2-pyr) heated from 28 °C to 130 °C at a rate of 1 °C min⁻¹.

Here, 2(thp)·3(2-pyr) provides a system for investigating the possibility of removing solvate molecules in a stepwise fashion i.e. 2(thp)·3(2-pyr) → (thp)·(2-pyr) → thp (form II)²³ and controlling the extent of removal within a given step. We first tested this by thermal routes. Thermogravimetry and calorimetry experiments previously demonstrated that non-isothermal heating of 2(thp)·3(2-pyr) results in a primarily one-step desolvation process (the associated TGA data are reproduced from Hasa et al. in ESI† Fig. S2).²² In the present study, we have carried out systematic variable-temperature X-ray powder diffraction (VT-XRPD) measurements at heating rates of 1, 5, and 10 °C min⁻¹, and the data are shown in Fig. 1(c) and ESI† Fig. S3 and S4, respectively. These measurements confirm that desolvation begins around 80–90 °C, where the 2(thp)·3(2-pyr) transforms into pure thp. At the slowest heating rate of 1 °C min⁻¹, (thp)·(2-pyr) is observed as a transient minority phase just above 80 °C.

We then tested the possibility for stepwise desolvation via mechanochemical milling. All milling experiments were run for 60 min (further details in ESI† section S3.1). First, neat milling of preformed 2(thp)·3(2-pyr) was performed. This did not result in any significant desolvation (ESI† Fig. S5). Next, a series of POLAG experiments were carried out using 200 mg of preformed 2(thp)·3(2-pyr) with varying amounts of different polymers. The repeat units for the polymers used are shown in ESI† Fig. S1. The mass ratio of polymer additive to reactant mass is designated as δ for the POLAG reactions here,²⁴ and the experiments were performed over a range of δ = 0.05–0.75. XRPD patterns of the products were measured, and multiphase Rietveld refinements^25–27 were performed to track the trends in phase transformation within the POLAG products. The resulting trends in phase fractions are plotted in Fig. 2.

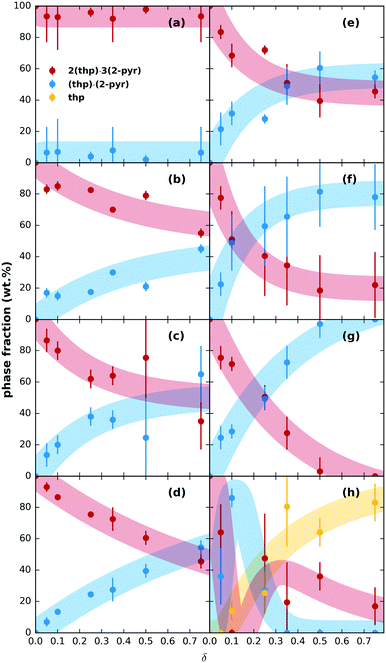Fig. 2 Relative phase fractions of 2(thp)·3(2-pyr), (thp)·(2-pyr), and pure thp with qualitative trends (thick shaded lines) of solid products after milling for 60 min with different amounts of polymer (given as a function of δ) for (a) PAM, (b) Kolliphor®, (c), PVP, (d) PVA, (e) PEGDME, (f) P4VP, (g) PEG, (h) PAA. Bars on the data points represent three standard deviations of the extracted values, and the trends were roughly approximated by fitting an appropriately shaped function to the extracted phase fractions (see ESI† for details).

The trends in phase transformation show three different outcomes: (1) no significant desolvation, (2) partial or (3) stepwise desolvation. The first outcome was observed for poly(acrylamide) (PAM), Fig. 2(a), where 2(thp)·3(2-pyr) remained the predominant phase even at δ = 0.75. The second outcome was the most common. Desolvation to pure (thp)·(2-pyr) was observed for poly(ethylene glycol) 1000 (PEG), Fig. 2(g). Most other polymers led to a partial transformation to (thp)·(2-pyr) to varying extents, Fig. 2(b–f), intermediate to the results for PAM and PEG. These polymers include poly(4-vinylpyridine) (P4VP) and derivatives of PEG (1. PEG dimethyl ether (PEGDME) where the OH groups of PEG are replaced with methyl groups, and 2. Kolliphor® P188, which is a poly(propylene oxide)–poly(ethylene oxide) triblock copolymer). Interestingly, grinding with polyvinylpyrrolidone (PVP), which is the polymer of 2-pyr, also resulted in only a partial transformation. Finally, the third outcome was observed for poly(acrylic acid) (PAA), Fig. 2(h). Low δ values led to a transformation of 2(thp)·3(2-pyr) into (thp)·(2-pyr), while pure thp (form II) became the predominant product at δ values in the range 0.35–0.75. The associated XRPD patterns for all samples can be found in ESI† Fig. S6–S13.

On further inspection of the trends at lower δ in Fig. 2, the amount of 2-pyr molecules supported by a given amount of polymer appears to be saturable, so more polymer is required to drive further desolvation. However, the total amount of desolvation achievable for a given polymer also appears to have limits. For instance, POLAG reaction with PVP and P4VP were extended to δ = 2.0 (extended plots shown in ESI† Fig. S14). The amount of transformation from 2(thp)·3(2-pyr) into (thp)·(2-pyr) appears to asymptote to ∼50% for PVP, and to ∼80% for P4VP with little change from δ = 0.5 to 2.0. For PEG, transformation to (thp)·(2-pyr) appears to go to 100% by δ ∼ 0.5. It is likely that different POLAG conditions can alter this behavior. Overall, our results reveal that the extent of desolvation through POLAG depends on both the type and amount of polymer. Controlled variation in other experimental parameters including the milling time, frequency, or the amount of the preformed solvate were not explored here, but could provide additional means to further optimize the selectivity.

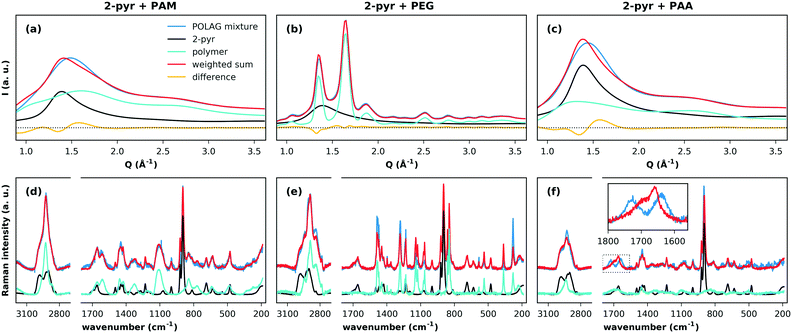
Based on the polymer screening presented above, PAM, PEG, and PAA were chosen as a basis to further investigate the driving forces underlying the desolvation behavior. Two sets of POLAG experiments were carried out. First, the given polymers and 2(thp)·3(2-pyr) were milled with δ = 0.75. Second, we also milled the polymers with either pure 2-pyr or pure thp using the same molar ratios of 2-pyr or thp as in the case with 2(thp)·3(2-pyr). Further details are given in ESI† section S3.2.1. The latter set of experiments gives us the opportunity to search for signals indicating specific interactions between pure 2-pyr or pure thp and the polymers. We could then look for these corresponding signals in the results for the POLAG experiments with 2(thp)·3(2-pyr). The phase pure samples and corresponding POLAG products were characterized using pattern fitting analysis of Raman spectra,²⁸ X-ray total scattering data, and the associated pair distribution functions (PDFs)^29–35 (see ESI† section S3.2). Raman allows us to probe changes in the molecular environments, while the XRPD and PDF data give insights into long- and short-range correlations in atomic density. For crystalline samples, XRPD measurements and Rietveld refinement were also further utilized.

We first discuss the effects of grinding the polymers with pure 2-pyr. The high-energy XRPD patterns for the milled 2-pyr-polymer mixtures and pure components are compared in Fig. 3(a–c). Each pattern was fitted by a weighted sum of the diffraction patterns of the pure components, and differences between the observed pattern and weighted sum in all three cases indicate changes in one or both of the pure phase structures. Since PEG is crystalline, this misfit for 2-pyr-PEG could simply result from a decrease in the crystallite size of PEG. These changes could also result from the take-up of 2-pyr, but this is unclear. The patterns for PAM and PAA on the other hand show that they are completely amorphous. The first sharp diffraction peaks for the amorphous mixtures with PAM and PAA cannot be described as a two-phase mixture of the pure components, and this suggests mixing at a molecular level. The associated Raman spectra and fits are shown in Fig. 3(d–f). For 2-pyr-PAM, all the peaks in the spectrum can be explained by the pure components. For 2-pyr-PEG, the peaks can also be explained by the pure components, but with misfits in the relative intensities that suggest modifications to the structure of PEG. Finally, the most notable case is for 2-pyr-PAA, which shows a significant modification to the bands from 1600–1780 cm⁻¹. The sharp peak at ∼1660 cm⁻¹ may be associated with the ν(C=O) stretch band (amide I) of 2-pyr,³⁶ where the broad shoulder feature at higher wavenumber may reflect the distribution of e.g. hydrogen bonding environments in the liquid state. The splitting of this peak into two distinct bands for 2-pyr-PAA gives direct evidence for distinctly different interaction environments for 2-pyr after grinding with PAA. Expanded plots for all Raman spectra and fits can be found in ESI† section S4.6.

Fig. 3 Measured, background-subtracted XRPD patterns of the pure components and mixtures obtained from milling 2-pyr with (a) PAM, (b) PEG, and (c) PAA. The corresponding Raman spectra are given in (d)–(f). Here, both XRPD and Raman spectra were assessed by least squares fitting of the background subtracted, pure component patterns. The boxed region in (f) highlights a zoomed view of modified peaks that are not explained by the pure component spectra.

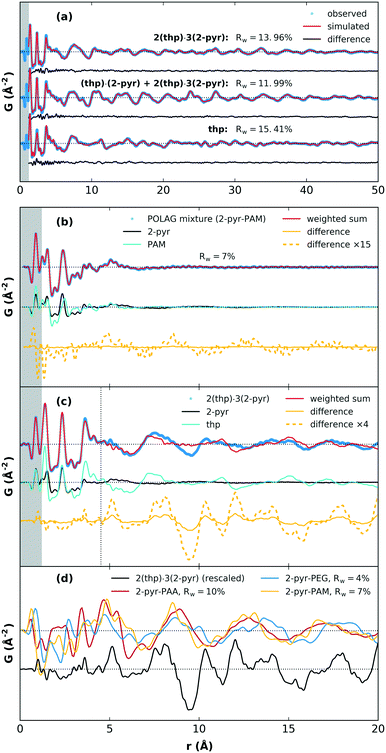
We next discuss the PDF analysis for products of POLAG with 2-pyr. PDF analysis in particular is a useful technique for distinguishing structural signals related to changes in local interactions and short-range order in molecular systems.^37–40 As a reference point for the assessment of materials with known structures, the crystal structure models for 2(thp)·3(2-pyr), (thp)·(2-pyr), and thp were refined to obtain the best match between simulated and experimental PDFs. The fits show very good agreement, Fig. 4(a). Model refinement was not feasible for the amorphous mixtures from the mechanomilling runs since we do not have accurate models of these complex materials. As an alternative, the structuring could be investigated by comparison of PDFs from the POLAG samples with linear combinations of the pure constituent phase datasets (Fig. 4(b), ESI† section S4.5). This also resulted in good agreement (e.g. R_w = 7% for PAM). Thus, most of the PDF signal of the POLAG samples can be explained as linear combination of polymer and 2-pyr structure, allowing a direct measurement of phase mixtures. However, close inspection reveals some signals in the difference curve (between the POLAG sample and the best-fit linear combinations) suggesting additional structural modifications in the constituents produced by the POLAG process. In particular, a long-wavelength oscillation in the difference curve may indicate modifications to the intermolecular packing, similar to that observed in amorphous drug–polymer dispersions^37,41 and saccharide mixtures.^42,43 As a further example, in Fig. 4(c), we show a similar comparison in which 2(thp)·3(2-pyr) is fit by the pure constituent phase thp and 2-pyr. Here, the fit is very good up to around 4–5 Å where the signal is dominated by the intramolecular structures. However, there are different intermolecular crystalline packing arrangements between thp and 2(thp)·3(2-pyr), and also a different local arrangement of 2-pyr in the liquid state. This is evidenced by peaks in the difference curve seen around 2.8–3.8 Å that correspond to the changed formation of N–H⋯O connections. At higher distances, a substantially larger difference is observed, which corresponds to the differences in intermolecular packing density between thp and 2(thp)·3(2-pyr) when they exhibit molecular level mixing. In general, the positive and negative signals in these difference curves represent an increase or decrease in the average density of the mixture with respect to the weighted contributions of pure components at a given distance. The resulting difference curves from all three POLAG mixtures with 2-pyr are plotted in Fig. 4(d) compared to the difference from the model case of 2(thp)·3(2-pyr) in Fig. 4(c). The long distance oscillations for 2-pyr-PAM and 2-pyr-PAA show a similar frequency while 2-pyr-PEG shows oscillations with a slightly different frequency. This may reflect the fact that PAM and PAA have amide and carboxyl groups respectively with the same frequency along the backbone that could act as preferential interaction sites for 2-pyr. PEG, on the other hand, is a polyether with no side groups. Thus, we could expect different modifications to the density distributions based on the different orientations 2-pyr might assume with respect to the polymers. We note that the difference in the wavelength of the oscillation of the residual versus that of liquid 2-pyr rules out that the observed oscillations are simply over-subtracted liquid 2-pyr. Distinct, sharp features are present in the residual from 2-pyr-PAA over a range of 3 < r < 6 Å. These are most likely coming from the addition or removal of specific bonding interactions between solvent and polymer molecules. This is supported by the similarity to the features observed in the model difference curve for 2(thp)·3(2-pyr) over this range. This then likely represents the local structural modification corresponding to the spectroscopic changes seen in the Raman spectrum.

Fig. 4 (a) Results of crystal structure model refinement to the PDFs of solvates and pure thp (form II), (b) POLAG mixture of 2-pyr-PAM described by summation of the pure components, (c) 2(thp)·3(2-pyr) compared to a summation of thp and 2-pyr, and (d) a comparison of the differences from pure component fits to 2-pyr-PAM, 2-pyr-PEG, 2-pyr-PAA, and 2(thp)·3(2-pyr) showing modifications to average atomic density correlations. The differences were obtained using a lower Q_max cutoff of the total scattering.

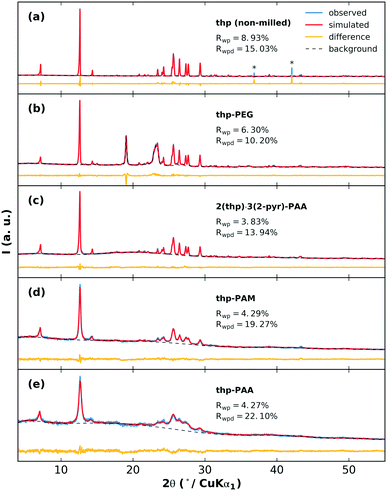
The effects of grinding the polymers with pure thp are next examined. The XRPD patterns of the milled thp-polymer mixtures and associated fits from Rietveld refinement are shown in Fig. 5. In each case, crystalline thp remains in the product but with varying extents of crystallite size reduction and/or structural disorder indicated by broadened diffraction peaks and increased diffuse scattering. The thp products in order from largest to smallest crystallite size are non-milled thp, thp-PEG, 2(thp)·3(2-pyr)-PAA, thp-PAM, thp-PAA. Modifications to small molecule crystallite size and size distribution on co-grinding with polymers is a well-established phenomenon and therefore not surprising in this case.⁴⁴ Differences between the POLAG samples and pure components of the thp-polymer mixtures observed by Raman and PDF (ESI† sections S4.5 and S4.6) suggest that the crystallite size reduction is accompanied by structural modifications to thp. The difference signal in the PDF could not be unambiguously identified by a modified thp form II structure or other known^45–47 or proposed⁴⁸ polymorphs (ESI† Fig. S42). We cannot rule out the possibility of nanocrystalline form III,⁴⁹ though no structure is currently available to confirm this. We note the following: (1) thp always remains, (2) the extent of crystallite size reduction does not strongly correlate with the polymers achieving the best desolvation, and (3) the thp product from milling 2(thp)·3(2-pyr)-PAA is more ordered than thp milled with PAA alone. The last point suggests that the processes related to mechanical disordering differ in the presence of 2-pyr. Thus, this is not likely the primary factor determining the mechanochemical desolvation behavior.

Fig. 5 Measured XRPD patterns and simulated patterns from Rietveld refinement for thp (a) without milling, and the POLAG products from (b) thp-PEG (background contains contribution from crystalline PEG), (c) 2(thp)·3(2-pyr)-PAA, (d) thp-PAM, and (e) thp-PAA. Relative crystallite size decreases from (a) to (e); asterisks (*) in panel (a) mark aberrations from the detector, which were excluded from the refinement.

Finally, having investigated the POLAG mixtures with 2-pyr or thp, we can look at the results for the target system of POLAG with 2(thp)·3(2-pyr). In this case, Rietveld refinements could again be used to track the extent of phase transformation (ESI† section S4.3). We observed minimal but similar levels of transformation from 2(thp)·3(2-pyr) to (thp)·(2-pyr) for both PAM and PEG under these conditions, but as expected, complete transformation to thp for PAA. Differences in the result for PEG here could be caused by slight changes either in the equipment used or the amount of material used in the reaction. These resulting Raman and PDF data were also subjected to multicomponent pattern fitting as above. Here additional components were added to the fits to account for the signals that could be expected due to the contributions from 2-pyr-polymer and thp-polymer. In particular, the signals of the 2-pyr-PAA and thp-PAA structural modification were detected by both PDF and Raman pattern fitting to the POLAG mixture of 2(thp)·3(2-pyr)-PAA (ESI† Fig. S36 and S50). This suggests that the desolvation of 2-pyr from 2(thp)·3(2-pyr) with PAA occurs via a similar mode of interaction observed in the POLAG product for 2-pyr-PAA. Thus, while it appears that 2-pyr can interact with each polymer investigated, at least from the liquid state, the development of distinct molecular environments and structural correlations on grinding either liquid 2-pyr or 2(thp)·3(2-pyr) with PAA results in a more favorable interaction between the PAA and 2-pyr, relative to PAM or PEG. This further drives the desolvation towards the pure unsolvated thp form II, as observed experimentally. We should also consider that the occurrence of signal resembling that of thp-PAA coincides with the largest degree of crystallite size reduction for this sample (Fig. 5(e)). This may suggest that the disordering effect seen on grinding thp-PAA may also be associated with some degree of mixing, and this may also contribute to the behavior seen for 2(thp)·3(2-pyr).

It is important to note that the polymers tested in this study are expected to absorb atmospheric moisture, to varying extents,⁵⁰ and such water content can potentially affect the ability to stabilize the removed 2-pyr molecules. However, this does not appear to be the primary factor for the observed desolvation effects. PAM, PEG, and PAA, for example, are all used in superabsorbent polymer technologies, but show widely varying desolvation behaviors for 2(thp)·3(2-pyr). Published sorption data (e.g. for PVP, P4VP, PAA, or PEG)^50–53 do not appear to suggest a clear correlation with relative desolvation behaviors, although moisture sorption can depend on specific chain length, polymer crystallinity, temperature, relative humidity, states of absorbed water, etc.^51,54 Thus, follow-up investigation of possible effects of moisture content may be warranted. Regardless, the observed behaviors could be justified without considering water, as follows.

To further understand the origin of the observed behavior, models for specific intermolecular interactions were prepared and reaction energies were computed as the sum of product energies minus the sum of reactant energies (weighted by the appropriate stoichiometries) using the Molecular Mechanics COMPASS-II forcefield⁵⁵ as implemented in Materials Studio. Since these are supramolecular reactions, such computations involve the calculation of the stability of all condensed phases involved. Lattice energies for crystalline systems were calculated by geometry optimization of their experimental crystal structures as found in the Cambridge Crystallographic Database: thp form II (BAPLOT01),⁴⁷ (thp)·(2-pyr) (PICMOG),²² and 2(thp)·3(2-pyr) (PICMIA).²² Consistent calculation of amorphous energies for all polymer and (polymer)·(2-pyr) systems required a comprehensive procedure to generate realistic amorphous models that were then geometry optimized (see ESI† section S5). Assuming that temperature and entropy effects are similar in reactants and products (i.e., they can be neglected), the reaction energy was used as a predictor of the reaction driving force.

For the 2(thp)·3(2-pyr) to (thp)·(2-pyr) conversion, reaction energies with all three polymers were computed to be negative (−1, −6, and −27 kJ mol⁻¹ for PEG, PAM, and PAA respectively) suggesting that all three polymers are in principle capable of converting sesquisolvate to the monosolvate. However, for the (thp)·(2-pyr) to thp conversion, only the reaction with PAA was computed to be negative (−18 kJ mol⁻¹) suggesting that only PAA is capable of further desolvating the monosolvate into pure thp, in agreement with the experimental observations. Solvation of PAA was calculated to provide a significantly higher driving force than with PAM or PEG. PAM was found to be slightly more stabilizing than PEG, contrary to that observed experimentally, which may suggest important kinetic or other factors at play that are not considered by these models.

These reactions can also be understood as a balance between crystalline desolvation and polymer solvation. Thus, the reaction energy can be calculated as

ΔE_reaction = ΔE^crystal_desolvation + ΔE^polymer_solvation

where ΔE^crystal_desolvation involves the removal of 2-pyr from the crystalline solvate (desolvation, a positive term), and ΔE^polymer_solvation involves the stabilization of the polymer via insertion of 2-pyr into its amorphous matrix (solvation, a negative term). In the absence of a polymer (neat grinding), only crystal desolvation takes place, which is unfavorable thermodynamically and thus explains why neat-grinding of the solvates does not result in phase changes.²² Thus for the reaction to occur, the energy released upon solvation of the polymer must be greater than the energy required to desolvate the crystalline form (Fig. 6).

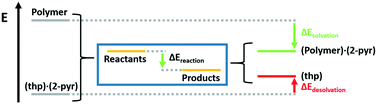Fig. 6 Scheme breaking down the reaction energy into the crystalline desolvation term and the polymer solvation term.

Solvation energies for the three polymers were calculated to be −67, −72, and −93 kJ mol⁻¹ for PEG, PAM, and PAA respectively. Crystal desolvation energies for 2(thp)·(2-pyr) and 2(thp)·3(2-pyr) were calculated to be −66 and −75 kJ mol⁻¹ respectively. These calculations support that PAA is the most active polymer and that desolvation of the monosolvate requires more energy than the sesquisolvate, because 2-pyr is more tightly bound to the thp molecules in the monosolvate than in the sesquisolvate structure.

Our previous study²² demonstrated that there is a favorable (negative) energy gain in forming 2(thp)·3(2-pyr) and that its formation involves (thp)·(2-pyr) as an intermediate product. In the present case, the thermodynamics of the system are altered by the presence of polymer, and the results above indicate that the driving force for desolvation of 2(thp)·3(2-pyr) depends strongly on the driving force for the solvation of the polymer, and thus on the polymer nature. In rationalizing the conversions, the system always goes to a state of lower energy. Thus upon milling of thp and 2-pyr only, the energy is progressively lowered in going from thp to (thp)·(2-pyr) to 2(thp)·3(2-pyr). Upon addition of polymers, the inverse reactions are observed because the polymer lowers its energy more than thp upon solvation with 2-pyr. The reaction energy is therefore a fine balance between the energy penalty needed to desolvate theophylline and the energy released upon solvation of the polymer.

Conclusions

In summary, we have shown the possibility of controlling desolvation of organic systems through POLAG by changing the amount and type of polymer. In general, there are two possible scenarios in a POLAG process. First, the polymer additive does not participate actively during the mechanochemical reactions. Such a case was previously demonstrated where the amount of the polymer additive does not significantly affect the kinetics of a solid state reaction.²⁴ In contrast, this study presents a second case where the polymer additive participates actively in the solid state reaction through specific interactions, and the amount used is crucial for obtaining the desired solid product.^20,56

A stepwise removal of solvent molecules from the selected solvate was not feasible through standard heating (with heating rates of 10, 5, and 1 °C min⁻¹), but milling for only 60 min in the presence of different polymers allowed for tuning the solvent removal from higher to lower stoichiometric solvation and even to the non-solvated solid. The combination of Raman spectroscopy and total scattering PDF analysis here has allowed us to specifically probe the vibrational and structural signals associated with these interactions. Features could be assigned to changes in hydrogen bonding interactions between the solvent 2-pyr in the liquid state versus in the polymer, and were subsequently observed to also occur in the case of desolvation from the solvate crystal.

Grinding with polymers (instead of heating alone) represents an important finding; that different polymers can remove only a certain amount of solvent from the crystal structure may open new avenues in the field of supramolecular chemistry. We believe that this process can be particularly useful for desolvating heat-sensitive materials, and for controlling solvation/desolvation processes in e.g. solid-state batteries. Finally, these experiments also highlight the importance of understanding the overall stability of multi-component mixtures and the various supramolecular forms that may result, as is important for tablets formulated as mixtures of solid-form active pharmaceutical ingredients and polymers.

Author contributions

MWT performed XRD, Raman, and PDF analysis. LM and MM performed the screening experiments. AJC devised and carried out the computational study. POO and JR performed the VT-PXRD experiments. ME provided resources and support for total scattering experiments. AS measured the Raman data. SJLB and RED provided useful discussion on the analysis and interpretation. DH conceptualized and supervised the work. MWT, AJC, and DH wrote the paper with review and input from all other authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

DH and MM would like to thank University of Trieste for partially funding this study through the “Fondo per la Ricerca di Ateneo (FRA 2020)” grant scheme. MWT gratefully acknowledges support from BASF. POO would like to acknowledge the Center for Intelligent Drug Delivery and Sensing Using Microcontainers and Nanomechanics (IDUN) funded by the Danish National Research Foundation (grant no. DNRF122) and the Velux Foundations (grant no. 9301) for funding of this project. JR would like to acknowledge funding from the Independent Research Fund Denmark [Grant No. 8022-00154B]. SJLB's contributions were supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences (DOE-BES) under contract No. DE-SC0012704. The authors acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for the provision of experimental facilities. Parts of this research were carried out at beamline P02.1. Open Access funding provided by the Max Planck Society.

Notes and references

1. J. M. Aguilera, A. Chiralt and P. Fito, Trends Food Sci. Technol., 2003, 14, 432–437.
2. U. J. Griesser, in Polymorphism: in the Pharmaceutical Industry, ed. R. Hilfiker, Wiley-VCH Verlag GmbH & Co. KGaA, 2006, pp. 211–233.
3. P. K. Kundu, G. L. Olsen, V. Kiss and R. Klajn, Nat. Commun., 2014, 5.
4. M.-L. C. Tong and X.-M. Chen, in Modern Inorganic Synthetic Chemistry, ed. R. Xu and Y. Xu, Elsevier, 2nd edn, 2017, pp. 189–217.
5. X. Zhang, Z. Chen, X. Liu, S. L. Hanna, X. Wang, R. Taheri-Ledari, A. Maleki, P. Li and O. K. Farha, Chem. Soc. Rev., 2020, 49, 7406–7427.
6. S. Thakral, R. Govindarajan and R. Suryanarayanan, in Polymorphism in the Pharmaceutical Industry: Solid Form and Drug Development, ed. R. Hilfiker and M. von Raumer, Wiley-VCH Verlag GmbH & Co. KGaA, 2nd edn, 2019, pp. 329–380.
7. G. G. Z. Zhang, D. Law, E. A. Schmitt and Y. Qiu, Adv. Drug Delivery Rev., 2004, 56, 371–390.
8. D. Raijada, L. Arnfast, A. D. Bond, J. Aho, J. Bøtker, N. Sandler and J. Rantanen, Cryst. Growth Des., 2017, 17, 3707–3715.
9. L. Arnfast, J. van Renterghem, J. Aho, J. Bøtker, D. Raijada, S. Baldursdóttir, T. De Beer and J. Rantanen, Pharmaceutics, 2020, 12, 116.
10. E. Boldyreva, Chem. Soc. Rev., 2013, 42, 7719.
11. T. Friščić, C. Mottillo and H. M. Titi, Angew. Chem., Int. Ed., 2020, 59, 1018–1029.
12. Joseph L. Howard, Q. Cao and D. L. Browne, Chem. Sci., 2018, 9, 3080–3094.
13. S. L. James, C. J. Adams, C. Bolm, D. Braga, P. Collier, T. Friščić, F. Grepioni, K. D. M. Harris, G. Hyett, W. Jones, A. Krebs, J. Mack, L. Maini, A. G. Orpen, I. P. Parkin, W. C. Shearouse, J. W. Steed and D. C. Waddell, Chem. Soc. Rev., 2012, 41, 413–447.
14. J.-L. Do and T. Friščić, ACS Cent. Sci., 2017, 3, 13–19.
15. T. Friščić, A. V. Trask, W. Jones and W. D. S. Motherwell, Angew. Chem., 2006, 118, 7708–7712.
16. D. Hasa and W. Jones, Adv. Drug Delivery Rev., 2017, 117, 147–161.
17. P. Wang, G. Li, Y. Chen, S. Chen, S. L. James and W. Yuan, CrystEngComm, 2012, 14, 1994.
18. F. C. Strobridge, N. Judaš and T. Friščić, CrystEngComm, 2010, 12, 2409.
19. D. Hasa, G. Schneider Rauber, D. Voinovich and W. Jones, Angew. Chem., 2015, 127, 7479–7483.
20. D. Scaramuzza, G. Schneider Rauber, D. Voinovich and D. Hasa, Cryst. Growth Des., 2018, 18, 5245–5253.
21. T. Kawakami, I. Shigemoto and N. Matubayasi, J. Chem. Phys., 2012, 137, 234903.
22. D. Hasa, M. Pastore, M. Arhangelskis, B. Gabriele, A. J. Cruz-Cabeza, G. S. Rauber, A. D. Bond and W. Jones, CrystEngComm, 2019, 21, 2097–2104.
23. Y. Ebisuzaki, P. D. Boyle and J. A. Smith, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1997, 53, 777–779.
24. L. S. Germann, S. T. Emmerling, M. Wilke, R. E. Dinnebier, M. Moneghini and D. Hasa, Chem. Commun., 2020, 56, 8743–8746.
25. R. E. Dinnebier, A. Leineweber and J. S. O. Evans, Rietveld refinement: practical powder diffraction pattern analysis using TOPAS, Walter de Gruyter GmbH & Co KG, 2018.
26. H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71.
27. A. A. Coelho, J. Appl. Crystallogr., 2018, 51, 210–218.
28. M. J. Pelletier, Appl. Spectrosc., 2003, 57, 20A–42A.
29. S. J. L. Billinge, in International Tables for Crystallography Volume H: Powder diffraction, ed. C. J. K. Gilmore, J. A. Kaduk and H. Schenk, 2019, pp. 649–672.
30. T. Egami and S. J. L. Billinge, Underneath the Bragg peaks : structural analysis of complex materials, Elsevier, Amsterdam, 2012.
31. P. J. Chupas, X. Qiu, J. C. Hanson, P. L. Lee, C. P. Grey and S. J. L. Billinge, J. Appl. Crystallogr., 2003, 36, 1342–1347.
32. A. A. Coelho, P. A. Chater and A. Kern, J. Appl. Crystallogr., 2015, 48, 869–875.
33. A. P. Hammersley, S. O. Svensson, M. Hanfland, A. N. Fitch and D. Hausermann, High Pressure Res., 1996, 14, 235–248.
34. P. Juhás, T. Davis, C. L. Farrow and S. J. L. Billinge, J. Appl. Crystallogr., 2013, 46, 560–566.
35. X. Yang, P. Juhás, C. L. Farrow and S. J. L. Billinge, arXiv, 2015, arXiv:1402.3163v3.
36. R. M. Silverstein, F. X. Webster, D. J. Kiemle and D. L. Bryce, Spectrometric identification of organic compounds, Wiley, Hoboken, NJ, 2015.
37. G. L. B. de Araujo, C. J. Benmore and S. R. Byrn, Sci. Rep., 2017, 7, 46367.
38. M. W. Terban, E. Y. Cheung, P. Krolikowski and S. J. L. Billinge, Cryst. Growth Des., 2015, 16, 210–220.
39. M. W. Terban, L. Russo, T. N. Pham, D. H. Barich, Y. T. Sun, M. D. Burke, J. Brum and S. J. L. Billinge, Mol. Pharmaceutics, 2020, 17, 2370–2389.
40. M. W. Terban and S. J. L. Billinge, Chem. Rev., 2021, 122, 1208–1272.
41. V. D. N. Bezzon, F. F. Ferreira, P. Smith, C. J. Benmore, S. R. Byrn and G. L. B. de Araujo, Int. J. Pharm., 2021, 600, 120500.
42. E. A. Morrow, M. W. Terban, J. W. Lee, L. C. Thomas, S. J. L. Billinge and S. J. Schmidt, J. Food Eng., 2019, 261, 87–99.
43. E. A. Morrow, M. W. Terban, L. C. Thomas, D. L. Gray, M. J. Bowman, S. J. L. Billinge and S. J. Schmidt, J. Food Eng., 2019, 243, 125–141.
44. I. Colombo, G. Grassi and M. Grassi, J. Pharm. Sci., 2009, 98, 3961–3986.
45. K. Fucke, G. J. McIntyre, C. Wilkinson, M. Henry, J. A. K. Howard and J. W. Steed, Cryst. Growth Des., 2012, 12, 1395–1401.
46. D. Khamar, R. G. Pritchard, I. J. Bradshaw, G. A. Hutcheon and L. Seton, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2011, 67, o496–o499.
47. S. Zhang and A. Fischer, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2011, 67, o3357–o3357.
48. M. D. Eddleston, K. E. Hejczyk, E. G. Bithell, G. M. Day and W. Jones, Chem. – Eur. J., 2013, 19, 7883–7888.
49. K. Matsuo and M. Matsuoka, Cryst. Growth Des., 2007, 7, 411–415.
50. H. M. L. Thijs, C. R. Becer, C. Guerrero-Sanchez, D. Fournier, R. Hoogenboom and U. S. Schubert, J. Mater. Chem., 2007, 17, 4864.
51. J. A. Baird, R. Olayo-Valles, C. Rinaldi and L. S. Taylor, J. Pharm. Sci., 2010, 99, 154–168.
52. H. T. Oyama and T. Nakajima, J. Polym. Sci., Polym. Chem. Ed., 1983, 21, 2987–2995.
53. J. Teng, S. Bates, D. A. Engers, K. Leach, P. Schields and Y. Yang, J. Pharm. Sci., 2010, 99, 3815–3825.
54. R. M. Hodge, G. H. Edward and G. P. Simon, Polymer, 1996, 37, 1371–1376.
55. H. Sun, Z. Jin, C. Yang, R. L. C. Akkermans, S. H. Robertson, N. A. Spenley, S. Miller and S. M. Todd, J. Mol. Model., 2016, 22, 47.
56. D. Hasa, E. Carlino and W. Jones, Cryst. Growth Des., 2016, 16, 1772–1779.

---

Footnote

† Electronic supplementary information (ESI) available: Details of materials and experimental methods, experimental (PXRD, PDF, Raman) data and fits, and further details of computational study. See DOI: 10.1039/d2ce00162d

---