 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Competing crystallization of α- and β-phase induced by β-nucleating agents in microdroplets of isotactic polypropylene†
Enrico
Carmeli
ab,
Sara
Ottonello
a,
Bao
Wang
a,
Alfréd
Menyhárd
c,
Alejandro J.
Müller
 de and
Dario
Cavallo
de and
Dario
Cavallo
 *a
*a
aDipartimento di Chimica e Chimica Industriale, Università degli studi di Genova, via Dodecaneso 31, 16146 Genova, Italy. E-mail: dario.cavallo@unige.it
bBorealis Polyolefine GmbH, Innovation Headquarters, St. Peterstrasse 25, 4021, Linz, Austria
cDepartment of Physical Chemistry and Materials Science, Faculty of Chemical Technology and Biotechnology, Budapest University of Technology and Economics, 1111 Budapest, Hungary
dPolymat and Department of Polymers and Advanced Materials: Physics, Chemistry and Technology, Faculty of Chemistry, University of the Basque Country UPV/EHU, Paseo Manuel de Lardizabal 3, 20018, Donostia-San Sebastián, Spain
eIKERBASQUE, Basque Foundation for Science, 48009 Bilbao, Spain
First published on 16th February 2022
Abstract
The nucleation efficiency of substrates towards a specific polymer is usually based on empirical methods, which depend on the employed experimental conditions. A more quantitative method to study the efficiency of nucleating agents promoting polypropylene β-phase is reported here. When a polymer is dispersed into sufficiently small droplets, the overall crystallization kinetics is controlled by nucleation, as growth can be orders of magnitude faster than nucleation. Confinement of polypropylene containing the nucleating agent particles into micro-domains (i.e., droplets) within a polystyrene matrix allows the isolation of the nucleation process and the determination of the surface free energy difference, Δσ. This parameter describes the intrinsic nucleation efficiency of a particular nucleating agent. Isothermal crystallization measurements were performed for dispersed polypropylene droplets containing three nucleating agents which catalyze the formation of both α- and β-phase (N,N′-dicyclohexylterephthalamide, quinacridone quinone, and tris-2,3-dimethyl-hexylamide of trimesic acid), and the data were analyzed via a first-order kinetics model. According to the calculated Δσ values, the nucleating efficiency scale is DCHT > TATA > QQ for α-phase, while DCHT > QQ for β-phase, in spite of the higher total amount of β-crystals generated by QQ particles.
1 Introduction
Isotactic polypropylene (PP) is one of the most employed polymers. Since its discovery in the 1950s,1 its crystallization behavior has attracted the interest of many researchers, and, after seventy years, fascinating surveys are still being conducted. The rich polymorphism of PP includes the monoclinic (α), trigonal (β), and orthorhombic (γ) forms.2,3 Other recently discovered crystalline phases are the trigonal form (δ)4 and the ε-phase.5 For the sake of completeness, a structure with a degree of order intermediate between crystalline and amorphous phase, named mesophase, is typically obtained through fast cooling from the melt.6 In the absence of specific nucleators, PP crystallizes essentially in the α-phase (a = 6.65 Å, b = 20.96 Å and c = 6.5 Å). In contrast, β-phase (a = b = 11.01 Å, c = 6.5 Å) becomes the main form only when selective nucleating agents are introduced into the polymer because of its intrinsic low nucleation rate.7–9 The PP β-phase was discovered shortly after the first production of isotactic polypropylene, but its detailed structure involving frustration of the chain packing was established only in the 90s.10–12 PP rich in β-crystals shows different mechanical properties from PP containing α-crystals. Lower modulus of elasticity, lower yield stress, and higher ductility characterize β-phase-rich PP with respect to α-phase-rich PP. This is related to the absence of the cross-hatching morphology formed by the α-lamellae during the growth process, in which the tangential lamellae increase the stiffness of the spherulites.8,13Usually, nucleating agents that are selective to PP β-phase also induce the formation of the monoclinic polymorph of PP. This versatility is caused by the various possible epitaxies between substrate and α-phase.14 The γ-modification of linear trans-quinacridone was the first highly active β-nucleating agent introduced. However, it is not completely selective towards the β-form since it nucleates a non-negligible amount of α-phase.8,15,16 The dual specificity is due to the epitaxial growth that occurs in the presence of the 6.5 Å periodicity between the substrate and those two crystalline phases of PP.16 Quinacridone quinone (QQ), another pigment based on the phthalocyanines, shows greater nucleation efficiency towards the β-form than γ-quinacridone.17 Moreover, N,N′-dicyclohexylterephthalamide (DCHT), whose crystalline structure was only recently disclosed,10 was found to nucleate PP β-phase through epitaxial growth10,18 due to a 6.5 and a 20 Å periodicity between the (001) DCHT plane and the (110) plane of PP β-form. PP α-crystals are nucleated by DCHT, although in minor amounts due to the higher potential energy involved in the interaction between the chains of the polymer and the cyclohexyl groups in DCHT molecules.10,18 Another substance with dual nucleating ability is tris-2,3-dimethyl-hexylamide of trimesic acid (TATA). The ability of this substance to enhance the crystallization rate of PP β-form has been recently studied.19,20 The amount of β-phase developed by TATA was reported to decrease after reaching a maximum at circa 10–100 ppm.20 Although several other substances were found to promote the formation of PP β-phase crystals,7,8,21–24 the present investigation focuses on QQ, DCHT and TATA.
The comparison of the nucleation efficiency between different nucleating agents is usually made empirically via non-isothermal experiments with differential scanning calorimetry (DSC), i.e., by detecting the enhancement of the crystallization temperature in the nucleated systems.25–28 Another method based on self-nucleation experiments was proposed by Fillon et al.25,29 It consists of comparing the enhancement of crystallization temperature caused by the presence of self-nuclei in the melt and by the added nucleating agent. Therefore, a relative efficiency scale can be obtained. However, a more intrinsic comparison implies the measurement of the actual nucleation rates, which are not commonly assessed in efficiently nucleated systems unless via indirect methods.30,31 In this respect, a method has been recently proposed that permits studying the absolute nucleation rate and the selectivity towards α- and/or β-phase for specific polymer/substrate pairs. The crystallizing polymer is confined into small domains within an inert matrix.32–36 If the dimension of the dispersed domains is at the micrometer scale, some droplets are free from the heterogeneities that favor nucleation, and, consequently, fractionated crystallization is observed.37 Indeed, domains containing the nucleating agent particle will nucleate at low undercooling (heterogeneous nucleation), while droplets free from any heterogeneity will nucleate at higher undercooling via homogeneous or surface-induced nucleation. It is noteworthy that due to the small dimensions of the dispersed phase, the growth time becomes negligible with respect to the time needed for nucleation to occur. Thus, the nucleation process can be isolated from the contribution of the crystal growth to the overall crystallization process. Furthermore, the direct measurement of the nucleation rate allows the calculation of the surface free energy difference (Δσ). Δσ describes the correlation between the surface tension properties of the substrate, the polymer crystal, and the polymer melt. In other words, Δσ corresponds to the difference in the system's surface free energy achieved with the replacement of a substrate/melt interface with a substrate/crystal and a crystal/melt interface. Given its independence of the experimental conditions and of the concentration of the nucleating agent in the polymer, this parameter permits drawing a universal efficiency scale.38,39
This method was already applied by us to study the nucleation efficiency of different substrates towards PP α-phase,40 and the present work is intended to extend the study to nucleating agents promoting PP β-phase. In particular, this article examines to what extent the crystallization rate of the α- and β-phase of PP can be enhanced by three nucleating agents, namely, DCHT, QQ, and TATA. DCHT and QQ induce both the α- and the β-phase to different extents, while TATA nucleates mainly the α-phase in the employed systems. The specificity towards a specific crystalline phase of PP is investigated by means of isothermal crystallization experiments, and the value of the interfacial free energy difference, characterizing the nucleation efficiency of the three substrates, is provided.
2 Experimental
2.1 Materials
An isotactic polypropylene grade, provided by Borealis Polyolefine GmbH (Austria), with weight-average molecular weight (MW) and polydispersity index (MW/Mn) of 365 kg mol−1 and 5.4, respectively, was employed as the crystallizing phase. Moreover, an atactic polystyrene (PS) from Sigma-Aldrich with MW and MW/Mn of 350 kg mol−1 and 2.1, respectively, was used as an inert medium in the prepared blends. Finally, three nucleating agents were used. N,N′-Dicyclohexyl-terephthalamide and quinacridone quinone were kindly provided by Borealis Polyolefine GmbH, and tris-2,3-dimethyl-hexylamide of trimesic acid was synthesized by us and the detailed synthesis method was published earlier.202.2 Methods
| Blend | PS [wt%] | PP [wt%] | DCHT [wt% in PP] | QQ [wt% in PP] | TATA [wt% in PP] |
|---|---|---|---|---|---|
| PS/PP | 80 | 20 | — | — | — |
| PS/PP(DCHT) | 80 | 20 | 2 | — | — |
| PS/PP(QQ) | 80 | 20 | — | 2 | — |
| PS/PP(TATA) | 80 | 20 | — | — | 2 |
Standard non-isothermal runs were performed by keeping the sample at 210 °C for 3 min to erase the crystalline memory of the material, cooling at 10 °C min−1 to 0 °C and, finally, heating to 210 °C at 10 °C min−1. A second thermal program was applied to PP samples containing the nucleating agents: heating to 210 °C and keeping this temperature for 3 min, cooling to 110 °C, and then heating to 210 °C at 10 °C min−1. This second heating scan reveals the nature of the crystals produced during cooling to 110 °C, ensuring the absence of recrystallization of β-phase crystals into α-phase crystals, as demonstrated in the literature.41–43
Isothermal crystallization measurements were carried out by keeping the sample at 210 °C for 3 min to erase the crystalline history, cooling at 20 °C min−1 to the crystallization temperature (Tc), keeping the sample at Tc for a certain time, and then heating at 20 °C min−1 to 210 °C for studying the melting behavior of the crystals formed during the isothermal step. Crystallization during cooling to Tc did not occur. This was proven by the absence of any melting peak during immediate heating from Tc. The above thermal cycle was repeated for different isothermal times at each selected Tc. A new sample was employed for every Tc to avoid degradation of the material that may affect the results.
3 Results and discussion
3.1 Morphological analysis of the blends
Images of the cryo-fractured surfaces of all the prepared blends are shown in Fig. 1. In all the mixtures, a homogeneous dispersion of the PP phase can be observed, regardless of the presence of nucleating agents, and the desired droplet matrix morphology was obtained.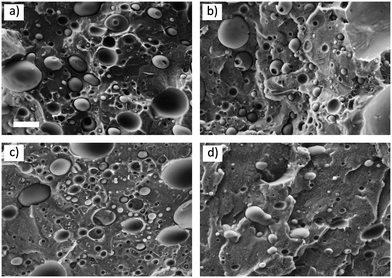 | ||
| Fig. 1 SEM images of the (a) PS/PP, (b) PS/PP(DCHT), (c) PS/PP(QQ), and (d) PS/PP(TATA) blend. The scale bar for all the images is the same and corresponds to 5 μm. | ||
The diameter of more than 250 droplets was measured for each blend and reported as a distribution in Fig. S1 of the ESI.† The number- and volume-average diameters (dn and dv, respectively), dispersity (D), volume fraction of droplets (Xv), and droplet concentration (Ni) were calculated according to the equations proposed in the literature44 and are reported in Table 2 for each blend. dn and Ni for the blends containing the nucleating agents are similar to those of the neat PS/PP blend. This means that as a first approximation, the effect of droplet size and polydispersity can be neglected when comparing the crystallization behavior of the different blends.
| Blend | d n [μm] | d v [μm] | D | X v | N i [cm−3] |
|---|---|---|---|---|---|
| PS/PP | 0.84 | 1.31 | 1.56 | 0.23 | 7.32 × 1011 |
| PS/PP(DCHT) | 1.03 | 1.46 | 1.41 | 0.23 | 3.92 × 1011 |
| PS/PP(QQ) | 0.84 | 1.32 | 1.57 | 0.23 | 7.28 × 1011 |
| PS/PP(TATA) | 0.87 | 1.29 | 1.48 | 0.23 | 6.57 × 1011 |
3.2 Thermal properties
The DSC standard cooling and second heating scans for neat PP and PP containing a specific nucleating agent are reported in Fig. 2a and b, respectively. The calculated values of Tc and melting temperature (Tm) are reported in Table 3.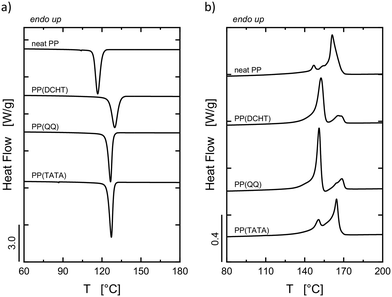 | ||
| Fig. 2 DSC standard (a) cooling and (b) second heating scans at 10 °C min−1 of neat PP and PP containing a nucleating agent. | ||
From the cooling scans in Fig. 2a, it can be observed that the crystallization of the α- and β-phase (demonstrated by the subsequent heating scans, Fig. 2b) takes place simultaneously, and only one peak is detectable despite the formation of two different polymorphs. However, the overall nucleating ability of the different nucleating agents can be inferred. All three substances enhance the Tc of PP by 10 °C or more with respect to neat PP. The most efficient additive in enhancing the overall crystallization rate of PP is DCHT, followed by TATA and then QQ.
Information about the type of crystalline structure formed during cooling is given by the subsequent heating scans in Fig. 2b. Neat PP gives rise to a main melting peak (at circa 160 °C) corresponding to the fusion of α-phase crystals. The small shoulder at about 145 °C indicates the presence of a certain amount of β-phase crystals, whose formation is favored at low cooling rates and in the absence of impurities with nucleating activity.45 PP containing the nucleating agents gives rise to two endotherms. The peaks located at lower temperature (150–153 °C) are due to the fusion of β-phase crystals, while the highest melting peaks (164–169 °C) correspond to the melting of α-phase crystals. Part of the latter type of crystals was formed via the well-known βα-recrystallization, which occurs when the sample is cooled below 100–105 °C.41,42,46,47 The growth rate of the β-phase becomes lower than the growth rate of the α-phase during cooling below 100–105 °C, and latent α-nuclei are produced in β-spherulites.41,42,48 The βα-recrystallization takes place upon heating samples previously cooled to room temperature, and it consists of melting of the β-crystals, recrystallization into α-phase crystals, and melting of such formed α-crystals.42 More recently, a different explanation was given by Lu et al.49 for the crystallization process taking place below 100 °C. A small fraction of thinner β-crystals is formed below 100 °C, and those lamellae melt at lower temperatures, favoring the formation of self-nuclei on which α-crystals can grow upon heating.
However, the three nucleating agents employed in this investigation are known to be versatile, i.e., they can nucleate both α- and β-phase crystals of PP. Therefore, DSC cooling scans from the melt to 110 °C and subsequent heating scans were obtained for samples of the three systems, and they are reported in Fig. S2 of the ESI.† At 110 °C, the overall crystallization process can be considered totally accomplished, and upon subsequent heating, the melting behavior of the developed crystals can be observed without βα-recrystallization. DCHT and QQ give rise to a larger content of β-crystals than α-crystals, as is apparent when observing the corresponding calculated enthalpies of melting. In contrast, for PP containing TATA, the opposite occurs. The dual nucleating ability of all the nucleating agents investigated is therefore demonstrated.
In Fig. 3, the DSC standard cooling and second heating scans for the blends are reported together with the curves for neat PP (scaled according to the content of PP in the blends) for comparison purposes. The presence of several separate crystallization events of PP in the blends is an indication of the occurrence of fractionated crystallization (Fig. 3a). This phenomenon, which can be better observed for each blend in Fig. S3 of the ESI,† happens when the number of dispersed particles is larger than the number of heterogeneities originally present in the bulk sample.33,44,46,50,51 During cooling from the melt, the droplets crystallize at different undercooling, giving rise to multiple crystallization exotherms. In fact, depending on their size, different amounts of heterogeneities can be present in the droplets, which in turn might determine different nucleating activities. On the one hand, droplets containing heterogeneities crystallize at low undercooling, corresponding to the nucleation efficiency of the specific heterogeneity, i.e., via heterogeneous nucleation. On the other hand, impurity-free droplets crystallize at large undercooling due to homogeneous or surface-induced nucleation.33,37,40,46,51 The enhancement of the crystallization rate of PP generated by the nucleating agents is also achieved in the blends, with the same efficiency scale obtained for bulk PP (DCHT > TATA > QQ). Therefore, it can be stated that the melt-mixing process did not meaningfully affect the distribution of nucleating agent particles in the dispersed phase, e.g., by means of complete migration of the heterogeneities towards the PS matrix.
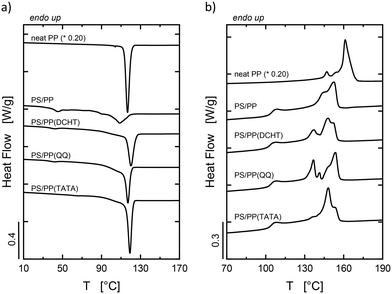 | ||
| Fig. 3 DSC standard (a) cooling and (b) second heating scans at 10 °C min−1 of neat PP (scaled by the amount of PP in the blends) and of the prepared blends. | ||
In Fig. 3b, the melting behavior of the PP phase in each blend can be observed. The highest melting peak of PP in the PS/PP blend is about 10 °C lower than the highest melting peak of neat PP related to the monoclinic structure, as stated above. The reason for such a decrease might be related to the difference in Tc between bulk PP and dispersed PP droplets, i.e., circa 10 °C. However, to establish the crystalline structure of the crystals present in the PP phase of the PS/PP blend, a WAXS measurement at room temperature was performed on a sample of the PS/PP blend after cooling from the melt. The acquired diffractogram, after subtraction of the PS amorphous halo, is shown in Fig. S4 in the ESI.† As can be observed, only typical features generated by α-crystals are present. Moreover, the small endothermic peak located at around 100 °C in the heating curves of each blend is related to the enthalpic relaxation of the PS matrix. This is due to the release upon heating of enthalpy gained during the physical aging of the material that occurred below its glass transition temperature.52 The melting curves of the samples containing the nucleating agents are substantially analogous to that of the PS/PP blend except for the presence of multiple melting peaks, especially for the blends containing DCHT and QQ. The lower melting endotherm can be reasonably assigned to the presence of a certain amount of β-phase.
3.3 Isothermal crystallization experiments
Given the low content of PP in the studied blends, the amount of latent heat released per unit time by PP during the isothermal crystallization is low. Therefore, the crystallization rate was estimated from the corresponding enthalpy of melting developed during the subsequent heating scans, as already done in previous publications, a protocol denoted as isothermal step crystallization.40,53–55Examples of heating scans obtained after isothermal crystallization steps at a certain Tc for different times are shown in Fig. 4a and c for the PS/PP(QQ) and the PS/PP(DCHT) blend, respectively. For both these systems, two melting peaks are distinguishable at ca. 143–147 and 152–155 °C, and they correspond to melting of β- and α-crystals, respectively. On the one hand, βα-recrystallization cannot occur because the heating scans were performed from the crystallization temperature, i.e., above 100–105 °C.42 On the other hand, the hypothesis that the high melting peak might be due to melting of β-crystals that were recrystallized from the β-crystals formed during the isothermal crystallization, namely ββ-recrystallization,42 was discarded for two reasons. The first reason is that no evidence of recrystallization was found in the non-reversing heat flow curve obtained upon heating by means of temperature-modulated DSC (TMDSC) that was performed for some samples after isothermal crystallization. The total, the non-reversing, and the reversing heat flow curves recorded for the PS/PP(QQ) and the PS/PP(DCHT) blends after isothermal crystallization at 131 °C for 120 min are shown in Fig. S5 of the ESI.† TMDSC permits the separation of melting and recrystallization processes.56,57 It was shown that exothermic transitions are present in the non-reversing heat flow curve between 140 and 150 °C when ββ- or βα-recrystallization occurs.20,57 However, in our case, no exothermic contributions are observable in that temperature range for the two blends, and thus it can be stated that the two phenomena do not occur upon heating the isothermally crystallized samples. In contrast, an exothermic peak is observable at about 154 °C in both samples, and it can be related to recrystallization of α-crystals into more perfect α-crystals (αα-recrystallization).49 The second reason is that melting of crystals developed in the PS/PP blend (without any nucleating agent) occurs at about 152 °C (see highest melting fraction of PP in the curve corresponding to the PS/PP blend in Fig. 3b). As discussed in section 3.2, the monoclinic nature of those crystals was assessed by means of WAXS measurements (Fig. S4†). Therefore, α- and β-crystals are both formed during the isothermal crystallization step.
As already discussed in section 3.2, DCHT and QQ are known to possess dual nucleating ability. Thus, the hypothesis is that in the droplets containing these substances, nucleation of α- or β-crystals occurs according to the selectivity of the specific nucleating agent, i.e., the probability of formation of a monoclinic or a trigonal nucleus at the selected crystallization temperature. In other words, among the droplets containing the nucleating agent, in some of them the α-form, and in some others the β-form, is nucleated. Furthermore, when observing the development of the two crystalline forms as a function of time in Fig. 4a and c, two different behaviors can be qualitatively identified for the PS/PP(QQ) and the PS/PP(DCHT) blend, respectively. With QQ, at short times, the quantity of developed α-phase, i.e., the area under the α-phase peak, is larger than that of β-phase, while at progressively longer times the amount of β-phase increases faster than the amount of α-phase. In contrast, with DCHT, the presence of the β-phase is significant already at short times, but the α-phase develops faster with increasing time. The different behaviors of the two systems were observed at all the crystallization temperatures employed in this investigation and are therefore peculiar to each nucleating agent.
In Fig. 4b and d, the heating scans of samples that were crystallized to saturation through the isothermal step crystallization procedure at different temperatures are shown for the PS/PP(QQ) and the PS/PP(DCHT) blend. For both systems, populations of β- and α-crystals (as indicated in the plots) are obtained in the whole crystallization temperature range employed in this investigation and give rise to double melting peaks. However, the probability of formation of trigonal crystals decreases faster than that of the monoclinic crystals when increasing the crystallization temperature. This is due to the increasing vicinity of the system to the equilibrium melting temperature  of the β-form (170 °C (ref. 58)) and to the inversely exponential dependence of the nucleation rate on
of the β-form (170 °C (ref. 58)) and to the inversely exponential dependence of the nucleation rate on 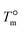 .38 In contrast,
.38 In contrast,  for the α-phase is at about 185 °C;58 thus, the decrease of α-phase nucleation rate is less significant with respect to that of the β-phase.
for the α-phase is at about 185 °C;58 thus, the decrease of α-phase nucleation rate is less significant with respect to that of the β-phase.
For the PS/PP(TATA) blend, examples of heating scans after isothermal crystallization at 129 °C for different times are reported in Fig. 5a. In Fig. 5b, the heating scans of samples that were crystallized to saturation through the isothermal step crystallization procedure at different temperatures are reported. In this system, the low melting peak related to the formation of β-phase crystals is not well developed like in the previous systems containing QQ and DCHT. This is due to the low content of β-crystals that are nucleated on top of TATA particles, in agreement with the PS/PP(TATA) heating scans from 110 °C in Fig. S2.† Furthermore, the same observations regarding the monoclinic nature of the crystals generating the main melting peak in the heating scans after the isothermal step crystallization are also valid for the PS/PP(TATA) blend. Therefore, only the main melting peak related to the fusion of α-crystals developed during the isothermal crystallization step was considered for further evaluation of the nucleation efficiency of TATA towards PP.
The enthalpy of melting was calculated as the area under the endotherms of the observed crystalline phases. Thus, for the PS/PP(QQ) and the PS/PP(DCHT) blends, a single baseline across the melting temperature range of α- and β-phase was drawn, and the corresponding areas were calculated by tracing a vertical separation line at the valley between the two melting peaks, as done in a previous investigation.19 In contrast, for the PS/PP(TATA) blend, the total area between the DSC curve and the baseline was assigned to the α-phase.
Confinement of the crystallizing polymer into small micro-domains within a matrix is a method that has been widely used to isolate the nucleation process from the growth process. This occurs when the contribution of the growth time is negligible with respect to the time needed for nucleation to happen, and thus nucleation becomes the rate-determining step for the overall crystallization process.32,34–36 To verify the compliance of our systems with this condition, the enthalpy of melting for both PP crystalline structures was calculated (see example in Fig. 6a), and the data were fitted with the Avrami equation as described below:
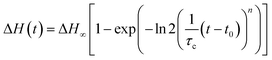 | (1) |
 | ||
| Fig. 6 (a) Enthalpy of melting of the PS/PP(QQ) blend for α-phase, β-phase and their sum (total) calculated from the heating scans after isothermal crystallization at 128 °C for different times. Fitting of (b) α-phase and (c) β-phase data reported in (a) with eqn (1); the calculated Avrami index (n) is also reported. | ||
The chosen range of crystallization temperatures is within the range in which the growth rate of β-crystals exceeds that of α-crystals, i.e., circa 100–140 °C.58–61 A polymorph that was nucleated first can nucleate another polymorph that grows faster, giving rise to cross-nucleation.62 However, cross-nucleation is a selective process, and β-phase was never found to cross-nucleate on top of α-crystals unless in oriented systems,48 while α-phase cross-nucleation onto β-phase crystals was already reported.58,59 Furthermore, we assume that given the very small dimension of the dispersed domains, only one nucleating agent particle can be present inside a droplet, and once the droplet is nucleated, growth of the crystalline embryo fills the small volume of the droplet very quickly. As reported in a previous publication of ours,40 the time to grow a crystal generated in a micro-droplet is 10 to 100 times shorter than the time for nucleation of that crystal to happen. Therefore, we can assume that transition from β-phase to α-phase by means of cross-nucleation cannot occur in the studied systems.
Saturation of the crystallization process was not achieved at all the employed crystallization temperatures, and especially at high Tc, since it would have been required to keep the sample at Tc for extremely long times. However, the fitting operation by means of eqn (1) allowed us to obtain an optimized value of ΔH∞ that is our best estimate of the enthalpy of melting at saturation. As an example, the evolution of the crystallization process (ΔH(t)/ΔH∞) for α- and β-phase as a function of time is reported for the PS/PP(QQ) blend in Fig. S6 in the ESI† for different crystallization temperatures.
The contribution of β-phase to the overall crystallinity that developed at the employed Tc, when saturation of the crystallization process was achieved, is different for the PS/PP(QQ) and the PS/PP(DCHT) blend. This information is reported in Fig. 7 as the β-phase content ratio (Xβ max), which was calculated as the ratio between the enthalpy of melting generated by β-crystals at saturation and the total enthalpy of melting at saturation. QQ is able to nucleate about double the amount of β-crystals with respect to DCHT, as apparent from the overlapped data at 128 and 131 °C.
 | ||
| Fig. 7 Maximum amount of β-phase (Xβ max) developed at different crystallization temperatures in the PS/PP(DCHT) and the PS/PP(QQ) blend. | ||
3.4 Quantitative evaluation of the nucleation efficiency
The kinetics of the nucleation process in the studied systems was quantitatively evaluated through the model of the first-order kinetics, which can be expressed by the following equation:34,37,63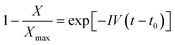 | (2) |
 | (3) |
The linearized version of eqn (2) was employed to fit the data. In Fig. 8a and b, examples of the fitting results for α- and β-phase crystallization data, respectively, are reported. The points within the whole conversion range to the semicrystalline state were used for fitting. The non-perfect linearity of the data is most likely due to the size polydispersity of the droplet system. As described by Ibarretxe et al.,35 the probability of nucleus formation increases with increasing dimension of the droplets. Therefore, larger droplets have a higher probability of nucleating at shorter times than smaller ones, while the latter crystallize at longer times than expected from the average droplet size.
 | ||
| Fig. 8 Fitting of data through the first-order kinetic model (eqn (2)) for (a) α-phase and (b) β-phase of the PS/PP(QQ) blend. Induction times are subtracted for the sake of clarity. | ||
The average droplet volume calculated from the volume-average diameter (see Table 2) was employed to obtain the nucleation rate value from the slope of the fitting lines. Values of I as a function of Tc are reported in Fig. 9a and b for α- and β-phase, respectively. DCHT is the nucleating agent with the highest nucleation rate and thus the highest efficiency towards both α- and β-phase of PP. TATA nucleates α-phase significantly faster than QQ in the extremes of the crystallization temperature window employed in this work, while at intermediate temperatures, TATA nucleates slightly faster than QQ and slightly slower than DCHT. Finally, QQ shows a lower nucleation rate than DCHT in the whole Tc range explored despite the higher total relative fraction of β-phase that was developed for the blend nucleated with QQ with respect to the blend containing DCHT (see Fig. 7).
 | ||
| Fig. 9 Nucleation rate for (a) α-phase in the three systems and (b) β-phase in the blends containing DCHT and QQ. | ||
To understand the reason for the differences in the nucleation rates observed among the studied nucleating agents, an intrinsic parameter of the polymer/substrate pair that is independent of experimental conditions and suitable for comparing the nucleating ability of different nucleating agents towards a specific polymer is the surface free energy difference (Δσ). This parameter describes the correlation between the surface tension properties of the substrate, the polymer crystal, and the polymer melt.39 The more favorable the substitution of a surface/melt interface with a surface/crystal and a crystal/melt interface, the lower is the value of Δσ and thus the more efficient the nucleating agent is. The evolution of the nucleation rate with the crystallization temperature allows us to calculate the value of Δσ.30,40,65
According to the theory of heterogeneous nucleation, the nucleation rate can be expressed in the linearized form as follows:38
 | (4) |
 , Δhf is the heat of fusion per unit volume of crystal at
, Δhf is the heat of fusion per unit volume of crystal at 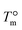 and f is a correcting factor
and f is a correcting factor  , which accounts for the variations of the heat of fusion with temperature when a large range of supercooling is investigated. Therefore, when plotting the nucleation rate data according to eqn (4), Δσ can be obtained from the slope of the line that fits the data (see Fig. 10). The employed values for the constant parameters in eqn (4) are reported in Table 4 for α- and β-phase.
, which accounts for the variations of the heat of fusion with temperature when a large range of supercooling is investigated. Therefore, when plotting the nucleation rate data according to eqn (4), Δσ can be obtained from the slope of the line that fits the data (see Fig. 10). The employed values for the constant parameters in eqn (4) are reported in Table 4 for α- and β-phase.
 | ||
| Fig. 10 Fitting of data through the first-order kinetic model for (a) the α-phase and (b) the β-phase of each blend containing the nucleating agents. The lines are the result of a linear regression. | ||
The calculated Δσ values for each pair of PP polymorph (α- or β-phase) and substrate (DCHT, QQ or TATA) are reported in Fig. 11. The efficiency scale of the different nucleating agents towards the two PP polymorphs agrees with the nucleation rate values reported in Fig. 9, i.e., DCHT > TATA > QQ for the α-phase and DCHT > QQ for the β-phase. The efficiency scale towards the α-phase reflects the overall nucleation ability that was noticeable from the non-isothermal cooling scans reported in Fig. 2. Nevertheless, Δσ is independent of the experimental conditions employed and of the concentration of the substance in the crystallizing polymer. The Δσ value for the PP β-phase/QQ pair is close to the value obtained in a previous investigation for a similar system.40 For DCHT and TATA, the Δσ values with the two PP polymorphs are reported here for the first time, and thus no comparison to values taken from the literature can be made.
For the PP β-phase/DCHT pair, the very low value of Δσ, i.e., below unity, is likely due to the occurrence of epitaxial growth of PP β-crystals on top of DCHT crystals.10 In previous investigations, values below one were found in systems where lattice matching between the crystallizing polymer and the nucleating substrate was proved.30,39,55,65,67 This result agrees with the known high nucleation efficiency of DCHT towards PP β-phase.8,15 For QQ, no specific reports about epitaxial crystallization with PP are present in the literature to the best of our knowledge. However, we note that epitaxy is confirmed for the structurally similar γ-quinacridone.18 The higher Δσ with respect to DCHT might indicate a worse crystallographic matching between PP and QQ compared to that between PP and DCHT.
Furthermore, the ratio between β-phase and α-phase Δσ is circa 0.5 and 0.6 for DCHT and for QQ, respectively. The lower is this ratio, the more favored is the formation of β-crystals. This reflects the higher nucleation rate of DCHT with respect to QQ towards PP β-phase. However, QQ generated a higher amount of β-phase crystals than DCHT (see Fig. 7). Therefore, we notice that selectivity and the ratio between β-phase and α-phase Δσ are not straightforwardly related.
4 Conclusions
Given the challenge in separating nucleation from crystal growth, several studies focused on the determination of the difference in the overall crystallization rate (for both α- and β-phase) of polypropylene containing different nucleating agents. In contrast, this work represents a first step towards the understanding of the nucleation rate in polypropylene containing a specific nucleating agent promoting β-phase crystals. Nucleation rate values and the surface free energy difference, Δσ, were obtained here for dispersed polypropylene droplets containing three nucleating agents with dual nucleating ability, namely N,N′-dicyclohexylterephthalamide (DCHT), quinacridone quinone (QQ), and tris-2,3-dimethyl-hexylamide of trimesic acid (TATA). In the employed range of isothermal crystallization temperatures, DCHT and QQ give rise to both α- and β-crystals, while TATA nucleates mainly α-crystals. According to the calculated Δσ values, the nucleation efficiency scale is DCHT > TATA > QQ for α-phase, while DCHT > QQ for β-phase. Furthermore, despite the faster nucleation rate of polypropylene containing DCHT, the total amount of β-phase developed during isothermal crystallization of the polypropylene/DCHT pair is about half of that achieved for the polypropylene/QQ pair.Author contributions
Enrico Carmeli: investigation, data curation, visualization, writing – original draft. Sara Ottonello: investigation, data curation. Bao Wang: validation, writing – review & editing. Alfréd Menyhárd: resources, writing – review & editing. Alejandro J. Müller: writing – review & editing. Dario Cavallo: conceptualization, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.References
- G. Natta, P. Pino, P. Corradini, F. Danusso, E. Mantica, G. Mazzanti and G. Moraglio, Crystalline high polymers of α-olefins, J. Am. Chem. Soc., 1955, 77, 1708–1710 CrossRef CAS.
- S. Brückner, S. V. Meille, V. Petraccone and B. Pirozzi, Polymorphism in isotactic polypropylene, Prog. Polym. Sci., 1991, 16, 361–404 CrossRef.
- G. Natta and P. Corradini, Structure and properties of isotactic polypropylene, in: Stereoregular Polymers and Stereospecific Polymerizations, Elsevier, 1967, pp. 743–746 Search PubMed.
- C. De Rosa, F. Auriemma, P. Vollaro, L. Resconi, S. Guidotti and I. Camurati, Crystallization behavior of propylene− butene copolymers: The trigonal form of isotactic polypropylene and form I of isotactic poly (1-butene), Macromolecules, 2011, 44, 540–549 CrossRef CAS.
- B. Lotz, A new ε crystal modification found in stereodefective isotactic polypropylene samples, Macromolecules, 2014, 47, 7612–7624 CrossRef CAS.
- R. Androsch, M. L. Di Lorenzo, C. Schick and B. Wunderlich, Mesophases in polyethylene, polypropylene, and poly (1-butene), Polymer, 2010, 51, 4639–4662 CrossRef CAS.
- A. Menyhárd, J. Varga and G. Molnár, Comparison of different-nucleators for isotactic polypropylene, characterisation by DSC and temperature-modulated DSC (TMDSC) measurements, J. Therm. Anal. Calorim., 2006, 83, 625–630 CrossRef.
- J. Varga, β-modification of isotactic polypropylene: preparation, structure, processing, properties, and application, J. Macromol. Sci., Part B: Phys., 2002, 41, 1121–1171 CrossRef.
- C. Grein, Toughness of neat, rubber modified and filled β-nucleated polypropylene: from fundamentals to applications, Intrinsic molecular mobility and toughness of polymers II, 2005, pp. 43–104 Search PubMed.
- Z. Wang, W. Yang, G. Liu, A. J. Müller, Y. Zhao, X. Dong, K. Wang and D. Wang, Probing into the epitaxial crystallization of β form isotactic polypropylene: From experimental observations to molecular mechanics computation, J. Polym. Sci., Part B: Polym. Phys., 2017, 55, 418–424 CrossRef CAS.
- D. R. Ferro, S. V. Meille and S. Brückner, Energy calculations for isotactic polypropylene: a contribution to clarify the β crystalline structure, Macromolecules, 1998, 31, 6926–6934 CrossRef CAS.
- D. Dorset, M. McCourt, S. Kopp, M. Schumacher, T. Okihara and B. Lotz, Isotactic polypropylene, β-phase: a study in frustration, Polymer, 1998, 39, 6331–6337 CrossRef CAS.
- P. Tordjeman, C. Robert, G. Marin and P. Gerard, The effect of α, β crystalline structure on the mechanical properties of polypropylene, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 4, 459–465 CrossRef CAS.
- C. Mathieu, A. Thierry, J. Wittmann and B. Lotz, “Multiple” nucleation of the (010) contact face of isotactic polypropylene, α phase, Polymer, 2000, 41, 7241–7253 CrossRef CAS.
- C. Mathieu, A. Thierry, J. Wittmann and B. Lotz, Specificity and versatility of nucleating agents toward isotactic polypropylene crystal phases, J. Polym. Sci., Part B: Polym. Phys., 2002, 40, 2504–2515 CrossRef CAS.
- F. Rybnikář, Transition of β to α phase in isotactic polypropylene, J. Macromol. Sci., Part B: Phys., 1991, 30, 201–223 CrossRef.
- M. Fujiyama, Structures and properties of injection moldings of β-crystal nucleator-added polypropylenes, Int. Polym. Process., 1996, 11, 271–274 CrossRef CAS.
- W. Stocker, M. Schumacher, S. Graff, A. Thierry, J.-C. Wittmann and B. Lotz, Epitaxial crystallization and AFM investigation of a frustrated polymer structure: isotactic poly (propylene), β phase, Macromolecules, 1998, 31, 807–814 CrossRef CAS.
- A. Menyhárd, G. Dora, Z. Horváth, G. Faludi and J. Varga, Kinetics of competitive crystallization of β-and α-modifications in β-nucleated iPP studied by isothermal stepwise crystallization technique, J. Therm. Anal. Calorim., 2012, 108, 613–620 CrossRef.
- J. Varga, K. Stoll, A. Menyhárd and Z. Horváth, Crystallization of isotactic polypropylene in the presence of a β-nucleating agent based on a trisamide of trimesic acid, J. Appl. Polym. Sci., 2011, 121, 1469–1480 CrossRef CAS.
- G. Y. Shi, X. D. Zhang and Z. X. Qiu, Crystallization kinetics of β-phase poly (propylene), Die Makromolekulare Chemie, Macromol. Chem. Phys., 1992, 193, 583–591 CrossRef CAS.
- M. Dong, Z. Guo, J. Yu and Z. Su, Crystallization behavior and morphological development of isotactic polypropylene with an aryl amide derivative as β-form nucleating agent, J. Polym. Sci., Part B: Polym. Phys., 2008, 46, 1725–1733 CrossRef CAS.
- Z. Zhang, Y. Tao, Z. Yang and K. Mai, Preparation and characteristics of nano-CaCO3 supported β-nucleating agent of polypropylene, Eur. Polym. J., 2008, 44, 1955–1961 CrossRef CAS.
- Q. Dou and Q. L. Lu, Effect of calcium malonate on the formation of β crystalline form in isotactic poly (propylene), Polym. Adv. Technol., 2008, 19, 1522–1527 CAS.
- B. Fillon, B. Lotz, A. Thierry and J. Wittmann, Self-nucleation and enhanced nucleation of polymers. Definition of a convenient calorimetric “efficiency scale” and evaluation of nucleating additives in isotactic polypropylene (α phase), J. Polym. Sci., Part B: Polym. Phys., 1993, 31, 1395–1405 CrossRef CAS.
- C. Marco, G. Ellis, M. Gomez and J. Arribas, Comparative study of the nucleation activity of third-generation sorbitol-based nucleating agents for isotactic polypropylene, J. Appl. Polym. Sci., 2002, 84, 2440–2450 CrossRef CAS.
- S. Jain, H. Goossens, M. van Duin and P. Lemstra, Effect of in situ prepared silica nano-particles on non-isothermal crystallization of polypropylene, Polymer, 2005, 46, 8805–8818 CrossRef CAS.
- A. Pozsgay, T. Fráter, L. Papp, I. Sajó and B. Pukánszky, Nucleating effect of montmorillonite nanoparticles in polypropylene, J. Macromol. Sci., Part B: Phys., 2002, 41, 1249–1265 CrossRef.
- A. Thierry, B. Fillon, C. Straupé, B. Lotz and J. Wittmann, Polymer nucleating agents: Efficiency scale and impact of physical gelation, in: Solidification Processes in Polymers, Springer, 1992, pp. 28–31 Search PubMed.
- H. Ishida and P. Bussi, Induction time approach to surface induced crystallization in polyethylene/poly (ε-caprolactone) melt, J. Mater. Sci., 1991, 26, 6373–6382 CrossRef CAS.
- C. Wang and L. Hwang, Transcrystallization of PTFE fiber/PP composites (I) crystallization kinetics and morphology, J. Polym. Sci., Part B: Polym. Phys., 1996, 34, 47–56 CrossRef CAS.
- M. L. Arnal and A. J. Müller, Fractionated crystallisation of polyethylene and ethylene/α-olefin copolymers dispersed in immiscible polystyrene matrices, Macromol. Chem. Phys., 1999, 200, 2559–2576 CrossRef CAS.
- M. L. Arnal, A. J. Müller, P. Maiti and M. Hikosaka, Nucleation and crystallization of isotactic poly (propylene) droplets in an immiscible polystyrene matrix, Macromol. Chem. Phys., 2000, 201, 2493–2504 CrossRef CAS.
- R. Cormia, F. Price and D. Turnbull, Kinetics of crystal nucleation in polyethylene, J. Chem. Phys., 1962, 37, 1333–1340 CrossRef CAS.
- J. Ibarretxe, G. Groeninckx, L. Bremer and V. Mathot, Quantitative evaluation of fractionated and homogeneous nucleation of polydisperse distributions of water-dispersed maleic anhydride-grafted-polypropylene micro-and nano-sized droplets, Polymer, 2009, 50, 4584–4595 CrossRef CAS.
- R. Tol, V. Mathot and G. Groeninckx, Confined crystallization phenomena in immiscible polymer blends with dispersed micro-and nanometer sized PA6 droplets, part 3: crystallization kinetics and crystallinity of micro-and nanometer sized PA6 droplets crystallizing at high supercoolings, Polymer, 2005, 46, 2955–2965 CrossRef CAS.
- L. Sangroniz, B. Wang, Y. Su, G. Liu, D. Cavallo, D. Wang and A. J. Müller, Fractionated crystallization in semicrystalline polymers, Prog. Polym. Sci., 2021, 101376 CrossRef CAS.
- B. Wunderlich, Macromolecular Physics, Academic Press, New York, 1976 Search PubMed.
- H. Ishida and P. Bussi, Surface induced crystallization in ultrahigh-modulus polyethylene fiber-reinforced polyethylene composites, Macromolecules, 1991, 24, 3569–3577 CrossRef CAS.
- B. Wang, R. Utzeri, M. Castellano, P. Stagnaro, A. J. Müller and D. Cavallo, Heterogeneous Nucleation and Self-Nucleation of Isotactic Polypropylene Microdroplets in Immiscible Blends: From Nucleation to Growth-Dominated Crystallization, Macromolecules, 2020, 53, 5980–5991 CrossRef CAS.
- B. Fillon, A. Thierry, J. Wittmann and B. Lotz, Self-nucleation and Recrystallization of Polymers. Isotactic Polypropylene, β Phase: β-α Conversion and β-α Growth Transitions, J. Polym. Sci., Part B: Polym. Phys., 1993, 31, 1407–1424 CrossRef CAS.
- J. Varga, Melting memory effect of the β-modification of polypropylene, J. Therm. Anal., 1986, 31, 165–172 CrossRef CAS.
- J. Varga, F. Schulek-Toth and A. Ille, Effect of fusion conditions of β-polypropylene on the new crystallization, Colloid Polym. Sci., 1991, 269, 655–664 CrossRef CAS.
- M. L. Arnal, M. E. Matos, R. A. Morales, O. O. Santana and A. J. Müller, Evaluation of the fractionated crystallization of dispersed polyolefins in a polystyrene matrix, Macromol. Chem. Phys., 1998, 199, 2275–2288 CrossRef CAS.
- E. Carmeli, G. Kandioller, M. Gahleitner, A. J. Müller, D. Tranchida and D. Cavallo, Continuous Cooling Curve Diagrams of Isotactic-Polypropylene/Polyethylene Blends: Mutual Nucleating Effects under Fast Cooling Conditions, Macromolecules, 2021, 54, 4834–4846 CrossRef CAS.
- D. S. Langhe, J. K. Keum, A. Hiltner and E. Baer, Fractionated crystallization of α-and β-nucleated polypropylene droplets, J. Polym. Sci., Part B: Polym. Phys., 2011, 49, 159–171 CrossRef CAS.
- F. Horváth, T. Gombár, J. Varga and A. Menyhárd, Crystallization, melting, supermolecular structure and properties of isotactic polypropylene nucleated with dicyclohexyl-terephthalamide, J. Therm. Anal. Calorim., 2017, 128, 925–935 CrossRef.
- J. Varga and J. Karger-Kocsis, Rules of supermolecular structure formation in sheared isotactic polypropylene melts, J. Polym. Sci., Part B: Polym. Phys., 1996, 34, 657–670 CrossRef CAS.
- Y. Lu, D. Lyu, D. Cavallo and Y. Men, Enhanced beta to alpha recrystallization in beta isotactic polypropylene with different thermal histories, Polym. Cryst., 2019, 2, e10040 Search PubMed.
- R. Morales, M. Arnal and A. Müller, The evaluation of the state of dispersion in immiscible blends where the minor phase exhibits fractionated crystallization, Polym. Bull., 1995, 35, 379–386 CrossRef CAS.
- O. Santana and A. Müller, Homogeneous nucleation of the dispersed crystallisable component of immiscible polymer blends, Polym. Bull., 1994, 32, 471–477 CrossRef CAS.
- B. Wunderlich, Thermal analysis of polymeric materials, Springer Science & Business Media, 2005 Search PubMed.
- V. Balsamo, N. Urdaneta, L. Pérez, P. Carrizales, V. Abetz and A. Müller, Effect of the polyethylene confinement and topology on its crystallisation within semicrystalline ABC triblock copolymers, Eur. Polym. J., 2004, 40, 1033–1049 CrossRef CAS.
- M. Galante, L. Mandelkern, R. Alamo, A. Lehtinen and R. Paukker, Crystallization kinetics of metallocene type polypropylenes: Influence of molecular weight and comparison with Ziegler-Natta type systems, J. Therm. Anal. Calorim., 1996, 47, 913–929 CrossRef CAS.
- E. Carmeli, S. E. Fenni, M. R. Caputo, A. J. Müller, D. Tranchida and D. Cavallo, Surface Nucleation of Dispersed Polyethylene Droplets in Immiscible Blends Revealed by Polypropylene Matrix Self-Nucleation, Macromolecules, 2021, 54, 9100–9112 CrossRef CAS.
- A. Genovese and R. Shanks, Crystallization and melting of isotactic polypropylene in response to temperature modulation, J. Therm. Anal. Calorim., 2004, 75, 233–248 CrossRef CAS.
- M. Dong, Z. Guo, Z. Su and J. Yu, The effects of crystallization condition on the microstructure and thermal stability of istactic polypropylene nucleated by β-form nucleating agent, J. Appl. Polym. Sci., 2011, 119, 1374–1382 CrossRef CAS.
- J. Varga, Y. Fujiwara and A. Ille, βα-bifurcation of growth during the spherulitic crystallization of polypropylene, Periodica Polytechnica, Chem. Eng., 1990, 34, 255–271 CAS.
- S. Looijmans, A. Menyhard, G. W. Peters, G. C. Alfonso and D. Cavallo, Anomalous temperature dependence of isotactic polypropylene α-on-β cross-nucleation kinetics, Cryst. Growth Des., 2017, 17, 4936–4943 CrossRef CAS.
- B. Lotz, α and β phases of isotactic polypropylene: a case of growth kineticsphase reentrency'in polymer crystallization, Polymer, 1998, 39, 4561–4567 CrossRef CAS.
- K. Nakamura, S. Shimizu, S. Umemoto, A. Thierry, B. Lotz and N. Okui, Temperature dependence of crystal growth rate for α and β forms of isotactic polypropylene, Polym. J., 2008, 40, 915–922 CrossRef CAS.
- L. Yu, Survival of the fittest polymorph: how fast nucleater can lose to fast grower, CrystEngComm, 2007, 9, 847–851 RSC.
- M. S. Sánchez, V. Mathot, G. V. Poel, G. Groeninckx and W. Bruls, Crystallization of polyamide confined in sub-micrometer droplets dispersed in a molten polyethylene matrix, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 815–825 CrossRef.
- P. Sajkiewicz, A. Gradys, A. Ziabicki and B. Misztal-Faraj, On the metastability of β phase in isotactic polypropylene: Experiments and numerical simulation, e-Polym., 2010, 124, 1–20 Search PubMed.
- E. Carmeli, B. Wang, P. Moretti, D. Tranchida and D. Cavallo, Estimating the nucleation ability of various surfaces towards isotactic polypropylene via light intensity induction time measurements, Entropy, 2019, 21, 1068 CrossRef CAS.
- C. Wang and C.-R. Liu, Transcrystallization of polypropylene composites: nucleating ability of fibres, Polymer, 1999, 40, 289–298 CrossRef CAS.
- W. Wang, B. Wang, A. Tercjak, A. J. Müller, Z. Ma and D. Cavallo, Origin of Transcrystallinity and Nucleation Kinetics in Polybutene-1/Fiber Composites, Macromolecules, 2020, 53, 8940–8950 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d2ce00087c |
| This journal is © The Royal Society of Chemistry 2022 |




