Microcrystalline solid–solid transformations of conformationally-responsive solvates, desolvates and a salt of N,N′-(1,4-phenylene)dioxalamic acid: the energetics of hydrogen bonding and n/π → π* interactions

Abstract

Oxalamic acid derivatives are model molecules used in crystal engineering and molecular recognition both in solution and in the solid state. Despite their growing importance, hardly any information on polymorphism, stability and interrelations of their solid forms can be found in the literature. In this work, the molecular and supramolecular structures of three cocrystal solvates of formula H₂pOx·2S (S = DMSO, DMF, ⅓(MeOH·2W); W = H₂O) and the dimethylammonium salt of N,N′-(1,4-phenylene)dioxalamic acid (H₂pOx) are described. The nature and energetics of non-covalent interactions were explored through computational methods including the evaluation of the Hirshfeld surface, two-dimensional fingerprint plots, energy-framework diagrams and crystal lattice energies. The X-ray structural parameters were correlated with experimental solid state IR, ¹³C-CPMAS, thermal analysis and SEM to elucidate the unknown molecular and supramolecular structures of two hydromorphs and three desolvated polymorphs of H₂pOx. The role of the crystallized solvents was demonstrated to fix the conformation of H₂pOx through hydrogen bonding and n/π → π* interactions, favoring the sp–ap conformation to fit the shape of the solvent. The interconversion pathways between the ten solid phases of H₂pOx were stablished, relying on the crystal size and temperature to yield a specific solvent-free polymorph.

---

1. Introduction

Oxalamides (oxamides), oxalamates (oxamates) and oxalamic (oxamic) acids are bifunctional compounds with high potential in crystal engineering and molecular recognition.¹ Oxalamides have been used as model compounds to design supramolecular β-sheets for a better understanding of supramolecular interactions in protein quaternary structures and in amyloids,² as well as in the design of compounds with anti-HIV activity.³ Oxalamides cocrystallize with pyridines, carboxylic acids, amines, halobenzenes, phenols, alcohols, and other oxalamides.⁴ On the other hand, the phenyldioxalamate moiety has become particularly important as a versatile supramolecular building block exploited for the formation of a wide variety of supramolecular architectures.⁵ For instance, diethyl N,N′-1,3-phenyldioxalamates have been shown to form molecular clefts whose conformation and cavity size can be controlled by steric hindrance and hydrogen-bonding effects.⁶ Furthermore, they have been used to explore the rotational isomerism of 1,3-benzenediols by cocrystallization.⁷ In the case of the oxalamic acid functionality, the only reported structures are related to the use of chiral oxalamic acids as resolving agents of racemic amines.^8,9

The title compound, N,N′-(1,4-phenylene)dioxalamic acid (H₂pOx), was first reported in the mid-70s as an antiallergic agent^10,11 as well as an anti-inflammatory and nontoxic compound.¹² Recently, it has attracted interest as a ligand for the synthesis of novel coordination mono and dinuclear Cu(II) complexes which showed intramolecular antiferromagnetic coupling.^13,14 Lately, heterobimetallic tetranuclear Cu^II₂M^II₂ (M = Cu, Ni) complexes have been reported, where the dianion of N,N′-(1,4-phenylene)dioxalamic acid (pOx²⁻) acts as a bridging ligand of four metallic centers.¹⁵ H₂pOx has also been used as a scaffold structure to build cuboid Ir–M (M = Cu, Ni, Zn) heterometallic coordination cages as catalysts.¹⁶ The chemistry of the H₂pOx ligand for metallic complexes and magnetochemistry have been summarized elsewhere.^17–19 In the context of biological activity, Cu(II) oxalamic acid complexes have been found active against Gram-positive bacteria.²⁰

Oxalamic acid derivatives are flat due to the formation of intramolecular hydrogen bonds between the amide NH and the COOH carbonyl oxygen atom. In addition, the relative disposition of the amide carbonyl group regarding the phenyl ring, as a plane of reference, gives rise to several conformers: antiperiplanar (ap) ±180–±150°, anticlinal (ac) ±150–±90°, synclinal (sc) ±90–±30°, and synperiplanar (sp) ±30–±0°. Considering the two oxalamic acid arms in anti disposition between the two oxalic carbonyls, six combinations are possible because of symmetry reasons: sp–sp, sp–sc, sp–ac, sc–sc, sc–ac, and sp–ap, Fig. 1.

Fig. 1 Conformations of N,N′-(1,4-phenylene)dioxalamic acid (H₂pOx) side arms in relation to the benzene ring.

Due to the growing importance of H₂pOx and the influence of conformational polymorphism on the geometry and properties of its metallic complexes, in this contribution, the molecular and supramolecular structures, IR spectroscopy, ¹³C-CPMAS NMR and thermal analysis of its neutral solvates of formula H₂pOx·2S (S = DMSO, DMF, ⅓(MeOH·2W); W = H₂O) and its dimethyl ammonium salt (HDMA)₂·pOx are described. The nature and energetics of non-covalent interactions involved in the stability of the crystal lattice were explored through computational methods, including the evaluation of the Hirshfeld surface (HS), two-dimensional fingerprint plots, energy-framework diagrams and lattice energies. Furthermore, the structures and hydrogen bonding (HB) patterns of two hydromorphs (H-I and H-II) of formula H₂pOx·2W and three H₂pOx desolvates (A-I, A-II and A-III) are proposed on the basis of IR spectroscopy, ¹³C-CPMAS NMR, PXRD, thermal analysis and SEM, as well as by comparison with the discussed X-ray crystal structures.

2. Experimental section

Detailed experimental descriptions are found in the ESI.†

2.1 Materials and crystal synthesis

See the ESI.†

2.2 Instrumentation

IR spectra were recorded neat at 25 °C using a Perkin Elmer Spectrum GX series with an FT system spectrophotometer using an ATR device. ¹³C CPMAS spectra were recorded on a Bruker Avance DPX-400 (101 MHz). X-ray powder diffraction data were collected on a PAN Analytical X'Pert PRO or on a D8 Focus Bruker AXS diffractometer with Cu Kα₁ radiation. DSC and TG measurements were performed on Q2000 equipment and a Thermobalance Q5000 IR, respectively, of TA instruments.

2.3 X-Ray structure determination

Single crystal X-ray diffraction data were collected on an Agilent SuperNova (dual source) diffractometer equipped with graphite-monochromatic Cu (λ = 1.54184 Å)/Mo (λ = 0.71073 Å) Kα radiation. The data collection was accomplished using CrysAlisPro software²¹ at 293(2) K under Cu (H₂pOx·2DMSO)/Mo (H₂pOx·2DMF, 3H₂pOx·2MeOH·4W, (HDMA)₂pOx) Kα radiation. The cell refinement and data reduction were carried out with the CrysAlisPro software.²¹ The models were refined and the structures solved using the SHELXL-2018/3 program²² of the WINGX package.²³ Platon²⁴ and Mercury²⁵ were used to prepare the material for publication. Hydrogen bonding motifs were described following the standard notation.²⁶ The CIF codes deposited at the CCDC are H₂pOx·2DMSO (1874282), H₂pOx·2DMF (1997487), 3H₂pOx·2MeOH·4W (1997485) and (HDMA)₂pOx (1997486). Crystal data, collection and refinement parameters are listed in Table S1.†

2.4 Hirshfeld surface (HS) analysis,²⁷ two-dimensional fingerprint plots,²⁸ and energy-framework diagrams²⁹

These calculations were performed with the software CrystalExplorer17.5.³⁰ The HS was mapped over d_norm, and the function of the normalized contact distance d_e and d_i was utilized, where d_e and d_i are the distance from a given point to the nearest atom outside and inside on the surface, respectively.³¹ The energy components E_elect (electrostatic potential), E_disp (dispersion) and E_total (total energy) were calculated linking the software with the Gaussian 09 software³² using the B3LYP/6-31G (d,p) level of theory. Scale factors³⁰ and % contribution of individual components to the stabilization energy³³ were also calculated.

2.5 Interaction and lattice energies

The interaction and lattice energy calculations were performed with the CLP-PIXEL software.^34–36

3. Results and discussion

3.1 The synthesis of crystals

Form I of the H₂pOx double-hydrate (H-I) precipitates after the neutralization reaction of the corresponding sodium dicarboxylate salt with HCl in an aqueous medium. The attempts to crystallize H-I from saturated water solutions yielded hydromorph II (H-II) as microcrystalline (mc) powder. After drying each of the two double-hydrates at 150 °C/3 h, anhydrous H₂pOx was obtained as polymorphic forms A-I and A-II, respectively. The powder X-ray diffraction patterns (PXRD) of A-I and A-II are very similar and they appear as finely dispersed powders of H₂pOx with no preferred orientation. The crystals of H₂pOx·2DMSO and H₂pOx·2DMF are formed by crystallization of H-I from their corresponding solutions and 3H₂pOx·2MeOH·4W from a methanol–water 1 : 1 solution. In addition, the grinding of H-I and DMSO or DMF quantitatively yielded the corresponding double-solvate. The PXRD patterns confirmed the formation of the same solid phases observed by crystallization from either DMSO or DMF solution. Desolvation of H₂pOx·2S (S = DMSO, DMF, ⅓(MeOH·2W)) resulted in the formation of A-I, A-II or A-III, depending on the conditions employed and the crystal size. Slow desolvation (45 °C/1–4 days) led to the formation of A-I, while rapid drying (160 °C/24 h) of DMSO and DMF solvates resulted in the formation of A-III, with the exception of grinded H₂pOx·2DMF which formed A-I under these conditions. In contrast, the A-II form is obtained from 3H₂pOx·2MeOH·4W after fast drying (150 °C/3 h). Nevertheless, no phase transitions by DSC were observed between A-I, A-II and A-III (vide infra). Finally, the dimethyl ammonium salt (HDMA)₂pOx was obtained from crystallization attempts of H-I in hot DMF by decomposition of DMF into dimethylamine and CO in an acid medium, as has been observed for other systems.³⁷ In every case, the identity of the solid phases as N,N′-(1,4-phenylene)dioxalamic acid was confirmed by ¹H-NMR in solution and the presence of different solid mc-forms, compared to the starting polymorph, was revealed by the corresponding PXRD patterns, as shown in Fig. 2.

Fig. 2 PXRD patterns of: (a) H₂pOx·2DMSO obtained from grinding procedures and (b) simulated from single crystal X-ray diffraction data; (c) H₂pOx·2DMF obtained from grinding procedures and (d) simulated from single crystal X-ray diffraction data; hydromorphs (e) H-I and (f) H-II; desolvates (g) A-I, (h) A-II and (i) A-III. Individual images of (g) and (h) are shown in Fig. S1.†

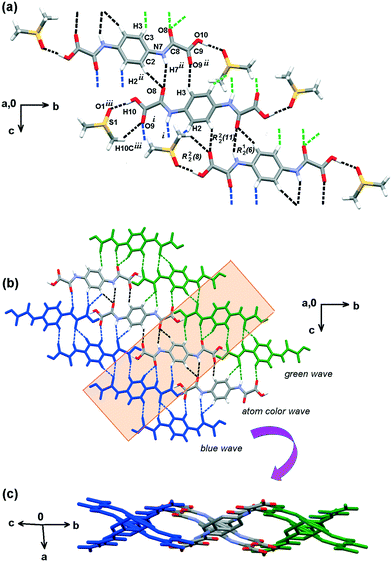
Hydration–dehydration experiments provided information about the hydrate stability as well as the role of water in the crystal network. Dehydration of H-I and H-II is accompanied by the structural reorganization of the lattice which is destabilized by the removal of the hydrogen-bonded water to give the corresponding anhydrate. Furthermore, rehydration experiments revealed that once formed, A-I and A-II reconstitute into the starting double-hydrated forms. The identity of A-I and A-II was always confirmed by rehydration experiments due to the high similarity between their PXRD patterns, as mentioned earlier. The vacant sites left behind after water removal are preserved in the mc-solids A-I and A-II, whose crystal networks are stable and capable of rearranging in the presence of moisture to restore the mc-lattice of the original double-hydrates under suitable conditions, as has also been observed in the tetrahydrate salt of HpOx⁻.³⁸ Conversely, hydration of A-III, obtained from either DMSO or DMF solvates, slowly progresses to form the mc-solid hydrate H-II. This result suggests that H₂pOx molecules are arranged into a more compact lattice in A-III than in A-I or A-II. Recalling that H-II is obtained by recrystallization of H-I from hot water, the latter can be considered as the kinetic hydromorph and the former as the thermodynamic hydromorph. The relationships between H₂pOx hydromorphs, solvomorphs, desolvates and HDMA⁺ salt are depicted in Fig. 3.

Fig. 3 Synthesis of hydromorphs (H-I and H-II), solvomorphs (H₂pOx·2S, S = DMSO, DMF; ⅓(MeOH·2W)), desolvates (A-I, A-II and A-III) and the dimethylammonium salt of N,N′-(1,4-phenylene)dioxalamic acid ((HDMA)₂pOx) as well as their interconversions.

The hydromorphs are pale beige solids, but H-I looks opaque while H-II appears to be composed of pearly fibers. SEM micrographs allowed the morphological changes of the solid forms to be observed. The SEM images reveal the shape of H-I as rectangular prisms whose form is lost by dehydration leading to the appearance of pores on the surface of the resulting agglomerated mass of A-I, Fig. 4(a) and (b). The narrow flat strips shaping H-II, Fig. 4(c), seem to fold by dehydration along their cross-cutting axis to shape long rectangular bars of A-II, Fig. 4(d). Drying of 3H₂pOx·2MeOH·4W leads to A-II, and large holes are left behind by solvent loss, Fig. 4(f), which after rehydration reconstitute into rectangular bars of H-II, Fig. 4(e). Finally, the A-III phase, obtained from H₂pOx·2DMSO, appears as piled plaques, Fig. 4(h), that once hydrated adopt the form of platelets, Fig. 4(g).

Fig. 4 SEM micrographs of: (a) H-I, (b) A-I, (c) H-II, (d) A-II, (e) H-II from rehydrated crystals of 3H₂pOx·2MeOH·4W, (f) A-II from crystals of 3H₂pOx·2MeOH·4W, (g) H-II from rehydration of A-III and (h) A-III from H₂pOx·2DMSO. (a)–(d), (g) and (h) ×5000, (e) and (f) ×200.

3.2 The molecular and supramolecular structures of H₂pOx·2S and (HDMA)₂pOx

The molecular structures of H₂pOx·2S (S = DMSO, DMF, ⅓(MeOH·2W)) and (HDMA)₂pOx are shown in Fig. S2, S3, S5 and S7.† Selected geometric parameters and those related to HB and n → π* interactions are listed in Tables S2–S9.†

3.2.1 H₂pOx·2DMSO. An inversion center of symmetry is imposed, thus only one-half molecule of H₂pOx and one molecule of DMSO are present in the asymmetric unit. The oxalamic acid arm is almost planar with a N7–C8–C9–O10 torsion angle of 176.58(18)°; the NCOCO₂H fragment is slightly tilted away from the aromatic ring plane, forming a torsion angle φ of 11.7(3)° (φ = C3–C1–N7–C8). For symmetry reasons, the oxalamic acid arms are anti positioned relative to each other.

Both ends of oxalamic acid are capped by DMSO molecules through O10–H10⋯O1 and C10–H10C⋯O9 hydrogen bonding (HB) to form a hetero-R²₂(8) ring motif. The linkage of this repetition unit is performed through N7–H7⋯O8, C3–H3⋯O9 and C2–H2⋯O8 HB interactions, forming two adjacent R²₂(11) and R¹₂(6) ring motifs and soft C10–H10C⋯O9 interaction to develop a weaving sheet within the bc plane, Fig. 5. O–H⋯OS values are similar to those observed in other carboxylic acid–DMSO complexes.³⁹ The third dimension is developed along the direction of the a-axis through S1⋯C8, O1⋯C9 and C10–H10B⋯O8 interactions, as depicted in Fig. 6. Because of the nature and bonding of the atoms involved, the sulfur–carbonyl synthon S⋯CO is similar to CO⋯CO interaction.⁴⁰ These n → π* interactions, also named as π-hole, have been found important for the stability of biomolecules and materials.⁴¹ Finally, DMSO molecules are bound together through weak C10–H10A⋯O1 interaction, developing channels along the direction of the c axis and filling the space between the H₂pOx weaving sheets.

Fig. 5 Hydrogen bonding pattern of the H₂pOx·2DMSO cocrystal solvate. (a) 0D is given by carboxylic acid interactions with DMSO forming hetero-R²₂(8) motifs that propagate in 1D by R²₂(11) and R¹₂(6) ring motifs, in black dotted lines. (b) 2D weaving sheets formed by the interlinkage of green, natural and blue colored waves. (c) View after rotating −48° in z and −84° in x. DMSO molecules are omitted for clarity.

Fig. 6 The third dimension developed by n → π* interactions. (a) DMSO–carbonyl interactions in H₂pOx·2DMSO: S1–O1⋯C9, O1–S1⋯C8; symmetry code (iv) = 1 + x, y, z. (b) Carbonyl–carbonyl interactions in H₂pOx·2DMF: C11–O11⋯C8, C9–O1O⋯C11; symmetry codes: (iv) = −1 + x, y, z; (v) = 1 − x, 1 − y, −z.

3.2.2 H₂pOx·2DMF. This crystal solvate is very similar to H₂pOx·2DMSO; therefore only differences between them are highlighted. The NCOCO₂H arm and the aromatic ring plane are almost coplanar (φ = 2.84(19)°) allowing the formation of shorter intermolecular HB (N–H⋯O and O–H⋯O) than those observed in H₂pOx·2DMSO. DMF and H₂pOx interact through carbonyl–carbonyl sheared interactions, Fig. 6, to develop the crystal network closely similar to that observed in the DMSO solvate. Lastly, this solvate is characterized by the absence of interactions between DMF molecules which run in channels along the c axis. The supramolecular structure is depicted in Fig. S4.†

3.2.3 3H₂pOx·2MeOH·4W. H₂pOx cocrystallizes as a mixed hydrate with methanol and water in a 3 : 2 : 4 proportion. An inversion center of symmetry is imposed; thus one complete and one-half molecule of H₂pOx are present in the asymmetric unit. The molecules of H₂pOx assemble with two molecules of either water or MeOH to form a bilayer of formula (H₂pOx·2W)₂, and a monolayer of formula H₂pOx·2MeOH, Fig. 7(a) and (b) and S6,† respectively. They arrange developing 1D tapes through the carboxylic acid O–H endings, amide carbonyl and water (O10–H10⋯O1–H1A⋯O18, O20–H20⋯O2–H2B⋯O8) or MeOH (O30–H30⋯O3–H3A⋯O28) forming, in both cases, R⁴₄(14) ring motifs that propagate along the [1 −1 12] direction. The 2D is developed in the (001) plane through the amide NH, the carbonyl of the COOH groups and the phenyl C–Hs HB to develop homo-R²₂(10) and hetero-R¹₂(6) ring motifs (N7–H7⋯O19, N17–H17⋯O9, C2–H2⋯O19, C5–H5⋯O9 in the bilayer; N27–H27⋯O29, C22–H22⋯O29 in the monolayer).

Fig. 7 Supramolecular architecture of 3H₂pOx·2MeOH·4W. (a) Alternated bilayers of formula (H₂pOx·2W)₂ and monolayer of formula H₂pOx·2MeOH in the (1 0 0) family of planes; a detail of the HB pattern between H₂pOx and water molecules W1 and W2 along the direction of the a axis. (b) HB scheme of one layer of H₂pOx·2W (0 0 1) family of planes; a similar HB scheme for H₂pOx·2MeOH is shown in Fig. S6.† (c) n → π* and π → π* interactions developing the 3D along the direction of the c axis.

Furthermore, the water molecule W2 rules the self-assembly of two centrosymmetric H₂pOx·2W layers through an R²₄(8) ring motif (O2–H2B⋯O8, O2–H2A⋯O8) partially filling the void space in between. In addition, the HB scheme of W2 is strong enough to deviate the N7C8O8C9O9O10 fragment out of the phenyl ring plane C1–C6 by φ = 19.5(3)° in comparison with the other oxalyl arm N17C18O18C19O19O20 which is almost coplanar (φ = 3.8(4)°). This distortion in the geometry allows the formation of a pair of antiparallel carbonyl–carbonyl (n → π*) interactions,⁴¹ C9O9⋯C18O18 and C18O18⋯C9O9, that contribute to strengthening the (H₂pOx·2W)₂ bilayer. Finally, the whole assembly is achieved through face-to-face stacking interactions (π → π*) between the aromatic rings (Cg1 = C1–C6, Cg2 = C21–C23) and the amide groups (Cg4 = N7–C8, Cg3 = N27–C28) (Cg1⋯Cg4 = 3.403(4) Å, Cg1_Perp = 3.378(4) Å; Cg2⋯Cg3 = 3.475(4) Å, Cg2_Perp = 3.471(4) Å).⁴² This kind of interaction has already been found to contribute to the supramolecular architecture of oxalamates⁴³ and proteins.⁴⁴ The n/π → π* interactions develop the 3D along the direction of the c axis [5 −8 0]. Fig. 7(c).

3.2.4 (HDMA)₂pOx. An imposed inversion center of symmetry leads to one-half of the dianion N,N′-(1,4-phenylene)dioxalamate (pOx²⁻) and one molecule of the dimethylammonium cation (HDMA⁺) in the asymmetric unit of (HDMA)₂pOx. The C–O lengths of the carboxylate ending are similar (O9C9 = 1.2273(13) Å, O10C9 = 1.2481(13) Å) in agreement with the anion formation. The oxalamate arm is almost planar with a N7–C8–C9–O10 torsion angle of 178.09(9)°. However, the NCOCO₂⁻ fragment is completely out of the phenyl ring plane, and they form an angle of 68.7(3)° between each other. Therefore, for symmetry reasons, the sc–ac conformation is observed. It is worth mentioning that this conformation has only been observed in anionic dinuclear M(II) metallacyclic complexes of the paracyclophane-type [M₂L₂]⁴⁻ (M = Cu, Pd)^14,17 and is in contrast to the almost planar conformation adopted in the monoanionic HpOx⁻ salt.³⁸

Several concurrent N–H⋯O and C–H⋯O interactions form intertwined ribbons to develop the 3D crystal network. The N1–H1AB⋯O10ⁱ and C11–H11A⋯O8^iv, forming C²₂(8) chains, the N7–H7⋯O9ⁱⁱⁱ, between the amide NH and the CO of the carboxylate group, forming an R²₂(10) motif, and bifacial C11–H11B⋯Cg^v,vi soft interactions form the individual ribbons along the [1 1 −1] direction. The latter interactions form adjacent R²₂(9) and R²₂(10) ring motifs on both faces of the phenyl ring allowing the methyls of HDMA⁺ to be placed up and down. Perpendicular families of ribbons are linked through bifurcated O10⋯H1A⋯O8 (N1–H1A⋯O8ⁱⁱ and N1–H1A⋯O10ⁱⁱ) strong ionic interactions in the [−1 1 1] direction. The full 3D HB scheme is depicted in Fig. 8.

Fig. 8 (a) Hydrogen bonding pattern of the (HDMA)₂pOx cocrystal salt, developing as a zig-zagging plane along the direction of the c axis. (b) Top view along the c axis.

3.3 Comparative Hirshfeld surface analysis of H₂pOx·2S and (HDMA)₂pOx

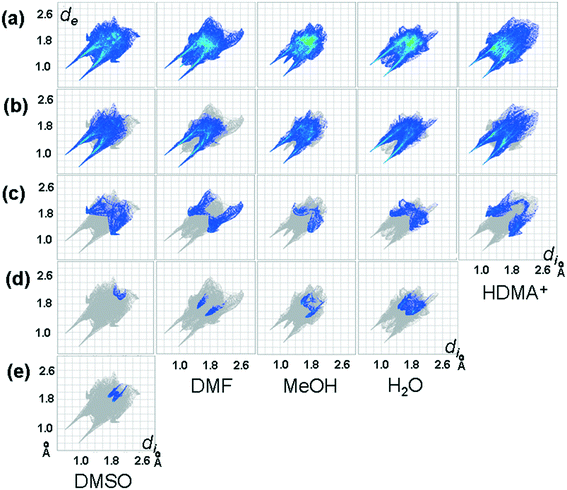
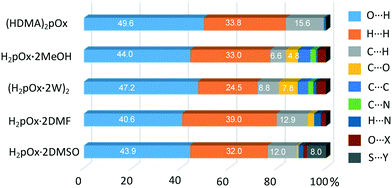
The sets of compounds herein crystallized are compared as a whole with the aim of highlighting their similarities and differences. The Hirshfeld surfaces (HSs) of H₂pOx·2S, mapped over the d_norm (range 0.4 Å to 3.0 Å), are shown in Fig. 9. The red bright spots mark the dominant interactions (O⋯H/H⋯O), which are given by D–H⋯O (D = O, N) HB, whereas the H⋯C/C⋯H contacts are also visible as small and light red spots. Among all the close interactions, H⋯H contacts (24.5–39.0%) represent the second largest interactions to the individual surfaces. The characteristic 2D fingerprint plots of the most significant attractive interactions and the percent contributions to the HSs are shown in Fig. 10 and 11, respectively. Most importantly, the O⋯H/H⋯O interactions (40.6–49.6%) appear as forceps-like profiles in the corresponding decomposed fingerprint plots Fig. 10(b), whereas the H⋯C (6.6–15.6%), C⋯O, O⋯S and their reciprocals appear as characteristic wing profiles, Fig. 10(c)–(e). C⋯O/O⋯C contacts significantly contribute to the HSs of the H₂pOx·2MeOH layer (4.8%) and (H₂pOx·2W)₂ bilayer (7.8%) of 3H₂pOx·2MeOH·4W, and to H₂pOx·2DMF (2.6%). The sum of S⋯Y/Y⋯S (Y = H, C, N, O) close contacts contributes to 8.0% to the HS of H₂pOx·2DMSO. The complete set of 2D fingerprint plots is shown in Fig. S8–S12.†

Fig. 9 Views of the Hirshfeld surfaces mapped over d_norm (ranges in a.u) for: (a) H₂pOx·2DMSO (−0.7837 to 1.3937), (b) H₂pOx·2DMF solvate (−0.7875 to 1.3212), 3H₂pOx·2MeOH·4W partitioned as (c) aqueous (H₂pOx·2W)₂ (−0.6139 to 1.2561) and (d) methanol H₂pOx·MeOH (−0.5936 to 1.3883) layers and (e) (HDMA)₂pOx (−0.7011 to 1.2605). Hydrogen bonding are represented by dashed lines.

Fig. 10 Selected views of the Hirshfeld 2D fingerprint over d_norm of the attractive interactions for H₂pOx·2S (DMSO, DMF, ⅓(MeOH·2W)) and HDMA⁺ salt. 3H₂pOx·2MeOH·4W is partitioned as H₂pOx·2MeOH and (H₂pOx·2W)₂ layers (a). Overall, (b) H⋯O/O⋯H, (c) H⋯C/C⋯H, (d) C⋯O/O⋯C and (e) O⋯S/S⋯O.

Fig. 11 Comparative percent contributions in the Hirshfeld surfaces of H₂pOx solvates and HDMA⁺ salt. 3H₂pOx·2MeOH·4W is partitioned as methanol (H₂pOx·2MeOH) and water layers (H₂pOx·2W)₂ (X = O, N, Y = H, C, N, O).

3.4 Quantitative interaction energy analysis of H₂pOx·2S and (HDMA)₂pOx

Selected results obtained from the interaction energy DFT calculations at the B3LYP/6-31G(d,p) level of theory, involving the H₂pOx·2S and (HDMA)₂pOx salt, are tabulated in Table 1. Most of the interaction energies, such as H⋯C/C⋯H, are calculated as assemblies of interactions whose HB motifs are depicted in Fig. 12. Those contacts with total interaction energy (E_tot) values smaller than −20.0 kJ mol⁻¹ are not considered for discussion. The environments about H₂pOx·2S or (HDMA)₂pOx are shown in Fig. S13–S17.† As expected, those HB motifs where the COOH⋯O contacts are involved give the greatest energies among the close contacts present in the crystals. Then, the E_tot values of the hetero-R²₂(8) and R²₂(7) HB motifs in DMSO and DMF solvates are −60.2 and −57.0 kJ mol⁻¹, respectively, larger than the COOH⋯O(sp³) HB in 3H₂pOx·2MeOH·4W with values which are in the range of −48.1 to −41.2 kJ mol⁻¹ or those O–H⋯O where water molecules act as H-donors with E_tot in the −20.4 to −27.0 kJ mol⁻¹ range. Nevertheless, the E_tot values of the hetero R²₂(n) n = 7, 8 are larger than those reported for other hetero R²₂(7) involving O–H⋯N(py) HB (−49.4 to −52.0 kJ mol⁻¹ range)⁴⁵ but smaller than the reported value for homo R²₂(8) in carboxylic acids (−73.0 kJ mol⁻¹).⁴⁶

Table 1 Calculated interaction energies (kJ mol⁻¹), %E_comp contributions to stabilization energy for selected HB and close contacts in H₂pOx·2S and (HDMA)₂pOx salt

Motif	Interaction	−Eele	−Epol	−Edis	E rep	−Etot	%Eele^a	%Edis^a	R
a The % contribution of Ecomp (%Ecomp) is calculated through (Ecomp/Estab) × 100 where Estab = Eele + Epol + Edisp. b R = distance between centroids in Å. c Cg1 and Cg2 are the centroids of the C1–C6 ring and C21–C23 rings, respectively; Cg3 and Cg4 are the centroids of the N7–C8 and N27–C28 amide bonds, respectively.
H2pOx·2DMSO
R^22(8)	O10–H10⋯O1	82.2	21.1	10.8	100.8	60.2	72.0	9.5	9.07
	C10–H10C⋯O9
R^22(11)	N7–H7⋯O8	25.5	6.2	18.5	29.5	29.4	50.8	36.9	7.91
	C3–H3⋯O9
R^12(6)	C2–H2⋯O8
D	O1–S1⋯C8	8.7	1.7	20.7	13.5	20.0	28.0	66.6	4.40
D	S1–O1⋯C9	19.0	4.6	16.9	17.7	27.6	46.9	41.7	6.25
C(4)	C10–H10A⋯O1	15.4	4.7	7.6	10.4	20.0	55.6	27.4	5.28
H2pOx·2DMF
R^22(7)	O10–H10⋯O11	93.5	22.0	10.9	109.4	57.0	74.0	8.6	9.35
	C11–H11⋯O9
R^22(11)	N7–H7⋯O8	25.4	6.1	17.9	29.2	28.9	51.4	36.2	8.39
	C3–H3⋯O9
R^12(6)	C2–H2⋯O8
D	C11–O11⋯C8	10.5	3.3	17.6	9.1	23.2	33.4	56.1	5.44
D	C9–O1O⋯C11	7.0	2.3	19.0	9.0	20.1	24.7	67.1	6.32
(H2pOx·2W)2
R^44(14)	O20–H20⋯O2	81.0	19.2	5.7	91.7	48.1	76.5	5.4	8.53
	O10–H10⋯O1	58.3	13.0	4.2	54.5	41.2	77.2	5.6	8.60
	O1–H1A⋯O18	41.7	8.0	7.2	47.7	26.8	73.3	12.7	6.61
	O2–H2B⋯O8	38.1	7.6	6.5	43.4	24.8	73.0	12.5	6.63
R^24(8)	O2–H2A⋯O8	31.0	6.1	9.3	31.5	25.8	66.8	20.0	4.17
R^22(10)	N7–H7⋯O19	42.5	8.1	18.5	52.1	34.8	61.5	26.8	9.55
	N17–H17⋯O9
R^12(6)	C2–H2⋯O19
	C5–H5⋯O9
D	O1–H1B⋯O2	16.7	1.5	4.6	4.0	20.4	73.2	20.2	14.48
C(5)	C9–O9⋯C18	10.4	2.7	61.7	36.9	43.9	13.9	82.5	3.93
	C18–O18⋯C9
H2pOx·2MeOH
R^44(14)	O30–H30⋯O3	77.1	19.8	8.8	90.9	47.6	72.9	8.3	8.78
	O3–H3A⋯O28	37.7	8.2	10.5	45.5	27.0	66.8	18.6	6.55
R^22(10)	N27–H27⋯O29	38.5	7.1	17.9	43.1	35.0	60.6	28.2	9.55
R^12(6)	C22–H22⋯O29
C(3)	Cg1⋯Cg4^c	8.6	2.8	61.1	32.8	44.1	11.9	84.3	4.91
	Cg2⋯Cg3
(HDMA)2pOx
R^22(10)	N7–H7⋯O9	53.2	12.2	15.9	54.8	45.0	65.4	19.6	9.20
R^21(5)	N1–H1A⋯O8	61.7	4.8	14.8	176.4	27.4	75.9	18.2	7.09
	N1–H1A⋯O10
D	N1–H1AB⋯O10	91.4	5.0	12.2	222.9	26.1	84.2	11.2	8.70

---

Fig. 12 Hydrogen bonding motifs formed through carboxylic acid (up) and amide (down) in H₂pOx·2S and (HDMA)₂pOx salt.

In addition, the amide N–H⋯O HB motif is the first directing energy contributor to the framework of the (HDMA)₂pOx salt, the second in H₂pOx·2S (S = DMSO, DMF), and the third in 3H₂pOx·2MeOH·4W. N–H⋯O can form hetero-rings R²₂(11) as a result of the combination of N–H⋯O with C–H⋯O or homo-rings R²₂(10) through the combination of two N–H⋯O interactions. They assemble as an adjacent combination of rings motifs {R¹₂(6) R²₂(11)} in both DMSO and DMF solvates with an E_tot mean value of −29.2(±3) kJ mol⁻¹, {R¹₂(6) R²₂(10)} in 3H₂pOx·2MeOH·4W with an E_tot mean value of −34.9(±1) kJ mol⁻¹ or as homo-R²₂(10) in the HDMA⁺ salt with E_tot = −45.0 kJ mol⁻¹. In any case the E_tot values are smaller than those calculated for homo-R²₂(10) with E_tot = −61.9 kJ mol⁻¹, in benzylic oxalamides.⁷

In both DMSO and DMF solvates, the third largest contributor to the E_tot are the D⋯CO (D = O, S) n → π* interactions with values in the −27.6 to −20.0 kJ mol⁻¹ range. The n → π* (CO⋯CO) and π → π* (amide–phenyl ring) interactions are mainly dispersive; in 3H₂pOx·2MeOH·4W, they reach E_tot mean values of −43.9 and −44.1 kJ mol⁻¹, respectively, similar to those values calculated for COO–H⋯O(carbonyl) hydrogen bonds, being the second contributors to the stability of this crystal network. The energy values herein calculated for n → π* and π → π* interactions are larger than those reported values of −22.3 kJ mol⁻¹ for antiparallel CO⋯CO⁴⁰ and 12.54 kJ mol⁻¹ for face-to face amide–phenyl ring stacking.⁴² These differences are explained because of cooperativity effects between two of each one of these interactions present in the crystal lattice of 3H₂pOx·2MeOH·4W, Fig. 7(c). Finally, D(sp³)–H⋯O (D = N, O) interactions are in the −27.4 to −20.4 kJ mol⁻¹ range, being the second contributors to the stability of the (HDMA)₂pOx salt.

The nature of the attractive energy involved in O–H⋯O HB motifs, as the dominant interaction, is mainly electrostatic with a mean percent contribution to the stabilization energy (%E_ele) value of 73(±3)%, Table 1. In contrast, the amide N–H⋯O, as the second HB contributor to the stabilization energy, is more dispersive with %E_disp values in the 36.9 to 19.6 range. The %E_disp value increases according the HB motifs: R²₂(10) < {R²₂(10) R¹₂(6)} < {R²₂(11) R¹₂(6)} reflecting the participation of the soft C–H⋯O contacts in the hetero-association. It is worth noting that the antiparallel CO⋯CO and face-to-face π⋯π* stacking (amide–phenyl ring) interactions present in the mixed solvate 3H₂pOx·2MeOH·4W are calculated as the largest dispersive energies, vide supra, with %E_disp = 82.5 (CO⋯CO) and %E_disp = 84.3 (π → π* of amide–phenyl ring), in comparison to the simple CO⋯CO interactions in DMSO and DMF solvates which are less dispersive with %E_disp in the 41.7 to 67.1 range. Thus, from the perspective of binding energetics, the contribution of n → π* and π → π* interactions to the stability of the crystal network of H₂pOx·2S must not be underestimated.

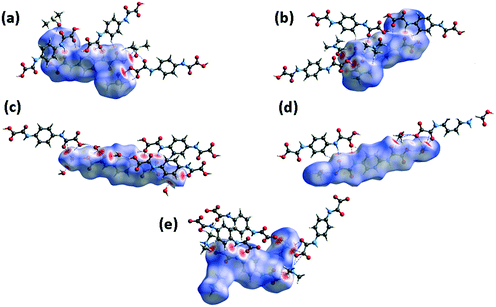
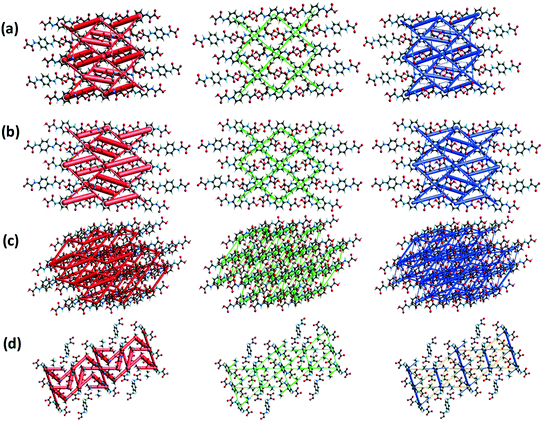
The visual representation of the energy-framework diagrams for E_ele (red), E_dis (green), E_tot (blue) and E_rep (yellow) for a cluster of nearest-neighbor molecules is shown in Fig. 13. Overall, the crystals of H₂pOx·2S (S = DMSO, DMF) are mainly dominated by the E_elec component, showing zig-zagging energy frameworks, Fig. 13(a) and (b), that overcome the E_disp as observed in the corresponding E_tot energy frameworks. On the other hand, the E_disp framework, owing to O–H⋯O, n → π* and π → π* medium strength interactions between the MeOH and water molecules with H₂pOx Fig. 13(c), strengthens the layers of the E_ele frameworks. In contrast, the large positive destabilizing ionic energies in the crystal of (HDMA)₂pOx, represented as yellow roads, strongly diminish the large stabilizing contribution from the E_ele term to the E_tot.

Fig. 13 Energy-framework diagrams for E_ele (red), E_dis (green), E_tot (blue) and E_rep (yellow) for a cluster of nearest-neighbor molecules in: (a) H₂pOx·2DMSO (bc plane), (b) H₂pOx·2DMF (bc plane), (c) 3H₂pOx·2MeOH·4W (ab plane) and (d) (HDMA)₂pOx (bc plane). All diagrams use the same cylinder scale of 80 for energies and cut-off = 9.7 kJ mol⁻¹ in 2³ unit cells.

Finally, the interaction (E_m–m, m = 1, 2) and lattice energies (E_L) of the H₂pOx solvatomorphs were calculated in the CLP-PIXEL software with the aim to estimate their relative crystal stability; their values in kJ mol⁻¹ are listed in Table S10.† As before, the 3H₂pOx·2MeOH·4W solvate was decomposed into H₂pOx·2W and H₂pOx·2MeOH fragments in order to appreciate the contribution of the interaction energies between the individual component layers. The strongest interaction energy between two H₂pOx moieties (E_1–1) is observed in 3H₂pOx·2MeOH·4W followed by H₂pOx·2DMSO and H₂pOx·2DMF. In contrast, the solvent molecules interact more strongly with H₂pOx, as judged by E_1–2 values, in the following order: DMF > W > DMSO > MeOH, whereas the interaction between two solvent molecules (E_2–2) is the largest in DMSO molecules followed by DMF and MeOH·2W. In general, the quotients E_1–1/E_1–2 and E_1–1/E_2–2 are in the 5.4–1.5 and 109–10 ranges, respectively. Then, the H₂pOx⋯H₂pOx interaction was found to be the largest contributor for all the solvates, where they should be critical for the stabilization of the lattice. Moreover, 3H₂pOx·2MeOH·4W is predicted to be the most stable crystalline solvatomorph with the largest negative value of E_L followed by DMF and DMSO solvates. On the other hand, the crystal density values suggest the following ranking order of solvatomorph stability: MeOH·2W > DMSO > DMF with the first being the densest (Table 2). Discrepancies in the stability order can be explained because the calculations were conducted at zero Kelvin and the density values are based on the structures measured at 293 K, as has been observed in other polymorphic systems.⁴⁸

Table 2 Selected thermal and crystal packing features of H₂pOx·2S

	H2pOx·2S
S	DMSO	DMF	⅓(MeOH·2W)
a Ref. 50. b ΔT = (peak temperature of the first S loss in DSC − Tb of the solvent). c (mc) micro-crystals. d (lc) large-crystals.
Theor./exp. step stoichiometry (%)	38.2/38.0	36.7/33.5 (18.4, 15.1) (mc)^c	15.3/15.3
		36.7/35.6 (9.5, 20.2, 5.9) (lc)^d
Desolvation temperature DSC, (°C)	178.0	77.3, 123.6 (mc)	96.4
		95.8, 123.0, 159.0 (lc)
Solvent boiling point, (°C)^a	189.0	153.0	64.6 (MeOH)
			100.0 (W)
ΔT, (°C)^b	−11.0	−75.7 (mc)	31.8 (MeOH)
		−57.2 (lc)	−3.6 (W)
Thermally formed desolvate	A-III	A-I (mc)	A-II
		A-III (lc)
Channel shape	Straight	Straight	Zig-zagging
Crystal density/g cm^−3	1.441	1.360	1.534
Packing fraction (PF)	0.682	0.682	0.719
Void space/Å^3	0	0	0
Void space/Å^3 (%) left by S	368.9 (39.2)	430.45 (44.3)	211.0 (21.9)
Lattice energy/kJ mol^−1	−134.75	−174.05	−367.80
E S–S/kJ mol^−1	−15.3	−9.8	−2.3

---

3.5 Thermal properties and crystal packing of H₂pOx·2S.

Thermogravimetry and differential scanning calorimetry curves (TG/DSC) confirmed the stoichiometric proportion of solvent molecules, Fig. S18–S21† according to the formula unit H₂pOx·2S (S = DMSO, DMF, ⅓(MeOH·2W)), and the thermal stability of the crystalline solid phases; data are listed in Table S11.† H₂pOx·2DMSO, in crystals or mechanochemically synthesized, released the solvent in one endothermic step at a peak temperature slightly below the boiling point of the solvent to form the A-III phase. In contrast, the thermal desolvation profile of H₂pOx·2DMF depends on the crystal size, Fig. S20.† Powdered mc-samples lost DMF in two stoichiometric well defined steps at 77.3/123.6 °C, whereas large crystals (lc) did it in several non-stoichiometric stages at 95.8 (9.5%), 123 (two overlapped steps, 20.2%) and 159 °C (5.9%) leading to A-I and A-III as the final desolvated forms, respectively. The difference in the slopes of the weight-loss steps suggests that the desolvation process of mc-H₂pOx·2DMF is more rapid than that of lc-H₂pOx·2DMF. This difference can be explained as a result of the isotropy of solvent diffusion in the mc-solid, whereas desolvation is highly anisotropic in the lc-solid,⁴⁹ beginning at the surface and traveling toward the center through a solvent gradient in the direction of the channels. In both cases, the DMF loss occurred at much smaller temperatures than the boiling point of the solvent⁵⁰ as has been observed in sulfamethazine–DMF⁵¹ or furosemide–DMF⁵² 1 : 1 solvates; in the last case the formation of different desolvated phases, according to the crystal size, has also been reported. The loss of DMF in two steps, in the range of 80–200 °C, has also been observed in the TG of the 1 : 1 betulin–DMF solvate⁵³ without DMF decomposition.⁵⁴ All these DMF-solvates, including the herein reported H₂pOx·2DMF, have very weak or null DMF–DMF interactions, as a common structural feature. Besides, their calculated packing fraction (PF) values are small, in the 0.659–0.687 range, with no void space.²⁵

In channel solvates, the low temperature of solvent loss compared to its boiling point has been associated with several crystal lattice features such as the compactness of the crystal packing, the cross-sectional area of the solvent channel, the void space in the lattice,⁵⁵ the number and strength of non-covalent interactions and the crystal size.⁵² Assuming similar crystal size between mc-DMF and mc-DMSO solvates, their large difference in thermal stability is analyzed in the context of their crystal packing characteristics. Selected crystal packing and thermal features of H₂pOx·2S are listed in Table 2. The packing fraction (PF) and void space were calculated using the packing coefficient algorithm in Mercury.²⁵ Furthermore, both solvates are equally packed (PF = 0.682) with no void spaces, forming straight channels running along the direction of the c axis. However, the calculated void space left behind after solvent loss is larger in the DMF solvate than in the DMSO solvate, according to the increase in crystal density and to the shape of the solvent molecule. At this point it is worth recalling that both solvent molecules have similar molecular weights but different shapes. In fact, the oxalamic acid arms of H₂pOx are twisted away from the aromatic ring to fit the curvature of the sphere-shaped DMSO geometry (φ = −11.7(3)°), whereas they are almost planar (φ = −2.84(19)°) in alignment to the right side of the cylinder-shaped DMF, Fig. 14. In addition, the spacing between the channels is greater in the DMF solvate than in the DMSO solvate, according to the length of the b axis (Table S1†) and in agreement with the calculated S⋯S pair-wise interaction energies (E_2–2/kJ mol⁻¹ = −15.0 (DMSO) and −9.8 (DMF)). Finally, both solvates are very similar in their supramolecular architecture but not in the calculated energetics involved (see Table 1). However, the differences in the crystal lattice features, above discussed, seem to overwhelm the E_L superiority of the mc-DMF solvate with regard to the mc-DMSO solvate resulting in the superior thermal stability of the latter.

Fig. 14 Voids in the H₂pOx·2S (S = DMSO, DMF, ⅓(MeOH·2W)) crystals, calculated with the module Solvate Analyzer of Mercury.²⁵ Conditions were set as follows: DMSO and DMF probe radius 1.2 Å, grid spacing 0.7 Å; and ⅓(MeOH·2W) probe radius 1 Å, grid spacing 0.1 Å. View in the ab plane, straight channels developing along the c axis (a) S = DMSO and (b) S = DMF. (c) S = ⅓(MeOH·2W) viewed in the ac plane, zig-zagging channels developing along the direction of the c axis.

On the other hand, the thermal stability of 3H₂pOx·2MeOH·4W crystals, where solvent loss is performed in one step, is well above the boiling point of MeOH (ΔT_b = 31.8 °C) and below that of water (ΔT_b = −3.6 °C). This result is easily explained as a consequence of the number and strength of non-covalent interactions, inherent crystal lattice features (large crystal density and PF, with no voids but the smallest void space left by solvent loss) and the largest E_L value. Nevertheless, the shape of MeOH–2W channels, which are zig-zagging along the direction of the c axis, should not be disregarded, Fig. 14. It is worth mentioning that the observed ΔT_b for MeOH–2W decomposition is in the observed range for other systems^56,57 but much smaller than that for isolated site methanolates.^58,59 In the case of (HDMA)₂pOx salt, its thermal stability was superior to 240 °C, Fig. S22.†

Finally, two water molecules per H₂pOx molecule in the H-I and H-II forms were confirmed, and they are equivalent to 12.5% of the initial masses, Fig. S23 and S24.† In H-I, the water molecules are tightly bound, and they are removed in one step at around 110 °C, disrupting the low symmetry of the crystal structure to further recrystallize into A-I. In the case of H-II, water is weakly bound, it is removed in one step near 92 °C to achieve the mc-powder A-II. This last behavior is similar to the dehydration of oxalic acid that occurs at 70 °C giving the most stable anhydrate (α-form).^60,61 According to their above described thermal properties and the reversibility in the hydration–rehydration process (vide supra), both H-I and H-II can be classified as stoichiometric channel hydrates.^62,63

Once formed by thermal desolvation, the mc-anhydrous phases A-I–A-III are stable up to approximately 200 °C, to reach decomposition at a peak temperature in the 228–233 °C range, leading to a residue at 270 °C of approximately 40% of the initial mass. Moreover, DSC analysis revealed the absence of thermal transitions between hydrates or anhydrates, suggesting the impossibility of thermally interconverting them.

3.6 Vibrational and ¹³C-CPMAS NMR analysis of crystalline H₂pOx·2S and (HDMA)₂pOx

A summary of the IR vibrational wavenumbers of the neutral solvates H₂pOx·2S and the salt (HDMA)₂pOx is listed in Table S12.† The carboxyl O–H and amide N–H stretching vibrations (ν) are observed in the 3323–3313 cm⁻¹ range. Besides, the symmetric (ν_C=Os) and antisymmetric (ν_C=Oas) stretching vibrations are in the 1730–1706 (weak) and 1686–1654 (strong) cm⁻¹ ranges, as expected when carbonyls are involved in HB.⁴⁷ In the case of H₂pOx·2DMSO, the ν_S=O is red shifted by 58 cm⁻¹ in agreement with its participation in strong HB,^64,65 whereas the ν_C=O of DMF in H₂pOx·2DMF remains unchanged. In general, the vibration spectroscopy is in agreement with the strong O–H⋯O and medium strength N–H⋯O HB length measurements performed by single crystal X-ray diffraction and the calculated interaction energies from them (vide supra). In the IR spectrum of the (HDMA)₂pOx salt, the amide ν_NH is observed at 3252 cm⁻¹ and the ν_C=Oas and ν_C=Os are observed at 1671 and 1652 cm⁻¹, in agreement with the large torsion between the oxalyl moiety and the phenyl ring as well as the strong N–H⋯O HB.

When the oxalyl unit is in the plane of the phenyl ring, the N lone pair of the amide is compromised with the aromatic ring resonance; therefore a partial positive charge is developed on the N atom resulting in the blue shift of the ν_NH band (usually beyond 3300 cm⁻¹). In contrast, the out of the phenyl plane conformations of the oxalyl unit exhibit N–H stretching vibration between 3200 and 3300 cm⁻¹, as previously reported for other phenyldioxalamates.⁶⁶ This approach has been used in the determination of conformational changes of peptides^67–69 and in the identification of crystal polymorphs.^70–72 Furthermore, taking into account the data of the four structures herein described and those oxalyl compounds whose N–H stretching frequencies and corresponding C3–C1–N7–C8 torsion angles (φ), measured from their X-ray structures, are known,^6,7 a good linear correlation is found in the wavenumber range of 3330–3225 cm⁻¹. The data, listed in Table S13,† fit to the general equation: φ = 2493(±268) − 0.748(±0.082)ν_NH (n = 10, R = 0.956, Sr = 9.4), Fig. S25.† This correlation is restricted to those structures whose COCO torsion angle is close to 180°. Based on this linear relationship, we are able to predict the conformation of the oxalamic arm of phenyloxalamic compounds knowing their ν_NH in the solid state, in this case the conformation of the hydrates and anhydrates herein reported (vide infra). It is important to highlight that, in compounds that have amide groups, most of the correlations found in the literature relate the conformation to the stretching frequency of the carbonyl group,⁷³ whereas in this work a correlation with the stretching frequency of the N–H, in oxalamic acid derivatives, is reported.

In addition, the ¹³C-Cross Polarization Magic Angle Spinning (¹³C-CPMAS) spectra of H₂pOx in the crystallized solvates and (HDMA)₂pOx are analyzed with the purpose of finding predictive patterns. A summary of the isotropic ¹³C-CPMAS chemical shifts of the H₂pOx·2S herein crystallized and (HDMA)₂pOx is listed in Table S14.† In solution, the ¹³C NMR spectrum of H₂pOx displays four signals, because of the characteristic C₂ molecular symmetry of symmetrically substituted 1,4-benzenes. The crystal structure of H₂pOx·2DMF reveled an almost planar disposition between the oxalyl arms and the phenyl ring (φ = 2.8(2)°). Therefore, only four signals are observed in the ¹³C-CPMAS NMR spectrum of H₂pOx·2DMF whose chemical shift values can be associated with a coplanar structure: δC1 = 135, δC3 = δC2 = 121, δC8 = 156 and δC9 = 163. In the case of H₂pOx·2DMSO, the oxalyl arm is tilted away from the phenyl ring by φ = 11.20(10)°, resulting in a small chemical shift difference between C2 and C3 atoms. In the mixed solvate 3H₂pOx·2MeOH·4H₂O, there are 1.5 molecules of H₂pOx in the asymmetric unit giving rise to unresolved broad signals.

In contrast to IR vibrational spectroscopy, both carbonyls are perfectly distinguishable in ¹³C-CPMAS, the amide carbonyl appears in the 156–157 ppm range, the carboxylic acid carbonyl is in the 162–163 ppm range, and the carboxylate is at 164 ppm. It is worth recalling that carboxylic acid forms R²₂(8), R²₂(7) or R⁴₄(14) hetero-rings in the set of H₂pOx·2S, but the R²₂(8) homo-ring is not formed. These results are in agreement with those ¹³C-CPMAS values reported for indomethacin⁷⁴ and 1H-pyrazole-4-carboxylic acid derivatives,⁷⁵ where the following trend has been found for δ¹³C: R²₂(8) homo-rings > C(n) homochains > C(n) heterochains > R²₂(n) hetero-rings > free carboxylic acid. Thus, according to the reported trends the δ¹³COOH in the R²₂(8) homo-ring is expected beyond 164 ppm for the oxalamic acid functional group herein analyzed.

(HDMA)₂pOx is discussed separately because of its salt nature. The solution (D₂O) spectrum of (HDMA)₂pOx strongly differs from the solid one; all carbon atoms are shifted to high frequencies by 4 ppm (C1) and ∼8–10 ppm (C2, C3) appearing at 137 ppm and in the 130–132 ppm range, respectively. This result is explained as a consequence of the large torsion angle between the oxalyl arms and the phenyl ring (φ = 68.7(3)°, vide supra). This conformation positions the cationic HDMA⁺ above and below the phenyl ring, forming a cation–π bifacial interaction as revealed by the crystal structure. The chemical shift of the amide carbonyl is the same in both solution and the solid (164 ppm), suggesting the existence of ionic triads 2HDMA⁺/pOx²⁻ in solution with very similar geometry than in the solid.

3.7 Molecular and supramolecular structures of hydrates and desolvates

In the above discussion, we have demonstrated the relation of some experimental molecular parameters and HB patterns, obtained from single crystal X-ray data, with IR and ¹³C-CPMAS spectroscopic values. On these grounds, the structures of polymorphic H₂pOx hydrates (H-I and H-II) and desolvates (A-I to A-III) are herein sketched.

A summary of the vibrational wavenumbers of hydrates and desolvates of H₂pOx is listed in Table S12† and the IR spectra are shown in Fig. 15. The IR spectrum of H-I is the same as has been reported elsewhere:¹⁷ two bands are observed for the stretching vibration of the N–H bond, whereas each ν_C=O stretching vibration is observed twice, with predicted φ values of 1.0 and 19.9°, vide supra. Besides, the ¹³C-CPMAS spectrum of H-I showed ten signals, corresponding to each one of the crystallographically different carbon atoms in the molecule, in agreement with the presence of one independent molecule of low symmetry in the asymmetric unit.

Fig. 15 Selected IR spectral windows of: (a) H-I, (b) H-II, (c) A-I, (d) A-II and (e) A-III.

In contrast, the IR spectra of H-II, A-I, A-II and A-III are much simpler. They show one band for the N–H and two broad bands for ν_C=Os and ν_C=Oas vibrations. In this context, the predicted φ values are: H-II, 13.1°; A-I, 16.9°; A-II, 31.1° and A-III, 30.3°. In addition, only four to five signals are observed in the ¹³C-CPMAS spectra of H-II, A-I, and A-II, revealing high symmetry. Thus, only one half of the H₂pOx molecule is observed, in agreement with an inversion center of symmetry located at the center of the benzene ring. In the case of desolvate A-III, seven signals are present in its ¹³C-CPMAS spectrum, whose small differences (∼1 ppm) in the chemical shifts (δ) are in agreement with one almost symmetric but independent molecule in the asymmetric unit.

In the context of supramolecular structure, efforts to relate the HB patterns to vibrational spectroscopy have been performed. An example closely related to H₂pOx is oxalic acid, which is known to crystallize into two polymorphs named α and β forms and also as the double-hydrate forming catemers (C(4)), homo-rings (R²₂(8)) and hetero-rings (R⁴₄(12)), respectively, Fig. 16. Each form presents its characteristic vibrational spectrum,^76,77 whose relevant data are summarized in Table S12.† Thus, clear ν_C=Oas (cm⁻¹) vibrations are observed according to the HB pattern of the carboxylic acid in the solid IR spectra: 1756 in the homochain, 1732 in the homo-ring and not observed in the heteroring because of centrosymmetry, but at 1738 in Raman spectroscopy. These findings are consistent with the values found in the vibrational study of a set of dicarboxylic acids forming homo-rings in the solid and the shift to 1780 cm⁻¹ for isolated COOH.⁷⁸ Each HB motif of oxalic acid can also be associated with the number and values of ν_OH frequencies: two strong bands beyond 3400 cm⁻¹ in the R⁴₄(12) hetero-ring with water, one strong band at 3114 cm⁻¹ for the C(4) homochain and several medium bands in the 3106–2677 cm⁻¹ range in the R²₂(8) homo-ring. In addition, a broad band assigned to O–H deformation mode (δ_OH), characteristic of hetero O–H⋯O motifs, is present in the IR spectrum of the dihydrate of oxalic acid at 1904 cm⁻¹ and in the trihydrate of the acid N,N′-(1,3-phenylene)dioxalamic⁷⁹ at 1998 cm⁻¹.

Fig. 16 Oxalic acid forms associated with their hydrogen bonding motifs.

The typical R²₂(8) homo-ring formed by carboxylic acids is absent in all of the crystal structures herein analyzed. Instead, in H₂pOx·2S (S = DMSO, DMF) the CO₂H forms an R²₂(n) (n = 7, 8) hetero-ring motif and R⁴₄(14) hetero-ring with both water and MeOH, when S = ⅓(MeOH·2W).

The vibrational pattern of the mc-forms of H₂pOx double-hydrates H-I and H-II, herein reported, shows close resemblance with the IR spectra of both 3H₂pOx·2MeOH·4W and the double-hydrate of the oxalic acid: ν_COas is in the 1733–1706 range, two ν_OH bands in 3550–3488 and 3390–3349 cm⁻¹ ranges and δ_OH in the 1954–1968 cm⁻¹ range. In this context, the carboxylic acid endings in H-I are proposed to form R⁴₄(14) HB motifs with water, similar to the motif shown in the (H₂pOx·2W)₂ bilayer of the mixed solvate 3H₂pOx·2MeOH·4W, as well as in H₂Mf(HpOx)₂·4W.³⁸ Besides, H-II is proposed to form R⁴₄(12) HB motifs with water similar to that found in the double-hydrate of oxalic acid. To support this proposal, it is worth recalling that crystals of 3H₂pOx·2MeOH·4W dried at RT form H-I, whereas the water molecules in H-II are weakly bound, and they are removed at 92.4 °C, similar to the dehydration of oxalic acid (vide supra). Furthermore, in H₂pOx desolvates A-I, A-II and A-III, the IR features are in agreement with carboxylic acid endings forming C(4) homochains and/or C(n) heterochains: ν_COas and ν_OH are in the 1765–1753 cm⁻¹ and 3293–3220 cm⁻¹ ranges, respectively. This conclusion is supported by ¹³C-CPMAS data, which revealed the absence of the R²₂(8) HB pattern in the H₂pOx hydrates and H₂pOx desolvates.

As far as the chemical shift of the amide carbonyl is concerned (¹³C-CPMAS), it is in the 156–158 ppm range in both the crystal solvates and the hydrates, and appears shifted to lower frequencies (154–155 ppm) in desolvates, Table S14.† Therefore, the amide carbonyl is proposed to be involved in X–H⋯OC (amide) (X = N, OH) HB in hydrates, developing C(n) chain motifs such as those observed in the triad of solvates herein crystallized. On the other hand, amide carbonyl is free of HB in desolvates, as a consequence of the lack of HB donors. These conclusions are in agreement with those observed by IR analysis and give support to the proposed structures of the conformational polymorphs depicted in Fig. 17.

Fig. 17 Supramolecular arrangement proposal in 1D for the double-hydrates H-I and H-II, and the solid phases A-I–A-III. Conformation sp–ap in: (a) H-I (1.0 and 19.9°), (b) H-II (13.1°), (c) A-I (16.1°) and A-II (16.9°). Conformation sc–ac in (c) A-III (30.3°). Estimated C3–C1–N7–C8 torsion angle values are in parentheses (φ = 2493(±268) − 0.748(±0.082)ν_NH (n = 10, R = 0.956, Sr = 9.4)).

4. Conclusions

The high propensity of N,N′-(1,4-phenylene)dioxalamic acid to form channel solvates of formula H₂pOx·2S was demonstrated and the interconversion pathways between the ten solid phases of H₂pOx herein reported were stablished. The crystal-solvates (S = DMSO, DMF, ⅓(MeOH·2W)) and the HDMA-salt were characterized by single X-ray crystallography. The evaluation of the Hirshfeld surface (HS), two-dimensional fingerprint plots and energy-framework diagrams allowed us to rank COOH⋯O (electrostatic) as the dominant HB interaction followed by N–H⋯O (electrostatic-dispersive) and lastly D⋯CO (D = O, S) n → π* and π → π* interactions (dispersive). The role of the crystallized solvent was demonstrated to fix the conformation of H₂pOx maximizing the HB capabilities of the whole system. In addition to the crystal packing features, the crystal stability relies on H₂pOx⋯H₂pOx interactions and the thermal stability on solvent–solvent interactions.

The X-ray structural features associated with ¹³C-CPMAS and IR vibrational spectroscopy allowed us to estimate the conformation of H₂pOx and to sketch the HB motifs that gave rise to the supramolecular architecture of non-crystallized polymorphs. Finally, the amide N–H⋯OCO intermolecular HB is proposed to maintain the crystal network that allows the reversibility in hydration–dehydration processes and the observed solid phase transformations of H₂pOx.

Abbreviations

DMSO	Dimethyl sulfoxide
DMF	Dimethyl formamide
DMA	Dimethyl amine
SEM	Scanning electron microscopy

Funding sources

This work was supported by CONACYT Grant 255354.

Author contributions

Conceptualization, I. I. P.-M., E. V. G.-B.; investigation, M. M.-S., S. C.-C., F. J. M.-M.; formal analysis, J. M. S.-Q., E. V. G.-B.; visualization, M. M.-S., S. C.-C., J. M. S.-Q., E. V. G.-B.; methodology, S. R.-L.; resources, S. R.-L., F. J. M.-M., A. C.; writing–review & editing, F. J. M.-M., E. V. G.-B., A. C., I. I. P.-M.; funding acquisition, supervision, validation, writing–original draft, I. I. P.-M. All the authors have read and agreed to the final version of the manuscript.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was supported by CONACYT Grants 255354 and 316892, Secretaria de Investigación y Posgrado del Instituto Politécnico Nacional (SIP-IPN) Grants 20211070 and 20201274, CONACYT Red Temática de Química Supramolecular Grant 271884, CGIC-UC (Coordinación General de Investigación Científica de la Universidad de Colima) and PROMEP-SEP.

References

1. F. J. Martínez-Martínez, E. V. García-Báez, J. S. González-González and I. I. Padilla- Martínez, Hydrogen Bonding in Pharmacy: Oxalic Acid Derivatives as a Case of Study, in Biotechnology: Health, Food, Energy and Environment Applications, ed. L. G. Torres-Bustillos and I. Garcia-Peña, Nova Science Publishers Inc., New York, 2013, pp. 189–206.
2. P.-N. Cheng, J. D. Pham and J. S. Nowick, The supramolecular chemistry of β-sheets, J. Am. Chem. Soc., 2013, 135, 5477.
3. N. Ohashi, S. Harada, T. Miuguchi, Y. Irahara, Y. Yamada, M. Kotani, W. Nomura, S. Matsushita, K. Yoshimura and H. Tamamura, Small-Molecule CD4 Mimics Containing Mono-cyclohexyl Moieties as HIV Entry Inhibitors, ChemMedChem, 2016, 11, 940.
4. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The Cambridge Structural Database ver. 2021.1, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171.
5. E. G. Ramírez-Milanés, F. J. Martínez-Martínez, N. E. Magaña-Vergara, S. Rojas Lima, Y. A. Avendaño-Jiménez, E. V. García-Báez, L. M. Morín-Sánchez and I. I. Padilla-Martínez, Positional isomerism and steric effects in the self-assemblies of phenylene bis-monothiooxalamides, Cryst. Growth Des., 2017, 17, 2513.
6. J. S. González-González, F. J. Martínez-Martínez, A. L. Peraza-Campos, M. J. Rosales-Hoz, E. V. García-Báez and I. I. Padilla-Martínez, Supramolecular architectures of conformationally controlled 1,3-phenyl-dioxalamic molecular clefts through hydrogen bonding and steric restraints, CrystEngComm, 2011, 13, 4748.
7. J. S. González-González, F. J. Martínez-Martínez, E. V. García-Báez, A. Cruz, L. M. Morín-Sánchez, S. Rojas-Lima and I. I. Padilla-Martínez, Molecular Complexes of Diethyl N,N′-1,3-Phenyldioxalamate and Resorcinols: Conformational Switching through Intramolecular Three-Centered Hydrogen-Bonding, Cryst. Growth Des., 2014, 14, 628.
8. L. Bereczki, P. Bombicz, J. Balint, G. Egri, J. Schindler, G. Pokol, E. Fogassy and K. Marthi, Optical resolution of 1-(1-naphthyl)ethylamine by its dicarboxylic acid derivatives: structural features of the oxalic acid derivative diastereomeric salt pair, Chirality, 2009, 21, 331.
9. J. Balint, G. Egri, M. Czugler, J. Schindler, V. Kiss, Z. Juvancz and E. Fogassy, Resolution of α-phenylethylamine by its acidic derivatives, Tetrahedron: Asymmetry, 2001, 12, 1511.
10. C. M. Hall and J. B. Wright, Antiallergic phenylenedioxamic acids, The Upjohn Company, Ger. Offen., DE2362409A1, 1974, p. 19740627.
11. J. B. Wright, C. M. Hall and H. G. Johnson, N,N’-(phenylene)dioxamic acids and their esters as antiallergy agents, Med. Chem., 1978, 21, 930.
12. G. P. Petyunin, Synthesis and pharmacological activity of phenylenedioxamic acids, Khim.-Farm. Zh., 1986, 20, 827–830.
13. E. Pardo, J. Faus, M. Julve, F. Lloret, M. C. Muñoz, J. Cano, X. Ottenwaelder, Y. Journaux, R. Carrasco, G. Blay, I. Fernández and R. Ruiz-García, Long-Range Magnetic Coupling through Extended π-Conjugated Aromatic Bridges in Dinuclear Copper(II) Metallacyclophanes, J. Am. Chem. Soc., 2003, 125, 10770.
14. J. Ferrando-Soria, M. Castellano, R. Ruiz-García, J. Cano, M. Julve, F. Lloret, C. Ruiz-Pérez, J. Pasán, L. Cañadillas-Delgado, D. Armentano, Y. Journaux and E. Pardo, Dicopper(II) Metallacyclophanes with Electroswitchable Polymethyl Substituted para-Phenylene Spacers, Chem. – Eur. J., 2013, 19, 12124.
15. E. Pardo, D. Cangussu, R. Lescouezec, Y. Journaux, J. Pasan, F. S. Delgado, C. Ruiz-Pérez, R. Ruiz-García, J. Cano, M. Julve and F. Lloret, Molecular-Programmed Self-Assembly of Homo- and Heterometallic Tetranuclear Coordination Compounds: Synthesis, Crystal Structures, and Magnetic Properties of Rack-Type Cu^II₂M^II₂ Complexes (M = Cu and Ni) with Tetranucleating Phenylenedioxamato Bridging Ligands, Inorg. Chem., 2009, 48, 4661.
16. H. Li, Y.-F. Han, Y.-J. Lin, Z.-W. Guo and G.-X. Jin, Stepwise Construction of Discrete Heterometallic Coordination Cages Based on Self-Sorting Strategy, J. Am. Chem. Soc., 2014, 136, 2982.
17. W. X. C. Oliveira, C. B. Pinheiro, M. M. da Costa, A. P. S. Fontes, W. C. Nunes, F. Lloret, M. Julve and C. L. M. Pereira, Crystal Engineering Applied to Modulate the Structure and Magnetic Properties of Oxamate Complexes Containing the [Cu(bpca)]⁺ Cation, Cryst. Growth Des., 2016, 16, 4094.
18. Y. Wang, Y. Zhang, B. Yang, A. Zhang and Q. Yao, N-(1-Oxy-2-picolyl)oxalamic acids as a new type of O,O-ligands for the Cu-catalyzed N-arylation of azoles with aryl halides in water or organic solvent, Org. Biomol. Chem., 2015, 13, 4101.
19. Y. Wang, J. Ling, Y. Zhang, A. Zhang and Q. Yao, N-(1-Oxy-2-picolyl)oxalamic Acid as an Efficient Ligand for Copper-Catalyzed Amination of Aryl Iodides at Room Temperature, Eur. J. Org. Chem., 2015, 19, 4153.
20. M. Sönmez, M. Çelebi, A. Levent, I. Berber and Z. Şentürk, A new pyrimidine-derived ligand, N-pyrimidine oxalamic acid, and its Cu(II), Co(II), Mn(II), Ni(II), Zn(II), Cd(II), and Pd(II) complexes: synthesis, characterization, electrochemical properties, and biological activity, J. Coord. Chem., 2010, 63, 848.
21. CrysAlis PRO, Agilent Technologies, Yarnton, UK, 2012.
22. G. M. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3.
23. L. J. Farrugia, WinGX and ORTEP for windows: An update, J. Appl. Crystallogr., 2012, 45, 849.
24. A. L. Spek, Structure validation in chemical crystallography, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148.
25. C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, V. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, Mercury CSD 2.0 - New Features for the Visualization and Investigation of Crystal Structures, J. Appl. Crystallogr., 2008, 41, 466.
26. J. Bernstein, R. E. Davis, L. Shimoni and N. L. Chang, Patterns in Hydrogen Bonding: Functionality and Graph Set Analysis in Crystals, Angew. Chem., Int. Ed. Engl., 1995, 34, 1555.
27. M. A. Spackman and J. J. McKinnon, Fingerprinting intermolecular interactions in molecular crystals, CrystEngComm, 2002, 66, 378.
28. J. J. McKinnon, M. A. Spackman and A. S. Mitchell, Novel tools for visualizing and exploring intermolecular interactions in molecular crystals, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 627.
29. M. J. Turner, S. P. Thomas, M. W. Shi, D. Jayatilaka and M. A. Spackman, Energy frameworks: insights into interaction anisotropy and the mechanical properties of molecular crystals, Chem. Commun., 2015, 51, 3735.
30. C. F. Mackenzie, P. R. Spackman, D. Jayatilaka and M. A. Spackman, CrystalExplorer model energies and energy frameworks: extension to metal coordination compounds, organic salts, solvates and open-shell systems, IUCrJ, 2017, 4, 575.
31. J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Towards quantitative analysis of intermolecular interactions with Hirshfeld surfaces, Chem. Commun., 2007, 3814.
32. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendel, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009.
33. A. Hasija, R. Bhowal and D. Chopra, Quantitative Investigation of Weak Intermolecular Interactions of −F and −CF₃ Substituted in Situ Cryocrystallized Benzaldehydes, Cryst. Growth Des., 2020, 20, 7921.
34. A. Gavezzotti, Calculation of Intermolecular Interaction Energies by Direct Numerical Integration over Electron Densities. 2. An Improved Polarization Model and the Evaluation of Dispersion and Repulsion Energies, J. Phys. Chem. B, 2003, 107, 2344.
35. A. Gavezzotti, Calculation of lattice energies of organic crystals: the PIXEL integration method in comparison with more traditional methods, Z. Kristallogr., 2005, 220, 499.
36. A. Gavezzotti, Equilibrium structure and dynamics of organic crystals by Monte Carlo simulation: critical assessment of force fields and comparison with static packing analysis, New J. Chem., 2013, 37, 2110.
37. M. M. Heravi, M. Ghavidel and L. Mohammadkhani, Beyond a solvent: triple roles of dimethylformamide in organic chemistry, RSC Adv., 2018, 8, 27832.
38. S. Chong-Canto, E. V. Garcia-Baez, F. J. Martinez-Martinez, A. A. Ramos-Organillo and I. I. Padilla-Martinez, Mechanochemical synthesis and structure of the tetrahydrate and mesoporous anhydrous metforminium(2+)-N,N'-1,4-phenylenedioxalamic acid (1:2) salt: the role of hydrogen bonding and n→π * charge assisted interactions, Pharmaceutics, 2020, 12, 998.
39. I. Csöregh, M. Czugler, A. Ertan, E. Weber and J. Ahrendt, Solid-state binding of dimethyl sulfoxide involving carboxylic host molecules: x-ray crystal structures of four inclusion species, J. Inclusion Phenom. Mol. Recognit. Chem., 1990, 8, 275.
40. F. H. Allen, C. A. Baalham, J. P. M. Lommerse and P. R. Raithby, Carbonyl-carbonyl interactions can be competitive with hydrogen bonds, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 320.
41. A. Bauzá, T. J. Mooibroek and A. Frontera, The bright future of unconventional σ/π-hole interactions, ChemPhysChem, 2015, 16, 2496.
42. M. Harder, B. Kuhn and F. Diederich, Efficient stacking on protein amide fragments, ChemMedChem, 2013, 8, 397.
43. L. C. Cabrera-Pérez, E. V. García-Báez, M. O. Franco-Hernández, F. J. Martínez-Martínez and I. I. Padilla-Martínez, Carbonyl–carbonyl interactions and amide p-stacking as the directing motifs of the supramolecular assembly of ethyl N-(2-acetylphenyl)- oxalamate in a synperiplanar conformation, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 381.
44. S. Dasari and B. S. Mallik, Conformational free-energy landscapes of alanine dipeptide in hydrated ionic liquids from enhanced sampling methods, Phys. Chem. B, 2020, 124, 6728.
45. S. L. Tan, N. R. Halcovitch and E. R. T. Tiekink, N,N'-Bis(pyridin-4-ylmethyl)oxalamide benzene monosolvate: crystal structure, Hirshfeld surface analysis and computational study, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2019, 75, 1133.
46. S. L. Tan and E. R. T. Tiekink, A 1:2 co-crystal of 2,20-dithiodibenzoic acid and benzoic acid: crystal structure, Hirshfeld surface analysis and computational study, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2019, 75, 1.
47. S. L. Tan and E. R. T. Tiekink, Crystal structure, Hirshfeld surface analysis and computational study of the 1:2 co-crystal formed between N,N'-bis(pyridin-4-ylmethyl)ethanediamide and 4-chlorobenzoic acid, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2020, 76, 245.
48. S. Long, P. Zhou, S. Parkin and T. Li, Polymorphism and solid-to-solid phase transitions of a simple organic molecule, 3-chloroisonicotinic acid, CrystEngComm, 2015, 17, 2389.
49. S. Varughese, M. S. R. N. Kiran, U. Ramamurty and G. R. Desiraju, Nanoindentation in crystal engineering: quantifying mechanical properties of molecular crystals, Angew. Chem., Int. Ed., 2013, 52, 2701.
50. NIST Standard Reference Database SRD Number 69, Last update to data: 2021 DOI: https://doi.org/10.18434/T4D303.
51. D. Ahuja, P. Bannigan and Å. C. Rasmuson, Study of three solvates of sulfamethazine, CrystEngComm, 2017, 19, 6481.
52. V. S. Minkov, A. A. Beloborodova, V. A. Drebushchak and E. V. Boldyreva, Furosemide solvates: can they serve as precursors to different polymorphs of furosemide?, Cryst. Growth Des., 2014, 14, 513.
53. D. Yang, N. Gong, L. Zhang, Y. Lu and G. Du, Structural and computational study of four new solvatomorphs of betulin: A combined X-ray, Hirshfeld surface, and thermal analysis, J. Pharm. Sci., 2017, 106, 826.
54. P.-H. Yuan, Y.-C. Bi, B. Su, D.-Z. Yang, N.-B. Gong, L. Zhang, Y. Lu and G.-H. Du, Analysis of four solvatomorphs of betulin by TG–DTA–EI/PI–MS system equipped with the skimmer-type interface, Nat. Prod. Bioprospect., 2020, 10, 141.
55. H. G. Brittain, K. R. Morris and S. X. M. Boerrigter, Structural aspects of solvatomorphic systems, in Polymorphism in Pharmaceutical Solids, ed. H. G. Brittain, Informa Healthcare, London, New York, 2nd edn, 2009.
56. J. Ouyang, B. Na, L. Zhou, S. Xiao, G. Xiong and T. Jin, Crystal structures and phase transformation of two novel solvates of valnemulin hydrochloride, CrystEngComm, 2018, 20, 563.
57. S.-R. Tak and Y.-T. Sohn, Crystal forms of a new 5-HT4 receptor agonist DA-6886, J. Therm. Anal. Calorim., 2016, 123, 2477.
58. M. Sorrenti, G. P. Bettinetti and A. Negri, Thermoanalytical characterization of pseudopolymorphs of sulfadimidine and sulfadimidine-trimethoprim molecular complexes, Thermochim. Acta, 1998, 321, 67.
59. D. Angira, A. Shaik, S. Kirubakaran and V. Thiruvenkatam, Exploring a solvated dimer of Gefitinib: a quantitative analysis, Acta Crystallogr., Sect. C: Struct. Chem., 2018, 74, 944.
60. D. Vojta, M. Vrankić, M. Bertmer and G. E. Schaumann, Dehydration of α-oxalic acid dihydrate: Structural, spectroscopic and thermal study with implications on the disruption of water molecular bridges in soil organic matter, Thermochim. Acta, 2016, 643, 73.
61. M. O. Okoth, R. M. Vrcelj, D. V. Sheen and J. N. Sherwood, Hydration studies of a simple molecular solid, CrystEngComm, 2012, 14, 1602.
62. A. M. Healy, Z. A. Worku, D. Kumar and A. M. Madi, Pharmaceutical solvates, hydrates and amorphous forms: A special emphasis on cocrystals, Adv. Drug Delivery Rev., 2017, 117, 25.
63. D. E. Braun, V. Kahlenberg and U. J. Griesser, Experimental and computational hydrate screening: cytosine, 5-flucytosine, and their solid solution, Cryst. Growth Des., 2017, 17, 4347.
64. F. A. Cotton, R. Francis and W. D. Horrocks, Sulfoxides as ligands II. The infrared spectra of some dimethyl sulfoxide complexes, J. Phys. Chem., 1960, 64, 1534.
65. K.-I. Oh, K. Rajesh, J. F. Stanton and C. R. Baiz, Quantifying hydrogen-bond populations in dimethyl sulfoxide/water mixtures, Angew. Chem., Int. Ed., 2017, 56, 11375.
66. J. S. González-González, O. Zuñiga-Lemus, F. J. Martínez-Martínez, E. V. García-Báez and I. I. Padilla-Martínez, Mechanochemical complexation of diethyl N,N'-[1,3-(2-methyl)phenyl]dioxalamate and resorcinol: conformational twist and x-ray helical supramolecular architecture, J. Chem. Crystallogr., 2015, 45, 244.
67. A. Dutta, A. Dutt, M. G. B. Drew and A. Pramanik, Supramolecular helix and β-sheet through self-assembly of two isomeric tetrapeptides in crystals and formation of filaments and ribbons in the solid state, Supramol. Chem., 2008, 20, 625.
68. J. Kong and S. Yu, Fourier transform infrared spectroscopic analysis of protein secondary structures, Acta Biochim. Biophys. Sin., 2007, 39, 549.
69. P. S. Walsh, R. Kusaka, E. G. Buchanan, W. H. James, B. F. Fisher, S. H. Gellman and T. S. Zwier, Cyclic Constraints on Conformational Flexibility in γ Peptides: Conformation Specific IR and UV Spectroscopy, J. Phys. Chem. A, 2013, 117, 12350.
70. N. J. Babu, S. Cherukuvada, R. Thakuria and A. Nangia, Conformational and Synthon Polymorphism in Furosemide (Lasix), Cryst. Growth Des., 2010, 10, 1979.
71. K. L. A. Chan, O. S. Fleming, S. G. Kazarian, D. Vassou, G. D. Chryssikos and V. Gionis, Polymorphism and devitrification of nifedipine under controlled humidity: A combined FT-Raman, IR and Raman microscopic investigation, J. Raman Spectrosc., 2004, 35, 353.
72. A. P. Mendham, R. A. Palmer, B. S. Potter, T. J. Dines, M. J. Snowden, R. Withnall and B. Z. Chowdhry, Vibrational spectroscopy and crystal structure analysis of two polymorphs of the di-amino acid peptide cyclo(L-Glu-L-Glu), J. Raman Spectrosc., 2010, 41, 288.
73. M. Jackson and H. Mathsch, Protein secondary structure from FT-IR spectroscopy: correlation with dihedral angles from three-dimensional Ramachandran plots, Can. J. Chem., 1991, 69, 1639.
74. X. Yuan, T.-X. Xiang, B. D. Anderson and E. J. Munson, Hydrogen bonding interactions in amorphous indomethacin and its amorphous solid dispersions with poly(vinylpyrrolidone) and poly(vinylpyrrolidone-co-vinyl acetate) studied using ¹³C solid-state NMR, Mol. Pharmaceutics, 2015, 12, 4518.
75. L. Infantes, M. A. García, C. López, R. M. Claramunt and J. Elguero, The structure and dynamic properties of 1H-pyrazole-4-carboxylic acids in the solid state, Z. Phys. Chem., 2013, 227, 841.
76. L. J. Bellamy and R. J. Pace, Hydrogen bonding in carboxylic acids-I. Oxalic acids, Spectrochim. Acta, 1963, 19, 435.
77. Q. X. Ma, H. He and C. Liu, Hygroscopic properties of oxalic acid and atmospherically relevant oxalates, Atmos. Environ., 2013, 69, 281.
78. I. Wolfs and H. O. Desseyn, Characteristic vibrational pattern for the cyclic dimer carboxylic acid function in the solid state, Appl. Spectrosc., 1996, 50, 1000.
79. L. Lisnard, L.-M. Chamoreau, Y. Li and Y. Journaux, Solvothermal synthesis of oxamate-based helicate: temperature dependence of the hydrogen bond structuring in the solid, Cryst. Growth Des., 2012, 12, 4955.

---

Footnote

† Electronic supplementary information (ESI) available: Details of the synthetic procedures, thermal analysis, molecular crystal structures, geometric structural parameters, correlation data and computational details. CCDC 1874282 and 1997485–1997487 contain the supplementary crystallographic data for this paper. For crystallographic data in CIF or other electronic format see DOI: 10.1039/d1ce01504d

---