Unexpected triaxial preferences in some all-syn 1,3,5-trifluorocyclohexanes

Abstract

Theory and solution NMR indicate that all-syn 1,3,5-trifluorocyclohexane 5 adopts the expected tri-equatorial conformation, however in the solid state the more polar triaxial conformation is observed. This and the favoured conformations of substituted (Me, OMe, NH(CO)Me, NHBoc) derivatives of 5 are investigated to explore triaxial C–F preferences.

---

It is a fundamental feature of substituted cyclohexane rings that the lower energy conformer tends to have the maximum number of equatorial substituents¹ due to unfavourable steric clashes associated with 1,3 diaxial interactions. Here we consider all-syn-1,3,5-trifluorocyclohexanes where electrostatic repulsion between tri-axial fluorines is anticipated to further favour the tri-equatorial conformers. Previously we prepared all syn-1,2,3,4,5,6-hexafluorocyclohexane 1 and found it to be a particularly polar aliphatic with a molecular dipole moment of μ = 6.2 D, the largest recorded for an aliphatic.² The polarity in 1 arises almost exclusively from the net dipole of the co-aligned tri-axial C–F bonds. Ring interconversion generates an iso-energetic conformer. Removing fluorines from 1 leads to non-equivalent interconverting conformers and it was anticipated that the conformer with more equatorial fluorines will be favoured. Polar organic motifs can offer advantageous properties to materials³ and therefore in order to maximise polarity in such systems, the challenge is to maintain tri-axial C–F bonds. We recently reported the synthesis and properties of all-syn 1,3,5-trifluoro-2,4,6-trialkyl cyclohexanes such as 2, and showed that they favour tri-axial C–F bonds as steric interactions between the Me groups are higher in energy than repulsion between the fluorines.⁴ These trialkyl systems have potential utility as the favoured conformers are also the most polar. For this study we wished to explore systems with less functionality and confined to unsubstituted all-syn-trifluorocyclohexane 5, and mono substituted derivatives (R = Me 6, OMe 7, NHAc 9, NHBoc 10) to explore their tendencies, or not, to adopt triaxial fluorine conformations. At the outset we re-calculated⁵ the conformational energy differences for all-syn pentafluoro- 3, tetrafluoro- 4 and trifluoro- 5 cyclohexanes at the PBE0-D3/def2-TZVP//B3LYP-D3/def2-TZVP level of theory, sequentially removing a fluorine from the rings as illustrated in Fig. 1. The B3LYP-D3/def2-TZVP level was chosen for the optimisation and frequency calculations since it reproduces accurately the experimental X-ray geometries of the compounds studied herein (Fig. S1 in the ESI†) and the PBE0-D3/def2-TZVP was chosen for single point energy calculations because it showed the lowest mean absolute error (MAE) with respect to DLPNO-CCSD(T) for similar molecular systems.⁴ The outcomes were similar to previous calculations⁵ where the gas phase structures favour the tri-equatorial conformers in each case, and most significantly so in the case of all-syn 1,3,5-trifluorocyclohexane 5, where the triaxial conformers 5_ax is 3.55 kcal mol⁻¹ higher in energy than 5_eq. Essentially in the gas phase the less polar conformers are favoured, however as we report here, the outcome can change in the condensed state and more polar conformers are often favoured.

Fig. 1 Comparative properties for cyclohexanes 1–5 calculated at the PBE0-D3/def2-TZVP//B3LYP-D3/def2-TZVP level of theory.

Trifluoro cyclohexane 5 could be readily prepared by a direct aryl hydrogenation of 1,3,5-trifluorobenzene as previously described by the Glorius lab.⁶ It is a solid (mp = 90 °C) and a suitable crystal of 5 proved amenable to X-ray diffraction analysis. The striking feature of the solid-state structure shown in Fig. 2a is the triaxial arrangement 5_ax of the C–F bonds. This was unexpected given that the relative gas phase energies favour 5_eq by 3.55 kcal mol⁻¹ and that 5_ax is a significantly more polar conformer (5_axμ = 5.12 D versus μ = 1.59 D for 5_eq). In order to rationalise this observation, the energy gained in condensing three molecules of 5 together was calculated in the gas phase, when they adopt either the 5_ax or the 5_eq conformations. The outcome summarised in Fig. 2a is quite striking. If three triaxial 5_ax conformers are stacked one on top of another, approximating the arrangement in the X-ray structure, then the interaction energy gained is −16.7 kcal mol⁻¹. Calculations were conducted using the London Dispersion-corrected Hartree–Fock method (HFLD)⁷ and the aug-cc-pVTZ basis set as implemented in ORCA 5.0.3⁸ due to its high accuracy – between that of DLPNO-CCSD and DLPNO-CCSD(T) schemes – and fast basis set convergence. However, if three tri-equatorial 5_eq conformers are similarly stacked, then the interaction energy is significantly lower at −1.23 kcal mol⁻¹. The stabilisation observed in condensing 5_ax comes from the inherent polarity and consequent electrostatic attraction accorded by intermolecular packing, where the electronegative fluorine faces contact the electropositive hydrogen faces of adjacent rings. The tri-equatorial conformer 5_eq is significantly less polar and the energy gained during condensation is far less significant (1.23 kcal mol⁻¹versus 16.7 kcal mol⁻¹).

Fig. 2 Equilibrium energies, X-ray structures (left hand side images – showing three molecules) and computational analysis indicating the energy gained from condensation of tri-axial and tri-equatorial conformers of 5 and 6 in the gas phase. (a) The condensation energy is greater for 5_ax than 5_eq and in (b) is greater for 6_ax than 6_eq.

¹H-NMR data in chloroform (CDCl₃) indicate a predominant tri-equatorial 5_eq conformation in solution for 5. There are no large ³J_HF coupling constants indicative of anti-periplanar HC–CF relationships. anti-Periplanar HC–CF relationship will normally have ³J_HF values in the range 20–35 Hz. The vicinal coupling constants are significantly smaller and measured at ³J_HF =11.5 Hz and ³J_HF = 4.5 Hz only, indicative of predominant gauche relationships in 5_eq.^9,10 It is interesting also to observe the change in the ¹J_CF coupling constants in the ¹³C-NMR spectra of 5 in solvents of varying polarity. The axial and equatorial conformers are not resolved due to rapid ring interconversion, thus the ¹J_CF coupling constant is an average of the triaxial 5 and tri-equatorial 5 populations.

The value of ¹J_CF = 179.4 Hz in cyclohexane, the least polar solvent, reduces to ¹J_CF = 173.5 Hz in acetone, the most polar solvent, and can be rationalised in terms of the Perlin effect.¹¹ The Perlin effect describes the phenomenon that the ¹J_CF coupling constants in NMR for an axial C–F bond has a lesser value than that for an equatorial C–F bond. This has been attributed to hyperconjugation from anti-periplanar C–H bonds donating electron density to the σ*_CF antibonding orbital and weakening (lengthening) the C–F bond, an effect that only occurs for axial C–F bonds. The observed reduction in the ¹J_CF coupling constant with increasing dielectric constants (e), progressing from cyclohexane, through toluene and chloroform to acetone as illustrated in Fig. 3 is consistent with more polar solvents increasingly accommodating the more polar 5_ax conformer, and computational outcomes suggest a 5_ax = 5_eq population at parity in acetone, which is significantly the most polar solvent explored (ε = 20.7). Such solvent effects have been observed for cis-fluorinated piperidines where the more polar conformers are stabilised by more polar solvents.¹² A similar situation is found for the methyl substituted trifluorocyclohexane 6 also prepared by aryl hydrogenation as illustrated in Fig. 2b. In the gas phase 6_eq is less polar and the lower energy conformer is favoured by 1.98 kcal mol⁻¹, however X-ray diffraction reveals that in the solid state 6_ax is the only conformer. A similar analysis to that carried out for 5, condensing three molecules of 6 in the gas phase and approximating the solid-state packing, resulted in significant intermolecular stabilisation after condensations of 6_ax (−16.62 kcal mol⁻¹), and much less so after condensations of 6_eq (−9.24 kcal mol⁻¹) (see Table S4, ESI†). Again, intermolecular interactions between the more polar conformers result in supramolecular stabilisation and this leads to the adoption of the triaxial conformer in the condensed phase. It was noted that stacking 6_eq one molecule on top of another did not result in a local minimum, and direct geometry optimization always led to a less organized trimeric arrangement. This is probably a result of the steric influence of the axial methyl group, evidencing that neither intermolecular interaction energy nor spatial organization favours the crystalline assembly of 6_eq. Therefore, Grimme's iterative-static metadynamics (iMTD-sMTD) protocol implemented in CREST software¹³ and GFN2-xTB method¹⁴ was used to explore the conformational space of the 6_eq trimer, and the global minimum was re-optimized in DFT and used for further calculations. The same procedure was carried out for 7_ax, 9_ax, 10_ax and 12_ax trimers, and in each case the global minimum was in good agreement with the experimental structures, evincing the reliability of the methodology (See ESI† for details).

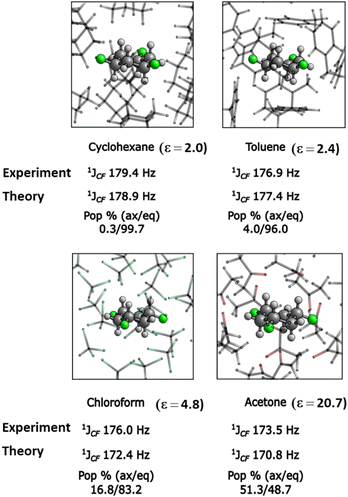Fig. 3 Experiment and theory (M06L/pcJ-1//M06L/pc-1)⁸ derived ¹J_CF NMR-coupling constants for 5 tend to lower values with increasing polarity (ε = dielectric constant) consistent with an increasing ratio of 5_ax in solution.

When a methoxy group is placed syn at C-2 of 1,3,5-trifluorocyclohexane 5, as in 7, the all-equatorial conformer 7_eq is favoured in the gas phase as might be expected. This compound was also prepared by aryl hydrogenation,⁶ in this case from the tri-fluoroanisole precursor and an X-ray structure (Fig. 4) also revealed the tri-equatorial structure 7_eq in the solid state, with the OMe group adopting an axial orientation. We have recently reported that unexpectedly, 4,4-difluoro-methoxycyclohexane 8 prefers a conformation with the OMe axial, displaying a pseudo anomeric effect.¹⁵ This was attributed in part to the accommodation of electrostatic non-conventional hydrogen bonds (NCHB) between the methoxy oxygen and 1,3 diaxial hydrogens in conformer 8_ax (see inset Fig. 4). Such NCHB interactions may also influence the preferred conformation of 7_eq. Although this might have been anticipated, it is against the trend so far in this series, where the more polar conformers emerge in the solid-state structures. It should be noted however that the polarity difference, as measured by the molecular dipole moment, is not so large between 7_ax (3.9 D) and 7_eq (2.0 D).

Fig. 4 X-Ray structures of 7_eq, 9_ax, 10_ax and 12_ax and equilibrium energies (PBE0-D3/def2-TZVP) of 7–12. The favoured conformers are the same in the gas and solid state phases. The preference for 8 (inset) was previously reported.¹⁵

Introduction of an amide (acetamide) and also a carbamate (NHBoc) substituent was also explored. Amide 9 and carbamate 10 were also prepared by aryl hydrogenation of their aromatic precursors.⁶ In both cases solid state structures were determined by X-ray structure analysis, and the outcomes are illustrated in Fig. 4. The structures 9_ax and 10_ax respectively each have their C–F bonds triaxial and the amide/carbamate equatorial. Unlike tri-fluorocyclohexane 5, the triaxial C–F conformers are unexpectedly found to be lower in energy and clearly the substituents are influencing the conformational preference in these molecules. This was not the case for –Me and –OMe in 6 and 7 respectively and clearly there are factors associated with the amide or carbamate groups in 9_ax and 10_ax over-riding electrostatic repulsion between the fluorines in the gas phase. This is consistent with the previously observed preference of an amide substituent to lie gauche to a vicinal fluorine.^16c Probably the most celebrated stereoelectronic associated with fluorine recognises unexpectedly, that 1,2-difluoroethane 13 has a lower energy gauche over anti conformer by about ∼0.8 kcal mol⁻¹ in the gas phase (see Fig. S5, ESI†).¹⁶ This contrasts with 1,2-dichloro-, 1,2-dibromo- and 1,2-iodo-ethanes which have lower energy anti conformers. The origin of the gauche effect is generally attributed to σ_CH → σ*_CF donation between anti-periplanar σ_C–H orbitals and lower energy σ*_CF antibonding orbitals, interactions not found in the anti conformer of 13. There are also competing electrostatic explanations for the gauche effect.¹⁷ Larger gauche preferences are found¹⁸ when one fluorine in 1,2-difluoroethane is replaced by other substituents such as the amide in 14. For 14 the preference has been reported^16c,18 to be 1.78 kcal mol⁻¹, twice that of the classical gauche effect and is attributed to several factors beyond hyperconjugation. For the lowest energy conformers in 14 the C–F and amide dipoles oppose each other, and there is an electrostatic attraction between the fluorine and the amide hydrogen, thus electrostatic factors reinforce the basic stereoelectronic origin of the gauche effect here. In order to explore this further, rotational energy profiles, rotating around the C–NAc 9_ax or C–NBoc 10_ax bonds, were conducted for each of the triaxial (and tri-equatorial see ESI†) conformers (see Fig. S4, ESI†). Both the cis-amide/carbamate (blue traces) and trans-amide/carbamate (black traces) geometries were explored, and in each case the trans-amides/carbamate gave the lowest energy conformer as expected. In both case there is a steep energy well of ∼14–15 kcal mol⁻¹ indicating a clearly preferred conformation. The lower energy conformers have the N–H bond aligned parallel to the three axial C–F bonds, and with the carbonyl group facing anti to the C–F bonds. This arrangement minimises the overall molecular dipole. It also introduces an electrostatic attraction between the proximal fluorines and the NH hydrogen, as previously discussed in the fluorine-amide gauche effect,^16c thus the system benefits from a combination of stereoelectronic and electrostatic effects. The influence of removing the distal fluorine was explored for 11 and 12, to reduce electrostatic repulsion between the axial fluorines (see Fig. 4). This significantly increased the equilibrium energy (−4.27 kcal mol⁻¹) in favour of 11_ax, relative to 9 (−2.01 kcal mol⁻¹) and also the equilibrium energy in favour of 12_ax (−3.15 kcal mol⁻¹) compared to 10 (−1.06 kcal mol⁻¹). Interestingly, 9_eq and 10_eq have smaller molecular dipoles than 11_eq and 12_eq, indicating that the distal C–F bond plays an important role in decreasing the overall polarity. Indeed, Natural Bond Orbital (NBO) analysis indicates that while hyperconjugative interactions rule the equilibria for 9 and 10, electrostatics are more important for 11 and 12. See ESI† for an expanded discussion.

This study demonstrates that the more polar triaxial conformer 5_ax is adopted in the solid state, although 5_eq is favoured in the gas phase and similarly for 6. For methoxy derivative 7, 7_eq with OMe axial is strongly favoured (5.87 kcal mol⁻¹) in the gas phase and not overturned in the solid state. For amide and carbamate derivatives 9–12 the fluoro diaxial and triaxial conformers are actually lower in energy than their equatorial counterparts, consistent with the fluorine-amide gauche effect.

We thank the Chinese Scholarship Council and FAPESP for studentships (BAP, #2021/09716-5) a Young Researcher Award (RAC, #2018/03910-1) and FAEPEX for a fellowship (RAC, #2479/21). CENAPAD-SP, CESUP and SDumont are acknowledged for computational resources.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. (a) O. Hassel and B. Ottar, Acta Chem. Scand., 1947, 1, 929; (b) D. H. R. Barton, J. Chem. Soc., 1953, 1027.
2. N. S. Keddie, A. M. Z. Slawin, T. Lebl, D. Philp and D. O’Hagan, Nat. Chem., 2015, 7, 483.
3. (a) O. Shyshov, S. V. Haridas, L. Pesce, H. Qi, A. Gardin, D. Bochicchio, U. Kaiser, G. M. Pavan and M. von Delius, Nat. Commun., 2021, 12, 3134; (b) R. Mondal, M. Agbaria and Z. Nairoukh, Chem. – Eur. J., 2021, 7193; (c) O. Shyshov, K. A. Siewerth and M. von Delius, Chem. Commun., 2018, 54, 4353; (d) P. Kirsch, Modern fluoroorganic chemistry-Synthesis, reactivity and applications, Wiley-VCH & Co, Weinheim, 2004.
4. T. J. Poskin, B. A. Piscelli, K. Yoshida, D. B. Cordes, A. M. Z. Slawin, R. A. Cormanich, S. Yamada and D. O’Hagan, Chem. Commun., 2022, 58, 7968.
5. Q. Luo, K. R. Randall and H. F. Schaefer, RSC Adv., 2013, 3, 6572.
6. (a) Z. Nairoukh, M. Wollenburg, C. Schlepphorst, K. Bergander and F. Glorius, Nat. Chem., 2019, 11, 264; (b) M. P. Wiesenfeldt, Z. Nairoukh, W. Li and F. Glorius, Science, 2017, 357, 908.
7. A. Altun, F. Neese and G. Bistoni, J. Chem. Theory Comput., 2019, 15, 5894.
8. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
9. (a) A. Lawer and L. Hunter, Eur. J. Org. Chem., 2021, 1184; (b) Y. Lizarme-Salas, A. D. Ariawan, R. Ratnayake, H. Luesch, A. Finch and L. Hunter, Beilstein J. Org. Chem., 2020, 16, 2663; (c) L. Hunter, P. Kirsch, A. M. Z. Slawin and D. O'Hagan, Angew. Chem., 2009, 48, 5457.
10. M. Giovanetti, L. F. F. Bitencourt, R. A. Cormanich and S. P. A. Sauer, J. Chem. Theory Comput., 2021, 17, 7712.
11. (a) A. C. Tsipis, New J. Chem., 2022, 46, 13940; (b) J. M. Silla, M. P. Freitas, R. A. Cormanich and R. Rittner, J. Org. Chem., 2014, 79, 6384; (c) S. Wolfe, B. M. Pinto, V. Varma and R. Y. N. Leung, Can. J. Chem., 1969, 68, 1051.
12. Z. Nairoukh, F. Strieth-Kalthoff, K. Bergander and F. Glorius, Chem. – Eur. J., 2020, 26, 6141.
13. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169.
14. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652.
15. B. A. Piscelli, D. O’Hagan and R. A. Cormanich, Phys. Chem. Chem. Phys., 2021, 23, 5845.
16. (a) M. Aufiero and R. Gilmour, Acc. Chem. Res., 2018, 51, 1701; (b) C. Thiehoff, Y. P. Rey and R. Gilmour, Isr. J. Chem., 2017, 57, 92; (c) D. O’Hagan, C. Bilton, J. A. K. Howard, L. Knight and D. J. Tozer, J. Chem. Soc., Perkin Trans. 2, 2000, 605.
17. J. C. R. Thacker and P. L. A. Popelier, J. Phys. Chem. A, 2018, 122, 1439.
18. (a) D. Y. Buissonneaud, T. van Mourik and D. O'Hagan, Tetrahedron, 2010, 66, 2196; (b) N. E. J. Gooseman, D. O’Hagan, M. J. G. Peach, A. M. Z. Slawin, D. J. Tozer and R. J. Young, Angew. Chem., 2007, 119, 6008.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2202377–2202382. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2cc05058g

---