 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stern–Volmer analysis of photocatalyst fluorescence quenching within hollow-core photonic crystal fibre microreactors†
Alexander S.
Gentleman‡
 ab,
Takashi
Lawson‡
ab,
Takashi
Lawson‡
 ab,
Matthew G.
Ellis
a,
Molly
Davis
a,
Jacob
Turner-Dore
c,
Alison S. H.
Ryder
c,
Michael H.
Frosz
ab,
Matthew G.
Ellis
a,
Molly
Davis
a,
Jacob
Turner-Dore
c,
Alison S. H.
Ryder
c,
Michael H.
Frosz
 d,
Maria
Ciaccia
e,
Erwin
Reisner
b,
Alexander J.
Cresswell
*c and
Tijmen G.
Euser
d,
Maria
Ciaccia
e,
Erwin
Reisner
b,
Alexander J.
Cresswell
*c and
Tijmen G.
Euser
 *a
*a
aNanophotonics Centre, The Cavendish Laboratory, University of Cambridge, JJ Thomson Avenue, Cambridge, CB3 0HE, UK. E-mail: te287@cam.ac.uk
bYusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1EW, UK
cDepartment of Chemistry, University of Bath, 1 South, Claverton Down, Bath, BA2 7AY, UK
dMax Planck Institute for the Science of Light, Staudtstr. 2, 91058, Erlangen, Germany
eSyngenta, Jealott's Hill Research Centre, Bracknell, Berkshire RG52 6EY, UK
First published on 26th August 2022
Abstract
We report the use of optofluidic hollow-core photonic crystal fibres as microreactors for Stern–Volmer (SV) luminescence quenching analysis of visible-light photocatalytic reactions. This technology enables measurements on nanolitre volumes and paves the way for automated SV analyses in continuous flow that minimise catalyst and reagent usage. The method is showcased using a recently developed photoredox-catalysed α-C–H alkylation reaction of unprotected primary alkylamines.
Photocatalysis is of pivotal significance in two critical fields of human endeavour: the conversion of solar energy (sunlight) into small molecule feedstocks or fuels (e.g., H2, CO, CH4),1,2 and the chemical synthesis of complex organic molecules such as pharmaceuticals and crop protection agents.3,4 Regardless of the application, it is important to attain an enhanced understanding of the mechanisms underlying photocatalytic reactions by providing experimental data for their verification.5 A factor of central mechanistic importance in photocatalysis is the kinetic partitioning of the catalyst's excited state, PC*, between productive quenching (which leads to the chemical reaction of interest) versus non-productive relaxation. The relaxation of PC* can be either radiative (i.e., fluorescence from 1PC* or phosphorescence from 3PC*), or it can be non-radiative (e.g., S1 → S0 internal conversion followed by vibrational relaxation), transferring thermal energy to the bulk medium in the latter case. These energy dispersal mechanisms have profound implications not only for the quantum efficiency of the catalysis – clearly of paramount importance for energy storage applications – but also for the catalytic turnover rate of the reaction.6 The fractionation between quenching and relaxation for a given photocatalyst-quencher combination is used for mechanistic interrogation in photocatalytic reaction development to identify or confirm which molecular species is engaging with the excited photocatalyst. A common technique is luminescence quenching (Stern–Volmer) analysis, which measures the rate of quenching of PC* by a given quencher species, as a function of its concentration, in competition with radiative decay processes.7 In fact, this technique has found application beyond the provision of mechanistic insight and has recently been leveraged as a high-throughput screening technology for the discovery of novel synthetic organic transformations.8,9
We have previously shown that energy dispersal mechanisms in photocatalytic reactions can be studied within liquid-filled hollow-core photonic crystal fibres (HC-PCFs):10,11 a novel class of optofluidic waveguides that allow light to be guided at the centre of a microfluidic channel.12,13 By infiltrating chemicals and monitoring their spectra (fluorescence, absorption, infrared, and/or Raman), reaction dynamics and steady-state concentrations can be probed in situ.14–21 Major advantages of these new ‘optofluidic microreactors’ over conventional sample cells are the enhanced detection sensitivity (from meter-scale optical-paths), tiny sample volumes of a few nL per cm fibre length (i.e., five orders of magnitude less than in conventional sample cells) and well-defined light-matter interactions: all key for the quantitative analysis of photochemistry.14–21 As such, they provide an ideal way to gain insight into the energy dispersal mechanisms of PCs under reaction conditions.
We introduce a new fibre-based, optofluidic microreactor approach to perform Stern–Volmer fluorescence quenching analysis on homogeneous photocatalytic reactions on a nanolitre scale.22–24 The principal motivation is to reduce by several orders of magnitude the quantities of catalysts and reagents necessary to perform such measurements by comparison to cuvette-based protocols. Ultimately, the longer-term objective is to design a fully-automated, high-throughput screening platform – based on HC-PCFs – to optimise or discover new photocatalysts or novel photocatalytic reactions.
As a proof-of-concept, we interrogate and verify the mechanism of a visible-light photoredox reaction recently developed by us for the α-C–H alkylation of unprotected primary amines (e.g., 1) with methyl acrylate 2 to access γ-lactams (e.g., 3) (Fig. 1).25 This transformation deploys the organophotocatalyst 2,4,5,6-tetra(9H-carbazol-9-yl)isophthalonitrile (4CzIPN) in union with an azide ion (N3−) as a hydrogen atom transfer (HAT) co-catalyst.26,27 The azide is introduced as tetrabutylammonium azide (Bu4NN3), which affords solubility in acetonitrile (MeCN).
 | ||
| Fig. 1 Scope for the photocatalytic α-C–H alkylation of unprotected amines, e.g. cyclohexylamine (1)) with methyl acrylate (2) to synthesise γ-lactams (3) using the 4CzIPN photocatalyst. | ||
We have previously utilised cuvette-based Stern–Volmer analyses to ascertain that the azide ion (N3−) co-catalyst serves as the primary reductive quencher for [4CzIPN]*, albeit with some very minor competitive quenching by the primary amine substrate (e.g., 1). Thus, we elected to reinvestigate the same reaction via Stern–Volmer fluorescence quenching analysis in an HC-PCF, to provide a head-to-head comparison with cuvette-based analysis for this system. Agreement with the former measurements would provide confidence that our HC-PCF approach provides robust and accurate experimental data, and would provide a pretext for its future use in the analysis of other photocatalytic processes.
For the in-fibre investigation of the fluorescence quenching dynamics of 4CzIPN, we employed a kagomé-style HC-PCF, a PCF type first used by Benabid et al.28 The kagomé-style HC-PCF implemented here was fabricated with a core diameter and wall thickness of 30 μm and 160 nm, respectively (Fig. 2a–c inset). This design allows for excellent guidance across the entire visible wavelength range when infiltrated with acetonitrile, as confirmed experimentally (Fig. S4, ESI†).
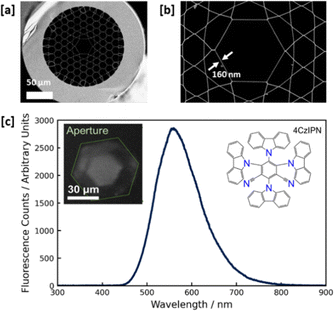 | ||
| Fig. 2 Dimensions and fluorescence transmission properties of the kagomé-style hollow-core photonic crystal fibre (HC-PCF). (a) Scanning electron microscope (SEM) image of the kagomé-style HC-PCF; (b) close-up SEM image of the fibre core with the inner strut thickness; (c) measured in-fibre fluorescence spectrum of the 4CzIPN photocatalyst (λexc = 365 nm). Inset: Camera image of 4CzIPN fluorescence emanating from the core region spatially selected using aperture A1 in Fig. S1a (ESI†) (green hexagon). | ||
A 20 cm length of kagomé HC-PCF was connected to liquid cells, and infiltrated with a sample solution using a standard syringe pump and PEEK tubing. A 5 cm long fibre section was side-irradiated with a diffuse LED source (Fig. S1, ESI†) in order to ensure homogenous irradiation of the infiltrated sample. This method of excitation allows for the fluorescence to be collected more efficiently over a longer fibre length than via in-coupling of the pump light as the excitation power becomes dependent on the sample concentration for the latter method (especially in cases where the quencher absorbance is high), thus confining any fluorescence emanating from the core to the first few centimetres of fibre.
Even though side-irradiation will result in excitation of the solution in the fibre cladding as well as the hollow core, the fluorescence signal emerging from the fibre core was spatially filtered and divided between a camera and spectrometer, ensuring that only core fluorescence is being monitored. The coupling to the spectrometer (Ocean Optics QE65000) was done through a multimode fibre with a 100 μm core diameter (see Fig. S1, ESI†). The fluorescence spectrum of 4CzIPN measured from this kagomé HC-PCF (Fig. 2c) compares well with that recorded using a commercial fluorometer from almost 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 times a larger sample volume within a conventional cuvette (see Fig. S2, ESI†), displaying similar fluorescence maxima at 546 nm (cuvette) and 558 nm (HC-PCF) in acetonitrile (Fig. 2c and Fig. S2, ESI†). As the comparison between the fluorescence spectra from both the cuvette and fibre is favourable, any difference in fluorescence resulting from surface-adsorbed molecules on the wall of the fibre core must be minute in comparison to that from free fluorescent molecules in the fibre core.
500 times a larger sample volume within a conventional cuvette (see Fig. S2, ESI†), displaying similar fluorescence maxima at 546 nm (cuvette) and 558 nm (HC-PCF) in acetonitrile (Fig. 2c and Fig. S2, ESI†). As the comparison between the fluorescence spectra from both the cuvette and fibre is favourable, any difference in fluorescence resulting from surface-adsorbed molecules on the wall of the fibre core must be minute in comparison to that from free fluorescent molecules in the fibre core.
In-fibre Stern–Volmer analysis was first conducted with tetrabutylammonium azide (Bu4NN3) to determine the rate at which it can quench the excited state of 4CzIPN, with the results presented in Fig. 3. A background (‘control’) fluorescence spectrum taken prior to loading with 4CzIPN samples shows that the background fluorescence from the HC-PCF infiltrated with pure acetonitrile was negligible (Fig. 3a). Stern–Volmer analysis is performed by fitting the normalised integrated counts (I0/In) to the linear function in eqn (1). Here, plotting I0/Invs. quencher concentration ([Q]n) whilst accounting for the fluorescence lifetime in the absence of a quencher, τ0 = 18.7 ns (inverse of the rate constant associated with the prompt fluorescence recorded from the 365 nm excitation of 4CzIPN in acetonitrile),29 gives a Stern–Volmer bimolecular quenching rate constant, ka, of (30.5 ± 1.1) × 109 L mol−1 s−1 with strong confidence (R2 = 0.995).
Fluorometer-based measurements (see Fig. S6, ESI†) with the same data analysis methodology and triplicate repeats gave a similar kq of (26.2 ± 2.0) × 109 L mol−1 s−1 with a slightly lower confidence R2 = 0.929, showing the reproducibility of our Stern–Volmer measurements between separate measurement platforms. In addition, fibre-based measurements enabled a bimolecular rate constant to be extracted on a 104 times smaller sample volume than fluorometer-based measurements (140 nL compared to 2 mL per measurement – Fig. S6, ESI†).
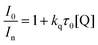 | (1) |
Fluorescence reabsorption by CHA or Bu4NN3 quenchers is expected to be negligible due to the marginal overlap between absorbance (Fig. S3, ESI†) and 4CzIPN fluorescence profiles (Fig. S2, ESI†). However, over the 10 cm propagation from the excitation region to the fibre end, residual quencher reabsorption may become noticeable due to the longer optical path length. The 4CzIPN spectrum at the highest concentration of the most absorbing quencher (1.2 mM Bu4NN3) shows a reduction of collected photons (ca. 4%) at the short-wavelength side of the spectrum compared to a sample without Bu4NN3. This shows that the effects of quencher reabsorption on the Stern–Volmer analysis are minimal (Fig. S7, ESI†). The small redshift of ca. 12 nm in the quencher-free fibre fluorescence spectrum (Fig. S2, ESI†), may be related to slight differences in the wavelength-response of the two spectrometers and/or residual reabsorption by 4CzIPN. However, this does not affect the Stern–Volmer analysis, as it is based on the relative reduction of total counts.
A similar in-fibre Stern–Volmer analysis was conducted with cyclohexylamine (1, CHA) to compare against Bu4NN3 (Fig. 4). We find that CHA as a quencher for 4CzIPN is less effective and report a bimolecular quenching rate constant, kq, of (2.3 ± 0.1) × 109 L mol−1 s−1 with moderate confidence (R2 = 0.970). Fluorometer-based measurements (see Fig. S8, ESI†) with the same data analysis methodology and triplicate repeats gave a similar kq of (2.2 ± 0.1) × 109 L mol−1 s−1 with a similar confidence R2 = 0.979.
To give a clearer interpretation of the azide anion and cyclohexylamine 1 as quenchers, the proportion of excited states interacting with each quencher (Fq) is calculated from the fluorescence lifetime (τ0) and bimolecular quenching rate constant, as shown in eqn (2). We observe that 36% of the exited state of 4CzIPN is quenched by 1 mM of azide compared to 4% with 1 mM of CHA.
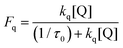 | (2) |
From our in-fibre Stern–Volmer analysis (Fig. 3b and 4b), the Bu4NN3 is shown to be much more efficient than CHA 1 at quenching the excited state of 4CzIPN, with kq values comparing very favourably to those derived from our cuvette-based measurements. These results are also consistent with previous observations by Cresswell et al., despite the kq values derived from their reported KSV values being at least an order of magnitude different due to systematic errors associated with the removal of oxygen contamination prior to fluorescence analysis (kq = 14.0 × 1010 M−1 s−1 and 6.69 × 108 M−1 s−1 for Bu4NN3 and CHA fluorescence quenchers, respectively).30 Even though the bimolecular quenching rate coefficient obtained for Bu4NN3 is of a similar magnitude to the rate of diffusion (kdiff ∼ 1010 s−1),31 our in-fibre Stern–Volmer analysis cannot distinguish between static and dynamic (collisional) quenching pathways and, as such, further experimentation is necessary for deeper understanding (e.g., excited-state lifetime studies). However, the comparison of kq values for Bu4NN3, and CHA 1 clearly affirms our previous assignment25 of the azide ion, N3−, as the primary reductive quencher of 4CzIPN* in the photoredox process. Single electron transfer (SET) is strongly implicated, based on EPR detection of spin-trapped N3˙ in studies of N3− oxidation by photoexcited 4CzIPN,32 as well as redox potentials w.r.t. SCE in MeCN (Ep/2 of N3− = +0.87 V; Ep/2 of CHA = +1.53 V; E1/2 (4CzIPN*/4CzIPN˙−) = +1.35 V).25,33 In the proposed mechanism (Fig. S9, ESI†), subsequent HAT from the relatively weak α-C–H bond of CHA 1 (BDE = 89–91 ± 2 kcal mol−1)34 by N3˙ occurs to give α-amino radical (4 – Fig. S9, ESI†), which undergoes addition to the acrylate acceptor 2 to give an α-carboxy radical (5 – Fig. S9, ESI†) [E1/2 ∼ –0.63 V vs. SCE35]. Reduction of this radical to the corresponding enolate (6 – Fig. S9, ESI†) by the [4CzIPN]˙− radical anion [E½ (PC/PC−•) = −1.21 V vs. SCE in MeCN] is presumably followed by proton transfer from HN3 (pKa = 7.9 in DMSO) to give the γ-amino ester product (7 – Fig. S9, ESI†) and regenerate the azide ion. A subsequent lactamisation step then converts 7 to γ-lactam 3.
In summary, we have shown that quantitative fluorescence spectroscopy can be performed on 140 nL volumes using optofluidic hollow-core photonic crystal fibre microreactors. PCF-microreactor Stern–Volmer analysis was successfully exemplified on a visible-light photoredox catalysed reaction using a widely used organophotocatalyst (4CzIPN). The resulting bimolecular quenching rate constant for [4CzIPN*] with N3− ion and with cyclohexylamine 1 were comparable to conventional fluorometer methods, despite the 104 times reduction in sample volume. This work provides a firm foundation for automated fluorescence screening of photoredox catalysts with quencher concentrations adjusted in continuous flow, while minimising the consumption of precious and expensive reagents.
T. G. E., E. R., and A. S. G. thank the Leverhulme Trust (RPG-2018-256), the Winton Programme for the Physics of Sustainability, and the Isaac Newton Trust. T. L. acknowledges the Cambridge NanoDTC (EPSRC Grant EP/L015978/1). A. J. C. thanks the Royal Society for a URF (UF150533), and the EPSRC and Syngenta for an iCASE PhD studentship (J. C. T.-D.).
Conflicts of interest
The authors have no conflict of interest to declare.Notes and references
- G. A. M. Hutton, B. C. M. Martindale and E. Reisner, Chem. Soc. Rev., 2017, 46, 6111–6123 RSC.
- A. Bachmeier, B. Siritanaratkul and F. A. Armstrong, in From Molecules to Materials, ed. E. A. Rozhkova and K. Ariga, Springer Intern. Publishing, Cham, 2015, pp. 99–123 Search PubMed.
- V. Balzani, G. Bergamini and P. Ceroni, Rend. Lincei, 2016, 28, 125–142 CrossRef.
- C. R. J. Stephenson, T. P. Yoon and D. W. C. MacMillan, Visible light photocatalysis in organic chemistry, Wiley-VCH Verlag, 2018 Search PubMed.
- T. Noël and E. Zysman-Colman, Chem. Catal., 2022, 2, 468–476 CrossRef.
- J. Z. Bloh, Front. Chem., 2019, 7, 128 CrossRef CAS PubMed.
- J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Springer-Verlag, New York, 2006 Search PubMed.
- F. Strieth-Kalthoff, C. Henkel, M. Teders, A. Kahnt, W. Knolle, A. Gómez-Suárez, K. Dirian, W. Alex, K. Bergander, C. G. Daniliuc, B. Abel, D. M. Guldi and F. Glorius, Chem, 2019, 5, 2183–2194 CAS.
- M. N. Hopkinson, A. Gómez-Suárez, M. Teders, B. Sahoo and F. Glorius, Angew. Chem., Int. Ed., 2016, 55, 4361–4366 CrossRef CAS PubMed.
- A. M. Cubillas, S. Unterkofler, T. G. Euser, B. J. M. Etzold, A. C. Jones, P. J. Sadler, P. Wasserscheid and P. S. J. Russell, Chem. Soc. Rev., 2013, 42, 8629–8648 RSC.
- M. Schmidt, A. M. Cubillas, N. Taccardi, T. G. Euser, T. Cremer, F. Maier, H.-P. Steinrück, P. S. J. Russell, P. Wasserscheid and B. J. M. Etzold, ChemCatChem, 2013, 5, 641–650 CrossRef CAS.
- P. Russell, Science, 2003, 299, 358–362 CrossRef CAS PubMed.
- G. Antonopoulos, F. Benabid, T. A. Birks, D. M. Bird, J. C. Knight, P. J. Russell, R. F. Cregan, B. J. Mangan, P. J. Roberts and D. C. Allan, Opt. Express, 2006, 14, 3000–3006 CrossRef CAS PubMed.
- P. Koehler, T. Lawson, J. Neises, J. Willkomm, B. C. M. Martindale, G. A. M. Hutton, D. Antón-García, A. Lage, A. S. Gentleman, M. H. Frosz, P. S. J. Russell, E. Reisner and T. G. Euser, Anal. Chem., 2021, 93, 895–901 CrossRef CAS PubMed.
- A. S. Gentleman, E. Miele, T. Lawson, P. Köhler, S. Kim, S. Yousaf, D. A. Garcia, A. Lage, C. P. Grey, J. J. J. Baumberg, M. H. Frosz, P. S. J. Russell, E. Reisner and T. G. Euser, in 14th Pacific Rim Conference on Lasers and Electro-Optics (CLEO PR 2020), OSA, Washington, DC, 2020.
- G. O. S. Williams, T. G. Euser, J. Arlt, P. S. J. Russell and A. C. Jones, ACS Photonics, 2014, 1, 790–793 CrossRef CAS.
- G. O. S. Williams, T. G. Euser, P. S. J. Russell and A. C. Jones, Methods Appl. Fluoresc., 2013, 1, 015003 CrossRef CAS PubMed.
- S. Smolka, M. Barth and O. Benson, Opt. Express, 2007, 15, 12783 CrossRef CAS PubMed.
- G. O. S. Williams, T. G. Euser, P. S. J. Russell, A. J. MacRobert and A. C. Jones, ChemPhotoChem, 2018, 2, 616–621 CrossRef CAS.
- D. Yan, J. Popp, M. W. Pletz and T. Frosch, ACS Photonics, 2017, 4, 138–145 CrossRef CAS.
- F. Schorn, M. Aubermann, R. Zeltner, M. Haumann and N. Y. Joly, ACS Catal., 2021, 11, 6709–6714 CrossRef CAS.
- M. H. Gehlen, J. Photochem. Photobiol., C, 2020, 42, 100338 CrossRef CAS.
- K. P. L. Kuijpers, C. Bottecchia, D. Cambié, K. Drummen, N. J. König and T. Noël, Angew. Chem., Int. Ed., 2018, 57, 11278–11282 CrossRef CAS PubMed.
- S. Bold, L. Zedler, Y. Zhang, J. Massin, V. Artero, M. Chavarot-Kerlidou and B. Dietzek, Chem. Commun., 2018, 54, 10594–10597 RSC.
- A. S. H. Ryder, W. B. Cunningham, G. Ballantyne, T. Mules, A. G. Kinsella, J. Turner-Dore, C. M. Alder, L. J. Edwards, B. S. J. McKay, M. N. Grayson and A. J. Cresswell, Angew. Chem., Int. Ed., 2020, 59, 14986–14991 CrossRef CAS PubMed.
- H. E. Askey, J. D. Grayson, J. D. Tibbetts, J. C. Turner-Dore, J. M. Holmes, G. Kociok-Kohn, G. L. Wrigley and A. J. Cresswell, J. Am. Chem. Soc., 2021, 143(39), 15936–15945 CrossRef CAS PubMed.
- J. D. Grayson and A. J. Cresswell, Tetrahedron, 2021, 81, 131896 CrossRef CAS.
- F. Benabid, J. C. Knight, G. Antonopoulos and P. S. J. Russell, Science, 2002, 298, 399–402 CrossRef CAS PubMed.
- R. Ishimatsu, S. Matsunami, K. Shizu, C. Adachi, K. Nakano and T. Imato, J. Phys. Chem. A, 2013, 117, 5607–5612 CrossRef CAS PubMed.
- A. S. H. Ryder, W. B. Cunningham, G. Ballantyne, T. Mules, A. G. Kinsella, J. Turner-Dore, C. M. Alder, L. J. Edwards, B. S. J. McKay, M. N. Grayson and A. J. Cresswell, Angew. Chem., Int. Ed., 2020, 59, 14986–14991 CrossRef CAS PubMed.
- N. A. Romero and D. A. Nicewicz, Chem. Rev., 2016, 116, 10075–10166 CrossRef CAS PubMed.
- M. Shee, S. S. Shah and N. D. P. Singh, Chem. – Eur. J., 2020, 26, 14070–14074 CrossRef CAS PubMed.
- J. Luo and J. Zhang, ACS Catal., 2016, 6, 873–877 CrossRef CAS.
- Y. R. Luo, Comprehensive Handbook of Chemical Bond Energies, CRC Press, Boca Ratan, FL, 2007 Search PubMed.
- N. Bortolamei, A. A. Isse and A. Gennaro, Electrochim. Acta, 2010, 55, 8312–8318 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cc03996f |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |


