Charge screening wormlike micelles affects extensional relaxation time and noodle formation

Abstract

A functionalised dipeptide that self-assembles to form wormlike micelles at high pH can be treated as a surfactant. By varying salt concentration, the self-assembled structures and interactions between them change, resulting in solutions with very different shear and extensional viscosity. From these, gel noodles with different mechanical properties can be prepared.

---

Interesting materials can be prepared from a range of self-assembling molecules using a so-called noodling approach.¹ A precursor solution is extruded into a crosslinking solution through a needle, leading to a gelled noodle-like structure. The process of forming these noodles controls the dimensions and the alignment of the self-assembled molecules within the noodle. Noodles have been used to prepare structures to direct cell growth,² form conductive^3,4 and directionally flexible materials,⁵ as well as threads that can be dried.⁶ Effective noodle formation requires long anisotropic micellar structures in the precursor solutions, leading to viscous solutions that also show significant extensional viscosity.^1,7 Forming well-defined structures that can maintain sufficient tensile stress to be useful relies on both a pushing force and a pulling force, as reported for effective silk formation.^8,9

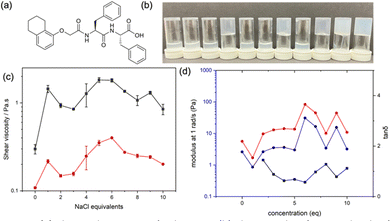
A suitable self-assembling molecule that can be used to form well-defined noodles is 1ThNapFF (Fig. 1a).⁷ At high pH, wormlike micelles (WLM) are formed as the terminal carboxylic acid is deprotonated. It is useful to consider such molecules simply as a surfactant,^10,11 although there is much discussion of similar molecules from the perspective of the peptide assembly.^12,13 Treating 1ThNapFF as a surfactant, the self-assembled structures would be expected to be affected by the concentration of added salt, which will screen the charges, leading to a lowering in the critical micelle concentration and so increased entanglements and interactions of the WLMs.

Fig. 1 (a) Chemical structure of 1ThNapFF; (b) photographs of inverted vials of solutions of 1ThNapFF at 10 mg mL⁻¹ at pH 11.3 with different NaCl equivalents; (c) plot of viscosity at 1 s⁻¹ (black data) and 10 s⁻¹ (red data) for the range of NaCl equivalents; (d) average tan δ (black data, right axis) and average storage and loss moduli (red and blue data respectively, left axis) obtained from frequency sweeps of the 1ThNapFF solutions at 1% strain and 1 rad s⁻¹. The tan δ data point for 0 and 1 eq. NaCl is >2 and not displayed to better show trends in the other data.

Solutions of 1ThNapFF were prepared at a concentration of 10 mg mL⁻¹ at a pH of 11.3 by deprotonation of the terminal carboxylic acid using sodium hydroxide, forming a viscous solution (Fig. 1b). Similar solutions were prepared at the same 1ThNapFF concentration and pH, but with the addition of different amounts of sodium chloride, ranging from 1–10 molar equivalents (eq.) with respect to 1ThNapFF, visibly affecting the samples (Fig. 1b).

Shear viscosity measurements were performed. Across the NaCl concentrations studied, all solutions have high viscosity compared to water alone and exhibit shear-thinning behaviour, indicative of WLM entanglement (Fig. 1c).¹⁴ The viscosity at low shear rate (1 s⁻¹) is higher when NaCl is added. There is a decrease in viscosity after 6 eq. Some of the solutions exhibited gel-like behaviour in that they could be inverted and seemingly did not flow (Fig. 1b). To investigate such effects more quantitatively, small amplitude oscillatory shear rheology was used (all data Fig. S2, ESI†). The data are best presented as NaCl concentration vs. tan δ (Fig. 1d), which is the ratio of the liquid-like (loss modulus G′′) to solid-like (storage modulus G′) characteristics. At 0 and 1 eq. NaCl, tan δ is >1, meaning that liquid-like behaviour is dominating and at 1 eq. NaCl tan δ is around 1. At all other NaCl eq. tan δ is <1 meaning that solid-like characteristics dominate. However, for all samples, tan δ is not sufficiently small for them to be designated as “true” gels. The data are also plotted as a function of G′ and G′′, where both increase with NaCl concentration until 4 eq. NaCl and remain unchanged as NaCl eq. are increased further. There is an apparent disconnect between the vial inversion and rheology data. We interpret this as being due to a complex interplay of changes in structure, persistence length and propensity to form transient crosslinks via lateral association (see below).

Extensional characteristics were probed using a dripping-onto-substrate (DoS) setup.¹⁵ This technique involves dispensing a fluid droplet onto a surface which results in the formation of an unstable liquid bridge. The subsequent thinning and break-up of the liquid bridge is governed by the material properties of the fluid.^15,16 In DoS measurements, polymer solutions and WLM solutions typically behave as viscoelastic liquids,¹⁷ where at intermediate and later stages of the thinning process a slender filament forms which undergoes, to a good approximation, purely uniaxial extensional flow. In this regime, the thinning dynamics can be fitted with an exponential decay to obtain the extensional relaxation time (eqn (1)) (more correctly, a characteristic time for extensional stress growth):

where G_E is the elastic modulus, λ_E the extensional relaxation time, R₀ radius of the dispensing needle, R filament radius and σ the surface tension.

DoS was used to study the λ_E of 1ThNapFF solutions with different NaCl eq. For each NaCl eq., three solutions were studied and three repeats performed for each solution, resulting in nine measurements. Exemplar data are shown in Fig. 2a with a summary shown in Fig. 2b. A wide range of behaviours were observed. For some samples, the filament broke very rapidly and, at the maximum frame rate (240 fps), an insufficient number of data points to fit the data accurately were collected (Fig. 2c). In other samples, filament thinning occurred over an intermediate timescale for which the thinning process was captured effectively (Fig. 2d) and could be accurately fitted. Finally, some samples did not break over reasonable timescales (>2 min) and λ_E was not calculated (Fig. 2e); this does not necessarily mean that λ_E is very high but that an unstable liquid bridge has not been formed and the thinning dynamics is arrested. A full summary of the results is shown in Section S3.3 (ESI†). Due to limitations with the experimental setup and difficulties associated with making highly reproducible samples, some of the results are more qualitative in nature.

Fig. 2 (a) Example data of normalised filament radius at later stages of thinning for 6 eq. NaCl (black) with an exponential decay fit (red); (b) plot of the average extensional relaxation times for each NaCl equivalent where measured. Full details of the different behaviours seen can be found in Table S1 (ESI†). Example images from the thinning process for (c) fast thinning (0 eq. NaCl); (d) intermediate thinning process fitted with an exponential decay (1 eq. NaCl) and (e) a filament that did not break (10 eq. NaCl).

The data at 0 eq. NaCl exhibited very fast break up, where λ_E < 0.1 s or was too small to be measured. At 1 eq. NaCl, all samples could be fitted to an exponential decay and showed an average relaxation time higher than 0 eq. NaCl. At 2 and 3 eq. NaCl, some filaments broke and λ_E could be measured but many did not break. Those that did break show an increasing λ_E with NaCl concentration. At 4 and 5 eq. NaCl, the liquid bridges did not break within the examined time period. As NaCl eq. increases further, a significant shift in behaviour is seen; at 6 and 7 eq. NaCl, all filaments broke but these were either too fast to measure or the λ_E ∼ 0.2 s. At 8 eq. NaCl and above, whilst the samples show irreproducibility, there are clear trends across the NaCl series. The NaCl concentration results in a modulation of λ_E. Surprisingly, 6 eq. NaCl possessed the highest shear viscosity at 1 s⁻¹ (Fig. 1) but a relatively small λ_E.

To understand how the structure of the WLMs change with NaCl and explain the above differences, we carried out small angle X-ray scattering (SAXS) and small angle neutron scattering (SANS) measurements, Fig. 3. To obtain the best contrast, SANS experiments were carried out in D₂O, whilst the SAXS experiments could be carried out in H₂O. The micellar structures present were not affected by this change in solvent (Section S3.4, ESI†). Similar long anisotropic structures are formed up until 5 eq. of NaCl, with the SAXS data fitting well to a cylinder model combined with a power law. The radius across this range of NaCl is 2.4 ± 0.1 nm, with the length (assigned to the persistence length) around 50 nm. The data at 6 eq. of NaCl fit best to an elliptical cylinder model with a radius of 1.9 nm and an axis ratio of 2.7. At 7 eq. NaCl, the data are best fit to a cylinder combined with a power law. Here the fit now depicts 1D structures with a larger radius of 4.6 nm as compared with lower NaCl concentrations. At 8 eq., an adequate fit to the data could not be obtained with any model. At 9 and 10 eq. of NaCl, the data were best fit again to a cylinder model combined with a power law, also with a radius of 4.6 nm, and a similar persistence length of around 50 nm. In all of this, we highlight that the data can generally be fitted well to a single model. Typically, when more than one species is present, the data cannot be fitted to a single model or significant polydispersity needs to be built in. These data do not preclude some further lateral association of these primary structures however. The SAXS data show that from low NaCl to high NaCl equivalents, the cylinder radius almost doubles. The structures formed at 6 eq. NaCl represent a point where there is a transition between structures. The requirement for an elliptical model, with a similar radius to those for 1–5 eq. points to lateral association of the WLM.¹⁸

Fig. 3 Scattering data (offset on y-axis for clarity) for solutions with different NaCl eq., (a) SANS data; (b) SAXS data; to scale cartoon of shape and cross-sectional areas of cylinders derived from fitting (c) SAXS and (d) SANS data. Scale bars = 2 nm; (e)–(g) TEM images for (e) 0 eq. NaCl; (f) 6 eq. NaCl; (g) 10 eq. NaCl. Scale bars = 40 nm. The arrow in (f) points to lateral association. The arrow in (g) points to the core of a hollow cylinder.

The SANS data at 0 eq. NaCl are best fit to a cylinder model at high Q, depicting 1.6 nm radius cylinders with a length of 27 nm. The fit was not extended to low Q owing to the presence of a structure factor peak at Q = 0.019 Å⁻¹. In the absence of salt, the WLM can be considered analogous to charged polyelectrolytes and this peak is attributed to the correlation length, ξ.¹⁹ This is the length at which all charges are screened (here 32.4 nm). At 1 eq. NaCl, the structure factor peak is no longer present, but the shape of the data is similar at high Q. These data were best fitted to a flexible cylinder model combined with a power law. The fit depicts similar structure to those at 0 eq. NaCl but the loss of the structure factor peak suggests that surface charge has been screened by the NaCl. From the SANS data, the structures at 10 eq. NaCl fit best to a hollow cylinder combined with a power law model, implying that the core does not have sufficient contrast to be resolved by the SAXS measurements (see above). The overall radius of the hollow tubes agrees with the cylinder radius found by SAXS.

Putting all these data together, we suggest that at 0 eq. NaCl, charged WLM that electrostatically repel each other are formed. From 1 to 5 eq. NaCl, the WLM structure remains the same, but surface charge is screened by the presence of NaCl. Significant lateral association of the cylindrical WLMs occurs at 6 eq. NaCl, captured in the fit as a need for ellipticity (see Fig. S9, ESI†).¹⁸ Between 7 and 10 eq. NaCl, the self-assembled structure change to hollow cylinders with a greater diameter. These data are confirmed by TEM (Fig. S10 (ESI†), although we highlight drying effects may be present). At 6 eq. NaCl, rigid structures are formed with evidence for lateral association (Fig. 3f). At 10 eq. NaCl, the core of a hollow cylinder is stained (Fig. 3g). Data for all samples is shown in Fig. S10 (ESI†). Across the series therefore, we have changes in micellar structure, changes in interactions and so propensity to laterally associate; all this leads to differences in the properties of the micellar solutions. The decrease in viscosity above 6 eq. NaCl for example can be linked to changes in micellar structure above this concentration.

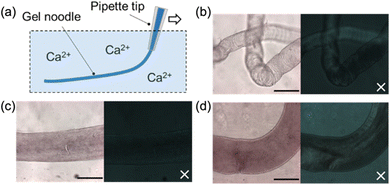
We investigated the formation of hydrogel noodles using the 1ThNapFF solutions at different NaCl eq. Gel noodles were readily formed at all NaCl equivalents by extruding the solutions into a bath containing calcium chloride (Fig. 4). Crosslinking of such solutions containing wormlike micelles occurs by chelation of the calcium ions by the carboxylates.⁷ In a bulk gel, TEM shows that the underlying wormlike structures exist in all cases on exposure to calcium chloride showing that significant structural changes are not occurring (Fig. S11, ESI†). Across all samples, limited birefringence is seen in cross polariser optical microscopy (CPOM), suggesting that the structures within the noodles are unaligned. The noodles formed from solutions at 0–5 eq. NaCl have a visibly rough surface whereas those formed from at 6–10 eq. NaCl appear much smoother (Fig. 4 and Fig. S12, ESI†).

Fig. 4 (a) Cartoon of noodle formation; (b)–(d) microscope images of noodles formed in a 50 mM CaCl₂ trigger bath using 1ThNapFF solutions with (b) 0 eq.; (c) 6 eq. and (d) 10 eq. NaCl. Images are at 5× magnification. Noodles are imaged wet in a pool of trigger medium. Left hand images are under normal light and right-hand images under cross polarised light. Scale bars = 0.4 mm. White crosses denote the polariser direction.

The gel noodles are sufficiently mechanically robust to be lifted out of solution with tweezers and bridged across a 3 cm wide gap. If left for an extended period (e.g., overnight), the noodles dry out, resulting in thin filaments. The dried filaments were imaged using both CPOM and scanning electron microscopy (SEM) (Fig. S13 and S14, ESI†). The drying process results in a thinning of the filaments to approximately 0.1 mm in diameter. In the CPOM images, the filament exhibit birefringence and in the SEM images the filaments appear to be comprised of bundles of fibres that are uniaxially aligned as observed for related systems.⁶ The alignment appears to be a result of drying.

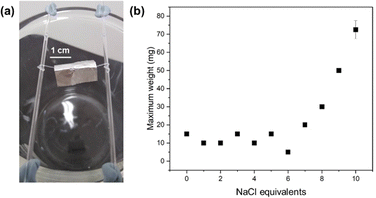
The hydrated gel noodles were more mechanically robust than the dry filaments, which were brittle and broke readily. We used a bridge loading experiment to investigate the mechanical strengths of the wet gel noodles (Fig. 5a). Gel noodles were prepared, lifted with tweezers and bridged (3 cm gap) between two glass capillaries. The excess length of noodle at each end was wrapped around the capillary to secure it, showing the high flexibility of the noodles. Then, 2 × 2 cm folds of aluminium foil were loaded onto the bridge. A different number of folds provided different weights. From 0 to 5 eq. NaCl, the gel noodle bridges could hold a mass of 10–15 mg (Fig. 5b). The noodles formed using 6 eq. NaCl were the weakest, suspending only 5 mg before breaking. Increasing from 7 to 10 eq. NaCl, the mass that was suspended increased to a maximum of 70 mg at 10 eq. NaCl. The structural changes to the WLM described above lead to a corresponding change to the mechanical properties of the resulting gel noodles. The gel noodles that can hold the greatest load are those that are prepared from hollow, cylindrical WLM.

Fig. 5 (a) Photograph of a gel noodle holding a 10 mg weight. Scale bar represents 1 cm. (b) Relationship between NaCl equivalents in the pre-gel solution with load. The data points show the maximum load the gel noodle bridge could support. Error bars represent the standard deviation across 7 repeat measurements and are small in most cases.

In conclusion, we have shown that the functionalised dipeptide 1ThNapFF forms WLMs in water at high pH resulting in viscous, shear-thinning solutions. Changing the NaCl concentration results in fundamental changes in the structure of the WLM and the interactions between them. The WLM structure remains unchanged until 6 eq. NaCl, where lateral association of cylindrical fibres occurs. As NaCl is increased further, large hollow cylinders form. These changes in structure and charge screening have a profound effect on both the shear and extensional viscosity of the fluids and directly impact on the properties of the gel noodles formed from the WLM.

Conceptualization: D. A., D. M., R. H., H. N.; methodology: all; software: H. N.; validation: R. H., D. M., H. N., D. A., R. P.; analysis: R. H., D. M., H. N., Y. A. H., D. A.; supervision: D. A.; project admin: D. A.; funding acquisition: D. A.; writing – all.

We thank the Leverhulme Trust for funding (RPG-2018-013). This work benefitted from the SasView software, originally developed by the DANSE project under NSF award DMR-0520547. We thank the EPSRC for funding the DL-SAXS instrument (EP/R042683/1).

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. S. Zhang, M. A. Greenfield, A. Mata, L. C. Palmer, R. Bitton, J. R. Mantei, C. Aparicio, M. O. de la Cruz and S. I. Stupp, Nat. Mater., 2010, 9, 594–601.
2. E. J. Berns, S. Sur, L. Pan, J. E. Goldberger, S. Suresh, S. Zhang, J. A. Kessler and S. I. Stupp, Biomaterials, 2014, 35, 185–195.
3. S. R. Diegelmann, N. Hartman, N. Markovic and J. D. Tovar, J. Am. Chem. Soc., 2012, 134, 2028–2031.
4. J. López-Andarias, M. J. Rodriguez, C. Atienza, J. L. López, T. Mikie, S. Casado, S. Seki, J. L. Carrascosa and N. Martín, J. Am. Chem. Soc., 2015, 137, 893–897.
5. J. Chen, F. K.-C. Leung, M. C. A. Stuart, T. Kajitani, T. Fukushima, E. van der Giessen and B. L. Feringa, Nat. Chem., 2018, 10, 132–138.
6. T. Christoff-Tempesta, Y. Cho, D.-Y. Kim, M. Geri, G. Lamour, A. J. Lew, X. Zuo, W. R. Lindemann and J. H. Ortony, Nat. Nanotechnol., 2021, 16, 447–454.
7. D. McDowall, M. Walker, M. Vassalli, M. Cantini, N. Khunti, C. J. C. Edwards-Gayle, N. Cowieson and D. J. Adams, Chem. Commun., 2021, 57, 8782–8785.
8. A. Koeppel, N. Stehling, C. Rodenburg and C. Holland, Adv. Funct. Mater., 2021, 31, 2103295.
9. A. Koeppel, P. R. Laity and C. Holland, Soft Matter, 2018, 14, 8838–8845.
10. K. McAulay, P. A. Ucha, H. Wang, A. M. Fuentes-Caparrós, L. Thomson, O. Maklad, N. Khunti, N. Cowieson, M. Wallace, H. Cui, R. J. Poole, A. Seddon and D. J. Adams, Chem. Commun., 2020, 56, 4094–4097.
11. R. Bordes and K. Holmberg, Adv. Coll. Inter. Sci., 2015, 222, 79–91.
12. S. Fleming and R. V. Ulijn, Chem. Soc. Rev., 2014, 43, 8150–8177.
13. G. Fichman and E. Gazit, Acta Biomater., 2014, 10, 1671–1682.
14. C. A. Dreiss, Soft Matter, 2007, 3, 956–970.
15. J. Dinic, Y. Zhang, L. N. Jimenez and V. Sharma, ACS Macro Lett., 2015, 4, 804–808.
16. J. Dinic, L. N. Jimenez and V. Sharma, Lab Chip, 2017, 17, 460–473.
17. R. Omidvar, S. Wu and H. Mohammadigoushki, J. Rheol., 2019, 63, 33–44.
18. E. R. Draper, B. Dietrich, K. McAulay, C. Brasnett, H. Abdizadeh, I. Patmanidis, S. J. Marrink, H. Su, H. Cui, R. Schweins, A. Seddon and D. J. Adams, Matter, 2020, 2, 764–778.
19. P.-G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca and London, 1979.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cc03646k

---