Semiconducting silicon–phosphorus frameworks for caging exotic polycations

Abstract

A series of novel semiconductors AAe₆Si₁₂P₂₀X (A = Na, K, Rb, Cs; Ae = Sr, Ba; X = Cl, Br, I) is reported. Their crystal structures feature a tetrahedral Si–P framework with large zeolite-like pores hosting two types of cations, monoatomic A⁺ and unprecedented octahedral X@Ae₆¹¹⁺. Mixing of the A and Ba cations was detected by single crystal X-ray diffraction and confirmed by multinuclear solid state NMR. The reported compounds are highly stable semiconductors with a bandgap range from 1.4 to 2.0 eV.

---

Semiconductors are of vital importance in modern society. Due to their many applications, the synthesis of novel semiconducting phases with specific properties is a commendable goal. However, rational design is challenging, and each application specifies additional requirements for the material. For example, photovoltaics require the band gap of the semiconductor to be between 1 and 2 eV to maximize absorption of the visible spectra.^1,2 Photocatalysts additionally require proper alignment of the valence and conduction bands based on the redox potential of the targeted reaction.³ For hard radiation detection, semiconductors must have a suitable band gap (1.5 to 2.4 eV) as well as a high crystal density.⁴ For nonlinear optical materials, the compound must have a noncentrosymmetric structure, suitable band gap, and high laser damage threshold.^5,6 A common requirement for almost all applications is stability in a number of conditions (ambient conditions, pressure, humidity, radiation, temperature, etc.). In terms of semiconductors based on earth-abundant silicon and phosphorus, binary SiP and SiP₂ exhibited high carrier mobilities and high stability.⁷ Orthorhombic SiP (Cmc2₁) has a layered crystal structure with a band gap of around 1.7 eV.⁸ Bulk and monolayer SiP hold promise for photodetection as well as nonlinear optics.^9,10 SiP₂ has been predicted to be a stable 2D material.¹¹ Ternary Si–P semiconductors, such as Ba₂Si₃P₆, MgSiP₂, ZnSiP₂, CdSiP₂, IrSi₃P₃, RuSi₄P₄, and BaSi₇P₁₀, exhibit a diverse variety of the silicon–phosphorus bonding motifs.^12–17 The compositional space of phosphides is less explored than the oxide and chalcogenide phase spaces, thus making it an underexplored frontier for finding new semiconductors.

This work originated from pursuing development of the flux synthesis for Si- and P-containing materials. The requirements that must be considered for flux growth are extensive.¹⁸ The combination of Si and P presents additional challenges when considering the typical approaches used for the constituents individually. While flux growth of silicides can be performed using Al, Ga, and In fluxes,¹⁹ the potential formation of AlP, GaP, and InP is undesirable. Sn is a great choice of flux for P containing materials, but Si has a low solubility in Sn, making Sn an undesirable choice. A less traditional flux choice is the salt flux,²⁰ which has been employed in silicates, germanates, and P-containing thiophosphates.²¹ Salt fluxes have been shown to promote the formation of highly complex crystal structures with multiple elements (quaternary and beyond).²² As a result of using salt flux, new salt inclusion semiconductors, AAe₆Si₁₂P₂₀X (A = Na, K, Rb, Cs; Ae = Sr, Ba; X = Cl, Br, I) were synthesized.

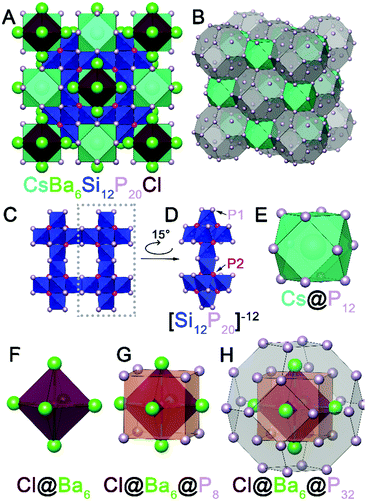
Initially, a reaction at 950 °C intended for crystal growth of BaCuSi₂P₃²³ with excess P and excess CsBr/CsI mixture resulted in the formation of CsBa₆Si₁₂P₂₀Br_1–xI_x. Large cuboidal single crystals with a deep red color were selected from the walls of the ampoule for single crystal X-ray diffraction (SXRD) (Fig. S1, ESI†). After the initial discovery, syntheses targeting the formation of AAe₆Si₁₂P₂₀X were carried out in similar conditions. These compounds can be made directly from the combination of the AX salt, Ae metal, Si, and P in the stoichiometric ratios (Fig. S2, ESI†). Alternatively, crystals suitable for SXRD can be grown with the addition of excess salt (Table S1, ESI†). The phase pure material CsBa₆Si₁₂P₂₀Cl is air-stable at room temperature on the order of weeks, water-stable, and stable up to 500 °C in air for at least 2 hours. CsBa₆Si₁₂P₂₀X does not melt below 1100 °C as evidenced by differential scanning calorimetry (Fig. S8, ESI†). So far, the crystal structures of 11 isostructural compounds have been determined (Table S3, ESI†). AAe₆Si₁₂P₂₀X compounds adopt a novel crystal structure type and exhibit exotic polycations [Ae₆X]¹¹⁺. Octahedral polycations such as Cs₆F have been observed in [Cs₆F][Cs₃AgF][Ge₁₄O₃₂] as well as cesium halide uranyl silicates.^24,25 However, the formal polycationic charge of Cs₆F is +5, which is less than half of what is expected for Ba₆Cl (+11). To our knowledge, there are no reports of a salt inclusion compound containing such a cationic fragment. Out of 11 synthesized isostructural compounds AAe₆Si₁₂P₂₀X, we will focus on CsBa₆Si₁₂P₂₀Cl which crystallizes in the space group Fm3̄m (No. 225) with a Wyckoff sequence of igfeba, which is a new structure type. The large charge of the [Ae₆X]¹¹⁺ polycation attests to the ability of silicon–phosphorus frameworks to accommodate charge. Silicon phosphides have been shown to accommodate charges from cations by adapting the bonding within the Si–P fragments. For instance, Si and P can form isolated SiP₄ tetrahedra (as in Li₁₄SiP₆),²⁶ corner-sharing tetrahedra (as in SiP₂),²⁷ and edge-sharing tetrahedra (as in Ba₄Si₃P₈).²⁸ In addition, Si–Si bonds can form to increase the magnitude of negative charge of the overall fragment or to balance the charge.²³ Conversely, P–P bonds can be formed to reduce the negative charge of the fragment. P is typically known for its trigonal pyramidal geometry, but P is versatile and is capable of being undercoordinated. Undercoordinated P atoms represent a way of increasing the magnitude of negative charge. In CsBa₆Si₁₂P₂₀Cl (Fig. 1A), due to the large charge of the [Ba₆Cl] polycation, the Si–P framework contains corner sharing as well as edge sharing SiP₄ tetrahedra with undercoordinated (2-coordinate) P atoms occupying the 48i site. The Si–P framework has a repeating fragment of six directionally oriented corner-sharing SiP₄ tetrahedra (Fig. 1C and D). This fragment is connected to an identical fragment facing the opposite direction through edge-sharing tetrahedra. All Si atoms in the structure are four-coordinate, however, the connectivity of the Si–P fragments leaves large voids in the crystal structure. The first void is filled by Cs. Cs is coordinated by 12 phosphorus atoms that form a cuboctahedron (Fig. 1E) with a volume of 132.6 ų. This is comparable to the volume of pentagonal dodecahedron cages in type I clathrates, Cs₈Cd₁₈As₂₈ (144.5 ų) and Cs₈Ga₂₇Sb₁₉ (149.9 ų).^29,30 The second void is extremely large with a volume of 575 ų and is filled with the Cl@Ba₆ octahedron (Fig. 1F). The distance between Cl and Ba is 3.40 Å. Each trigonal face of the Cl@Ba₆ octahedron is capped with a P atom, which forms a cube around the octahedron (Fig. 1G). Furthermore, a truncated octahedron with 24 P atoms at each vertex encapsulates the Cl@Ba₆@P₈ unit (Fig. 1H). The 8 P atoms forming the cube intersect the center of the hexagonal faces of the truncated octahedron. This giant truncated octahedra share square faces with the cuboctahedra and thus not completely isolated by the silicon phosphorus framework. The truncated octahedron and cuboctahedron pack together in a rock-salt sublattice (Fig. 1B). The distance between the two P atoms in the square face of the cuboctahedron that connects with the truncated octahedron is 5.48 Å. The large channels between Cs and Ba are comparative to small channel zeolites. Conventional zeolite channels range between 4.2 and 7.4 Å.³¹ Another interesting structural feature is that the cation-filled voids are connected in all directions, i.e. the channels are three dimensional.

Fig. 1 (A) Unit cell view of CsBa₆Si₁₂P₂₀Cl along [100]. (B) Rock-salt packing of truncated octahedra and cuboctahedra. (C) Si–P framework viewed along [100]. (D) Si–P repeating fragment featuring two groups of 6 directionally oriented corner-sharing SiP₄ tetrahedra. (E) Cs@P₁₂ cuboctahedron. (F) Cl@Ba₆ octahedron. (G) Cl@Ba₆ octahedron encapsulated in a P₈ cube. (H) Cl@Ba₆@P₈ unit inside of a truncated octahedron formed by 24 P atoms.

While the atomic assignments from SXRD were made by considering the connectivity of the structure as well as the composition, it should be noted that X-ray diffraction is not sensitive enough to indisputably distinguish Cs from Ba. In CsBa₆Si₁₂P₂₀Cl, the best refinement was obtained when Cs solely occupies the 4b site and Ba solely occupies the 24e site. Attempts at refining a mixture of Cs/Ba at either site resulted in unstable refinements due to similarities of Cs and Ba scattering factors. However, when Cs is replaced with Rb, K, or Na with different enough scattering factors the site occupancies of the 4b and 24e sites clearly indicate that the alkali and Ba cations are mixing in both sites. There is a clear trend of the smaller alkali metal avoiding the 4b site in the center of the cuboctahedra and instead shifting to the 24e site, forming shorter A–P distances (Fig. S3 and Table S4, ESI†). The smaller alkaline-earth metal, Sr, does not mix with Rb or Cs, which are both larger than Sr, and has yet to be synthesized with Na or K. The iodine containing analogs (CsBa₆Si₁₂P₂₀I, RbBa₆Si₁₂P₂₀I) have additional complexity as the iodine position is partially vacant. To account for the charge imbalance, the Ba is replaced by Rb/Cs making the actual composition close to Rb_1.1Ba_5.9Si₁₂P₂₀I_0.9. To validate atomic assignments of Si and P, as well as understand the cation mixing, we employed magic angle spinning (MAS) solid-state nuclear magnetic resonance (NMR) spectroscopy.

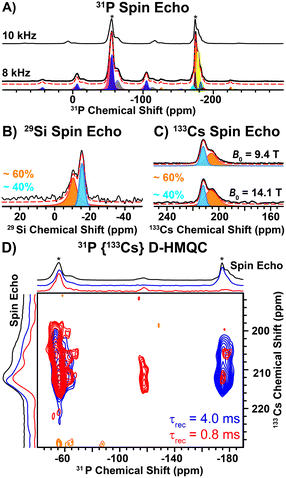
Direct excitation ³¹P solid-state NMR spectra reveal two main groups of NMR signals centered at ca. –56 and –175 ppm (Fig. 2A). The high frequency ³¹P NMR signals (−56 ppm) exhibit larger chemical shift anisotropy (CSA; span (Ω) ~ 115 ppm) than the low frequency signals (−175 ppm; Ω ∼ 62 ppm, Table S7, ESI†). The magnitude of the CSA is dependent on the local symmetry at the nucleus; symmetric environments give rise to small CSA. Therefore, the ³¹P NMR signals at −56 ppm and −175 ppm correspond to the 2- and 3-coordinate P sites, respectively. The ratio of the 2 and 3-coordinate ³¹P NMR signals is ca. 3 : 2, consistent with the structure determined by SXRD (Table S7, ESI†). We note that each group of ³¹P NMR signals exhibits multiple peaks (shoulders), which likely arises from structural (substitutional) disorder. Interestingly, a direct excitation ²⁹Si NMR spectrum reveals two relatively broad ²⁹Si NMR signals at −11 ppm and −16 ppm with relative populations of ca. 60 and 40%, respectively (Fig. 2B and Table S8, ESI†). In addition, direct excitation ¹³³Cs NMR spectra also reveal two sites centered at ca. 206 ppm (ca. 60%) and 212 ppm (ca. 40%) (Fig. 2C and Table S9, ESI†). Only one unique Si and Cs site is expected from the SXRD structure.

Fig. 2 (A) 1D ³¹P spin echo NMR spectra recorded with a (lower) 8 kHz or (upper) 10 kHz MAS frequency. Asterisks denote isotropic NMR signals. (B) 1D ²⁹Si spin echo NMR spectrum. (C) 1D ¹³³Cs spin echo NMR spectra recorded at B₀ = (upper) 9.4 T or (lower) 14.1 T. Experimental (black solid line) and analytically simulated (red dashed line) spectra are shown. (D) 2D ³¹P {¹³³Cs} D-HMQC NMR spectra recorded with either (red) 0.8 ms or (blue) 4 ms of heteronuclear dipolar recoupling applied to the ³¹P spins.

To further probe the two unique ¹³³Cs NMR signals, we recorded 2D ³¹P{¹³³Cs} D-HMQC NMR spectra. The ³¹P{¹³³Cs} D-HMQC NMR spectrum recorded with a short duration of heteronuclear dipolar recoupling (0.8 ms) reveals that the 2-coordinate ³¹P NMR signals (ca. −56 ppm) correlate to both ¹³³Cs sites (Fig. 2D, red). The short duration of dipolar recoupling primarily probes ³¹P–¹³³Cs spin pairs in close spatial proximity. Closer examination of the 2-coordinate ³¹P NMR signal suggests two unique 2-coordinate sites, where the lower or higher frequency ³¹P NMR signals correlate with the higher or lower frequency ¹³³Cs NMR signals, respectively (Fig. S5, ESI†). In addition, weak ³¹P–¹³³Cs correlations are observed for the 3-coordinate ³¹P NMR signals, where the center of the ³¹P NMR signal is shifted to a lower frequency than that observed in the ³¹P spin echo NMR spectrum (Fig. 2D, red). It is not surprising that the most intense 3-coordinate ³¹P NMR signal (−174 ppm) shows weak correlations in the 2D HMQC spectrum as these P atoms are quite distant from Cs (6.44 Å). However, the lower frequency ³¹P shoulder (−177 ppm) has increased intensity in the HMQC spectrum and significantly lower intensity in the ³¹P spin echo NMR spectrum as compared to the −174 ppm ³¹P NMR signal. Furthermore, the lower frequency ³¹P NMR signal (−177 ppm) primarily correlates with the lower frequency ¹³³Cs NMR signal, suggesting it is in closer spatial proximity to Cs (Fig. 2D). At long durations of heteronuclear dipolar recoupling (4 ms), all ³¹P NMR signals reveal correlations to both ¹³³Cs NMR signals (Fig. 2D, blue). The observation of two unique ²⁹Si and ¹³³Cs sites, in addition to the ³¹P{¹³³Cs} D-HMQC correlations discussed above, suggests site mixing between Cs and Ba. The ¹³³Cs NMR signal at ca. 206 ppm is assigned to Cs replacing a Ba site based on the correlations observed with the lower frequency 3-coordinate ³¹P NMR signal (−177 ppm) in the 2D ³¹P{¹³³Cs} D-HMQC spectrum. We note that the ¹³³Cs NMR signal at ca. 206 ppm is broader than the ¹³³Cs NMR signal at ca. 212 ppm, consistent with a more asymmetric environment. A ³⁵Cl spin echo NMR spectrum reveals a sharp NMR signal assigned to Cl coordinated by 6 Ba atoms (Fig. S4, ESI†). In addition, there is a broadened ³⁵Cl NMR signal, consistent with a more asymmetric environment when Cl is coordinated by both Ba and Cs (Fig. S4, ESI†).

Since there are no Si–Si or P–P bonds, the electron balance in the produced compounds can be rationalized either as (Cs⁺)(Ba²⁺)₆(Si⁴⁺)₁₂(P³⁻)₂₀(Cl¹⁻) when Si–P bonding is treated as ionic or (Cs⁺)(Ba²⁺)₆(Si⁰)₁₂(P⁰)₈(P¹⁻)₁₂(Cl¹⁻) when Si–P bonding is covalent. Band structure calculations underestimated the band gap of materials by 0.4–0.5 eV against experimental values from UV-vis diffuse reflectance spectroscopy (Fig. 3A). For CsBa₆Si₁₂P₂₀Cl, the band structure shows a direct band gap of about 1.45 eV at the Γ-point, which correlates with the direct experimental gap shown in the Tauc plot to be 1.92 eV (Fig. S9, ESI†). The valence band maximum (VBM) is mostly populated with P states with contributions from Ba, while the conduction band minimum (CBM) has nearly equal contributions from Si, P, and Ba. Electron localization function (ELF) analysis (Fig. 3C) found covalent bonds for Si–P interactions and additional electron lone pairs located on P atoms. Cs and Cl appear ionic as demonstrated by the spherical shaped ELF density. The ELF distribution around Ba is not entirely spherical, which indicates weak directed interactions between the Ba and P atoms as in Ba₃S₄I₂.³² Because of the lack of states near the VBM and CBM for the A and X, the band gaps are not affected by the substitution of these elements. However, replacing Ba with Sr results in a shrinking of the gap and a transformation from a direct to an indirect bandgap (Fig. S9 and S10, ESI†).

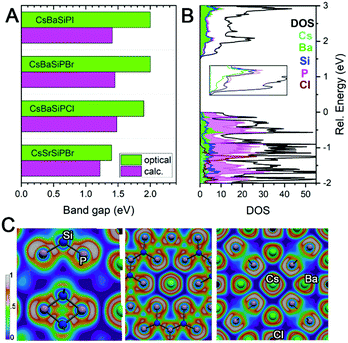Fig. 3 (A) Comparison of calculated and experimental band gaps. (B) Density of states with inset showing the CBM. (C) ELF visualizations.

In conclusion, we have synthesized a novel family of semiconductors that appear to be versatile in composition. Their bandgaps range from 1.4 to 2.0 eV which is within the range for photovoltaic, photocatalytic, and radiation detection materials. The large cage-like structure contains unique cluster cations. The Si–P framework which forms the cages has large pores (diameter > 5 Å), similar to zeolite materials. High chemical and thermal stabilities of the reported compounds demonstrate the promise of Si–P frameworks for functional materials in optical and ion transport applications.

This research was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Science and Engineering, grant DE-SC0022288. Solid-state NMR spectroscopy experiments (A. P. P., R. W. D., and A. J. R.) were supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials Science and Engineering Division. Ames Laboratory is operated for the U.S. DOE by Iowa State University under Contract DE-AC02-07CH11358. A. J. R. acknowledges additional support from the Alfred P. Sloan Foundation through a Sloan research fellowship. V. K. was supported by the U.S. Department of Energy Office of Science, Science Undergraduate Laboratory Internships (SULI).

All authors contributed to this work. The authors are thankful to Prof. J. Vela (ISU) for access to the UV-vis spectrometer.

Conflicts of interest

There are no conflicts to declare.

References

1. P. K. Nayak, G. Garcia-Belmonte, A. Kahn, J. Bisquert and D. Cahen, Energy Environ. Sci., 2012, 5, 6022–6039.
2. D. H. Fabini, M. Koerner and R. Seshadri, Chem. Mater., 2019, 31, 1561–1574.
3. M.-Y. Qi, M. Conte, M. Anpo, Z.-R. Tang and Y.-J. Xu, Chem. Rev., 2021, 121, 13051–13085.
4. S. L. Nguyen, C. D. Malliakas, J. A. Peters, Z. Liu, J. Im, L.-D. Zhao, M. Sebastian, H. Jin, H. Li, S. Johnsen, B. W. Wessels, A. J. Freeman and M. G. Kanatzidis, Chem. Mater., 2013, 25, 2868–2877.
5. D. F. Eaton, Science, 1991, 253, 281–287.
6. K. M. Ok, E. O. Chi and P. S. Halasyamani, Chem. Soc. Rev., 2006, 35, 710–717.
7. B. Huang, H. L. Zhuang, M. Yoon, B. G. Sumpter and S.-H. Wei, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 121401.
8. C. Li, S. Wang, X. Zhang, N. Jia, T. Yu, M. Zhu, D. Liu and X. Tao, CrystEngComm, 2017, 19, 6986–6991.
9. C. Li, S. Wang, C. Li, T. Yu, N. Jia, J. Qiao, M. Zhu, D. Liu and X. Tao, J. Mater. Chem. C, 2018, 6, 7219–7225.
10. H. Sar, J. Gao and X. Yang, Sci. Rep., 2021, 11, 6372.
11. F. Shojaei, B. Mortazavi, X. Zhuang and M. Azizi, Mater. Today Energy, 2020, 16, 100377.
12. J. Mark, J. Wang, K. Wu, J. G. Lo, S. Lee and K. Kovnir, J. Am. Chem. Soc., 2019, 141, 11976–11983.
13. J. Chen, Q. Wu, H. Tian, X. Jiang, F. Xu, X. Zhao, Z. Lin, M. Luo and N. Ye, Adv. Sci., 2022, 2105787.
14. J. E. Jaffe and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 741–756.
15. K. T. Zawilski, P. G. Schunemann, T. C. Pollak, D. E. Zelmon, N. C. Fernelius and F. K. Hopkins, J. Cryst. Growth, 2010, 312, 1127–1132.
16. S. Lee, S. L. Carnahan, G. Akopov, P. Yox, L.-L. Wang, A. J. Rossini, K. Wu and K. Kovnir, Adv. Funct. Mater., 2021, 31, 2010293.
17. A. Haffner, V. Weippert and D. Johrendt, Z. Anorg. Allg. Chem., 2021, 647, 326–330.
18. J. Wang, P. Yox and K. Kovnir, Front. Chem., 2020, 8, 186.
19. M. G. Kanatzidis, R. Pöttgen and W. Jeitschko, Angew. Chem., Int. Ed., 2005, 44, 6996–7023.
20. V. V. Klepov, C. A. Juillerat, K. A. Pace, G. Morrison and H.-C. zur Loye, Front. Chem., 2020, 8, 518.
21. M. G. Kanatzidis, Curr. Opin. Solid State Mater. Sci., 1997, 2, 139–149.
22. D. E. Bugaris and H.-C. zur Loye, Angew. Chem., Int. Ed., 2012, 51, 3780–3811.
23. P. Yox, S. J. Lee, L. Wang, D. Jing and K. Kovnir, Inorg. Chem., 2021, 60, 5627–5634.
24. N. R. Spagnuolo, G. Morrison and H.-C. zur Loye, Solid State Sci., 2019, 97, 105973.
25. G. Morrison, M. D. Smith and H.-C. zur Loye, J. Am. Chem. Soc., 2016, 138, 7121–7129.
26. S. Strangmüller, H. Eickhoff, D. Müller, W. Klein, G. Raudaschl-Sieber, H. Kirchhain, C. Sedlmeier, V. Baran, A. Senyshyn, V. L. Deringer, L. van Wüllen, H. A. Gasteiger and T. F. Fässler, J. Am. Chem. Soc., 2019, 141, 14200–14209.
27. T. Wadsten, Acta Chem. Scand., 1967, 21, 593–594.
28. J. Mark, J.-A. Dolyniuk, N. Tran and K. Kovnir, Z. Anorg. Allg. Chem., 2019, 645, 242–247.
29. H. He, A. Zevalkink, Z. M. Gibbs, G. J. Snyder and S. Bobev, Chem. Mater., 2012, 24, 3596–3603.
30. B. Owens-Baird, J. Wang, S. G. Wang, Y. S. Chen, S. Lee, D. Donadio and K. Kovnir, J. Am. Chem. Soc., 2020, 142, 2031–2041.
31. G. A. Ozin, A. Kuperman and A. Stein, Angew. Chem., Int. Ed. Engl., 1989, 28, 359–376.
32. J. Wang, K. Lee and K. Kovnir, Inorg. Chem. Front., 2016, 3, 306–312.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2168162–2168172. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2cc02304k

---