Isomer dynamics of the [Au₆(NHC-S)₄]²⁺ nanocluster

Abstract

The use of metal nanoclusters is strongly reliant on their size and configuration; hence, studying the potential isomers of a cluster is extremely beneficial in understanding their performance. In general, the prediction and identification of isomer structures and their properties can be challenging and computationally expensive. Our work describes an investigation to find local isomers for the previously experimentally characterized small gold cluster [Au₆(NHC-S)₄]²⁺ protected by bidentate mixed carbene-thiolate ligands. We employ the molecular dynamics simulation method where the interatomic forces are calculated from density functional theory. We find several isomers that are more stable than the isomer corresponding to the experimental crystal structure, as well as a significant impact of the finite-temperature atom dynamics on the electronic structure and optical properties. Our work highlights the growing need to investigate ligand-stabilized metal clusters to uncover isomerism and temperature effects on their properties.

---

Ligand-protected metal nanoclusters (NCs) have a wide range of applications due to their unique properties.^1–3 In order to investigate metal NCs and their characteristics, it is important to consider the influence of ligand groups.^4,5 A broad range of different ligands like chalcogenates, phosphines, alkynyls and N-heterocyclic carbenes (NHCs) have already been used.^6–20 Among all, gold clusters, in particular, have sparked considerable attention, for example due to their catalytic activity when supported by metal oxides.²¹ A rising number of research studies have shown that the physicochemical properties of metal NCs are substantially impacted by the presence of different isomers, which influences the crystallization of the main NC.^22,23 However, this study demonstrates that the crystallized structure is not automatically the most stable isomer in the gas phase or in solution, which raises intriguing questions regarding how the presence of isomers affects crystallization or the catalytic activity of NCs in different conditions.

Computational methods provide a controlled way to study isomers. Properties of thiolate-protected gold NCs have been extensively studied using density functional theory (DFT) techniques. As an example, a study on the Au₂₈(SR)₂₀ cluster²⁴ suggested a novel isomer with relatively high stability composed of the same Au₁₄ kernel but a different ligand shell compared to the two experimentally reported structures. It showed also that the new isomer is an important link in the formation of Au₂₂(SR)₁₈, Au₃₄(SR)₂₂ and Au₄₀(SR)₂₄ clusters. In another DFT study,²⁵ two low-lying Au₂₈(SR)₂₀ isomers were suggested successfully and three isomerism mechanisms were identified by studying the crystallized Au₃₈(SR)₂₄, Au₂₈(SR)₂₀, and Au₃₀(SR)₁₈ clusters.

DFT studies offer significant insight on isomerism, but finding the potential structures can be a considerable challenge. Here, combining DFT with molecular dynamics (MD) methods can help. A DFT-MD study, performed on Au₃₈(SCH2CH2Ph)₂₄²⁶ revealed that from the two empirically discovered isomers^27,28 the prolate shaped one is more stable than the oblate one.

Although many experimental techniques are successful to determine the atomic structure of metal NCs,^29–34 finding the presence of isomers is a difficult task by itself. In this regard, computational work can inspire new experimental investigations. In a recent work, a new isomer structure for the widely studied thiolate-protected gold cluster Au₂₅(SR)₁₈ was predicted from DFT-MD calculations in 2020,³⁵ and soon after, the presence of this isomer was confirmed both in gas-phase studies³⁶ and in solution.³⁷

In this work, we investigate the previously characterized [Au₆(NHC-S)₄]²⁺ cluster, protected by bidentate mixed carbene-thiolate ligands, with the experimental crystal structure provided in ref. 6. We performed DFT-MD simulations at three temperatures (approximately 145 K, 280 K and 475 K) with a goal to characterize the impact of temperature on the structural, electronic and optical properties. Our study reveals a systematic understanding of how temperature impacts the structure–property relations of the above-mentioned cluster. The most important findings are: (i) new isomers with a lower total energy than the structure reported from the experiment, (ii) demonstration of the effect of crystal environment on the isomer structure, (iii) a strong temperature dependence of the energy gap between the highest occupied and the lowest unoccupied molecular orbital (i.e. HOMO and LUMO), (iv) a clear correlation between the size of the HOMO–LUMO energy gap and a descriptive structural parameter of the cluster, and (v) shifting and splitting of the absorption peaks in the UV-vis spectrum due to temperature effects (dynamics of single-electron orbitals) as compared to the calculations for the known static structure.

The experimental crystal structure (ref. 6) was used as our initial point for the calculations. Density-functional theory (DFT) implemented in the real-space code-package GPAW³⁸ was used to calculate the wave functions and eigenenergies for the Kohn–Sham states. Relativistic effects for gold are included in GPAW setups. All DFT calculations were performed using the PBE (Perdew–Burke–Ernzerhof) functional.³⁹ The structural optimization has been done by 0.2 Å grid spacing and 0.01 eV Å⁻¹ convergence criterion for the maximum forces acting on atoms in the cluster. Molecular dynamics (MD) simulations were done using the Langevin thermostat with 0.01 friction parameter and 2 fs time step that is justified by treating all hydrogen atoms as deuteriums during the simulation. The dynamics was collected at three different temperatures 145 K, 280 K and 475 K. The total length of the simulation runs were 20 ps for 145 K, 10 ps for 280 K and 30 ps for 475 K including heating. Analysis was done after the thermalization stage, which takes less than 2 ps at 475 K, ∼4 ps at 148 K and 2 ps in the 280 K run. From these results, the 475 K run was continued after the 280 K run. 120 optical spectra were calculated after thermalization for the MD snapshot structures with an increment of 65 steps using 145 K and 475 K data and 50 spectra with an increment of 65 steps using 280 K data. Absorption spectra were calculated using linear response time dependent density functional theory (lr-TDDFT) as implemented in GPAW software.⁴⁰ Spectra were calculated using 0.25 Å grid spacing and the PBE functional for the wavefunctions and for the lr-TDDFT kernel.

A previous study on [Au₆(NHC-S)₄]²⁺ revealed that this cluster is made up of an anti-prismatic central Au₆ core supported by four NHC-thiolate ligand groups composed of two neutral [(NHC-S)₂Au₂] staple-type units. The PBE-relaxed single crystal structure, shown in Fig. 1, was used as our starting point to run DFT-MD calculations at three different temperatures: 145 K, 280 K, and 475 K. Fig. 1a depicts two gold atoms Au_a and Au_b, which are uniquely positioned as part of the SR–Au–SR staple units, and the distance between the two gold atoms and the dihedral angle shown in Fig. 1b and c, respectively, are used as two of the key parameters to study the isomer configurations.

Fig. 1 (a) PBE-optimized structure of [Au₆(NHC-S)₄]²⁺. (b) Au_a-Au_b distance – 4.74 Å part of the SR-Au-SR linear motif. (c) Dihedral angle – 89.10° in S–Au–Au–S. (Au: golden, S: red, N: blue, C: gray, H: white).

Fig. 2 shows the total energy behavior of the system at three temperatures 145 K, 280 K and 475 K as a function of time. To find potential isomer configurations, seven structures from the MD-runs were chosen and optimized (labeled in Fig. 2 and visualized in Fig. S2, ESI†) based on their proximity to the local minimum in terms of energy. The previously introduced Au_a–Au_b bond and dihedral angle were determined to analyse the differences of the structures. The results presented in Table S1 (ESI†) indicate that the Au_a–Au_b distance varies between 3.51 Å−3.83 Å, and the dihedral angles get values between 94° and 106°. Compared to the crystal structure there is a considerable change in the structure that gets more compact and twisted by the two protecting unit ends, which happens without any bond breaking. As a general trend, the largest twisting connects to the most compact structures. Interestingly, the crystal structure is not part of the structural phase space seen in the MD-simulation. With an energy of 0.19–0.42 eV per cluster, all the observed isomers are more stable than the single crystal structure. The most stable structure is the isomer number 2 as labeled in Fig. 2 at 145 K (check the structure for isomer 2 in Fig. S1a (ESI†).

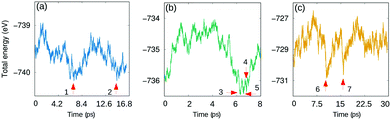Fig. 2 Total energy as a function of time for DFT-MD runs in (a) 145 K, (b) 280 K and (c) 475 K. The selected isomers are labeled 1–7.

Next, we studied systematically dynamical and structural effects on the electronic structure of the cluster at different temperatures. Fig. 3 shows the distribution of the energy gap values between the HOMO and LUMO as a function of the Au_a–Au_b distance at 145 K, 280 K, and 475 K.

Fig. 3 Heat and distribution maps of the HOMO–LUMO gap variation with respect to the Au_a–Au_b distance at three temperatures: (a) 145 K, (b) 280 K and (c) 475 K. Lighter colors in the heat maps indicate the most densely populated area with similar HOMO–LUMO energy gap values.

The initial distance for the relaxed single crystal cluster is 4.74 Å, and the HOMO–LUMO gap is 3.22 eV. As shown in Fig. 3, universal correlation can be seen at all three temperatures; the HOMO–LUMO energy gap value is lower for configurations with shorter Au_a–Au_b distance. Furthermore, the distribution of the HOMO–LUMO gap values (Fig. 3 right vertical panels) is centered at about 2.85 eV for 145 K, 2.78–2.85 eV for 280 K and 2.6–2.8 eV for 475 K. The shape approaches normal distribution at higher temperatures. The central region is the most densely populated area also based on the scatter map plots. Note that the thermalization part has been removed from the data.

Fig. 4 shows a diagram of the energy levels for occupied states (a) and unoccupied states (b) as a function of time at 145 K. The energy of the HOMO state fluctuates strongly, within 0.5 eV, and over time this eigenenergy splits from the “band” of lower-lying states. The energies of the other states either increase or decrease in comparison to the PBE-relaxed crystal structure, but with much smaller fluctuations than the HOMO.

Fig. 4 Energies of the electron states (drawn in diverse colors) as a function of time at 145 K for (a) occupied and (b) unoccupied states.

It is now intriguing to see how the optical absorption spectrum as one of the key signatures of electronic structure changes. Optical absorption spectra were calculated for three temperatures. Fig. 5 shows computed lr-TDDFT spectra of the static single crystal structure after structural optimization presented as a folded spectrum of electron–hole excitations compared to the dynamical multi-structure spectrum calculated from 145 K DFT-MD simulation. Temperature dependent spectra are combined from the single particle transitions calculated and collected for 120 snapshot structures that are chosen in every 65 steps after thermalization.

Fig. 5 Optical absorption spectra in 145 K as combined from 120 snapshot structures (purple lines) chosen in every 65 steps compared to the single crystal structure (yellow curve). Spectrum for the dynamic structures is shown as a stick spectrum including all single particle transitions and their oscillator strengths from the 120 structures that are collected into energy bins (peaks I–IV). The spectrum of the optimized single crystal structure is broadened by 0.1 eV Gaussians (peaks a–d).

Absorption spectra show that even minor changes in the structure have a considerable impact on optical behaviour (Au_a–Au_b bond lengths and dihedral angle values of the selected isomers and single crystal structure are listed in Table S1, ESI†). Optical absorption spectra of DFT-MD findings in Fig. 5 show four absorption bands. The first peak appears around 400 nm (I) which is absent in the PBE-optimized single crystal structure. The remaining peaks appear at about 350 nm (II), 310 nm (III) and 285 nm (IV) whereas the single crystal structure displays two prominent peaks at 290 nm (d) and 335 nm (b) as well as two weak shoulders at 305 nm (c) and 355 nm (a). The first three absorption peaks (a), (b) and (c) in the single crystal structure are blue-shifted, while the fourth peak (d) shows a comparable agreement with that for DFT-MD (IV). Absorption spectra calculated for 280 K display four peaks, however, there are no discrete peaks in 475 K (check Fig. S3 for 280 K and Fig. S4 for 475 K results, ESI†).

To understand the origin of the optical absorption peaks for the single crystal structure and dynamic structures, we computed the dipole transition contribution maps (DTCMs). Fig. S5 (ESI†) shows DTCMs for the selected dynamic structure in 145 K. Red/blue dots in DTCMs represent the relative (strengthening/screening) contributions of single electron–hole excitations to the total transition dipole moment. To reduce the computational load, one representative structure from 120 configurations was selected for analysing the origin of the first and the fourth absorption peaks. The selected structure has the highest resemblance of peak locations to those of the combined spectrum shown in Fig. 5, so that less costly DTCM computations could be obtained. The first and fourth absorption peaks at 396 nm and 288 nm (shown by the arrows in the bottom right panels) are analyzed in Fig. S5 (ESI†). The bottom horizontal and right vertical panels illustrate the occupied (negative energies) and the unoccupied (positive energies) electron states. The absorption for the first peak at 396 nm arises from the HOMO to LUMO+1 transition (Fig. S5a, ESI†), whereas the second peak (Fig. S5b, ESI†) has several contributions from states below the HOMO to states above the LUMO. Higher energy peaks are composed of increasing numbers of transitions and are more collective (DTCMs for the third and the fourth peaks at 145 K shown in Fig. S6a and b, ESI†). Fig. S5c (ESI†) depicts DTCMs for the optimized single crystal structure. The first peak at 355 nm is combined of two main transitions from HOMO to LUMO+1 and HOMO−1 to LUMO. Note that the finite-temperature dynamics splits this peak into two in Fig. S5a (ESI†). This is due to the splitting and decoupling of the HOMO away from the deeper states as shown in Fig. 4a. (DTCMs for the third and fourth peaks for the chosen dynamic structure shown in Fig. S6, ESI,† and DTCMs for the second, third and fourth peaks for the relaxed crystal presented in Fig. S7, ESI†).

To relate the observed crystal structure to the optimal gas phase isomer, we did a 7.4 ps MD simulation starting from the lowest-energy gas phase isomer 2, surrounding it with counterions (10 PF₆⁻) and solvent molecules (2 EtOH) in the crystal structure symmetry.⁶ The total charge was set to 8- and the central P- and C-atoms of PF₆⁻ and EtOH were fixed. Interestingly, the cluster changes spontaneously back to the crystal structure conformation when heating starts, as shown in Fig. S8 (ESI†). Compared to gas phase isomers (Table S1 and Fig. S2, ESI†), the Au–Au distance increases drastically and fluctuates around 4.6 Å. Simultaneously, the S–Au–Au–S dihedral angle decreases and oscillates around 85°. Hence, isomerization happens spontaneously in both directions between the gas and crystal phases. Optimization of the packing and interactions to counterions and solvent molecules in the crystal stabilizes a structure that is not seen in the gas phase isomers.

We have shown that DFT-MD calculation is an effective approach to analyze previously studied cluster [Au₆(NHC-S)₄]²⁺ in order to find possible isomers at different temperatures. The current findings show the presence of at least seven isomers at three different temperatures: 145 K, 280 K, and 475 K. The isomer transition occurs at low temperature without any bond breakage and is shown to be reversible if the cluster environment is changed. In general, we have shown that the optical and electronic properties of a cluster can be very different depending on the exact structure and therefore understanding the isomerism better for protected metal clusters aids designing them for different applications. In this study, we imply that the crystallized structure is not automatically the lowest energy isomer in the gas phase or vice versa. In contrast to the small molecules, protected metal clusters are computationally more demanding and it is not self-evident whether their crystal, gas or solution phase structures should or should not be the same – even less is understood regarding how isomerization affects properties such as the catalytic activity.

This work was supported by the Academy of Finland (grants 315549 and 319208). The computations were done at the JYU node of the Finnish national FCCI infrastructure.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. R. Jin, C. Zeng, M. Zhou and Y. Chen, Chem. Rev., 2016, 116, 10346–10413.
2. P. M. Clusters, From Fundamentals to Applications, Elsevier, Amsterdam, 2015, vol. 9.
3. Q.-Y. Zhang and L. Zhao, Tetrahedron Lett., 2018, 59, 310–316.
4. I. Chakraborty and T. Pradeep, Chem. Rev., 2017, 117, 8208–8271.
5. R. R. Nasaruddin, T. Chen, N. Yan and J. Xie, Coord. Chem. Rev., 2018, 368, 60–79.
6. K. Salorinne, R. W. Man, P. A. Lummis, M. S. A. Hazer, S. Malola, J. C.-H. Yim, A. J. Veinot, W. Zhou, H. Häkkinen and M. Nambo, et al. , Chem. Commun., 2020, 56, 6102–6105.
7. H. Shen, Z. Xu, M. S. A. Hazer, Q. Wu, J. Peng, R. Qin, S. Malola, B. K. Teo, H. Häkkinen and N. Zheng, Angew. Chem., Int. Ed., 2021, 60, 3752–3758.
8. M. Brust, M. Walker, D. Bethell, D. J. Schiffrin and R. Whyman, J. Chem. Soc., Chem. Commun., 1994, 801–802.
9. Q. Yao, T. Chen, X. Yuan and J. Xie, Acc. Chem. Res., 2018, 51, 1338–1348.
10. S. Hossain, Y. Niihori, L. V. Nair, B. Kumar, W. Kurashige and Y. Negishi, Acc. Chem. Res., 2018, 51, 3114–3124.
11. R. L. Whetten, H.-C. Weissker, J. J. Pelayo, S. M. Mullins, X. López-Lozano and I. L. Garzón, Acc. Chem. Res., 2019, 52, 34–43.
12. Y. Pei, P. Wang, Z. Ma and L. Xiong, Acc. Chem. Res., 2018, 52, 23–33.
13. J. Yan, B. K. Teo and N. Zheng, Acc. Chem. Res., 2018, 51, 3084–3093.
14. H. Yang, Y. Wang, H. Huang, L. Gell, L. Lehtovaara, S. Malola, H. Häkkinen and N. Zheng, Nat. Commun., 2013, 4, 1–8.
15. H. Yang, Y. Wang, X. Chen, X. Zhao, L. Gu, H. Huang, J. Yan, C. Xu, G. Li and J. Wu, et al. , Nat. Commun., 2016, 7, 1–8.
16. W. Kurashige, Y. Niihori, S. Sharma and Y. Negishi, J. Phys. Chem. Lett., 2014, 5, 4134–4142.
17. Y. Song, S. Wang, J. Zhang, X. Kang, S. Chen, P. Li, H. Sheng and M. Zhu, J. Am. Chem. Soc., 2014, 136, 2963–2965.
18. Z. Lei, X.-K. Wan, S.-F. Yuan, Z.-J. Guan and Q.-M. Wang, Acc. Chem. Res., 2018, 51, 2465–2474.
19. K. Konishi, M. Iwasaki and Y. Shichibu, Acc. Chem. Res., 2018, 51, 3125–3133.
20. Q.-F. Zhang, X. Chen and L.-S. Wang, Acc. Chem. Res., 2018, 51, 2159–2168.
21. M. Haruta, N. Yamada, T. Kobayashi and S. Iijima, J. Catal., 1989, 115, 301–309.
22. W. Chen and S. Chen, Functional nanometer-sized clusters of transition metals: Synthesis, properties and applications, Royal Society of Chemistry, 2014, vol. 7.
23. K. M. Jensen, P. Juhas, M. A. Tofanelli, C. L. Heinecke, G. Vaughan, C. J. Ackerson and S. J. Billinge, Nat. Commun., 2016, 7, 1–8.
24. X. Sun, P. Wang, L. Xiong and Y. Pei, Chem. Phys. Lett., 2018, 704, 68–75.
25. W. W. Xu, X. C. Zeng and Y. Gao, Nanoscale, 2018, 10, 9476–9483.
26. R. Juarez Mosqueda, S. Malola and H. Häkkinen, Eur. Phys. J. D, 2019, 73, 62.
27. H. Qian, W. T. Eckenhoff, Y. Zhu, T. Pintauer and R. Jin, J. Am. Chem. Soc., 2010, 132, 8280–8281.
28. S. Tian, Y.-Z. Li, M.-B. Li, J. Yuan, J. Yang, Z. Wu and R. Jin, Nat. Commun., 2015, 6, 1–7.
29. K. Taylor, C. Pettiette-Hall, O. Cheshnovsky and R. Smalley, J. Chem. Phys., 1992, 96, 3319–3329.
30. F. Furche, R. Ahlrichs, P. Weis, C. Jacob, S. Gilb, T. Bierweiler and M. M. Kappes, J. Chem. Phys., 2002, 117, 6982–6990.
31. P. Weis, Int. J. Mass Spectrom., 2005, 245, 1–13.
32. A. Fielicke, A. Kirilyuk, C. Ratsch, J. Behler, M. Scheffler, G. von Helden and G. Meijer, Phys. Rev. Lett., 2004, 93, 023401.
33. P. Gruene, D. M. Rayner, B. Redlich, A. F. van der Meer, J. T. Lyon, G. Meijer and A. Fielicke, Science, 2008, 321, 674–676.
34. X. Xing, B. Yoon, U. Landman and J. H. Parks, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 165423.
35. M. F. Matus, S. Malola, E. K. Bonilla, B. M. Barngrover, C. M. Aikens and H. Häkkinen, Chem. Commun., 2020, 56, 8087–8090.
36. E. Kalenius, S. Malola, M. F. Matus, R. Kazan, T. Burgi and H. Hakkinen, J. Am. Chem. Soc., 2021, 143, 1273–1277.
37. Y. Cao, S. Malola, M. F. Matus, T. Chen, Q. Yao, R. Shi, H. Häkkinen and J. Xie, Chem, 2021, 7, 2227–2244.
38. J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola and H. Hansen, et al. , J. Phys.: Condens. Matter, 2010, 22, 253202.
39. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
40. M. Walter, H. Häkkinen, L. Lehtovaara, M. Puska, J. Enkovaara, C. Rostgaard and J. J. Mortensen, J. Chem. Phys., 2008, 128, 244101.

---

Footnote

† Electronic supplementary information (ESI) available: Details of the atomic structure of the Au₆ cluster, optical spectra and their analysis, and simulations in the crystal environment. See DOI: 10.1039/d2cc00676f

---