The rise of an exciton in solid ammonia

Abstract

We trace a polymorphic phase change in solid ammonia films through the emergence of a Frenkel exciton at 194.4 nm, for deposition temperatures of 48 K, 50 K and 52 K. Observations on a timescale of hours give unparalleled access to the individual processes of nucleation and the phase change itself. The excitonic transition is forbidden in the low temperature phase, but greater flexing of the solid state structure in the higher temperature phase makes the transition allowed, as the nano-crystals approach ∼30 unit cells through nucleation. We find activation energies of 21.7 ± 0.6 kJ mol⁻¹ for nucleation and 22.8 ± 0.6 kJ mol⁻¹ for the phase change, corresponding to the breaking of two to three hydrogen bonds.

---

Solid state phase transformations, or polymorphic phase transitions,^1–3 are encountered in an array of fields ranging from drug manufacture,⁴ electronics,⁵ chocolate production⁶ to the interstellar medium.⁷ Polymorphic transitions can be described by two consecutive and distinct processes, the nucleation phase in the parent matrix and the growth of these nuclei to complete the transformation. Despite their broad importance, the processes occurring during nucleation and recrystallization at the molecular scale have proved largely inaccessible. We show here how vacuum ultraviolet (VUV) absorption spectra, recorded for thin cryo-films of ammonia, reveal separately the nucleation rate for crystallite formation in solid ammonia in real time and the growth rate of these nuclei, until the phase conversion nears completion.

We study films a few nanometres thick, deposited by physical vapour deposition under ultra-high vacuum (UHV). It is known from earlier work that such films form in only two crystalline phases,^8–10 displaying a polymorphic phase transition at a deposition temperature, T_d, of ∼50 K. These phases are referred to below as phase II, for low T_d and phase I, for high T_d.¹¹ The ammonia moieties lie on a cubic unit cell in the space group P213–T⁴, which enables hydrogen bonding.^12,13 Films belong to the family of ‘spontelectric’ solids,¹⁴ displaying spontaneously generated electric fields created on deposition, so-called ‘spontelectric fields’. Phases I and II differ in their spontelectric properties.⁸ Fields arise through dipole orientation, which results in a bound polarization charge at the surface/vacuum interface of the film. In phase II, the average angle of ammonia moieties to the horizontal varies between 1.79° at T_d = 20 K and 1.58° at 50 K. In phase I, values are 0.54° at 55 K falling to 0.27° at 80 K,⁸ demonstrating subtle differences in average orientation in the structures of phase I and II.

VUV absorption spectra of ammonia ices condensed between 48 K and 52 K were observed to change with time, most prominently via the emergence of a sharp peak at 194.4 nm, which we attribute to the emergence of a Frenkel exciton. Rate of emergence of the exciton peak is associated with a polymorphic transition between phase II and phase I, gives the rate of the phase change and the delayed emergence of the peak gives the nucleation rate.

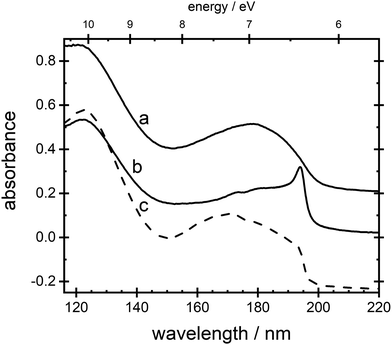
General features of VUV absorption spectra for thin films of ammonia are shown in Fig. 1. Curve a displays the absorption spectrum for a film with T_d = 20 K, phase II, and curve b with T_d = 65 K, phase I. The sharp absorption peak around 194.4 nm (curve b) can be observed, immediately following deposition, only in films prepared with T_d ≥ 55 K. It forms after minutes or hours at lower temperatures and it is altogether absent below 48 K. Curve c in Fig. 1, was recorded through deposition at 20 K and subsequent anneal to 65 K. There is a shoulder evident at 194.4 nm.

Fig. 1 VUV absorption spectrum for a thin film of ammonia prepared with a T_d = 20 K, b T_d = 65 K and c T_d = 20 K and annealed to 65 K showing a shoulder around 194.4 nm. Spectra a and c have been offset in absorbance for clarity.

Absorption lines are associated with transitions involving excitation of the X̃¹A₁ ground state of NH₃ to Rydberg states, well characterised in gas phase spectra.^15,16 The Rydberg states of NH₃ in the gas phase are planar and of D_3h symmetry, whereas the ground state is pyramidal, belonging to C_3v. We propose here that in the low temperature phase II, excited states of NH₃ remain C_3v, whereas only in phase I do they become D_3h. The à ← X̃ transition has a maximum at 193.85 nm in gas phase spectra, in the ν₂ umbrella mode progression. Thus in phase I, the 194.4 nm absorption line may be attributed to the transition, with the molecules able to flex inter-molecular hydrogen bonds¹² and tunnel through the planar D_3h structure in the X̃ state.

The wavelength of the 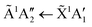transition is independent of T_d over the range of temperature between 48 K and 80 K, and thus of changes in the T_d-dependent spontelectric field in the film.⁸ The 194.4 nm transition therefore involves a Frenkel exciton, in which the hole and electron reside on the same molecular species and the absorption wavelength is insensitive to the electric field, in contrast to Wannier–Mott excitons.⁸

In the low temperature phase II, we suggest that NH₃ has a vanishingly small probability of assuming D_3h symmetry. This arises through inhibition of the ν₂ umbrella motion, which we attribute to a significantly higher barrier to inversion in phase II, than in phase I. This results in a negligible amplitude in the transition. A tunnelling frequency of 1 MHz was reported for solid ND₃ at 2 K.¹⁷ The gas phase tunnelling frequency is 1.6 GHz for ND₃,¹⁸ where this factor of >10³, between the gas phase and the solid state, illustrates the influence of a barrier to inversion in phase II, as suggested, albeit for the deuterated species. If the ground state remains X̃¹A₁, that is, effectively lacking umbrella motion, and the à state also remains in C_3v as proposed above, then the à ← X̃ is forbidden and the 194.4 nm line is absent in phase II, as observed.

Spectra of phases I and II remain virtually indistinguishable between 145 nm and 115 nm, curves a and b, Fig. 1, involving D̃, Ẽ, F̃ and G̃ ← X̃ transitions. This is consistent with symmetry considerations which show that these transitions are all allowed, whether the excited states are of C_3v or D_3h symmetry.

An example of the observed growth with time of the 194.4 nm peak, and the rise of the exciton for T_d = 52 K, is presented in Fig. 2. Data in Fig. 2 were collected over a period of 4 hours and demonstrate the absence of any absorption peak at 194.4 nm at the earliest times,¹⁹ followed by the growth of the peak over this time period. Each individual spectrum in Fig. 2 was fit with two Gaussians to extract the change in amplitude of the peak at 194.4 nm as a function of time. As an example, Gaussian fits to the final spectrum, when the peak is fully developed at long time, are presented as an inset to Fig. 2.

Fig. 2 VUV absorption spectra for a 6 nm thick ammonia film deposited at 52 K. Spectra were recorded as a function of time, starting at effective time zero,¹⁹ moving from blue to red at later times. All spectra are background-subtracted such that absorbance at 200 nm is set to zero. The inset shows a 2-Gaussian peak fit to the final absorption spectrum, obtained after 4 hours, with G1 representing the peak at 194.4 nm, and G2 representing the background.

The change in amplitude of the peak at 194.4 nm, labelled G1 in Fig. 2, is shown as a function of time, for 3 different films prepared with T_d = 48 K, 50 K and 52 K, in Fig. 3. Changing T_d has three notable effects on the shape of the growth curves in Fig. 3. First, we note the variation with T_d of the maximum absorbance, A_max. This quantity is higher for higher T_d, with A_max = 0.14 for 52 K, A_max = 0.11 for 50 K and A_max = 0.015 for T_d = 48 K. Second, there is a time offset, t_offset, before the peak begins to grow for data with T_d = 48 K, a shorter offset with T_d = 50 K, and the peak is already vestigially present for the shortest measurable times of 120 seconds for T_d = 52 K. Third, the rate at which the peak grows is strongly temperature dependent. Table 1 collates these results. Additional data collected at T_d = 50 K, for 4.2 nm and 8.4 nm films, show that the rate of peak growth is independent of film thickness. From this we conclude that phase change in our thin films occurs via bulk processes and is not significantly influenced by the presence of interfaces.

Fig. 3 The change in amplitude of the exciton peak at 194.4 nm as a function of time, for ammonia films of thickness 6 nm prepared at three different T_d. Data are shown as points and error bars as light lines. Errors result from the error in the Gaussian fits presented in Fig. 2.

Table 1 Parameters describing the change in amplitude of the absorption peak at 194.4 nm in 6 nm films of ammonia, deposited at various T_d. Values are peculiar to 6 nm films, since data derive from absorbance, effectively containing units of volume

T d/K	t offset/s^19	Initial rate of peak growth/absorbance/s^−1	Rate of growth of nuclei/s^−1
48	7870 ± 350	1.49 × 10^−6 ± 8 × 10^−8	1.27 × 10^−4 ± 6 × 10^−6
50	1220 ± 44	1.95 × 10^−5 ± 8 × 10^−7	8.2 × 10^−4 ± 3 × 10^−5
52	120 ± 8	1.19 × 10^−4 ± 6 × 10^−6	8.33 × 10^−3 ± 6 × 10^−4

---

The polymorphic recrystallization from phase II to phase I may be seen to involve two distinct stages. The first stage is maintained for the offset times in Table 1. This stage is associated with fluctuations leading to the accumulation of nuclei, that is, local structures tending to a phase 1 structure, which once formed, fail to survive and decay back towards their phase II conformation. These metastable nuclei decay because they are generated in an energetically unfavourable environment. In the experiment, the observation of this stage is consistent with the absence of any absorption in the excitonic transition for the period t_offset. This transition is indicative of the presence of phase I.

The system thus remains quiescent for t_offset but then, through some fluctuation, finds sufficient extent of material in a crystallite for the  excitonic transition to take place, via umbrella motion. These may then give rise to zones of critical size and the formation of critical nuclei, which grow rather than decay. Such nuclei conform more to the phase I than the phase II environment and become the seeds of the new and larger crystallites of phase I, yielding the 194.4 nm absorption. New here is that we reveal the unsuccessful attempts to form phase I structures of sufficient conformity to survive within this new phase.

Following classical nucleation theory, we consider a rate, J, for the formation of nuclei of the target phase I, that will grow instead of shrink, on forming from nuclei of phase II. This rate is given by an Arrhenius activated process with a Gibbs free-energy barrier, ;^20,21

where k is Boltzmann's constant, T is temperature, and εl represents the absorption coefficient of solid NH₃ times the film thickness, with units of volume (see caption to Table 1). We take this effective rate for nucleation to be proportional to the inverse of t_offset. The ability to explore configurations may therefore be expressed as 1/t_offset ∝ exp(−/kT). Application of this expression is shown in Fig. 4. This yields a barrier to attainment of a critical configuration, , of 21.7 ± 0.6 kJ mol⁻¹. The activation energy barrier, 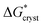, of the re-crystallization process itself, may be determined from the initial rates of 194.4 nm peak growth, in Table 1, column 3, for T_d = 48 K, 50 K and 52 K. An Arrhenius analysis gives a free energy barrier of 22.8 ± 0.6 kJ mol⁻¹, within the errors the same value as that for nucleation.

Fig. 4 An Arrhenius analysis, based upon eqn (1), using values of t_offset, Table 1, yielding , of 21.7 ± 0.6 kJ mol⁻¹; see eqn (1).

With regard to the values of 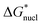and 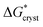, the strength of the hydrogen bond in ammonia has been calculated to be 9.3 kJ mol⁻¹.²² The values of and therefore suggest the breaking of two to three hydrogen bonds to form the transition state, in both nucleation and crystallization stages of the phase change. The result that ≈ reflects the fact that the physical processes for nucleation and crystallization are very comparable, requiring similar rupture of the lattice structure. We note that the activation energy associated with the phase change falls below the energy required for molecular desorption, measured to be 29 kJ mol⁻¹ and calculated to be 31.4 kJ mol⁻¹.²³

We have shown in previous work that in phase I, crystallites formed at 65 K contain 422 unit cells, at 60 K, 189 unit cells and at 55 K, 59 unit cells.⁸ Extrapolation of these figures suggests 34 ± 8 at 52 K, 20 ± 4 at 50 K and 10 ± 2 unit cells at 48 K (1σ). Thus crystallites may contain on average between 2 × 2 × 2 and 3 × 2 × 2 unit cells, at 48 K, 2 × 3 × 3 to 3 × 3 × 3 unit cells at 50 K, and 3 × 3 × 3 to 3 × 4 × 4 unit cells at 52 K. Results in Fig. 3 show that the maximum absorbance, after 14 000 s, drops markedly with T_d between 52 K and 48 K, in parallel with crystallite size. We postulate that there is some minimum crystallite size which gives sufficient elbow room for the hydrogen bonds to flex and enable the excitonic transition. For any T_d, there is a distribution of crystallite sizes and the proportion of crystallites with some necessary minimum size is lower for lower T_d. We suggest that the average size of crystallites at 48 K, with 8 to 12 unit cells, is too small for sufficient flexing to allow the excitonic transition. Therefore only the tail of the distribution of sizes is sufficient to support this transition. At higher T_d, crystallites progress to 2 × 3 × 3 to 3 × 3 × 3 unit cells at 50 K and 3 × 3 × 3 to 3 × 4 × 4 at 52 K, with an increasingly higher proportion able to support the 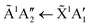excitonic transition.

The crystal structure of ammonia can be considered as an intermediate step on the scale between the H-bond-dominated structure of water ice and the quantum cryo-crystals of methane,²⁴ the latter lacking any hydrogen bonding. It is likely that the phenomenon, reported here for solid ammonia, could be transferred to these other species in an effort to compare the dynamics of crystallisation. Water, as a polar molecule, would also be a good candidate in which to pursue the spontelectric effect and the nature of phase changes, noting the contribution that studies of the spontelectric effect in ammonia have made to our understanding of the current system. Polarisation behaviour in water ices has been reported elsewhere^25,26 but temperature dependent VUV absorption data for water-ice films are not available.

AC thanks the Danish National Research Foundation (Center for Interstellar Catalysis, DNRF150). RJ acknowledges the STFC for her PhD Studentship under grant no. ST/N50421X/1. The research leading to this result has been supported by the project CALIPSOplus under the Grant Agreement 730872 from the EU Framework Programme for Research and Innovation HORIZON 2020. We acknowledge the Centre for Storage Ring Facilities and staff at Aarhus (ISA) for granting access to the AU-UV beamline on the ASTRID2 storage ring with special thanks to Nykola Jones.

Conflicts of interest

There are no conflicts of interest to declare.

Notes and references

1. J. D. Dunitz, Pure Appl. Chem., 1991, 63, 177–185.
2. J. Anwar and D. Zahn, Adv. Drug Delivery Rev., 2017, 117, 47–70.
3. S. Karthika, T. K. Radhakrishnan and P. Kalaichelvi, Cryst. Growth Des., 2016, 16, 6663–6681.
4. S. Datta and D. J. W. Grant, Nat. Rev. Drug Discovery, 2004, 3, 42–57.
5. P. Yu, Y. Zhen, H. Dong and W. Hu, Chem, 2019, 5(11), 2814–2853.
6. R. L. Wille and E. S. Lutton, J. Am. Oil Chem. Soc., 1966, 43, 491–496.
7. K. I. Öberg, A. C. A. Boogert, K. M. Pontoppidan, S. van den Broek, E. F. van Dishoeck, S. Bottinelli, G. A. Blake and N. J. Evans, ApJ, 2011, 740, 109.
8. A. Cassidy, R. L. James, A. Dawes and D. Field, ChemistryOpen, 2020, 9, 983–990.
9. A. Dawes, R. J. Mukerji, M. P. Davis, P. D. Holtom, S. M. Webb, B. Sivaraman, S. V. Hoffmann, D. A. Shaw and N. J. Mason, J. Chem. Phys., 2007, 126, 244711.
10. W. Zheng and R. I. Kaiser, Chem. Phys. Lett., 2007, 440, 229–234.
11. The literature has labelled a phase of solid ammonia stable at pressures above 5.1 kbar as phase II. There is no evidence that the low T_d phase II in the present manuscript forms in these high pressure environments. Our phase II bears no relation to this high pressure phase save that it is another stable phase of crystalline ammonia. For details on the phase diagram for ammonia at high pressures we refer the reader to: L. Huang, Y. Han, J. Liu, X. He and J. Li, Sci. Rep., 2020, 10, 7546.
12. I. Olovsson and D. H. Templeton, Acta Crystallogr., 1959, 12, 827–832.
13. R. Boese, N. Niederprüm, D. Bläser, A. Maulitz, M. Y. Antipin and P. R. Mallinson, J. Phys. Chem. B, 1997, 101, 5794–5799.
14. D. Field, O. Plekan, A. Cassidy, R. Balog, N. C. Jones and J. Dunger, Int. Rev. Phys. Chem., 2013, 32, 345–392.
15. S. Leach, H.-W. Jochims and H. Baumgärtel, Phys. Chem. Chem. Phys., 2005, 7, 900–911.
16. P. Limão-Vieira, N. C. Jones, S. V. Hoffmann, D. Duflot, M. Mendes, A. I. Lozano, F. Ferreira da Silva, G. García, M. Hoshino and H. Tanaka, J. Chem. Phys., 2019, 151, 184302.
17. A. W. Hewat and C. Riekel, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1979, 35, 569–571.
18. J. van Wijngaarden and W. Jäger, J. Chem. Phys., 2001, 114, 3968–3976.
19. A 120s delay occurs between the completion of film dosing and the collection of the first spectrum. Time zero represents the recording of the first spectrum.
20. K. A. Jackson, Kinetic Processes: Crystal Growth, Diffusion, and Phase Transitions in Materials, John Wiley & Sons, 2010.
21. J. W. P. Schmelzer, J. Non-Cryst. Solids, 2010, 356, 2901–2907.
22. C. A. Morrison and M. M. Siddick, Chem. – Eur. J., 2003, 9, 628–634.
23. L. L. Shipman, A. W. Burgess and H. A. Scheraga, J. Phys. Chem., 1976, 80, 52–54.
24. A. Leont’eva, A. Prokhorov, V. Romanusha and V. Efimov, Low Temp. Phys., 2019, 45, 260–267.
25. M. J. Iedema, M. J. Dresser, D. L. Doering, J. B. Rowland, W. P. Hess, A. A. Tsekouras and J. P. Cowin, J. Phys. Chem. B, 1998, 102, 9203–9214.
26. C. Bu, J. Shi, U. Raut, E. H. Mitchell and R. A. Baragiola, J. Chem. Phys., 2015, 142, 134702.

---