Towards reliable three-electrode cells for lithium–sulfur batteries

Abstract

Three-electrode measurements are valuable to the understanding of the electrochemical processes in a battery system. However, their application in lithium–sulfur chemistry is difficult due to the complexity of the system and thus rarely reported. Here, we present a simple three-electrode cell format with relatively good life time and minimum interference with the cell operation.

---

Lithium–sulfur (Li–S) batteries have been regarded as a promising electrochemical energy storage system of the next generation due to their high theoretical energy density and the abundance of sulfur as a by-product of the petroleum industry.^1,2 However, the development of the system has been challenged by the catholyte nature of the system and the metallic lithium electrode, of which the interaction adds to the complexity.^2–4 In the positive electrode, as elemental sulfur is reduced, soluble intermediates (Li₂S_x, x = 2–8, lithium polysulfides) are formed before turning into insoluble lithium sulfide (Li₂S) at the end of discharge.⁵ Upon charging, the overall reaction reverses though the exact distribution of intermediates differs.⁶ The repeated dissolution and precipitation of the insulating sulfur and Li₂S require a large host electrode surface area, which is commonly provided by porous carbonaceous materials.⁷ In the literature, the complicated reaction mechanism in the positive electrode is often blamed for the fast degradation of Li–S cells.^7,8 Frequently addressed issues include the loss of soluble active material, worsening mass transport, sluggish kinetics and chemical redox shuttle of the soluble polysulfides.^2,3,9 Various strategies for improving the S/C composite electrode are typically demonstrated in “half-cells”.^7,8 Conveniently, for the Li–S system, full-cells and half-cells for studying the positive electrode share the same components, with the major difference being the excess of the Li metal negative in the latter. Such a setup enables the comparison between different S/C electrodes by assuming that the smaller working electrode is the limiting factor.

However, this assumption of a non-limiting Li counter electrode is often invalid. As mentioned, the application of the metallic Li electrode, even in excess, is itself a challenge of Li–S batteries.^2,10 In addition to the general issues facing Li metal batteries,¹¹ the Li–S system encounters extra problems stemming from the interplay between the soluble polysulfides and metallic Li.^2,4 For example, the solid–electrolyte interphase (SEI) on Li in Li–S batteries is less robust due to its reduced sulfur components that can dissolve again when oxidised by the polysulfides in the electrolyte¹² Although electrolyte additives can mitigate this issue,¹³ fragile SEI indicates that Li will consume electrolyte continuously throughout cycling.^14,15 This phenomenon, along with nonuniform stripping and plating,¹⁶ raises the resistance of the counter electrode, which may not be negligible in comparison to the cell resistance.

In order to distinguish the electrochemical responses from the working and counter electrodes (WE and CE, respectively), a reference electrode (RE) has to be introduced.¹⁷ Despite the abundance of literature on three-electrode Li-ion batteries, there are scarce reports of three-electrode Li–S cells. Moreover, three-electrode setups are mostly used for electrochemical impedance spectroscopy (EIS) measurements on fresh electrodes.^13,18 There are only few reports on separate impedance contributions from the positive and negative electrodes of an Li–S cell at different states of charge (SoC).^19,20 Hence, the resistance contribution of the Li counter electrode over extended cycling in the Li–S system has not yet been well-investigated.

A significant challenge in the construction of three-electrode Li–S cells arises from the sensitivity of the cell response to the electrolyte volume.¹⁵ As an example, we initially investigated the construction of three-electrode cells both vacuum-sealed pouch cell and a reusable three-electrode cell housing from a commercial supplier. The results are presented in the ESI,† Fig. S1 and S2. Cells constructed in each of these cell formats showed shorter cycle life and higher cell resistance in comparison to the two- and three-electrode coin cells described later in this work. We attribute the major differences to the following: the vacuum sealing process of the pouch cells removes an uncontrolled amount of electrolyte, while the O-rings of the customised cells appear not to provide a sufficient seal. We have found a coin cell inserted with a polyimide-coated gold (Au) microwire, as depicted in Fig. 1, enables three-electrode cells which behave in a comparable matter to their two-electrode equivalent. This cell design is a combination of a previously proposed cell geometry²⁰ and RE.²¹ The polyimide coating insulates the Au microwire throughout the cell, leaving only a small cross section between WE and CE, which makes it easy to ensure good electrode alignment.^17,21,22 Crucially for the Li–S system, we find that the Au microwire electrode provides a valuable function both lithiated, as a conventional RE, or as an unlithiated pseudo-RE.

Fig. 1 Scheme of the cross sections of the three-electrode coin cell setup.

The Au microwire can be electrochemically lithiated by the CE after cell assembly, which has been previously reported for three-electrode measurements of comparable Li-ion cells.²¹ The Li_xAu (x = 0–1) alloy exhibits a consistent potential of 0.31 V vs. Li/Li⁺ and can serve as a RE given a constant concentration of Li-ions in the electrolyte.^21,23 The alternative is to use the Au microwire without lithiation as a pseudo-reference electrode. Although it is known that Au pseudo-RE causes artefacts at low frequencies in the impedance spectra of a Li-ion cell,²¹ in a Li–S catholyte the potential of the pseudo-RE is comparatively stabilised by the dissolved polysulfides, which set the potential of the pseudo-RE at around 2.35 and 2.15 V vs. Li/Li⁺ at the upper and lower plateaus, respectively.²⁴ Secondly, in this work we use our previously reported Intermittent Current Interruption (ICI) method for following resistance,^15,25,26 in which the measurement time is 1 s, and short enough that low frequency/long timescale instability does not significantly affect the measurement. Third, although LiAu has a constant potential when in contact with a fixed concentration of Li⁺ in the electrolyte, the latter changes locally in an operating cell. This leads to ∼20 mV variation in the potential of LiAu, which is not obvious in Fig. 2 but can be read from the raw data.²⁷

Fig. 2 Potential (E), internal resistance (R) and diffusion resistance coefficient (k) of the cell, working (WE) and counter (CE) electrodes in the 10th cycle. The E/S ratio, RE of each cell are marked. The sulfur-loading of the cell marked with ‘HL’ is 3.2 mg_S cm⁻² while that of the other three cells is 2.5 mg_S cm⁻². R and k of the WE, CE and the cell in all cells are higher during discharging than during charging, except for R at the end of charging of the two cells with E/S = 6. Note that the CE potential is approximately 0 V − E_RE, and the cell voltage is identical for all cell.

After the formation cycle, the cells were cycled galvanostatically at C/10 (C = 1672 mA h g_S⁻¹) between 1.8 and 2.6 V. Resistance measurements were made using the abovementioned ICI method, with one-second current interruptions every five minutes. Analysis of the potential change during the interruption (ΔE) gives an internal resistance (R) and a diffusion resistance coefficient (k), which is proportional to the coefficient of the Warburg element (σ) typically used in equivalent circuit model fitting of EIS results, as shown in eqn (1).²⁶

where t is time since the current is switched off. To demonstrate this cell format, a comparison was made with both lithiated and unlithiated Au microwire as a RE, together with measurements using the lithiated version at two electrolyte-to-sulfur ratios (E/S = 6 and 7 μL mg_S⁻¹) and two sulfur-loadings (2.5 and 3.2 mg_S cm⁻²). The higher E/S ratio is selected to compensate for the extra separator, which absorbed about 2.3 μL according to its porosity,²⁸ while the higher sulfur-loading is chosen since the potential profile of S/C composite electrodes showed noticeable difference below and above 3 mg_S cm⁻² in previous work.²⁹ The potential and resistance profiles in the 10th cycle for each of these cases are plotted in Fig. 2.

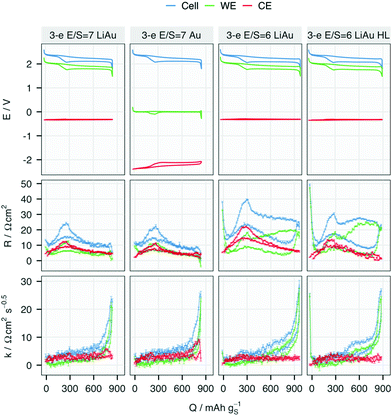
Despite the differences in the potential profiles, the resistances measured with both lithiated (LiAu) and unlithiated (Au) REs agree closely at the same E/S ratio. In the cells with E/S = 7, the overall R, which corresponds to the charge-transfer and solution resistances,¹⁵ is equally contributed by the WE and CE. However, in the cells with E/S = 6, R on the lower discharge plateau has a larger contribution from the WE, especially in the cell with higher sulfur loading. Given that the RE is positioned halfway between the WE and CE, the solution resistance measured at both WE and CE should be approximately equal. Therefore, the higher R from the WE at lower E/S ratio and higher loading can be attributed to a higher charge-transfer resistance, or passivation of the electrode surface. The higher R from both the WE and CE in the cell ‘3-e E/S = 6 LiAu’ may be a mixed effect of higher solution resistance from the increased polysulfide concentration and higher charge-transfer resistance of the CE. However, it is difficult to distinguish the two effects since both resistances are included in R in an ICI measurement.

The diffusional resistance, quantified by k, is mostly contributed by the WE in all cells. This observation indicates that the mass transport inside or to the porous carbon matrix in the WE is the main contribution to diffusional resistance in a Li–S cell. Except for a small increase at the end of discharge in the cells with E/S = 7, k of the CE stays invariant at all SoC. A steep increase in k can be observed in all WE near the end of discharge, indicating a transport limitation in the sulfur electrode. With E/S = 6, the increase of k starts around 400 mA h g_S⁻¹, which appears as a slope in the cell with a standard sulfur-loading of 2.5 mg_S cm⁻² but a plateau when the loading is increased to 3.2 mg_S cm⁻² (cell marked with ‘HL’). Such two-stage growth of k has been proposed to be associated with both surface passivation and replacement of electrolyte volume inside the porous carbon matrix, which are caused by the formation of insulating Li₂S.²⁶

The evolution of the resistance from both electrodes in the cell with an Au RE is presented in Fig. 3. In the 70th cycle, R of the Li CE increases for all SoC except for the vicinity of 0% (∼700 mAh g_S⁻¹) while R of the WE stays at the same level as in previous cycles. An increase in k of the CE can also be observed at the end of discharge, in contrast to the relative lack of change in k at the WE with increasing cycle number. Despite the more noisy signal in the 80th cycle, further increases in resistance can be attributed to R and k in both electrodes.

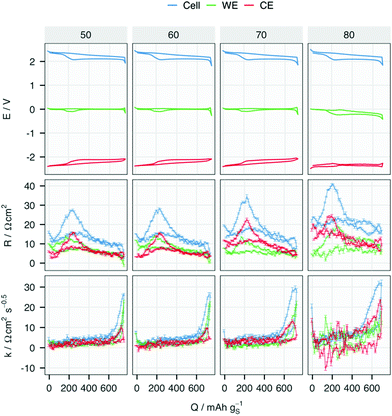Fig. 3 Potential (E), internal resistance (R) and diffusion resistance coefficient (k) of the cell, working (WE) and counter (CE) electrodes in the 50th, 60th 70th and 80th cycle of the cell with E/S = 7 and a Au pseudo-RE, i.e. ‘3-e E/S = 7 Au’ in Fig. 2.

The changes in R for each electrode, as summarised by the minimum, maximum and media per cycle, are plotted for all four cells in Fig. 4. The potential and resistance profiles of the remaining cells are presented for selected cycles in Fig. S4–S6 (ESI†). The same summary of k can be found in Fig. S7 (ESI†). An earlier and faster increase of R from the CE can be found in all the cells, except for the one with higher sulfur-loading. At 2.5 mg_S cm⁻², the median resistance of the metallic Li electrode surpasses that of the WE the earliest in the cell with E/S = 6. This is also reflected by the shorter cycle life of the cell with lower E/S. Although the three-electrode cells show a shorter cycle life as the standard two-electrode cells, the same impact of the E/S ratio on the cycle life of two-electrode cells can be seen in Fig. S2 and S8 (ESI†) and in previous work.¹⁵ Moreover, the dominant resistance contribution from the Li metal electrode can be found in all the cells with the standard sulfur loading as they approach the end of their cycle life. It can thus be inferred that the E/S ratio has a strong impact on the onset of the rapid resistance growth of the metallic Li electrode, which offers an explanation for its strong influence on the cycle life of the cell.¹⁵

Fig. 4 The median (solid line), maximum and minimum (ribbon) of the internal resistance (R) in each cycle of cells with (a) E/S = 7 and (b) E/S = 6. Note that the scales are different in parts (a and b). The maximum of the y-axis is set to 60 (a) and 350 (b) for the clarity. The data from first 9 cycles of the cell ‘3-e E/S = 7 LiAu’ have large noise in R due to the insufficient resolution of the potentiostat, which is therefore left out of the graph. The potentiostat was changed afterwards.

The RE in the cell with high sulfur loading stops to function properly after the 30th cycle, which can be observed in the negative R values from both WE and CE in Fig. 4. Although the LiAu alloy provides a constant potential of 0.31 V vs. Li/Li⁺ in the beginning of cycling, the low potential leads to reduction of polysulfides with simultaneous delithiation of the Au wire. This ultimately results in a potential shift to that of the polysulfides, as exhibited in Fig. S4 and S6 (ESI†). Despite this, the Au wire still functions as a pseudo-RE in the rest of cycles in the cells with the standard sulfur-loading, but not in the cell with high sulfur-loading: as shown in Fig. S6 (ESI†), the potential of the CE first decreased from −0.31 V to around −2.1 V, but from around 25 cycles drifts to around −0.9 V vs. CE. This potential does not correspond to any expected process, and the negative resistance values indicate that the RE fails to function properly after the 35th cycle in this cell. This indicates a soft short-circuit between the RE and CE, which may be a consequence of the larger morphological changes of the Li CE due to the higher current density.

In summary, this work demonstrates that the increase in the internal resistance of a Li–S half-cell can be significantly affected by the metallic Li counter electrode when the cell approaches the end of the cycle life, even with large excesses of Li metal and electrolyte. This observation has crucial implications to the majority of the studies on the Li–S system, which are carried out in various comparable half-cells. The general assumption that the counter electrode should not limit the cell performance, whether in terms of capacity, resistance or cycle life, may not hold throughout the cycling test, especially when the cell resistance starts to grow substantially in later cycles. In addition, to the best of our knowledge, this work is the first report of long-duration cycling of a three-electrode Li–S cell. We conclude the introduction of a Au microwire into a standard coin cell contributes the smallest increase in resistance and negative effect on cycle life, following an investigation of several different concepts. The use of unlithiated Au as a pseudo-RE together with ICI to follow resistance also presents a uniquely convenient analytical method for the Li–S system.

The authors acknowledge the financial support from the ÅForsk Foundation, Swedish Energy Agency and StandUP for Energy consortium.

Conflicts of interest

There are no conflicts to declare.

References

1. P. Bonnick, E. Nagai and J. Muldoon, J. Electrochem. Soc., 2018, 165, A6005–A6007.
2. M. Zhao, B. Li, X.-Q. Zhang, J. Huang and Q. Zhang, ACS Cent. Sci., 2020, 6, 1095–1104.
3. M. Wild, L. O’Neill, T. Zhang, R. Purkayastha, G. Minton, M. Marinescu and G. J. Offer, Energy Environ. Sci., 2015, 8, 3477–3494.
4. D. Aurbach, E. Pollak, R. Elazari, G. Salitra, C. S. Kelley and J. Affinito, J. Electrochem. Soc., 2009, 156, A694–A702.
5. K. H. Wujcik, D. R. Wang, A. A. Teran, E. Nasybulin, T. A. Pascal, D. Prendergast and N. P. Balsara, in Electrochemical Engineering, John Wiley & Sons, Ltd, 2018, pp. 41–74.
6. U. Košir, I. Kralj Cigić, J. Markelj, S. Drvarič Talian and R. Dominko, Electrochim. Acta, 2020, 363, 137227.
7. M. A. Pope and I. A. Aksay, Adv. Energy Mater., 2015, 5, 1–22.
8. Z. Li, Y. Huang and L. Yuan, Carbon, 2015, 92, 41–63.
9. J. Lei, T. Liu, J. Chen, M. Zheng, Q. Zhang, B. Mao and Q. Dong, Chem, 2020, 6, 2533–2557.
10. X.-B. Cheng, J.-Q. Huang and Q. Zhang, J. Electrochem. Soc., 2018, 165, A6058–A6072.
11. A. Varzi, K. Thanner, R. Scipioni, D. Di Lecce, J. Hassoun, S. Dörfler, H. Altheus, S. Kaskel, C. Prehal and S. A. Freunberger, J. Power Sources, 2020, 480, 228803.
12. M. J. Lacey, A. Yalamanchili, J. Maibach, C. Tengstedt, K. Edström and D. Brandell, RSC Adv., 2016, 6, 3632–3641.
13. S. S. Zhang, Electrochim. Acta, 2012, 70, 344–348.
14. X. B. Cheng, C. Yan, J. Q. Huang, P. Li, L. Zhu, L. Zhao, Y. Zhang, W. Zhu, S. T. Yang and Q. Zhang, Energy Storage Mater., 2017, 6, 18–25.
15. M. J. Lacey, ChemElectroChem, 2017, 4, 1997–2004.
16. K.-H. Chen, K. N. Wood, E. Kazyak, W. S. LePage, A. L. Davis, A. J. Sanchez and N. P. Dasgupta, J. Mater. Chem. A, 2017, 5, 11671–11681.
17. R. Raccichini, M. Amores and G. Hinds, Batteries, 2019, 5, 1–24.
18. S. S. Zhang and J. A. Read, J. Power Sources, 2012, 200, 77–82.
19. J. Fang, W. Shen, S. H. S. Cheng, S. Ghashghaie, H. K. Shahzad and C. Y. Chung, J. Power Sources, 2019, 441, 227202.
20. C. Barchasz, J.-C. Leprêtre, F. Alloin and S. Patoux, J. Power Sources, 2012, 199, 322–330.
21. S. Solchenbach, D. Pritzl, E. J. Y. Kong, J. Landesfeind and H. A. Gasteiger, J. Electrochem. Soc., 2016, 163, A2265–A2272.
22. L. H. J. Raijmakers, M. J. G. Lammers and P. H. L. Notten, Electrochim. Acta, 2018, 259, 517–533.
23. P. Bach, I. Valencia-Jaime, U. Rütt, O. Gutowski, A. H. Romero and F. U. Renner, Chem. Mater., 2016, 28, 2941–2948.
24. M. J. Lacey, K. Edström and D. Brandell, Electrochem. Commun., 2014, 46, 91–93.
25. M. J. Lacey, K. Edström and D. Brandell, Chem. Commun., 2015, 51, 16502–16505.
26. Y.-C. Chien, A. S. Menon, W. R. Brant, D. Brandell and M. J. Lacey, J. Am. Chem. Soc., 2020, 142, 1449–1456.
27. Y. Chien, D. Brandell and M. J. Lacey, Supporting data for “Towards reliable three-electrode cells for lithium–sulfur batteries” [Data set], Zenodo, 2021 DOI:10.5281/zenodo.5211151.
28. D. R. Rajagopalan Kannan, P. K. Terala, P. L. Moss and M. H. Weatherspoon, Int. J. Electrochem., 2018, 2018, 1–7.
29. M. J. Lacey, V. Österlund, A. Bergfelt, F. Jeschull, T. Bowden and D. Brandell, ChemSusChem, 2017, 10, 2758–2766.

---

Footnote

† Electronic supplementary information (ESI) available: Cycling statistics, cell voltage and resistance profiles of all cells, potential and resistance profiles in the later cycles of the three-electrode cells, statistics of the diffusion resistance coefficient (k). See DOI: 10.1039/d1cc04553a

---