Monitoring off-resonance signals with SHARPER NMR – the MR-SHARPER experiment

Abstract

We demonstrate an extension to the SHARPER (Sensitive Homogenous and Refocussed Peaks in Real Time) NMR experiment which allows more than one signal to be monitored simultaneously, while still giving ultra-sharp, homo- and hetero-decoupled NMR signals. This is especially valuable in situations where magnetic field inhomogeneity would normally make NMR a problematic tool, for example when gas evolution is occurring during reaction monitoring. The originally reported SHARPER experiment only works for a single, on-resonance NMR signal, but here we demonstrate the Multiple Resonance SHARPER approach can be developed, which in principle can acquire multiple on-/off-resonance signals simultaneously while retaining the desirable properties of the parent sequence. In practice, the case of two resonances, e.g. those of a reactant and a product, will most of the time be considered for MR-SHARPER, as illustrated here.

---

Introduction

Monitoring chemical reactions by following changes in reactant, intermediate and product concentrations can allow chemists to determine reaction kinetics and reaction mechanisms.¹ NMR spectroscopy is well suited to reaction monitoring and mechanistic studies because it is inherently quantitative, is able to observe a wide array of different nuclei,² and simultaneously provides a wealth of structural information.³ However, most standard NMR spectroscopic techniques rely on maintenance of a highly stable homogenous magnetic field. This may be challenging when applied to reaction monitoring, for example if a chemical reaction evolves a gas⁴ or requires additional hardware inside the magnetic field, such as in photochemical^5,6 or electrochemical⁷ reactions. Several NMR experiments have been reported which are capable of compensating for magnetic field inhomogeneity, for example the UPSIF⁸ experiment, which yields a broadband pure shift spectrum. However, it does not work in real time (i.e. within the time period of a single FID) and so is unsuitable for monitoring fast chemical reactions. Shim pulses⁹ offer real-time compensation for magnetic field inhomogeneity, but require significant calibration and cannot compensate for dynamic changes to the magnetic field inhomogeneity over the course of a reaction.

Extending previous reports,^10,11 the recently reported SHARPER NMR experiment works both in real time and requires no prior calibration of the field inhomogeneity.⁴ This is achieved for a single, on-resonance NMR signal, by repeatedly refocussing it using a train of 180° refocussing pulses between acquired data chunks, with the pulse sequence of non-selective SHARPER shown in Fig. 1. This train of spin echoes, in addition to removing heteronuclear coupling evolution, serves to refocus undesirable evolution of magnetisation, such as that due to magnetic field inhomogeneity as long as the Δ periods are sufficiently short. Indeed, SHARPER proves to be capable of removing residual magnetic field inhomogeneity even in well shimmed spectra, reducing T_2(ΔB0) contributions to and resulting in narrower linewidths and thus more intense signals than standard NMR spectroscopic approaches.² A modified selective version of the sequence, sel-SHARPER is also capable of refocussing the effects of homonuclear couplings.⁴ Collapsing of multiplicity can further enhance the improvements in signal intensity from the SHARPER experiment.

Fig. 1 The SHARPER pulse sequence. Flip angles and signs of gradients are as indicated. “X” can be any nucleus of interest. Phase cycle as follows φ1 = 2x, 2(−x), 2y, 2(−y); φ2 = 2(y, −y), 2(x, −x); φ3 = 2(−y, y), 2(−x, x); and receiver phases are 2x, 2(−x), 2y, 2(−y).

An inherent attribute of the SHARPER sequences is that the 180° pulses also serve to refocus chemical shift evolution between the data chunks, which leads to significant and regular sideband artefacts in the Fourier transformed spectra for any off-resonance magnetisation, should this be not removed prior to the acquisition. i.e. the spectrum works only for a single, on-resonance signal.

In reaction monitoring applications it is usually desirable to monitor at least two signals (starting material and product), if not more where intermediates are also of interest. While this could be achieved by running interleaved experiments where each resonance is measured in alternate scans, this reduces the time resolution of the experiment, even if a single scan version of the SHARPER experiment is used (which does not lead to significant phase cycle related artefacts). Another solution is to run the same chemical reaction multiple times, monitoring a different resonance each time and this has been shown to be possible with minimal experimental error.¹² However, a more elegant solution is to modify the SHARPER experiment to relax the requirement for the signal to be precisely on-resonance, thus in principle allowing multiple frequencies to be accessed in a single experiment. Two resonances, e.g. those of a reactant and a product, can be sampled by this approach.

Off-resonance SHARPER

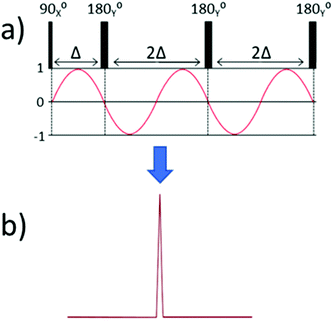
To explain how off-resonance SHARPER can be achieved, it is first helpful to explore the immediate consequence of running a standard SHARPER spectrum while acquiring an off-resonance signal. In these cases, the chemical shift evolution is repeatedly perturbed between the acquired chunks. Fig. 2(a) presents a simplified cartoon version of the standard SHARPER sequence along with the evolution of the X component of magnetisation during the sequence. Following the initial 90⁰_X pulse, the X component of magnetisation is 0, however chemical shift during the subsequent data chunk occurs to give a sinusoidal X magnetisation. The effect of the first 180⁰_Y refocussing pulse is to invert the sign of the X component of magnetisation i.e. creating jumps in phase. Fourier transformation of the resulting FID leads to intense regular sideband artefacts centred on the frequency of the off-resonance signal (Fig. 2(b)).

Fig. 2 (a) The X component of magnetisation due to chemical shift evolution in a SHARPER experiment, and (b) a cartoon of the resulting Fourier transform.

Our approach to MR-SHARPER exploits the special case where the 180⁰_Y refocussing pulses are applied after a precise duration, Δ, which is chosen to be the wave period of the off-resonance frequency i.e. the point at which the X component of magnetisation has returned to 0. This is illustrated in Fig. 3 and should avoid the phase jumps shown in Fig. 2, and thus lead to an essentially normal FID and a sharp singlet in the subsequent Fourier transformed NMR spectrum.

Fig. 3 (a) The X component of magnetisation due to chemical shift evolution in a SHARPER experiment, where the wave period has been matched to the data chunk duration, and (b) a cartoon of the resulting Fourier transform.

More generally, the value of Δ can take multiple values for off-resonance SHARPER experiments, as it can be any integer or half integer multiple, n, of the wave period of the off-resonance frequency, v_off, present, described in eqn (1):The timing required for off-resonance SHARPER experiments.

However, it should be noted that the upper limit of Δ is defined by the magnitude of any scalar couplings and magnetic field inhomogeneity that need to be refocussed in these experiments. In typical applications, this means Δ < 20 ms is desirable to achieve Δ < 1/(4J) where J is the largest scalar coupling constant for the signal.

To demonstrate this experimentally, an off-resonance SHARPER experiment (pulse sequence in Fig. 4) was acquired on the residual HDO signal in a sample of 99% D₂O. The transmitter offset was adjusted to place the HDO signal exactly 100 Hz off-resonance which thus has a wave period of 10 ms i.e. the bulk magnetisation will rotate exactly 360° over 10 ms. Consequently the Δ duration was set to 10 ms, giving a full length data chunk (2Δ) of 20 ms. As anticipated, acquiring 500 data chunks using this sequence results in a perfect SHARPER-like FID (Fig. 5a) with slow relaxation arising from removal of T_2(ΔB0) contributions to , but in an off-resonance acquisition. Closer examination of the FID (Fig. 5b) shows there is no jump in phase observed and the resulting Fourier transformed spectrum (Fig. 5c) presents the expected sharp singlet, with a very narrow half-height linewidth (0.1 Hz). Indeed, the only apparent difference between this and an on-resonance SHARPER spectrum is that the peak is located 100 Hz away from the transmitter offset.

Fig. 4 Pulse sequence diagram for a simplified SHARPER pulse sequence. Flip angles and phases are as shown. Chemical shift evolution during the delays K – typically tens of microseconds are cancelled out, but are required for the avoidance of ringdown.

Fig. 5 Experimental data showing (a) full FID and (b) 80 ms region of the FID from an off-resonance SHARPER experiment examining residual HOD in D₂O, with the signal exactly 100 Hz off-resonance. (c) Shows the resulting Fourier transform.

Multiple resonance SHARPER

When multiple resonances are present in a spectrum, the frequency differences between resonances are fixed (for a given sample and experimental conditions) so in this case the value of Δ must be suitable for all of the frequencies present. In the following we discuss cases where either, only two resonances are present in the spectrum (e.g. two ¹⁹F signals), or, two resonances are selected through selective excitation (e.g. in ¹H spectra). Such experiments can be performed in two different ways, by placing the transmitter offset either on one resonance (Fig. 6a) or exactly between two resonances, (Fig. 6b). This yields either (a) a spectrum with an on-resonance and off-resonance peak or (b) a spectrum with two off-resonance peaks. In (a), where the off-resonance frequency is doubled, the wave period is halved. This is beneficial as shorter wave periods allow a greater number of suitable Δ values to be found, while still regularly refocussing the magnetic field inhomogeneity. However in (b), both signals are at identical off-resonance frequencies and thus frequency dependent imperfections should affect both resonances equally, and the bandwidth required for such pulses is also minimised. If both resonances are at a fixed frequency throughout a chemical reaction the latter solution may be preferred because equivalent behaviour of both monitored peaks is helpful to provide quantitative comparison of the peak intensities. However, in situations where one resonance changes frequency, we found it generally best to set the offset to the immobile resonance – and this was the case in the experimental data presented below.

Fig. 6 Optimal transmitter offset placement for MR-SHARPER spectra with only two resonances.

Experimentally, to achieve precise values of Δ, this requires equally precise values of the dwell time between the data-points in the chunks to be set. We note that whilst delay periods in modern NMR spectrometers can be trivially set with a high degree of precision (∼12.5 ns on Bruker hardware)¹³ defining precise dwell times is more challenging. We found that the precise values to which acceptable dwell times can be set are 33–133 ns on the Bruker spectrometers tested. Thus, some values of Δ which satisfy eqn (1) may not be experimentally accessible with sufficient precision due to hardware limitation. To minimise this issue we wrote scripts (see ESI†) to examine a matrix of all possible values of Δ (<40 ms) which fitted eqn (1) for the frequency differences present in the NMR spectrum of interest within upper and lower bounds for spectral width and maximum and minimum Δ duration. The script then calculates the optimal Δ value based on the closest possible fit to integer multiples of experimentally-accessible dwell times given the spectrometer hardware. Further discussion on this selection of Δ and hardware limitations is given in the ESI.†

In order to demonstrate MR-SHARPER experimentally, a sample of CD₃OD was used, which gives a ¹H spectrum with two resonances, relating to residual amounts of two methanol isotopologues, CHD₂OD and CD₃OH. The transmitter offset was placed exactly between the two resonances, yielding a single 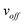of ± 387.63 Hz on our 500 MHz spectrometer. Ideal potential values for Δ were constrained to between 3 and 6 ms to ensure adequate J-refocussing, with spectral widths of between 10 and 25 ppm allowed. This gave an optimal experimental Δ value of 3.87 ms, with a dwell time of 43.0 μs. Sufficient data chunks were collected to yield a MR-SHARPER FID of 11.6 s duration. Fig. 7(a) shows the result SHARPER style spectrum with two sharp and intense singlets at the resonances frequencies of the corresponding 1D ¹H spectrum (Fig. 7(b)). Linewidth for both MR-SHARPER resonances was significantly narrowed to 0.14 Hz and 0.19 Hz for CHD₂OD and CD₃OH respectively cf 1.19 Hz and 1.56 Hz in the 1D ¹H spectrum. This, combined with the reduction in multiplicity for the CHD₂OD, provides a dramatic increase in signal-to-noise ratio of 21.9× for CHD₂OD and 7.8× for the CD₃OH.

Fig. 7 (a) MR-SHARPER and (b) 1D ¹H spectra of residual CHD₂OD and CD₃OH isotopologues in a sample of neat CD₃OD. SHARPER spectrum zero-filled to 2048 K, both apodised with a 0.1 Hz Gaussian. Signal intensity of the CD₃OH signal has been normalised in both cases.

One consequence of this approach is that greater frequency differences between the monitored resonances will result in shorter wave periods and thus more freedom in selecting the value of Δ. Increased frequency differences could come either from use of a higher field spectrometer or acquisition on nuclei with a broader range of chemical shifts (such as ¹⁹F). Thus, higher quality (increased signal-to-artefact ratio) MR-SHARPER spectra will be acquired on these systems. Conversely, lower performance can be expected when utilising lower field instruments where, matching a theoretically valid value of Δ with an experimentally feasible one becomes more difficult.

MR-SHARPER applications

Mutarotation of glucose

In the first example of reaction monitoring, MR-SHARPER was used to monitor the mutarotation of 99+% α-D-glucose in D₂O into an isomeric mixture of α- and β-D-glucose equilibrium states.^14,15 A selective version of the MR-SHARPER experiment, MR-sel-SHARPER, was used, allowing precise setting of the number of points in each Δ acquisition period. A 50 ms doubly selective Gaussian refocussing pulse and a pre-saturation of the HDO residual solvent signal were applied (sequences provided in ESI†). The ratio of the integrals of the ¹H signals of the anomeric protons of glucose (∼5.2 ppm and ∼4.6 ppm) was monitored as the sample reached equilibrium after 400 minutes, Fig. 8. The reaction was also monitored by acquiring simple ¹H NMR spectra, two interleaved single-resonance sel-SHARPER experiments using a single-pulsed field gradient spin-echo (SPFGSE) for the initial signal selection⁴ and a MR-sel-SHARPER experiment using a double-selective pulse to simultaneously invert both anomeric protons (example spectra are shown in Fig. S9 of the ESI†).

Fig. 8 Mutarotation of glucose: ratio of the integrals from sel-SHARPER, MR-sel-SHARPER and 1D ¹H spectra (integrals measured by signal deconvolution to account for overlap of β anomeric proton with HDO).

Table 1 gives a comparison of the different equilibrium constants, K, and rate constants, k, derived from 1D ¹H, SPFGSE, sel-SHARPER and MR-sel-SHARPER experiments for the mutarotation. It was found that integrating the MR-sel-SHARPER signals from both the main (central) resonance and 1^st sideband, for the off-resonance β anomeric proton provided a slightly better fit to the equilibrium data from the ¹H NMR spectra (see Fig. S6–S8, ESI† to see detail on this integration) but still provided a good fit to the kinetics.

Table 1 Comparison of different methods to monitor the equilibration of α- to β-glucose. Integrals for the ¹H spectrum were measured by lineshape fitting to account for the overlap with the water signal. Detailed rate equations provided in ESI† ^15,16

Method	Rate constant, k = kf + kr ×10^−4/s^−1	Equilibrium constant, K = [β]eq/[α]eq
^1H spectrum	2.09 ± 0.06	1.607 ± 0.006
SPFGSE	2.09 ± 0.02	1.584 ± 0.006
sel-SHARPER	2.08 ± 0.04	1.568 ± 0.006
MR sel-SHARPER main band only	2.11 ± 0.01	1.465 ± 0.006
MR sel-SHARPER main + 1^st sidebands	2.17 ± 0.07	1.594 ± 0.006
Inhomogeneous conditions
SPFGSE	—	1.603
sel-SHARPER	—	1.600
MR sel-SHARPER main + 1^st sideband	—	1.730

---

In order to demonstrate that the magnetic field inhomogeneity compensation is retained for both on- and off-resonance signals, the composition of the equilibrated glucose sample was re-measured with the z shim coil deliberately miss-set by +200 units from its optimal value. As can be seen in Fig. 9, both sel-SHARPER and MR-sel-SHARPER give sharp singlets, both compensating for magnetic field inhomogeneity and removing splitting due to proton–proton interactions whereas the corresponding 1D ¹H SPFGSE shows significant broadening of multiplets and subsequent deterioration of the signal-to-noise ratio. Under these conditions the SPFGSE, sel-SHARPER and MR-sel-SHARPER spectra produce comparable equilibrium constants (Table 1, ‘Inhomogeneous conditions’), as they did under optimum shimming conditions.

Fig. 9 Overlay of NMR spectra recorded under poor magnetic homogeneity (z shim miss-set by 200). 1D ¹H SPFGSE spectrum, MR-sel-SHARPER spectra and sel-SHARPER spectrum. All spectra are plotted on the same vertical scale. For clarity SPFGSE spectrum is replotted using a 10-fold vertical expansion.

Protodeboronation of aromatic boronic acid

A more challenging protodeboronation reaction shown in Fig. 10 was also studied with the MR-SHARPER sequence. In basic conditions aromatic boronic acids decompose to the corresponding aromatic compound, a process that has previously been studied by NMR in detail.^4,16

Fig. 10 Protodeboronation reaction for 4.9 mg 2,6-difluoro-4-methoxyphenylboronic acid, 1, 27 °C 1 : 1 H₂O : dioxane solvent, 0.2 M KOH.

The 1D ¹⁹F spectrum of the reaction mixture (Fig. 11) contains only two signals, one from the reactant (1) and the other from the product (2). Note that the signal from the reactant is broadened by the chemical exchange between its boronic acid and boronate forms (Fig. 11, bottom), which cannot be removed using the chunk lengths of tens of milliseconds. However, any broadening due to unresolved ¹⁹F–^10/11B couplings should be refocussed by the SHARPER pulse sequence. The corresponding MR-SHARPER spectrum (Fig. 11, top) showed the expected significantly sharper resonances from the elimination of ¹H–¹⁹F splittings and magnetic field inhomogeneity, with a three-fold SNR improvement for 1 and eight-fold for 2.

Fig. 11 Comparison of simple 1D ¹⁹F pulse-acquire spectrum (time = 1603 s) and MR-SHARPER (time = 1536 s) for the protodeboronation of 1 measured consecutively. The integral region for the off-resonance SHARPER signal is indicated in red.

The protodeboronation of 1 was monitored by alternately measuring a simple 1D ¹⁹F pulse-acquire spectrum and ¹⁹F MR-SHARPER every 67 seconds. Over the course of the reaction the ¹⁹F resonance frequency of 2 drifted by approximately 10 Hz. As illustrated previously,⁴ a mismatch between the carrier and resonance frequencies causes a redistribution of signal intensities with sidebands signals becoming more intense, while the intensity of the central signal decreases. At the same time, their sum is constant. Absolute integrals therefore were measured using a wider region (indicated in red in Fig. 11) to include the contribution from side-bands for the off-resonance signal.

When monitoring the reaction, a good agreement was observed for the calculated rate constants, k_obs, obtained from fitting the absolute integrals in 1D ¹⁹F and MR-SHARPER spectra (Fig. 12). It should be noted that the early period of the reaction could not be measured due to practical considerations in transporting and loading the sample, combined with optimising the MR-SHARPER parameters. Nevertheless, these data clearly demonstrate that the MR-SHARPER experiment has equal quantitative value to the standard 1D pulse-acquire experiment and is a good solution to reaction monitoring in cases where inhomogeneity and other factors reduce resolution and sensitivity of NMR experiments.

Fig. 12 Absolute integrals measured for protodeboronation of 1 measured using interleaved 1D ¹⁹F pulse-acquire and ¹⁹F MR-SHARPER experiments. See ESI† for determination of k_obs and discussion of measurements of integrals for the off-resonance signal.

Conclusion

We have shown that the previously reported SHARPER experiment can be extended to more than one resonance simultaneously through use of a precise timing of acquisition intervals, which is both sample and spectrometer frequency specific. This is demonstrated for the common case where two signals are of interest, e.g. from a product and a reactant.

The advantages of the SHARPER experiment over simple 1D spectra, which make it desirable for reaction monitoring, are retained in MR-SHARPER. Compensation for magnetic field inhomogeneity and refocussing of scalar couplings results in signal-to-noise ratios significantly greater than is possible for regular 1D spectra; this is achieved without a requirement to pulse on any nuclei or resonance other than those being acquired.

Experimental

NMR experiments described in the Off-Resonance SHARPER section were acquired using a sample of Neat 99% D₂O (Sigma) using a 500 MHz spectrometer equipped with a DCH Cryoprobe.

The mutarotation of glucose was measured for 24.8 mg 99% α-D(+)-glucose (Acros Organics) in 0.6 ml D₂O at 27 °C. The protodeboronation of 1 was measured for 4.9 mg of 2,6-difluoro-4-methoxyphenylboronic acid, 1 (provided by Lloyd-Jones research group, University of Edinburgh) in 0.7 ml 1 : 1 water : 1,4-dioxane solvent with a final concentration of 0.2 M potassium hydroxide at 27 °C. NMR experiments described in the mutarotation of glucose and protodeboronation sections were acquired using a three-channel 400 MHz Bruker Avance III NMR spectrometer equipped with a 5 mm z gradient BB TBO ¹H, ¹⁹F probe.

The full experimental and processing parameters for the NMR spectra measured are provided in the ESI.† The Python scripts for calculation of Δ values require Python2.7 with Numpy and SciPY modules. Scripts as well as the matrices required to use them with Topspin 3.6 equipped spectrometer are included in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. D. thank C4X Discovery and the EPSRC National Productivity Investment Fund (NPIF) for Doctoral Studentship funding.

EPSRC (Grant Reference EP/S016139/1) provided financial support of this work. Instrument support was in part provided by the EPSRC grant EP/R030065/1.

References

1. M. Hall, J. C. Chouler, A. Codina, P. T. Gierth, J. P. Lowe and U. Hintermair, Catal. Sci. Technol., 2016, 66, 8406–8417.
2. M. H. Levitt, Spin Dynamics: Basics of Nuclear Magnetic Resonance, John Wiley & Sons, 2013.
3. M. V. Gomez and A. de la Hoz, Beilstein J. Org. Chem., 2017, 13, 285–300.
4. A. B. Jones, G. C. Lloyd-Jones and D. Uhrín, Anal. Chem., 2017, 89, 10013–10021.
5. L. Bliumkin, R. Dutta Majumdar, R. Soong, A. Adamo, J. P. Abbatt, R. Zhao, E. Reiner and A. J. Simpson, Environ. Sci. Technol., 2017, 50, 5506–5516.
6. M. V. Gomez, A. Juan, F. Jiménez-Márquez, A. De La Hoz and A. H. Velders, Anal. Chem., 2018, 90, 1542–1546.
7. F. Gomes, P. F. da Silva, C. M. S. Lobo, M. da Silva Santos and L. A. Colnago, Anal. Chim. Acta, 2017, 983, 91–95.
8. Y. Huang, S. Cao, Y. Yang, S. Cai, H. Zhan, C. Tan, L. Lin, Z. Zhang and Z. Chen, Anal. Chem., 2017, 89, 7115–7122.
9. D. Topgaard, R. W. Martin, D. Sakellariou, C. A. Meriles and A. Pines, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 17576–17581.
10. R. Freeman and H. D. W. Hill, J. Chem. Phys., 1974, 54, 301–313.
11. J. Bocan, G. Pileio and M. H. Levitt, Phys. Chem. Chem. Phys., 2012, 14, 16032–16040.
12. R. Wei, A. M. Hall, R. Behrens, M. S. Pritchard, E. J. King and G. C. Lloyd-Jones, Eur. J. Org. Chem., 2021, 2331–2342.
13. NMR Software Department, Introduction to Bruker NMR Pulse Programming User Manual Version 2, Bruker Corporation, 2016.
14. J. C. Kendrew and E. A. Moelwyn-Hughes, Proc. R. Soc. London, Ser. A, 1940, 176, 352–367.
15. E. Lin, C. J. Yu, C. L. Chen, L. D. Chou and C. Chou, J. Phys. Chem. A, 2010, 114, 1665–1669.
16. P. A. Cox, M. Reid, A. G. Leach, A. D. Campbell, E. J. King and G. C. Lloyd-Jones, J. Am. Chem. Soc., 2017, 139, 13156–13165.

---

Footnote

† Electronic supplementary information (ESI) available: Details of experimental methods, pulse sequences, resulting data and data analysis methods, including links to Github for easier access to code. See https://doi.org/10.1039/d2an00134a

---