Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the dopant induced effects on SFX-MeOTAD for perovskite solar cells: a spectroscopic and computational investigation†
Fraser
Gunn
 a,
Paheli
Ghosh
b,
Michal
Maciejczyk
c,
Joseph
Cameron
a,
Paheli
Ghosh
b,
Michal
Maciejczyk
c,
Joseph
Cameron
 d,
Dennis
Nordlund
e,
Satheesh
Krishnamurthy
d,
Dennis
Nordlund
e,
Satheesh
Krishnamurthy
 b,
Tell
Tuttle
b,
Tell
Tuttle
 f,
Peter
Skabara
f,
Peter
Skabara
 d,
Neil
Robertson
d,
Neil
Robertson
 c and
Aruna
Ivaturi
c and
Aruna
Ivaturi
 *a
*a
aSmart Materials Research and Device Technology (SMaRDT) Group, Department of Pure and Applied Chemistry, University of Strathclyde, Thomas Graham Building, Glasgow, G1 1XL, UK. E-mail: aruna.ivaturi@strath.ac.uk
bSchool of Engineering & Innovation, The Open University, Milton Keynes, MK7 6AA, UK
cEastCHEM, School of Chemistry, University of Edinburgh, King's Buildings, Edinburgh, EH93FJ, UK
dWestCHEM, School of Chemistry, University of Glasgow, Joseph Black Building, University Place, Glasgow, G12 8QQ, UK
eStanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, Menlo Park, CA 94025, USA
fStrathclyde Computational and Theoretical Chemistry (ScoTCH) Hub, Department of Pure and Applied Chemistry, University of Strathclyde, Thomas Graham Building, Glasgow, G1 1XL, UK
First published on 12th October 2021
Abstract
SFX-MeOTAD [2,2′,7,7′-tetrakis(N,N-di(4-methoxyphenyl)amino)-spiro-(fluorene-9,9′-xanthene)] (also known as X60) has emerged as a cost-effective alternative to the ubiquitous, but excessively-expensive, spiro-MeOTAD hole transport material (HTM) in perovskite solar cells. Using its pre-oxidised dicationic salt, SFX-(TFSI)2, a controlled concentration dependent conductivity tuning of this HTM without the requirement of air (oxygen) exposure has been carried out. This study details the modifications in the optical and electrical properties of this low cost HTM as a function of the concentration of the dicationic salt (0–100 mol%) using UV-vis absorption and electrical conductivity measurements. X-ray absorption and photoelectron spectroscopy investigations have been carried out to elucidate the role of the dicationic salt in the enhanced electronic properties of SFX-MeOTAD. By incorporating the dicationic SFX-(TFSI)2 it has been shown that the conductivity of SFX-MeOTAD increased by 4 orders of magnitude from 2.55 × 10−8 S cm−1 to 9.4 × 10−4 S cm−1 when using an optimal dopant concentration of 20.5 mol%. The degree of oxidation of SFX-MeOTAD was determined through UV-vis absorption and consolidated using the computational calculations. The XPS study reveals that doping SFX-MeOTAD with SFX(TFSI)2 not only results in the oxidation of the HTM but also leads to a variation in the local chemistry around carbon and nitrogen which directly influences the conductivity of the doped films. NEXAFS studies indicate that doping enhances the aromatic nature of the molecule initially but increasing the dopant concentration further affects the aromaticity and possibly the π stacking, similar to the trend seen in dopant concentration dependent conductivity of the SFX-MeOTAD films. These findings have implications on the choice of dopant concentration and counterions more generally for triarylamine based HTMs.
1. Introduction
Perovskite solar cells (PSCs) evolved from dye-sensitised solar cells (DSSCs) after Kojima et al. utilised a lead halide perovskite as a sensitiser in the DSSC.1 Following on from this, there has been a surge of research interest in PSCs due to their extraordinary material properties e.g. tuneable bandgap of the absorber material, long charge carrier diffusion lengths and lifetimes and lower production costs due to easy manufacturing via solution processing.2,3 To date, the highest power conversion efficiency (PCE) recorded for PSCs is 25.5%.4 Perovskites are ambipolar in nature and hence can be used in different device architectures.5 PSCs are layered devices that contain the perovskite absorber sandwiched between an n-type electron transport layer (ETL) and a p-type hole transport layer (HTL). The role of the hole transport layer is to transport the photogenerated holes, increase selectivity and reflectivity of the top contact and increase the internal quantum efficiency of the PSC.6 An appropriate hole transport material (HTM) must meet certain criteria such as high thermal stability, optimum energy level alignment with the perovskite material and good solubility for solution processing.7One of the most common HTMs used in PSCs is 2,2′,7,7′-tetrakis[N,N-di(4-methoxyphenyl)amino]-9,9′-spirobifluorene (spiro-MeOTAD); however, it has a relatively low conductivity with values varying between 2 × 10−8 S cm−1 and 2.5 × 10−7 S cm−1 reported in the literature.8,9 In order to improve its conductivity chemical dopants are used. These dopants are p-type and are used to increase the concentration of the charge carriers which in turn increases the conductivity of the HTM.10–15 The most prevalent dopant used in spiro-MeOTAD is lithium bis(trifluoromethanesulfonyl)imide (LiTFSI). LiTFSI, however, does not directly oxidise spiro-MeOTAD, and after mixing, the HTM must be exposed to the air in order to be oxidised.16,17 This is an issue as it is difficult to control and regulate the degree of the oxidation of the spiro-MeOTAD. The production of unpredictable variations of the oxidised spiro-MeOTAD has been shown to have an effect on the repeatability/reproducibility of PSC performance and stability.8 LiTFSI also promotes pinhole formation in spiro-MeOTAD, which has detrimental effects on the performance of PSC (e.g. PSCs without pinholes in the HTL are shown to have 10 times longer life time than those with pinholes).18,19 Applying other dopants such as cobalt complexes tris(2-(1H-pyrazol-1-yl)pyridine)cobalt(III) tri[bis(trifluoromethane)sulfonimide] (FK102) and tris(2-(1H-pyrazol-1-yl)-4-tert-butylpyridine)cobalt(III)tri[bis(trifluoromethane)sulfonimide] (FK209), benzoyl peroxide (BPO) and H3PO4, also does not result in the direct oxidation of spiro-MeOTAD and requires co-doping with LiTFSI. These dopants form the spiro-MeOTAD radical cation; however, for an effective charge generation a TFSI counter anion is required.10–13,16 Other p-type dopants are metal complexes. One such example is the copper(II) complex, bis[2,2′-(chloromethylene)-dipyridine]copper(II) bis[bis(trifluoromethylsulfonyl)imide] [Cu(bcpm)2], in which the TFSI counter anion is used to increase the solubility of the Cu(II) complex in organic solvents.14 Another metal complex used is molybdenum tris(1-(trifluoroacetyl)-2-(trifluoromethyl)ethane-1,2-dithiolene) [Mo(tdf-COCF3)3] which exhibits reversible reduction to its stable monoanion. This monanion oxidises spiro-MeOTAD to its monocation and without the requirement of LiTFSI.15 Introducing a pre-oxidised form of spiro-MeOTAD, 2,2′,7,7′-tetrakis[N,N-di(4-methoxyphenyl)amino]-9,9′-spirobifluorene di[bis-(trifluoromethanesulfonyl)imide] i.e. spiro-(TFSI)2, has been demonstrated to remove the requirement of air exposure and hence addresses the unpredictability of producing different variations of oxidised spiro-MeOTAD.8 Spiro-MeOTAD is also costly due to the tedious multistep synthesis of the spiro core, thus explaining why no large-scale commercial deployments of perovskite solar cells using this HTM exist.20 An alternative HTM that contains a spiro[fluorene-9,9′-xanthene] core obtained from one-pot reaction of fluorenone and phenol in the presence of methane sulfonic acid without any solvent, is SFX-MeOTAD [2,2′,7,7′-tetrakis(N,N-di(4-methoxyphenyl)amino)-spiro-(fluorene-9,9′-xanthene), shown in Fig. 1(a)] which is five times more cost effective than spiro-MeOTAD.21 SFX-MeOTAD (also referred to as X60 in the literature) has been demonstrated to be a suitable HTM candidate for PSCs with efficiencies ranging from 12.4% to 19.8% by using different perovskite absorbers and electron transport layers in the n-i-p device architecture.21–23 The dicationic salt of SFX-MeOTAD, SFX-(TFSI)2, shown in Fig. 1(b), has also been explored recently as a dopant and has shown promise with the conductivity increasing by two orders of magnitude with an increase in dopant concentration from 0–20 mol%, and efficient devices with PCEs of 19% have been reported.24 In the present study a detailed analysis of the optical and electrical properties of SFX-MeOTAD as a function of the dicationic salt SFX-(TFSI)2 dopant concentration has been extended to cover a wide range (0–100 mol%). To understand the role of SFX-(TFSI)2 in the oxidation of SFX-MeOTAD, resulting in the observed modifications in the electrical and optical properties, detailed X-ray photoelectron spectroscopy (XPS) and near edge X-ray absorption fine structure spectroscopy (NEXAFS) of the doped and undoped thin film samples have been carried out. To investigate the molecular structure, and the electronic and optical properties of the neutral SFX-MeOTAD and its various oxidised forms, density functional theory (DFT) and time-dependent density functional theory (TD-DFT) calculations have been carried out, revealing excellent correlation between the experimental observations and theoretical calculations.
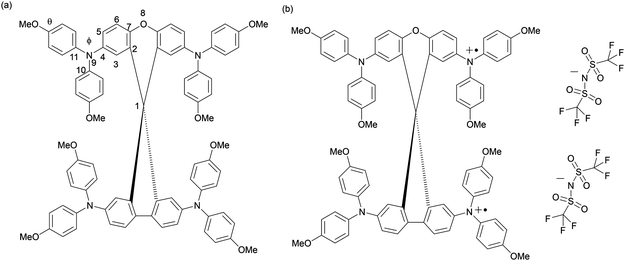 | ||
| Fig. 1 (a) Chemical structure of SFX-MeOTAD with main geometries; (b) chemical structure of SFX-(TFSI)2. | ||
2. Experimental
2.1 Synthesis of SFX-MeOTAD and SFX-(TFSI)2
Synthesis of SFX-MeOTAD was carried out as reported in the literature.21 Synthesis of SFX-(TFSI)2 was similar to that of spiro(TFSI)2 as reported by Nguyen et al.8 Briefly, SFX-MeOTAD and silver bis(trifluoromethanesulfonyl)imide were mixed in dry dichloromethane under nitrogen. The mixture was stirred for 24 hours at room temperature. The resulting mixture was then diluted with methylene chloride, filtered and the solvent was removed by rotary evaporation. The residual solid was dissolved in dichloromethane and then precipitated in dry diethyl ether twice. The resulting powder was dried under vacuum and the composition was confirmed by CHN elemental analysis (%): calculated C 56.66, H 3.80, and N 4.66. Result: C 56.50, H 3.68, and N 4.59.2.2. Deposition of SFX(TFSI)2 doped SFX-MeOTAD films
Different concentrations [0–100 mol%] of SFX-(TFSI)2 were mixed with SFX-MeOTAD in anhydrous chlorobenzene to a combined concentration of 0.15 M. To this 0.12 M 4-tert-butylpyridine was added before spin coating on cleaned glass (for absorbance and conductivity measurements) or FTO coated glass (for XPS and NEXAFS measurements) at 2000 rpm for 1 minute. For conductivity measurements aluminium electrodes (∼80 nm) were deposited by thermal evaporation (∼10−6 mbar) on doped and undoped SFX-MeOTAD thin films coated on glass.2.3. Characterisation techniques
Elemental analyses of SFX-MeOTAD and SFX-(TFSI)2 were carried using a Carlo Erba CE1108 Elemental Analyser. For evaluating the conductivity of the SFX-MeOTAD films doped with varying concentrations of SFX-(TFSI)2 (0–100 mol%), I–V measurements were carried out in the dark inside a N2 filled glovebox via a two-point probe method using a Keithley 4200-SCS Parameter Analyser. For each dopant concentration an average of four I–V measurements has been recorded. The conductivity was evaluated using the inverse of the gradient of the I–V plots, the area between the electrodes and thickness of the films. The film thickness was measured in air using an atomic force microscope (AFM) (Digital Instruments, Dimension 3100) in the tapping mode (using TESPA-V2 probes and Nanoscope III software) with ten measurements per sample used to determine the average thickness. In order to handle the AFM data, WSXM software was used.25 The absorbance of the SFX-MeOTAD thin film samples with different SFX(TFSI)2 doping concentrations (0–100%) was studied using a UNICAM UV 300 spectrophotometer in the range of 290–1100 nm. The electronic properties of the undoped and SFX-(TFSI)2 doped SFX-MeOTAD films were investigated using XPS with a load-locked KRATOS XSAM-800 instrument equipped with a dual anode X-ray source using a Mg Kα (1253.6 eV) excitation source. For C 1s, F 1s, O 1s and N 1s core levels, the photoelectrons were collected using a high magnification analyser more from the smallest possible area on the specimen. CasaXPS version 2.3.16 software was used for analysing the XPS data. NEXAFS experiments were performed at the beam-line 8-2 of the Stanford Synchrotron Radiation Lightsource of SLAC National Accelerator Laboratory.26 The samples were vacuum sealed and packed with molecular sieves during transport to carry out XPS and NEXAFS experiments. The samples were mounted on an aluminium stick with a conductive carbon tape and measurements were performed under ultra-high vacuum conditions (<1 × 10−9 Torr). The energy of the incident beam was calibrated at the carbon dip (284.7 eV) arising from the contaminations in the beamline optics. Beamline slits and the pass energy of the analyser were set to achieve a total energy resolution of 0.3 eV. To eliminate the effects of sample orientation on the intensities of the resonances, the C and N K-edge spectra were acquired in the total electron yield (TEY) mode at 54.7° (magic angle) incidence of the soft X-ray beam between 280.0 to 330.0 eV and 380.0 to 440.0 eV, respectively. The spectra were then normalised to a linear background following the protocol developed by Wang et al.27,28 The incoming flux (I0) was measured using a gold mesh in the beamline and the signal was divided by the incident flux for normalisation. Pre- and post-edge normalisation were carried out from 275–285 eV and 320–330 eV for the C K-edge and the edge jump was normalised to unity. C and N K-edge NEXAFS spectra of the pristine SFX-MeOTAD and SFX-(TFSI)2 doped SFX-MeOTAD films were probed individually to understand the variations in the electronic properties as a function of dopant concentration.2.4. Computational details
The molecular structures of SFX-MeOTAD and its oxidised forms i.e. SFX-MeOTAD+, SFX-MeOTAD2+ and SFX-MeOTAD4+ were optimised in chlorobenzene solvent using the PBE0 functional and the 6-311G(d,p) basis set.29,30 The calculations were carried out using Gaussian 16.31 The solvation model used in the calculations was the default IEF-PCM solvation model.32 The changes in the electronic structure and the absorption spectra, which are instigated by the oxidation from SFX-(TFSI)2, was investigated using the TDDFT calculations that also employed the PBE0 functional and the 6-311G(d,p) basis set. The solvation model used was the default IEF-PCM model in chlorobenzene. For all the species, 60 excitation states were calculated.3. Results and discussion
3.1 Electrical and optical properties of SFX(TFSI)2 doped SFX-MeOTAD
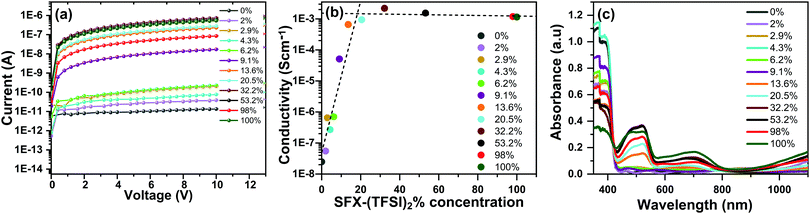
Conductivity values of the SFX-MeOTAD films doped with varying molar percentages of SFX-(TFSI)2 were evaluated from the I–V measurements carried out in the dark inside a N2 filled glovebox using a two-point probe method. As shown in Fig. 2(a) and (b), pristine SFX-MeOTAD has a rather low conductivity of 2.55 × 10−8 S cm−1 and as the molar concentration of SFX-(TFSI)2 is increased, the conductivity improves. At a dopant concentration of 20.5 mol% of SFX-(TFSI)2, the conductivity of SFX-MeOTAD was observed to increase by four orders of magnitude to a value of 9.43 × 10−4 S cm−1. The conductivity values of undoped SFX-MeOTAD reported in the literature lie within a wide range of 1.96 × 10−6 S cm−1 and 1.1 × 10−4 S cm−1, similar to the conductivity values in a wide range reported for undoped spiro-MeOTAD.22,24 It is important to note that, in the present study, the conductivity measurements were carried out in the dark inside the N2 glovebox to avoid any photo-oxidation of SFX-MeOTAD in air. Recent work utilising pre-oxidised SFX-MeOTAD reported in the literature quoted an increase in conductivity by 2 orders of magnitude from 1.96 × 10−6 S cm−1 to 8.84 × 10−4 S cm−1 upon increasing the doping concentration from 0% to 20%.24 A study using spiro-(TFSI)2 doping in spiro-MeOTAD, on the other hand, reported an increase in conductivity by 5 orders of magnitude, increasing from 2 × 10−8 S cm−1 to 1.43 × 10−3 S cm−1 upon increasing the dopant concentration from 0% to 14%.8 This increase in conductivity by 5 orders of magnitude is analogous to the level of conductivity increase that is observed in the present study (from 2.55 × 10−8 S cm−1 to 2.2 × 10−3 S cm−1); however, a higher doping concentration of 32.2 mol% of SFX-(TFSI)2 is required for SFX-MeOTAD. From Fig. 2(b) it was observed that the conductivity increased linearly and started to plateau after 20.5 mol% concentration. Using a linear fit, it was found that the point of inflection lies at ∼20.5 mol%, which is the optimal dopant concentration for SFX-MeOTAD. Fig. 2(c) shows the absorbance spectra of undoped and doped SFX-MeOTAD. The undoped SFX-MeOTAD film has a maximum absorbance at ca. 387 nm and the peak decreases as the concentration of SFX-(TFSI)2 increases. The measured maximum absorbance is in agreement with the previous reported values in the range of 367–388 nm for SFX-MeOTAD.21,22 Spiro-MeOTAD shows absorbance bands at ca. 385 nm showing that SFX-MeOTAD exhibits similar optical properties to spiro-MeOTAD.33 As the concentration of SFX-(TFSI)2 increases, the absorption band at 387 nm decreases, and there is an increase in the bands at around 520 nm and 680 nm. This corresponds to the production of the oxidised radical species [e.g., SFX-MeOTAD+ and SFX-MeOTAD2+].22,24 This phenomenon is also reported in spiro-MeOTAD with peaks appearing at 520–524 nm and 687–690 nm upon oxidation.8,10,14–16,34 When measured on thin films, the absorption peak of spiro-MeOTAD at ca. 522 nm increases as the molar% of spiro-(TFSI)2 increases and there is also an increase in the peak at ca. 700 nm.35 Recently, the absorbance spectrum of spiro-(TFSI)2 single crystals dissolved in acetonitrile was studied in a wide wavelength range (300–2000) and peaks were observed at 371 nm, 521 nm, 691 nm, 908 nm and 1527 nm.36To understand the changes induced by the oxidation process on the electronic structure and absorption spectrum and to optimise the geometries of the possible oxidised species of SFX-MeOTAD, DFT and TD-DFT computational calculations were carried out. The optimised structure of neutral SFX-MeOTAD shows that both the xanthene and fluorene units of the spiro[fluorene-9,9′-xanthene] core are planar, and the appended triarylamine units are not planar, but are in a propeller orientation (see S1 in ESI†). When the neutral SFX-MeOTAD is oxidised to the +1 species it leads to the formation of a doublet ground state and when this is further oxidised to the +2 species an open shell triplet state is formed. The triplet state for the +2 species was calculated to be 7.08 kcal mol−1 more stable than the singlet state. The nature of a possible +4 species that might form in the oxidation process was also calculated and it was found that the triplet state was more stable than the singlet state by 13.97 kcal mol−1 for this oxidation state.
Fig. 1(a) shows the label assignment and the geometrical parameters of the optimised species of SFX-MeOTAD and its oxidised forms (1+, 2+, 4+) are given in Table 1. When the optimised structure of neutral SFX-MeOTAD in vacuo is compared to that in chlorobenzene solvent, as given in Table 1 (column 2 and 3), slight variations in the bond lengths, the dihedral angle (Φ) (which shows the out of plane alterations of the phenyl-OMe groups in relation to the spiro[fluorene-9,9′-xanthene] core), and the angle of the OMe group that protrudes from the phenyl group are observed. Nonetheless, the effect of solvent was anticipated to be significant in the calculated spectra of the oxidised species. Thus, all the DFT and TD-DFT calculations for the oxidised species have been carried out in chlorobenzene solvent. Further investigation shows that there are variations in the geometries of the different oxidised states in the solvent as compared to that in vacuo. As the level of oxidation increases, the spiro[fluorene-9,9′-xanthene] core reacts by constricting the C7–O8 bond (1.365 Å in the neutral species and 1.354 Å in the +4 species). There is also the shrinking of the C1–C2 from the neutral species to the +2 species but the length of the same bond increases when oxidised to +4. The C2–C7 bonds lengthen from neutral to +4. It can however be seen that the C4–N9 bond decreases from neutral to +2 but increases when further oxidised to +4. There is an increase in Φ angle when going from the neutral to +2 but then decreases when going into the +4 state. There was no change in the OMe-phenyl angle when the oxidation state was increased.
| Parametera | Neutral (vacuo) | Neutral (chlorobenzene) | 1+ (chlorobenzene) | 2+ (chlorobenzene) | 4+ (chlorobenzene) |
|---|---|---|---|---|---|
| a Bond lengths are in angstroms and bond angles are in degrees. | |||||
| C1–C2 | 1.528 | 1.523 | 1.520 | 1.520 | 1.530 |
| C2–C3 | 1.395 | 1.396 | 1.396 | 1.388 | 1.391 |
| C2–C7 | 1.389 | 1.389 | 1.390 | 1.393 | 1.393 |
| C3–C4 | 1.389 | 1.392 | 1.392 | 1.400 | 1.394 |
| C4–C5 | 1.400 | 1.403 | 1.403 | 1.408 | 1.402 |
| C4–N9 | 1.415 | 1.408 | 1.407 | 1.392 | 1.411 |
| C5–C6 | 1.380 | 1.380 | 1.379 | 1.375 | 1.376 |
| C6–C7 | 1.395 | 1.394 | 1.395 | 1.396 | 1.396 |
| C7–O8 | 1.362 | 1.365 | 1.363 | 1.359 | 1.354 |
| N9–C10 | 1.416 | 1.414 | 1.415 | 1.416 | 1.403 |
| N9–C11 | 1.409 | 1.414 | 1.413 | 1.414 | 1.393 |
| Φ(C3C4N9C11) | 124 | 142 | 143 | 148 | 139 |
| Θ | 116 | 116 | 116 | 116 | 116 |
An isosurface representation of the molecular frontier orbital of neutral SFX-MeOTAD is shown in Fig. 3 (a full table of energies can be found in the ESI;† see S2). For the neutral species there are two quasi-degenerate highest occupied molecular orbitals (HOMO/HOMO−1) that are delocalised across the fluorene core of the molecule and the triarylamine groups attached (HOMO), and also due to the contribution of the lone pairs on the O atom within the spiro[fluorene-9,9′-xanthene] core, lone pairs from the nitrogen atoms and the phenyl ligands into the top of the molecule (HOMO−1) (see Fig. 3(a)). When going down in energy to the HOMO−2 and HOMO−3 energy levels it can be seen that the orbitals are delocalised within the phenyl ligands and the nitrogen lone pairs contributing to delocalisation (Fig. 3(b)).
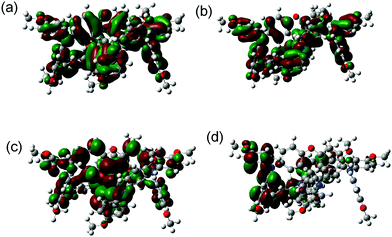 | ||
| Fig. 3 Isodensity plot showing the frontier orbitals of neutral SFX-MeOTAD (a) HOMO/HOMO−1, (b) HOMO−2/HOMO−3, (c) LUMO/LUMO+1, and (d) LUMO+10. | ||
The two lowest unoccupied molecular orbitals (LUMO/LUMO+1) show π* character [Fig. 3(c)]; the delocalisation is spread across the spiro[fluorene-9,9′-xanthene] core into the phenyl ligands attached to the xanthene part of the core of the molecule and at higher energy levels, such as LUMO+10, the orbitals are localised in the outer N-phenyl-OMe ligands (Fig. 3(d)). The HOMO energy level was calculated to be −4.87 eV and is in good accordance with both the experimental and other computational values reported for SFX-MeOTAD (experimental value of −5.16 eV and computational values of −5.11 eV and −5.61 eV).22,24,37 Deng et al. also calculated the HOMO of SFX-MeOTAD using different functional methods of BMK, PBE0, B3LYP, CAM-B3LYP, M06 and M06-2X, all using the 6-31G(d) basis set. In their study, the BMK method was explored in detail as it was found to give a value close to that measured experimentally; however, the method led to an energy gap of 4.87 eV (largest reported for SFX-MeOTAD). B3LYP and M06-2X gave values for the HOMO for SFX-MeOTAD at −4.55 eV and −5.87 eV.38 The LUMO ranged from −0.28 eV to −1.05 eV using the different functional methods mentioned above.38 Additionally, there have been reports with the LUMO determined to be 0.48 eV, −1.15 eV and −2.56 eV.22,24,37 The HOMO–LUMO gap was calculated to be 3.85 eV computationally and using the absorbance onset for pristine SFX-MeOTAD from Fig. 2(c) the experimental HOMO–LUMO gap was calculated to be 2.96 eV. The HOMO–LUMO gaps of SFX-MeOTAD have been determined experimentally in other studies to be 2.96 eV and 3.05 eV21,22 and computationally the energy gaps have been calculated to be 3.10 eV and 5.45 eV.37,38
When oxidised to the +1 i.e. SFX-MeOTAD+ species, a doublet ground state is formed and the orbitals within this are split into α and β manifolds that have different spatial wave functions and so this results in different energies for each manifold as seen in Fig. 4. The HOMO in the α manifold is stabilised by 0.74 eV with respect to its β manifold counterpart and is almost degenerate and corresponds to the HOMO−1 of the neutral species. It can be seen that the HOMO and LUMO gap in the α manifold is 3.33 eV. An electron has been removed from the β orbital and so contains the HOMO–LUMO of the monocation species which are delocalised in the spiro[fluorene-9,9′-xanthene] core and the (N-phenyl-OMe)2 ligands that protrude from the core. The +2 species, i.e. SFX-MeOTAD2+, is in a triplet state that has two singly occupied orbitals in the α manifold that are quasi-degenerate with a HOMO–LUMO gap of 3.77 eV. The HOMO/HOMO−1 in the α manifold is now localised similarly to the HOMO/HOMO−1 of the neutral SFX-MeOTAD species but there is more localisation of the orbitals in one of the N-phenyl-OMe ligands that is part of the xanthene core than the other. The LUMO of the α manifold corresponds to the LUMO of the neutral and +1 species as the orbitals are localised in the fluorene part of the spiro[fluorene-9,9′-xanthene] core. The HOMO/HOMO−1 shows that the orbitals are localised in half of the SFX-MeOTAD molecule and the LUMO shows localisation similar to the LUMO of the monocation and neutral species. Within the β manifold, the HOMO/HOMO−1 has the same nature as the HOMO−1/HOMO−2 of the neutral species whereas the LUMO/LUMO+1 corresponds to the HOMO/HOMO−1 of the neutral SFX-MeOTAD. The +4 species, i.e. SFX-MeOTAD4+, exists in a triplet state, which is more favourable than the singlet state for this species. This gives rise to two singly occupied molecular orbitals and a gap of 1.66 eV between the HOMO and HOMO−1 in the α manifold. These have a character that is similar to the HOMO/HOMO−1 of the neutral, although there is more delocalisation of the orbital in one of the triarylamine branches of the lower fluorene section of the central core than the other. The HOMO–LUMO gap of the α manifold was calculated to be 2.28 eV. In the β manifold, the HOMO−3 where the electron sits lies 1.72 eV lower than the HOMO−2 orbital (see S3, ESI† for the HOMO–LUMO frontier orbitals of each oxidation state in the α and β manifolds).
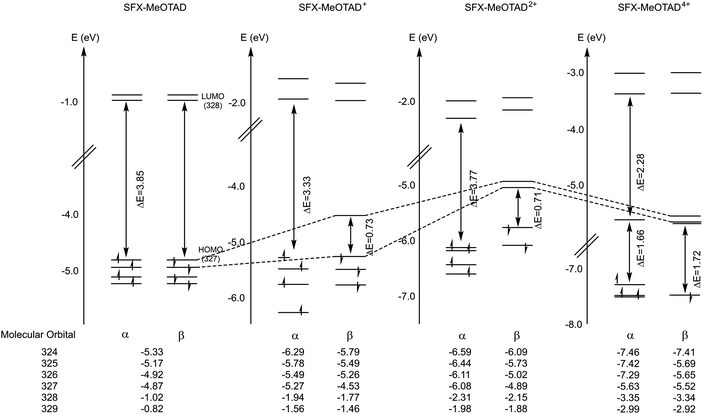 | ||
| Fig. 4 Schematic representation of the molecular frontier orbitals of SFX-MeOTAD and its oxidised species with orbital energies given below in eV. | ||
There has always been a great interest in the optical properties of doped HTMs to ascertain the oxidation states that contribute to particular absorptions. Fig. 5 gives a comparison of the experimental and computational absorption spectra of undoped (neutral) SFX-MeOTAD. The calculated spectrum (red curve in Fig. 5) showed an absorption maximum at 400 nm compared to the experimentally measured 367 nm in chlorobenzene solution (magenta curve in Fig. 5) and 387 nm when measured on a thin film (blue curve in Fig. 5), providing reasonable agreement (red shifted by 0.28 eV compared to solution and 0.10 eV compared to the thin film) between the calculated and experimental bands. The absorbance of SFX-MeOTAD in its neutral state has been investigated by Deng et al. with maximum reported at 348 nm and 403 nm using different functional methods.38 Sun et al. carried out a study using the PBE33 method and the 6-31G* basis set for SFX-MeOTAD and maximum absorbance was reported at 346 nm in agreement with the value obtained in the present study.37 Other experimental absorption maxima values of 367 nm in dichloromethane21 and 389 nm in toluene solvent22 have been reported, whereas for thin film it has been reported at 358 nm.23 It has been reported that SFX-MeOTAD also absorbs at ca. 300 nm.22 In this study, though this was not observed in the thin film experimental UV-vis measurements, a peak was observed at 308 nm in the experimental solution measurements. When compared to the computational value of 308 nm, there is no deviation between the experimentally measured value and the absorbance observed computationally. This peak was not observed in the thin film samples as the thin films were deposited on glass substrates. However, a small absorbance between ca. 500–600 nm and 700–800 nm was observed in the measured absorbance curve of the SFX-MeOTAD film without any added SFX(TFSI)2 (blue curve in Fig. 5), which is associated with photo-doping in the presence of oxygen that might have occurred during transferring the samples from the glovebox to the UV-vis spectrophotometer. In the solution samples, a small peak is observed at ca. 890 nm for all solution samples, but this is possibly due to debris interfering with the beam inside the spectrophotometer.
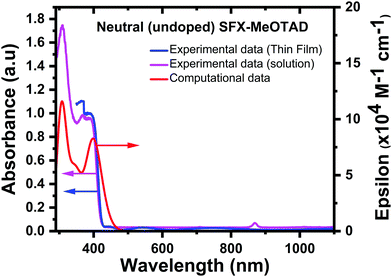 | ||
| Fig. 5 Comparison of experimental [thin film (blue) and solution (magenta)] and computational absorption spectra (red) for neutral (undoped) SFX-MeOTAD. | ||
From the calculated TD-DFT eigenvalues the transitions that are involved in the band centred at 400 nm are from the HOMO to the LUMO and show strong local excitation character and also correspond to π–π* transitions. Whereas the transitions from the HOMO/HOMO−1 to the LUMO+11 and LUMO+8 result in a peak at 308 nm with a predominant charge transfer (CT) character but also some local excitation character at one of the triarylamine groups bonded to the xanthene part of the core and both triarylamine groups attached to the fluorene part of the core. This peak was found to be more intense than that found at 400 nm (see S4, ESI† for all MO isodensity plots of transitions mentioned).
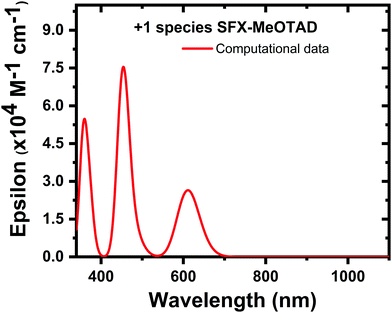
In addition to this, the experimental and calculated spectra of the +2 species were compared and benchmarked with each other. The spectrum of the pristine SFX-(TFSI)2 dicationic salt is shown in Fig. 6. Computationally it was shown the peaks that correspond to this species appear at 389 nm, 459 nm and 681 nm. From analysing the TD-DFT eigenvalues, it can be inferred that the transition from low-lying HOMO orbitals HOMO−13 to the LUMO+1 in the β manifold corresponds to the 459 nm peak. Transitions in the α manifold, HOMO−1 to the LUMO also corresponds to the band at 459 nm, whereas the transitions from the HOMO−7/HOMO−5 orbitals to the LUMO/LUMO+1 correspond to the band at 681 nm in the β manifold. These transitions show π–π* character and predominantly local excitation character but there is some partial CT character. Further analysis of the eigenvalues shows that a transition from the HOMOα to the LUMO+3α corresponds to the peak at 389 nm with a mixture of local excitation and CT character. When comparing this to the experimental data, which show an absorbance peak at 386 nm, there is a very good correlation between the experimental and computational values. The experimental spectrum shows peaks at 520 nm and 703 nm, which again provides good agreement between the calculated (blue shifted by 0.3 eV for peaks found at ca. 500 nm and <0.1 eV for the peaks at ca. 700 nm) and experimental thin film bands. When measured in solution, the absorbance bands were measured as ca. 350 nm, 524 nm and 709 nm (0.35 eV blue shifted, 0.33 eV red shifted, and 0.07 eV red shifted compared to the computational results, respectively). In all cases, the difference between the calculated and experimental bands is within the limits of accuracy of the TD-DFT approach for the PBE0 method (ΔE = ± 0.2–0.3 eV for singlet excitations and up to 0.5 eV for triplet excitations).39 The intensities of the calculated bands after 400 nm (red line, Fig. 6) are the same as the experimental UV bands (blue line, Fig. 6). An opposite behaviour was observed in the simulated absorption spectrum of spiro-MeOTAD as compared to the experimentally obtained UV-vis absorbance.40 As shown by Zhang et al., the +2 oxidation state of spiro-MeOTAD can absorb around 2000 nm.36 This behaviour was also observed in the SFX-MeOTAD2+ calculations, where a peak was observed at 1937 nm and corresponds to the transitions between the HOMO−1β orbital and the LUMO+1β orbital (see S5, ESI† for visualised MO transitions for SFX-MeOTAD2+). This band was not able to be measured experimentally due to the limitations of the equipment.39
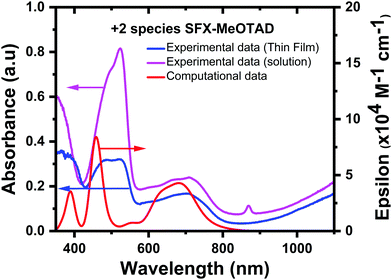 | ||
| Fig. 6 Comparison of experimental [thin film (blue) and solution (magenta)] and computational absorption (red) spectra for SFX-MeOTAD2+. | ||
When doping SFX-MeOTAD with the dicationic salt of SFX-MeOTAD the following mechanism is assumed to take place, in analogy to spiro-MeOTAD:35
| SFX-MeOTAD2+ + SFX-MeOTAD → 2SFX-MeOTAD+ |
From the above experimental and calculated data and using the equation for oxidising SFX-MeOTAD with a dicationic salt we can extrapolate that as we increase the concentration of the dicationic salt, for concentrations that are below 50% dopant, all the SFX-(TFSI)2 is utilised to convert the neutral SFX-MeOTAD to the monocation so this gives rise to an increase in the intensity of the peak found at ca. 522 nm. At concentrations over 50%, there is an excess of the dication; therefore, this describes the increase in the band ca. 680 nm. This means that for the optimal dopant concentration of 20.5%, all of the dicationic salt is used to convert the neutral SFX-MeOTAD to the SFX-MeOTAD monocation. Using the redox potentials known for SFX-MeOTAD, the doping efficiency of the optimal dopant mol% can be found.21 Combining neutral SFX-MeOTAD and the dicationic salt would result in a compositional mixture containing the neutral, monocation and dication species at equilibrium. The equilibrium constant of the redox reaction was calculated using the Nernst equation and thus the contribution of each species can be calculated. See S10 in the ESI† for the full calculation. From the calculation, a solution that initially contained neutral SFX-MeOTAD and 20.5 mol% SFX-(TFSI)2 should have almost no dication species at equilibrium. The final concentrations of the individual species in this optimal dopant mol% are 59.08%, 40.84% and 0.08% for neutral, monocation and dication, respectively. Taking this into account we were able to create a computational absorption spectrum, using the oscillator strengths and their corresponding wavelengths, for the 20.5% doped sample (redline, Fig. 8). See S7–S9 in the ESI† for a full list of oscillator strengths and the corresponding orbital contributions. The calculated maximum absorption bands were found to be 389 nm, 459 nm and 681 nm. When compared to the experimental data (thin film (blue) and solution (magenta), Fig. 8), these values are in excellent agreement as the difference between the calculated and experimental bands are within the limits of accuracy of the TD-DFT approach (band 1 ΔE = ±0.16 eV (solution), ΔE = ±0 eV (thin film); band 2 ΔE = ±0.32 eV (solution), ΔE = ±0.32 eV (thin film) and band 3 ΔE = ±0.07 eV (solution), ΔE = ±0.05 eV (thin film)).39 As mentioned above, a simplistic picture proposed earlier for spiro-MeOTAD was assumed to be true for SFX-MeOTAD as well, where it is assumed that all the dicationic salt is used to convert SFX-MeOTAD into its monocation. However, conversion of SFX-MeOTAD2+ to SFX-MeOTAD4+, as proposed by Zhang et al.,36 cannot be ruled out. DFT and TD-DFT computational calculations were also carried out for the +4 triplet, and the absorbance maxima were found at ca. 630 nm and ca. 760 nm. These peaks were not seen in the experimental data of the doped samples [Fig. 2(c)]; therefore, we can assume that +4 SFX-MeOTAD is not present in the measured films.
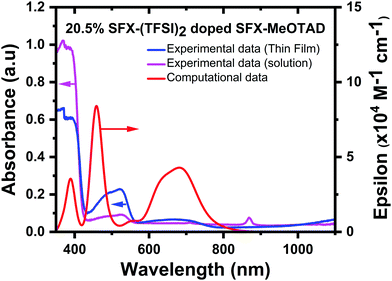 | ||
| Fig. 8 Comparison of experimental [thin film (blue) and solution (magenta)] and computational absorption spectra (red) for 20.5% SFX-(TFSI)2 doped SFX-MeOTAD. | ||
3.2 Electronic properties of SFX(TFSI)2 doped SFX-MeOTAD
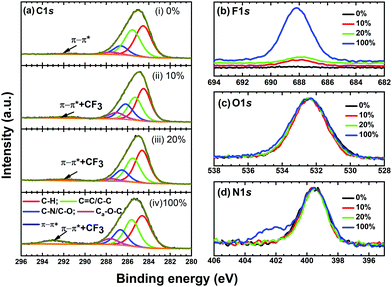
X-Ray photoelectron spectroscopy (XPS) is a highly surface-sensitive, element-specific technique which is used to probe the variation in local chemistry around the carbon, nitrogen and oxygen atoms as a result of the nearest-neighbour interaction during the doping of SFX-MeOTAD with different concentrations of SFX(TFSI)2. High resolution core level XPS spectra were acquired and deconvoluted to understand the effect of the dopant and mechanism of dopant–HTM interaction. Fig. 9 compares the (a) C 1s, (b) F 1s, (c) O 1s and (d) N 1s core level XPS spectra of pristine SFX-MeOTAD [0%], SFX-MeOTAD doped with 10 mol% SFX(TFSI)2 [10%], and 20 mol% SFX(TFSI)2 [20%] and the dopant SFX(TFSI)2 [100%]. The C 1s spectra of all the samples have been deconvoluted into five components each as shown in Fig. 9(a), namely C–H, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/C–C, C–N/C–O, Ca–O–C, and π–π* at 284.5 ± 0.1 eV, 285.5 ± 0.1 eV, 286.4 ± 0.2 eV, 287.3 ± 0.3 eV and 291.5 eV, respectively, corresponding to the peak position for spiro-MeOTAD.18 The peak at 285.5 eV is expected to have a contribution from both sp2 and sp3 hybridised carbon since the disorder-induced peak (sp3) occurs at a 0.5 eV higher binding energy than the graphitic (sp2) peak41 but cannot be resolved using the 0.9 eV resolution XPS equipment used in this study. The 287.3 eV peak has a contribution from both C–N and C–O bonds whereas the π–π* plasmon feature, which originates from the delocalisation of electron density over the carbon atoms and is a signature of the aromatic nature of the molecule, is reported at ∼291.5 eV. In SFX(TFSI)2 doped SFX-MeOTAD samples, broadening of the 291.5 eV peak can also be attributed to the presence of the CF3 groups in the TFSI anions since it has not been possible to deconvolute the effect of π–π* and CF3. The fitting parameters extracted from the core level XPS spectra of pristine and SFX-(TFSI)2 doped SFX-MeOTAD are summarised in Table S11 in the ESI.† A decrease in the percentage of the C–H component is observed from pristine SFX-MeOTAD (46.7%) to 10 mol% doped sample (41.4%) before increasing again in the case of 20 mol% (45.4%), whereas pure SFX(TFSI)2 records the lowest C–H percentage at 41.2%. The initial reduction in the C–H component is attributed to the air-exposure of the samples prior to measurements being undertaken as in the case of spiro-OMeTAD.18 There is negligible variation in the C
C/C–C, C–N/C–O, Ca–O–C, and π–π* at 284.5 ± 0.1 eV, 285.5 ± 0.1 eV, 286.4 ± 0.2 eV, 287.3 ± 0.3 eV and 291.5 eV, respectively, corresponding to the peak position for spiro-MeOTAD.18 The peak at 285.5 eV is expected to have a contribution from both sp2 and sp3 hybridised carbon since the disorder-induced peak (sp3) occurs at a 0.5 eV higher binding energy than the graphitic (sp2) peak41 but cannot be resolved using the 0.9 eV resolution XPS equipment used in this study. The 287.3 eV peak has a contribution from both C–N and C–O bonds whereas the π–π* plasmon feature, which originates from the delocalisation of electron density over the carbon atoms and is a signature of the aromatic nature of the molecule, is reported at ∼291.5 eV. In SFX(TFSI)2 doped SFX-MeOTAD samples, broadening of the 291.5 eV peak can also be attributed to the presence of the CF3 groups in the TFSI anions since it has not been possible to deconvolute the effect of π–π* and CF3. The fitting parameters extracted from the core level XPS spectra of pristine and SFX-(TFSI)2 doped SFX-MeOTAD are summarised in Table S11 in the ESI.† A decrease in the percentage of the C–H component is observed from pristine SFX-MeOTAD (46.7%) to 10 mol% doped sample (41.4%) before increasing again in the case of 20 mol% (45.4%), whereas pure SFX(TFSI)2 records the lowest C–H percentage at 41.2%. The initial reduction in the C–H component is attributed to the air-exposure of the samples prior to measurements being undertaken as in the case of spiro-OMeTAD.18 There is negligible variation in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/C–C component upon the addition of 10 mol% dopant but the contribution of carbon bonded to carbon increases from 29.9% for undoped SFX-MeOTAD to 33.7% for 20 mol% doped sample, which is possibly due to the complex formation between SFX-MeOTAD and SFX(TFSI)2 dopant or oxidised SFX-MeOTAD+ species. The increase in the C–N/C–O component from SFX-MeOTAD to 10 mol% SFX(TFSI)2 sample before reducing for 20 mol% SFX(TFSI)2 sample can be corroborated with the variation in local chemistry due to the additional nitrogen environment from SFX(TFSI)2 dopant and follows the N K-edge resonances as will be discussed later. The increase in % concentration of the aromatic carbon Ca–O–C component initially upon doping with 10% SFX(TFS)2 could be an indication of the oxidation of molecules.42 As can be observed from the overlaid F 1s spectra in Fig. 9(b), pristine SFX-MeOTAD [0 mol%] shows no signature of F 1s whereas 10 mol%, 20 mol% and 100 mol% [or pure SFX(TFSI)2] show an additional peak at ∼688.0 eV which can be attributed to the CF3 groups in the TFSI anions. As can be observed from Fig. 9(a)(iv), SFX(TFSI)2 shows the presence of a strong CF3 signature which can be attributed to the TFSI groups in the dopant. The intensity of CF3 decreases in the doped samples since they are expected to contain 10 mol% and 20 mol% of the TFSI groups as compared to 100 mol% in SFX(TFSI)2. The O 1s spectra of SFX-MeOTAD and SFX-MeOTAD doped with different concentrations of SFX(TFSI)2 are compared in Fig. 9(c). The O 1s spectra are fitted with one peak at ∼532.4 eV corresponding to the Ca–O species in the samples. The FWHM of O 1s spectra of SFX-MeOTAD and SFX-MeOTAD doped with different concentrations of SFX(TFSI)2 do not show any appreciable variation, though SFX(TFSI)2 dopant shows the highest FWHM at 2.5 eV which can be attributed to the presence of the highest concentration of oxidised SFX-MeOTAD in the sample. Fig. 9(d) shows the overlaid N 1s spectra of SFX-MeOTAD and SFX-MeOTAD doped with different concentrations [10 mol% and 20 mol%] of SFX(TFSI)2 and pure SFX(TFSI)2. The presence of a single peak corresponding to amine nitrogen is observed for SFX-MeOTAD and SFX-MeOTAD doped with different concentrations of SFX(TFSI)2, whereas the pure SFX(TFSI)2 sample shows an additional peak at 402.2 eV corresponding to the oxidised nitrogen component.
C/C–C component upon the addition of 10 mol% dopant but the contribution of carbon bonded to carbon increases from 29.9% for undoped SFX-MeOTAD to 33.7% for 20 mol% doped sample, which is possibly due to the complex formation between SFX-MeOTAD and SFX(TFSI)2 dopant or oxidised SFX-MeOTAD+ species. The increase in the C–N/C–O component from SFX-MeOTAD to 10 mol% SFX(TFSI)2 sample before reducing for 20 mol% SFX(TFSI)2 sample can be corroborated with the variation in local chemistry due to the additional nitrogen environment from SFX(TFSI)2 dopant and follows the N K-edge resonances as will be discussed later. The increase in % concentration of the aromatic carbon Ca–O–C component initially upon doping with 10% SFX(TFS)2 could be an indication of the oxidation of molecules.42 As can be observed from the overlaid F 1s spectra in Fig. 9(b), pristine SFX-MeOTAD [0 mol%] shows no signature of F 1s whereas 10 mol%, 20 mol% and 100 mol% [or pure SFX(TFSI)2] show an additional peak at ∼688.0 eV which can be attributed to the CF3 groups in the TFSI anions. As can be observed from Fig. 9(a)(iv), SFX(TFSI)2 shows the presence of a strong CF3 signature which can be attributed to the TFSI groups in the dopant. The intensity of CF3 decreases in the doped samples since they are expected to contain 10 mol% and 20 mol% of the TFSI groups as compared to 100 mol% in SFX(TFSI)2. The O 1s spectra of SFX-MeOTAD and SFX-MeOTAD doped with different concentrations of SFX(TFSI)2 are compared in Fig. 9(c). The O 1s spectra are fitted with one peak at ∼532.4 eV corresponding to the Ca–O species in the samples. The FWHM of O 1s spectra of SFX-MeOTAD and SFX-MeOTAD doped with different concentrations of SFX(TFSI)2 do not show any appreciable variation, though SFX(TFSI)2 dopant shows the highest FWHM at 2.5 eV which can be attributed to the presence of the highest concentration of oxidised SFX-MeOTAD in the sample. Fig. 9(d) shows the overlaid N 1s spectra of SFX-MeOTAD and SFX-MeOTAD doped with different concentrations [10 mol% and 20 mol%] of SFX(TFSI)2 and pure SFX(TFSI)2. The presence of a single peak corresponding to amine nitrogen is observed for SFX-MeOTAD and SFX-MeOTAD doped with different concentrations of SFX(TFSI)2, whereas the pure SFX(TFSI)2 sample shows an additional peak at 402.2 eV corresponding to the oxidised nitrogen component.
The results show that doping with SFX(TFSI)2 not only results in the oxidation of SFX-MeOTAD but also variation in the local chemistry around carbon, oxygen and nitrogen. The studies have been extended to NEXAFS spectroscopy to understand the variation in the electronic properties and structural variation in SFX(TFSI)2 doped SFX-MeOTAD.
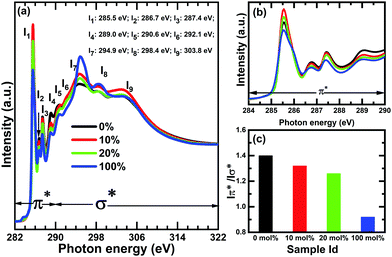
Fig. 10 shows the C K-edge spectra of undoped SFX-MeOTAD, SFX-MeOTAD doped with 10% and 20% SFX(TFSI)2 dopant and 100% of the dopant SFX(TFSI)2. The spectra are dominated by sharp π* and σ* resonances around 285.0 eV and 292.0 eV, respectively.43–48 The molecular orbital diagram shows that π* resonances occur due to the transitions from the core level to the unoccupied antibonding π molecular states (1s → 2p), whereas the σ resonances occur because of the transitions of core electrons to different antibonding σ molecular states. Five π* resonances at 285.6, 286.7, 287.4, 289.0 and 290.6 eV and four σ* resonances at 292.1, 294.4, and 298.6 along with a broad band at 303.0 eV are observed.
The I1, I2, I4 and I5 resonances can be assigned to the transitions from the C2,3 → π1*(a2) and C2,3,4 → π2*(b1), C1 to the π2*(b1), C2,3,4 to π3* and C1 → π3*(b1) orbitals, respectively. Resonance I3 at 287.5 eV has contribution from C 1s → π*(C–H) with some σ*C–H/3p Rydberg-like excitations (details of the assignments provided in Table S12 in the ESI†).49 The resonance between 286 and 287.4 eV may have multiple contribution from N-substituted aromatic C which is often reported to be overlapped with the oxygen moieties.50–52 Significant broadening of the π* resonances, the low atomic concentration of nitrogen and the overlap with the C–O features, may result in lack of any clear signature of C–N at the C K-edge spectra. Table S7 (ESI†) summarises the peak positions and assignments of the C K-edge NEXAFS resonances of SFX-MeOTAD and SFX-MeOTAD doped with SFX(TFSI)2.
The C K-edge spectra of SFX-MeOTAD, SFX-MeOTAD doped with different concentrations of SFX(TFSI)2 and pure SFX(TFSI)2 consist of the same number of absorption bands which have close energy positions but variation in intensities is clearly discernible [Fig. 10(a)]. This intensity variation stems from the change in the π* and σ* states of SFX-MeOTAD upon doping with SFX(TFSI)2. The strong interaction between the localised π* and σ* states in aromatic molecules gives rise to significantly separated energy and two or more degenerate states, resulting in splitting of the π* antibonding orbitals. Intensity of the first π* feature increases significantly upon using SFX(TFSI)2 as a dopant compared to pristine SFX-MeOTAD as observed from Fig. 10(b) which is also evident from the increase in the Iπ*/Iσ* ratio from 100% at 0.92 to 1.32 for the 10% sample [Fig. 10(c)]. This would suggest an increase in the aromaticity of the molecules when the pre-oxidised form of SFX-MeOTAD is used as the dopant. However, increasing the concentration of the dopant to 20% affects the Iπ*/Iσ* ratio adversely, evident from a decrease in value to 1.26. Moreover, the Iπ*/Iσ* ratio is reportedly highest at 1.38 for pristine 0% doped samples. It can be proposed that SFX-MeOTAD forms a charge transfer complex with SFX(TFSI)2 during the doping procedure, which probably has several decay channels available for π* transitions due to the electron-donating methoxy groups in undoped samples and the nitrogen-based counterion (TFSI) in the dopant. This results in a decrease in the Iπ*/Iσ* ratio from pristine to doped samples. However, the increase in the dopant concentration possibly results in localisation of the charge density due to enhanced concentration of the TFSI anions, which in turn reduces the π* and σ* intensities. A similar phenomenon is observed in case of spiro(TFSI)2, where intermolecular charge transfer is hindered as well as orbital overlap and π–π interaction due to the anions involved in the molecules.36 Significant broadening of I1 in the case of 100% dopant implies delocalisation of the π* orbitals. The variation in line shape may also suggest the difference in charge transfer in 100% dopant and other doping concentrations. TFSI is a good nitrogen-based counterion as the anionic charge is appreciably delocalised over the bis(sulfonyl) imide moiety. The electron-withdrawing inductive effects of the CF3 groups along with the electron-donating methoxy moieties have a synergistic effect on the charge transfer properties of the dopant resulting in delocalisation of the charge density over the molecules. However, upon using it as a dopant in SFX-MeOTAD, formation of a complex between them may result in the loss of delocalisation of charge carriers, thereby affecting the broadening of I1. The reduction in intensities of I3, I4 and I5 of 10% and 20% doped samples in comparison to undoped 0% sample may be explained in terms of the fact that the presence of an electronegative nearest neighbour to carbon may make the π*e2u molecular orbital non-degenerate which reduces the probability of transitions from C 1s → π*(C–H), C 1s → π3*(C2,3,4) and π3*(C1). The transitions from the C 1s → σ* molecular orbitals give rise to the σ* shape resonances beyond 291.0 eV and are significantly broader as a result of multiple transitions or interaction of the in-plane carbon orbitals. The σ* resonances, I6, I7, I8 and I9 have been assigned to σ*C–C + σ*C–N,53–55 σ1* with contribution from b2g π* shake-up character, σ2* and σ* C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C43,44,56–62 transitions, respectively. The resonance at 292.1 eV may have a contribution from σ*C–F63–66 in the case of 100%, 10% and 20% doped samples. An overall enhancement in the intensity of σ* resonances has been observed upon doping SFX-MeOTAD with SFX(TFSI)2. Thus, it can be proposed that doping SFX-MeOTAD with SFX(TFSI)2 helps in enhancing the aromatic nature of the molecule initially but increasing the dopant concentration further detrimentally affects the aromaticity and possibly the π stacking. The conductivity values of the doped samples follow a similar trend, where the conductivity increases with increase in the dopant concentration till around 20.5 mol% above which it plateaus. This suggests that the choice of counterion of the dopants for HTMs is crucial since the counterions can interact strongly with the oxidised HTM molecules and affect conductivity. So, a wider range of counterions should be explored when optimising the dopants for triarylamine based HTMs. Thus, the choice of counterion is something that needs to be considered when exploring new hole transport materials. This has been observed in some studies reported in the literature. For example, a larger aggregation was observed when Na+ was used as the counterion in conjugated polyelectrolytes containing a π-delocalised backbone with charged pendant groups as compared to the same material having CH3NH3+ counterion. PSCs fabricated utilising these hole transport materials showed that devices made with HTM containing Na+ counterion were around 50% less efficient than devices made using HTM with CH3NH3+ counterion.67 An improvement in hole conductivity and homogeneity was observed in an ionic type HTM containing TFSI− counterions as compared to the same HTM that did not contain the counterions.68 Counterions used in ionic liquids such as PF6−, CF3SO3− and BF4− are also found in conducting polymers used for photovoltaic applications because the counterions are weakly interacting due to a shielded charge.69 A halide counterion (Br−) in the A–D–A type ionic molecule as HTM was compared with the same HTM with TFSI− counterions. It was found that HTMs with the TFSI− counterions showed better performance in PSCs than those with Br− as the counterion. Although devices made with the TFSI− containing HTM exhibited higher efficiencies, the performance of devices using HTM with Br− counterions was still better than that of devices where the HTM did not contain any counterions. This is because the HOMO is located at a deeper energy level due to the high electron withdrawing effect of the quarternarised part of the HTM that helps to modify the HOMO.70
C43,44,56–62 transitions, respectively. The resonance at 292.1 eV may have a contribution from σ*C–F63–66 in the case of 100%, 10% and 20% doped samples. An overall enhancement in the intensity of σ* resonances has been observed upon doping SFX-MeOTAD with SFX(TFSI)2. Thus, it can be proposed that doping SFX-MeOTAD with SFX(TFSI)2 helps in enhancing the aromatic nature of the molecule initially but increasing the dopant concentration further detrimentally affects the aromaticity and possibly the π stacking. The conductivity values of the doped samples follow a similar trend, where the conductivity increases with increase in the dopant concentration till around 20.5 mol% above which it plateaus. This suggests that the choice of counterion of the dopants for HTMs is crucial since the counterions can interact strongly with the oxidised HTM molecules and affect conductivity. So, a wider range of counterions should be explored when optimising the dopants for triarylamine based HTMs. Thus, the choice of counterion is something that needs to be considered when exploring new hole transport materials. This has been observed in some studies reported in the literature. For example, a larger aggregation was observed when Na+ was used as the counterion in conjugated polyelectrolytes containing a π-delocalised backbone with charged pendant groups as compared to the same material having CH3NH3+ counterion. PSCs fabricated utilising these hole transport materials showed that devices made with HTM containing Na+ counterion were around 50% less efficient than devices made using HTM with CH3NH3+ counterion.67 An improvement in hole conductivity and homogeneity was observed in an ionic type HTM containing TFSI− counterions as compared to the same HTM that did not contain the counterions.68 Counterions used in ionic liquids such as PF6−, CF3SO3− and BF4− are also found in conducting polymers used for photovoltaic applications because the counterions are weakly interacting due to a shielded charge.69 A halide counterion (Br−) in the A–D–A type ionic molecule as HTM was compared with the same HTM with TFSI− counterions. It was found that HTMs with the TFSI− counterions showed better performance in PSCs than those with Br− as the counterion. Although devices made with the TFSI− containing HTM exhibited higher efficiencies, the performance of devices using HTM with Br− counterions was still better than that of devices where the HTM did not contain any counterions. This is because the HOMO is located at a deeper energy level due to the high electron withdrawing effect of the quarternarised part of the HTM that helps to modify the HOMO.70
From the results obtained in the present study the optimal doping concentration is 20.5% as this is where the conductivity values started to plateau. It is important to note that the doping affects not only conductivity but also other properties like hydrophobicity, energy levels, film processing ability etc., and hence the best performing devices might not always correspond to optimal doping. Upon using spiro-(TFSI)2 as the dopant, a downshift in the ionisation potential of spiro-OMeTAD was observed. The best performing device was shown with 14 mol% spiro-(TFSI)2. At an optimal dopant concentration, the hydrophobicity of the film was shown to increase as the contact angle increases from 72.2° for the Li-TFSI doped spiro-OMeTAD to 83.3° for the spiro-OMeTAD with optimal spiro-(TFSI)2 doping. Cross-sectional SEM imaging showed that voids appeared in the Li-TFSI doped spiro-OMeTAD devices after aging for 300 hours at 50 °C but this was not observed in the optimal spiro-(TFSI)2 devices. These observations showed that the spiro-(TFSI)2 doped films have a greater stability in high moisture and oxygen environments.35 When (MeO-TPC)TFSI was used as the dopant, the conductivity of spiro-OMeTAD increased drastically at 50% dopant but the best performing device was made with 30% dopant with an efficiency of 17.9%. The contact angle also increased showing that the film hydrophobicity increased. The film morphology showed that there were no visible cracks or aggregation of the film unlike the film made with FK209.71 Using acid additives to help in enhancing the conductivity of spiro-OMeTAD was observed to decreases the ionisation energy of the HTM and also the Fermi level. There was no noticeable change in the ionisation energy and Fermi level between spiro-OMeTAD doped with LiTFSI and cobalt(III) complexes and those that had the acid additives. It was concluded that the increase in conductivity was due to hydrogen-bonding that increases the delocalisation of electrons.12
NEXAFS studies have also been carried around the N K-edge to understand the effect of SFX(TFSI)2 doping on SFX-MeOTAD. The positions and assignments of the N K-edge resonances of pristine and doped samples are summarised in Table S13 in the ESI.† N K-edge NEXAFS spectra of samples analysed are shown in Fig. 11 and are dominated by four resonances at 401.1, 402.7, 405.1 and 407.7 eV. Splitting of the N 1s → π* resonance in the 10%, 20% and 100% samples may be attributed to the difference in bond length between the N–C molecules as has been previously observed for spiro-MeOTAD40 and SFX-MeOTAD in this study. A modest difference in C–N bond length in the case of spiro(TFSI)2 has been reported36 and a similar variation in bond length in the case of SFX(TFSI)2 has been observed in this study [Table 1]. This trend would corroborate the fact that the presence of electron-donating methoxy groups affects the charge density of the molecules and plays a crucial role in influencing the charge transfer process. The resonance at 402.9 eV can be attributed to the transitions to the antibonding orbitals localised on amine moieties.72 An increase in the area under the curve from the pristine 0% to 10% and 20% doped samples signifies an enhancement in the nitrogen content of the molecules as the edge-jump intensity is proportional to the total nitrogen content in the molecules. SFX(TFSI)2 can have multiple nitrogen environments stemming from the different oxidation potentials on the amine N in the two halves of SFX-MeOTAD and the nitrogen from the dopant. The substantial enhancement in the nitrogen content of doped molecules point towards an increase in the π* and σ* density of states (DOS) over nitrogen and may also indicate the presence of additional decay channels available to the 10% and 20% doped samples via the formation of a charge transfer complex similar in lines to the spiro-MeOTAD+TFSI− which creates additional DOS over N through the (CF3SO2)2N− counteranion in spiro(TFSI)2. Pristine 0% sample has the lowest area under the curve due to the lower nitrogen environment available compared to the 10%, 20% and 100% samples. Interestingly, increasing the dopant concentration beyond 10% shows a decrease in the area under the curve which can probably be associated with the localisation of charge density due to enhanced TFSI concentration and can be corroborated with the C K-edge spectra where the aromaticity is found to decrease upon using a dopant concentration beyond 10% (Fig. 10).
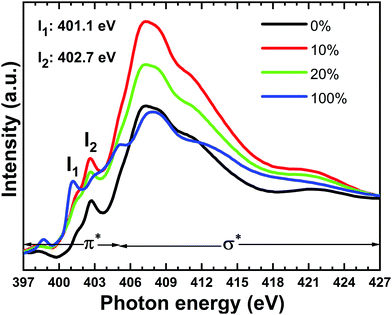 | ||
| Fig. 11 Comparison of N K-edge NEXAFS spectra corresponding to SFX-MeOTAD [0%], SFX-MeOTAD doped with 10% SFX(TFSI)2 [10%], SFX-MeOTAD doped with 20% SFX-(TFSI)2 [20%] and SFX(TFSI)2 dopant [100%]. | ||
Thus, it can be concluded that doping SFX-MeOTAD with SFX(TFSI)2 results in an enhancement in the aromatic nature which might possibly suggest improved π stacking between the molecules until an optimal concentration is reached, at which point a decrease is observed.
4. Conclusion
This study presents a detailed investigation of the modifications in the molecular structure and the electronic and optical properties of SFX-MeOTAD by doping it with its pre-oxidised form viz., a dicationic salt SFX(TFSI)2, probed using XPS, NEXAFS and detailed DFT, and TD-DFT computational calculations. By varying the doping concentration of the dicationic salt over a larger range [0–100%], it was possible to find the optimal doping concentration which resulted in four orders of increase in the conductivity of the pristine SFX-MeOTAD. An optimal doping concentration of 20.5% SFX-(TFSI)2 resulted in films with a conductivity of 9.43 × 10−4 S cm−1. Computational calculations provided detailed understanding of the geometric structure and the electronic and optical properties of SFX-MeOTAD and its oxidised forms. This allowed us to computationally calculate the absorbance spectrum for SFX-MeOTAD doped with the optimal dopant concentration of 20.5% SFX-(TFSI)2. XPS data reveals that doping with SFX(TFSI)2 results not only in the oxidation of SFX-MeOTAD but also in variations of the local chemistry around carbon and nitrogen which would influence the conductivity of the doped films, indicating that the counterion of the dopant can strongly interact with the oxidised HTM molecules and affect conductivity. Doping SFX-MeOTAD with SFX(TFSI)2 helps in enhancing the aromatic nature of the molecule initially but increasing the dopant concentration further affects the aromaticity and possibly the π stacking. The conductivity values of the doped samples follow a similar trend. Based on the results of the present study, the following considerations are important for doping triarylamine based HTM for perovskite solar cells (a) proper choice of the counterion in the dopant as it interacts strongly with the HTM; (b) although the HTM may contain multiple triarylamines, each molecule is likely to be not more than singly charged at the optimal dopant concentration; and (c) optimising the dopant concentration will strongly affect the conductivity.Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. I. acknowledges UK Research and Innovation (UKRI), Engineering and Physical Sciences Research Council (EPSRC) for the Fellowship grant (EP/P011500/1), EPSRC DTP (2120149) and Strathclyde's Research Excellence Award (REA) for funding Fraser's studentship. DFT and TD-DFT results were obtained using the ARCHIE-WeSt High-Performance Computer (http://www.archie-west.ac.uk) based at the University of Strathclyde. S. K. acknowledges Royal Society IES\R2\170272 and Royal Academy of Engineering Newton fund for the funding support. M. R. M. and N. R. acknowledge the European Union's Horizon 2020 Research and Innovation Programme H2020-MSCA-IF-2014-659237 and the EPSRC Supersolar Hub for financial support.References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- G. Xing, N. Mathews, S. S. Lim, Y. M. Lam, S. Mhaisalkar and T. C. Sum, Science, 2013, 342(6156), 344–347, DOI:10.1126/science.1243167.
- G. Hodes, Science, 2013, 342(6156), 317–318, DOI:10.1126/science.1245473.
- NREL, Best Research-Cell Efficiency Chart|Photovoltaic Research|NREL, https://www.nrel.gov/pv/assets/pdfs/best-research-cell-efficiencies.20200104.pdf.
- M. Liu, M. B. Johnston and H. J. Snaith, Nature, 2013, 501, 395–398, DOI:10.1038/nature12509.
- W. Tress, N. Marinova, O. Inganas, M. K. Nazeeruddin, S. M. Zakeeruddin and M. Graetzel, in 2014 IEEE 40th Photovoltaic Specialist Conference, PVSC 2014, 2014, pp. 1563–1566.
- T. Liu, K. Chen, Q. Hu, R. Zhu and Q. Gong, Adv. Energy Mater., 2016, 6, 1–17 Search PubMed.
- W. H. Nguyen, C. D. Bailie, E. L. Unger and M. D. Mcgehee, J. Am. Chem. Soc., 2014, 136, 10996–11001 CrossRef CAS PubMed.
- H. J. Snaith and M. Grätzel, Appl. Phys. Lett., 2006, 89, 262114, DOI:10.1063/1.2424552.
- J. Burschka, A. Dualeh, F. Kessler, E. Baranoff, N.-L. L. Cevey-Ha, C. Yi, M. K. Nazeeruddin and M. Grätzel, J. Am. Chem. Soc., 2011, 133, 18042–18045 CrossRef CAS PubMed.
- J. Burschka, F. Kessler, M. K. Nazeeruddin and M. Grätzel, Chem. Mater., 2013, 25, 2986–2990 CrossRef CAS.
- Z. Li, J. Tinkham, P. Schulz, M. Yang, D. H. Kim, J. Berry, A. Sellinger and K. Zhu, Adv. Energy Mater., 2017, 7, 1–8 Search PubMed.
- Q. Liu, L. Fan, Q. Zhang, A. Zhou, B. Wang, H. Bai, Q. Tian, B. Fan and T. Zhang, ChemSusChem, 2017, 10, 3098–3104 CrossRef CAS PubMed.
- C. Chen, W. Zhang, J. Cong, M. Cheng, B. Zhang, H. Chen, P. Liu, R. Li, M. Safdari, L. Kloo and L. Sun, ACS Energy Lett., 2017, 2, 497–503 CrossRef CAS.
- A. Pellaroque, N. K. Noel, S. N. Habisreutinger, Y. Zhang, S. Barlow, S. R. Marder and H. J. Snaith, ACS Energy Lett., 2017, 2, 2044–2050 CrossRef CAS.
- A. Abate, T. Leijtens, S. Pathak, J. Teuscher, R. Avolio, M. E. Errico, J. Kirkpatrik, J. M. Ball, P. Docampo, I. McPherson and H. J. Snaith, Phys. Chem. Chem. Phys., 2013, 15, 2572 RSC.
- U. B. Cappel, T. Daeneke and U. Bach, Nano Lett., 2012, 12, 4925–4931 CrossRef CAS PubMed.
- Z. Hawash, L. K. Ono, S. R. Raga, M. V. Lee and Y. Qi, Chem. Mater., 2015, 27, 562–569 CrossRef CAS.
- L. K. Ono, S. R. Raga, M. Remeika, A. J. Winchester, A. Gabe and Y. Qi, J. Mater. Chem. A, 2015, 3, 15451–15456 RSC.
- A. T. Murray, J. M. Frost, C. H. Hendon, C. D. Molloy, D. R. Carbery and A. Walsh, Chem. Commun., 2015, 51, 8935–8938 RSC.
- M. Maciejczyk, A. Ivaturi and N. Robertson, J. Mater. Chem. A, 2016, 4, 4855–4863 RSC.
- B. Xu, D. Bi, Y. Hua, P. Liu, M. Cheng, M. Grätzel, L. Kloo, A. Hagfeldt and L. Sun, Energy Environ. Sci., 2016, 9, 873–877 RSC.
- K. Liu, Y. Yao, J. Wang, L. Zhu, M. Sun, B. Ren, L. Xie, Y. Luo, Q. Meng and X. Zhan, Mater. Chem. Front., 2017, 1, 100–110 RSC.
- J. Qu, X. Jiang, Z. Yu, J. Lai, Y. Zhao, M. Hu, X. Yang and L. Sun, Sci. China: Chem., 2018, 61, 172–179 CrossRef CAS.
- I. Horcas, R. Fernández, J. M. Gómez-Rodríguez, J. Colchero, J. Gómez-Herrero and A. M. Baro, Rev. Sci. Instrum., 2007, 78, 013705, DOI:10.1063/1.2432410.
- K. G. Tirsell and V. P. Karpenko, Nucl. Instrum. Methods Phys. Res., Sect. A, 1990, 291, 511–517, DOI:10.1016/0168-9002(90)90113-K.
- H. Wang, C. Y. Ralston, D. S. Patil, R. M. Jones, W. Gu, M. Verhagen, M. Adams, P. Ge, C. Riordan, C. A. Marganian, P. Mascharak, J. Kovacs, C. G. Miller, T. J. Collins, S. Brooker, P. D. Croucher, K. Wang, E. I. Stiefel and S. P. Cramer, J. Am. Chem. Soc., 2000, 122, 10544–10552, DOI:10.1021/ja000945g.
- H. Wang, P. Ge, C. G. Riordan, S. Brooker, C. G. Woomer, T. Collins, C. A. Melendres, O. Graudejus, N. Bartlett, S. P. Cramer, C. G. Woomer, T. Collins, C. A. Melendres, X. O. Graudejus, O. N. Bartlett and S. P. Cramer, J. Phys. Chem. B, 1998, 102, 8343–8346 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. E. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, O. Farkas, J. B. Foresman and J. D. Fox, Gaussian, Inc., Wallingford CT, 2016.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- R. S. Sanchez and E. Mas-Marza, Sol. Energy Mater. Sol. Cells, 2016, 158, 189–194 CrossRef CAS.
- C. T. Weisspfennig, M. M. Lee, J. Teuscher, P. Docampo, S. D. Stranks, H. J. Joyce, H. Bergmann, I. Bruder, D. V. Kondratuk, M. B. Johnston, H. J. Snaith and L. M. Herz, J. Phys. Chem. C, 2013, 117, 19850–19858 CrossRef CAS.
- B. Tan, S. R. Raga, A. S. R. Chesman, S. O. Fürer, F. Zheng, D. P. McMeekin, L. Jiang, W. Mao, X. Lin, X. Wen, J. Lu, Y. B. Cheng and U. Bach, Adv. Energy Mater., 2019, 9, 1–10 Search PubMed.
- W. Zhang, L. Wang, Y. Guo, B. Zhang, V. Leandri, B. Xu, Z. Li, J. M. Gardner, L. Sun and L. Kloo, Chem. Commun., 2020, 56, 1589–1592 RSC.
- Z. Z. Sun, Y. L. Xu, R. Zhu and H. Y. Liu, Org. Electron., 2018, 63, 86–92 CrossRef CAS.
- J. Deng, W. Hu, W. Shen, M. Li and R. He, Phys. Chem. Chem. Phys., 2019, 21, 1235–1241 RSC.
- D. Jacquemin, B. Mennucci and C. Adamo, Phys. Chem. Chem. Phys., 2011, 13, 16987–16998 RSC.
- S. Fantacci, F. De Angelis, M. K. Nazeeruddin and M. Grätzel, J. Phys. Chem. C, 2011, 115, 23126–23133 CrossRef CAS.
- W. Huang and S. Ptasinska, Appl. Surf. Sci., 2016, 367, 160–166 CrossRef CAS.
- R. Schoelin, M. H. Karlsson, S. K. Eriksson, H. Siegbahn, E. M. J. Johansson and H. Rensmo, J. Phys. Chem. C, 2012, 116, 26300–26305 CrossRef CAS.
- J. A. Horsley, J. Stöhr, A. P. Hitchcock, D. C. Newbury, A. L. Johnson and F. Sette, J. Chem. Phys., 1985, 83, 6099 CrossRef CAS.
- J. L. Solomon, R. J. Madix and J. Stohr, Surf. Sci., 1991, 255, 12–30 CrossRef CAS.
- M. P. Keane, A. N. de Brito, N. Correia, S. Svensson and S. Lunell, Chem. Phys., 1991, 155, 379–387 CrossRef CAS.
- A. Baiardi, M. Mendolicchio, V. Barone, G. Fronzoni, G. A. Cardenas Jimenez, M. Stener, C. Grazioli, M. De Simone and M. Coreno, J. Chem. Phys., 2015, 143(20), 204102, DOI:10.1063/1.4935715.
- R. P. Gandhiraman, D. Nordlund, C. Javier, J. E. Koehne, B. Chen and M. Meyyappan, J. Phys. Chem. C, 2014, 118, 18706–18712 CrossRef CAS PubMed.
- A. Ganguly, S. Sharma, P. Papakonstantinou and J. Hamilton, J. Phys. Chem., 2011, 115, 17009–17019 CrossRef CAS.
- J. Lehmann, D. Solomon, J. Brandes, H. Fleckenstein, C. Jacobsen and J. Thieme, Biophysico-Chemical Processes Involving Natural Nonliving Organic Matter in Environmental Systems, 2009, pp. 729–781 Search PubMed.
- Y. Zubavichus, A. Shaporenko, M. Grunze and M. Zharnikov, J. Phys. Chem. A, 2005, 109, 6998–7000 CrossRef CAS PubMed.
- E. Apen, A. P. Hitchcock and J. L. Gland, J. Phys. Chem., 1993, 97, 6859–6866 CrossRef CAS.
- R. V. Dennis, B. J. Schultz, C. Jaye, X. Wang, D. A. Fischer, A. N. Cartwright and S. Banerjee, J. Vac. Sci. Technol., B, 2013, 31, 041204 CrossRef.
- N. Graf, E. Yegen, T. Gross, A. Lippitz, W. Weigel, S. Krakert, A. Terfort and W. E. S. Unger, Surf. Sci., 2009, 603, 2849–2860 CrossRef CAS.
- M. Nyberg, J. Hasselström, O. Karis, N. Wassdahl, M. Weinelt, A. Nilsson and L. G. M. Pettersson, J. Chem. Phys., 2000, 112, 5420–5427 CrossRef CAS.
- C. Dri, G. Fronzoni, G. Balducci, S. Furlan, M. Stener, Z. Feng, G. Comelli, C. Castellarin-Cudia, D. Cvetko, G. Kladnik, A. Verdini, L. Floreano and A. Cossaro, J. Phys. Chem. C, 2016, 120, 6104–6115 CrossRef CAS.
- Y. Luo, M. Bernien, A. Krüger, C. F. Hermanns, J. Miguel, Y. M. Chang, S. Jaekel, W. Kuch and R. Haag, Langmuir, 2012, 28, 358–366 CrossRef CAS PubMed.
- U. Oran, S. Swaraj, A. Lippitz and W. E. S. Unger, Plasma Processes Polym., 2006, 3, 288–298 CrossRef CAS.
- K. H. Hwang, W. H. E. Schwarz, T. C. Chang and U. Seeger, Chem. Phys., 1987, 117, 73–89 CrossRef.
- J. W. Chiou, S. C. Ray, S. I. Peng, C. H. Chuang, B. Y. Wang, H. M. Tsai, C. W. Pao, H. Lin, Y. C. Shao, Y. F. Wang, S. C. Chen, W. F. Pong, Y. C. Yeh, C. W. Chen, L. Chen, K. Chen, M. Tsai, A. Kumar, A. Ganguly, P. Papakonstantinou, H. Yamane, N. Kosugi, T. Regier, L. Liu and T. K. Sham, J. Phys. Chem. C, 2012, 116, 16251–16258 CrossRef CAS.
- S. C. Ray, H. M. Tsai, J. W. Chiou, B. Bose, J. C. Jan, K. Kumar, W. F. Pong, D. Dasgupta and M.-H. Tsai, J. Phys.: Condens. Matter, 2004, 16, 5713–5719 CrossRef CAS.
- E. Yegen, A. Lippitz, D. Treu and W. E. S. Unger, Surf. Interface Anal., 2008, 40, 176–179 CrossRef CAS.
- D. Solomon, J. Lehmann, J. Kinyangi, B. Liang, K. Heymann, L. Dathe, K. Hanley, S. Wirick and C. Jacobsen, Soil Sci. Soc. Am. J., 2008, 73, 1817–1830 CrossRef.
- A. V. Syugaev and A. N. Maratkanova, J. Electron Spectrosc. Relat. Phenom., 2014, 195, 71–77 CrossRef CAS.
- T. Ohta, K. Seki, T. Yokoyama, I. Morisada and K. Edamatsu, Physica, 1990, 41, 150–153 CAS.
- K. Heymann, J. Lehmann, D. Solomon, M. W. I. Schmidt and T. Regier, Org. Geochem., 2011, 42, 1055–1064 CrossRef CAS.
- H. Agren, V. Carravetta, L. G. M. Pettersson and O. Vahtras, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 848–855 CrossRef PubMed.
- X. Li, Y. C. Wang, L. Zhu, W. Zhang, H. Q. Wang and J. Fang, ACS Appl. Mater. Interfaces, 2017, 9, 31357–31361 CrossRef CAS PubMed.
- J. Zhang, B. Xu, L. Yang, A. Mingorance, C. Ruan, Y. Hua, L. Wang, N. Vlachopoulos, M. Lira-Cantú, G. Boschloo, A. Hagfeldt, L. Sun and E. M. J. Johansson, Adv. Energy Mater., 2017, 7, 1–8 Search PubMed.
- M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629 CrossRef CAS PubMed.
- M. Cheng, K. Aitola, C. Chen, F. Zhang, P. Liu, K. Sveinbjörnsson, Y. Hua, L. Kloo, G. Boschloo and L. Sun, Nano Energy, 2016, 30, 387–397 CrossRef CAS.
- W. Zhang, F. Zhang, B. Xu, Y. Li, L. Wang, B. Zhang, Y. Guo, J. M. Gardner, L. Sun and L. Kloo, ACS Appl. Mater. Interfaces, 2020, 12, 33751–33758 CrossRef CAS PubMed.
- B. J. Schultz, R. V. Dennis, J. P. Aldinger, C. Jaye, X. Wang, D. A. Fischer, A. N. Cartwright and S. Banerjee, RSC Adv., 2014, 4, 634–644 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc04172j |
| This journal is © The Royal Society of Chemistry 2021 |