Open Access Article
Open Access ArticleEffects of polarized light on the optical and self-oscillation behaviors of liquid crystal network polymers†
Rana
Zibaei
ab,
Mohammad Sadegh
Zakerhamidi
 *abc,
Sirous
Korram
ab and
Amid
Ranjkesh
d
*abc,
Sirous
Korram
ab and
Amid
Ranjkesh
d
aFaculty of Physics, University of Tabriz, Tabriz, Iran. E-mail: Zakerhamidi@tabrizu.ac.ir; Fax: +98-41-33347050; Tel: +98-41-33393353
bResearch Institute for Applied Physics and Astronomy, University of Tabriz, Tabriz, Iran
cPhotonics Center of Excellence, University of Tabriz, Tabriz, Iran
dCondensed Matter Department, J. Stefan Institute, Jamova 39, Ljubljana, Slovenia
First published on 29th September 2021
Abstract
The phenomenon of self-oscillation is abundant in nature, which often occurs in response to various environmental stimuli. The most common stimuli for these processes are heat and light. Oscillations based on bending are one type of self-oscillating phenomenon. In this study, the oscillation frequency and amplitude of liquid crystalline polymer network (LCN) structures with light are investigated. Due to the anisotropy of LCN, which originates from a specific orientation in the LCN surfaces, all studies are performed with polarized light to accurately determine the effect of different orientations of these networks on frequency and oscillation parameters. The different polarizations of light show different oscillating behaviors in terms of amplitude and frequency of the LCN oscillation. To investigate the factors affecting the amplitude and frequency, such as temperature and optical behaviors, the effect of increasing the power of the polarized light source on the behavior of these materials is evaluated.
1. Introduction
By living in nature and observing its various phenomena and wonders, humankind has always thought of using and creating these phenomena for himself and his goals. Seeing birds, humans thought of flying and built airplanes, and perceiving the different properties and activities of animals and plants over a long period led to the creation of many synthetic materials that were nature-inspired and exhibited the properties seen in nature.1–3 Today, soft and intelligent materials are used in the field of soft robotics, thus making it possible to achieve numerous goals with various dimensions. Among them, stimuli-responsive materials that undertake macroscopic deformations in response to different stimuli are of great interest to scientists as they do not require complex installations to operate.4,5One important class of these materials is liquid crystalline polymer networks (LCNs), which are almost entirely prepared from LC monomer precursors. Materials within this class are famous for their elasticity, intrinsic anisotropy, and self-assembly.6 They could be elastomeric or in glassy form. The glassy form LCNs generally tend to have glass transition temperatures ranging from 60 to 100 °C with moduli parallel to the nematic director in the range of 1–2 GPa.7
Among various and effective stimuli in the LCN systems, light is the most favorable stimulus, which can be precisely controllable, and has safe availability.8–10 Indeed, light characteristics such as wavelength, intensity, etc., can strongly influence the photophysical and photomechanical outputs observed in the LCN systems.11,12 To enhance the photomechanical effects in the LC systems, embedding light-sensitive dyes into LCNs13–20 and the molecular alignment and the structure of LCNs21–23 affect in reversible mechanical deformations18,24,25 and, self-oscillation,26,27 upon photo actuation.
Self-oscillation is especially interesting for scientists due to its great potential in various fields, such as flying robots, power generation, and sensors.28 Many researchers have studied the mechanism and necessities of self-oscillation.29,30 LCN self-oscillators with different structures has been designed mostly based on Azo dyes/moieties. The first photo actuated LCN oscillator was reported by White's group. They used a monodomain azobenzene-containing LCN to obtain a 30 Hz photo-driven oscillation. The mechanism of these Azo-LCNs was established on the trans to cis isomerization of azobenzene linkages and sequentially irradiating both sides of the cantilever.31 They also observed an increase in the frequency (up to 270 Hz) by diminishing the cantilever length, as well as reducing the air pressure.32 Polarization of light as another essential characteristic was studied for deformations and oscillation of Azo-LCN cantilevers.33,35 Flexural-torsional self-oscillation was illustrated in Azo-LCNs with less azobenzene concentration. Correspondingly, different LCN cuts based on the angle of the long axis of the cantilever with the nematic molecular direction axis were exposed to light, and oscillations with different frequencies and amplitudes were observed. It was demonstrated that increasing the intensity and temperature leads to an increase in the oscillation amplitude.34 Some advanced self-sustained oscillation modes have been developed using the Azo LCN mixture with the following basic forms of oscillation: bending, twisting, contraction–expansion and self-sustained freestyle oscillation.29 Also, a chaotic oscillation for fluoro-azobenzene LCNs derived by sun-light was described.36 In all the mentioned reports, the photo-sensibility of the LCN structure is based on the utilization of an azobenzene chromophore. Recently, a new LCN, without Azo dyes, using photo stabilizers has been reported that could self-oscillate in bending mode with splay molecular alignment. Indeed, the photo-thermal effect in the critical position of the cantilever bending, self-shadowing, causes self-sustained oscillations at ∼6 Hz.30,37
The above-mentioned studies mostly focused on the oscillation behaviours based on the materials characteristics. But light as a leading factor should be investigated in more detail. There is no doubt that different light characteristics can impact on the mechanical responses of the LCN. Indeed, depending on incident beam intensity, light-matter interactions are classified into two optical domains: “linear and non-linear.” Indeed, according to the optical properties of LCNs including anisotropy, molecular direction, and refractive index, investigating the linear and non-linear optical responses of LCNs is essential. For the detailed investigation on polarized light-driven oscillation behaviours in LCN, we study linear and non-linear optical responses of LCNs. By understanding those properties in the LCNs and obtaining their optical responses, we develop LCN applications as well.
This work concentrates on the LCN films containing a photo-thermal component as the photo-responsive moiety, illustrating self-oscillation when exposed to the light source. We study the polarized light effect on these LCNs and explore the role of polarization on parameters like temperature, oscillation, and linear and non-linear optical behavior. For the first time, the non-linear optical behavior of LCN films like the non-linear absorption coefficient is reported using open-aperture Z-scan setups. This investigation reveals new aspects of the processes involved in the mechanical behavior of LCN polymers.
2. Experimental
2.1. Materials
The reactive monomer mesogen used for the syntheses of the LCN was RM82 (Mw = 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Sigma Aldrich) and was used without purification. Irgacure 651 (supplied by Ciba, Basel, Switzerland) is a highly effective UV photoinitiator for initiating the polymerization of unsaturated RM82 mesogen prepolymer systems.38 Tinuvin 460 (BASF) was used as a UV light absorber. The chemical structures of the component materials in LCN polymer film are shown in Fig. 1. To obtain parallel (homogeneous orientation) and vertical (homeotropic orientation) alignment layers, we used polyvinyl alcohol (PVA) and lecithin aqueous solution (1 wt%), respectively. They were purchased from Merck with the highest purity.
000, Sigma Aldrich) and was used without purification. Irgacure 651 (supplied by Ciba, Basel, Switzerland) is a highly effective UV photoinitiator for initiating the polymerization of unsaturated RM82 mesogen prepolymer systems.38 Tinuvin 460 (BASF) was used as a UV light absorber. The chemical structures of the component materials in LCN polymer film are shown in Fig. 1. To obtain parallel (homogeneous orientation) and vertical (homeotropic orientation) alignment layers, we used polyvinyl alcohol (PVA) and lecithin aqueous solution (1 wt%), respectively. They were purchased from Merck with the highest purity.
2.2. Polymerization of the liquid crystalline networks
For the LCN polymerization, RM82 (96.5 wt%, Merck Co. Ltd) monomers were used, and for photo stabilization of the LCN, 2.5 wt% of Tinuvin 460 was added to the RM82 monomers. Irgacure 651 (1 wt%, Merck Co. Ltd) photoinitiator was used for easy polymerization inside quartz cells with splay surface alignment. RM82 monomers, Tinuvin 460, and Irgacure 651 were dissolved inside the dichloromethane (highest available purity from Merck Co. Ltd) and mixed using a Laboratory Mixer (50 rpm 60 min), so the solvent completely evaporates. The obtained mixture was melted and drawn into 20 μm thick quartz cells by capillary action in the isotropic phase (103 °C). The splay cells were made of one rubbed planar quartz (coated with PVA) and one homeotropic quartz (coated with lecithin). The cell gaps were adjusted to 20 μm using spherical spacers that glued planar and homeotropic quartz sheets together with Nova65 UV glue. For photo-curing, the mixture sample was cooled to the nematic phase (91 °C) and subjected to a 365 nm UV light (power density 12 mW cm−2) for about 30 min followed by a thermal post-curing at 120 °C for 10 min.2.3. Characterization instruments
A Vertex 70, FT-IR spectrophotometer, was used to record the vibration spectra over the wavenumber range 400–4000 cm−1. A double beam Shimadzu UV-2450 UV-visible spectrophotometer was used to record the absorption spectra over a wavelength range of 200–900 nm. Spectroscopic instruments were combined with a cell temperature controller with an accuracy of ±0.10 °C. The scanning electron microscopy (SEM) images of the LCN films that illustrated mesogen alignment at the films’ thickness were collected with a MIRA3 FEG-SEM instrument. The atomic force microscope (AFM) analysis was performed on a Nanosurf Mobile S instrument.2.4. Optical setup
We used two optical setups in our experiments. Firstly, measuring the photo-driven oscillation of the LCN and secondly, recording the optically non-linear behavior of the LCN. Photo-driven oscillation of the LCN cantilevers was directed with a linearly polarized 405 nm collimated UV-light (a diode laser, with a spatial mode close to Gaussian TEM00, works at the wavelength of 405 nm). Fig. 2 shows the photo-driven oscillation of the LCN setup. The beam was expanded and collimated with a spherical lens, and the polarization direction of the beam was controlled with a Fresnel rhomb (Newport). Cantilevers were in 2.5 mm × 2 cm dimensions and were exposed to the light at the point about 2 mm below the clamp. The focused beam irradiates the planar side of the film, which is hanged by a clamp. Oscillations of the LCN cantilevers were characterized by using a camera operating at a frame rate of 60 Hz. The oscillation frequency was determined optically (with a photodiode and an oscilloscope). The amplitude of the oscillations was measured from the captured images using video analysis software (Tracker). | ||
| Fig. 2 Photo-driven oscillation of the LCN setup, (a) LCN placement and oscillation in set-up, and (b) measurement of temperature, frequency and amplitude of LCN oscillation. | ||
The open aperture Z-scan technique was performed to obtain the non-linear absorption coefficient. Fig. 3 shows the Z-scan setup. A Gaussian light beam with a wavelength of 405 nm was employed for the Z-scan experiment to study the non-linear properties of the LCN films. A lens with a focal length of 100 mm was placed in front of the sample, and a lens with f = 5 cm was used after the sample to collect the output light from the sample on the detector. In the focal point, the radius of the focused light beam (obtained via knife-edge experiment) was approximately 0.35 mm. The non-linear absorption coefficients can be determined according to the changes in the obtained transmission curves, collected via a photodiode and an oscilloscope.
3. Results and discussion
3.1. Morphology of the liquid crystal network polymers
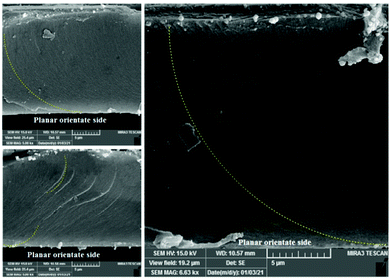
Glassy LCN films were formed by photo-polymerization of the crosslinking nematic monomers RM 82, and FT-IR spectra before and after photo-polymerization of RM 82 are presented in Fig. S1 in the ESI,† according to the presented method in Section 2.2 in a splay alignment. The splay configuration causes a gradual change of molecules’ director in the thickness of the film. This type of configuration, oriented structures such as LC, has two refractive indices (ne and no), generating a refractive index gradient. This configuration is extra-important when using polarized light. It should be noted that acrylate functional groups in the RM 82 cause the formation of a polymer network. The polymerization of the LCN network is affected by the initial orientation of the nematic RM 82 mesogen monomers, so polymerization forms anisotropic structures under the surface alignment layer. Due to the polymerization of LCN inside oriented cells, study of the surface morphology of the LCN samples is necessary using AFM and SEM. Fig. 4 shows the AFM images in the planar orientate side (front). AFM image analysis in the planar and homeotropic oriented side of LCN presented in Fig. S2 in the ESI† showed grooves of 0.7 μm wide and 0.5 nm deep in the surface. In the homeotropic oriented side grooves with an approximate average width of 0.2 μm and a depth of 0.7 nm were determined. The surface roughness (Ra) is about 0.14 nm on the parallel oriented side and 0.32 nm on the homeotropic part orientated side. Increasing the roughness increases the surface area.39The cross-section of the LCN in the SEM is shown in Fig. 5, which clearly demonstrates the change of orientation from a homogeneous to homeotropic alignment pattern. The AFM and SEM show that the surface orientations are present in the surface of the synthesized LCN polymer, and these orientation gradients continue in the LCN bulk.
3.2. Polarized light effects on the self-oscillation behaviors of the liquid crystal network polymers
Thin transparent LCN films attached to the retaining clip in the setup (Fig. 2), and the sample cantilever were exposed to light. The long axis of the cantilever (x) is in the same direction as the rubbed planar side, and (E) represents the polarization direction of light.Subjecting this cantilever to a polarized collimated exposure (405 nm and 162 mW cm−2 at distance of 50 cm from the sample) causes bending of the planar orientated side of the LCN film towards the light followed by continues self-oscillation, LCN oscillation with Parallel and perpendicular Polarized Light presented in Video files S1 and S2 in the ESI,† as shown in Fig. 2. The oscillations were continuous for about 1 hour, and when they stopped, the cantilever restarts its oscillation after a while, with the frequency close to the previous. The actuation is triggered with a polarization parallel to the long axis of the cantilever (E ‖ x), establishing oscillations with a frequency of 8 Hz. The polarization perpendicular to the x (E ⊥ x), and the 45° polarized light to the long axis of the cantilever (E45°) resulted in oscillations in the direction of the exposure light with the frequency and amplitude parameters given in Table 1.
| Polarization | Frequency (Hz) | Amplitude (mm) |
|---|---|---|
| Parallel (E ‖ x) | 8 | 1.3 |
| Perpendicular (E ⊥ x) | 6 | 2.5 |
| 45° to the x (E45°) | 14 | 2 |
As shown in Table 1, the highest oscillation frequency is observed in light with a polarization of 45°, and the largest amplitude is obtained in light with perpendicular polarization. It should be noted that in the case where the polarization of light is parallel or perpendicular to the x-axis, in principle, the components of ne (at the front side of the LCN surface) and no (at the backside of the LCN surface) are to adjust the main factor in light absorption on both sides of the sample and cause oscillation, respectively. But in the case where the polarization of light is 45°, refractive index components are effective in all parts of the LCN and cause light absorption and oscillation. Although the obtained oscillation frequencies in all cases are extremely low frequencies (ELF), their sum in 45° polarized light is interesting.
| Oscillation frequency (E ‖ x) + Oscillation frequency (E ⊥ x) = Oscillation frequency (E45°) | (1) |
The natural frequency equation for this type of cantilever (non-damped) is given by:40
 | (2) |
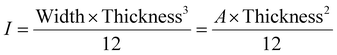 | (3) |
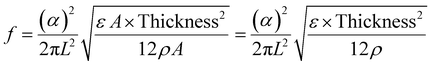 | (4) |
 | (5) |
 | (6) |
It is clear that the studied cantilever changes in frequency are related to its tensile modulus and thickness. Of course, it should be noted that the temperature variations in the LCN cantilever with light at different polarizations are almost the same, and the density changes are negligible. Indeed, a series of experiments using a thermal infrared camera verified that the temperature at both sides of the LCN cantilever varies when exposed to the different polarizations of light. When the film was exposed to parallel polarization (E ‖ x) of light, with a laser light power of 162 mW cm−2, the planar side (front) of it had a higher (∼1 °C) temperature than that of the homeotropic side (planar oriented side temperature = 59 °C). When a perpendicular polarized light was irradiated on the sample, with a power of 162 mW cm−2, the temperature was higher (∼0.5 °C) at the homeotropic surface, as compared to the sample planar side (homeotropic side temperature = 58 °C). In 45° polarized light, temperatures at the planar-oriented side of the film (temperature = 58 °C) are higher (∼1 °C) than that of the homeotropic side.
It is noteworthy that in the same LCN sample, changing light polarization would lead to differences in oscillation frequency. The oscillation frequency variations in the studied LCN sample with polarized light depend on two parameters. The first effective parameter in the LCN frequency of the oscillation with polarized light is the modulus of elasticity. Its temperature dependency at high temperature differences is very important in the oscillation frequency.41 However, in the same sample of LCN the modulus of elasticity is constant and when this sample is exposed to different polarized light, changes in the modulus of elasticity are negligible.42
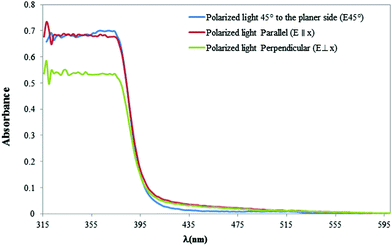
The second effective parameter in the oscillation frequency of the LCN sample with polarized light is the sample's thickness. The parallel polarized light is absorbed in the planer-oriented layer. For the perpendicular polarized light, the highest absorption occurs in the homeotropic oriented layer, and for the 45° polarized light, all of the LCN samples contribute to light absorption. Therefore, it can be assumed that the effective thickness in the absorbance of differently polarized light will be different. Consequently, it can be said that the reason for the higher oscillation frequency of 45° polarized light is due to the higher effective absorption thickness in the sample compared to the parallel and perpendicular polarized light. Due to the larger oscillation frequency with parallel polarized light compared to perpendicular polarized light, it seems that the thickness of the planer-oriented layer is larger than the thickness of the homeotropic layer in the LCN polymer bulk. However, due to the fact that the surface anchorage between the rubbed PVA (∼10−3 J m−2)43 and the LCN surface during polymerization is much larger than lecithin (∼10−5 J m−2)44 with a LCN surface, it seems logical that after LCN polymerization, the thickness of the planar layer is greater than the homeotropic layer. Fig. 6 shows the polarized absorption spectra of the LCN sample. The amount of absorbance with parallel and 45° polarized light is more than the amount of absorption with perpendicular polarized light. This difference in thickness can also justify the absorbance and temperature difference between the two sides of the LCN sample.
It should be noted that in polarized light at 45°, the orientation of LCN molecules (parallel to the surface at the front and vertical to the surface at the rear) causes the absorbance of this polarized light in the parallel and vertical layer to follow Malus's law.45 So the vector component of 45° polarized light for absorbance in the studied LCN should be broken into two components. The parallel component in the parallel layer and the vertical component in the vertical molecular layer of the LCN can interact. Resultant vector components in the parallel and vertical directions are smaller than the main component. Therefore, the amount of absorbance in each parallel and vertically oriented layer is less than the absorbance as compared to parallel polarization in the parallel oriented layer and vertically polarized light in the vertically oriented layer. However, both layers have an absorbance component, even less for the 45° polarized light. The total absorbance spectrum is presented in Fig. 6. It shows the sum of absorbance of each resultant vector component of 45° polarized light in each layer. As is shown, the amount absorbance of 45° polarized is slightly higher than the absorbance of parallel polarized light.
Another interesting point in the oscillation results presented in Table 1 is the oscillation amplitude. It seems that the different orientation RM polymer network structure at the two sides of the cantilever surface, which resulted from the orientation in the polymerization step, causes different oscillations in the two sides of the cantilever. The front side of the cantilever shows oscillation (E ‖ x) with a lower amplitude. The backside of the cantilever shows oscillation (E ⊥ x) with higher amplitude. Of course, the amplitude of each side can indicate the maximum expansion of that surface and, therefore, the possible amplitude in that situation. Consequently, it can be assumed that at light polarization of 45°, the oscillation of the LCN with a specific frequency occurs. In this case, the combination of the planer and homeotropic alignment side layer oscillation occurs, Fig. 7a, with a constant frequency of 14 Hz. In this case, the combined oscillation, destructive oscillation, shows amplitude with a range of 2 mm for 45° polarized light. By increasing the power of the laser light to 300 mW cm−2 (at a distance of 50 cm from the sample) the temperature at both sides of the LCN cantilever changes compared to the 162 mW cm−2 laser power. So the parallel polarization results in the temperature of 60 °C for the planar side and 59 °C for the homeotropic (back) side. For perpendicular polarized light, the planar side had a temperature of 59 °C and the homeotropic side 60 °C. Finally, for the 45° polarized light, the temperature at the planar and homeotropic oriented sides of the film was 60 °C. This increase in laser power did not affect the oscillation frequency but led to irregular oscillation amplitude compared to the 162 mW cm−2 laser power.
 | ||
| Fig. 7 Mechanical oscillations, amplitude and temperature changes at the Hinge point, of the LCN during irradiation with UV laser light. (a) 162 mW cm−2 and (b) 300 mW cm−2. | ||
The amplitude of the oscillation at two different powers of the laser light source is shown in Fig. 7. The amplitudes obtained for each state are fitted with a sine function as the dotted line. In the low power mode (162 mW cm−2), the amplitude is exactly fitted in a sinusoidal function with high regression, R2 = 0.98. In the oscillation mode with parallel, 45° and vertical polarized light, the amplitude values are the same for each case. Also, the range of temperature changes at the Hinge point, the LCN exposed area with light, is about 2 °C.
In a low power light source, it seems that the factors affecting the oscillation process reached a state of equilibrium. Consequently, regular oscillation amplitude was observed in the LCN sample (Fig. 7a). However, as the power of the light source increases, the influence of the effective factors on the oscillation of the LCN changes in comparison with the previous state, in other words, it becomes out of balance, which results in an irregular oscillation amplitude.
At high power laser light, due to the intervention of other effective factors the system is de-balanced. As shown in Fig. 7b, by increasing the power of the laser light source to 300 mW cm−2, the amplitudes for each case cannot be fitted by a single sine function, and the frequency still is constant.
The fitting result in this situation by combining the sine functions gives an acceptable result with R2 = 0.9. It means that there are different amplitudes in each oscillating state and in comparison with low laser power light; a specific range for the oscillation of each case cannot be attributed. Also, the range of temperature changes at the Hinge point is about 4 °C. The general increase of the LCN surface temperature changes at the Hinge point, by increasing the power of the laser, can be explained via two reasons.
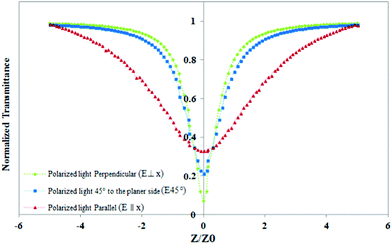
The first reason is the increase in light intensity, which can lead to an increase in the linear light absorption in the LCN that leads to an overall increase in the temperature in the LCN sample. The second reason is the high intensity of the laser light resulting in the non-linear behavior of the LCN sample. Higher non-linear absorption in the homeotropic side of the LCN can increase the temperature in this part of the LCN and eliminate the temperature gradient between the two sides of the LCN surfaces with 45° polarized light. For this purpose, the non-linear absorption of LCN with parallel, perpendicular and 45° polarized light, relative to the planer-oriented side with a 300 mW cm−2 laser light source, was recorded. In the simplest case, the light-induced changes in total absorption of materials are equal to:46,47
| α(I) = αo + βI | (7) |
The non-linear absorption of the LCN has the valley pattern, meaning a positive non-linear absorption and a reverse saturable absorption (RSA) mechanism for the LCN. According to Fig. 7, the light transmission through the sample is significantly reduced at high laser powers, and linear absorption and nonlinear absorption coefficients of the studied LCN presented in Table S1 in the ESI,† which means increased light absorption. Higher absorption will lead to an increase in the temperature. Henari48 has shown that excitation under a CW laser leads to thermal effects, which increases the excited-state absorption (ESA). Moreover, two-photon absorption (TPA) needs a pulse laser source with a beam intensity higher than 108 (w cm−2).49 So for the LCN in parallel, perpendicular, and 45° polarized light, RSA occurs by ESA.
High non-linear absorption in the homeotropic oriented side is the reason for the increase in the temperature of the homeotropic oriented surface compared to the 162 mW cm−2 laser exposed power case.
4. Conclusions
Optical designs normally focus on the wavelength and intensity of the light while neglecting its polarization. Understanding the polarized light's effect on oriented and anisotropic materials is crucial for many optical responses and applications. Polarized light provides accurate information regarding the ability of the oriented layers of LCN. Examining the LCN oscillations with a planar and homeotropic oriented surface with polarized light showed that the surface orientation is an essential parameter in creating oscillation, frequency, and oscillation amplitude. The importance of planar and homeotropic surface alignment in the polymerization stage of the LCN polymer and the difference in light absorption components on both sides of LCN causes temperature and refractive index gradients on both sides of the LCN. These gradients control the frequency and amplitude of the oscillation.The results showed that the oscillation frequency of the LCN with polarized light and the temperature dependency depends on the thickness of the planar and homeotropic oriented side. In addition, the overall frequency of the studied LCN sample is directly related to the vibration frequency of both oriented sides. In the oscillation amplitude with polarized light, both oriented sides have specific amplitudes with parallel and perpendicular polarized light, and the destructive wave composition of these amplitudes occurs with 45° polarized light.
Finally, increasing the power results in an increment in the non-linear optical behavior of the LCN, and this leads to temperature variations between the two sides of the LCN. On the other hand, the oscillation behavior in this situation shows irregular amplitude.
Author contributions
R. Zibaie performed the experiments, analyzed the data and collected data. M. S. Zakerhamidi conceived and designed the experiments, analyzed and evaluated the data, and wrote and edited the manuscript. S. Korram analyzed and evaluated the data. A. Ranjkesh analyzed and evaluated the data and edited the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was part of a project that has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (Grant agreement no. 884928-LOGOS).References
- S. Schuhladen, F. Preller, R. Rix, S. Petsch, R. Zentel and H. Zappe, Adv. Mater., 2014, 26, 7247 Search PubMed.
- H. Shahsavan, S. M. Salili, A. Jákli and B. Zhao, Adv. Mater., 2017, 29, 1604021 Search PubMed.
- X. Q. Wang, C. F. Tan, K. H. Chan, X. Lu, L. Zhu, S. W. Kim and G. W. Ho, Nat. Commun., 2018, 9, 3438 Search PubMed.
- N. El-Atab, R. B. Mishra, F. Al-Modaf, L. Joharji, A. A. Alsharif, H. Alamoudi, M. Diaz, N. Qaiser and M. M. Hussain, Adv. Intell. Syst., 2020, 2, 2000128 Search PubMed.
- M. Pishvar and R. L. Harne, Adv. Sci., 2020, 7, 2001384 Search PubMed.
- T. Ube and T. Ikeda, In Photomechanical Materials, Composites, and Systems: Wireless Transduction of Light into Work, John Wiley & Sons, Hoboken, New Jersey, 2017, pp. 1–35 Search PubMed.
- T. J. White, In Photomechanical Materials, Composites, and Systems: Wireless Transduction of Light into Work, Wiley & Sons, Hoboken, New Jersey, 2017, pp. 153–177 Search PubMed.
- H. Zeng, P. Wasylczyk, C. Parmeggiani, D. Martella, M. Burresi and D. S. Wiersma, Adv. Mater., 2015, 27, 3883 Search PubMed.
- M. Pilz da Cunha, S. Ambergen, M. G. Debije, E. F. G. A. Homburg, J. M. J. den Toonder and A. P. H. J. Schenning, Adv. Sci., 2020, 7, 1902842 Search PubMed.
- S. Nocentini, C. Parmeggiani, D. Martella and D. S. Wiersma, Adv. Opt. Mater., 2018, 6, 1800207 Search PubMed.
- Y. Yu, M. Nakano and T. Ikeda, Nature, 2003, 425, 145 Search PubMed.
- L. Dong and Y. Zhao, Mater. Chem. Front., 2018, 2, 1932 Search PubMed.
- D. Corbett and M. Warner, Phys. Rev. Lett., 2007, 99, 174302 Search PubMed.
- K. M. Lee and T. J. White, Macromolecules, 2012, 45, 7163 Search PubMed.
- J. H. Yun, C. Li, S. Kim and M. Cho, J. Phys. Chem. C, 2018, 122, 6310 Search PubMed.
- M. Pilz Da Cunha, E. A. J. Van Thoor, M. G. Debije, D. J. Broer and A. P. H. J. Schenning, J. Mater. Chem. C, 2019, 7, 13502 Search PubMed.
- B. K. Juluri, A. S. Kumar, Y. Liu, T. Ye, Y. W. Yang, A. H. Flood, L. Fang, J. F. Stoddart, P. S. Weiss and T. J. Huang, ACS Nano, 2009, 3, 291 Search PubMed.
- J. A. Lv, Y. Liu, J. Wei, E. Chen, L. Qin and Y. Yu, Nature, 2016, 537, 179 Search PubMed.
- M. Chen, B. Yao, M. Kappl, S. Liu, J. Yuan, R. Berger, F. Zhang, H. J. Butt, Y. Liu and S. Wu, Adv. Funct. Mater., 2020, 30, 1906752 Search PubMed.
- Y. Yue, Y. Norikane, R. Azumi and E. Koyama, Nat. Commun., 2018, 9, 3234 Search PubMed.
- M. Lahikainen, H. Zeng and A. Priimagi, Nat. Commun., 2018, 9, 4148 Search PubMed.
- Z. Jiang, Y. Xiao, X. Tong and Y. Zhao, Angew. Chem., 2019, 131, 5386 Search PubMed.
- T. Ube, K. Kawasaki and T. Ikeda, Adv. Mater., 2016, 28, 8212 Search PubMed.
- R. Yang and Y. Zhao, ACS Macro Lett., 2018, 7, 353 Search PubMed.
- K. M. Lee, N. V. Tabiryan, T. J. Bunning and T. J. White, J. Mater. Chem., 2012, 22, 691 Search PubMed.
- T. J. White and D. J. Broer, Nat. Mater., 2015, 14, 1087 Search PubMed.
- T. Ikeda, J. I. Mamiya and Y. Yu, Angew. Chem., Int. Ed., 2007, 46, 506 Search PubMed.
- A. Jenkins, Phys. Rep., 2013, 525, 167 Search PubMed.
- H. Zeng, M. Lahikainen, L. Liu, Z. Ahmed, O. M. Wani, M. Wang, H. Yang and A. Priimagi, Nat. Commun., 2019, 10, 5057 Search PubMed.
- A. H. Gelebart, G. Vantomme, E. W. Meijer and D. J. Broer, Adv. Mater., 2017, 29, 1606712 Search PubMed.
- T. J. White, N. V. Tabiryan, S. V. Serak, U. A. Hrozhyk, V. P. Tondiglia, H. Koerner, R. A. Vaia and T. J. Bunning, Soft Matter, 2008, 4, 1796 Search PubMed.
- S. Serak, N. Tabiryan, R. Vergara, T. J. White, R. A. Vaia and T. J. Bunning, Soft Matter, 2010, 6, 779 Search PubMed.
- T. J. White, S. V. Serak, N. V. Tabiryan, R. A. Vaia and T. J. Bunning, J. Mater. Chem., 2009, 19, 1080 Search PubMed.
- K. M. Lee, M. L. Smith, H. Koerner, N. Tabiryan, R. A. Vaia, T. J. Bunning and T. J. White, Adv. Funct. Mater., 2011, 21, 2913 Search PubMed.
- S. Liu, X. Liao, L. T. de Haan, Y. You, H. Ye, G. Zhou and D. Yuan, Soft Matter, 2021, 17, 748 Search PubMed.
- K. Kumar, C. Knie, D. Bléger, M. A. Peletier, H. Friedrich, S. Hecht, D. J. Broer, M. G. Debije and A. P. H. J. Schenning, Nat. Commun., 2016, 7, 11975 Search PubMed.
- G. Vantomme, A. H. Gelebart, D. J. Broer and E. W. Meijer, J. Polym. Sci., Part A: Polym. Chem., 2018, 56, 1331 Search PubMed.
- A. Bagheri and J. Jin, ACS Appl. Polym. Mater., 2019, 1, 593 Search PubMed.
- L. Lai and E. A. Irene, Area evaluation of microscopically rough surfaces, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.–Process., Meas., Phenom., 1999, 17, 33 Search PubMed.
- R. D. Blevins, Formulas for Natural Frequency and Mode Shape, Van Nostrand Reinhold Co., New York, NY, USA, 1979 Search PubMed.
- N. Lagakos, J. Jarzynski, J. H. Cole and J. A. Bucaro, J. Appl. Phys., 1986, 59, 4017 Search PubMed.
- L. Liu, D. J. Broer and P. R. Onck, Soft Matter, 2019, 15, 8040 Search PubMed.
- H. Yokoyama, Mol. Cryst. Liq. Cryst., 1988, 165, 265 Search PubMed.
- S. I. Baek, S. J. Kim and J. H. Kim, AIP. Adv., 2015, 5, 097170 Search PubMed.
- S. C. Gladden, Am. J. Phys., 1950, 18, 395 Search PubMed.
- M. Khadem Sadigh and M. S. Zakerhamidi, Opt. Laser Technol., 2018, 100, 216 Search PubMed.
- M. Sheik-Bahae, A. A. Said and V. Stryland, Opt. Lett., 1989, 14, 955 Search PubMed.
- F. Z. Henari, J. Opt. A: Pure Appl. Opt., 2001, 3, 188 Search PubMed.
- G. Sreekumar, P. G. Louie, C. I. Muneera, K. Sathiyamoorthy, C. Vijayan and C. Mukherjee, J. Opt. A: Pure Appl. Opt., 2009, 11, 125204 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: FT-IR spectra before and after photo-polymerization of RM 82, AFM image analysis in the planar and homeotropic oriented side of LCN, linear absorption and nonlinear absorption coefficients in LCN, video file of LCN oscillation with parallel polarized light and video file of LCN oscillation with perpendicular polarized light. See DOI: 10.1039/d1tc03870b |
| This journal is © The Royal Society of Chemistry 2021 |