Effect of electric hysteresis on fatigue behavior in antiferroelectric bulk ceramics under bipolar loading

Abstract

Antiferroelectric ceramics are exploited for applications in high energy-density capacitors due to their reversible electric-field-induced phase transitions. The difference in the fields between the forward and reverse transition is termed electric hysteresis. As accumulation of hysteresis loss is detrimental to antiferroelectric capacitors, especially in high-frequency applications, the effect of hysteresis on the long-term operation performance must be evaluated. We investigate the effect of hysteresis on fatigue behavior in two antiferroelectric ceramic compositions with comparable recoverable energy densities (0.56 vs. 0.64 J cm⁻³), having a large and small hysteresis of 23.9 kV cm⁻¹ and 3.9 kV cm⁻¹, respectively. In test cycles of 2.5 × 10⁶ of ±60 kV cm⁻¹ bipolar fields, the ceramic with large hysteresis exhibits a 72% decrease in the recoverable energy density and a 71% decrease in the energy efficiency. In contrast, the small hysteresis ceramic shows a 4.5% degradation in energy density and 0% degradation in energy efficiency. These results demonstrate that reducing the electric hysteresis of antiferroelectric capacitors is essential for higher energy efficiency and longer service lifetime.

---

1. Introduction

The rapid increase in energy generation from renewable resources, especially over the last decade, has led to a growing demand for high energy-density capacitors. Antiferroelectric (AFE) materials are considered as one of the best candidates for these high-energy/high-frequency power conditioning applications, like DC inverters in renewable sources and electric cars, due to their near zero remanent polarization and fast discharge rates.^1–3 During the charging stage of the AFE capacitor, it undergoes a field-induced transition to ferroelectric (FE) phase storing energy (W_st), and then releases part of the stored energy (W_re) as it returns to the AFE phase when the electric field is removed during the discharge stage.⁴ The phase transitions, however, are associated with electric hysteresis (ΔE), corresponding to dissipated energy (W_loss) which cannot be recovered during the operation of the capacitor and reduces its operating efficiency. Like ferroelectrics, AFE capacitors undergo deterioration in their performance when exposed to extended periods of dynamic fields.^5,6 Such deterioration limits the operational life of an AFE capacitor.

Electric fatigue is the decay in material performance under the impact of a prolonged application of alternating electric fields. In a FE material, fatigue manifests as the reduction in maximum polarization, remanent polarization, and the maximum induced strain with increasing cycles of electric field.^7–9 A deterioration in the properties adversely affects the operation reliability and life of FE devices. The origin of fatigue has been attributed primarily to (i) electrochemical factors: pinning of domain walls by charge carriers that inhibit domain wall movement and (ii) mechanical factors: formation and propagation of microcracks that disintegrate the active material. Fatigue from electrochemical origin can be generally recovered by annealing over 300 °C, but the damage from mechanical factors is permanent. AFE ceramics (like ferroelectrics) also undergo fatigue: i.e., loss in the maximum polarization and maximum strain when subjected to repeated electric loading.^5,6,10 Although the fatigue resistance of AFE ceramics is presumably superior to the FE counterparts,¹¹ the degradation of polarization and strain poses a great hindrance in their widespread application as high energy-density capacitors and large-displacement actuators.

The fatigue behavior can be affected by both intrinsic and extrinsic factors. Intrinsic factors are characteristic to the ceramic like (i) composition, (ii) domain structure, and (iii) grain morphology; while the extrinsic factors depend on external conditions like (i) applied electric field amplitude, (ii) electrode material, (iii) test temperature, (iv) frequency of the loading signal, (v) polarity of loading, and (vi) sample surface conditions. Influences of these factors on fatigue have been mostly studied in ferroelectrics.^7,8,12–14 During its service, an AFE capacitor undergoes back-and-forth phase-transition cycles, each of which is associated with an electric hysteresis. An accumulation of the hysteresis loss energy can prove detrimental to the capacitor, especially in high-frequency applications. As such, there is an urgent need to evaluate the effect of hysteresis on the long-term operation performance of AFE capacitors. In the literature, there are only a few reports on the fatigue behavior of AFE ceramics^{5,6,10,13–15} and, to the best of our knowledge, there has been no study on the influence of hysteresis on the fatigue of AFE materials.

Here, fatigue behavior is studied and compared for two AFE compositions with drastically different electric hysteresis (ΔE) but with comparable recoverable energy densities (W_re). Both compositions are La- and Sn-doped lead zirconate titanate. The ceramic with small hysteresis is (Pb_0.925La_0.05)(Zr_0.42Sn_0.40Ti_0.18)O₃, as reported in a previous study,¹⁶ which is abbreviated as PZ-S (S: small hysteresis). The large hysteresis composition is (Pb_0.97La_0.02)(Zr_0.59Sn_0.31Ti_0.10)O₃ and is abbreviated as PZ-L (L: large hysteresis). The effect of hysteresis on fatigue mechanism, its manifestation on maximum polarization, strain and energy storage properties are thoroughly investigated. This study will be instrumental in the design of high energy-density AFE capacitors aimed for reliable performance with a long lifetime.

2. Experimental procedure

The ceramics in the present study are prepared with the solid-state reaction route. High-purity oxides (>99.9%) of PbO, La₂O₃, ZrO₂, SnO₂, and TiO₂ were weighed in stoichiometric quantities for both compositions: (Pb_0.97La_0.02)(Zr_0.59Sn_0.31Ti_0.10)O₃ (PZ-L) and (Pb_0.925La_0.05)(Zr_0.42Sn_0.40Ti_0.18)O₃ (PZ-S). A 3–5% excess of PbO was included to compensate for the lead loss in the subsequent high-temperature processing steps. The oxides were milled in ethanol for 6 hours. After drying, the milled powders were uniaxially pressed into a cylinder and calcined at 935 °C for 4 hours. After another milling and drying, 10 wt.% polyvinyl alcohol binder was added, and pressed pellets were buried in PbZrO₃ powders in a double crucible arrangement during sintering at 1350 °C for 3 hours.

The top 200 μm layer was polished off from both flat surfaces of the sintered pellets. The disk samples were then annealed at 250 °C for 30 minutes to relieve any stresses incurred. The density of the sintered pellets was determined using the Archimedes method. The phase purity and crystal structure were analyzed with X-ray diffraction from the annealed samples. Scanning electron microscopy (SEM) was performed on the fractured surface of the sintered pellets to reveal the grain morphology. For the dielectric property measurement, silver paste electrodes were fired on at 800 °C for 5 minutes. The temperature dependent dielectric constant and loss tangent were measured at 1, 10 and 100 kHz at a rate of 4 °C min⁻¹ during heating.

For bipolar electric field cycling and electric property measurements, the sintered pellets were polished to ∼0.4 mm thick disks. Ag–Pt bilayer 6 mm diameter electrodes were sputtered on the flat surfaces. The samples were submerged in a dielectric fluid (Fluorinert™ FC-40, 3M) to prevent arcing during the bipolar fatigue tests under a triangular waveform with a peak field (E_max) of ±60 kV cm⁻¹ at a frequency of 10 Hz. The E_max was selected nearly 25 kV cm⁻¹ above the critical transition fields of the compositions to ensure the ceramics attain polarization saturation during the electric cycling. Three samples of each composition were tested for 2.5 × 10⁶ cycles at room temperature. During the fatigue tests, polarization (P) vs. electric field (E) curves were recorded with a standardized ferroelectric test system (Precision LC II, Radiant Technologies) at the first cycle and after a preset number of cycles. In addition, the macroscopic longitudinal strain (S₃) vs. electric field (E) was recorded at the first cycle and after 2.5 × 10⁶ cycles. These P vs. E and S₃vs. E curves were all recorded at the frequency of 1 Hz.

After fatigue tests, the Ag–Pt bilayer electrodes were chemically etched away to expose the fatigued surfaces underneath the electrodes, which were then examined with SEM. Then, the top 100 μm layer of the ceramic under the electrode was mechanically polished off to inspect the fatigue damage in the interior of the sample.

3. Results

3.1 Structure of the AFE ceramics

X-ray diffraction patterns of the sintered ceramics are shown in Fig. 1 for the two compositions (PZ-L and PZ-S). Both compositions exhibit a perovskite structure. Impurities, if any, are in quantities below the detection limit of the X-ray diffractometer. The peaks of the patterns are indexed with the pseudo-cubic unit cell.^17,18 The splitting of the (200) pseudo-cubic peaks in both compositions indicates a tetragonal distortion of the perovskite structure.¹⁹ The peaks for PZ-S shift towards higher 2θ angles, compared to PZ-L, suggesting smaller lattice parameters. Such decrease in PZ-S is expected due to the higher concentration of smaller ionic radii La³⁺ (1.36 Å) ions, which substitutes a much larger Pb²⁺ (1.49 Å) on the A-site of the perovskite structure. Moreover, PZ-S also has a high Ti⁴⁺ (0.605 Å) concentration on the B-site, which is smaller than Sn⁴⁺ (0.69 Å) and Zr⁴⁺ (0.72 Å).²⁰ The lattice parameters of PZ-L were determined to be a = 4.109 Å and c = 4.081 Å, and for PZ-S, a = 4.083 Å and c = 4.065 Å. The unit cell volume of PZ-S is 67.767 ų, which is smaller than that of PZ-L (68.886 ų). The splitting of the (200) pseudo-cubic peak is much more prominent in PZ-L than in PZ-S, as illustrated in Fig. 1b. This suggests a stronger tetragonal distortion in the crystal structure, as also evidenced from the 1 − (c/a) ratio (tetragonality) of the two lattices (0.7% for PZ-L and 0.4% for PZ-S). A c/a ratio closer to unity (in PZ-S) indicates a near cubic structure and minimum lattice distortion.⁴ The relative density of the AFE ceramics was determined to be 96.9% for PZ-L and 97.5% for PZ-S.

Fig. 1 X-ray diffraction spectra of the two AFE ceramics PZ-L and PZ-S. (a) The whole spectra in the 2θ range of 20–70°. (b) The close view of the 200 pseudo-cubic peak.

The as-sintered ceramics were mechanically fractured and then thermally etched at 1140 °C for 30 minutes to better reveal the grain boundaries during SEM imaging. The grain size and morphology of the two AFE ceramics are illustrated in Fig. 2. The average grain size was quantified using the linear intercept method. The PZ-L ceramic has a larger grain size of 11.9 ± 2.7 μm while PZ-S shows a smaller grain size of 2.8 ± 0.4 μm. The suppressed grain growth in PZ-S can be attributed to the higher content of La³⁺ which is known to inhibit grain growth.^16,21 It should be noted that the two AFE ceramics display distinctive fracture features. The PZ-L ceramic fractures in a conchoidal mode, suggesting a strong grain-boundary mechanical strength. On the other hand, PZ-S shows primarily intergranular fracture.

Fig. 2 SEM micrographs of the fracture surface of as-sintered ceramics: (a) PZ-L, (b) PZ-S.

3.2 Properties of the AFE ceramics

3.2.1 Dielectric properties. Fig. 3 shows the temperature dependence of the dielectric constant (ε_r) and loss tangent (tan δ) of the two ceramics at 1 kHz, 10 kHz and 100 kHz. For PZ-L (Fig. 3a), the dielectric constant increases continuously from its room temperature value to reach a maximum at 149 °C (T_m), after which it shows a plateau region before it drops after 181 °C. PZ-L is in AFE state at room temperature, indicated by its low tan δ values. At the first anomaly at T_m, the tetragonal AFE phase transforms to a paraelectric multicell cubic structure. At the second anomaly, the multicell cubic transforms to a single-cell cubic structure. No frequency-dependent dispersion is observed in the ε_r, characteristic to the AFE behavior. The loss tangent (tan δ) remains low in a large range of temperature and increases at high temperatures in the single-cell-cubic paraelectric phase.

Fig. 3 Temperature dependence of dielectric constant (ε_r) and loss tangent (tan δ) of the AFE ceramics measured during heating. (a) PZ-L, (b) PZ-S.

The dielectric behavior of PZ-S is presented in Fig. 3b. The room-temperature value of ε_r is much higher than PZ-L. The ε_r increases to reach its maximum at ∼77 °C (T_m) but there is no plateau region. Also, the AFE to paraelectric transition is much more diffuse compared to that of PZ-L. The ε_r and tan δ show apparent frequency dispersion at temperatures below T_m. The loss tangent is higher at room temperature than PZ-L and decreases to remain low up to 200 °C until it increases at high temperatures. The high room-temperature ε_r, lowered T_m, suppression of the plateau region, and the increased frequency dispersion are similar to earlier studies and are attributed to the high La³⁺ concentration.^16,22 La³⁺ is expected to promote the formation of polar nano-regions that facilitate diffuse phase transitions and introduce relaxor characteristics in lead zirconate titanate ceramics. It is interesting to note that in the Pb_1−1.5xLa_x(Zr_0.42Sn_0.40Ti_0.18)O₃ (x = 0.00–0.06) series, La³⁺ disrupts the long-range FE order and impose both relaxor and AFE characteristics to the compositions of x = 0.04, 0.05, and 0.06.¹⁶ La³⁺ was also reported to further stabilize the AFE order in Pb(Yb_1/2Nb_1/2)_0.92Ti_0.08O₃ ceramics.²³

3.2.2 Electric field-induced polarization. The polarization response of the AFE ceramics to the first cycle of applied electric field is presented in Fig. 4a. Both compositions show double hysteresis loops characteristic to AFE materials. When the applied electric field increases, the ceramic undergoes a field-induced AFE to FE phase transition at a critical field (E_F). This forward transition in the PZ-L ceramic is indicated by an abrupt increase in polarization at 35.3 kV cm⁻¹ after which the polarization saturates when the entire ceramic transforms to the FE phase,^19,24 reaching a maximum (P_max) of 38.1 μC cm⁻² at 60 kV cm⁻¹. During unloading of the electric field, the induced FE phase remains stable at electric fields much below E_F and eventually transforms back to the AFE phase at another critical field (E_A) revealed by the sharp drop in polarization. The remanent polarization (P_r) at 0 kV cm⁻¹ is near 0 (0.1 μC cm⁻²), indicating an almost complete recovery of the AFE phase. The difference in the applied fields, measured at half-maximum polarization, is the electric hysteresis (ΔE),²⁵ which is 23.9 kV cm⁻¹ for PZ-L. Such a hysteretic transition behavior is consistent with previous reports on similar AFE compositions.^26,27

Fig. 4 (a) The P vs. E and (b) S₃vs. E hysteresis loops measured on the PZ-L (black) and PZ-S (red) ceramics at their virgin state.

In contrast, the PZ-S ceramic transforms to the FE phase in a more gradual and diffuse manner. The resulting P vs. E loop is oblique and slim. Such slim loops were also observed by Chen et al.¹⁶ in AFE ceramics with high La³⁺ concentrations. An increase in La³⁺ concentration is expected to introduce random local fields that disrupt the long-range AFE order and promote diffuse phase transitions and slanted hysteresis loops.^25,28,29 The higher La³⁺ concentration in PZ-S also leads to a lower saturation polarization, with a P_max of 26.7 μC cm⁻² at 60 kV cm⁻¹. The electric hysteresis ΔE for PZ-S is 3.9 kV cm⁻¹, significantly smaller than the PZ-L ceramic.

In capacitor applications, the forward AFE to FE transition occurs during charging as energy is stored (W_st) and the reverse FE to AFE transition takes place during discharging as part of the stored energy is released as useful recoverable energy (W_re). The unrecovered stored energy is the energy loss (W_loss), which leads to heat dissipation in the capacitor. The energy properties of a capacitor are quantified as follows:

W_loss = W_st − W_re (3)

η = (W_re/W_st) × 100% (4)

where E is electric field, P is polarization, P_r is the remanent polarization at 0 kV cm⁻¹ field and P_max is the maximum polarization at peak field. The energy efficiency η quantifies the effectiveness of the capacitor in releasing the stored energy; a higher value of η is always desired.

In the PZ-L ceramic, the sharp increase in polarization at E_F and the high maximum polarization result in a high W_st of 1.36 J cm⁻³. Nevertheless, owing to the large hysteresis, a major portion of the stored energy is unrecovered with W_loss of 0.80 J cm⁻³. This results in a W_re of 0.56 J cm⁻³, corresponding to an η of 41%. The slanted shape of the loop and a low maximum polarization in PZ-S lead to a much lower W_st of 0.73 J cm⁻³. However, the reduced hysteresis indicates an extremely low W_loss (0.09 J cm⁻³), which results in an even higher W_re (0.64 J cm⁻³) than that of PZ-L. The energy efficiency η of PZ-S is 88%, more than twice that of PZ-L.

3.2.3 Electric field-induced strain. The macroscopic longitudinal strain (S₃) induced by the applied electric field is displayed in Fig. 4b. The S–E loops show the same hysteretic behavior as their corresponding P–E loops. For PZ-L, S₃ remains almost zero when the ceramic is in AFE till E_F is reached, where it shows a sharp increase marking the AFE to FE phase transition. S₃ reaches a maximum of 0.32% (S_max) at the peak field of 60 kV cm⁻¹. The strain gradually decreases upon field removal when the FE to AFE transition occurs. Under the fields in the opposite polarity, a highly symmetric lobe of the strain loop is developed.

The PZ-S ceramic does not show an abrupt increase in S₃ as field increases. The AFE to FE transition is diffuse around E_F, which leads to a slanted S–E loop. The loops display a small offset to the negative field with a minor asymmetry. The S_max is 0.11% in positive lobe (S⁺) and 0.09% in the negative lobe (S⁻). The maximum strains in PZ-S are significantly lower than PZ-L, which may be attributed to the correlation between strain and polarization in these compounds.^30,31

3.3 Fatigue of the AFE ceramics

Fig. 5 and 6 show the evolution of the hysteresis loops of the two AFE ceramics under bipolar cyclic electric fields. Selected P–E loops for PZ-L at the first cycle (blue) and after 1.6× 10⁵, 6.5 × 10⁵, 1.3 × 10⁶ and 2.5 × 10⁶ cycles are displayed in Fig. 5a. It is evident that E_F gradually shifts to lower values during cycling and eventually the AFE to FE transition becomes very diffuse. The maximum polarization (P_max) decreases while the remanent polarization (P_r) increases with the number of cycles. After 2.5 × 10⁶ cycles, the double loops almost become a slanted single loop with considerable P_r and apparent coercive fields, suggesting the stabilization of the induced FE phase upon electric cycling.³²

Fig. 5 Hysteresis loops of the PZ-L ceramic during fatigue under bipolar electric fields. (a) The P vs. E loops. (b) The S–E loops.

Fig. 6 Hysteresis loops of the PZ-S ceramic during fatigue under bipolar electric fields. (a) The P vs. E loops. (b) The S–E loops.

The fatigue effect on the field-induced strain in PZ-L is shown in Fig. 5b. After 2.5 × 10⁶ cycles, the S–E loop becomes slanted asymmetric, analogous to the P–E loop. The S_max decreases by 52% in the S⁺ lobe while by 65% in the S⁻ lobe. Development of asymmetry in the S–E loop after fatigue was also observed in previous studies on AFE ceramics.^5,6,10 Another notable feature in the S–E loop after fatigue is the presence of negative strains in the S⁻ lobe. A negative strain is indicative of FE behavior. Therefore, the strain behavior confirms the stabilized FE state in the fatigued sample revealed by the P–E loops.

The P–E loops of PZ-S were measured at the first cycle, and after 1.6 × 10⁵, 6.5 × 10⁵, 1.3 × 10⁶ and 2.5 × 10⁶ cycles and are displayed in Fig. 6a. In contrast to PZ-L, PZ-S shows almost no change in the loop characteristics even after 2.5 × 10⁶ cycles, with all the loops overlapping on each other. The S–E loops at the first cycle and after fatigue of PZ-S display very minor reduction in S_max, indicating a high resistance to electric cycling (Fig. 6b). Both lobes of the double loops become slightly more slanted after fatigue owing to an increase in the diffuseness of the phase transitions. The S_max in the S⁺ lobe remains larger than that in the S⁻ lobe after fatigue.

The evolution of P_max and P_r are compared in Fig. 7 for PZ-L and PZ-S, averaged for three samples in each composition. The P_max in PZ-L shows minor drop till 3.2 × 10⁵ cycles after which the decline is almost logarithmic. After 2.5 × 10⁶ cycles, the P_max reduces by 23.7% from its virgin state value. The P_r remains stable till 3.2 × 10⁵ cycles before it shows a dramatic increase. On the other hand, the PZ-S ceramic displays a small reduction of 3.0% in P_max after 2.5 × 10⁶ cycles of bipolar fields. Apart from the behavior of the average values, PZ-L shows a greater variation in their polarization values indicated by the large error bars. The deviation shows an increase with the number of cycles, indicating a poor reliability at high cycles in AFE capacitors made of PZ-L due to electric fatigue. The error bars in Fig. 7b for PZ-S are smaller than the symbols on the curves, indicating that the variation in its polarizations remains low throughout the cycles of fatigue tests. Therefore, the ceramic with small hysteresis (PZ-S) not only shows excellent resistance to fatigue but also high stability and reliability in the performance.

Fig. 7 The maximum polarization (P_max) and remanent polarization (P_r) as a function of the cycle number of during fatigue of (a) PZ-L, and (b) PZ-S. The polarization values were averaged over three samples for each composition. The error bars are smaller than the symbols in (b) for PZ-S.

4. Discussion

4.1 Energy storage properties against fatigue

The energy storage properties of AFE capacitors can be extracted from the recorded P–E loops. Fig. 8 illustrates the evolution of W_st and W_loss of the two ceramics during bipolar cycling. Both W_st and W_loss in PZ-L show an initial gradual decrease till 3.2 × 10⁵ cycles. During this period, the P_max and P_r are stable, and the P vs. E loops become more diffuse at the forward and reverse transitions. The small reduction in W_st is attributed to the gradual reduction in the P_max, while the reduction in W_loss stems from the increase in diffuseness of the phase transitions which makes the loops slanted and slimmer, reducing the enclosed loop area. After 3.2 × 10⁵ cycles, W_loss in PZ-L shows a drastic rise while W_st exhibits a small increase. The increase in W_loss (∼50%) is attributed to the sharp rise in P_r which marks the gradually stabilized FE phase in PZ-L. In contrast, both W_st and W_loss in PZ-S change very little throughout the 2.5 × 10⁶ cycles. Compared to their initial values, W_st decreases by 5% while W_loss decreases by 7% after fatigue.

Fig. 8 Evolution of W_st and W_loss during cycling of bipolar electric fields in (a) PZ-L, and (b) PZ-S. The values are extracted from P–E loops in Fig. 5 and 6.

For energy storage capacitors, the most important properties are the recoverable energy density W_re and the energy efficiency η. The evolution of these two properties during electric cycling are comparatively shown in Fig. 9. Even though W_st and W_loss are quite different in the two compositions, the initial W_re in PZ-L and PZ-S are comparable (0.56 vs. 0.64 J cm⁻³). However, after multiple cycles of bipolar loading, the two ceramics show distinctions in performance. The W_re of PZ-L shows a gradual increase till 3.2 × 10⁵ cycles after which it drops sharply, by 72% from its initial value after 2.5 × 10⁶ cycles. The large decrease in W_re is due to the sharp increase in W_loss during the late stage of fatigue test. On the other hand, PZ-S has a higher initial value of W_re and it remains mostly steady during fatigue, only a 4.5% decrease after 2.5 × 10⁶ cycles. The energy efficiency η shows a similar trend as W_re. It drops to 12% in PZ-L after 2.5 × 10⁶ cycles, indicating 88% of the stored energy cannot be released. PZ-S, in contrast, demonstrates a remarkable stability. Its η value remains constant at 88% even after 2.5 × 10⁶ cycles due to the proportional decrease in W_st and W_loss. For an operating capacitor at a designated energy density and operating field, it can be seen that the ceramic with a small hysteresis, such as PZ-S, would display a much longer service life with excellent stability in performance. It should be noted that PZ-S can be referred to as a relaxor antiferroelectric ceramic. The strategy of designing relaxor antiferroelectric compositions for high performance energy-storage capacitors has been recently demonstrated in both lead-containing¹⁷ and lead-free perovskite compounds.^33–35

Fig. 9 Evolution of (a) the recoverable energy density, W_re, and (b) the energy efficiency, η, during cycling of bipolar electric fields in PZ-L and PZ-S. The values are extracted from P–E loops in Fig. 5 and 6.

4.2 Fatigue mechanisms of the AFE ceramics

4.2.1 Electrochemical factors. The fatigue in bulk FE and AFE ceramics have been attributed primarily to two main types of factors: (i) migration and accumulation of electrochemical charge species or (ii) mechanical impairment by microcracks. In most cases, both factors can work concurrently to contribute to electric fatigue. Mechanical damage is easier to identify since it results in microcracks that can be detected with a microscope. Electrochemical causes of fatigue originate from the formation, migration and accumulation of charged species or defects that lead to pining of domain walls or phase boundaries and hinder their movement under electric field. In lead zirconate titanate ceramics, these defects can be the donor or acceptor dopants at A or B sites of the ABO₃ perovskite lattice, or oxygen vacancies due to doping or PbO loss during sintering.^36,37

The increase in the diffuse nature of the AFE–FE transitions during repeated bipolar cycling can be attributed to the pinning of both domain walls and phase boundaries. Pinning of the phase boundary impedes the phase transitions. If the impediment is strong, many domains or grains may not even transform into the FE phase, which can lead to the decrease in the maximum polarization and make the phase transition gradual and to occur over a range of fields. In the meantime, charged point defect pinning can occur to the FE domain walls in the induced FE phase.³⁸ A higher field may be required to overcome the increased energy barrier and move the domain walls.

The increase in the remanent polarization in PZ-L suggests that bipolar electric cycling tends to stabilize the induced FE phase. As the amount of FE phase is negligible in the virgin state, the increase in the fraction of the metastable FE phase is attributed to the accumulated charged point defects during fatigue cycling. The polar nature of the charged defects favors the polar FE phase to minimize net charges and to reduce the electrostatic energy. The accumulation of charged defects, and their pinning of the FE domain walls and AFE/FE phase boundaries are also suggested to be responsible for the asymmetric degradation of the strain loops after fatigue, especially in the PZ-L composition. Development of asymmetry is more commonly seen during fatigue in the FE ceramics^12,39 and also in some AFE,⁵ as FE domains progressively freeze with a preferred polarization direction favored by clusters of point defects (, , , etc.) and their complexes (e.g.).⁴⁰ Under the applied field during electric fatigue, the charged point defects and their complexes tend to align themselves and form low-energy configurations. As a result, internal-bias fields gradually develop, favoring certain FE domains. These directionally biased FE domains give rise to an ‘offset polarization’ and an ‘offset strain’.^40–42

4.2.2 Microcracking. Mechanical damage during electric cycling is also one of the mechanisms of fatigue in FE and AFE materials. The damage incurred by microcracking cannot be relieved by heat treatments below the sintering temperature and is thus, considered permanent. The surfaces of two fatigued samples were examined after etching the electrode and are displayed in Fig. 10. The PZ-L ceramic displays extensive microcracks underneath the electrode (Fig. 10a). The surface prior to electrical loading does not have any cracks and has similar appearance to the flat part in the upper right portion of this micrograph. The cracks in the fatigued sample are situated primarily along grain boundaries and sometimes within grains (Fig. 10b). A large portion of the top layer of grains on the ceramic surface appears to have been pulled away after the etching process. Similar microcracking behavior was also observed by Jiang et al.⁷ in ferroelectric ceramics. Microcracks adversely affect the phase transition in adjacent grains because they can shield the applied electric field. As lesser number of grains transform, the achievable maximum polarization drops, as seen in the reduction of P_max values in PZ-L. The non-uniform transition in grains gives rise to incompatible stresses at grain boundaries, further promoting crack growth.⁷

Fig. 10 SEM micrographs of the surfaces of fatigued samples after the electrodes were chemically etched. (a) PZ-L at lower magnification. (b) PZ-L at higher magnification where microcracks along grain boundaries (arrow II) as well as within grains (arrows I and III) are seen. (c) PZ-S.

A closer examination of the microcracks in PZ-L reveals three types of microcracks (Fig. 10b): (i) transgranular cracks enclosed inside grains (arrows marked I), (ii) intergranular cracks along grain boundaries (arrow II), and (iii) transgranular cracks across multiple grains (arrow III). These distinct types of microcracks seem to indicate their different origins: the transgranular crack is likely to be caused by the incompatible strain at the AFE/FE phase boundary within the grain while the intergranular crack is resulted from the incompatible strain at the grain boundary due to anisotropic nature of the piezoelectric effect. During electric cycling, the AFE to FE transition is accompanied with an increase in the crystal volume, which in turn creates internal stress at the AFE/FE phase boundary as well as the grain boundary. The piezoelectric and electrostrictive strains under applied field depend on crystallographic orientations of individual grains. A mismatch in the strains between two adjacent grains leads to stress concentrations at the grain boundary. When the stress is sufficiently high, the repeated action during electric cycling leads to microcracks formation. It is interesting to note that virgin state PZ-L mechanically fractures in the conchoidal mode (Fig. 2), indicating the grain boundaries are not mechanically weak initially. The extensive intergranular microcracks in the electrically fatigued sample indicate the large differences in local stresses under mechanical and electric loadings.

In stark contrast, the ceramic with small hysteresis, PZ-S, shows an intact surface underneath the electrode after fatigue (Fig. 10c). Even in small and scattered pockets where the grain structure underneath is revealed, no microcracks either along grain boundaries or within grains are observed.

To further inspect if microcracks exist in the interior of fatigued samples, a layer of 100 μm under the electrode surface was polished off from both PZ-L and PZ-S samples. PZ-L displays macrocracks along the rim of electroded region and clouds of propagating microcracks within the electroded region. Another distinct feature is the presence of discoloration beneath the electroded region in PZ-L, as shown in the optical image in the table of contents entry. In contrast, PZ-S shows neither microcracks nor discoloration, in line with the SEM micrographs in Fig. 10c. Such discoloration and macrocrack patterns are similar to those observed by Zhang et al.¹² in fatigued FE lead zirconate titanate ceramics. The accumulated charged point defects can act as color centers. Also the production of 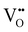during electric cycling is likely to be accompanied with cation reduction, darkening the ceramic.^12,30 Furthermore, the formation of microcracks can drastically increase light scattering, discoloring the electrically fatigued ceramic.

4.3 Hysteresis-dependent fatigue resistance

The large electric hysteresis seen in PZ-L during the phase transitions is indicative of incompatible AFE and FE phases at the phase boundary. The situation should be qualitatively similar to the martensitic transitions in shape memory alloys.⁴³ The hysteretic energy (W_loss) would then be largely expended in moving the high energy phase boundaries. During repeating forward and reverse transitions, these phase boundaries can act as sites for crack initiation and also promote the accumulation of charged defects, to relieve the elastic and electrostatic energies. In contrast, the smaller tetragonal distortion in PZ-S may result in more compatible AFE and FE phases with a smaller hysteresis in the displacive transitions.¹⁷

The hysteresis-dependent fatigue resistance can be rationalized to be consistent with the strain-dependent fatigue resistance. Zhou et al.⁶ reported that the AFE composition with a higher electric field-induced strain (S₃) suffered more severe microcracking after fatigue. In the present work, the higher macroscopic field-induced strain in PZ-L also corresponds to more severe mechanical damage. In our previous work,¹⁸ we found that the longitudinal strain S₃ during phase transition in PbZrO₃-based AFE polycrystalline ceramics is 4 to 5 times of the transverse strain (S₁). So S₃ can be used as an indicator of the volume strain (S₃ + 2S₁). A higher S₃ suggests a larger volume expansion from the AFE unit cell to the FE unit cell, and in turn, a larger lattice mismatch at the AFE/FE interface. An incompatible AFE/FE phase boundary manifests itself as large electric hysteresis ΔE. High S₃ and large ΔE are hence, expected to come hand in hand, and both lead to fast and severe fatigue damage. This is indeed the case in the previous work by Zhou et al.,⁶ as well as in the present work (Fig. 4b).

The two compositions with largely distinct electric hysteresis not only show a variation in their fatigue resistance but also in their fatigue mechanisms. For the large hysteresis composition PZ-L, fatigue is believed to result from both electrochemical and mechanical factors. The severe structural damage and propensity of microcracks indicate that mechanical factors may be the dominant mechanism in fatigue of PZ-L. The limited change in P_max and P_r in PZ-L till 3.2 × 10⁵ cycles (Fig. 7a) and the low variability (small error bars) indicates a homogeneous and mild degradation, which is similar to the incubation period of fatigue seen in many FE ceramics.³⁸ The nucleation and fast growth of microcracks are presumed to occur after this period till the measured 2.5 × 10⁶ cycles. Since microcracking in ceramics varies significantly from sample to sample, the dispersion in the data increases beyond 3.2 × 10⁵ cycles. In contrast, in the small hysteresis composition PZ-S, the absence of any microcracks and limited degradation in P_max and P_r suggest that electrochemical factors are the prevailing fatigue mechanism. The lower field-induced strain also indicates a lower lattice mismatch. In addition, the higher concentration of La³⁺ donor dopant in PZ-S may reduce the amount of oxygen vacancies in the ceramic, thereby reducing the charged defects responsible for domain wall pinning.⁴⁴

5. Conclusions

The fatigue behavior in bulk AFE ceramics with a comparable recoverable energy density shows a strong association with electric hysteresis. The mechanism of fatigue also exhibits a correlation with the hysteretic nature of the electric-field-induced phase transition. Mechanical damage seems to be dominant in the composition with large hysteresis and electrochemical factors are prevalent in the small-hysteresis composition. The large-hysteresis composition shows a much more severe fatigue deterioration in the maximum polarization, increase in remanent polarization with asymmetric strain behavior after fatigue, compared to the small-hysteresis composition. The recoverable energy of the large-hysteresis composition deteriorates dramatically by a 72% reduction after 2.5 × 10⁶ cycles, while the small-hysteresis composition shows remarkable fatigue resistance and stability with only a 4.5% reduction in recoverable energy and no change in the energy efficiency. Thus, for the design of high energy-density capacitors for long life and stable performance, compositions with low hysteresis should be used.

Author contributions

P. M. and X. T. designed the research plan. P. M. conducted the experiments and drafted the manuscript. J. C. and X. T. advised the thesis research. All authors participated data analysis and manuscript writing.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This material is based upon work supported by the U.S. Department of Energy's Office of Energy Efficiency and Renewable Energy (EERE) under the Advanced Manufacturing Office (AMO) Award Number DE-EE0009105.

References

1. A. Chauhan, S. Patel, R. Vaish and C. R. Bowen, Materials, 2015, 8, 8009–8031.
2. P. Liu, B. Fan, G. Yang, W. Li, H. B. Zhang and S. L. Jiang, J. Mater. Chem. C, 2019, 7, 4587–4594.
3. W. Chao, T. Q. Yang and Y. X. Li, J. Mater. Chem. C, 2020, 8, 17016–17024.
4. H. Liu, L. Fan, S. Sun, K. Lin, Y. Ren, X. Tan, X. Xing and J. Chen, Acta Mater., 2020, 184, 41–49.
5. L. Zhou, R. Z. Zuo, G. Rixecker, A. Zimmermann, T. Utschig and F. Aldinger, J. Appl. Phys., 2006, 99, 044102 /1–8.
6. L. Zhou, G. Rixecker, A. Zimmermann and F. Aldinger, Mater. Sci. Forum, 2005, 475–479, 1193–1196.
7. Q. Jiang, E. C. Subbarao and L. E. Cross, Acta Metall. Mater., 1994, 42, 3687–3694.
8. N. Balke, D. C. Lupascu, T. Blair and A. Gruverman, J. Appl. Phys., 2006, 100, 114117 /1–7.
9. X. J. Lou, J. Appl. Phys., 2009, 105, 024101 /1–24.
10. L. Zhou, G. Rixecker, A. Zimmermann and F. Aldinger, J. Eur. Ceram. Soc., 2006, 26, 883–889.
11. X. J. Lou, Appl. Phys. Lett., 2009, 94, 072901 /1–3.
12. Y. Zhang, D. C. Lupascu, E. Aulbach, I. Baturin, A. Bell and J. Rödel, Acta Mater., 2005, 53, 2203–2213.
13. M. D. Nguyen, J. Eur. Ceram. Soc., 2020, 40, 1886–1895.
14. Q. Jiang, E. C. Subbarao and L. E. Cross, J. Appl. Phys., 1994, 75, 7433–7443.
15. H. R. Jo and C. S. Lynch, J. Appl. Phys., 2016, 119, 024104 /1–7.
16. X. Chen, X. Dong, G. Wang, F. Cao, F. Hu and H. Zhang, J. Am. Ceram. Soc., 2018, 101, 3979–3988.
17. P. Mohapatra, Z. Fan, J. Cui and X. Tan, J. Eur. Ceram. Soc., 2019, 39, 4735–4742.
18. J. Frederick, X. Tan and W. Jo, J. Am. Ceram. Soc., 2011, 94, 1149–1155.
19. C. T. Blue, J. C. Hicks, S. E. Park, S. Yoshikawa and L. E. Cross, Appl. Phys. Lett., 1996, 68, 2942–2944.
20. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
21. Y. Dan, K. Zou, G. Chen, Y. Yu, Y. Zhang, Q. Zhang, Y. Lu, Q. Zhang and Y. He, Ceram. Int., 2019, 45, 11375–11381.
22. F. Zhuo, Q. Li, J. Gao, Y. Wang, Q. Yan, Z. Xia, Y. Zhang and X. Chu, J. Mater. Chem. C, 2016, 4, 7110–7118.
23. Y. Bao, X. Dong and G. Wang, ACS Appl. Energy Mater., 2019, 2, 6939–6951.
24. S.-E. Park, M.-J. Pan, K. Markowski, S. Yoshikawa and L. E. Cross, J. Appl. Phys., 1997, 82, 1798–1803.
25. Y. Feng, Z. Xu, H. Li and X. Yao, Ceram. Int., 2004, 30, 1393–1396.
26. P. Qiao, X. Chen, Z. Liu, G. Wang and X. Dong, Mater. Lett., 2020, 260, 126877 /1–4.
27. Z. Liu, Y. Bai, X. Chen, X. Dong, H. Nie, F. Cao and G. Wang, J. Alloys Compd., 2017, 691, 721–725.
28. C. Xu, Z. Liu, X. Chen, S. Yan, F. Cao, X. Dong and G. Wang, J. Appl. Phys., 2016, 120, 074107 /1–6.
29. R. Xu, Z. Xu, Y. Feng, X. Wei and J. Tian, J. Appl. Phys., 2016, 120, 144102 /1–6.
30. J. Nuffer, D. C. Lupascu, A. Glazounov, H. J. Kleebe and J. Rödel, J. Eur. Ceram. Soc., 2002, 22, 2133–2142.
31. C. Verdier, D. C. Lupascu and J. Rödel, J. Eur. Ceram. Soc., 2003, 23, 1409–1415.
32. X. Liu and X. Tan, Appl. Phys. Lett., 2015, 107, 072908 /1–4.
33. H. Qi, R. Zuo, A. Xie, A. Tian, J. Fu, Y. Zhang and S. Zhang, Adv. Funct. Mater., 2019, 29, 1903877.
34. A. Tian, R. Zuo, H. Qi and M. Shi, J. Mater. Chem. A, 2020, 8, 8352–8359.
35. K. Han, N. Luo, Z. Chen, L. Ma, X. Chen, Q. Feng, C. Hu, H. Zhou, Y. Wei and F. Toyohisa, J. Eur. Ceram. Soc., 2020, 40, 3562–3568.
36. T. F. Zhang, X. G. Tang, Q. X. Liu, S. G. Lu, Y. P. Jiang, X. X. Huang and Q. F. Zhou, AIP Adv., 2014, 4, 1–11.
37. C. Slouka, T. Kainz, E. Navickas, G. Walch, H. Hutter, K. Reichmann and J. Fleig, Materials, 2016, 9, 945 /1–22.
38. J. Nuffer, D. C. Lupascu and J. Rödel, Acta Mater., 2000, 48, 3783–3794.
39. M. Ozgul, S. Trolier-Mckinstry and C. A. Randall, J. Electroceram., 2008, 20, 133–138.
40. D. C. Lupascu, Fatigue in Ferroelectric Ceramics and Related Issues, Springer-Verlag Berlin Heidelberg, 2004.
41. Y. A. Genenko, J. Glaum, M. J. Hoffmann and K. Albe, Mater. Sci. Eng., B, 2015, 192, 52–82.
42. Y. Zhang, I. S. Baturin, E. Aulbach, D. C. Lupascu, A. L. Kholkin, V. Y. Shur and J. Rödel, Appl. Phys. Lett., 2005, 86, 012910 /1–3.
43. J. Cui, Y. S. Chu, O. O. Famodu, Y. Furuya, J. Hattrick-Simpers, R. D. James, A. Ludwig, S. Thienhaus, M. Wuttig, Z. Zhang and I. Takeuchi, Nat. Mater., 2006, 5, 286–290.
44. K. Amanuma, T. Mori, T. Hase, T. Sakuma, A. Ochi and Y. Miyasaka, Jpn. J. Appl. Phys., 1993, 32, 4150–4153.

---