A plethora of structural transitions, distortions and modulations in Cu-doped BiMn₇O₁₂ quadruple perovskites

Abstract

The presence of strongly competing electronic instabilities in a crystalline material can produce fascinating structural phenomena. For example, the A-site-ordered quadruple perovskite BiMn₇O₁₂ hosts both active polar instabilities of the Bi³⁺ lone pair electrons and Jahn–Teller instabilities of Mn³⁺ cations that drive the following sequence of phase transformations on cooling, Im-3 > I2/m > Im > P1, corresponding to orbital ordering and polar distortions. Carrier doping by Cu²⁺ tunes the two instabilities in BiCu_xMn_7−xO₁₂ solid solutions and significantly complicates the system behavior. The x = 0.05 and 0.1 members show the following sequence of phase transformations on cooling, Im-3 > I2/m > R-1(αβγ)0 > R3(00γ)t, and are examples of materials with the electric dipole helicoidal texture in the ground state and a dipole density wave structure in the intermediate R-1(αβγ)0 phase (Science 2020, 369, 680–684). Here, the detailed behavior of the BiCu_xMn_7−xO₁₂ solid solutions with x = 0.2–0.8 was investigated by laboratory X-ray, synchrotron X-ray, and neutron powder diffraction between 5 K and 620 K, and differential scanning calorimetry measurements. Nearly every composition (with a step Δx = 0.1) has a unique behavior when considering both the sequence of phase transitions and the presence of incommensurate superstructure reflections. The sequence Im-3 > HT-Immm(t)* > Immm* > LT-Immm(t)* is realized for x = 0.2 and 0.3 (where t denotes pseudo-tetragonal), Im-3 > I2/m* > Immm(t)* – for x = 0.4, Im-3 > I2/m* > I2/m* – for x = 0.5, Im-3 > I2/m* > Im-3 – for x = 0.6 and 0.7, and Im-3 > R-3 > I2/m > Im-3 – for x = 0.8, where asterisks denote the presence of additional incommensurate reflections. Re-entrance of the high-temperature cubic phase was observed at low temperatures for x = 0.6–0.8 suggesting strong competition between the different electronic instabilities. The re-entrant cubic phases have nearly zero thermal expansion.

---

1. Introduction

Perovskite-structure (formally trivalent) manganites have surprisingly versatile chemical compositions varying from R³⁺MnO₃ (R = Bi, La-Lu and Y)¹ to R³⁺_1−xMn_xMnO₃ (x is from 0 up to 0.4 depending on the size of R³⁺ cation)² to R³⁺Mn₃O₆ (R = Gd–Tm and Y)³ and finally to R³⁺Mn₇O₁₂ (R = Bi, La-Er and Y).^4–21 Even without any doping they show a broad range of interesting chemical and physical properties originating from an interplay between spin and orbital degrees of freedom, such as one of the largest spin-induced ferroelectric polarization for multiferroic materials of type II²² and good catalytic activity.²³

Aliovalent doping introduces a new variable: charge degrees of freedom. This produces more complex phenomena, such as a wider variety of different ground states (including charge- and orbital-ordered insulating antiferromagnets and related stripe structures, ferromagnetic metals, and spin-glass states) and colossal magnetoresistance coupled with phase separation. Doped R³⁺_1−xA²⁺_xMnO₃ perovskites were used as model systems to develop concepts of small polarons, electron–phonon and Jahn–Teller couplings, and double exchange.

In the case of R = Bi a new variable appears: polar instabilities of the Bi³⁺ lone pair electrons. The simple BiMnO₃ perovskite was a controversial compound for many years, but experimental²⁴ and theoretical²⁵ studies have now established that bulk BiMnO₃ crystallizes in a centrosymmetric space group with antipolar displacements of Bi³⁺ cations. On the other hand, A-site-ordered quadruple perovskite BiMn₇O₁₂ shows two low symmetry polar phases^12,13 and the following sequence of phase transformations on cooling, Im-3 > I2/m > Im > P1,²⁰ where all phases are commensurate. Remarkably, large incommensurate modulations of the structure appear through aliovalent doping by Cu²⁺ in BiCu_xMn_7−xO₁₂ solid solutions at small x values of 0.05 and 0.1.²⁶ These compositions exhibit the following sequence of phase transformations on cooling, Im-3 > I2/m > R-1(αβγ)0 > R3(00γ)t, and are the first example of materials with an electric dipole helicoidal texture in the ground state.²⁶ Moreover, they show a dipole density wave structure in the intermediate R-1(αβγ)0 phase.²⁶

At high enough doping levels (x ≥ 1.2), BiCu_xMn_7−xO₁₂ solid solutions adopt the cubic Im-3 structure at all temperatures.²⁷ At slightly smaller doping levels (0.9 ≤ x ≤ 1.1),²⁷ where the average oxidation state of B-site manganese is about +3.25, a charge-ordered and orbital-ordered structure at the B sites is first realized, BiCu²⁺Mn₂³⁺(Mn³⁺₃Mn⁴⁺)O₁₂ – the same structure found in A²⁺Mn₇O₁₂ (= A²⁺Mn³⁺₃(Mn³⁺₃Mn⁴⁺)O₁₂) perovskites.²⁸ However, this charge and orbital order in BiCuMn₆O₁₂ are stable in a limited temperature range of 300 to 130 K. Below 130 K the charge and orbital orders collapse and the cubic Im-3 phase is reentered.²⁷

The structural behavior of BiCu_xMn_7−xO₁₂ solid solutions is remarkable and unique. In this work, we have established the detailed structural properties of BiCu_xMn_7−xO₁₂ solid solutions in the composition range of 0.2 ≤ x ≤ 0.8. We found that almost every composition (with a step Δx = 0.1) has unique behavior when considering both phase transition sequences and incommensurately modulated superstructure reflections. A Im-3 > HT-Immm(t)* > Immm* > LT-Immm(t)* sequence is realized for x = 0.2 and 0.3 (where t denotes pseudo-tetragonal, and asterisks denote the presence of additional incommensurate reflections), Im-3 > I2/m* > Immm(t)* – for x = 0.4, Im-3 > I2/m(1)* > I2/m(2)* – for x = 0.5 (where 1 and 2 distinguish different phases with the same symmetry), Im-3 > I2/m* > Im-3 – for x = 0.6 and 0.7, and Im-3 > R-3 > I2/m > Im-3 – for x = 0.8. A complete composition–temperature phase diagram of BiCu_xMn_7−xO₁₂ solid solutions was constructed.

2. Experimental part

2.1. Sample preparation

BiCu_xMn_7−xO₁₂ samples with x = 0.2–0.8 and a step of 0.1 were prepared from stoichiometric mixtures of CuO (99.99%), Bi₂O₃ (99.9999%), Mn₂O₃, and MnO_1.839. MnO_1.839 is a commercial chemical (‘MnO₂’ from Alfa Aesar, 99.997%), whose oxygen content was determined to be MnO_1.839 from the weight loss after heating in air at 923 K for 24 h (MnO_1.839 was a mixture of Mn₂O₃ and MnO₂ by X-ray powder diffraction). Single-phase Mn₂O₃ was prepared from ‘MnO₂’ (99.997%) by heating in air at 923 K for 24 h. The mixtures were placed in Au capsules and treated at 6 GPa in a belt-type high-pressure apparatus at about 1370 K for 90 min (heating time to the desired temperature was 10 min). After the heat treatment, the samples were quenched to room temperature, and the pressure was slowly released. The samples were black dense pellets.

2.2. X-ray and neutron powder diffraction

Laboratory X-ray powder diffraction (XRPD) data were collected at room temperature using a RIGAKU MiniFlex600 diffractometer using Cu Kα radiation (2θ range of 10–80°, a step width of 0.02°, and a counting speed of 1° min⁻¹). Some of the BiCu_xMn_7−xO₁₂ samples contained trace amounts of Bi₂O₂CO₃ impurity. Low-temperature (LT) (from 10 K to 300 K) and high-temperature (HT) (from 298 K to 620 K) laboratory XRPD data were collected on a RIGAKU SmartLab using Cu Kα₁ radiation (45 kV, 200 mA; a 2θ range of 10–110°, a step width of 0.02°, and a scan speed of 2–4° min⁻¹) with a cryostat system and a furnace attachment. XRPD patterns were analyzed and lattice parameters were obtained by the Rietveld method using RIETAN-2000.²⁹ In the LT XRPD experiments, powder samples were fixed with Apiezon-N grease. The surface roughness of the grease/sample mixtures and its evolution with temperature under high vacuum conditions resulted in a larger dispersion of the lattice parameters determined by LT XRPD compared to the lattice parameters determined by HT XRPD.

Synchrotron XRPD data were measured (1) between 110 K and 520 K on a large Debye–Scherrer camera at the undulator beamline BL15XU of SPring-8,^30,31 where the intensity data were collected between 2° and 60.23° at 0.003° intervals in 2θ, and the incident beam was monochromatized at λ = 0.65298 Å, and (2) between 100 K and 460 K on the beamline BL02B2 of SPring-8,³² where the intensity data were collected between 2.08° and 78.22° at 0.006° intervals in 2θ, and the incident beam was monochromatized at λ = 0.420138 Å. The samples were put into Lindemann glass capillaries (inner diameter: 0.1 mm), which were rotated during measurements. Synchrotron XRPD data were analyzed by the Rietveld method using the RIETAN-2000 program.²⁹ Sample cooling was performed in air by cold N₂ gas flow; therefore, ice sometimes accumulated on capillaries and produced additional artifact reflections on data collected on BL15XU; those ice reflections could be easily identified in the Rietveld fitting.

Neutron powder diffraction data for BiCu_0.5Mn_6.5O₁₂ were measured at the ISIS pulsed neutron and muon facility of the Rutherford Appleton Laboratory (UK) on the WISH diffractometer located at the second target station.³³ The sample (∼1.7 g) was loaded into a cylindrical 6 mm diameter vanadium can and measured from 1.5 K up to 400 K on heating. Rietveld refinements of the crystal structures were performed using the FullProf program³⁴ against the data measured in detector banks at average 2θ values of 58°, 90°, 122°, and 154°, each covering 32° of the scattering plane.

2.3. Thermal properties

Differential scanning calorimetry (DSC) curves of powder samples (and pellets in a few cases) were recorded on a Mettler Toledo DSC1 STAR^e system at heating/cooling rates of 10 K min⁻¹ between 130 K and maximum 650 K in Al capsules. Three runs were performed to check and confirm very good reproducibility.

3. Results and discussion

3.1. BiCu_xMn_7−xO₁₂ solid solutions with x = 0.2 and 0.3

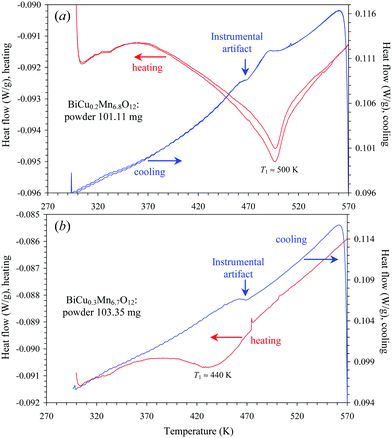
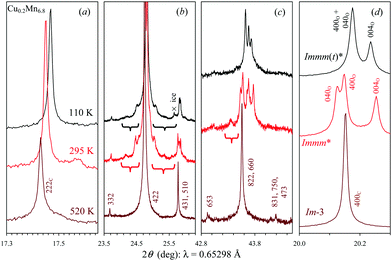
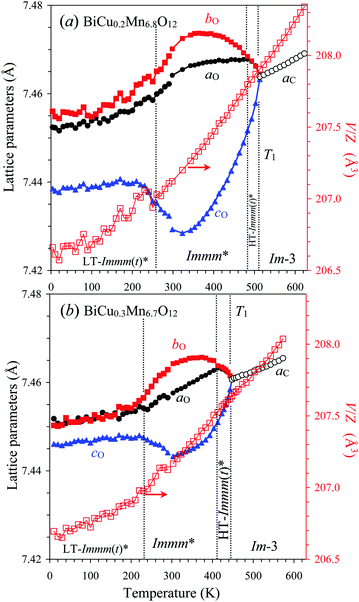
DSC measurements (Fig. 1a) of BiCu_0.2Mn_6.8O₁₂ showed the presence of a broad peak on heating, which was centered at T₁ ≈ 500 K, with tails on both sides from the maximum. In the case of BiCu_0.3Mn_6.7O₁₂, the DSC peak was significantly broader on heating with T₁ ≈ 440 K (Fig. 1b), and no DSC anomalies were detected on cooling. No DSC anomalies were detected below 300 K in both samples (Fig. S1, ESI†).

Fig. 1 DSC curves of (a) BiCu_0.2Mn_6.8O₁₂ (two runs) and (b) BiCu_0.3Mn_6.7O₁₂ (one run) on heating (left-hand axes) and cooling (right-hand axes) at 10 K min⁻¹. Note that the heating and cooling difference scale ranges are different. Small bumps near 470 K on cooling curves are instrumental artifacts.

Laboratory and synchrotron (Fig. 2) XRPD measurements showed that above T₁ reflections could be indexed in a cubic system, and below T₁ down to 10 K – in an orthorhombic system. The 222 cubic reflection remained unsplit even in the synchrotron XRPD data (Fig. 2a) suggesting no deviations from the orthorhombic structure. Synchrotron XRPD data clearly showed the presence of modulated reflections at RT and at low temperatures (Fig. 2b and 3b), a few weak modulated reflections were also observed in laboratory XRPD data (Fig. S2, ESI†). The temperature dependence of the lattice parameters and unit-cell volume is given in Fig. 4, where the Immm model was used in the Rietveld fitting below T₁. Both samples showed the existence of narrow HT regions where the refined orthorhombic (O) lattice parameters a_O and b_O exactly matched indicating that the crystal system became metrically tetragonal. However, there are no tetragonal subgroups of the parent cubic Im-3 structure. Therefore, the real symmetry should remain orthorhombic, and we label it HT-Immm(t)*, where t stands for pseudo-tetragonal and the asterisk denotes the presence of additional incommensurately modulated reflections. Modulated reflections were observed at all temperatures below T₁ (Fig. S2 and S3, ESI†). There were also LT regions, where the refined lattice parameters a_O and b_O nearly (x = 0.2) or exactly (x = 0.3) matched. The pseudo-tetragonality can also be seen from the merging of the (400) and (040) orthorhombic reflections in the synchrotron XRPD data (Fig. 2d and 3d). Incommensurately modulated reflections remained in the low-temperature Immm(t)* phase (LT-Immm(t)*, Fig. 2b and 3b), they were only slightly changed compared with the RT data (that is, with the Immm* phase).

Fig. 2 Fragments of synchrotron XRPD data (BL15XU) of BiCu_0.2Mn_6.8O₁₂ in different 2θ regions at T = 110 K, 295 K and 520 K. Some reflection indexes for the cubic phase (without notations and with the C notation) and the orthorhombic (O) phase are given. A cross marks a possible reflection from ice. Braces show modulated reflections.

Fig. 3 Fragments of synchrotron XRPD data (BL15XU) of BiCu_0.3Mn_6.7O₁₂ in different 2θ regions at T = 110 K and 295 K. Some reflection indexes for the orthorhombic (O) phase are given. Braces show modulated reflections.

Fig. 4 Temperature dependence of the lattice parameters (left-hand axes) and the unit-cell volume (V/Z) (right-hand axes) in (a) BiCu_0.2Mn_6.8O₁₂ and (b) BiCu_0.3Mn_6.7O₁₂ from laboratory XRPD data. All measurements are performed on heating. C: cubic, O: orthorhombic, t: pseudo-tetragonal. HT: high-temperature, LT: low-temperature. Stars indicate the presence of additional incommensurately modulated reflections. α_V = 1.8(4) × 10⁻⁵ at 300–610 K for x = 0.2, α_V = 1.5(5) × 10⁻⁵ at 300–560 K and α_V ∼ 5 × 10⁻⁶ at 10–210 K for x = 0.3.

Therefore, there are four different crystallographic phases in BiCu_0.2Mn_6.8O₁₂ and BiCu_0.3Mn_6.7O₁₂, Im-3 > HT-Immm(t)* > Immm* > LT-Immm(t)*, appearing on cooling.

3.2. BiCu_xMn_7−xO₁₂ solid solutions with x = 0.4

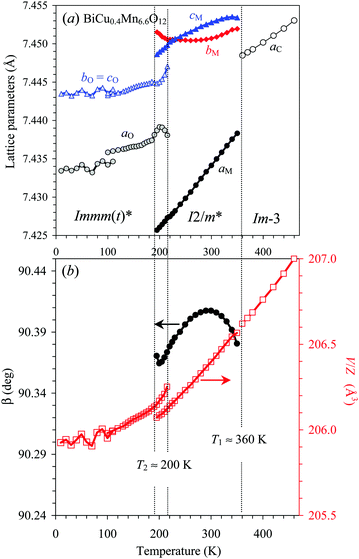
DSC data of the x = 0.4 sample (Fig. 5a and Fig. S5 of the ESI†) showed the presence of one relatively sharp peak on heating (at T₁ ≈ 360 K) and cooling and one very broad peak centered at T₂ ≈ 200 K, which was only observed on heating curves.

Fig. 5 DSC curves of (a) BiCu_0.4Mn_6.6O₁₂ (three runs) and (b) BiCu_0.5Mn_6.5O₁₂ (one run) on heating (left-hand axes) and cooling (right-hand axes) at 10 K min⁻¹. Note that the heating and cooling difference scale ranges are the same.

Above T₁, all reflections in the synchrotron XRPD data of the x = 0.4 sample can be fitted by the cubic Im-3 model, and between T₁ and T₂ in the monoclinic I2/m model (Fig. S6, ESI†), which was observed in pure BiMn₇O₁₂ and slightly doped BiCu_xMn_7−xO₁₂ with x = 0.1.^20,26 Clear splitting of the 222 cubic reflection was observed below T₁, which then disappeared below T₂. The presence of a single reflection, corresponding to the 222 cubic reflection, confirms that the symmetry is orthorhombic below T₂ (Fig. 6a). However, the 040 and 004 orthorhombic reflections merge at all temperatures below T₂ on synchrotron and laboratory XRPD data. Therefore, lattice parameters below T₂ were refined in space group Immm with a constraint, b_O = c_O. The temperature dependence of the lattice parameters of BiCu_0.4Mn_6.6O₁₂ is shown in Fig. 7. Therefore, there are three different crystallographic phases in BiCu_0.4Mn_6.6O₁₂, Im-3 > I2/m* > Immm(t)*, appearing on cooling, where again the asterisks indicate the presence of additional incommensurate reflections.

Fig. 6 Fragments of synchrotron XRPD data (BL02B2) of BiCu_0.4Mn_6.6O₁₂ in different 2θ regions at T = 100 K, 170 K, 230 K, 295 K and 380 K. Some reflection indexes for the cubic phase (without notations and with the C notation), the monoclinic (M) phase and the orthorhombic (O) phase are given. Braces show incommensurately modulated reflections.

Fig. 7 Temperature dependence of (a) the lattice parameters and (b) monoclinic β angle (left-hand axis) and the unit-cell volume (V/Z) (right-hand axis) in BiCu_0.4Mn_6.6O₁₂ from laboratory XRPD data (from 10 K to 110 K) and synchrotron XRPD data (from 100 K to 460 K). All measurements were performed on heating. M: monoclinic, C: cubic, O: orthorhombic. Stars indicate the presence of additional incommensurately modulated reflections. α_V = 1.8(2) × 10⁻⁵ at 360–440 K in the C phase, α_V = 1.5(3) × 10⁻⁵ at 195–330 K in the M phase and α_V = 8.1(1.6) × 10⁻⁶ at 100–175 K in the O phase (based on synchrotron XRPD data).

3.3. BiCu_xMn_7−xO₁₂ solid solutions with x = 0.5

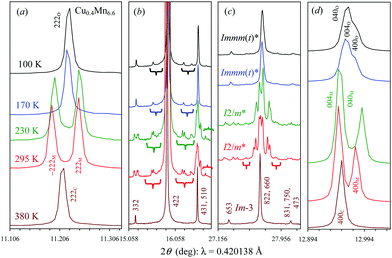
DSC data of the x = 0.5 sample (Fig. 5b) showed the presence of one sharp peak on heating (at T₁ ≈ 365 K) and cooling. The behavior in BiCu_0.5Mn_6.5O₁₂ below T₁ was similar to that of BiCu_0.4Mn_6.6O₁₂ with one exception in that the monoclinic splitting of reflections (e.g., the 222 cubic reflection) could be observed in laboratory and synchrotron XRPD data at all temperatures below T₁ down to 10 K (Fig. 8 and Fig. S6 of the ESI†). Therefore, the lattice parameters were refined in the space group I2/m. Fig. 9 gives the temperature dependence of the lattice parameters of BiCu_0.5Mn_6.5O₁₂ (similar temperature dependence of the lattice parameters was obtained based on neutron diffraction data (Fig. S7, ESI†)); these data show that BiCu_0.5Mn_6.5O₁₂ has the second structural transition near T₂ ≈ 120 K, where there were steps in the lattice parameters and an abrupt change in the behavior of the monoclinic angle. This temperature was below the reach of our DSC experiments; therefore, only one sharp peak was observed in the DSC curves at T₁ ≈ 365 K (Fig. 5b).

Fig. 8 Fragments of synchrotron XRPD data (BL15XU) of BiCu_0.5Mn_6.5O₁₂ in different 2θ regions at T = 110 K, 170 K, 295 K and 385 K. Some reflection indexes for the cubic phase (without notations and with the C notation) and the monoclinic (M) phase are given. A cross marks a possible reflection from ice. Braces show incommensurately modulated reflections.

Fig. 9 Temperature dependence of (a) the lattice parameters and (b) monoclinic β angle (left-hand axis) and the unit-cell volume (V/Z) (right-hand axis) in BiCu_0.5Mn_6.5O₁₂ from laboratory XRPD data. Measurements were performed on heating. C: cubic, M: monoclinic. Stars indicate the presence of additional incommensurately modulated reflections. α_V = 2.0(3) × 10⁻⁵ at 370–510 K in the C phase and α_V ∼ 5 × 10⁻⁶ at 10–100 K in the M phase.

Therefore, there are three different crystallographic phases in BiCu_0.5Mn_6.5O₁₂, Im-3 > I2/m(1)* > I2/m(2)*, appearing on cooling, where (1) and (2) mean different phases with the same symmetry. The behavior of BiCu_0.4Mn_6.6O₁₂ and BiCu_0.5Mn_6.5O₁₂ is quite similar between T₁ and T₂ including the dome-like changes of the monoclinic angle and the crossing in the temperature dependence of the monoclinic b_M and c_M lattice parameters when approaching T₂. However, below T₂ they adopt different distortions.

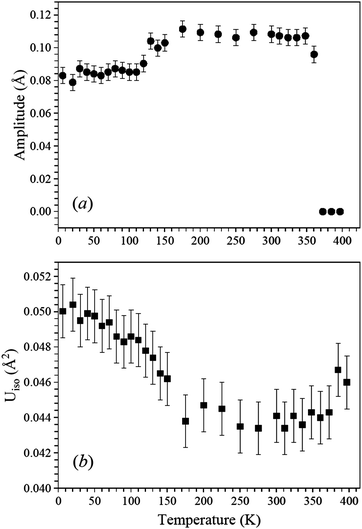
The structural evolution of BiCu_0.5Mn_6.5O₁₂ through the phase transitions was studied in detail by neutron diffraction. The most prominent features are presented in Fig. 10. Structural parameters in the average I2/m and Im-3 models at some selected temperatures are summarized in Tables S1 and S2 (ESI†), and Rietveld refinement fits are shown in Fig. S8 (ESI†). As neutron scattering lengths of Cu (7.718 fm) and Mn (−3.73 fm) are very different the Cu/Mn distribution can be precisely studied. Our analysis of the cubic modification (with the minimum number of refined structural parameters) showed that the B sites are solely occupied by Mn. The refined occupation of the A’ site (0.149(4)Cu + 0.851Mn) was close to the nominal value (0.167Cu + 0.833Mn). The Im-3 > I2/m(1)* transition is driven by the Jahn–Teller instability of Mn³⁺ cations located at the B sites, and the corresponding orbital order is similar to that observed in the prototype Jahn–Teller perovskite system LaMnO₃; the associated structural distortion transforms as the M₂⁺ irreducible representation of the parent cubic Pm-3m space group (for a general ABO₃ perovskite).³⁵ The amplitude of the M₂⁺ distortive mode therefore can be taken as a quantitative measure of the Jahn–Teller distortion averaged over the two symmetry independent B-site Mn cations in the average monoclinic structure of BiCu_0.5Mn_6.5O₁₂. As shown in Fig. 10, at the I2/m(1)* > I2/m(2)* transition Jahn–Teller distortions are reduced and at the same time the atomic displacement parameter of the Bi atom is enhanced. The latter most likely indicates an increase in the static off-centric displacements optimizing the lone pair instability. Thus, these experimental findings further support the presence of strong competitions between the lone pair and Jahn–Teller electronic instabilities. Apparently, the LT (iso)structural transitions in other compositions of the series with x = 0.2, 0.3 and 0.4 are similar in origin, although additional studies and quantitative characterizations of the structural modulations are required to confirm this assumption.

Fig. 10 Temperature dependence of (a) the average amplitude of the Jahn–Teller distortions for two octahedral sites (Mn4 and Mn5) and (b) the atomic displacement parameter of the Bi site in the ideal (0, 0, 0) positions in BiCu_0.5Mn_6.5O₁₂ from neutron diffraction data.

3.4. BiCu_xMn_7−xO₁₂ solid solutions with x = 0.6 and 0.7

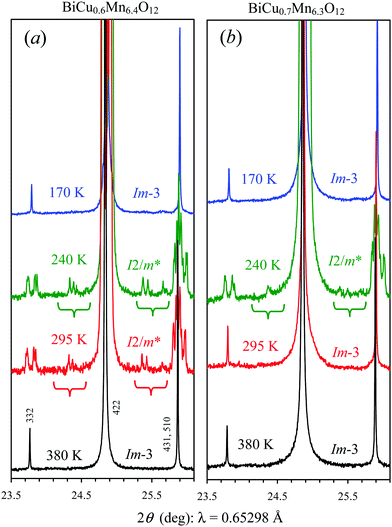
DSC data (Fig. 11) showed the presence of two relatively sharp peaks on heating with T₁ ≈ 330 K (x = 0.6), T₁ ≈ 289 K (x = 0.7), T₂ ≈ 206 K (x = 0.6) and T₂ ≈ 206 K (x = 0.7). Cooling curves revealed large hysteresis at T₂; the hysteresis reached about 25 K for x = 0.7 (as a peak was centered near 181 K on cooling). The hysteresis was probably larger for x = 0.6; this is why no clear peaks were observed on cooling as the peak may have been hidden by extrinsic effects (below about 160–170 K the DSC system could not support a constant cooling rate of 10 K min⁻¹ resulting in peak-like artifacts).

Fig. 11 DSC curves of BiCu_0.6Mn_6.4O₁₂ (black), BiCu_0.7Mn_6.3O₁₂ (red), and BiCu_0.8Mn_6.2O₁₂ (blue) on (a) heating and (b) cooling at 10 K min⁻¹. Note the heating and cooling difference scale ranges are the same.

Above T₁ and below T₂, reflections on laboratory and synchrotron XRPD data could be indexed in the cubic space group Im-3, and between T₁ and T₂ – in the monoclinic space group I2/m (Fig. 12 and Fig. S9 of the ESI†). The temperature dependence of the lattice parameters and unit-cell volume is given in Fig. 13. The monoclinic angle β (Fig. 13b) shows a dome-like feature in both compounds, but this feature was less pronounced in comparison with the dome-like feature of BiCu_0.5Mn_6.5O₁₂ in the I2/m(1)* phase (Fig. 9b). It is also interesting that the monoclinic b_M and c_M lattice parameters were the same in BiCu_0.6Mn_6.4O₁₂ in the whole temperature range where this phase is stable. Therefore, both BiCu_0.6Mn_6.4O₁₂ and BiCu_0.7Mn_6.3O₁₂ show a re-entrant phase transition to the cubic phase and the following sequence of phase transformations, Im-3 > I2/m* > Im-3. Note that the I2/m* phases should actually be slightly different in both compounds as they have different incommensurately modulated reflections (Fig. 12).

Fig. 12 Fragments of synchrotron XRPD data (BL15XU) of (a) BiCu_0.6Mn_6.4O₁₂ and (b) BiCu_0.7Mn_6.3O₁₂ in a 2θ region of 23.5–26.1 deg at T = 170 K, 240 K, 295 K and 380 K. Some reflection indexes for the cubic phase (without notations) are given. Braces show modulated reflections.

Fig. 13 Temperature dependence of (a) the lattice parameters and (b) monoclinic β angle (left-hand axis) and the unit-cell volume (V/Z) (right-hand axis) in BiCu_0.6Mn_6.4O₁₂ (triangles) and BiCu_0.7Mn_6.3O₁₂ (circles) from laboratory XRPD data (below 300 K). Synchrotron XRPD data were used above 300 K. C: cubic, M: monoclinic. Stars indicate the presence of additional modulated reflections. α_V ∼4 × 10⁻⁶ at 10–180 K in the C phase for x = 0.6 and 0.7.

3.5. BiCu_xMn_7−xO₁₂ solid solutions with x = 0.8

DSC data (Fig. 11) showed the presence of two relatively sharp peaks on heating with T₁ ≈ 296 K and T₂ ≈ 183 K. Cooling curves revealed only one peak centered at 287 K, the second peak could not be seen due to extrinsic effects on DSC cooling curves.

Laboratory and synchrotron XRPD data revealed the following sequence of phase transitions on cooling: Im-3 > R-3 > I2/m > Im-3 (Fig. 14 and Fig. S10 of the ESI†). However, the R-3 phase was not observed as purely single-phase on synchrotron XRPD data: at 290 K, about 35 wt% of the cubic Im-3 phase remained, and about 15 wt% of the monoclinic I2/m phase already appeared at 275 K. A smaller measurement step would probably be needed to detect a single R-3 phase. The R-3 and I2/m phases coexisted from 275 K down to 223 K. The single I2/m phase was only observed at 206 K. Because of the complex phase co-existence, the temperature dependence of the lattice parameters was extracted from synchrotron XRPD data between 120 and 300 K; below 160 K, where the cubic phase is stable, laboratory XRPD data were used (Fig. 15). It should be noted that no modulated reflections were observed in this monoclinic I2/m phase. Also, no modulated reflections were found in the R-3 phase.

Fig. 14 Fragments of synchrotron XRPD data (BL15XU) of BiCu_0.8Mn_6.2O₁₂ in different 2θ regions at different temperatures. Some reflection indexes for the cubic phase (without notations and with the C notation), the monoclinic (M) phase, and the R-3 phase (R) are given. Crosses mark a reflection from ice. tr.: trace.

Fig. 15 Temperature dependence of (a) the lattice parameters and (b) monoclinic β angle (left-hand axis) and the unit-cell volume (V/Z) (right-hand axis) in BiCu_0.8Mn_6.2O₁₂ from laboratory XRPD data (open circles; 10–160 K) and synchrotron XRPD data (filled symbols; 120–440 K). All measurements were performed on heating. C: cubic, M: monoclinic. R: R-3. α_V = 1.93(13) × 10⁻⁵ in the HT C phase, α_V = 2.3(6) × 10⁻⁵ in the R phase, α_V = 3(1) × 10⁻⁵ in the M phase and α_V = 6(3) × 10⁻⁶ at 120–180 K in the LT C phase.

3.6. Composition–temperature phase diagram of BiCu_xMn_7−xO₁₂

A complete composition–temperature phase diagram of the BiCu_xMn_7−xO₁₂ system (Fig. 16) can be constructed based on the results of this work for x = 0.2–0.8 and the literature data for x = 0,²⁰ 0.05, 0.1,²⁶ 0.9, 1.0, 1.1 and 1.2.²⁷ We emphasize that available laboratory and synchrotron XRPD data do not allow us to distinguish between centrosymmetric and non-centrosymmetric space groups at the moment. Therefore, we always assigned centrosymmetric space groups. Detailed structural analysis or other methods will be needed in future studies to determine the presence or absence of a center of symmetry. For example, a polar space group of R3(00γ)t was found in BiCu_0.1Mn_6.9O₁₂ below about 400 K based on the crystal structure analysis of neutron diffraction data and the observation of a ferroelectric P–E hysteresis loop.²⁶ Very detailed structural studies will also be needed in the future to determine full structural models, which could account for all observed modulated reflections. The construction of such models is out of the scope of the present study.

Fig. 16 Composition–temperature phase diagram of BiCu_xMn_7−xO₁₂ solid solutions for 0 ≤ x ≤ 1.2. Stars indicate the presence of additional incommensurately modulated reflections, t stands for pseudo-tetragonal. Shaded regions show mixed-phase regions. Magnetic transition temperatures (T_mag: red and pink symbols) are also plotted for completeness (but detailed magnetic studies will be reported elsewhere). T₁ denotes a phase transition from the high-temperature cubic Im-3 phase. T₂ denotes the lowest temperature structural phase transition.

Here we mention that for both monoclinic and orthorhombic structures there are several non-equivalent non-centrosymmetric structures. For instance, in the case of the Immm space group, there are four non-centrosymmetric isotropy subgroups with the same reflection conditions as Immm, namely I222, I2mm, Im2m and Imm2. In spite of the fact that the latter three are Imm2 in the standard setting, the corresponding structures are non-equivalent and imply different directions to become polar. The I2/m space group has Im and I2 non-centrosymmetric isotropy subgroups.

At high temperatures, the parent cubic Im-3 structure is stable for all the compositions. On cooling, the cubic structure transforms into different modifications driven by the orbital ordering of Mn³⁺ cations (as in the I2/m phases) and/or charge ordering of Mn³⁺/Mn⁴⁺ cations (realized, for example, in the R-3 phase for x = 0.8–1.1), where Mn⁴⁺ cations appear as a result of Cu²⁺ doping. Neutron diffraction demonstrated that Cu²⁺ cations are localized in the square-planar A’ site as expected because Cu²⁺ cations strongly prefer Jahn–Teller-distorted sites. As Mn⁴⁺ cations cannot be located in square-planar sites they should exclusively appear at the octahedral B sites.

The first HT structural transition from the cubic phase (at T₁) appears to be first-order for x = 0–0.1 and 0.4–1.1 judging from sharp peaks on DSC curves, hysteresis between the heating/cooling DSC curves and abrupt changes of the lattice parameters. However, no detectable jumps of the (normalized) unit-cell volume were observed, for example, for x = 0.4 (Fig. 7) and 0.5 (Fig. 9). On the other hand, the first HT transition showed all signs of a second-order phase transition for x = 0.2 and 0.3, where the HT-Immm(t)* phase first emerges from the cubic phase. Namely, the orthorhombic lattice parameters merged gradually (Fig. 4), no detectable jumps of the (normalized) unit-cell volume were observed, and there were very broad DSC anomalies (Fig. 1). However, any transition from the cubic Im-3 to either Immm, I2/m or R-3 must be first order based on the symmetry grounds. It is related to the fact that the relevant irreducible representations, mediating the corresponding symmetry lowering, allow a third power invariant in the Landau free-energy decomposition. So, all these representations do not satisfy the Landau criteria for continuous phase transitions. LT structural phase transitions for x = 0.4–1.1 are characterized by large DSC hysteresis for all compositions (if observable), abrupt changes of the lattice parameters and jumps on the (normalized) unit-cell volume suggesting their strong first-order nature.

During the first HT structural transition large structural distortions are realized. However, at lower temperatures, structural distortions are suppressed for x = 0.2–0.5 as can be seen from the reduced reflection splitting, the merging of some lattice parameters, and temperature evolution of the Jahn–Teller distortions (Fig. 10a). For the x = 0.6–1.1 compositions, structural distortions are completely suppressed with the re-entrance of the cubic phase. There are no (static) polar, orbital and charge orderings in the cubic phase. Therefore, the re-entrance of the cubic phase suggests that competition among different instabilities in BiCu_xMn_7−xO₁₂ is very strong and of comparable strength and intensifies with decreasing temperature, and the system is frustrated to a degree when it cannot choose a preferable instability. We note that the re-entrant low-temperature cubic phases demonstrate nearly zero thermal expansion with the volumetric coefficient of thermal expansion (α_V = (1/V)*ΔV/ΔT) of about 4 × 10⁻⁶.

The BiCu_0.8Mn_6.2O₁₂ composition is located between two major structural distortions, I2/m and R-3. This fact could be the origin of its complex behavior. The R-3 phase is characterized by B-site Mn³⁺/Mn⁴⁺ charge ordering (where the ideal 3 : 1 ratio of Mn³⁺ : Mn⁴⁺ is realized in BiCuMn₆O₁₂).²⁷ As the Mn³⁺ : Mn⁴⁺ ratio at the B sites approaches the ideal value in BiCu_0.8Mn_6.2O₁₂ the charge-ordered distortion first wins. But the R-3 phase has unusual compressed Mn³⁺ octahedra, and such Jahn–Teller distortions are very unstable.³⁶ Therefore, the I2/m phase wins on further cooling as it has usual elongated Jahn–Teller distortions. Polar instabilities from the presence of Bi³⁺ cations could add additional frustration to the system eventually leading to the cubic symmetry on further cooling. We note that even small compositional inhomogeneity could complicate the behavior of BiCu_0.8Mn_6.2O₁₂ even though we did not observe any evidence of inhomogeneity in the cubic modifications (such as, reflection broadening or splitting).

The behavior of the x = 0.6–1.1 compositions can also be discussed from the opposite direction, that is, during heating. Different ordered states, such as spin-, charge-, orbital-ordered, and superconducting states, are destroyed when temperature increases in the vast majority of condensed-matter systems. A famous exception to this general rule is the so-called Pomeranchuk effect, when the liquid ground state of ³He transforms to a solid when temperature increases.^37,38 The BiCu_xMn_7−xO₁₂ solid solutions with x = 0.6–1.1 can also be considered as exceptions to the general rule as their disordered cubic ground states transform to the orbital-ordered state (x = 0.6 and 0.7) or the orbital- and charge-ordered states (x = 0.8–1.1) when temperature increases.

4. Conclusion

Undoped BiMn₇O₁₂ has active electronic instabilities related to Bi³⁺ lone-pair electrons and Jahn–Teller Mn³⁺ cations. Both instabilities are in play resulting in the orbital order transition, Im-3 > I2/m, and in polar distortions, I2/m > Im > P1. Carrier doping by Cu²⁺ was found to tune the competing electronic instabilities of BiMn₇O₁₂ resulting in a complex composition–temperature phase diagram of the BiCu_xMn_7−xO₁₂ solid solution, with the appearance of a number of different crystallographic phases the majority of which hosted additional incommensurate structural modulations. Competition between instabilities in BiCu_xMn_7−xO₁₂ intensifies for x = 0.6–1.1 resulting in the re-entrance of the high-temperature cubic phase in the ground state. The re-entrant cubic phases have nearly zero thermal expansion.

Author contributions

Alexei A. Belik: conceptualization, investigation, formal analysis, data curation, writing – original draft, writing – review and editing. Yoshitaka Matsushita: investigation. Masahiko Tanaka: investigation. Roger D. Johnson: formal analysis, investigation, writing – review & editing. Dmitry D. Khalyavin: formal analysis, investigation, writing – review and editing.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was partly supported by JSPS KAKENHI Grant Numbers JP19H05819 and JP20H05276, a research grant (40–37) from Nippon Sheet Glass Foundation for Materials Science and Engineering, and Innovative Science and Technology Initiative for Security (Grant Number JPJ004596) from Acquisition, Technology, and Logistics Agency (ATLA), Japan. The synchrotron radiation experiments were performed at SPring-8 with the approval of the NIMS Synchrotron X-ray Station (Proposal Numbers: 2016B4504, 2017A4503 and 2019A4501) and Japan Synchrotron Radiation Research Institute (JASRI) (Proposal No. 2021A1334). We thank Dr Y. Katsuya for his assistance at BL15XU of SPring-8, and Dr S. Kobayashi for his assistance at BL02B2 of SPring-8. RDJ acknowledges support from a Royal Society University Research Fellowship.

References

1. J.-S. Zhou and J. B. Goodenough, Unusual evolution of the magnetic interactions versus structural distortions in RMnO₃ perovskites, Phys. Rev. Lett., 2006, 96, 247202.
2. L. Zhang, A. Dönni, V. Y. Pomjakushin, K. Yamaura and A. A. Belik, Crystal and magnetic structures and properties of (Lu_1−xMn_x)MnO₃ solid solutions, Inorg. Chem., 2018, 57, 14073–14085.
3. L. Zhang, Y. Matsushita, K. Yamaura and A. A. Belik, Five-fold ordering in high-pressure perovskites RMn₃O₆ (R = Gd–Tm and Y), Inorg. Chem., 2017, 56, 5210–5218.
4. A. N. Vasil’ev and O. S. Volkova, New functional materials AC₃B₄O₁₂ (Review), Low Temp. Phys., 2007, 33, 895–914.
5. B. Bochu, J. Chenavas, J. C. Joubert and M. Marezio, High pressure synthesis and crystal structure of a new series of perovskite-like compounds CMn₇O₁₂ (C = Na, Ca, Cd, Sr, La, Nd), J. Solid State Chem., 1974, 11, 88–93.
6. A. Prodi, E. Gilioli, R. Cabassi, F. Bolzoni, F. Licci, Q. Huang, J. W. Lynn, M. Affronte, A. Gauzzi and M. Marezio, Magnetic Structure of the high-density single-valent e_g Jahn-Teller system LaMn₇O₁₂, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 085105.
7. H. Okamoto, M. Karppinen, H. Yamauchi and H. Fjellvag, High-temperature synchrotron X-ray diffraction study of LaMn₇O₁₂, Solid State Sci., 2009, 11, 1211–1215.
8. R. Cabassi, F. Bolzoni, E. Gilioli, F. Bissoli, A. Prodi and A. Gauzzi, Jahn-Teller-induced crossover of the paramagnetic response in the singly valent eg system LaMn₇O₁₂, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 214412.
9. F. Mezzadri, M. Calicchio, E. Gilioli, R. Cabassi, F. Bolzoni, G. Calestani and F. Bissoli, High-pressure synthesis and characterization of PrMn₇O₁₂ polymorphs, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 014420.
10. M. Verseils, F. Mezzadri, D. Delmonte, B. Baptiste, Y. Klein, S. Shcheka, L. C. Chapon, T. Hansen, E. Gilioli and A. Gauzzi, Effect of chemical pressure induced by La³⁺/Y³⁺ substitution on the magnetic ordering of (AMn₃)Mn₄O₁₂ quadruple perovskites, Phys. Rev. Mater., 2017, 1, 064407.
11. N. Imamura, M. Karppinen, T. Motohashi, D. Fu, M. Itoh and H. Yamauchi, Positive and negative magnetodielectric effects in A-site ordered (BiMn₃)Mn₄O₁₂ perovskite, J. Am. Chem. Soc., 2008, 130, 14948–14949.
12. F. Mezzadri, G. Calestani, M. Calicchio, E. Gilioli, F. Bolzoni, R. Cabassi, M. Marezio and A. Migliori, Synthesis and characterization of multiferroic BiMn₇O₁₂, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 100106(R).
13. W. A. Slawinski, H. Okamoto and H. Fjellvag, Triclinic crystal structure distortion of multiferroic BiMn₇O₁₂, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2017, 73, 313–320.
14. N. Imamura, M. Karppinen and H. Yamauchi, Synthesis and properties of monoclinic and cubic forms of the A-site-ordered (BiMn₃)Mn₄O₁₂ perovskite, Chem. Mater., 2009, 21, 2179–2183.
15. H. Okamoto, N. Imamura, M. Karppinen, H. Yamauchi and H. Fjellvag, Square coordinated MnO₂-units in BiMn₇O₁₂, Inorg. Chem., 2010, 49, 8709–8712.
16. H. Okamoto, N. Imamura, M. Karppinen, H. Yamauchi and H. Fjellvag, Crystal structure of the monoclinic and cubic polymorphs of BiMn₇O₁₂, J. Solid State Chem., 2010, 183, 186–191.
17. F. Mezzadri, M. Buzzi, C. Pernechele, G. Calestani, M. Solzi, A. Migliori and E. Gilioli, Polymorphism and multiferroicity in Bi_1−x/3(Mn^III₃)(Mn^III_4−xMn^IV_x)O₁₂, Chem. Mater., 2011, 23, 3628–3635.
18. N. Imamura, K. Singh, D. Pelloquin, C. Simon, T. Sasagawa, M. Karppinen, H. Yamauchi and A. Maignan, Magnetodielectric response of square-coordinated MnO₂ unit in cubic BiMn₇O₁₂, Appl. Phys. Lett., 2011, 98, 072903.
19. A. Gauzzi, G. Rousse, F. Mezzadri, G. L. Calestani, G. Andre, F. Bouree, M. Calicchio, E. Gilioli, R. Cabassi, F. Bolzoni, A. Prodi, P. Bordet and M. Marezio, Magnetoelectric coupling driven by inverse magnetostriction in multiferroic BiMn₃Mn₄O₁₂, J. Appl. Phys., 2013, 113, 043920.
20. A. A. Belik, Y. Matsushita, Y. Kumagai, Y. Katsuya, M. Tanaka, S. Y. Stefanovich, B. I. Lazoryak, F. Oba and K. Yamaura, Complex structural behavior of BiMn₇O₁₂ quadruple perovskite, Inorg. Chem., 2017, 56, 12272–12281.
21. L. Zhang, N. Terada, R. D. Johnson, D. D. Khalyavin, P. Manuel, Y. Katsuya, M. Tanaka, Y. Matsushita, K. Yamaura and A. A. Belik, High-pressure synthesis, structures, and properties of trivalent A-site-ordered quadruple perovskites RMn₇O₁₂ (R = Sm, Eu, Gd, and Tb), Inorg. Chem., 2018, 57, 5987–5998.
22. T. Kimura, T. Goto, H. Shintani, K. Ishizaka, T. Arima and Y. Tokura, Magnetic control of ferroelectric polarization, Nature, 2003, 426, 55–58.
23. I. Yamada, Novel catalytic properties of quadruple perovskites, Sci. Technol. Adv. Mater., 2017, 18, 541–548.
24. A. A. Belik, S. Iikubo, T. Yokosawa, K. Kodama, N. Igawa, S. Shamoto, M. Azuma, M. Takano, K. Kimoto, Y. Matsui and E. Takayama-Muromachi, Origin of the monoclinic-to-monoclinic phase transition and evidence for the centrosymmetric crystal structure of BiMnO₃, J. Am. Chem. Soc., 2007, 129, 971–977.
25. P. Baettig, R. Seshadri and N. A. Spaldin, Anti-polarity in ideal BiMnO₃, J. Am. Chem. Soc., 2007, 129, 9854–9855.
26. D. D. Khalyavin, R. D. Johnson, F. Orlandi, P. G. Radaelli, P. Manuel and A. A. Belik, Emergent helical texture of electric dipoles, Science, 2020, 369, 680–684.
27. A. A. Belik, Y. Matsushita and D. D. Khalyavin, Reentrant structural transitions and collapse of charge and orbital orders in quadruple perovskites, Angew. Chem., Int. Ed., 2017, 56, 10423–10427.
28. Y. S. Glazkova, N. Terada, Y. Matsushita, Y. Katsuya, M. Tanaka, A. V. Sobolev, I. A. Presniakov and A. A. Belik, High-pressure synthesis, crystal structures, and properties of CdMn₇O₁₂ and SrMn₇O₁₂ perovskites, Inorg. Chem., 2015, 54, 9081–9091.
29. F. Izumi and T. Ikeda, A Rietveld-analysis program RIETAN-98 and its applications to zeolites, Mater. Sci. Forum, 2000, 321-324, 198–205.
30. M. Tanaka, Y. Katsuya and A. Yamamoto, A new large radius imaging plate camera for high-resolution and high-throughput synchrotron X-ray powder diffraction by multiexposure method, Rev. Sci. Instrum., 2008, 79, 075106.
31. M. Tanaka, Y. Katsuya, Y. Matsushita and O. Sakata, Development of a synchrotron powder diffractometer with a one-dimensional X-ray detector for analysis of advanced materials, J. Ceram. Soc. Jpn., 2013, 121, 287–290.
32. S. Kawaguchi, M. Takemoto, K. Osaka, E. Nishibori, C. Moriyoshi, Y. Kubota, Y. Kuroiwa and K. Sugimoto, High-throughput powder diffraction measurement system consisting of multiple MYTHEN detectors at beamline BL02B2 of SPring-8, Rev. Sci. Instrum., 2017, 88, 085111.
33. L. C. Chapon, P. Manuel, P. G. Radaelli, C. Benson, L. Perrott, S. Ansell, N. J. Rhodes, D. Raspino, D. Duxbury, E. Spill and J. Norris, Wish: the new powder and single crystal magnetic diffractometer on the second target station, Neutron News, 2011, 22, 22–25.
34. C. J. Rodriguez, Recent advances in magnetic structure determination by neutron powder diffraction, Phys. B, 1993, 193, 55–69.
35. M. A. Carpenter and C. J. Howard, Symmetry rules and strain/order-parameter relationships for coupling between octahedral tilting and cooperative Jahn-Teller transitions in ABX₃ perovskites. I. Theory, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2009, 65, 134–146.
36. S. V. Streltsov and D. I. Khomskii, Jahn-Teller distortion and charge, orbital, and magnetic order in NaMn₇O₁₂, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 201115.
37. I. Pomeranchuk, On the theory of liquid ³He, Zh. Eksp. Teor. Fiz., 1950, 20, 919–926.
38. Y. Saito, F. Y. Yang, J. Y. Ge, X. X. Liu, T. Taniguchi, K. Watanabe, J. I. A. Li, E. Berg and A. F. Young, Isospin Pomeranchuk effect in twisted bilayer graphene, Nature, 2021, 592, 220–224.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc02344f

---