Magnetocaloric Ln(HCO₂)(C₂O₄) frameworks: synthesis, structure and magnetic properties

Abstract

This study probes the structure and the magnetic properties of members of the Ln(HCO₂)(C₂O₄) (Ln = Sm³⁺–Er³⁺) family of coordination frameworks. These frameworks adopt Pnma orthorhombic symmetry with one-dimensional chains arranged on a distorted triangular lattice. The magnetic properties of the Gd–Ho members of this series indicate they remain paramagnetic down to 2 K, with Dy(HCO₂)(C₂O₄) magnetically ordering at 0.6 K. The magnetocaloric effect of Gd(HCO₂)(C₂O₄) is amongst the highest found in frameworks with a peak entropy change of 55.97 J kg⁻¹ K⁻¹ (218.42 mJ cm⁻³ K⁻¹) for a 5–0 T field change at T_max = 2 K, making this material a very good candidate for ultra-low temperature magnetic cooling. In contrast with related magnetocaloric materials lanthanides with high magnetocrystalline anisotropy do not generally improve the magnetocaloric performance of this family at higher temperatures and lower fields. Neutron diffraction experiments suggest that Tb(HCO₂)(C₂O₄) and Ho(HCO₂)(C₂O₄) lack significant local magnetic correlations, highlighting the key role these play in optimising the magnetocaloric performance in low fields in related phases; this emphasises the importance of designing materials with specific magnetic interactions to optimise magnetocaloric performance.

---

1. Introduction

Low temperature cooling is an essential requirement for both scientific research and modern society due to it being required for applications such as quantum computing,¹ spintronics,² sensing and generating large magnetic fields, such as those used in medical imaging. Liquid cryogenics are conventionally used for this purpose and allow for cooling at different temperature ranges. For instance, liquid nitrogen is used for cooling down to 80 K, liquid helium (⁴He) for T > 2 K while mixtures of ⁴He and ³He are employed for cooling down to 20 mK. The increasing cost and scarcity of liquid helium, however, requires the exploration of cost-effective alternative materials to these conventional cryogens.^3,4 Materials exhibiting the paramagnetic magnetocaloric effect (MCE) are a promising and thermodynamically efficient candidate for low temperature magnetic refrigeration, in which the cooling is driven by the disorder of spins aligned by the magnetic field as the field is reduced. The MCE is an entropically-driven phenomenon occurring when paramagnets are subject to a cycled magnetic field and the cooling limit is established by the magnetic ordering temperature of each individual material.⁵

Lanthanide ions are the most suited for the fabrication of MCE materials due to their high number of unpaired spins and thus greater magnetic moments, which results in high magnetocaloric entropy change. The maximum magnetic entropy (−ΔS^max_m) that can be theoretically extracted is assumed to be nR ln(2S + 1) where n is the number of unpaired spins and S is the total spin quantum number. This neglects any contribution of the total orbital angular momentum L and, for this reason, Gd³⁺ is generally considered the best candidate with exactly half-filled f-orbitals and S = 7/2. As a consequence, research on materials containing Gd³⁺ has been generally favoured for their potential MCE performance.⁶ Recently particular interest has been devoted to the development of magnetocalorics with high MCE at low applied field.^7–12 Achieving this goal is important for their use with permanent magnets, generally characterised by a field limit of 2 T, avoiding reliance on superconducting magnets.^13,14 Optimising such MCE materials for use above 4 K offers the potential to replace liquid helium for a wider range of cryogenic applications.

While most magnetocalorics are dilute magnetic salts, alloys or oxides, coordination frameworks, which feature polyatomic ligands, have recently attracted significant interest as magnetocalorics.^6,15–17 This takes advantage of the wide variety of structures they can adopt, because their ligands direct structures away from the simple close packed structures favoured by most alloys and oxides, which in turn allows their magnetic properties to be tuned in ways not readily possible in other materials.^18,19 Work on compounds such as Gd(HCO₂)₃, GdOHCO₃ and GdPO₄ attracted initial interest for having greater MCE than Gd₃Ga₅O₁₂ (GGG), the benchmark compound for magnetic cooling below 10 K.^13,20,21 Such materials are optimised for large field changes of 5–7 T and for use at or below 2 K. As best exemplified by more detailed studies of GdPO₄ the performance of these materials is largely attributed to a high density of Gd cations, with their high S = 7/2 magnetic moment coupled with weak magnetic exchange interactions and low magnetocrystalline anisotropy preventing order to well below 1 K.²¹ The performance of these materials under lower applied magnetic fields and higher temperatures, which facilitates a wider range of applications, is more modest.

It has been shown that replacing Gd with cations with high magnetocrystalline anisotropy, such as Ising-like Tb, Ho or Dy centres, in Gd(HCO₂)₃ and GdOHCO₃ shifts the maximum entropy change in low applied fields to higher temperatures, as is also seen less dramatically in e.g. Dy₃Ga₅O₁₂ (DGG).^10,11,22,23 Neutron scattering studies of magnetocrystalline anisotropic Ln(HCO₂)₃ (Ln = a lanthanide) and LnOHCO₃ phases observe significant magnetic diffuse scattering in those materials whose performance peaks above 4 K.^24,25 Interpretation of this scattering suggests their enhanced magnetocaloric properties at higher temperatures arises from ferromagnetic chains with frustrated antiferromagnetic interactions between them, in contrast to the weak negligible interactions observed in gadolinium based frameworks. This enables the chains to readily align with a magnetic field when it is applied and antiferromagnetic correlations are suppressed, increasing their magnetisation rapidly under low applied fields and thereby enhancing their entropy changes.²⁶ Geometric frustration has long been identified as a way of improving the MCE performance of materials, including GGG itself,²⁷ due to it suppressing long-range magnetic order to much lower temperatures, which allows dense magnetic materials to be used leading to a higher −ΔS^max_m. Coupling this with ferromagnetic chains is, however, a newer concept and it is important to establish if such strong local magnetic order is always associated with enhancing paramagnetic magnetocalorics for high temperature applications.

Inspired by the interesting properties shown by the Ln(HCO₂)₃ phases,¹⁰ our interest focused on understanding how the modification of the crystal structure, achieved by the introduction of a different ligand, could modify the magnetic properties and the MCE of analogous systems. This has driven us towards the synthesis of the Ln(HCO₂)(C₂O₄) series of coordination polymers, previously reported for Ce and Tb.^28–30 In the Ln(HCO₂)(C₂O₄) phases two of the formate ligands in Ln(HCO₂)₃ are exchanged for an oxalate ligand resulting in a lowering of the symmetry from the rhombohedral R3m to the orthorhombic Pnma space group and the face-sharing chains becoming zig-zag rather than linear. In this work, we have synthesised and characterised different members of this family of compounds with a combination of powder and single-crystal diffraction. We have then characterised the magnetic properties of the A(HCO₂)(C₂O₄) (A = Gd–Ho) phases as these are the most likely to be of interest as magnetocalorics. We find Gd(HCO₂)(C₂O₄) to be a very good candidate for magnetic cooling at low temperatures and high magnetic fields, with an MCE comparable to that of the best Gd-based coordination frameworks.^13,20,21 We also found that Dy(HCO₂)(C₂O₄) modestly outperforms Gd(HCO₂)(C₂O₄) at temperatures above 5 K for low field changes due to the high magnetocrystalline anisotropy of the Dy³⁺ cation, with indications of antiferromagnetic order at lower temperatures that is likely associated with its inverse MCE near 2 K. In contrast to the Ln(HCO₂)₃ phases,¹⁰ the Tb³⁺ and Ho³⁺ analogues do not show a significant improvement compared to Gd(HCO₂)(C₂O₄) under any condition. Neutron diffraction patterns of Tb(HCO₂)(C₂O₄) and Ho(HCO₂)(C₂O₄) lack any evidence of short or long range magnetic order. This suggests the subtle change in crystal structure from Ln(HCO₂)₃ phases to their isoelectronic Ln(HCO₂)(C₂O₄) compounds is enough to disrupt the local magnetic correlations and also the improved magnetocaloric performance at higher temperatures. This highlights the importance of tuning local magnetic interactions to optimise magnetocalorics for solid state cooling under more moderate conditions.

2. Experimental

Samples were synthesised under solvothermal conditions following a previously reported procedure for Tb(HCO₂)(C₂O₄) with modifications.³⁰ 2 mmol of the appropriate Ln(NO₃)₃·xH₂O (99%, x = 6 for Sm³⁺, Eu³⁺, Gd³⁺ and Tb³⁺, Acros Organics and x = 5 for Dy³⁺, Ho³⁺ and Er³⁺ Alfa Aesar), 2 mmol of oxalic acid (98%, Acros Organics), 0.8 mmol of Na₂CO₃ (99.5%, Acros Organics), 3 mL of N,N-dimethylformamide (DMF, Fisher Scientific, 99% reagent grade) and 3 mL of distilled water were mixed in a 25 mL Teflon-lined autoclave. These were then sealed and heated under autogenous pressure at 150 °C in an oven and left for 72 hours. After solvothermal treatment, the crystalline products were filtered off and washed with ethanol. About 2 g of both Tb(DCO₂)(C₂O₄) and Ho(DCO₂)(C₂O₄) were used for neutron diffraction experiments and were synthesised using the same method described but with a combination of different batches of samples, using D₂O (99.8%, Acros Organics) and d7-DMF (99%, Goss Scientific).

Fourier-transform infrared spectra were measured using a Shimadzu IR-Affinity1. Thermal analyses were carried out using a Netzsch STA 409 PC thermal analyzer with coupled thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC) measurements in a 24–800 °C temperature range with a heating rate of 10 °C min⁻¹ under an air atmosphere.

Sample purity was assessed by powder X-ray diffraction (PXRD) using a Bragg–Brentano PANalytical X’PERT 3 diffractometer equipped with an Empyrean CuKα LFF source (λ = 1.5046 Å) and a X’Celerator linear detector with the sample mounted on zero-background silicon sample holders. The resulting patterns were analysed for phase purity using the program Rietica employing the Le Bail fitting method.^31,32

All samples showed needle-shaped crystals of approximately 0.1 μm size, with Ho(HCO₂)(C₂O₄) and Er(HCO₂)(C₂O₄) crystals slightly bigger in size enabling their structure to be determined by single crystal X-ray diffraction (SCXRD). This was carried out at 120 K using a Supernova Rigaku Oxford Diffraction diffractometer using a CuK_α microfocus source and an Atlas S2 CCD detector. The data obtained were indexed, integrated and reduced using the CrysAlisPro software suite, version 1.171.40.53, with empirical absorption corrections performed using the same packages. The structure was solved using a direct method in SHELXT-2015³³ and refinements subsequently carried out using a least-squares method with SHELXL-2015³⁴ using the Olex2 graphical user interface (see Table 1 for crystallographic details and Tables S1 and S2 (ESI†) for selected bond distances).³⁵

Table 1 Crystallographic data for the structure of Ho(HCO₂)(C₂O₄) and Er(HCO₂)(C₂O₄) determined by single-crystal X-ray diffraction

Compound	Ho(HCO2)(C2O4)	Er(HCO2)(C2O4)
Formula	HoC3HO6	ErC3HO6
Formula weight (g mol^−1)	297.97	300.30
Crystal system	Orthorhombic	Orthorhombic
Space group	Pnma	Pnma
Temperature (K)	120	120
a (Å)	6.9473(3)	6.9198(4)
b (Å)	10.5261(4)	10.4221(6)
c (Å)	6.5526(4)	6.5331(4)
V (Å^3)	479.18(4)	474.32(5)
Z	4	4
ρ calc (g cm^−3)	4.130	4.205
μ (cm^−1)	30.72	32.72
Refl. meas./unique	2037/489 [Rint = 2.83%]	1003/483 [Rint = 2.33%]
Parameters refined	52	52
R 1, wR2 (all)	2.03%, 4.56%	2.17%, 4.30%
R 1, wR2 (obs)	1.89%, 4.50%	1.90%, 4.20%
Goodness of fit	1.04	1.04

---

DC susceptibility data for Gd(HCO₂)(C₂O₄) were collected using a Quantum Design MPMS SQUID magnetometer with powder samples placed in gelatin capsules enclosed inside a pierced straw with a uniform diamagnetic background. DC susceptibility data on Ln(HCO₂)(C₂O₄) (Ln = Tb³⁺, Dy³⁺ and Ho³⁺) and magnetisation data of all four samples measured were collected using a Quantum Design MPMS 3 VSM SQUID magnetometer while heat capacity data on Dy(HCO₂)(C₂O₄) between 250 mK and 4 K were obtained using a Quantum Design PPMS-Dynacool at the ISIS Support Laboratories, Rutherford Appleton Laboratories, UK. Time-of-flight neutron powder diffraction experiments were conducted using the GEM powder diffractometer at the ISIS Neutron and Muon Source, Rutherford Appleton Laboratories, UK.^36–38 The reciprocal-space range covered is 0.25 < Q < 15 Å⁻¹ and data were collected at temperatures between 1.6 K and 300 K. The samples were cooled in an 8 mm vanadium can using an Oxford Instruments Variox Cryostat. Data were fitted using the Rietveld refinement method in the GSAS software package using the EXPGUI user interface.^39,40 Refinements were carried out fitting the background using shifted Chebyschev polynomial functions and the peak profiles were fitted using a profile function consisting of the convolution of exponentials and a pseudo-Voigt function.

3. Results and discussion

3.1 Structural characterisation

Single-crystal diffraction data for Ho(HCO₂)(C₂O₄) and Er(HCO₂)(C₂O₄) indicated both coordination polymers are isostructural and crystallise in the orthorhombic Pnma space group at 120 K (see Fig. 1 for structure). For the sake of brevity we will only describe the Ho(HCO₂)(C₂O₄) structure here, which is composed of Ho³⁺ cations occupying one unique Ho site (Ho1) and coordinated by nine oxygen atoms from the surrounding ligands, three oxygens from three formates (one O2 and two O1) and six oxygens from three oxalates (two O3 and four O4), with the latter acting as a bichelating ligand utilising both carboxylate groups. The resulting HoO₉ face-sharing polyhedra can be described as distorted monocapped square antiprisms with Ho–O distances of 2.391(3) Å and 2.451(3) Å for O1, 2.402(3) Å for O2, 2.390(2) Å for O3 and 2.413(2) Å and 2.437(2) Å for O4. The face-sharing HoO₉ polyhedra propagate along the a-axis forming infinite zig-zag chains with intrachain Ho–Ho distances of 3.7948(3) Å and Ho–O1–Ho angles of 103.21(12)° and 102.98(8)° for Ho–O4–Ho. Each chain is then joined to the neighbouring ones into a distorted triangular lattice via the bridging formate ligand along the c-axis and oxalate ligands along the [011] and [011̄] axis. The interchain Ho–Ho distances are 6.5526(6) Å and 6.2367(3) Å for those connected by the formate and oxalate ligands, respectively. Overall this gives a coordination framework with three dimensional connectivity, I¹O² type according to the nomenclature of Cheetham et al.⁴¹

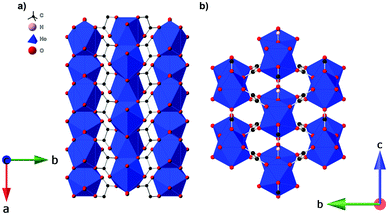Fig. 1 (a) Crystal structure of Ho(HCO₂)(C₂O₄) with infinite one-dimensional chains grow along the a-axis. (b) Arrangement of the chains in a triangular lattice on the bc-plane.

Powder X-ray and (for the Tb and Ho members of the series) neutron diffraction are consistent with all members of this series, from Sm to Er, adopting the same structure at ambient temperature. Le Bail fits to powder X-ray diffraction data confirmed that all the samples used in this study are phase pure and adopt the orthorhombic Pnma structure at room temperature (see Fig. S1–S7, ESI†). It should be noted at this point that significant attempts were made to synthesise phases containing lanthanides larger than Sm but this was unsuccessful. This is despite a modified method, which utilised Ce(OH)₄, enabling the synthesis of Ce(HCO₂)(C₂O₄).²⁸ Issues were also encountered in repeatedly synthesising pure samples of Er(HCO₂)(C₂O₄), with most batches containing small amounts of unknown impurities. Since Ln(OH)₄ is not available as a reagent for most lanthanides we suggest that Sm–Er is the limit for which Ln(HCO₂)(C₂O₄) phases can be readily prepared with Ce(HCO₂)(C₂O₄) also accessible due to its unique chemistry.

3.2 Infrared spectra and thermal behaviour

Fourier-transform infrared spectra (FTIR) for Ln(HCO₂)(C₂O₄) (Ln = Sm–Er) show all members of the series have a similar spectra (see Fig. S8, ESI†). A strong signal around 1735 cm⁻¹, usually attributed to the stretching of the C=O group, can be associated with a shortened C–O bond length while bands at 1367 and 1345 cm⁻¹ can be attributed to C–H bending modes due to the presence of the formate ligand within the structure. Results from thermogravimetric analysis show a significant loss of weight at ∼450 °C, indicating all samples thermally decompose around this temperature (see Fig. S9–S15, ESI†). Differential Scanning Calorimetry (DSC) measurements suggesting these compounds typically decompose exothermically, with the exception of Gd(HCO₂)(C₂O₄).

3.3 Magnetic properties

The Ln(HCO₂)(C₂O₄) phases have similar structures to the Ln(HCO₂)₃ and LnOHCO₃ families in having face-sharing chains packed into a distorted triangular lattice.^20,42 We therefore chose to explore the magnetic properties of the A(HCO₂)(C₂O₄) (A = Gd³⁺, Tb³⁺, Dy³⁺ and Ho³⁺) members of the Ln(HCO₂)(C₂O₄) series, since these lanthanides have been reported to have promising magnetocaloric properties in the Ln(HCO₂)₃ and LnOHCO₃ phases.^10,11,13,20 Field cooled (FC) and zero-field cooled (ZFC) susceptibility χ(T) data of these compounds, measured in a 0.1 T magnetic field from 2 to 300 K, do not show any significant features suggesting the materials remain paramagnetic down to 2 K (see Fig. 2 and Fig. S16–S19, ESI†). Inverse susceptibility data were well fitted using the Curie–Weiss law consistent with antiferromagnetic behaviour (see Table 2 for resulting values). The Curie–Weiss temperature (θ_CW) obtained for Gd(HCO₂)(C₂O₄) is a clear indication of its antiferromagnetic behaviour. Other members of the series also have negative θ_CW, consistent with antiferromagnetic interactions. These must, however, by interpreted more tentatively for the Tb³⁺–Ho³⁺ members of this series since their significant orbital angular momentum can also be quenched at low temperatures due to crystal-field effects. The θ_CW of these phases remain negative when fit across both high and low temperature ranges, which supports the existence of antiferromagnetic interactions.

Fig. 2 ZFC molar susceptibility χ(T) for A(HCO₂)(C₂O₄) measured from 2–300 K in a field of 0.1 T; inverse molar susceptibility χ⁻¹(T) is presented in the inset.

Table 2 Bulk magnetic properties of A(HCO₂)(C₂O₄) with A = Gd–Ho

Sample	Theoretical μeff (μB)	High-T fit (K)	θ CW (K)	Experimental μeff (μB)	Low-T fit (K)	θ CW (K)	Experimental μeff (μB)	Theoretical Msat = gJJ/2 (μB atom^−1)	M at T = 2 K and B = 5 T (μB atom^−1)
Gd(HCO2)(C2O4)	7.9	50–300	−0.8	7.5	2–20	−0.5	7.5	3.5	7.5
Tb(HCO2)(C2O4)	9.7	50–300	−5.6	9.8	2–20	−1.9	9.3	4.5	5.5
Dy(HCO2)(C2O4)	10.6	50–300	−6.4	10.8	2–20	−1.3	9.8	4.9	5.7
Ho(HCO2)(C2O4)	10.6	50–300	−9.9	10.9	8–30	−4.2	10.2	5.0	5.7

---

To better highlight any features of the inverse susceptibility curves, C/χ|θ_CW| − 1 was plotted as a function of T/|θ_CW| and linearly fitted between T/|θ_CW| = 6–15 (see Fig. S20–S23, ESI†).⁴³ It can be observed that for Gd(HCO₂)(C₂O₄) the linear trend is maintained down to the lowest temperature, indicating a lack of magnetic interactions. For Tb(HCO₂)(C₂O₄) and Ho(HCO₂)(C₂O₄) there may be a small deviation from linearity below T/|θ_CW| = 2; this is in a direction suggestive of very weak antiferromagnetic coupling but may also be linked to crystal field effects. However, the deviation from linearity is especially significant in the Dy member, indicating a more significant coupling among the spins and presumably resulting significant short-range order. The effective magnetic moments of all phases were found to be close to the expected theoretical values for the trivalent lanthanide cations (see Table 2).

Magnetisation measurements down to 2 K are consistent with paramagnetic behaviour (see Fig. 3 and Fig. S24–S27, ESI†). Ising-like systems are expected to have saturation values M_max close to g_JJ/2 while Heisenberg-like ones should have values close to g_JJ. The observed values for the saturation magnetisation for Gd(HCO₂)(C₂O₄) are therefore consistent with Heisenberg spins while those for the Dy³⁺, Tb³⁺ and Ho³⁺ compounds are closer to the Ising limit, albeit higher than the expected values (see Table 2). These results indicate that these systems feature significant single ion anisotropy, although they are insufficient to conclusively show Ising-like spins we note similar deviations were found for Ln(HCO₂)₃ and LnOHCO₃ phases, which were then found to be Ising-like by neutron scattering.^10,11,24,25 Inelastic neutron measurements are required to confirm the precise nature of the anisotropy of these cations.

Fig. 3 Magnetisation plot of A(HCO₂)(C₂O₄) (A= Gd³⁺–Ho³⁺) collected at 3 K for fields up to 5 T.

Interestingly, Dy(HCO₂)(C₂O₄) shows a greater increase in magnetisation than Gd(HCO₂)(C₂O₄) for low applied fields and temperatures above 3 K. It is also notable that the magnetisation of Dy(HCO₂)(C₂O₄) decreases between 3 K and 2 K for fields higher than 0.1 T. This suggests that a magnetic transition might occur for Dy(HCO₂)(C₂O₄) close to 2 K, but below this given there is no discontinuity observed in the susceptibility data. Furthermore, the decrease in magnetisation suggests this transition is likely antiferromagnetic in nature. Consistent with this, heat capacity measurements for Dy(HCO₂)(C₂O₄) show a peak at 0.6 K under zero-field conditions, indicating that this compound undergoes a magnetic transition at such low temperatures. Furthermore, consistent with a magnetic phase transition, it can be observed that the feature in the heat capacity is partially suppressed upon increasing the applied magnetic field up to 1 T, with the heat capacity increasing towards higher temperatures (see Fig. 4). This is consistent with other systems, such as the lanthanide gallium garnets Ln₃CrGa₄O₁₂ (Ln = Tb³⁺, Dy³⁺, Ho³⁺), where heat capacity data have shown higher applied magnetic fields result in the transition temperature shifting to higher values and a gradual broadening of the heat capacity maxima.⁹

Fig. 4 Magnetic heat capacity data for Dy(HCO₂)(C₂O₄) measured between 250 mK and 4 K with applied fields of 0, 0.5 and 1 T.

The magnetic entropy change, ΔS_m, was calculated from the magnetisation data using the Maxwell relation, , from 2 K to 12 K for ΔB = 5–0 T for A(HCO₂)(C₂O₄). This gave −ΔS^max_m of 55.97, 14.72, 16.45, 11.70, J kg⁻¹ K⁻¹ for ΔB = 5–0 T and T_max of 2, 4, 5, 9 K for Gd³⁺, Tb³⁺, Dy³⁺ and Ho³⁺ corresponding to volumetric values of 218.42, 58.18, 66.44, 48.33 mJ cm⁻³ K⁻¹ (see Fig. 5). The values observed for Gd(HCO₂)(C₂O₄) are amongst the highest known for magnetocaloric coordination frameworks, exceeding that of the closely related Gd(HCO₂)₃,¹⁰ well above that of Ca₄GdO(BO₃)₃,⁸ and other carboxylate-based systems containing one-dimensional chains, such as Gd(OAc)₃(MeOH), Gd(OAc)₃(H₂O)_0.5, or Gd(HCOO)(OAc)₂(H₂O)₂, where weaker interchain interactions are present.^44,45 Gd(HCO₂)(C₂O₄) is also very likely superior to Gd₆O(OH)₄(ClO₄)(H₂O)₆](OH)₄, Gd₄(SO₄)₄(OH)₄(H₂O) and Gd₄(SO₄)₃(OH)₄(C₂O₄)(H₂O)₅·H₂O, which possess three-dimensional structures containing Gd clusters, and Gd₂O(OH)₄(H₂O)₂, which features a layered structure, with at least comparable values for a 5–0 T field change than these materials are reported to have for a 7–0 T change (5–0 T values are unavailable for these materials).^46–48 The −ΔS^max_m values observed are, however, lower than that of GdOHCO₃,^10,11 GdPO₄²¹ and Gd(OH)₃.⁴⁶ Beyond coordination frameworks the benchmark oxide, GGG has values of about 35 J kg⁻¹ K⁻¹ or 248 mJ cm⁻³ K⁻¹ for a field change of 5–0 T meaning Gd(HCO₂)(C₂O₄) significantly outperforms GGG with respect to entropy change per mass but is slightly lower with respect to entropy change per volume.⁴⁹ Similarly, Gd(HCO₂)(C₂O₄) performs better than GdBWO₉ with respect to the entropy change per mass, whereas the entropy change per volume is significantly lower.⁵⁰ GdF₃ has the highest MCE of all of these materials.⁵¹ This makes Gd(HCO₂)(C₂O₄) a very good candidate for ultra-low magnetic cooling at high magnetic fields (see Fig. 6).

Fig. 5 Magnetic entropy changes for the A(HCO₂)(C₂O₄) series for ΔB = 5–0 T. The filled and hollow symbols mark the gravimetric and volumetric units, respectively.

Fig. 6 The reported maximum volumetric and gravimetric entropy change for high performance magnetocaloric coordination frameworks and selected oxides and halides. These values are generally shown for a of 5–0 T applied field change, except Gd(OH)₃, GdPO₄, Gd₂O(OH)₄(H₂O)₂, Gd₂(C₂O₄)₃(H₂O)₆·0.6H₂O, Gd(HCOO)(OAc)₂(H₂O)₂, Gd₄(SO₄)₄(OH)₄(H₂O), Gd₆O(OH)₈(ClO₄)(H₂O)₆](OH)₄ and Gd₄(SO₄)₃(OH)₄(C₂O₄)(H₂O)₅·H₂O, for which values are shown for a 7–0 T field change, and Ca₄GdO(BO₃)₃, which is for a 9–0 T field change.

It should be noted that for all lanthanides other than Gd, the materials have higher T_max, which is associated with use for higher temperature applications, with the exception of Tb(HCO₂)(C₂O₄) for small (1–0 T) field changes. In the context of the performance of related anisotropic materials in low applied fields it is important to note that the −ΔS^max_m of these materials are 22.72, 24.10 and 5.66 mJ cm⁻³ K⁻¹ with T_max = 2, 4 and 6 K for Tb³⁺, Dy³⁺ and Ho³⁺, respectively, for a 1–0 T field change, whereas the values are 39.86, 47.00 and 17.02 mJ cm⁻³ K⁻¹ with T_max = 4, 5 and 7 K for a 2–0 T field change (see Fig. 7 and Fig. S28, ESI†). Even at these lower fields, however, only Dy(HCO₂)(C₂O₄) appears to outperform Gd(HCO₂)(C₂O₄), which occurs above 5 K for a 1–0 T field change and above 7 K for a 2–0 T change, with the gap in performance increasing further at higher temperatures. This enhancement in performance is, however, smaller than that observed for some highly magnetocrystalline anisotropy cations in the Ln(HCO₂)₃ and LnOHCO₃ phases. For instance, for the latter family of frameworks and a field change of 2–0 T, the −ΔS^max_m values are 168.62, 186.15 and 112.67 mJ cm⁻³ K⁻¹ (T_max = 4 K) for Tb³⁺, Dy³⁺ and Ho³⁺ respectively,¹¹ while for the Ln(HCO₂)₃ series the values are 46.9, 61.2 and 46.2 mJ cm⁻³ K⁻¹ with T_max = 3, 2, 4 K, respectively.¹⁰ In both cases it has been shown that, for lower applied fields, compounds with magnetic anisotropy outperform their Gd-analogues at higher temperatures, typically above 4 K. It should also be highlighted that the −ΔS_m of Dy(HCO₂)(C₂O₄) decreases below 4 K and with inverse MCE (ΔS_m > 0) exhibited near 2 K. The loss of entropy is consistent with the drop in magnetisation observed for this compound at low temperatures. Inverse MCE is not common but has been observed due to crystal field effects, such as in PrNi₅,^52,53 in transition metal alloys showing first-order magnetic transitions,⁵⁴ and more recently in Ba₃Tb(BO₃)₃.⁵⁵ In the case of Dy(HCO₂)(C₂O₄), the inverse MCE is likely due to approaching the magnetic transition indicated by the heat capacity measurements with the behaviour of the magnetisation along with the deviation from linearity of the inverse susceptibility suggesting this is antiferromagnetic in nature. However, confirming the origins of this inverse MCE in Dy(HCO₂)(C₂O₄) – whether this is due solely to the suppression of antiferromagnetic correlations under applied field or other factors – would require further information about the magnetic structure achievable via neutron diffraction; this would include its local structure since the material remains paramagnetic until well below the temperature at which negative entropy emerges. We anticipate this would present a significant challenge due to the high neutron absorption of Dy and, hence, require the use of less adsorbing isotopes. This would be a particularly costly task to carry out for Dy(HCO₂)(C₂O₄), which cannot be made with the near 100% atomic efficiency of solid state reactions.

Fig. 7 Magnetic entropy changes for the A(HCO₂)(C₂O₄) series for ΔB = 1–0 T. The filled and hollow symbols mark the gravimetric and volumetric units, respectively.

3.4 Low temperature neutron diffraction

In the related Ln(HCO₂)₃ and LnOHCO₃ frameworks it has been shown that the enhancement of magnetocaloric properties at higher temperatures is associated with short range magnetic order, as indicated by the appearance of diffuse magnetic scattering in neutron diffraction patterns. ^10,11,24 Comparing the behaviour of the A(HCO₂)(C₂O₄) compounds to the closely related Ln(HCO₂)₃ phases there is a striking difference in the lack of improvement in the magnetocaloric entropy change of the Tb(HCO₂)(C₂O₄) and Ho(HCO₂)(C₂O₄) compounds at higher temperatures and lower applied fields compared to the analogous Ln(HCO₂)₃ phases. This offers the opportunity to confirm if the strong local magnetic interactions in the Ln(HCO₂)₃ phases are indeed related to their magnetocaloric properties. To establish this we measured the neutron diffraction patterns of both Tb(HCO₂)(C₂O₄) and Ho(HCO₂)(C₂O₄) at a series of temperatures between 1.5 K and 20 K (see Fig. 8). This did not show any difference in the scattering observed between these temperatures, either in terms of additional intensity of the Bragg reflections or diffuse scattering; the latter confirmed by looking at a difference pattern that were rebinned to optimise signal to noise. The lack of observable magnetic diffuse scattering indicates that Tb(HCO₂)(C₂O₄) and Ho(HCO₂)(C₂O₄) likely lack any significant magnetic correlations above 1.5 K, in sharp contrast to the Tb(HCO₂)₃ and Ho(HCO₂)₃ where strong diffuse magnetic scattering is observed below 10 K. ^10,24 This would support the hypothesis that the 1D ferromagnetic correlations in Tb(HCO₂)₃ and Ho(HCO₂)₃ play a key role in enhancing their magnetocaloric properties under low applied fields and higher temperatures by enhancing the rate of change in their magnetisation under applied fields. ^10,11,24,25 Conversely, the likely lack of such correlations in Tb(HCO₂)(C₂O₄) and Ho(HCO₂)(C₂O₄) probably leads to them not offering such enhanced properties.

Fig. 8 Comparison of neutron diffraction patterns collected at 20 K and 1.6 K from bank 2 on GEM for (a) Tb(HCO₂)(C₂O₄) and (b) Ho(HCO₂)(C₂O₄). For both compounds, the difference line has been magnified ten times and shows no appreciable variation upon lowering the temperature.

When comparing the closely related Ln(HCO₂)₃ and Ln(HCO₂)(C₂O₄) phases we find that replacing two formate linkers with one oxalate linker leads to the symmetry being lowered from the rhombohedral R3m for the Ln(HCO₂)₃ to the orthorhombic Pnma structure of the Ln(HCO₂)(C₂O₄) phases and a modification between having linear LnO₉ chains in the Ln(HCO₂)₃ phases to zig-zag chains in the Ln(HCO₂)(C₂O₄) compounds. Despite this, the superexchange pathways appear to remain similar among the two families of compounds. In Tb(HCO₂)₃, the superexchange pathway was found to have a total length of 4.975(3) Å while for Tb(HCO₂)(C₂O₄) this distance is 4.937(2) and 4.887(2) Å for O1 and O4, respectively. Similarly, the Tb–O–Tb angles in Tb(HCO₂)(C₂O₄) have an average value of 103.04(8)°, close to the 105° angles found in Tb(HCO₂)₃.¹⁰ Thus it is expected that the interactions within the chains in both series should remain similar for a given f-electron configuration, although small differences in exchange pathways may affect the nature of these interactions. Since the interchain coupling in both series occurs via carboxylate groups, with one syn–anti bidentate oxygen atom and the other coordinated in an anti-fashion in all cases, both families have the same broad magnetic motif. It is therefore most likely the change in symmetry plays a key role in the suppression of the strong magnetic interactions seen in Tb(HCO₂)₃ and Ho(HCO₂)₃ in their Ln(HCO₂)(C₂O₄) analogues, although we cannot rule out other factors such as dipolar interactions and small changes in crystal-field effect also playing a role in this. Thus, despite the modest properties of the magnetically anisotropic A(HCO₂)(C₂O₄) phases, the results presented here both highlight the importance of searching for lanthanide frameworks with strong local magnetic correlations when looking for enhanced magnetocaloric properties and that small changes in the structures of such materials can have a significant effect on their performance.

4. Conclusions

In this work we have reported the synthesis of members of the Ln(HCO₂)(C₂O₄) (Ln = Sm³⁺–Er³⁺) family of coordination frameworks. We have probed the magnetic, including magnetocaloric, properties of the A(HCO₂)(C₂O₄) members (A = Gd³⁺–Ho³⁺). We have found Gd(HCO₂)(C₂O₄) has a high magnetocaloric performance with a peak entropy change, −ΔS^max_m, of 55.97 J kg⁻¹ K⁻¹ (218.42 mJ cm⁻³ K⁻¹), comparable to that of the best performing coordination frameworks, at 2 K for a field change of 5–0 T. This makes Gd(HCO₂)(C₂O₄) a very good candidate for magnetic cooling at low temperature and high magnetic fields. We have shown that Dy(HCO₂)(C₂O₄) can outperform Gd(HCO₂)(C₂O₄) at higher temperatures for field changes of less than 2 T, although not as significantly as observed in related families of coordination polymers; Dy(HCO₂)(C₂O₄) also exhibits inverse MCE near 2 K. This study has shown that, in contrast with their isoelectronic Ln(HCO₂)₃ analogues, Tb(HCO₂)(C₂O₄) and Ho(HCO₂)(C₂O₄) lack significant magnetic correlations above 1.5 K; this is likely the cause of their poorer MCE compared to the analogous magnetically anisotropic formates. These results highlight that it is of paramount importance to optimise the local magnetic correlations in magnetocalorics to optimise their performance at lower applied magnetic fields and higher temperatures, showing such optimisation is vulnerable to disruption by relatively small structural changes.

Author contributions

M. F. synthesised the samples, performed powder X-ray diffraction experiments as well as single-crystal diffraction measurements and magnetic susceptibility data on the Gd(HCO₂)(C₂O₄); he also carried out the fits to all diffraction data. G. B. G. S. collected susceptibility data (Tb–Ho), magnetisation data and heat capacity measurement. I. d. S. performed neutron diffraction experiments on the GEM diffractometer. P. J. S. supervised the project and conceptualised the paper, writing this jointly with M. F. with contributions from all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank the Leverhulme Trust and Engineering and Physical Sciences Research Council for funding this work through RPG-2018-268 and EP/T027886/1, respectively. We would also like to thank the Science and Technologies Facilities Council for granting experiment time on the GEM powder diffractometer at the ISIS Neutron and Muon Source.

References

1. L. Gyongyosi and S. Imre, Comput. Sci. Rev., 2019, 31, 51–71.
2. C. Mitra, Nat. Phys., 2015, 11, 212–213.
3. A. H. Olafsdottir and H. U. Sverdrup, Biophys. Econ. Sustainable, 2020, 5, 6.
4. A. Cho, Science, 2009, 326, 778–779.
5. A. Smith, Eur. Phys. J. H., 2013, 38, 507–517.
6. Y. Z. Zheng, G. J. Zhou, Z. Zheng and R. E. P. Winpenny, Chem. Soc. Rev., 2014, 43, 1462–1475.
7. R. Li, P. Manuel, F. Orlandi and C. Greaves, J. Mater. Chem. A, 2018, 6, 21149–21155.
8. N. D. Kelly and S. E. Dutton, Inorg. Chem., 2020, 59, 9188–9195.
9. P. Mukherjee and S. E. Dutton, Adv. Funct. Mater., 2017, 27, 1–7.
10. P. J. Saines, J. A. M. Paddison, P. M. M. Thygesen and M. G. Tucker, Mater. Horiz., 2015, 2, 528–535.
11. R. J. C. Dixey and P. J. Saines, Inorg. Chem., 2018, 57, 12543–12551.
12. M. Evangelisti and E. K. Brechin, Dalton Trans., 2010, 39, 4672.
13. G. Lorusso, J. W. Sharples, E. Palacios, O. Roubeau, E. K. Brechin, R. Sessoli, A. Rossin, F. Tuna, E. J. L. L. McInnes, D. Collison and M. Evangelisti, Adv. Mater., 2013, 25, 4653–4656.
14. A. Smith, C. R. H. Bahl, R. Bjork, K. Engelbrecht, K. K. Nielsen and N. Pryds, Adv. Energy Mater., 2012, 2, 1288–1318.
15. N. R. Ram, M. Prakash, U. Naresh, N. S. Kumar, T. S. Sarmash, T. Subbarao, R. J. Kumar, G. R. Kumar and K. C. B. Naidu, J. Supercond. Novel Magn., 2018, 31, 1971–1979.
16. K. A. Gschneidner and V. K. Pecharsky, Annu. Rev. Mater. Sci., 2000, 30, 387–429.
17. Y. Mozharivskyj, Magnetocaloric Effect and Magnetocaloric Materials, Elsevier Inc., 2016.
18. M. Kurmoo, Chem. Soc. Rev., 2009, 38, 1353–1379.
19. P. J. Saines and N. C. Bristowe, Dalton Trans., 2018, 47, 13257–13280.
20. Y.-C. Chen, L. Qin, Z.-S. Meng, D.-F. Yang, C. Wu, Z. Fu, Y.-Z. Zheng, J.-L. Liu, R. Tarasenko, M. Orendáč, J. Prokleška, V. Sechovský and M.-L. Tong, J. Mater. Chem. A, 2014, 2, 9851–9858.
21. E. Palacios, J. A. Rodríguez-Velamazán, M. Evangelisti, G. J. McIntyre, G. Lorusso, D. Visser, L. J. de Jongh and L. A. Boatner, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 214423.
22. T. Numazawa, Phys. B, 2003, 329–333, 1656–1657.
23. P. Mukherjee, Y. Wu, G. I. Lampronti and S. E. Dutton, Mater. Res. Bull., 2018, 98, 173–179.
24. R. J. C. Dixey, F. Orlandi, P. Manuel, P. Mukherjee, S. E. Dutton and P. J. Saines, Philos. Trans. R. Soc., A, 2019, 377, 20190007.
25. R. J. C. Dixey, G. B. G. Stenning, P. Manuel, F. Orlandi and P. J. Saines, J. Mater. Chem. C, 2019, 7, 13111–13119.
26. R. J. C. Dixey, P. Manuel, F. Orlandi, P. Mukherjee, S. E. Dutton, G. B. G. Stenning and P. J. Saines, J. Mater. Chem. C, 2020, 8, 12123–12132.
27. J. A. M. Paddison, H. Jacobsen, O. A. Petrenko, M. T. Fernandez-Diaz, P. P. Deen and A. L. Goodwin, Science, 2015, 350, 179–181.
28. J. C. Tan, J. D. Furman and A. K. Cheetham, J. Am. Chem. Soc., 2009, 131, 14252–14254.
29. S. Romero, A. Mosset and J. C. Trombe, J. Solid State Chem., 1996, 127, 256–266.
30. C. Kittipong, P. Khemthong, F. Kielar and Y. Zhou, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2016, 72, 87–91.
31. A. Le Bail, H. Duroy and J. L. Fourquet, Mater. Res. Bull., 1988, 23, 447–452.
32. B. Hunter, AINSE Symp. Neutron Scatt. Powder Diffraction; Aust. Neutron Beam Gr. Meet., 2000, 31, 20.
33. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2015, 71, 3–8.
34. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct, Chem., 2015, 71, 3–8.
35. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
36. W. Williams, R. Ibberson, P. Day and J. Enderby, Phys. B, 1997, 241–243, 234–236.
37. P. Day, J. Enderby, W. Williams, L. Chapon, A. Hannon, P. Radaelli and A. Soper, Neutron News, 2004, 15, 19–23.
38. I. da Silva, P. J. Saines and M. Falsaperna, Probing 1D Magnetism in Lanthanide Formate Oxalate Frameworks, 2020 DOI:10.5286/ISIS.E.RB2010596.
39. H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71.
40. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213.
41. A. K. Cheetham, C. N. R. Rao and R. K. Feller, Chem. Commun., 2006, 4780–4795.
42. A. Pabst, J. Chem. Phys., 1943, 11, 145–149.
43. B. C. Melot, J. E. Drewes, R. Seshadri, E. M. Stoudenmire and A. P. Ramirez, J. Phys.: Condens. Matter, 2009, 21, 216007.
44. F.-S. Guo, J.-D. Leng, J.-L. Liu, Z.-S. Meng and M.-L. Tong, Inorg. Chem., 2012, 51, 405–413.
45. G. Lorusso, M. A. Palacios, G. S. Nichol, E. K. Brechin, O. Roubeau and M. Evangelisti, Chem. Commun., 2012, 48, 7592–7594.
46. Y. Yang, Q.-C. Zhang, Y.-Y. Pan, L.-S. Long, L.-S. Zheng, Y. Yang, Q.-C. Zhang, Y.-Y. Pan, L.-S. Long and L.-S. Zheng, Chem. Commun., 2015, 51, 7317–7320.
47. S.-D. Han, X.-H. Miao, S.-J. Liu and X.-H. Bu, Chem. – Asian J., 2014, 9, 3116–3120.
48. Y.-L. Hou, G. Xiong, P.-F. Shi, R.-R. Cheng, J.-Z. Cui and B. Zhao, Chem. Commun., 2013, 49, 6066.
49. B. Daudin, R. Lagnier and B. Salce, J. Magn. Magn. Mater., 1982, 27, 315–322.
50. Z. Yang, H. Zhang, M. Bai, W. Li, S. Huang, S. Ruan and Y.-J. Zeng, J. Mater. Chem. C, 2020, 8, 11866–11873.
51. Y.-C. Chen, J. Prokleška, W.-J. Xu, J.-L. J. Liu, J.-L. J. Liu, W.-X. Zhang, J.-H. Jia, V. Sechovský and M.-L. Tong, J. Mater. Chem. C, 2015, 3, 12206–12211.
52. P. J. von Ranke, V. K. Pecharsky, K. A. Gschneidner and B. J. Korte, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 14436–14441.
53. J. A. Barclay and W. A. Steyert, Cryogenics, 1982, 22, 73–80.
54. T. Krenke, E. Duman, M. Acet, E. F. Wassermann, X. Moya, L. Mañosa and A. Planes, Nat. Mater., 2005, 4, 450–454.
55. N. D. Kelly, C. Liu and S. E. Dutton, J. Solid State Chem., 2020, 292, 121640.

---

Footnote

† Electronic supplementary information (ESI) available: Tables and figures of crystallographic details, neutron diffraction refinements and magnetic measurements. CCDC 2078968 and 2078969. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1tc01831k

---