Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Accurately predicting optical properties of rare-earth, aluminate scintillators: influence of electron–hole correlation†
Christopher N.
Singh
 *,
Ghanshyam
Pilania
*,
Ghanshyam
Pilania
 ,
Jan
Bárta
,
Jan
Bárta
 ,
Blas Pedro
Uberuaga
,
Blas Pedro
Uberuaga
 and
Xiang-Yang
Liu
and
Xiang-Yang
Liu
Materials Science and Technology Division, Los Alamos National Laboratory, Los Alamos, New Mexico, USA
First published on 24th May 2021
Abstract
A theoretical and computational analysis of two approaches to simulate luminescent profiles of rare-earth perovskite scintillators is given. This work establishes the importance of many-particle corrections in the prediction of the principal excitation wavelength, revealing that they lead to differences of nearly one hundred nanometers from the standard Δ-SCF approach. We show the electronic structure of this class of materials uniquely necessitates a many-particle treatment because, in contrast to traditional semiconductors, rare-earth scintillator materials are weakly screened and relatively few bands dominate the radiative decay channels. This makes accounting for long-range electron–hole correlations a central issue in accurate predictions, and we discuss the trade-off between accuracy and performance of various popular approaches. Understanding the strengths and weaknesses of available theoretical tools will help define search parameters for new scintillator development.
Introduction
The conversion of high energy particles such as γ-rays, α-particles, X-rays, and neutrons to lower-energy visible or ultraviolet photons is of great scientific and technological importance.1 Scintillators are materials that accomplish this conversion. They are an important subset of the broader class of luminescent materials, and these have key applications in radiation detection for national security, high energy physics, lasers and light emitting diodes, medical imaging and therapy, oil drilling, and more.2 In light of this, accurate predictions of scintillator performance and fundamental notions for how to tune that performance to the desired application have become increasingly sought after,3–7 but achieving this goal requires accounting for radiative and non-radiative decay channels in complex, quantum light-matter interactions.8 Properties at the macroscopic level such as light yield, response time, and stability under irradiation conditions are of pivotal importance for scintillators,9,10 yet a full quantum mechanical treatment of the properties remains a significant theoretical challenge.5 In fact, the large difference between theory and experiment indicates we are far from a complete theoretical understanding of the phenomena.11,12 It is therefore worthwhile to benchmark the efficacy of standard approaches in predicting the luminescent profiles of scintillator materials, while also expounding the different fundamental physical assumptions that constitute these approaches.When a material is (γ)-irradiated, three types of interaction processes can unfold – photoelectric absorption, Compton scattering, or pair creation13 – but for inorganic scintillators, photoelectric absorption is the primary light–matter interaction. While the intimate relationship between photoelectric absorption, electronic structure, and efficient recombination of photo-excited carriers is standard canon from a band-engineering (single-particle) perspective,8,10,14,15 the many-particle contribution is much less considered in the context of scintillators.16 It is however well established in traditional semiconductors,17,18 and therefore ought be considered even more important in weakly-screened, wide-gap systems with dispersionless manifolds. In addition to many-body effects, an accurate theory must distinguish intrinsic from extrinsic degrees of freedom that contribute to scintillator performance.12 For example, crystalline defects, precise stoichiometry, non-uniformity, and the like are extrinsic factors, often uncontrollable at the level of fabrication. Excitation density, relaxation rate, excitation energy – these are intrinsic to a given system, defined by the chemistry and atomic structure. Because it has been recognized that a set of theoretical criteria is highly desired for predicting new, as well as tuning known, scintillator materials,19–21 this task of accurate modeling naturally must begin with handling the intrinsic properties of photo-excited carriers including many-body effects.‡
In this article, we compare the accuracy and performance of two endpoint theories§ commonly used to access principal luminescence wavelengths from first principles – the Δ-Self-Consistent-Field (Δ-SCF) aspproach,22 and many-body perturbation theory using the Bethe–Salpeter Equation (BSE).23–25 We find that for the cerium-doped perovskites, a particularly promising class of materials due to their ease of manufacture and wide range of optoelectronic properties,26 solution of the BSE gives excitation wavelengths within a few percent of experimental measurements for approximately half the computational cost of Δ-SCF. Meanwhile, the Δ-SCF approach generally gives excitation wavelengths at best to within 20% of experiment, and our general finding with this method is similar to previous results pertaining to systems with different chemistries,27,28 supporting the conclusion that the general performance of the Δ-SCF approach is constant across chemistries. We discuss the approximations of electron–hole correlations as the origin of these discrepancies.
Theoretical approaches
The Δ-SCF method is a way to approximate the electron excitation, addition, and removal energies in localized systems (Martin section 10.629). It is closely related to Slater's transition state argument.30 The transition energy in this formulation,¶ ΔE, is approximated by the energy eigenvalue, ε, of a many-particle state with one-half an electron transferred between the initial and final states of interest. In other words, if E1 is the energy of an initial state parameterized by a set of manifolds, {α}, such that E1 = E1(αi = 1, αj = 0), and E2 is the energy of the final state such that E2 = E2(αi = 0, αj = 1), then E2 − E1 = ΔE can be approximated by a state with {αi = 1/2, αj = 1/2} and energy ε. That is, the difference in energy between two states, in which an electron is transferred between two orbitals, is best approximated by a state that has half an electron transferred between each orbital. Please see Slater30 for the details, but the important notion here is that to leading order ΔE ≈ ε, suggesting the excitation energy will best be approximated by the eigenvalue of a state that is halfway between the two states.In current density functional implementations, the Δ-SCF method consists of two independent, self-consistent calculations, one for the first state with density n1 and total energy E1, and one for the second state with density n2 and total energy E2. The excitation energy is given by the difference of the two ΔE21 = E2 − E1.31,32 To see this more concretely, we follow Gavnholt et al.22 and first restate the Kohn–Sham equation33
 | (1) |
 | (2) |
 | (3) |
 | (4) |
It is however important to discuss some salient features of this approach now, as well as previous results, before contrasting it with the solution of the BSE. First, a “special, unknown orbital-dependent exchange–correlation potential should be used for the excited states”,22,35 but this is unknown, and often the ground state exchange–correlation functional is used. Second, it is formally only a statement about the total energy difference between non-degenerate pairs of states. This suggests that any interpretation of the excited state spectrum as physical retains the same ambiguity as interpreting the ground-state Kohn–Sham orbitals as single particle excitation energies,36 and that degeneracies invalidate the approach.34 Third, there is the practical difficulty in choosing which Kohn–Sham state to occupy at each point in momentum space.22 Finally, the Δ-SCF method by construction requires finding two self-consistent solutions, which, for complex oxides lightly doped with heavy f-manifold activators, can become prohibitively expensive as these systems often require relativistic corrections and hybrid functionals. We will expand on this point later.
However, in spite of its axiomatic failings, the simplicity inherent in this approach is often leveraged to gain some insight into scintillator emission wavelengths. For example, Marsman et al.3 and Canning et al.19,51 deploy this method for Ce3+ with reasonable effect. Jia et al.27 also use it, although state “…like in previous studies using Δ-SCF, we work beyond formal justification,” and a study looking at thirteen different scintillating chemistries finds 50–80 percent agreement with experimental absorption, emission, and Stokes' shift energies.28 Lastly, and perhaps most importantly, the Δ-SCF method does not provide a means to access, even in principle, the scintillator brightness, and this coupled with all the aforementioned reasons indicates there is room to improve beyond the predictive power of the Δ-SCF for scintillator performance.
Unlike the Δ-SCF approach, excitation energies by solution of the Bethe–Saltpeter equation23 are not plagued by the same ambiguity of interpretation. In fact, the precise manner in which the BSE improves upon the Δ-SCF (in the context of luminescent scintillators) is that, in the BSE approach, the assumption is that the excited state crystal wavefunction |S(q)〉 is a linear combination of two-particle (electron–hole) basis functions52,53 as
 | (5) |
 | (6) |
 | (7) |
 | (8) |
| H|S(q)〉 = ES|S(q)〉. | (9) |
We can understand the fundamental change in perspective afforded by eqn (5) by comparing the expression for the imaginary component of the macroscopic dielectric function in the independent-particle picture to that in the excitonic picture. At the single-particle level, the dielectric function is53
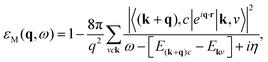 | (10) |
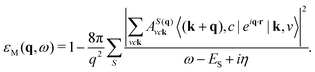 | (11) |
From these expressions, the effect of the two-particle correlations is to admix contributions from different inter-band excitations to the final spectrum that are just summed individually at the single-particle level. In eqn (10), a zero in the denominator at the fundamental gap (when ω − [E(k+q)c − Ekv] = 0) usually dominates the spectrum; however, in eqn (11), the poles depend on the eigenvalues (ES) of eqn (9). These eigenvalues ES correspond to linear combinations of electron–hole states that can be of mixed orbital character. In the rare-earth doped scintillators, it is a theoretical challenge to understand the role played by partially delocalized activator states that interact with the host conduction band,19,51 and the ambiguity in the Δ-SCF approach is thus exacerbated if the first available virtual band is composed of partially delocalized, dipole-forbidden orbital character. The BSE approach however handles this aspect, and in fact goes beyond it because not only are excitation and relaxation rates weighted by the dipole matrix elements,** but the electron–hole coupling is considered explicitly. These differences are schematically illustrated in Fig. 1.
Finally, for simplicity, we focus only on zero temperature. Our assumption is that the initial and final states have the same number of phonon fluctuations. The consequence is that the emission and excitations energies are equal in this approach. In general, however, the emission spectrum is a reflection of the absorption spectrum across the zero-phonon line,56 meaning the same physical process usually has a lower energy during emission than during absorption. Nevertheless, if electron–hole correlations have the tendency to red-shift features in the absorption spectrum, then elements in the emission will be blue-shifted, leading to the observed minimal Stokes shift in these materials.
Methods
Computational
As alluded to, Ce3+ activated inorganic complex oxides are of particular interest because of high light yield and efficient 5d → 4f (parity allowed) transitions. The energetics of activator states have been investigated (semi-empirically) to this end by Dorenbos et al.;57,58 thus, we use the cerium-doped perovskites (MAlO3:Ce for M = Lu, Gd, Y, La) as a model series of rare-earth scintillating systems in a first principles analysis. The electronic structure and dielectric function of LuAlO3:Ce, GdAlO3:Ce, YAlO3:Ce, and LaAlO3:Ce are determined in this study using Density Functional Theory (DFT) as implemented in the Vienna Ab Initio Simulation Package (VASP)59–63 with PBE+U64–69 or HSE0670,71 exchange–correlation functionals to obtain both the instantaneous ionic-electronic ground state and the Δ-SCF22 excited states, and solve the Bethe–Salpeter equation (BSE)23–25 beyond the Tamm–Dancoff approximation.72The LuAlO3:Ce, GdAlO3:Ce, and YAlO3:Ce perovskites crystallize in an orthorombic Pnma (space group 62) structure while the LaAlO3:Ce compound has trigonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c (space group 167) symmetry. As a starting point, we use the experimental lattice parameters from Dernier et al.,73 Boulay et al.,74 Diehl et al.,75 and Takata et al.76 for the lutetium, gadolinium, yttrium, and lanthanum compounds respectively. Using these parameters as inputs, we replace one leading cation by Ce, and perform standard lattice relaxations at the PBE+U level to find the ground state ionic positions. These atomic positions are then used in single-point hybrid calculations that constitute our approximation to the ground and excited states for Δ-SCF calculations. The PBE+U+SO quasi-particle spectrum is then used to solve the BSE equation and evaluate either eqn (10) or eqn (11) to understand the optical absorption processes.
c (space group 167) symmetry. As a starting point, we use the experimental lattice parameters from Dernier et al.,73 Boulay et al.,74 Diehl et al.,75 and Takata et al.76 for the lutetium, gadolinium, yttrium, and lanthanum compounds respectively. Using these parameters as inputs, we replace one leading cation by Ce, and perform standard lattice relaxations at the PBE+U level to find the ground state ionic positions. These atomic positions are then used in single-point hybrid calculations that constitute our approximation to the ground and excited states for Δ-SCF calculations. The PBE+U+SO quasi-particle spectrum is then used to solve the BSE equation and evaluate either eqn (10) or eqn (11) to understand the optical absorption processes.
In this study, we conceptualize the Hubbard U term to be a free parameter in the sense that, while the ionic relaxation and electronic structure are U-dependent, the precise value of U does not change the qualitative behavior.†† We fix Ueff = 4 eV and J = 0 for all f states within the Dudarev scheme66 unless otherwise noted. Due to computational limitations in the Δ-SCF calculations, we neglect the spin–orbit interaction when comparing several chemistries (Table 1); however, we provide some discussion below on its importance.
While GdAlO3 is an antiferromagnet at 0 K,77 again for computational simplicity, in the Δ-SCF calculations we do not attempt to use the antiferromagnetic ground state, but instead use, as an approximation, the computationally simpler ferromagnetic state. This is a reasonable approximation because the antiferromagnetic ordering temperature is 3.9 K.77 Therefore, the exchange interaction should not contribute significantly to the free energy at high temperature. Where the HSE06 hybrid functional is used for final electronic structure calculations, we use 33% exact exchange instead of the usual 25%.78 The screening parameter is 0.2 Å−1. In all cases, we maintain a minimum momentum space resolution of 0.7 Å−1.
Experimental
For comparison to the theoretical calculations, Ce-doped perovskites YAlO3:0.5% Ce and GdAlO3:0.5% Ce were synthesized by melting the mixture of constituent oxides under an argon atmosphere in an optical floating zone furnace and subsequent quenching of the melt. A single-lamp, single-mirror optical floating zone furnace FZ-S15065X(HV) (Asgal Corp., Japan) equipped with a 6.5 kW Xe arc lamp was utilized with an Al2O3 crucible serving as a receptacle for the molten droplets. Phase purity of the samples was confirmed by X-ray powder diffraction on a Bruker Nano D8 Advance diffractometer equipped with a LynxEye XE-T position sensitive detector and copper X-ray tube. The lattice parameters determined from the observed diffraction peak positions matched the reported literature values and database records, confirming their composition. Thin opaque pellets were fabricated from as-prepared powders with 5 wt% methylcellulose binder and their photoluminescence emission and excitation spectra were measured using custom-built PTI Quantamaster double-grating spectrofluorometer using 75 W Xe arc lamp as a light source and Hamamatsu R928P photomultiplier tube as the detector. After removing the scattered light background, the transition energies for observed overlapping excitation bands (monitored wavelength was at Ce3+ emission maximum of 358 and 365 nm for GdAlO3:Ce and YAlO3:Ce, respectively) were determined from a multiple Gaussian curve fit in the spectra transformed into ∼W/eV = f(E[eV]).Results
Table 1 represents the main result, and compares the theoretical and experimental fundamental electronic gaps as well as principal luminescence wavelengths. We find that generally hybrid functionals give the best Eg for these rare-earth aluminates. The range of λex measurements taken from literature is summarized in Table 1, and the experimental gap is taken from experiments performed on high quality bulk films. This table shows that the BSE predictions are within a few percent of the average wavelength measured across several experiments, while the Δ-SCF prediction can vary by nearly 100 nanometers. For example, in the lutetium compound, the Δ-SCF underestimated the excitation energy, while in the yttrium compound, the excitation energy was overestimated. The reason for this, we suspect, has to do with the character of the virtual state wave functions. For example, the lowest conduction band states in LuAlO3:Ce and YAlO3:Ce vary in orbital content and degree of localization. Enforcing the occupation of these Kohn–Sham eigenstates states does not account for selection rules, energy and momentum conservation, or the fact that the Δ-SCF approach is meant to deal with localized states. Solution of the BSE does account for each of these, and we attribute the difference between the Δ-SCF approach and experiment to these factors.Fig. 2 summarizes the electronic structure of LuAlO3:Ce at various levels of theory. Panels (a) and (b) show the ground and excited state density of states using HSE with spin–orbit (SO) coupling. Panels (c) and (d) demonstrate the effect of the Hubbard U correction. Similar to Ning et al.,79 we find that increasing the Hubbard U correction on the Ce f states nearly linearly drives them toward the valence band. We see that in the un-relaxed structure, the single Ce f electron remains in the gap and never becomes part of the valence band for 2 < U < 8 (eV), but in the relaxed structure for a large enough U value, this state can be driven into the valence band. Panel (e) shows the dispersion of LuAlO3:Ce, and panel (f) shows the projected density of states. From the latter four panels, we know that the Hubbard U term can slide the position of the occupied Ce f level within the gap. Although the states are largely dispersionless, we do find significant orbital mixing in the conduction band. The projected density of states in Fig. 1(f) shows that, because the lowest lying conduction band states do have significant Ce d and f character, we expect the Δ-SCF approach to be less accurate. Nevertheless, we can still investigate the difference between the electronic structure in the ground and excited states as given in the first two panels of Fig. 2. We find using the Δ-SCF approach that the localized Ce f level becomes unoccupied in the excited state as expected (Fig. 2b), but additionally that the d character is pulled down in energy. This is evidence that the excited state solution has not fallen back into the ground state, i.e., we have not suffered a variational collapse.
Based on our discussion of the Δ-SCF approach in the Theoretical Approaches section, we seek to move half an electron between the Ce 4f and 5d orbitals. However, the difficulty of using the eigenstates as a reference basis is clear from Fig. 3. It shows the change in the DFT energy between the ground and excited states, ΔE, as well as the change in f orbital occupancy, Δnf, for LuAlO3:Ce including spin–orbit coupling with various functionals and pseudopotentials. Fig. 3 also serves to illustrate that the spin–orbit interaction does not improve the Δ-SCF prediction appreciably. In principle, the spin–orbit coupling can affect the system in three ways. First, it splits the degeneracy between the Lu f states, better aligning the simulations with synchrotron valence band spectra. Second, it allows inter-system crossings between bright and dark exciton states,80 effectively changing the nature of the available decay channels. Third, because Ce3+ is susceptible to nephelauxetic expansion,81 the spin–orbit interaction increases the delocalization of virtual Ce d states relative to the non-spin–orbit coupled solution. In spite of these, we find that including the spin–orbit coupling only changes the result by a few nanometers, and suspect each of these effects to generally be a weak correction to the predicted wavelengths. In fact, this same trend holds regardless of the functional chosen or pseudopotentials used – the principal luminescence wavelength is approximately 20% deviated from experiment, and at the same time, we do not reach the transfer of one-half an electron. The results in this plot are a manifestation of the difficulty inherent in the Δ-SCF approach, which we suspect will hold across solid state chemistries. We attribute the deviations from experiment in Table 1 to these same factors.
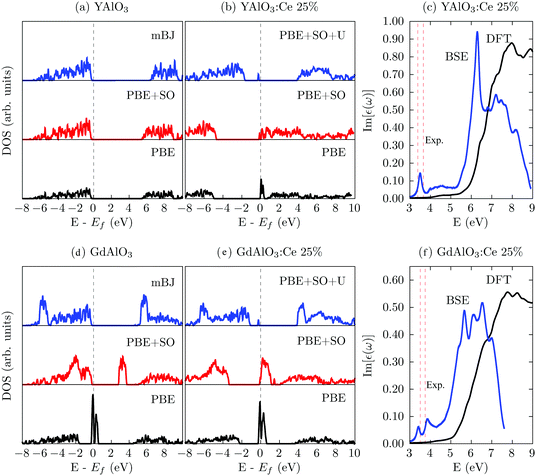
Fig. 4 shows the electronic structure and dielectric function for the yttrium and gadolinium compounds, respectively. Much like the lutetium compound, the spin–orbit interaction lowers the degeneracy in the Ce f states, and a Hubbard U correction is necessary to gap the spectrum. The single particle spectrum is compared against the BSE spectrum in part (c) and (f). We find that, in both cases, accounting for the electron–hole interaction via the BSE results in the emergence of new low energy peaks that align well with experimental measurements (indicated by dashed vertical lines), but also significantly red-shifts the spectra. Because we need very few (only 4) occupied bands and relatively few (20–40) unoccupied bands to capture the experimental excitation wavelength, this is evidence that a primary radiative decay event in the cerium doped aluminates is driven by the Coulomb interaction between a hole localized on the Ce f state and a partially delocalized state that can be of mixed orbital character. Our finding is in contrast to previous work suggesting that, without localized in-gap states, there can be no luminescence.51 In other words, there are actually two energy scales that contribute here – thermal and correlation. It is usually thought that Ce3+ d states must lie far enough (≫kBT) below the conduction band so that thermal quenching will not preclude scintillation. However, it is possible that correlation effects (spectral properties) can outweigh distribution effects (the temperature only enters the Fermi function), if localized holes are negligibly screened. At the single-particle level (DFT), the theoretical peaks in Fig. 4(c and f) align with the thermal-only picture because the Ce3+ d are buried in the conduction band and no peak is predicted near the experimentally measured wavelength. However, by including the electron–hole correlation effects, we do see a peak at the same energy as the measurement, even though the Ce3+ d states are slightly hybridized, forming part of the conduction band. Of course there is no way experimentally to see what will happen in the absence of correlations, but theoretically we are showing what will happen with correlations “on” (BSE) and correlations “off” (DFT). By doing so, we find an optically active channel at the same energy found in experiment. This data then is evidence that electron–hole correlations play an important role in scintillator properties. At this point, we now turn to a discussion of these results.
Discussion
Treatment of electron–hole correlations
Earlier, we pointed out that the Δ-SCF method and the BSE approach vary in multiple ways, but one of the most important ways they differ is in their treatment of electron–hole correlations. In the Δ-SCF method, we have found that local exchange–correlation functionals perform rather poorly, with predictions more than 100 nm deviated from experiment, while hybrid functionals perform better with wavelength predictions ≤100 nm from experiment. This is evidence that non-local correlations are important because the result improved by adding a portion of exact exchange. In light of the approximations used in the Δ-SCF approach that may obscure the interpretation, achieving better results by incorporating a portion of the screened Coulomb potential suggests that accounting for the electron–hole interaction may be necessary. If, then, by explicit treatment of the direct and exchange couplings through the BSE, one achieves predictions even more in line with measurement, the conclusion that electron–hole correlations are important becomes even stronger. What then precludes always solving the BSE? The issue is often one of computational expense.The computational burden usually associated with solution of the BSE is however decreased (or absent) for this specific class of materials, and the computational cost of the Δ-SCF method is increased. This is because a large portion of the computational cost for solving the BSE comes in converging the evaluation of the interaction kernel with respect to momentum sampling, but for the rare-earth scintillators studied here, we were able to achieve good agreement with experiment with relatively few bands and k points. This suggests that only a few dispersionless bands dominate the spectrum. In other words, a sufficient approximation is that the wave functions do not change appreciably between momenta that compose the radiative decay channel. Additionally, because the dimension of the exciton Hamiltonian scales only with bands and k points (dim(H) = NcNvNk), large supercells with light doping are accessible as long as the radiative decay channels are comprised of relatively few dispersionless bands. Access to the excitation energy by the Δ-SCF method on the other hand scales cubically with the number of electrons, ultimately requiring multiple hybrid simulations of large supercells. Couple that with the absence of ambiguity in the excited state interpretation with the BSE, and the BSE provides a more accurate, cheaper alternative to the Δ-SCF approach for investigation and discovery of rare-earth scintillator materials.
Extensions of the Δ-SCF method
It is worth discussing the fact that the Δ-SCF method is most studied for molecular systems,32,82 and the dubious choice of number of electrons to excite in long-range-ordered solids has been addressed with the development of the Δ-sol method.36 The Δ-sol method, however, is formulated to predict the fundamental electronic gap in solids, which is not the excitation spectrum, because numerous processes occur below the fundamental gap (single- and multi-phonon production by infrared irradiation, Urbach tailing, recombination at in-gap/defect states, exciton recombination etc.83). This alone suggests the Δ-sol method would be of limited general utility for scintillator prediction, even compared to the standard Δ-SCF. Additionally, the theory is based on dielectric screening in a homogeneous electron gas within the random phase approximation, and it is unlikely this will be a valid starting point for excitations from atomic-like states in wide gap systems. Dielectric screening is generally a power law function of the gap,84 and explains why the materials tested in the Δ-sol study all have a gap less than 4 eV (and are mostly s and p valence systems). This means the most salient feature of the Δ-sol method, namely, a way to choose the correct number of valence electrons in the thermodynamic limit based on the assumption of complete screening at 5–7 kf−1, is not applicable to rare-earth scintillators because the screening length will be ∼10 times larger in these systems. All this suggests that accurate predictions of rare-earth scintillators cannot be approached from the viewpoint of refinements of the Δ-SCF method.Conclusions
We have shown that accurate predictions of the principal luminescence wavelength across the cerium-doped, rare-earth aluminates can be achieved by solving the Bethe–Salpeter equation from first principles. The efficacy of this approach reflects the importance of the electron–hole interaction in this class of scintillating materials. The computational burden usually associated with solving the BSE is reduced in these systems because the radiative decay processes are dominated by relatively few, dispersionless bands. Therefore, a smaller basis set is needed to achieve reasonable accuracy. A comparison of the BSE approach against the Δ-SCF method has presented at least two sources of error for the Δ-SCF method. The first is that electron–hole interactions are not explicitly accounted for, even though they are expected to play an important role in weakly-screened, wide-gap systems. To partially circumvent this, advanced (ground-state) functionals may be employed in the Δ-SCF method, but this leads to significant computational expense. Still, ground state exchange–correlation functionals are not expected to properly account for the orbital dependent potentials actually realized in the excited state. The second source of deviation is the difficulty in obtaining the desired occupations in partially hybridized bands. In this case, optical selection rules may be inadvertently broken, leading to incorrect transition energies. Although it can be computationally taxing in certain circumstances, solution of the BSE has neither of these problems. Therefore, development of new scintillating materials can leverage the accuracy and affordability of the BSE approach to accelerate materials discovery.Author contributions
Christopher N. Singh: conceptualization, methodology, formal analysis, investigation, writing – original draft, writing – review & editing, visualization. Ghanshyam Pilania: writing – review & editing, supervision. Jan Bárta: formal analysis, investigation, writing – review & editing. Blas Pedro Uberuaga: writing – review & editing, resources, supervision, project administration, funding acquisition. Xiang-Yang Liu: conceptualization, validation, resources, writing – review & editing, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Los Alamos National Laboratory (LANL) Directed Research and Development Program, and used resources provided by the LANL Institutional Computing Program. LANL is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy under Contract No. 89233218CNA000001. We would like to thank J. A. Valdez for X-ray powder diffraction measurements and B. W. Wiggins for access to photoluminescence setup.References
- S. K. Gupta and Y. Mao, Front. Optoelectron., 2020, 13, 156–187 CrossRef.
- C. Dujardin, E. Auffray, E. Bourret-Courchesne, P. Dorenbos, P. Lecoq, M. Nikl, A. Vasilev, A. Yoshikawa and R.-Y. Zhu, IEEE Trans. Nucl. Sci., 2018, 65, 1977–1997 CAS.
- M. Marsman, J. Andriessen and C. W. E. van Eijk, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 16477–16490 CrossRef CAS.
- A. N. Vasil'ev and A. V. Gektin, IEEE Trans. Nucl. Sci., 2013, 61, 235–245 Search PubMed.
- D. J. Vogel and D. S. Kilin, J. Phys. Chem. C, 2015, 119, 27954–27964 CrossRef CAS.
- F. Zhou, B. Sadigh, P. Erhart and D. Åberg, npj Comput. Mater., 2016, 2, 1–7 CrossRef.
- R. Williams, J. Q. Grim, Q. Li, K. Ucer, G. Bizarri, S. Kerisit, F. Gao, P. Bhattacharya, E. Tupitsyn, E. Rowe, et al., Hard X-Ray, Gamma-Ray, and Neutron Detector Physics XV, 2013, p. 88520J Search PubMed.
- M. Korzhik, G. Tamulaitis and A. N. Vasil'ev, Physics of Fast Processes in Scintillators, Springer Nature, 2020 Search PubMed.
- J. C. de Mello, H. F. Wittmann and R. H. Friend, Adv. Mater., 1997, 9, 230–232 CrossRef CAS.
- M. Nikl, Phys. Status Solidi A, 2000, 178, 595–620 CrossRef CAS.
- W. Moses, G. Bizarri, R. T. Williams, S. Payne, A. Vasil'Ev, J. Singh, Q. Li, J. Grim and W.-S. Choong, IEEE Trans. Nucl. Sci., 2012, 59, 2038–2044 Search PubMed.
- A. Gektin, A. N. Vasilev, V. Suzdal and A. Sobolev, IEEE Trans. Nucl. Sci., 2020, 880–887 CAS.
- T. Yanagida, Proc. Jpn. Acad., Ser. B, 2018, 94, 75–97 CrossRef CAS PubMed.
- J. Ueda, P. Dorenbos, A. J. Bos, K. Kuroishi and S. Tanabe, J. Mater. Chem. C, 2015, 3, 5642–5651 RSC.
- H. Luo, A. J. Bos and P. Dorenbos, J. Phys. Chem. C, 2016, 120, 5916–5925 CrossRef CAS.
- P. Erhart, A. Schleife, B. Sadigh and D. Åberg, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 075132 CrossRef.
- W. Hanke and L. J. Sham, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 4656–4673 CrossRef CAS.
- J. Paier, M. Marsman and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 121201 CrossRef.
- A. Canning, A. Chaudhry, R. Boutchko and N. Grønbech-Jensen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 125115 CrossRef.
- G. Pilania, K. J. McClellan, C. R. Stanek and B. P. Uberuaga, J. Chem. Phys., 2018, 148, 241729 CrossRef CAS PubMed.
- G. Pilania, S. K. Yadav, M. Nikl, B. P. Uberuaga and C. R. Stanek, Phys. Rev. Appl., 2018, 10, 024026 CrossRef CAS.
- J. Gavnholt, T. Olsen, M. Engelund and J. Schiøtz, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075441 CrossRef.
- E. E. Salpeter and H. A. Bethe, Phys. Rev., 1951, 84, 1232–1242 CrossRef.
- S. Albrecht, L. Reining, R. Del Sole and G. Onida, Phys. Rev. Lett., 1998, 80, 4510–4513 CrossRef CAS.
- M. Rohlfing and S. G. Louie, Phys. Rev. Lett., 1998, 81, 2312–2315 CrossRef CAS.
- Z. Song, J. Zhao and Q. Liu, Inorg. Chem. Front., 2019, 6, 2969–3011 RSC.
- Y. Jia, A. Miglio, S. Poncé, M. Mikami and X. Gonze, Phys. Rev. B, 2017, 96, 125132 CrossRef.
- Y. Jia, S. Poncé, A. Miglio, M. Mikami and X. Gonze, Adv. Opt. Mater., 2017, 5, 1600997 CrossRef.
- R. M. Martin, Electronic structure of atoms, Cambridge University Press, 2004, p. 187–203 Search PubMed.
- J. C. Slater Statistical Exchange–Correlation in the Self-Consistent Field, Academic Press, 1972, vol. 6, pp. 1–92 Search PubMed.
- R. O. Jones and O. Gunnarsson, Rev. Mod. Phys., 1989, 61, 689–746 CrossRef CAS.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037 CrossRef CAS PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- Y. Jia, S. Poncé, A. Miglio, M. Mikami and X. Gonze, Phys. Rev. B, 2019, 100, 155109 CrossRef CAS.
- U. von Barth, Phys. Rev. A: At., Mol., Opt. Phys., 1979, 20, 1693–1703 CrossRef CAS.
- M. K. Y. Chan and G. Ceder, Phys. Rev. Lett., 2010, 105, 196403 CrossRef CAS PubMed.
- V. Kolobanov, V. Mikhailin, N. Petrovnin, D. Spassky and Y. Zorenko, Phys. Status Solidi B, 2006, 243, R60–R62 CrossRef CAS.
- C. Dujardin, C. Pedrini, W. Blanc, J. Gacon, J. Van't Spijker, O. Frijns, C. Van Eijk, P. Dorenbos, R. Chen and A. Fremout, et al. , J. Phys.: Condens. Matter, 1998, 10, 3061 CrossRef CAS.
- A. Lempicki, M. H. Randles, D. Wisniewski, M. Balcerzyk, C. Brecher and A. J. Wojtowicz, IEEE Trans. Nucl. Sci., 1995, 42, 280–284 CAS.
- P. Dorenbos, E. Bougrine, J. De Haas, C. Van Eijk and M. Korzhik, Radiat. Eff. Defects Solids, 1995, 135, 321–323 CrossRef CAS.
- J. Verweij, M. T. Cohen-Adad, D. Bouttet, H. Lautesse, B. Moine and C. Pedrini, Chem. Phys. Lett., 1995, 239, 51–55 CrossRef CAS.
- H. Luo and P. Dorenbos, J. Mater. Chem. C, 2018, 6, 4977–4984 RSC.
- T. Inoue, T. Morimoto and Y. Ohki, Appl. Phys. A: Mater. Sci. Process., 2015, 119, 1423–1429 CrossRef CAS.
- T. De Queiroz, C. Ferrari, D. Ulbrich, R. Doyle and A. De Camargo, Opt. Mater., 2010, 32, 1480–1484 CrossRef CAS.
- Y. Parganiha, J. Kaur, V. Dubey and R. Shrivastava, Superlattices Microstruct., 2015, 85, 410–417 CrossRef CAS.
- Y. Zorenko, M. Nikl, J. Mares, V. Gorbenko, V. Savchyn, T. Voznyak, M. Kucera, A. Beitlerova, R. Kucerkova and A. Fedorov, Phys. Status Solidi A, 2009, 206, 2586–2592 CrossRef CAS.
- Y. V. Zorenko, A. Voloshinovskii, G. Striganyuk and V. Gorbenko, Opt. Spectrosc., 2005, 98, 555–558 CrossRef CAS.
- S.-G. Lim, S. Kriventsov, T. N. Jackson, J. Haeni, D. G. Schlom, A. Balbashov, R. Uecker, P. Reiche, J. Freeouf and G. Lucovsky, J. Appl. Phys., 2002, 91, 4500–4505 CrossRef CAS.
- X. Wang, T. Pan, T. Zang, J. Li, Z. Zhao, L. Zhang and J. Xu, Sci. China, Ser. E: Technol. Sci., 2009, 52, 3678 CrossRef CAS.
- X. Zeng, L. Zhang, G. Zhao, J. Xu, Y. Hang, H. Pang, M. Jie, C. Yan and X. He, J. Cryst. Growth, 2004, 271, 319–324 CrossRef CAS.
- A. Canning, R. Boutchko, A. Chaudhry and S. E. Derenzo, IEEE Trans. Nucl. Sci., 2009, 56, 944–948 CAS.
- C. D. Spataru, S. Ismail-Beigi, R. B. Capaz and S. G. Louie, Phys. Rev. Lett., 2005, 95, 247402 CrossRef PubMed.
- M. Gatti and F. Sottile, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 155113 CrossRef.
- F. Wu, F. Qu and A. H. MacDonald, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 075310 CrossRef.
- R. J. Elliott, Phys. Rev., 1957, 108, 1384–1389 CrossRef CAS.
- G. D. Mahan, Many-particle physics, Springer Science & Business Media, 2013 Search PubMed.
- P. Dorenbos, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 165107 CrossRef.
- P. Dorenbos, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035118 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467–R5470 CrossRef CAS PubMed.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954 CrossRef CAS PubMed.
- V. I. Anisimov, I. V. Solovyev, M. A. Korotin, M. T. Czyżyk and G. A. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 16929–16934 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- T. Sander, E. Maggio and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 045209 CrossRef.
- P. Dernier and R. Maines, Mater. Res. Bull., 1971, 6, 433–439 CrossRef CAS.
- D. d. Boulay, N. Ishizawa and E. N. Maslen, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2004, 60, i120–i122 CrossRef PubMed.
- R. Diehl and G. Brandt, Mater. Res. Bull., 1975, 10, 85–90 CrossRef CAS.
- H. Takata, M. Iiduka, Y. Notsu and M. Harada, J. Alloys Compd., 2006, 408, 1190–1192 CrossRef.
- A. Cooke, N. England, N. Preston, S. Swithenby and M. Wells, Solid State Commun., 1976, 18, 545–547 CrossRef CAS.
- X.-Y. Liu, G. Pilania, A. A. Talapatra, C. R. Stanek and B. P. Uberuaga, ACS Appl. Mater. Interfaces, 2020, 12, 46296–46305 CrossRef CAS PubMed.
- L. Ning, F. Yang, C. Duan, Y. Zhang, J. Liang and Z. Cui, J. Phys.: Condens. Matter, 2012, 24, 055502 CrossRef PubMed.
- E. Eizner, L. A. Martnez-Martnez, J. Yuen-Zhou and S. Kéna-Cohen, Sci. Adv., 2019, 5, eaax4482 CrossRef CAS PubMed.
- D. N. Petrov and B. Angelov, Phys. B, 2020, 579, 411912 CrossRef CAS.
- Y. C. Park, M. Krykunov and T. Ziegler, Mol. Phys., 2015, 113, 1636–1647 CrossRef CAS.
- M. Korzhik and A. Gektin, Engineering of scintillation materials and radiation technologies, Springer, 2017, pp. 3–11 Search PubMed.
- R. Ravichandran, A. X. Wang and J. F. Wager, Opt. Mater., 2016, 60, 181–187 CrossRef CAS.
- J. F. Janak, Proof that ∂E/∂ni = ε in density-functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 18(12), 7165–7168 CrossRef CAS.
- A. Görling, Density-functional theory beyond the Hohenberg–Kohn theorem, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59(5), 3359–3374 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc01151k |
| ‡ Extrinsic factors will contribute most to inter-sample variation, while the intrinsic factors will contribute most to inter-system variation. |
| § There are in fact many first principles approaches to excited state phenomena, but many are more nuanced, less widely applied, or more applicable to molecular systems. See Dreuw et al.32 or Park et al.82 for more information. |
| ¶ Extensions to density functional theory were given later by Janak85 and Görling.86 |
| || We use the word exciton in the same way as Mahan p. 592:56 “the modification of the absorption rate of photons due to the Coulomb interaction between the electron and valence band hole”. |
| ** This point will be elaborated on later. |
| †† These compounds are metallic at the PBE level, and while the value of U can rigidly shift the precise location of the Ce f state, we mainly need it to open a gap for cheaper-than-hybrid ionic relaxations. |
| This journal is © The Royal Society of Chemistry 2021 |