Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The local atomic structure and thermoelectric properties of Ir-doped ZnO: hybrid DFT calculations and XAS experiments†
Andrei
Chesnokov
 a,
Denis
Gryaznov
a,
Denis
Gryaznov
 *a,
Natalia V.
Skorodumova
bc,
Eugene A.
Kotomin
ad,
Andrea
Zitolo
*a,
Natalia V.
Skorodumova
bc,
Eugene A.
Kotomin
ad,
Andrea
Zitolo
 e,
Martins
Zubkins
e,
Martins
Zubkins
 a,
Alexei
Kuzmin
a,
Alexei
Kuzmin
 a,
Andris
Anspoks
a,
Andris
Anspoks
 a and
Juris
Purans
a
a and
Juris
Purans
a
aInstitute of Solid State Physics, University of Latvia, Kengaraga 8, Riga, LV-1063, Latvia. E-mail: gryaznov@mail.com
bDepartment of Materials Science and Engineering, School of Industrial Engineering and Management, KTH-Royal Institute of Technology, Brinellvägen 23, Stockholm, Sweden
cDepartment of Physics and Astronomy, Uppsala University, Box 516, 751 20 Uppsala, Sweden
dMax Planck Institute for Solid State Research, Heisenbergstr. 1, Stuttgart, D-70569, Germany
eSynchrotron SOLEIL, L’orme des Merisiers, BP 48 Saint Aubin, 91192, Gif-sur-Yvette, France
First published on 15th March 2021
Abstract
We combined the hybrid density functional theory (DFT) calculations and X-ray absorption spectroscopy (XAS) experiments in the study of the local atomic structure around Ir ions in ZnO thin films with different iridium content. This was then used in the first principles analysis of the thermoelectric properties of material. The emphasis has been put on the conditions for a positive Seebeck coefficient and p-type electrical conductivity as the functions of the Fermi level. We studied both computationally and experimentally several possible IrOx polyhedra (complexes) with a different number of surrounding oxygens and Ir oxidation states, including those with the formation of peroxide ions (O22−). In particular, octahedral coordination of iridium ions was identified by reverse Monte Carlo (RMC) simulations of the Ir L3-edge EXAFS spectra of ZnO:Ir thin films as the predominant complex, which is supported by the calculated lowest interstitial oxygen incorporation energies. All the calculated IrOx (x = 4, 5, 6) complexes, regardless of Ir the oxidation state, demonstrate potential for p-type conduction if the Fermi level (μF) falls in the range of 0–0.8 eV from the valence band maximum (VBM) and the Ir concentration is high enough (12.5% in the present DFT calculations). Even though the corresponding calculated Seebeck coefficient (S) around 80–89 μV K−1 slightly exceeds the experimental values, we emphasise the presence of an important plateau in the dependence of S on μF in this range for two complexes with the formation of peroxide ions (O22−). We predicted also that peroxide ions O22− are characterized by the calculated phonon frequencies of 810–942 cm−1 in agreement with our previous Raman experimental results. In this light, we discuss the high sensitivity of calculated S(μF) dependences to the atomic and electronic structure.
Introduction
Zinc oxide (ZnO) is widely used in semiconductor and optoelectronic industries. Despite more than two decades of intensive research, the capabilities of ZnO are still not exhausted. It can be grown as large bulk single crystals of high quality, deposited as thin films, or made amorphous.1–3 It has a 3.4 eV wide band gap, strong luminescence, high electron mobility, high thermal conductivity and large exciton binding energy. Due to these properties, ZnO is regarded as a promising material for a wide variety of applications, including but not limited to transparent conductors, sensors/emitters of blue and UV light, and to functional coatings.4,5 In particular, modern electronics requires stable p-type thin films with sufficiently high transparency and p-type conductivity. Modified ZnO can be a stable n-type conductor, and the current research focuses on achieving stable p-type conductivity. Concurrently, as a result of advances in growing methods, the research scope is also shifting towards an amorphous phase of ZnO.6To date, there has been room for more details on a study of the behaviour of intrinsic and impurity defects in ZnO. A comprehensive analysis of intrinsic defect behaviour by using advanced optical measurements was recently performed for defect-rich single ZnO7 crystals. In the interpretation of photo-luminescence spectra the oxygen vacancies (VO), the vacancy pairs (VO–VZn), Zn interstitials and their complexes were identified. In ZnO electronic donors are formed spontaneously leading to intrinsic doping asymmetry.8 Even though the oxygen vacancy possesses the lowest formation energy under Zn and O-rich conditions in most theoretical studies on bulk material, understanding conditions for the growth of the thin films plays a very important role. The literature indicates that the analysis of defects in thin films should be done with caution. For instance, the Mn-doped ZnO thin films required theoretical computations to explain discrepancies in the interpretation of XANES (X-ray absorption near edge structure) spectra.9 It was established that neither O nor Zn vacancies are detectable in the XANES spectra. Their presence is less important than local structure changes induced by the Mn impurity. The present study focuses on the d-electron impurity, Ir. ZnO:cIr thin films (c is the Ir concentration) have demonstrated the change in the sign of the Seebeck coefficient from negative to positive for Ir concentration ranging from c = 12.4 to 16.4%.10 High oxygen partial pressure during the ZnO:cIr thin film deposition and film transformation into the amorphous phase with the Ir concentration c = 7–16% at room temperature allows us to suggest an important role of oxygen interstitials (Oi's).10 However, atomistic understanding of the changes in the ZnO:cIr thin film properties was missing. Notice that the present experiments considered a wider range of Ir concentrations and were mainly focused on the local atomic structure around Ir. Raman spectroscopy results revealed10 the existence of a vibrational band at 720 cm−1, and it was argued that its presence is not due to the IrO2 phase but is rather related to the formation of a peroxide moiety (O22−). The existing body of work5 relating to ZnO largely agrees on the fact that Oi tends to form an O–O ‘dumbbell’ or ‘split interstitial’. This may show both donor- and acceptor-like qualities as discussed based on DFT calculations.11
Notice that previous DFT calculations of Ir-doped ZnO did not discuss the thermoelectric properties and the effect of Seebeck coefficient sign change.12–14 Thus, the present DFT calculations address these peculiar properties of ZnO:Ir thin films and explore the connection between the role of Ir impurity and Oi for the electronic structure, thermoelectrical properties and p-type conduction. We use several models of IrOx polyhedra (called, hereafter, IrOx complexes) in ZnO, distinguished by the number of oxygens surrounding Ir, the oxidation state of Ir, incorporation energy of Oi's and the presence of peroxide defects. Thus, we can find interpretations in the Seebeck coefficient dependences on μF for potential p-type conduction in Ir-doped ZnO.
The experimental section describes details of preparing Ir-doped ZnO and pure IrOx thin films and synchrotron radiation XAS measurements at the Ir L3-edge. Subsequent sections on methods introduce the models for the calculation of IrOx complexes in ZnO and present computational details, including those regarding the thermoelectric properties. The results section is divided into several subsections to discuss the results of the extended X-ray absorption fine structure (EXAFS) spectra analysis using reverse Monte Carlo (RMC) simulations, the calculated structural properties of IrOx complexes in ZnO and those of the parent compounds, the electronic structure properties of IrOx complexes in ZnO, and the main results of thermoelectric property calculations.
Methods
Experimental
Mixed zinc-iridium oxide (ZnO:cIr) and pure IrOx amorphous thin films were deposited on polyimide tape substrates at room temperature by reactive DC magnetron co-sputtering in an Ar (20 sccm) + O2 (10 sccm) atmosphere (10 mTorr working pressure). A metallic Zn (99.95 wt%) target with Ir (99.6 wt%) pieces placed on the target erosion zone were used for sputtering. The thin film thickness was about 200–300 nm. The iridium concentration (c = 7%, 16%, 29%, 54% and 67%) was determined using X-ray fluorescence measurements. X-ray diffraction measurements confirm the amorphous structure of all films. More details about the experimental procedure can be found in ref. 10.X-ray absorption spectra (XAS) at the Ir L3-edge were measured at room temperature at the SAMBA bending-magnet beamline15 of the Synchrotron SOLEIL storage ring. The experiments were performed in transmission mode using the focusing Si(220) monochromator and two ionization chambers. For each sample, a multi-layered sandwich was prepared to obtain a sufficiently large total thickness of samples with an absorption edge jump close to 1. The processing of XAS was performed using a conventional procedure,9 as implemented in the XAESA code.16
The Ir L3-edge EXAFS spectra in mixed zinc–iridium oxide (ZnO:cIr) and pure IrOx thin films were analysed using the reverse Monte Carlo (RMC) method17 based on the evolutionary algorithm (EA), which is implemented in the EvAX code.18
DFT calculations
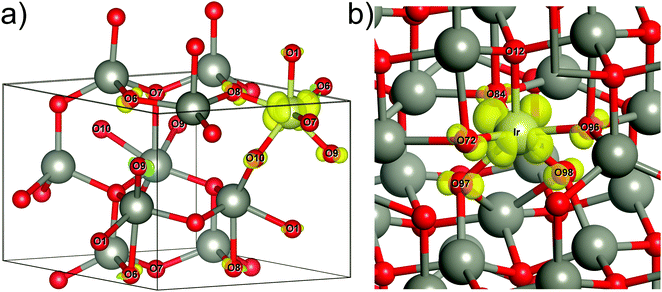
We have performed all DFT calculations using the Crystal17 v 1.0.219–22 computer code. We used the supercell approach,23 and as such we have modelled defective structures of ZnO (wurtzite structure with four atoms per unit cell, space group P63mc) using 2 × 2 × 1 (i.e. four times extended unit cell L4, consisting of 16 atoms) or 4 × 4 × 3 (L48, 192 atoms) supercells. These supercells represented 12.5 (L4) and 1.04 (L48) atomic % concentrations of Ir. In all cases, Ir ion substituted a regular Zn ion. In the following analysis, we refer to this defect as the IrnOx complex, where n denotes the oxidation state24 and x is the number of oxygen ions adjacent to Ir. In the wurtzite structure, Zn has four nearest O ions. Thus, we first model Ir surrounded by four host oxygen ions. In the results section we will show that n = 2+ in this case, i.e. Ir2+O4. Other complexes included the Oi ions. In our calculations we considered numerous atomic configurations and used the incorporation energy of Oi’s (discussed below) to choose the most important ones. There is a different complex with four oxygen ions surrounding Ir but with n = 3+, i.e. Ir3+O4, due to only one Oi adjacent to Ir and simultaneously forming O22− with a host oxygen (our first complex with the formation of O22−). There is the complex with five oxygen ions surrounding Ir with n = 4+, i.e. Ir4+O5, due to two Oi's close to Ir. In this complex one of the Oi ions forms O22− with the host oxygen (our second complex with the formation of O22−). Lastly, there is the complex with six oxygen ions surrounding Ir with n = 4+, i.e. Ir4+O6, due to two Oi's close to Ir and without formation of O22−. The atomic structure of each complex after the full structure relaxation can be seen in Fig. 5 and in Fig. S1 (ESI†).We analyse the oxidation state n of IrnOx in the different complexes by comparing it to reference materials: IrO2 (formal oxidation state of iridium is 4+), a hypothetical Ir2O3 (formal oxidation state 3+), and to ZnIr2O4 (formal oxidation state 3+). All these materials were modelled in their common reported structures: tetragonal (space group P42/mn, rutile structure) for IrO2, rhombohedral (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c, corundum structure) for Ir2O3, and cubic (space group Fd
c, corundum structure) for Ir2O3, and cubic (space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, spinel structure) for ZnIr2O4. To the best of our knowledge, the preparation of single-crystal Ir2O3 is not yet reported. However, its presence in IrO2 powders was discussed in ref. 25 and 26, and corundum Ir2O3(001) surface oxide was synthesized at high oxygen pressure27 in the oxidation of the Ir(111) surface. Besides, several papers describe and report measurements of properties of devices based on corundum-structured Ir2O3, although without discussing the actual structure of the material.28,29
m, spinel structure) for ZnIr2O4. To the best of our knowledge, the preparation of single-crystal Ir2O3 is not yet reported. However, its presence in IrO2 powders was discussed in ref. 25 and 26, and corundum Ir2O3(001) surface oxide was synthesized at high oxygen pressure27 in the oxidation of the Ir(111) surface. Besides, several papers describe and report measurements of properties of devices based on corundum-structured Ir2O3, although without discussing the actual structure of the material.28,29
Our DFT calculations are based on the method of linear combination of atomic orbitals (LCAO). We use atom-centered basis sets (BS) of Gaussian-type functions adopted from the literature. The relativistic effective core pseudopotential with 60 core electrons30 and basis set of triple-zeta valence with f-polarization function30,31 for Ir were taken from the Basis Set Exchange resource32 and used earlier by Ping et al.33 All-electron BSs for O and Zn were taken from ref. 33 and Gryaznov et al.,34 respectively. We modified the basis set for Zn by optimizing exponent values of the two most diffuse orbitals: one from the sp series and one from the d series (see the ESI† for details). We optimized these values with respect to the total electronic energy of the system with constant volume and atomic positions. The convergence limit of this procedure, based on the Powell's conjugate direction method and used as implemented in the OPTBAS35 interface to CRYSTAL, was set to 10−5 a.u. For all other calculations, the convergence limit on the total energy for the self-consistent field procedure was set to 10−7 a.u. for both electronic and lattice structure relaxation.
As the exchange–correlation functional we chose a hybrid PBE0 functional with 25% of Hartree–Fock exchange.36 We should mention that the bandgap value of pure ZnO obtained in the present calculations with the PBE0 functional is 3.45 eV, a value that is reasonably close to the experimental value of 3.44 eV37 and which did not require an increase of the amount of exact exchange suggested in the literature for the HSE functional.38 Indeed, our test calculation with the HSE functional showed a band gap of 2.93 eV, suggesting that this effect is basis-independent. The Brillouin zone was sampled with either 4 × 4 × 4 (for the L4 supercell) or a 2 × 2 × 2 (L48) Γ-centered k-point mesh generated with the Monkhorst–Pack39 method. All calculations of defective structures in the neutral supercells were spin-polarized and did not include the spin–orbit effects; the use of symmetry operations was explicitly omitted. Computational parameters (the choice of basis sets, functional and integration precision) have been validated to faithfully represent the bulk properties of ZnO, IrO2 and Ir2O3, and ZnIr2O4.
Oi incorporation energy
As discussed above, the IrOx complexes with n exceeding 2+ are not obtainable in the wurtzite structure by simply substituting Zn with Ir. The number of oxygen neighbours for each cation in the wurtzite structure is 4. Therefore, the additional Oi atoms are required. Thus, in our calculations for the Ir3+O4, Ir4+O5 and Ir4+O6 complexes defective L4 supercells contain 18 ions (8 metals and 10 oxygens) meaning two Oi's were added. The large supercell L48, containing 194 ions (96 metals and 98 oxygens) was used for the Ir4+O6 only. Optimization of atomic positions in a defective supercell may lead to very different atomic configurations; therefore, energetic criteria are important for their comparison. To compare systems of different atomic configurations we use the so-called incorporation energy, calculated from total electronic energies:| Einc(Oi) = E(Oi) − E(Ir) − E(O2), | (1) |
Calculation of thermoelectric properties
CRYSTAL17 allows post-process DFT wavefunctions for evaluating the electron transport properties by solving the Boltzmann equation. Unlike other approaches implemented in popular codes such as BoltzTrap41 or BoltzWann,42 CRYSTAL17 performs analytical derivatives of the electronic bands. Several studies have shown that all these codes, despite their differences, yield similar results.43,44 At the core of the equations for the transport coefficients (such as Seebeck coefficient and electronic conductivity) is the transport distribution function, cast here as the energy projected tensor: | (2) |
By integrating the conductivity distributions written with tensors of eqn (2), it is possible to obtain conductivity tensors, for instance, the electrical conductivity σ:
 | (3) |
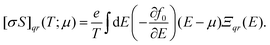 | (4) |
Results and discussion
Structural properties of synthesized samples
Careful examination of the experimental EXAFS spectra and their FTs (Fig. 1) suggests that the local environment around iridium atoms is quite disordered, being typical for nanocrystalline or amorphous IrOx films.47 Indeed, reliable structural contributions are present in FTs up to about 4 Å and consist of three peaks: the main peak at 1.5 Å is due to the nearest oxygen atoms of the first coordination shell, while the origin of the next two peaks at 2.5 and 3.5 Å should be clarified. Our previous experience suggests that in metal oxide thin films such peaks can be due to multiple-scattering (MS) effects within the first coordination shell of the metal atom48 with additional contributions originating from metal atoms located in the second coordination shell.49 Thus, the structural model required to describe the local environment of iridium should be cluster-like, i.e. containing a few atoms. Besides, the closeness of the experimental Ir L3-edge XANES and EXAFS spectra for pure IrOx and Ir-doped ZnO thin films gives strong evidence for the similarity of their structures. The Ir L3-edge XANES is dominated by the white line at ∼11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 217 eV due to the dipole allowed transition 2p3/2(Ir) → 5d(Ir) + 2p(O).50 A decrease of the iridium concentration leads to the appearance of the shoulder at 11
217 eV due to the dipole allowed transition 2p3/2(Ir) → 5d(Ir) + 2p(O).50 A decrease of the iridium concentration leads to the appearance of the shoulder at 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 eV, also visible in the EXAFS spectra at 2.5 Å−1; it is due to the damped high-frequency contribution originating from peaks at 2–4 Å in FTs. Thus, all samples can be roughly divided into two groups, having close XANES and EXAFS spectra; the first group with c ≤ 29% and the second group with c ≥ 54% and pure IrOx.
240 eV, also visible in the EXAFS spectra at 2.5 Å−1; it is due to the damped high-frequency contribution originating from peaks at 2–4 Å in FTs. Thus, all samples can be roughly divided into two groups, having close XANES and EXAFS spectra; the first group with c ≤ 29% and the second group with c ≥ 54% and pure IrOx.
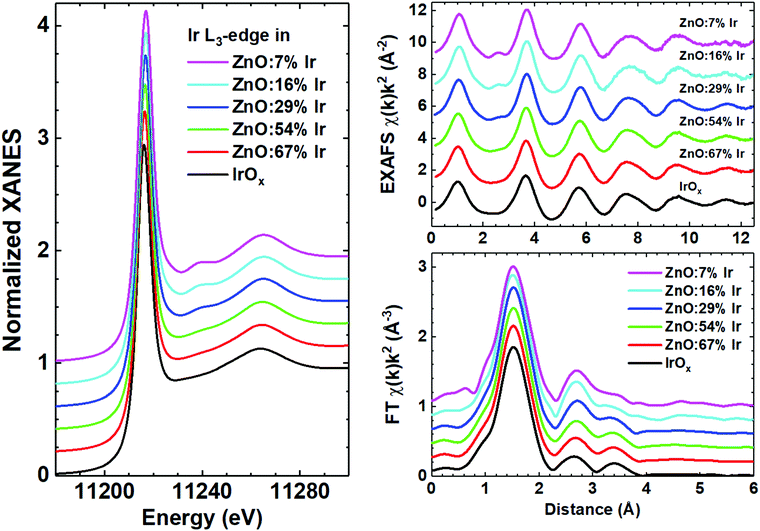 | ||
| Fig. 1 Experimental Ir L3-edge XANES (left panel), EXAFS and their Fourier transforms (FT) (right panel) for mixed zinc-iridium oxide (ZnO:cIr) and pure IrOx thin films. | ||
Crystalline IrO2 adopts the rutile-type structure (space group P42/mnm) with slightly distorted (2 × 1.96 Å and 4 × 2.00 Å) octahedral coordination of iridium atoms by oxygens.51
The IrO6 octahedra are joined by edges along the c-axis direction forming chains, which are cross-linked by shared corners to four neighbouring chains.51 Therefore, we used different fragments of the rutile IrO2 structure to construct two structural models for RMC simulations. The first model included a single IrO6 octahedron, whereas the second model contained two IrO6 octahedra joined by the edge. In both cases, a 5 × 5 × 5 supercell (a simulation box) was constructed (Fig. 2) and used in the RMC/EA simulations to get sufficient statistics from 125 independent structural units (IrO6 or Ir2O10). Each iridium-oxygen unit was placed in the centre of the cell with a large enough size (10 Å × 10 Å × 10 Å) to exclude the influence of units located in the neighbouring cells on each other.
 | ||
| Fig. 2 Two 5 × 5 × 5 supercell models used in the RMC simulations and composed of single IrO6 octahedra (left) and groups of two IrO6 octahedra joined by the edge (right). | ||
The details of the RMC/EA method were described previously.17,18 The number of simultaneously used atomic configurations in the EA method was 32. At each iteration, the new atomic configuration was generated by randomly displacing all atoms in the simulation box with the maximally allowed shift of 0.4 Å to get the best possible agreement between the Morlet wavelet transforms (WTs) of the experimental and calculated EXAFS spectra χ(k)k2. The calculations were performed in the k-space range from 1.5 to 11 Å−1 and in the R-space range from 0.8 to 4.0 Å. No significant improvement in the residual was observed after 5000 iterations.
The configuration-averaged EXAFS spectra during each RMC/EA simulation were calculated using ab initio real-space multiple-scattering (MS) FEFF8.50L code,52,53 including the MS effects up to the 4th order. The scattering potential and partial phase shifts were calculated for each absorption edge only once within the muffin-tin (MT) approximation52,53 for the cluster with a radius of 5 Å, constructed from the rutile IrO2 structure and centred at the absorbing iridium atom. Small variations of the cluster potential due to atom displacements during the RMC/EA simulations were neglected. The complex exchange–correlation Hedin-Lundqvist potential was used to account for the photoelectron inelastic losses within the one-plasmon approximation.54 The amplitude reduction factor S02 was included in the scattering amplitude,52,53 calculated by the FEFF code, and no additional correction of the EXAFS amplitude was performed.
The results of the RMC/EA simulations for two selected samples from each group are reported in Fig. 3 and 4. As one can see, two simple structural models (Fig. 2) provide good agreement with the experimental data, reproducing contributions from all peaks observed in FTs. In ZnO:cIr samples with c ≤ 29%, iridium atoms are octahedrally coordinated by six oxygens with R(Ir–O) = 1.93 ± 0.02 Å and the mean square relative displacement (MSRD) σ2(Ir–O) = 0.0050 ± 0.0005 Å2. The group of peaks located at longer distances in FT is solely due to the MS effects within the IrO6 octahedron. In ZnO:cIr samples with c ≥ 54% and pure IrOx, iridium atoms are also octahedrally coordinated by six oxygens with slightly longer mean bonds R(Ir–O) = 1.96 ± 0.02 Å, having slightly larger MSRD σ2(Ir–O) = 0.0065 ± 0.0005 Å2. However, there is an additional iridium atom from the neighbouring octahedron located at R(Ir–Ir) = 3.15 ± 0.02 Å with MSRD σ2(Ir–Ir) = 0.0056 ± 0.0005 Å2, whose EXAFS, together with that from the remaining 4 oxygen atoms, interferes with the MS contribution from the first shell, resulting in the two-peak structure in FT. Thus, at high Ir dopant concentration and in pure IrOx films, structural groups of two IrO6 octahedra joined by the edge can be evidenced. These groups form chains in crystalline rutile-type IrO2.51
 | ||
| Fig. 3 Experimental and calculated by RMC Ir L3-edge EXAFS spectra χ(k)k2 and their Fourier and Morlet wavelet transforms for the ZnO:7% Ir thin film. | ||
 | ||
| Fig. 4 Experimental and calculated by RMC Ir L3-edge EXAFS spectra χ(k)k2 and their Fourier and Morlet wavelet transforms for the pure IrOx thin film. | ||
DFT atomic structures of iridium–oxygen complexes in ZnO and parent compounds
We focus our discussion of the oxidation state n of Ir in the IrnOx complex in ZnO on an analogy with “pure” reference compounds: IrO2, Ir2O3, and ZnIr2O4 (see the computational details in Methods section). In either structure, Ir is six-fold coordinated, and in both IrO2 and Ir2O3 the six neighbouring oxygens are split into two groups (orbits) by symmetry, yielding long (axial) and short (azimuthal) Ir–O distances. The calculated lattice parameters of IrO2 and ZnIr2O4 are consistent with the experimental data (Table S1, ESI†). Our results show several possible ways to distinguish Ir3+ from Ir4+ (Table 1). First, the magnetic moment (μIr) of Ir demonstrates that Ir in all these oxides is in the low-spin state with electron configurations 5d5 (n = 4+, IrO2) and 5d6 (n = 3+, Ir2O3 and ZnIr2O4). Second, the effective atomic charge of Ir (qIr) is quite different for n = 3+ and 4+, which makes it a useful descriptor for comparing different IrnOx complexes. Thus, the larger (qIr) in IrO2 than in Ir2O3 and ZnIr2O4 is in accordance with a larger n in the former. Third, the Ir–O distances are typically longer for Ir3+ than for Ir4+ as shown in Table 1.| Crystal | d Ir–O, Å | q Ir, e | μ Ir, μB | q O, e | μ O, μB | ΔE, eV |
|---|---|---|---|---|---|---|
| IrO2 | Short: 1.942 | 1.712 | 0.625 | −0.856 | 0.171 | Metal |
| Long: 1.999 | ||||||
| Ir2O3 | Short: 2.053 | 1.241 | 0.000 | −0.827 | 0.000 | 3.39 |
| Long: 2.085 | ||||||
| ZnIr2O4 | 2.069 | 1.067 | 0.000 | −0.824 | 0.000 | 3.44 |
The smaller ionic radius of Ir4+ leads to a smaller lattice constant in IrO2 and, therefore, stronger hybridization between the Ir and O electronic states. Interestingly, the bandgap (ΔE) values in Ir2O3 and ZnIr2O4 are quite close. It was discussed earlier that the use of the hybrid exchange–correlation functional is critical to reproduce the bandgap in ZnIr2O4.13 The calculated ΔE for ZnIr2O4 in the present study is well comparable with the recently obtained experimental data in ref. 55.
In Tables 2 and 3 we present basic properties of the most important configurations of IrnOx complexes, distinguished by the number of surrounding oxygens, incorporation energy (eqn (1)), oxidation state n, and formation of peroxide fragments (or lack thereof). The main difference between the configurations is due to the number of oxygens surrounding Ir. We, thus, obtain the configurations with the number of surrounding oxygens ranging from 4 to 6, whereas n varies from 2+ to 4+. The obtained n-values are consistent with the oxidation states analysis for amorphous IrOx powders.56 It was shown in that work that the average oxidation state of Ir is around 3.6 indicating the presence of Ir3+ and Ir4+ in the powders. The Ir oxidation state is 2+ if the interstitial oxygens are absent (Ir2+O4). In this case, dIr–O, qIr and μIr are obviously different from the other oxidation states and configurations in Table 2.
| Complex | d Ir–O, Å | d Ir–O, Å (avg) | q Ir, e | μ Ir, μB |
|---|---|---|---|---|
| Ir2+O4 | 2.136–2.176 | 2.147 | 0.751 | 2.530 |
| Ir3+O4 | 1.846–1.920 | 1.885 | 1.193 | 1.795 |
| Ir4+O5 | 1.828–2.024 | 1.954 | 1.095 | 0.695 |
| Ir4+O6 | 1.893–1.972 (1.892–2.047) | 1.938 (1.936) | 1.325 (1.366) | 0.514 (0.507) |
| Complex | Peroxide | d O–O, Å | E inc(Oi), eV | ν, cm−1 |
|---|---|---|---|---|
| Ir3+O4 | Yes | 1.47 | −3.77 | 942 |
| Ir4+O5 | Yes | 1.54 | −4.37 | 810 |
| Ir4+O6 | No | — | −5.15 | — |
In the case of the Ir3+O4 complex, Ir has four neighbors, too, and yet in this case the properties of Ir are not the same as in the Ir2+O4 case. In Ir3+O4, the value of μIr corresponds to n = 3+ and an intermediate spin state (the formal value of μIr = 2 μB). However, dIr–O in the Ir3+O4 complex differs from that in Ir2O3 and ZnIr2O4 (Table 1). It is smaller than in the parent oxides whereas qIr in Ir3+O4 is close to the one of Ir in Ir2O3. The other two cases of Ir4+O5 and Ir4+O6 are characterized by small magnetic moments of Ir, consistent with the low spin configuration of the 5d5 orbital. Such magnetic moments of Ir are very close to that in IrO2 (Table 1). In contrast to other complexes, the Oi ions are Ir's nearest neighbors in the Ir4+O6 complex, and do not participate in the formation of peroxide defects.
The Ir–O distances are shorter in the complexes containing the Oi ions than in the Ir2+O4 case and parent compounds, which is connected with a greater overlap of the orbitals and results in an increased oxidation state of Ir. The calculated average Ir–O bond length of the Ir4+O6 complex matches experimental data obtained with EXAFS (1.94 Å vs. 1.96 Å). Interestingly, the larger supercell (L48) used for the Ir4+O6 complex did not demonstrate any changes in the basic properties (Table 1).
Table 3 indicates that the six-fold coordinated Ir is the energetically preferable state, as it is characterized by the lowest energy of incorporation. However, the Ir3+O4 and Ir4+O5 complexes contain the peroxide defects, formed by one Oi ion and one host oxygen ion. The interatomic distances (dO–O) between these two oxygens are consistent with the values known for this type of defect (dumbbell) in other materials and ZnO from the DFT calculations.11,57–59
From the experimental viewpoint, the O–O bond in O22− has been reported to have a length varied from 1.47 to 1.54 Å for Ir(O2) complexes in organic compounds.60–62 The stretching vibration of the O–O bond has been assigned62 an IR absorption band at ν = 833 cm−1. Likewise, dO–O of 1.47 Å has been reported for a cubic zinc peroxide (ZnO2).63 In the latter study, authors have observed a strong Raman peak centred at 835 cm−1, which they attribute to the O–O stretching vibration through comparison with other published data.64,65 However, a larger calculated dO–O equal to 1.75 Å for ZnO2 was associated with the experimentally measured ν of 748 cm−1 taken from the literature (see ref. 66 and references therein). Importantly, the present calculated ν's of peroxide defect are only slightly larger than the measured one of 720 cm−1 for Ir-doped ZnO.10
Analysis of the electronic structure
Even without Oi's, Ir induces a non-zero spin on neighbouring oxygen ions in the Ir2+O4 complex. The magnetic moment of its 4 O neighbours varies from 0.10–0.12 μB. Such values of the magnetic moment are of the same order as those for the oxygens surrounding Ir in the complexes with Oi's. This is also well demonstrated by the spin density distribution shown in Fig. S1a–c (ESI†) and Fig. 5. The maximum spin density is localized on Ir whereas there is some part of the spin density on the nearest oxygen neighbours. A non-zero spin of oxygen ions surrounding Ir and the fact that these ions have a decreased charge (not shown) in comparison with other oxygen ions are very much in line with the same properties of IrO2 in contrast to Ir2O3 and ZnIr2O4 (Table 1). Ir is fully oxidized, and the electrons given to surrounding oxygens are distributed between them, including Oi's. This facilitates hole localization in Ir-doped ZnO. Interestingly, in the case of peroxide defect, the resultant fragment is asymmetric, with different magnetic moments of the two oxygens. Notice, however, that the magnetic moments of oxygens in O22− are more pronounced in the Ir4+O5 complex than in the Ir3+O4 one due to the smaller O–O distance in the former case.Analysis of the calculated density of states (DOS) for the Ir4+O6 complex (Fig. 6 and 7c) revealed that the top of the valence band consists of Ir states and states of oxygens surrounding Ir (Ir–O band). It is the band of the width of ∼0.4 eV (small supercell, L4). The states of the same oxygens are extended to deeper energies and hybridized with the states of other oxygens in the lattice (the total width of this band is around 5 eV). The Zn states contribute at even deeper energies. In the large supercell (L48, Fig. 7d), the Ir–O band is separated from the extended O-band which should have an impact on the calculated thermoelectric properties. The band gap in Ir-doped ZnO is between the occupied and unoccupied Ir–O bands and changes from 1.75 to 2.50 eV for the small (L4, c = 12.50%) and large (L48, c = 1.04%) supercell.
Even though the overall characteristics in the calculated complexes are similar, there are still some differences to mention (Fig. S2, ESI† and Fig. 7b). The hybridization effect as discussed above is stronger in Ir3+O4 than in Ir4+O6. Essentially, the top of the valence band in Ir3+O4 is formed of Ir states and all oxygens in the lattice. In the case of the Ir4+O5 complex, the picture is similar with Ir4+O6, but the Ir–O band is wider (almost 1 eV).
Analysis of thermoelectric properties
In the present analysis, we discuss the calculated thermoelectric properties, i.e. the Seebeck coefficient (S) and electrical conductivity (σ), for the IrOx complexes in ZnO and reference systems: perfect ZnO, ZnIr2O4 and IrO2. Thermoelectric properties are extremely sensitive to the electronic structure. Perfect ZnO is not expected to demonstrate good potential for the p-type conduction. We suggest that this property of ZnO is reflected in the steep increase of the calculated S to unrealistically high values (see Fig. S2a, ESI†) in the proximity of VBM.In the calculations the exact Fermi level μF is unknown but a comparison with the available experimental data could help with its identification. Therefore, S and σ dependence on μF referenced at the VBM, i.e. S(μF) and σ(μF), lies at the heart of our analysis. Typically, such dependencies have two parts for positive and negative values of S standing for holes and electrons, respectively. We, therefore, focus our analysis on the positive S-values only to estimate the potential of Ir-doped ZnO for the p-type conduction.
In Table 4 the calculated σ- and S-values at fixed μF are compared with the corresponding data found in the experimental literature and our previous experimental results.10 Notice that the experimental results differ by the sample preparation and treatment, leading to some scatter in data. Interestingly, it is almost the same value of μF = μ − EVBM ≈ 0.7 eV for all systems for both S and σ in Table 4 to find better correspondence with the experimental values and is, therefore, a good compromise for such a comparison.
| Compound | S, μV K−1 | S exp, μV K−1 | σ, Ω−1 m−1 | σ exp, Ω−1 m−1 |
|---|---|---|---|---|
| a Measured at room temperature; two values for σ for polycrystalline and epitaxial thin films whereas the Seebeck coefficient was measured for polycrystalline films only; the thin films prepared by PLD between 773 and 973 K. b The values are taken at room temperature for the 100 nm thin films prepared by PLD and oxidized at 0.05–0.2 mBar and 500 °C. c The bulk value measured at room temperature. d The Ir concentration c = 16.4%. | ||||
| ZnO | 2510 | Non-conducting | 6.05 × 10-8 | Non-conducting |
| ZnIr2O4 | 92.3 | 53.9a68 | 1.72 × 102 | 2.09 × 102, 3.39 × 102a68 |
| IrO2 | 63.9 | — | 1.32 × 106 | 1.15–2.90 × 10669,70 |
| 0.68–1.67 × 106b71 | ||||
| 2.94 × 106c71 | ||||
| Ir2O3 | 105 | — | 8.98 × 101 | — |
| Ir2+O4 | 80.1 | 6.8d10 | 2.57 × 102 | 47.6d10 |
| Ir3+O4 | 88.7 | 3.20 × 101 | ||
| Ir4+O5 | 89.4 | 4.13 × 101 | ||
| Ir4+O6 (c = 12.5%, L4) | 83.8 | 1.62 × 102 | ||
| Ir4+O6 (c = 1.04%, L48) | 2335 | 3.49 × 10−8 | ||
The calculated σ-value for ZnIr2O4 and IrO2 agree very well with the experimental data. The cation vacancies and anti-sites are detrimental defects in spinels13,67 explaining, at least in part, the p-type conductivity. Thus, it should be reflected in the S-values as well. Indeed, we emphasize significant differences in the behaviour of S(μF) for bulk ZnIr2O4 in a comparison with perfect ZnO. It has a well distinguished plateau in the range of μF between 0 and 0.8 eV (Fig. 7a) followed by a steep increase to very high values. A positive Seebeck coefficient of 92.3 μV K−1 at μF = 0.7 eV is in agreement with the experimental values (Table 4).
The Ir-doped ZnO is characterized by a high sensitivity of thermoelectric properties to the electronic structure as well. All IrOx complexes as discussed in the present study show different behaviour of S(μF). However, we again emphasize the presence of a plateau and steep increase to very high values for some of the complexes. The positive Seebeck coefficient is in the range 60–80 and 55–90 μV K−1 for the complex without the interstitial oxygens, (Ir2+O4), and in the Ir4+O6 complex in the small supercell (c = 12.5%, L4), respectively, depending on μF (in the range of μF between 0 and 0.8 eV) at 308 K. Neither the Ir2+O4 nor Ir4+O6 complex in the small supercell (L4) are characterized by the steep increase of S(μF) as were found in perfect ZnO and ZnIr2O4. Here S(μF) increases smoothly approaching the maximum value at μF ∼ 0.70–0.75 eV (Fig. 7b and c). In contrast, the Ir4+O5 and Ir3+O4 complexes (Fig. S2, ESI†) show very similar behavior of S(μF) with ZnIr2O4 and demonstrate much smaller changes for the S-values in the range of μF between 0 and 0.8 eV. In Fig. S2b and c (ESI†) it is demonstrated that the plateau in the range of μF between 0 and 0.8 eV is present and leads to the values of S of the order of ∼89 μV K−1 (see also Table 4). The presence of a plateau and formation of O22− are, in our opinion, interconnected.
We do not expect perfect agreement for the absolute S-values between the experiment and simplified model in the calculation but rather present a qualitative picture explaining the p-type conduction in Ir-doped ZnO. Also, we notice a significant decrease of σ for the Ir concentration c = 1.04% (Ir4+O6, L48). In this case there is again a steep increase of the calculated S to very high values (see Fig. 7d) in the proximity of VBM similar to perfect ZnO. In the complexes with the plateau, the steep increase is shifted to higher μF. At the values of μF = 0.8–1.9 eV for Ir3+O4 and 0.8–1.6 for Ir4+O5 the steep increase of S is observed and transformation into the n-type conductor follows. Furthermore, S(μF) is differently influenced by temperature T in the two ranges of μF, 0.0 < μF ≤ 0.8 eV and 0.8 < μF ≤ 1.9(1.6) eV, in Fig. 7(f–h) and Fig. S2(d and e) (ESI†). At μF ≤ 0.8 eV, S(μF) increases with T, and an opposite behaviour is found in the range 0.8 < μF ≤ 1.9(1.6) eV for the complexes with the steep increase. Qualitatively speaking, this picture is very close to what was observed for ZnIr2O4 as well (Fig. 7e).
Conclusions
We have successfully combined hybrid DFT calculations and Ir L3-edge XAS experiments to gain insight into the local atomic structure around iridium ions in Ir-doped ZnO. The ZnO:cIr (c = 7%, 16%, 29%, 54% and 67%) and IrOx thin films of thickness 200–300 nm were deposited by reactive DC magnetron co-sputtering on polyimide tape substrates. The role of interstitial oxygens was emphasized in such experiments. Thus, the analysis of EXAFS spectra using the reverse Monte Carlo simulations revealed that iridium ions are predominantly octahedrally coordinated by oxygens. Consequently, several IrOx (x = 4–6) polyhedra (complexes) inside the wurtzite ZnO lattice were selected for the calculations of the atomic and electronic structure, vibrational and thermoelectric properties from the first principles.The hybrid PBE0 exchange–correlation functional and Gaussian basis-set described very well the basic properties of ZnO, ZnIr2O4, and IrO2 crystals, which justified further computational study of Ir-doped ZnO. The complexes (IrnOx) were distinguished by the oxidation state of Ir (n) and formation of peroxide defects, and as a consequence, by the different number of oxygens (x) surrounding Ir ions. Their corresponding formulas were chosen as Ir2+O4 – the system without interstitial oxygens Oi's, Ir3+O4 – the first system with the interstitials and formation of peroxide defects O22−, Ir4+O5 – the second system with the formation of peroxide defect, and lastly, Ir4+O6 the system with Ir ions which are octahedrally coordinated by oxygens. It is worth mentioning that the selected complexes containing two interstitial Oi ions were found by a careful treatment of numerous spatial configurations with different total energies. However, we were able to choose the three most important ones and focus our study on the analysis of the relevant Seebeck coefficient, electrical conductivity and density of states for them. Moreover, the Ir4+O6 complex was calculated with two Ir concentrations, namely 12.50 and 1.04%. We compared the calculated thermoelectric properties for the chosen complexes with those for the reference systems, i.e. perfect ZnO, ZnIr2O4, and IrO2. Each calculated IrOx complex demonstrated some differences in the calculated DOS. However, the main DOS feature of calculated complexes for the Ir concentration 12.5% is due to (1) the mixed Ir–O band contributing to the VBM, (2) the states of oxygens surrounding Ir and their extension and hybridization with the other oxygens states in the lattice, and (3) as a consequence, the predicted positive Seebeck coefficient and electrical conductivity for the Fermi level μF (referenced at the VBM) lying in the range 0 ≤ μF ≤ 0.8 eV. In this μF-range the calculated Seebeck coefficients are close for the four calculated complexes including the one without Oi's. In contrast, the calculation of smaller Ir concentration (1.04%) for the Ir4+O6 complex revealed the Seebeck coefficient behaviour similar with the hypothetical perfect ZnO which is reflected in its steep increase in the proximity of VBM. It can be explained by a separate Ir–O band characterized by much weaker hybridization effect with the host oxygens and smaller width in a comparison with the larger concentration 12.5%. Such differences between the Ir concentrations should explain the sign change in the Seebeck coefficient behaviour observed experimentally in ref. 10. Lastly, the calculated local vibrational frequencies of O22− peroxides entering two complexes, Ir3+O4 and Ir4+O5, are close to those in the Raman measurements in ref. 10. The complexes with the formation of peroxide defects, i.e. Ir3+O4 (Ir4+O5), also have the steep increase of Seebeck coefficient in the range 0.8 < μF ≤ 1.9(1.6) eV similar to ZnIr2O4.
Author contributions
A. C.: investigation, formal analysis, writing – original draft, visualization. D. G.: methodology, writing – review & editing. N. V. S.: project administration, supervision. E. A. K.: project administration, supervision. A. Z.: investigation, M. Z.: investigation. A. K.: investigation, formal analysis, writing – review & editing, visualization. A. A.: investigation. J. P.: funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We greatly acknowledge the financial support via the ERAF Project No. 1.1.1.1/18/A/073. Calculations have been performed under the Project HPC-EUROPA3 (INFRAIA-2016-1-730897), with the support of the EC Research Innovation Action under the H2020 Programme. A. C. gratefully acknowledges the technical support received from KTH-PDC. Institute of Solid State Physics, University of Latvia as the Center of Excellence has received funding from the European Union's Horizon 2020 Framework Programme H2020-WIDESPREAD-01-2016-2017-TeamingPhase2 under grant agreement No. 739508, project CAMART2.Notes and references
- P. Novák, T. Kozák, P. Šutta, M. Kolega and O. Bláhová, Phys. Status Solidi A, 2018, 215, 1700951 CrossRef.
- P. Novák, J. Očenášek, T. Kozák and J. Savková, Thin Solid Films, 2018, 660, 471–476 CrossRef.
- J. Rezek, P. Novák, J. Houška, A. D. Pajdarová and T. Kozák, Thin Solid Films, 2019, 679, 35–41 CrossRef CAS.
- D. C. Look, B. Claflin, Y. I. Alivov and S. J. Park, Phys. Status Solidi A, 2004, 201, 2203–2212 CrossRef CAS.
- A. Janotti and C. G. Van de Walle, Rep. Prog. Phys., 2009, 72, 126501 CrossRef.
- D. Mora-Fonz and A. L. Shluger, Phys. Rev. B, 2019, 99, 014202 CrossRef CAS.
- A. V. Uklein, V. V. Multian, G. M. Kuz’micheva, R. P. Linnik, V. V. Lisnyak, A. I. Popov and V. Ya. Gayvoronsky, Opt. Mater., 2018, 84, 738–747 CrossRef CAS.
- S. Lany, J. Osorio-Guillén and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 241203 CrossRef.
- A. Kuzmin and J. Chaboy, IUCrJ, 2014, 1, 571–589 CrossRef CAS PubMed.
- M. Zubkins, R. Kalendarev, J. Gabrusenoks, A. Plaude, A. Zitolo, A. Anspoks, K. Pudzs, K. Vilnis, A. Azens and J. Purans, Thin Solid Films, 2017, 636, 694–701 CrossRef CAS.
- P. Erhart, A. Klein and K. Albe, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085213 CrossRef.
- D. Muñoz Ramo and P. D. Bristowe, J. Phys.: Condens. Matter, 2016, 28, 345502 CrossRef PubMed.
- D. M. Ramo and P. D. Bristowe, J. Chem. Phys., 2014, 141, 084704 CrossRef PubMed.
- D. Muñoz Ramo and P. D. Bristowe, Thin Solid Films, 2014, 555, 112–116 CrossRef.
- S. Belin, V. Briois, A. Traverse, M. Idir, T. Moreno and M. Ribbens, Phys. Scr., 2005, 980 CrossRef CAS.
- A. Kalinko, XAESA, https://github.com/aklnk/xaesa, 2020.
- J. Timoshenko, A. Kuzmin and J. Purans, Comput. Phys. Commun., 2012, 183, 1237–1245 CrossRef CAS.
- J. Timoshenko, A. Kuzmin and J. Purans, J. Phys.: Condens. Matter, 2014, 26, 055401 CrossRef CAS PubMed.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, WIREs Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D’Arco, M. Llunell, M. Causà, Y. Noël, L. Maschio, A. Erba, M. Rerat and S. Casassa, CRYSTAL17 User's Manual, University of Torino, Torino, 2017 Search PubMed.
- F. Pascale, C. M. Zicovich-Wilson, F. López Gejo, B. Civalleri, R. Orlando and R. Dovesi, J. Comput. Chem., 2004, 25, 888–897 CrossRef CAS PubMed.
- C. M. Zicovich-Wilson, F. Pascale, C. Roetti, V. R. Saunders, R. Orlando and R. Dovesi, J. Comput. Chem., 2004, 25, 1873–1881 CrossRef CAS PubMed.
- R. A. Evarestov, Quantum chemistry of solids: LCAO treatment of crystals and nanostructures, Springer, Berlin, New York, 2nd edn, 2012 Search PubMed.
- IUPAC Compendium of Chemical Terminology: Gold Book, ed. M. Nič, J. Jirát, B. Košata, A. Jenkins and A. McNaught, IUPAC, Research Triagle Park, NC, 2.1.0., 2009 Search PubMed.
- M. Peuckert, Surf. Sci., 1984, 144, 451–464 CrossRef CAS.
- M. Hara, K. Asami, K. Hashimoto and T. Masumoto, Electrochim. Acta, 1983, 28, 1073–1081 CrossRef CAS.
- W.-H. Chung, D.-S. Tsai, L.-J. Fan, Y.-W. Yang and Y.-S. Huang, Surf. Sci., 2012, 606, 1965–1971 CrossRef CAS.
- S. Kan, S. Takemoto, K. Kaneko, I. Takahashi, M. Sugimoto, T. Shinohe and S. Fujita, Appl. Phys. Lett., 2018, 113, 212104 CrossRef.
- S. Kan, S. Takemoto, K. Kaneko, T. Shinohe and S. Fujita, 2018 IEEE CPMT Symposium Japan (ICSJ), IEEE, Kyoto, 2018, pp. 95–98.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- A. W. Ehlers, M. Böhme, S. Dapprich, A. Gobbi, A. Höllwarth, V. Jonas, K. F. Köhler, R. Stegmann, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 208, 111–114 CrossRef CAS.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- Y. Ping, G. Galli and W. A. Goddard, J. Phys. Chem. C, 2015, 119, 11570–11577 CrossRef CAS.
- D. Gryaznov, E. Blokhin, A. Sorokine, E. A. Kotomin, R. A. Evarestov, A. Bussmann-Holder and J. Maier, J. Phys. Chem. C, 2013, 117, 13776–13784 CrossRef CAS.
- R. A. Evarestov, A. I. Panin, A. V. Bandura and M. V. Losev, J. Phys.: Conf. Ser., 2008, 117, 012015 CrossRef.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- C. M. Bertoni, G. Cappellini, F. Finocchi, P. Monachesi, G. Chiarotti and P. Chiaradia, 7.3.3 II-VI compound surfaces: Datasheet from Landolt-Börnstein – Group III Condensed Matter, “Physics of Solid Surfaces” in SpringerMaterials, Springer-Verlag, Berlin Heidelberg, 2015, vol. 45A Search PubMed.
- F. Oba, M. Choi, A. Togo, A. Seko and I. Tanaka, J. Phys.: Condens. Matter, 2010, 22, 384211 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- R. W. Grimes and C. R. A. Catlow, Philos. Trans. R. Soc., A, 1991, 335, 609–634 CrossRef CAS.
- G. K. H. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71 CrossRef CAS.
- G. Pizzi, D. Volja, B. Kozinsky, M. Fornari and N. Marzari, Comput. Phys. Commun., 2014, 185, 422–429 CrossRef CAS.
- G. Sansone, A. Ferretti and L. Maschio, J. Chem. Phys., 2017, 147, 114101 CrossRef PubMed.
- J. Linnera, G. Sansone, L. Maschio and A. J. Karttunen, J. Phys. Chem. C, 2018, 122, 15180–15189 CrossRef CAS PubMed.
- Ü. Özgür, Ya. I. Alivov, C. Liu, A. Teke, M. A. Reshchikov, S. Doğan, V. Avrutin, S.-J. Cho and H. Morkoç, J. Appl. Phys., 2005, 98, 041301 CrossRef.
- S. Jantrasee, S. Pinitsoontorn and P. Moontragoon, J. Electron. Mater., 2014, 43, 1689–1696 CrossRef CAS.
- A. Kuzmin, R. Kalendarev, J. Purans and D. Pailharey, Advanced Optical Devices, Technologies, and Medical Applications, 2003, vol. 5123 Search PubMed.
- A. Kuzmin and R. Grisenti, Philos. Mag. B, 1994, 70, 1161–1176 CAS.
- J. Gaidelene, R. Kalendarev, A. Kuzmin and J. Purans, Nucl. Instrum. Methods Phys. Res., Sect. A, 2004, 531, 321–326 CrossRef CAS.
- A. Balerna, E. Bernieri, E. Burattini, A. Kuzmin, A. Lusis, J. Purans and P. Cikmach, Nucl. Instrum. Methods Phys. Res., Sect. A, 1991, 308, 240–242 CrossRef.
- A. A. Bolzan, C. Fong, B. J. Kennedy and C. J. Howard, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 373–380 CrossRef.
- A. L. Ankudinov, B. Ravel, J. J. Rehr and S. D. Conradson, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7565–7576 CrossRef CAS.
- J. J. Rehr and R. C. Albers, Rev. Mod. Phys., 2000, 72, 621–654 CrossRef CAS.
- L. Hedin and B. I. Lundqvist, J. Phys. C, 1971, 4, 2064–2083 CrossRef.
- M. J. Wahila, Z. W. Lebens-Higgins, A. J. Jackson, D. O. Scanlon, T.-L. Lee, J. Zhang, K. H. L. Zhang and L. F. J. Piper, Phys. Rev. B, 2019, 100, 085126 CrossRef CAS.
- V. Pfeifer, T. E. Jones, J. J. Velasco Vélez, C. Massué, R. Arrigo, D. Teschner, F. Girgsdies, M. Scherzer, M. T. Greiner, J. Allan, M. Hashagen, G. Weinberg, S. Piccinin, M. Hävecker, A. Knop-Gericke and R. Schlögl, Surf. Interface Anal., 2016, 48, 261–273 CrossRef CAS.
- R. A. Evarestov, A. Platonenko, D. Gryaznov, Y. F. Zhukovskii and E. A. Kotomin, Phys. Chem. Chem. Phys., 2017, 19, 25245–25251 RSC.
- A. de Jamblinne de Meux, G. Pourtois, J. Genoe and P. Heremans, J. Appl. Phys., 2018, 123, 161513 CrossRef.
- R. Thapa, S. Ghosh, S. Sinthika, E. Mathan Kumar and N. Park, J. Alloys Compd., 2015, 620, 156–163 CrossRef CAS.
- D. Bridget Williams, W. Kaminsky, J. M. Mayer and K. I. Goldberg, Chem. Commun., 2008, 4195 RSC.
- M. G. Crestani, A. Steffen, A. M. Kenwright, A. S. Batsanov, J. A. K. Howard and T. B. Marder, Organometallics, 2009, 28, 2904–2914 CrossRef CAS.
- H. Baumgarth, T. Braun, B. Braun, R. Laubenstein and R. Herrmann, Eur. J. Inorg. Chem., 2015, 3157–3168 CrossRef CAS.
- A. Escobedo-Morales, R. Esparza, A. García-Ruiz, A. Aguilar, E. Rubio-Rosas and R. Pérez, J. Cryst. Growth, 2011, 316, 37–41 CrossRef CAS.
- N. Uekawa, N. Mochizuki, J. Kajiwara, F. Mori, Y. J. Wu and K. Kakegawa, Phys. Chem. Chem. Phys., 2003, 5, 929–934 RSC.
- M. Sun, W. Hao, C. Wang and T. Wang, Chem. Phys. Lett., 2007, 443, 342–346 CrossRef CAS.
- G. L. Gutsev, B. K. Rao and P. Jena, J. Phys. Chem. A, 2000, 104, 11961–11971 CrossRef CAS.
- M. N. Amini, H. Dixit, R. Saniz, D. Lamoen and B. Partoens, Phys. Chem. Chem. Phys., 2014, 16, 2588 RSC.
- M. Dekkers, G. Rijnders and D. H. A. Blank, Appl. Phys. Lett., 2007, 90, 021903 CrossRef.
- Y. Liu, H. Masumoto and T. Goto, Mater. Trans., 2004, 45, 3023–3027 CrossRef CAS.
- W. D. Ryden, A. W. Lawson and C. C. Sartain, Phys. Rev. B: Solid State, 1970, 1, 1494–1500 CrossRef.
- S. G. Bhat, A. M. Koshy, S. Pittala and P. S. A. Kumar, AIP Conf. Proc., 2017, 1859, 020007 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc00223f |
| This journal is © The Royal Society of Chemistry 2021 |