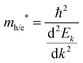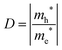Revisiting the structural, electronic and photocatalytic properties of Ti and Zr based perovskites with meta-GGA functionals of DFT
Received
21st December 2020
, Accepted 8th March 2021
First published on 9th March 2021
Abstract
The strongly constrained and appropriately normed (SCAN) functional of density functional theory (DFT) conforms to all possible exact constraints required of a meta-GGA functional and offers good approximations for structural and energetic properties of solids in comparison to experiments. However, SCAN is unable to fully overcome the underestimation of band gap for perovskite oxide materials suitable for photocatalysis. In the present work, we use a combination of meta-GGAs SCAN and modified Becke–Johnson local density approximation (mBJ-LDA) potential functional to accurately compute the structural, energetic, mechanical, vibrational and optoelectronic properties of Ti and Zr based ABO3 (A = Sr, Ba and B = Ti and Zr) perovskite oxides. In addition to evaluating their physical properties, the potential applications of these materials as photocatalyst operating in the UV region of the electromagnetic spectrum are also examined. We show that the structural, energetic, mechanical and vibrational properties calculated using SCAN are in better agreement with experimental data as compared to the commonly used semi-local functionals of DFT. However, the optoelectronic properties of the large band gap Ti and Zr based perovskite oxides are further improved if computed with the mBJ-LDA potential functional, whereby an even higher level of accuracy than with SCAN is achieved, with results that are comparable to the computationally expensive hybrid DFT functionals. On the whole, our DFT calculations indicate that a combination of SCAN and mBJ-LDA functionals for exploring the physical properties of large band gap perovskite oxides provide the means for identifying photocatalysts suitable for hydrogen production at low computational costs.
1. Introduction
In condensed matter physics and related sciences, Kohn–Sham (KS) density functional theory (DFT) has become a standard ab initio tool for exploring materials. For this reason DFT is being rigorously used for understanding the physical properties of materials and has proven to be particularly instrumental in predicting novel materials.1–5 Since the precision of KS DFT calculations is strongly dependent on the selected approximation for computing exchange–correlation energy (i.e. Exc = Ex + Ec), efforts for developing reliable functionals for determining Exc have seen a steady progress.3,6,7 By examining self-consistent one-electron equations, one expects that a universal exchange–correlation energy functional for KS DFT, wholly dependent on the ground-state electron density, ρ, can be obtained since Exc[ρ] is expressed by half of the Coulomb interaction in a double integral over space between electron and exchange–correlation hole. However, an approximate functional is always needed in real applications of KS DFT where semi-local approximations have traditionally allowed to formally compute Exc[ρ] from a single integral through a computationally efficient procedure.
Over the years, many DFT functionals have been developed which can be assigned to one of the four rungs of Jacob's ladder based on their level of sophistication and acquired accuracy.8 Among these four rungs of Jacob's ladder of DFT functionals, the first three rungs are occupied by semi-local approximations.8,9 A common feature of all the semi-local DFT functionals is that they can be expressed as single integral, 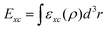 , where εxc is the exchange–correlation energy density per volume. For the first and second rungs, respectively, εxc is expressed in terms of electron density, ρ, alone (as in the case of local density approximation (LDA))10 and ρ and its first gradient, ∇ρ, (as in the case of generalized gradient approximation (GGA)).11 On the other hand, combining electron density and its first derivative with kinetic-energy density and/or ∇2ρ gives us the so-called meta-GGA functionals, which occupy the third rung of Jacob's ladder.7,9 Apart from the semi-local functionals, there also exist DFT functionals which allow computing Exc[ρ] through a double integral or Hartree–Fock (HF) exchange. Although accurate, these so-called hybrid functionals are computationally much more expensive than the semi-local functionals and thus occupy the fourth rung of the Jacob's ladder.12
, where εxc is the exchange–correlation energy density per volume. For the first and second rungs, respectively, εxc is expressed in terms of electron density, ρ, alone (as in the case of local density approximation (LDA))10 and ρ and its first gradient, ∇ρ, (as in the case of generalized gradient approximation (GGA)).11 On the other hand, combining electron density and its first derivative with kinetic-energy density and/or ∇2ρ gives us the so-called meta-GGA functionals, which occupy the third rung of Jacob's ladder.7,9 Apart from the semi-local functionals, there also exist DFT functionals which allow computing Exc[ρ] through a double integral or Hartree–Fock (HF) exchange. Although accurate, these so-called hybrid functionals are computationally much more expensive than the semi-local functionals and thus occupy the fourth rung of the Jacob's ladder.12
Recently, meta-GGA functionals have been increasingly employed to compute physical properties of complex oxide semiconductors. This can mainly be attributed to the fact that earlier theoretical studies clearly show that the structural and energetic properties of these materials in general,9,13 and optoelectronic properties of large band gap semiconductors in particular,14 are not accurately predicted by LDA and GGA functionals. The quest for improving accuracy in determining the physical properties of perovskite oxides can partly be ascribed to their potential applications in advance oxidation processes (AOPs) for which various research groups are making efforts in designing new and efficient photocatalysts.15,16 In this context, perovskite oxides having the chemical composition ABO3 constitute a potential class of ceramic materials which are candidates for numerous device applications. This can mainly be ascribed to the presence of BO6 octahedra where the electronic states of the B and O atoms play dominant roles in the conduction and valence band edges, respectively. Consequently, this provides huge opportunities to considerably alter the physical properties of these materials through chemical as well as physical means.17,18 In particular, strontium titanate (SrTiO3), barium titanate (BaTiO3), strontium zirconate (SrZrO3) and barium zirconate (BaZrO3) are important perovskite oxides in which the 3d and 4d electrons of Ti and Zr, respectively, are bonded with the 2p electrons of oxygen. The d electrons introduced by the presence of transition metals in the titanium and zirconium based perovskite oxides bring about interesting physical properties for these materials which substantiate the exceptional importance of these materials. These materials have therefore been thoroughly studied both experimentally and theoretically in the past for a wide range of applications. In their pristine forms, both the titanates and zirconates of Sr and Ba show an insulating nature under ambient conditions that persists even at very high temperatures despite structural phase transitions. Owing to their chemical and mechanical stabilities at high temperature, these compounds have found applications in hydrogen sensors, fuel cells and electronic devices.19–21 Importantly, there are several reports available in the literature which place these materials among the most suitable candidates for photocatalysis applications.16 Owing to these facts, it is inevitable that an accurate account of the structural, energetic and optoelectronic properties of ABO3 (where A = Sr and Ba; B = Ti and Zr) perovskite oxides should be obtained using DFT calculations.
In 2015, Sun et al.13 proposed the strongly constrained and appropriately normed (SCAN) meta-GGA functional, which conforms to all the known exact constraints for a meta-GGA. These include six constraints each for the exchange and correlation together with 5 constraints for the sum of the two.13 In SCAN, the orbital kinetic energy densities of each spin are also added along with other ingredients (e.g. local spin density approximation (LSDA) and spin-density gradients) to obtain exchange and correlation energies, while the exchange and correlation potentials can still be computed using the Perdew–Burke–Ernzerhof (PBE) GGA.11 As a result, structural and energetic properties computed using the SCAN functional show better accuracy for most types of bonds as compared to standard semi-local functionals of DFT.22,23 In fact, the SCAN functional has proven to be more efficient than hybrid DFT for structural and energetic properties at only a fraction of the computational cost.13,22,23 Despite these advantages, the underestimation of band gaps and incorrect optical properties for transition metal oxides computed using SCAN still requires one to resort to either semi-empirical methods23 or hybrid DFT calculations.24,25 In order to remain truly ab initio and within the regime of meta-GGA functionals of DFT with low computational cost, it is intuitive to compute the optoelectronic properties of large band gap Ti and Zr based perovskite oxides by employing modified Becke–Johnson local density approximation (mBJ-LDA) functional proposed by Tran and Blaha14 using the ground state structural properties obtained from SCAN functional. Motivated by this, in the present study we use a combination of SCAN and mBJ-LDA meta-GGA functionals for computing the structural, energetic, mechanical, vibrational, electronic and optical properties of ABO3 (where A = Sr and Ba; B = Ti and Zr) perovskite oxides using the all-electron full-potential linearized augmented plane wave method (FP-LAPW) of DFT. As the compounds under study are potential candidates for photocatalysis,16 we examine their photocatalytic properties for producing hydrogen through water splitting using the electronic properties computed with SCAN and mBJ-LDA functional. We expect that the results provided in this study would prove helpful in designing and improving the photocatalytic activities of the ABO3 perovskite oxides in future studies.
2. Computational methods
In this work, the DFT calculations are performed using the WIEN2k package.26 For the FP-LAPW method employed in the present work, the core and valence states are separated by muffin-tin spheres such that the electron wave function inside these spheres is augmented plane waves having spherical harmonics, while in the interstitial region the electron wave function is modeled using plane waves. The muffin-tin radii are chosen to be 2.1, 2.3, 1.8, 1.85. and 1.6 a.u. for Sr, Ba, Ti, Zr, and O atoms, respectively, while an energy separation of −6.0 Ry is used between the core and the valence states. With the present choice of muffin-tin radii and energy separation between the core and valence states, the Sr (4s, 4p, 5s), Ba (5s, 5p, 6s), Ti (3s, 3p, 3d, 4s), Zr (4s, 4p, 4d, 5s) and O (2s, 2p) states are treated as valence states. For the interstitial region, the plane wave cutoff ROKmax (where RO is the muffin-tin radius of oxygen and Kmax is the largest K vector of the plane wave expansion) and the Fourier expansion of charge density vector Gmax are set to be 8.0 and 24 Bohr−1, respectively. For the case of cubic perovskite unit cell, 84 k-points in the irreducible wedge of the first Brillouin zone (corresponding to a 14 × 14 × 14 k-mesh) are used and the energy and charge convergence criteria are set to 10−5 Ry and 10−3 e, respectively. During geometry optimization the atomic forces are always minimized to a value less than 1 mRy a.u.−1 using the SCAN functional for obtaining ground state atomic positions.
Since SCAN has previously been shown to perform better in calculating structural and energetic properties of band gap materials as compare to other functionals,13 it has been used for computing all the ground state geometries and energetic properties in this work. On the other hand, the electronic and optical properties are computed using both SCAN and mBJ-LDA functionals using the SCAN optimized structures, where improved parameters of mBJ-LDA for semiconductors proposed by Koller et al. are utilized.27 Thus, we combine the good structure from SCAN with the good electronic structure of mBJ-LDA (i.e. SCAN//mBJ-LDA simulations), since the latter is a potential functional and cannot be used for computing structural properties.14 It is worth pointing out here that the correlation energy and correlation potential parts of mBJ-LDA can be computed using the PBE GGA. Since the SCAN functional uses PBE GGA for the correlation potential,13,26 one might desire the same parameterization scheme and perform SCAN//mBJ-GGA simulation of the electronic properties. However, we note that the electronic band structure computed using mBJ-GGA yield band gaps that are farther from experiment, compared to mBJ-LDA. This can be ascribed to the fact that parametric optimization27 for this potential functional has only been carried out for the default exchange–correlation energy obtained from LDA26 and can lead to alightly larger deviation in band gap values when used for mBJ-GGA calculations.
For the present study, we consider the prototype cubic crystal (space group No. 221, Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structure of SrTiO3, BaTiO3, SrZrO3 and BaZrO3 perovskites and compute the structural properties using the SCAN functional. Since the energetic properties presented in this study also required computation of ground state properties of the oxygen molecule, elemental solids and binary oxides, all the structural parameters for these molecules and solids are also optimized using the SCAN functional. In the case of oxygen molecule, force minimization is performed for computing the optimized bond length. On the other hand, lattice parameters of elemental solids, binary oxides and ternary oxides are computed using self-consistent calculation for a series of fixed volumes of their respective unit cells. Where necessary, the c0/a0 and b0/a0 ratios have also been optimized. The SCAN optimized unit cells of all the ABO3 compounds are subsequently used for computing the electronic and optical properties. For computing the mechanical properties, we have utilized the Elastic Constants for Cubic Cases (ELAS) program provided within the WIEN2k package.26 For the computation of the vibrational properties of the ABO3 compounds (using a 40-atom supercell), the frozen phonon approximation was employed using the phonopy code.28 For all the calculations involving phonons, a force convergence criteria of 0.01 mRy a.u.−1 was used. In order to eliminate numerical noise in our phonon calculations, the charge density grid has been enlarged by a factor of 2, while symmetrization of the force constants was also taken into account during post processing of the forces with the phonopy code.29
m) structure of SrTiO3, BaTiO3, SrZrO3 and BaZrO3 perovskites and compute the structural properties using the SCAN functional. Since the energetic properties presented in this study also required computation of ground state properties of the oxygen molecule, elemental solids and binary oxides, all the structural parameters for these molecules and solids are also optimized using the SCAN functional. In the case of oxygen molecule, force minimization is performed for computing the optimized bond length. On the other hand, lattice parameters of elemental solids, binary oxides and ternary oxides are computed using self-consistent calculation for a series of fixed volumes of their respective unit cells. Where necessary, the c0/a0 and b0/a0 ratios have also been optimized. The SCAN optimized unit cells of all the ABO3 compounds are subsequently used for computing the electronic and optical properties. For computing the mechanical properties, we have utilized the Elastic Constants for Cubic Cases (ELAS) program provided within the WIEN2k package.26 For the computation of the vibrational properties of the ABO3 compounds (using a 40-atom supercell), the frozen phonon approximation was employed using the phonopy code.28 For all the calculations involving phonons, a force convergence criteria of 0.01 mRy a.u.−1 was used. In order to eliminate numerical noise in our phonon calculations, the charge density grid has been enlarged by a factor of 2, while symmetrization of the force constants was also taken into account during post processing of the forces with the phonopy code.29
3. Results and discussion
3.1. Structural and energetic properties
Since thermodynamic quantities, such as enthalpy of formation, require one to find the difference between the cumulative total energies of atomic species in their stable reference phases and the total energies of the compounds constituted by these atoms, it is important that the exchange–correlation functional is able to provide good approximation of the ground state energies. For this reason, we first examine the performance of the SCAN functional in determining the energetic properties of all the atoms constituting the ABO3 (where A = Sr and Ba; B = Ti and Zr) compounds. Table 1 presents the structural properties and cohesive energies of O2 dimer, fcc Sr, bcc Ba, hcp Ti and hcp Zr computed using the SCAN functional. In the present work, we have computed the cohesive energy, Ec, as the difference between the total energy of the above-mentioned stable reference phases of an atom X and the energy of the same atom X placed inside a large supercell, i.e.| | | Ec = Estable–phaseX − EatomX | (1) |
Table 1 Structural properties (Å) and cohesive energies (eV per atom) of oxygen molecule, face centered cubic unit cell of strontium, body centered cubic unit cell of barium, hexagonal closed packed unit cell of titanium and hexagonal closed packed unit cell of zirconium computed using the SCAN functional. For the sake of comparison, results of the GGA functional reported in previous DFT studies and experimental data are also presented
| System |
SCAN (this work) |
GGA (previous DFT studies) |
Experiment |
| O2 (molecule) |
|
|
|
|
r
0
|
1.215 |
1.21930 |
1.21031 |
|
E
c
|
−2.756 |
−2.97530 |
−2.56031 |
Sr (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
|
|
|
|
a
0
|
6.059 |
5.92132 |
6.04033 |
|
E
c
|
−1.774 |
−1.77932 |
−1.72034 |
Ba (Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
|
|
|
|
a
0
|
5.067 |
4.88735 |
5.02033 |
|
E
c
|
−1.985 |
−2.05235 |
−1.90034 |
| Ti (P63/mmc) |
|
|
|
|
a
0
|
2.932 |
2.93136 |
2.95037 |
|
c
0
|
4.653 |
4.67036 |
4.68637 |
|
E
c
|
−4.685 |
−5.45036 |
−4.85034 |
| Zr (P63/mmc) |
|
|
|
|
a
0
|
3.160 |
3.17832 |
3.23038 |
|
c
0
|
5.134 |
5.12632 |
5.14938 |
|
E
c
|
−6.157 |
−6.92532 |
−6.25036 |
In the case of oxygen, Estable–phaseX in eqn (1) is the total energy of a SCAN optimized O2 dimer, which is simulated in a large asymmetric orthorhombic cell using only the Γ-point. On the other hand, Estable–phaseX values in the case of Sr, Ba, Ti and Zr are computed from their respective SCAN optimized crystal unit cells. EatomX in eqn (1) is the energy of an isolated single atom which has been computed by placing a single atom in an asymmetric orthorhombic unit cell using the Γ-point. For a correct determination of the Estable–phaseX and EatomX energies, spin-polarized calculations are adopted which ensure proper occupation.
It is evident from Tables 1 and 2 that the lattice parameters for elemental as well as binary solids obtained using the SCAN functional are in better agreement with experimental data compared to the GGA functional.30–48 Importantly, the SCAN calculated values of Ec for Sr, Ba, Zr and Ti also a show significantly smaller deviation from experimental data which is usually much larger for semi-local DFT functionals.13 Importantly, it is evident from our calculated values of bond length and cohesive energy for O2 molecules that the SCAN functional does not suffer from the over-binding issue faced in other semi-local exchange–correlation energy functionals, thus providing an accuracy comparable to hybrid DFT calculations.13,40,41 On the whole, better agreement of the structural properties and cohesive energies of O2 and elemental metals computed using SCAN with the experimental data (Table 1) clearly indicates that this meta-GGA exchange–correlation functional of DFT facilitates accurate determination of the thermodynamic properties of ABO3 perovskite oxides.
Table 2 Lattice parameters (Å) and enthalpies of the formation (eV per f.u.) of cubic unit cell of strontium oxide, cubic unit cell of barium oxide, tetragonal unit cell of titania and monoclinic unit cell of zirconia computed using the SCAN functional. For the sake of comparison, results of the GGA functional reported in previous DFT studies and experimental data are also presented
| Compound |
SCAN (this work) |
GGA (previous DFT studies) |
Experiment |
SrO (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
|
|
|
|
a
0
|
5.163 |
5.12832 |
5.16139 |
| ΔHf |
−6.079 |
−6.41432 |
−6.14043 |
BaO (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
|
|
|
|
a
0
|
5.553 |
5.49335 |
5.53944 |
| ΔHf |
−5.604 |
−5.96735 |
−5.68043 |
| TiO2 (P42/mnm) |
|
|
|
|
a
0
|
4.597 |
4.65345 |
4.59046 |
|
b
0
|
2.973 |
2.96945 |
2.95646 |
| ΔHf |
−10.080 |
−10.42545 |
−9.74046 |
| ZrO2 (P21c) |
|
|
|
|
a
0
|
5.174 |
5.13332 |
5.15147 |
|
b
0
|
5.238 |
5.21232 |
5.20347 |
|
c
0
|
5.364 |
5.41132 |
5.31647 |
| ΔHf |
−11.371 |
−12.11732 |
−11.41048 |
As the primary result of a DFT calculation for solids is the determination of total energy, an important thermodynamic quantity that can be derived from the calculated total energy is the reaction energy, EReact, which plays an important role for identifying the application of the subject material in various technologies.42 For the present study, EReact is the energy of perovskite oxides relative to cumulative energies of the binary oxides corresponding to the chemical reaction AO + BO2 → ABO3. For this reason, we can compute EReact by subtracting the sum of total energies of its binary oxides AO (EAOt) and BO2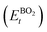 from the total energy of ABO3
from the total energy of ABO3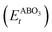 according to the relation42
according to the relation42
| | 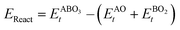 | (2) |
However, since the total energies of ABO3, AO and BO2 compounds are also related to their respective enthalpies of formation by the formulas
| | 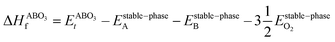 | (3) |
| | 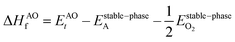 | (4) |
and
| |  | (5) |
respectively, we can see that
EReact can also be expressed as
| | 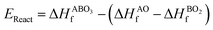 | (6) |
In the above equations, Et is the total energy of the optimized unit cells of the concerned oxides. It is evident from eqn (2) to (6) that only a good determination of the ground state total energies of AO, BO2 and ABO3 would ensure accurate computation of EReact. For the present study, we have computed the ground state lattice parameters and enthalpies of formation of the relevant AO and BO2 binary oxides using the SCAN meta-GGA functional, which are presented in Table 2. A comparison of the lattice parameters presented in Table 2 clearly shows that the SCAN functional gives a much better account of the structural properties of SrO, BaO, TiO2 and ZrO2 compared to the common semi-local functionals belonging to the first two rungs of the Jacob's ladder.8 At the same time, the calculated enthalpies of the formation for the four AO and BO2 oxides clearly show that large overestimation commonly seen in the GGA calculations is eliminated by the employment of the SCAN functional. This can mainly be ascribed to the fact that the SCAN functional does not suffer from the over-binding of oxygen bonds, which allows it to perform better for both molecules and solids.13,23
The lattice parameters of the ABO3 (where A = Sr and Ba; B = Ti and Zr) compounds under consideration computed using the SCAN meta-GGA functional are presented in Table 3, while the total energy vs volume and pressure vs volume data are shown in Fig. 1. When compared to experimental data, the SCAN calculated lattice parameters of SrTiO3 and BaZrO3 are only slightly larger (<0.5%), while the lattice parameters for BaTiO3 and SrZrO3 are slightly smaller (<0.12%). It is also evident from Table 3 that the enthalpies of formation computed using the SCAN functional for ABO3 compounds are in better agreement with experimental values compared to GGA. These results further confirm the superior performance of this meta-GGA functional in determining the thermodynamics of complex oxides. From Fig. 1, it can also be seen that the pressure vs. volume data computed using the Birch–Murnaghan's equations of state give a linear variation of pressure with volume for the SCAN calculations. Since the mechanical properties of perovskite materials (discussed later) are strongly dependent on smooth variation of pressure vs volume of the unit cell, Fig. 1 already indicates good performance of the SCAN meta-GGA functional.13 It is also worth pointing out here that the experimental enthalpies of the formation for the ABO3 compounds are less than the sum of enthalpies of the formation of the concerned binary oxides (i.e.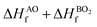 ), which indicates that the structure of the cubic perovskite oxides is energetically stable.49 Since experimental studies have shown the existence of BaTiO3 in the cubic phase,51,52 our calculated values of the enthalpies of the formation of BaTiO3, BaO and TiO2 clearly satisfy
), which indicates that the structure of the cubic perovskite oxides is energetically stable.49 Since experimental studies have shown the existence of BaTiO3 in the cubic phase,51,52 our calculated values of the enthalpies of the formation of BaTiO3, BaO and TiO2 clearly satisfy 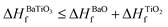 , showing that the SCAN meta-GGA functional has good agreement with experimental observations which have earlier been satisfied only through the use of the semi-empirically corrected GGA+U method.42
, showing that the SCAN meta-GGA functional has good agreement with experimental observations which have earlier been satisfied only through the use of the semi-empirically corrected GGA+U method.42
Table 3 Lattice parameters (Å) and enthalpies of the formation (eV per f.u.) of cubic perovskite unit cells of strontium titanate, barium titanate, strontium zirconates and barium zirconate computed using SCAN functional. For the sake of comparison, results of GGA reported in previous DFT studies and experimental data are also presented
| Compound |
SCAN (this work) |
GGA (previous works) |
Experiment |
| SrTiO3 |
|
|
|
|
a
0
|
3.909 |
3.94350 |
3.89051 |
| ΔHf |
−17.533 |
−17.80545 |
−17.00052 |
| BaTiO3 |
|
|
|
|
a
0
|
3.996 |
4.03550 |
4.00051 |
| ΔHf |
−17.233 |
−17.43545 |
−17.26552 |
| SrZrO3 |
|
|
|
|
a
0
|
4.149 |
4.19845 |
4.15453 |
| ΔHf |
−17.994 |
−18.08045 |
−18.32054 |
| BaZrO3 |
|
|
|
|
a
0
|
4.207 |
4.25645 |
4.19055 |
| ΔHf |
−18.226 |
−18.24045 |
−18.27054 |
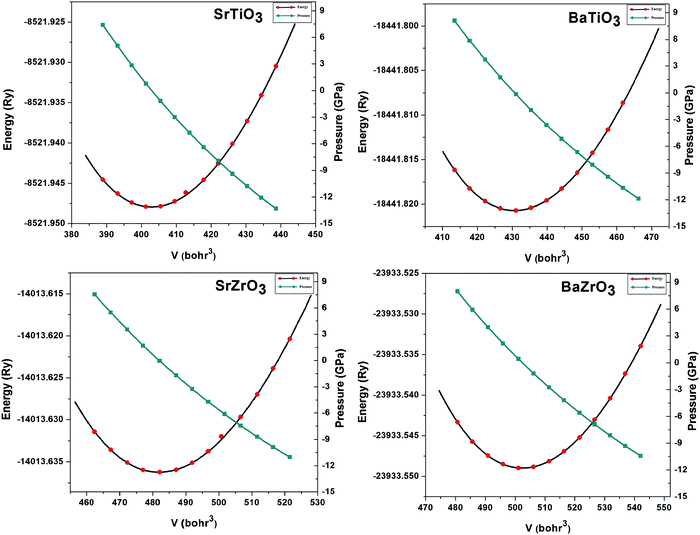 |
| | Fig. 1 The calculated total energy vs. volume and pressure vs. volume plots for SrTiO3, BaTiO3, SrZrO3 and BaZrO3 computed using the SCAN meta-GGA functional. | |
As mentioned earlier, determination of EReact for the chemical reaction AO + BO2 → ABO3 is important for determining the suitability of a perovskite oxide for various applications.42 In addition, EReact computed using DFT have also been used to examine the suitability of one-step and two-step techniques for synthesizing novel ternary compounds.5 In the case of compounds crystallizing in the perovskite structure, one can relate EReact with the dimensionless Goldschmit's tolerance factor, t.56 As the value of Goldschmit's tolerance factor indicates the stability of the perovskite structure, one expects an increase in t with increase in the values of EReact.57 In Fig. 2 we present our SCAN calculated EReact values as a function of increasing t of the four perovskite oxides. The comparison of our calculated results with the previous GGA+U calculations42 and experimental data58 as shown in Fig. 2 makes it evident that the SCAN meta-GGA functional is efficient in predicting reaction energies. Importantly, the EReact values obtained for SrTiO3, BaTiO3 and BaZrO3 with SCAN are found to be in excellent agreement with experimental ones.
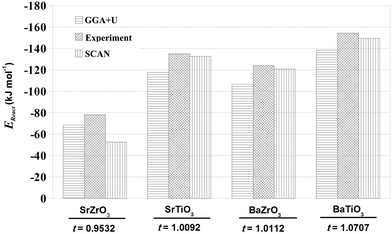 |
| | Fig. 2 The reaction energies, EReact (kJ mol−1), for SrTiO3, BaTiO3, SrZrO3 and BaZrO3 plotted as a function of increasing Goldsmith tolerance factor, t. The GGA+U and experimental values are derived from data reported by Hautier et al.42 and Kubaschewski et al.,58 respectively. | |
3.2. Mechanical properties
Since the mechanical response of a material to applied forces can be derived from its elastic constants, DFT calculations are commonly employed to supplement experimental results59 or to predict mechanical properties60 of ABO3 (where A = Sr and Ba; B = Ti and Zr) perovskite oxides. In the case of cubic crystals the mechanical properties can be completely defined in terms of three independent elastic constants C11, C12 and C44, which correspond to longitudinal compression, transverse expansion and shear elastic modulus, respectively.61 Since the three elastic constants for cubic structure can be computed from straight forward total energy calculations, in the present study, we have used the SCAN meta-GGA functional to compute the elastic constants of the cubic perovskite structure of alkaline earth metal titanates and zirconates, which are presented in Table 4. The comparison of our SCAN results with previous GGA59 calculations for SrTiO3 reveals that both these functionals show small deviations from experimental data.62 However, larger deviations of both SCAN and GGA results from the experimental data are evident in the case of BaTiO3.51 Since the large deviation of our calculated values of elastic constants for BaTiO3 can be due to the fact that this compound generally adopts a distorted perovskite structure, it is difficult to judge the performance of SCAN functional based solely on the comparison between the data presented in Table 4.
Table 4 Elastic constants (GPa) of cubic perovskite unit cells of strontium titanate, barium titanate, strontium zirconates and barium zirconate computed using SCAN functional. For comparison GGA and experimental data are also presented where available
| Compound |
SCAN (this work) |
GGA (previous works) |
Experiment |
| SrTiO3 |
|
|
|
|
C
11
|
344.90 |
319.3059 |
317.2062 |
|
C
12
|
110.90 |
97.5059 |
102.5062 |
|
C
44
|
109.01 |
113.0059 |
123.5062 |
| BaTiO3 |
|
|
|
|
C
11
|
310.34 |
310.4059 |
206.0051 |
|
C
12
|
113.67 |
107.2059 |
140.0051 |
|
C
44
|
130.21 |
139.8059 |
126.0051 |
| SrZrO3 |
|
|
|
|
C
11
|
327.26 |
338.6060 |
— |
|
C
12
|
78.32 |
71.0060 |
— |
|
C
44
|
82.00 |
77.0060 |
— |
| BaZrO3 |
|
|
|
|
C
11
|
320.95 |
322.5060 |
— |
|
C
12
|
84.22 |
79.0060 |
— |
|
C
44
|
94.93 |
70.0060 |
— |
Although various important mechanical parameters (e.g. shear modulus, Young's modules, Zener anisotropy factor, and Kleinman parameter) can be derived from C11, C12 and C44 using simple mathematical formulas,61 we note that only experimental data of elastic constants for SrTiO3 and BaTiO3 are available in the literature.51,62 However, Yamanak et al.63,64 have carried out studies for measuring the thermophysical properties of SrZrO3 and BaZrO3 in which they report the shear modulus, G (GPa), and Young's modulus, Y (GPa), of these perovskite oxides. For this reason, we first compute the bulk modulus, B (GPa), Voigt's shear modulus, SV (GPa), and Reuss's shear modulus, SR (GPa) for the four ABO3 compounds using the formulas
| | 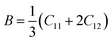 | (7) |
| | 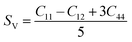 | (8) |
and
| | 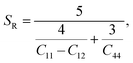 | (9) |
respectively. The values computed using
eqn (7) through
(9) are subsequently used for computing
G and
Y from
| | 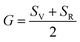 | (10) |
and
| | 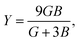 | (11) |
respectively. On comparing our calculated values of
G and
Y with GGA and experimental data presented in
Fig. 3, it is clear that the SCAN meta-GGA functional performs better than the semi-local GGA functionals for predicting the mechanical properties of perovskites considered in this work.
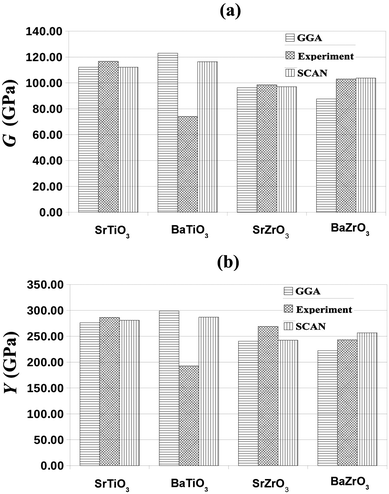 |
| | Fig. 3 The SCAN calculated shear modulus, G (GPa), and Young's modulus, Y (GPa), of SrTiO3, BaTiO3, SrZrO3 and BaZrO3 together with the GGA and experimental values reported in ref. 59, 60 and ref. 51, 62–64, respectively. | |
3.3. Vibrational properties
Vibrational properties of solids can be evaluated in terms of phonons that represent the collective dynamic excitations in a periodic lattice. Apart from being significantly important in indicating phase stability and structural transitions, phonons are crucial in modulating the transport properties of charge carriers in bulk65–67 and nano-materials.68,69 Since lattice vibrations can provide additional momentum to charge carriers of indirect band gap materials,70 phonons also play a key role in interband transitions. For this reason, a reliable knowledge of the phonon modes in a perovskite photocatalyst can prove useful in designing improved absorption of electromagnetic radiations71,72 as well as controlling the electron–hole recombination rates.73,74 For the five atom cubic unit cell of the perovskites considered in this work, there are five triply degenerate phonons at the Brillouin zone center (Γ-point). Among these phonons, one of the triply degenerate phonons is acoustic while the remaining four are optical. The coherent movement of charges in the acoustic phonons gives them zero frequency at the Γ-point, while the four triply degenerate optical phonons in a cubic perovskite structure have non-zero frequencies at the Γ-point.75 Three of these four triply degenerate optical phonons are infrared active and are designated as Γ15(TO1), Γ15(TO2) and Γ15(TO3); corresponding to A–BO3 ferroelectric soft mode, O–B–O bend mode and B–O stretch mode, respectively.75 On the other hand, the fourth triply degenerate (designated as Γ25) phonon mode is optically inactive and corresponds to a B–O3 torsion mode.75
It is well know that the dielectric and ferroelectric properties of the cubic ABO3 perovskite oxides are controlled by phonons,51,53,55,76 which can be modified by varying the stress or temperature. It is therefore intuitive to assess the performance of a DFT functional in predicting experimentally observed phonon modes and instabilities (e.g. ferroelectric at low temperatures). Unfortunately, a correct description of the vibrational properties from the frozen phonon approximation using semi-local as well as advanced functionals of DFT at 0 K has remained a challenge.50,77–81 For instance, plane wave (PW) based DFT calculations by Wahl et al.50 utilizing both semi-local and Heyd–Scuseria–Ernzerhof (HSE06) schemes only confirm the experimentally observed Sr–TiO3 ferroelectric soft mode of SrTiO3 to be real within the LDA approximation (see Table 5). On the contrary, all of LDA, GGA and HSE06 confirm the imaginary Ba–TiO3 ferroelectric soft mode of BaTiO3.50 However, recent employment of the SCAN functional for computing phonon modes of SrTiO3 and BaTiO3 at the Γ-point using the projector augmented wave (PAW) method has shown better performance of this meta-GGA exchange–correlation parameterization scheme.79 Since the PW/PAW based DFT calculations of phonons for the considered class of compounds are found to be sensitive to the choice of pseudopotentials as well as the treatment of semi-core states as valence or core states,79,80,82 an accurate all-electron account of vibrational frequencies at the Γ-point through FP-LAPW method of DFT using the SCAN meta-GGA functional is therefore mandated.
Table 5 The Γ-point optical phonon frequencies (THz) for the cubic phase of ABO3 (where A = Sr and Ba; B = Ti and Zr) compounds computed using the SCAN meta-GGA functional in the present study compared with the available theoretical results computed using the SCAN, LDA, GGA and HSE06 functionals and experimental data. Imaginary frequencies are indicated by imaginary unit, i, after the value
| Compound symmetry |
DFT method-functional |
Experiment |
| FP-LAPW-SCAN |
PW-SCAN |
PW-LDA |
PW-GGA |
PW-HSE06 |
| SrTiO3 |
|
|
|
|
|
|
|
Γ
15 (TO1) |
2.811 |
2.39879 |
2.39850 |
3.448 i50 |
2.248 i50 |
2.74983 |
|
Γ
15 (TO2) |
5.060 |
5.18679 |
5.30650 |
4.40750 |
4.85750 |
5.06683 |
|
Γ
25
|
7.309 |
7.49579 |
6.77450 |
7.01550 |
7.49550 |
7.94583 |
|
Γ
15 (TO3) |
16.128 |
16.36979 |
16.87850 |
15.34950 |
15.97950 |
16.39983 |
| BaTiO3 |
|
|
|
|
|
|
|
Γ
15 (TO1) |
4.532 i |
6.595 i79 |
2.248 i50 |
3.837 i78 |
7.225 i50 |
— |
|
Γ
15 (TO2) |
5.130 |
5.48679 |
5.78650 |
5.57678 |
5.54650 |
5.45684 |
|
Γ
25
|
8.733 |
8.69479 |
8.57450 |
8.45478 |
9.29650 |
9.23784 |
|
Γ
15 (TO3) |
14.022 |
14.27079 |
14.39050 |
14.06078 |
14.39050 |
14.45084 |
| SrZrO3 |
|
|
|
|
|
|
|
Γ
15 (TO1) |
1.874 i |
— |
3.41880 |
2.608 i82 |
— |
— |
|
Γ
15 (TO2) |
6.074 |
— |
6.44680 |
— |
— |
— |
|
Γ
25
|
3.528 |
— |
5.36680 |
— |
— |
— |
|
Γ
15 (TO3) |
16.877 |
— |
16.30980 |
— |
— |
— |
| BaZrO3 |
|
|
|
— |
|
|
|
Γ
15 (TO1) |
2.883 |
— |
2.87881 |
2.72875 |
— |
3.44885 |
|
Γ
15 (TO2) |
5.961 |
— |
5.78681 |
5.69675 |
— |
6.29685 |
|
Γ
25
|
5.735 |
— |
— |
5.45675 |
— |
— |
|
Γ
15 (TO3) |
14.788 |
— |
15.37981 |
14.48075 |
— |
15.14085 |
Since performance evaluation of various DFT functionals in predicting the vibrational properties of ABO3 perovskites can be carried out on the basis of optical phonon frequencies at the Γ symmetry point,50,75–78 in Table 5 we present our SCAN results together with the available earlier theoretical and experimental values. It is worth pointing out here that unlike the usual space group dependent unit cell calculations performed within the WIEN2k code for structural and electronic properties, the phonopy code requires forces caused by finite atomic displacements to be computed within supercells which are deprived of space group.28 For this reason, in this work, the atomic forces for the 40-atom supercells have been computed using Γ-point sampling. From Table 5 it is evident that the Γ-point phonon frequencies computed using SCAN in the present FP-LAPW calculations are in excellent agreement with the available experimental data.83–85 One can clearly see that both SrTiO3 and BaZrO3 show no tendency for ferroelectric distortion at low temperatures. On the other hand, both BaTiO3 and SaZrO3 show a tendency to ferroelectric distortions at low temperatures, which has also been observed in earlier studies.50,82,84 It is particularly important to notice that our calculated values for SrTiO3 and BaTiO3 are in better agreement with the experimental data compared to HSE06.50 Moreover, our FP-LAPW results of the A–BO3 ferroelectric soft mode for SrTiO3 and BaZrO3 computed using SCAN are the closest to the experimental data when compared with earlier theoretical results.79,82,83,85 The better performance of SCAN can mainly be attributed to the fact that an accurate determination of the vibrational properties using the frozen phonon approximation requires very precise computation of the curvature of the total energy surface with respect to the atomic displacements introduced in the solid. As SCAN already shows good performance in determining the total energy dependent physical properties of atoms, molecules and solids,13 from Table 5 it is evident that it also performs better than the computationally expensive HSE06 functional in determining the vibrational properties of ABO3 perovskites.50,79
3.4. Electronic properties
Using the lattice parameters optimized with the SCAN functional, we have computed the electronic density of states (DOS) and band structure diagrams of the selected alkaline earth metal titanates and zirconates, which are presented in Fig. 4 and 5, respectively. For these properties both SCAN and mBJ-LDA functionals are employed since the former DFT functional is known to underestimate the band gaps of solids despite its good performance for structural and energetic properties.13,23 By comparing Fig. 4 and 5, one can see that the overall features of the electronic properties for SrTiO3, BaTiO3, SrZrO3 and BaZrO3 computed using the two meta-GGA functionals are similar. However, both the DOS and band structure diagrams show that the positioning of the electronic states belonging to conduction and valence bands computed using SCAN//mBJ-LDA simulations are modified, which results in increase of the band gaps. From Fig. 4 we can see that the upper valence bands for SrTiO3 and BaTiO3 are mainly composed of the O-2p states along with a minor contribution coming from the Ti-3d states. In a similar fashion, Fig. 5 shows that the upper valence bands for SrZrO3 and BaZrO3 are mainly composed of the O-2p states along with a minor contribution coming from the Zr-4d states. Irrespective of the choice of the functional, it is also evident that for all the ABO3 perovskites considered in this study the conduction band edge is mainly composed of the B atom's d states along with a minor contribution coming from the O-2p states. Moreover, the contribution of Sr-5s and Ba-6s states in the conduction band minimum is negligible; however, these states dominate the conduction band at higher energies. This is understandable since the ABO3 perovskite oxides are composed of alternating layers of AO and BO2, such that stronger covalent bonding between B and O atoms dominates the conduction and valence band edges, respectively.32,35
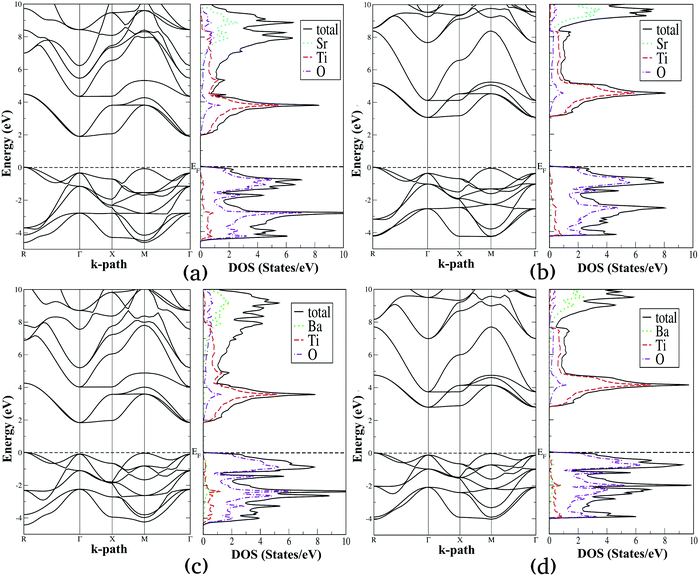 |
| | Fig. 4 Calculated electronic band structure diagrams and density of states plots for SrTiO3 (a and b) and BaTiO3 (c and d) computed using SCAN (a and c) and mBJ-LDA (b and d) meta-GGA functionals. | |
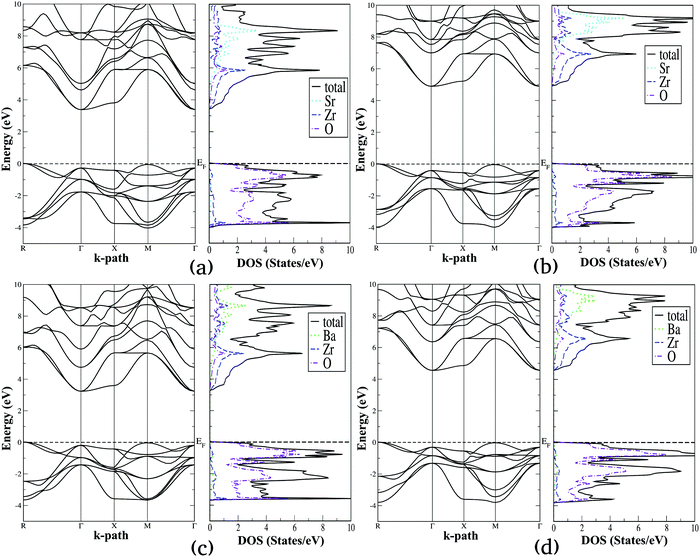 |
| | Fig. 5 Calculated electronic band structure diagrams and density of states plots for SrZrO3 (a and b) and BaZrO3 (c and d) computed using SCAN (a and c) and mBJ-LDA (b and d) meta-GGA functionals. | |
From the electronic properties of ABO3 (where A = Sr and Ba; B = Ti and Zr) shown in Fig. 4 and 5, it is evident that the fundamental energy band gap between the O-2p states at the valence band edge and the B atom's d states at the conduction band edge is along the R → Γ direction. On the other hand, the optical band gap for all these compounds is slightly larger than the fundamental band gap, which is along the Γ → Γ direction. The SCAN and mBJ-LDA calculated band gaps for ABO3 (where A = Sr and Ba; B = Ti and Zr) along the R → Γ and Γ → Γ directions are presented in Table 6 and compared with earlier theoretical results computed using GGA and HSE06 functionals as well as with experimental data.86–91 It is clear that the SCAN meta-GGA functional employed in this study underestimates band gaps for the perovskite oxides considered here, which are only slightly larger than the band gaps predicted by the GGA functional.23,86,92 The comparison of the fundamental band gaps computed using SCAN//mBJ-LDA simulations and the ones computed using hybrid DFT in ref. 86 shows that a relatively smaller shift of the B atom's d states making up the conduction band edge at the Γ symmetry point is achieved with the meta-GGA (i.e. mBJ-LDA) functional employed here. Since the band structures shown in Fig. 4 and 5 reveal that the application of mBJ-LDA does not shift the O-2p states located at the R symmetry point, our calculated mBJ-LDA R → Γ band gaps are smaller than the ones obtained using the HSE06 functional.86 On the other hand, Fig. 4 and 5 clearly show that the O-2p states located at the Γ symmetry point below the Fermi level are pushed towards more negative energies with the application of the mBJ-LDA functional. As a consequence, the optical band gaps of SrTiO3 and SrZrO3 computed using the SCAN//mBJ-LDA simulations (Table 6) are in better agreement with the experimental data.87–91 On the other hand, optical band gaps of cubic BaTiO3 and BaZrO3 are slightly smaller when compared with the hybrid DFT results.86 Despite the fact that different experimental values for the optical band gaps of BaZrO3 are reported in the literature,90,91 comparison of our calculated band gap with earlier works suggests that the performance of the mBJ-LDA functional for barium compounds is also satisfactory. In particular, the small difference in the fundamental and optical band gap of cubic BaTiO3 (0.11 eV) is in good agreement with the previous experimental reports which reported difficulty in determining the direct or indirect nature of the band gap for this material.88 Thus, our results allow us to claim that the SCAN//mBJ-LDA simulations are a better choice than HSE06 for reliably evaluating the optical properties and photocatalytic performance of ABO3 (where A = Sr and Ba; B = Ti and Zr) perovskite oxides.
Table 6 The calculated fundamental (R → Γ) and optical (Γ → Γ) band gaps (eV) of SrTiO3, BaTiO3, SrZrO3 and BaZrO3 perovskites computed using SCAN and mBJ-LDA meta-GGA functionals along with the GGA and HSE06 band gaps reported in a previous theoretical study and experimental data
|
|
Fundamental band gap (along R → Γ direction) |
Optical band gap (along Γ → Γ direction) |
| SCAN |
mBJ-LDA |
GGA |
HSE06 |
SCAN |
mBJ-LDA |
GGA |
HSE06 |
Experiment |
|
Temperature extrapolated value derived from optical band gap of tetragonal BaTiO3.
|
| SrTiO3 |
1.90 |
3.07 |
1.8786 |
3.2986 |
2.23 |
3.42 |
2.2486 |
3.6986 |
3.4387 |
| BaTiO3 |
1.84 |
2.80 |
1.7886 |
3.1486 |
1.92 |
2.91 |
1.9386 |
3.2786 |
∼3.20a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 88 88 |
| SrZrO3 |
3.38 |
4.89 |
3.4486 |
4.9386 |
3.65 |
5.30 |
3.6886 |
5.2986 |
5.6089 |
| BaZrO3 |
3.23 |
4.55 |
3.2286 |
4.6786 |
3.42 |
4.85 |
3.4686 |
4.9986 |
5.30,90 5.0591 |
3.5. Optical properties
For practical purposes, the application of a material in optical devices can be directly related to its absorption properties. Since the optical band gaps of ABO3 (where A = Sr and Ba; B = Ti and Zr) ceramics make them suitable for applications in devices operating in the 220 nm–360 nm wavelength range, it is intuitive to examine their optical properties. As a long range of absorption appears to be plausible for transition between states having varying degrees of spatial overlaps, the band gap alone does not give complete information of absorption properties. To address this issue, optical absorption in a wide range of wavelength has been obtained for SrTiO3, BaTiO3, SrZrO3 and BaZrO3 perovskite oxides by computing the real and imaginary parts of the complex dielectric function.93,94 The optical absorption plots calculated using the SCAN and mBJ-LDA meta-GGA functionals are presented in Fig. 6. Irrespective of the choice of the functional used, it is evident that the optical absorption is maximum in the far-UV region (<200 nm) of the electromagnetic spectrum. Since the SCAN functional is unable to accurately reproduce the experimental band gaps of the compounds under study, one can see that the threshold of the optical absorption for this functional is in the visible region for the titanates and UV region for the zirconates. However, the results computed using SCAN//mBJ-LDA simulations show that the threshold of optical absorption for all the compounds under consideration is in the UV region, in agreement with the experimental observations.87–91
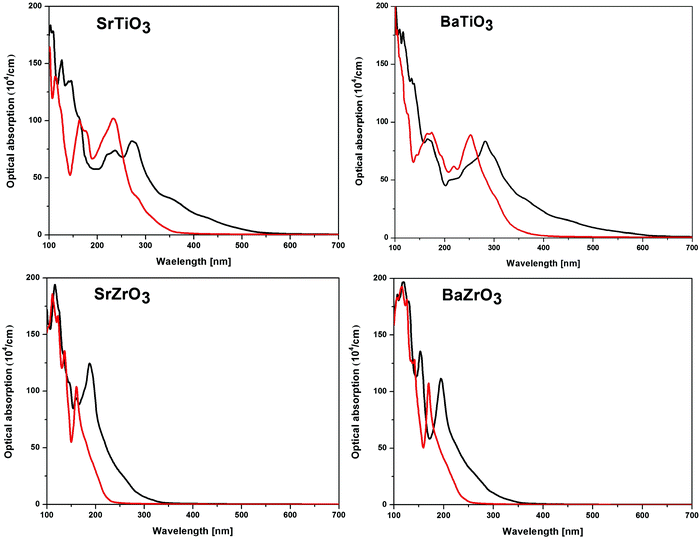 |
| | Fig. 6 The calculated optical absorption of SrTiO3, BaTiO3, SrZrO3 and BaZrO3 perovskite oxides computed using the SCAN (black line) and mBJ-LDA (red line) meta-GGA functionals. | |
3.6. Photocatalytic performance
Despite the fact that the optical absorption plots shown in Fig. 6 indicate that SrTiO3, BaTiO3, SrZrO3 and BaZrO3 are suitable for applications in optical devices operating in the UV region of the electromagnetic spectrum, the application of these perovskite oxides for hydrogen production through photocatalysis requires that the band edge potentials are appropriate with reference to water oxidation and reduction potentials.16 It is well known that for successfully producing hydrogen by water splitting, a material's conduction band minima (CBM) should be more negative than the reduction potential of H+/H2, while the valence band maxima (VBM) should be more positive than the oxidation potential of H2O/O2.16 In order to estimate positions of the conduction and valence band edges of the compounds under study, we have computed band edge potential using the procedure detailed in ref. 95–98 for the SCAN, mBJ-LDA and experimental optical band gaps presented in Table 6. The calculated results are presented in Fig. 7, where one can see that the edge potential of CBM computed using SCAN//mBJ-LDA simulations is located −0.89 eV, −0.71 eV, −1.81 eV and −1.66 eV above the reduction potential of water for SrTiO3, BaTiO3, SrZrO3 and BaZrO3, respectively. On the other hand, the band edge potentials of VBM for SrTiO3, BaTiO3, SrZrO3 and BaZrO3 computed using SCAN//mBJ-LDA simulations are found to be 2.53 eV, 2.20 eV, 3.49 eV and 3.20 eV below the oxidation potential of water, respectively. A comparison of the results presented in Fig. 7 again makes it evident that the mBJ-LDA functional is able to provide better agreement with experiment as compared to the SCAN functional.
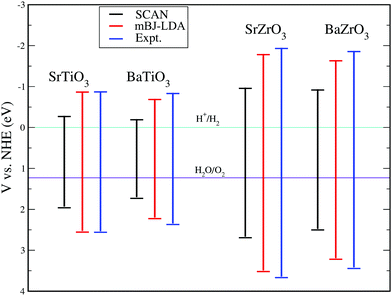 |
| | Fig. 7 The band edge potentials for SrTiO3, BaTiO3, SrZrO3 and BaZrO3 perovskite oxides calculated using the SCAN, mBJ-LDA and experimental optical band gaps.87–91 | |
An important feature evident from our calculated mBJ-LDA results and experimental data presented in Fig. 7 is that the Ti based compounds have both their CBM and VBM edge potentials located close to the H+/H2 and H2O/O2 potentials, respectively, when compared to the Zr based compounds. Since reports from 1980s already show insignificant photocatalytic activity of pristine SrTiO3 for splitting water,99,100 one might suspect that pristine perovskite oxides with band gap > 4 eV (e.g. LiTaO3101 and BaZrO3102) are more suited for hydrogen production. However, this is not the case, because SrTiO3 loaded with a co-catalyst show an improved photocatalytic activity. This is due to the lower rate of recombination of the photogenerated electron and holes achieved in Rh loaded SrTiO3, which results in better hydrogen evolution (628 μmol h−1)103 when compared to pristine BaZrO3 (104.5 μmol h−1).102 Therefore, recombination is an important factor influencing the photocatalytic performance of a material104 that can be evaluated in terms of the transfer rate of photogenerated electrons and holes in the reduction and oxidation processes.105 Unfortunately, the transfer rate of photogenerated electrons and holes cannot be directly measured from DFT calculations, however, it can indirectly be evaluated from the absolute ratio of the effective masses of the photogenerated holes and electrons
| | 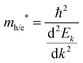 | (12) |
in valence and conduction bands, respectively, according to the formula
105| | 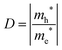 | (13) |
A large value of D would indicate a better transfer rate of photogenerated electrons and holes, hence lower rate of recombination. On the other hand, smaller values of D would indicate higher rate of recombination. In eqn (12), Ek is the energy corresponding to wavevector k. Since the fundamental band gaps of Ti and Zr based perovskite oxides considered in this work are along the R → Γ symmetry points, we have considered the curvatures of the bands at Γ point for computing the effective mass of electron and the curvatures of the bands at R point for computing the effective mass of holes.105 A comparison of the results computed using SCAN and mBJ-LDA (Table 7) clearly indicates that effective masses obtained from the former meta-GGA functional are slightly smaller; indicating that SCAN gives a larger curvature for both the conduction and valence band edges. This inability of the SCAN functional in predicting the accurate band structures of materials having band gaps > 1 eV is analogous to the results obtained with a GGA functional23 which also results in an underestimation of the effective masses.106 On the contrary, application of mBJ-LDA causes narrowing of the band dispersion that results in large effective masses, which are overestimated as compared to experimental data.106,107 Nevertheless, the values of D computed using both the SCAN and mBJ-LDA functionals clearly show that an improved separation of charges should be expected from Zr based perovskite oxides. These results are in accordance with the photocatalytic hydrogen evolution under UV irradiation of pristine SrTiO399,100 and BaZrO3.102 We therefore conclude that the employment of SCAN//mBJ-LDA simulations for investigating oxide semiconductors using DFT allows a reliable account of the structural, electronic and photocatalytic properties which are usually possible through computationally expensive hybrid functionals or GW methods.13,14 Moreover, our results clearly suggest that the employment of a combination of SCAN and mBJ-LDA meta-GGA functionals for examining the modulation of band edge potentials of large band gap ceramics by means of doping can be important in predicting new photocatalysts.
Table 7 The electron and hole effective masses (in units of free electron mass me) corresponding to the curvatures of conduction band at Γ point and curvature of valence band along R point, respectively, along with ratios of me* and mh* computed using the SCAN and mBJ-LDA meta-GGA functionals
| Compound |
SCAN |
mBJ-LDA |
|
m
e* Γ → R |
m
h* R → Γ |
D
|
m
e* Γ → R |
m
h* R → Γ |
D
|
| SrTiO3 |
0.80 |
−2.36 |
2.95 |
1.07 |
−2.70 |
2.53 |
| BaTiO3 |
0.83 |
−2.34 |
2.82 |
1.10 |
−2.69 |
2.44 |
| SrZrO3 |
0.60 |
−2.47 |
4.14 |
0.71 |
−2.87 |
4.03 |
| BaZrO3 |
0.59 |
−2.42 |
4.08 |
0.70 |
−2.82 |
4.01 |
4. Conclusions
In conclusions, we have performed a systematic analysis of combined application of SCAN and mBJ-LDA meta-GGA functionals for computing the physical properties of alkaline earth metal titanate and zirconate in cubic perovskite structure using the FP-LAPW method of DFT. The potential of these perovskite oxides for photocatalytic hydrogen production by splitting water is also examined. Our results clearly show that the experimentally observed structural, energetic, mechanical and vibrational properties of large band gap perovskite oxides are accurately predicted by the SCAN functional. In particular, the accurate prediction of the structural and energetic properties of atomic species and the binary oxides involved in synthesis of the concerned perovskite oxides shows that SCAN meta-GGA functional is able to provide an accuracy comparable to that of hybrid DFT calculations. The comparison of SCAN calculated reaction energies for SrTiO3, BaTiO3, SrZrO3 and BaZrO3 shows good agreement with experimental observations, which have previously been achieved through GGA+U calculations. By computing the elastic constants and frequencies of the optical phonons at the Brillouin zone center of the concerned perovskite oxides, we also show that SCAN functional performs better than the semi-local GGA as well as HSE06 functional for accurately predicting the mechanical and vibrational properties of these materials. Despite its good performance for the above-mentioned physical properties of perovskite oxides, SCAN functional is found to fall short of reproducing the experimentally observed band gaps of alkaline earth metal titanates and zirconates. To address this issue, we show that the application of SCAN//mBJ-LDA simulations allows one to achieve better accuracy in determining the optoelectronic properties of SrTiO3, BaTiO3, SrZrO3 and BaZrO3. In agreement with experiments, all four compounds are found to be indirect band gap materials showing absorption thresholds in the UV region of the electromagnetic spectrum. Using the electronic band gaps predicted by mBJ-LDA meta-GGA functional we also show that our ab initio predicted band edge potentials and effective masses of photogenerated electrons and holes are consistent with photocatalytic hydrogen evolution observed in SrTiO3 and BaZrO3. Since ab initio calculations provide the means to simulate changes in material's properties, our results clearly demonstrate that combining SCAN and mBJ-LDA functionals of DFT would prove useful as a computationally economical and robust technique for designing new photocatalysts based on Ti and Zr based perovskite oxides. This can particularly prove useful in future DFT studies for exploring the surface properties of photocatalysts where hybrid functionals become impractical owing to their huge computational costs.
Author contributions
Waqas Zulfiqar: Conceptualization, data curation, and writing – original draft. Syed Muhammad Alay-e-Abbas: Conceptualization, writing – original draft, validation, and supervision. Ghulam Abbas: Formal analysis and validation. Amel Laref: Validation and visualization. J. Andreas Larsson: Writing – review & editing, supervision, and validation. Ali Shaukat: Writing – review & editing and supervision.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors are grateful to the Higher Education Commission of Pakistan for financial support under the National Research Program for Universities grant No. 7107/Punjab/NRPU/R&D/HEC/2017. S. M. A. A. and J. A. L. thank the Knut and Alice Wallenberg Foundation, and Kempestiftelserna for financial support. This research project was supported by a grant from the “Research Centre of Female Scientific and Medical Colleges”, Deanship of Scientific Research, King Saud University. The computations were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) at HPC2N and NSC partially funded by the Swedish Research Council through grant agreement no. 2018-05973.
References
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and J. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- K. Burke, J. Chem. Phys., 2012, 136, 150901 CrossRef PubMed.
- A. Jain, Y. Shin and K. A. Persson, Nat. Rev. Mater., 2016, 1, 15004 CrossRef CAS.
- P. Canepa, S. H. Bo, G. S. Gautam, B. Key, W. D. Richard, T. Shi, Y. Tian, Y. Wang, J. Li and G. Ceder, Nat. Commun., 2017, 8, 1759 CrossRef PubMed.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 15, 2315 CrossRef.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2015, 142, 074111 CrossRef PubMed.
- J. P. Perdew, A. Ruzsinszky, J. Tao, V. N. Staroverov, G. E. Scuseria and G. I. Csonka, J. Chem. Phys., 2005, 123, 062201 CrossRef PubMed.
- F. Tran, J. Stelzl and P. Blaha, J. Chem. Phys., 2016, 144, 204120 CrossRef PubMed.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, J. Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- B. G. Janesko, T. M. Henderson and G. E. Scuseria, Phys. Chem. Chem. Phys., 2009, 11, 443–454 RSC.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 15, 036402 CrossRef PubMed.
- F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS PubMed.
- J. Xing, W. Q. Fang, H. J. Zhao and H. G. Yang, Chem. – Asian J., 2012, 7, 642–657 CrossRef CAS PubMed.
- N. Dehnhardt, H. Borkowski, J. Schepp, R. Tonner and J. Heine, Inorg. Chem., 2018, 57, 633–640 CrossRef CAS PubMed.
- S. Zlotnik, D. M. Tobaldi, P. Seabra, J. A. Labrincha and P. M. Vilarinho, Chem. Phys. Chem., 2016, 17, 3570–3575 CrossRef CAS PubMed.
- H. Iwahara, T. Yajima, T. Hibino and H. Ushida, J. Electrochem. Soc., 1993, 140, 1687 CrossRef CAS.
- T. Yajima, K. Koide, H. Takai, N. Fukatsu and H. Iwahara, Solid State Ionics, 1995, 79, 333–337 CrossRef CAS.
- U. De, K. R. Sahu and A. De, Solid State Phenom., 2015, 232, 235–278 Search PubMed.
- P. Kovács, F. Tran, P. Blaha and G. K. H. Madsen, J. Chem. Phys., 2019, 150, 164119 CrossRef PubMed.
- G. S. Gautam and E. A. Carter, Phys. Rev. Mater., 2018, 2, 095401 CrossRef.
- J. Muscat, A. Wander and N. M. Harrison, Chem. Phys. Lett., 2001, 342, 397–401 CrossRef CAS.
- P. Borlido, T. Aull, A. W. Huran, F. Tran, M. A. L. Marques and S. Botti, J. Chem. Theory Comput., 2019, 10, 5069–5079 CrossRef PubMed.
-
P. Blaha, K. Schwarz, G. Madsew, D. Kvasnicka and J. Luitz, WIEN2k: An Augmented Plane Wave Plus Local Orbital Program, Vienna University of Technology, Austria, 2014.
- D. Koller, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155109 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- J. M. Skelton, D. Tiana, S. C. Parker, A. Togo, I. Tanaka and A. Walsh, J. Chem. Phys., 2015, 143, 064710 CrossRef PubMed.
- F. Tran, R. Laskowski, P. Blaha and K. Schwarz, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 115131 CrossRef.
-
K. P. Huber, Molecular spectra and molecular structure: IV. Constants of diatomic molecules, Spr. Sci. & Bus. Med., 2013 Search PubMed.
- S. M. Alay-e-Abbas, M. W. Yousaf, G. Abbas, N. Amin and A. Laref, Ceram. Int., 2019, 45, 18281–18290 CrossRef CAS.
- M. S. Anderson, C. A. Swenson and D. T. Peterson, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 3329 CrossRef CAS PubMed.
-
C. Kittel and P. McEuen, Introduction to solid state physics, Wiley, New York, 2005, p. 105 Search PubMed.
- S. M. Alay-e-Abbas, F. Javed, G. Abbas, N. Amin and A. Laref, J. Phys. Chem. C, 2019, 123, 6044–6053 CrossRef CAS.
- P. Janthon, S. Luo, S. M. Kozlov, F. Vines, J. Limtrakul, D. G. Truhlar and F. Illas, J. Chem. Theory Comput., 2014, 10, 3832 CrossRef CAS PubMed.
-
G. Chiarotti, Interaction of Charged Particles and Atoms with Surfaces, LandoltBornstein-Group III Condensed Matter. Spr. Ber. Heid. 24c 1995.
-
J. Donohue, The Structures of the Elements, Wiley, New York, 1974, p. 191 Search PubMed.
- M. C. Verbraeken, E. Suard and J. T. Irvine, J. Mater. Chem., 2009, 19, 2766–2770 RSC.
-
J. Rogal, PhD thesis, Freie Universität, Berlin, 2006.
- L. Schimka, J. Harl and G. Kresse, J. Chem. Phys., 2011, 134, 024116 CrossRef PubMed.
- G. Hautier, S. P. Ong, A. Jain, C. J. Moore and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155208 CrossRef.
-
M. W. Chase Jr., NIST-JANAF Thermochemical Tables, 4th edn, J. Phys. Chem. Ref. Data 4 (1998) 9.
- L. G. Liu and W. A. Bassett, J. Geophys. Res., 1972, 77, 4934 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
-
G. V. Samsonov, The Oxide Handbook IFI, Plenum, New York, 1982 Search PubMed.
- R. E. Hann, P. R. Suitch and J. L. Pentecost, J. Am. Ceram. Soc., 1985, 68, 285 CrossRef.
-
J. G. Speight, Lange's Handbook of Chemistry, McGrawHill, New York, 6 2005 Search PubMed.
-
D. R. Lide, CRC Handbook of Chemistry and Physics. CRC Press, Boca Raton, 2007 Search PubMed.
- R. Wahl, D. Vogtenhuber and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 104116 CrossRef.
-
K. H. Hellwege and A. M. Hellwege, Ferroelectrics and Related Substances, New Series, Landolt-Bornstein, Springer Verlag, Berlin, vol. 3 1969 Search PubMed.
-
O. Kubaschewski, C. B. Alcock and P. J. Spencer, Materials Thermochemistry, Pergamon, New York, vol. 6, 1993, p. 257 Search PubMed.
- B. J. Kennedy, C. J. Howard and B. C. Chakoumakos, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 4023 CrossRef CAS.
- M. E. Huntelaar, A. S. Booij and E. H. P. Cordfunke, J. Chem. Thermodyn., 1994, 26, 1095 CrossRef CAS.
-
W. Pies and A. Weiss, Simple Oxocompounds of Zirconium (Oxozirconates); K.-H. Hellwege, A. M. Hellwege, Springer Materials, New York, 1976 Search PubMed.
- V. M. Goldschmidt, Die Naturwissen, 1926, 21, 477 CrossRef.
-
S. Stølen, Chemical thermodynamics of materials. John Wiley & Sons, New York 2005 Search PubMed.
-
O. Kubaschewski, C. B. Alcock and P. J. Spencer, Materials Thermochemistry, Pergamon, New York, 1993, pp. 257–323 Search PubMed.
- S. Piskunov, Comput. Mater. Sci., 2004, 29, 165–178 CrossRef CAS.
- R. Terki, H. Feraoun, G. Bertrand and H. Aourag, Phys. Status Solidi B, 2005, 242, 1054–1062 CrossRef CAS.
-
C. Kittel, Introduction to Solid State Physics, John Wiley & Sons, Inc., USA, 1996 Search PubMed.
- R. O. Bell and G. Rupprecht, Phys. Rev., 1963, 129, 90 CrossRef CAS.
- J. S. Yamanaka, J. Am. Ceram. Soc., 2005, 88, 1496–1499 CrossRef.
- S. Yamanaka, H. Fujikane, T. Hamaguchi, H. Muta, T. Oyama, T. Matsuda, S. Kobayashi and K. Kurosaki, J. Alloys Compd., 2003, 359, 109–113 CrossRef CAS.
- J. S. Kang, M. Li, H. Wu, H. Nguyen and Y. Hu, Science, 2018, 361, 575–578 CrossRef CAS PubMed.
- J.-J. Zhou, O. Hellman and M. Benardi, Phys. Rev. Lett., 2018, 121, 226603 CrossRef CAS PubMed.
- Y. Kang and S. Han, Phys. Rev. Appl., 2018, 10, 044013 CrossRef CAS.
- K. Kaasbjerg, K. S. Thyhesen and K. W. Jaconbsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115317 CrossRef.
- B. Liao, J. Zhou, B. Qiu, M. S. Dresselhaus and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 235419 CrossRef.
- J. Noffsinger, E. Kioupakis, C. G. Van de Walle, S. G. Louie and M. L. Cohen, Phys. Rev. Lett., 2012, 108, 167402 CrossRef PubMed.
- X. Gong, O. Voznyy, A. Jain, W. Liu, R. Sabatini, Z. Piontkowski, G. Walters, G. Bappi, S. Nokhrin, O. Bushuyev, M. Yuan, R. Comin, D. McCamant, S. O. Kelley and E. H. Sargent, Nat. Mater., 2018, 17, 550–556 CrossRef CAS PubMed.
- T. Ghosh, S. Aharon, L. Etgar and S. Ruhman, J. Am. Chem. Soc., 2017, 139, 18262–18270 CrossRef CAS PubMed.
- J. He, A. S. Vasenko, R. Long and O. V. Prezhdo, J. Phys. Chem. Lett., 2018, 9, 1872–1879 CrossRef CAS PubMed.
- L. Cheng, C. Zhang and Y. Liu, JPhys Mater., 2019, 2, 045005 CrossRef CAS.
- P. G. Sundell, M. E. Björketun and G. Wahnström, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 104112 CrossRef.
- R. Schafranek, J. D. Baniecki, M. Ishii, Y. Kotaka, K. Yamanka and K. Kurihara, J. Phys. D: Appl. Phys., 2012, 45, 055303 CrossRef.
- R. D. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5828–5844 CrossRef CAS PubMed.
- D. I. Bilc, R. Orlando, R. Shaltaf, G.-M. Rignanese, J. Íñiguez and P. Ghosez, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 165107 CrossRef.
- Y. Zhang, J. Sun, J. P. Perdew and X. Wu, Phys. Rev. B, 2017, 96, 03514 Search PubMed.
- R. Vali, J. Phys. Chem. Solids, 2008, 69, 876–879 CrossRef CAS.
- A. R. Akbarzadeh, I. Kornev, C. Malibert, L. Bellaiche and J. M. Kiat, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 205104 CrossRef.
- S. Amisi, E. Bousquet, K. Katcho and P. Ghosez, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 064112 CrossRef.
- W. G. Stirling, J. Phys. C, 1972, 5, 2711–2730 CrossRef CAS.
- Y. Luspin, J. L. Servoin and F. Gervais, J. Phys. C, 1980, 13, 3761–3773 CrossRef CAS.
- C. H. Perry, D. J. McCarthy and G. Rupprecht, Phys. Rev., 1965, 138, A1537 CrossRef.
-
M. Schlipf, PhD thesis, Forschungszentrum Jülich, 2013.
-
H. Dittrich, N. Karl, H. W. Schock and S. Kuck, Ternary Compounds, Organic Semiconductors: Supplement, Springer, 2000 Search PubMed.
- S. H. Wemple, Phys. Rev. B: Solid State, 1970, 2, 2679 CrossRef.
- Y. S. Lee, J. S. Lee, T. W. Noh, D. Y. Byun, K. S. Yoo, K. Yamaura and E. Takayama-Muromachi, Phys. Rev. B: Solid State, 2003, 67, 113101 CrossRef.
- J. Robertson, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.–Process., Meas., Phenom., 2000, 18, 1785–1791 CrossRef CAS.
- H. Zhang, J. Qiao, G. Li, S. Li, G. Wang, J. Wang and Y. Song, Ultrason. Sonochem., 2018, 42, 356 CrossRef CAS PubMed.
- G. S. Gautam, T. P. Senftle and E. A. Carter, Chem. Mater., 2018, 30, 4543 CrossRef.
-
F. Wooten, Optical properties of solids, Academic Press, New York, 1972 Search PubMed.
- C. Ambrosch-Draxl and J. O. Sofo, Comput. Phys. Commun., 2006, 175, 1 CrossRef CAS.
- S. Akhtar, S. M. Alay-e-Abbas, G. Abbas, M. I. Arshad, J. Batool and N. Amin, J. Appl. Phys., 2018, 123, 161569 CrossRef.
- M. A. Butler and D. S. Ginley, J. Electrochem. Soc., 1978, 125, 228 CrossRef CAS.
- Y. Xu and M. A. Schoonen, Am. Miner., 2000, 85, 543–556 CrossRef CAS.
- H. L. Zhuang and R. G. Hennig, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 115314 CrossRef.
- K. Domen, S. Naito, M. Soma, T. Onishi and K. Tamaru, J. Chem. Soc., Chem. Commun., 1980, 12, 543–544 RSC.
- J. M. Lehn, J. P. Sauvage and R. Ziessel, Nouv. J. Chim., 1980, 4, 623–627 CAS.
- A. Kudo, Catal. Surv. Asia, 2003, 7, 31–38 CrossRef CAS.
- Y. Yuan, X. Zhang, L. Liu, X. Jiang, J. Lv, Z. Li and Z. Zou, Int. J. Hydrogen Energy, 2008, 33, 5941–5946 CrossRef CAS.
- J. M. Lehn, J. P. Sauvage, R. Ziessel and L. Hilaire, Isr. J. Chem., 1982, 22, 168–172 CrossRef CAS.
- K. Ozawa, M. Emori, S. Yamamoto, R. Yukawa, S. Yamamoto, R. Hobara, K. Fujikawa, H. Sakama and I. Matsuda, J. Phys. Chem. Lett., 2014, 5, 1953–1957 CrossRef CAS PubMed.
- X. Meng, N. Yun and Z. Zhang, Can. J. Chem. Eng., 2019, 97, 1982–1998 CrossRef CAS.
- Y. S. Kim, M. Marsman and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205212 CrossRef.
- B. Traoré, G. Bouder, W. Lafargue-Dit-Hauret, X. Rocquefelte, C. Katan, F. Tran and M. Kepenekian, Phys. Rev. B, 2019, 99, 035139 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Ghulam
Abbas
*ab,
Ghulam
Abbas
 cd,
Amel
Laref
cd,
Amel
Laref
 e,
J. Andreas
Larsson
b and
Ali
Shaukat
f
e,
J. Andreas
Larsson
b and
Ali
Shaukat
f
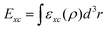 , where εxc is the exchange–correlation energy density per volume. For the first and second rungs, respectively, εxc is expressed in terms of electron density, ρ, alone (as in the case of local density approximation (LDA))10 and ρ and its first gradient, ∇ρ, (as in the case of generalized gradient approximation (GGA)).11 On the other hand, combining electron density and its first derivative with kinetic-energy density and/or ∇2ρ gives us the so-called meta-GGA functionals, which occupy the third rung of Jacob's ladder.7,9 Apart from the semi-local functionals, there also exist DFT functionals which allow computing Exc[ρ] through a double integral or Hartree–Fock (HF) exchange. Although accurate, these so-called hybrid functionals are computationally much more expensive than the semi-local functionals and thus occupy the fourth rung of the Jacob's ladder.12
, where εxc is the exchange–correlation energy density per volume. For the first and second rungs, respectively, εxc is expressed in terms of electron density, ρ, alone (as in the case of local density approximation (LDA))10 and ρ and its first gradient, ∇ρ, (as in the case of generalized gradient approximation (GGA)).11 On the other hand, combining electron density and its first derivative with kinetic-energy density and/or ∇2ρ gives us the so-called meta-GGA functionals, which occupy the third rung of Jacob's ladder.7,9 Apart from the semi-local functionals, there also exist DFT functionals which allow computing Exc[ρ] through a double integral or Hartree–Fock (HF) exchange. Although accurate, these so-called hybrid functionals are computationally much more expensive than the semi-local functionals and thus occupy the fourth rung of the Jacob's ladder.12![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structure of SrTiO3, BaTiO3, SrZrO3 and BaZrO3 perovskites and compute the structural properties using the SCAN functional. Since the energetic properties presented in this study also required computation of ground state properties of the oxygen molecule, elemental solids and binary oxides, all the structural parameters for these molecules and solids are also optimized using the SCAN functional. In the case of oxygen molecule, force minimization is performed for computing the optimized bond length. On the other hand, lattice parameters of elemental solids, binary oxides and ternary oxides are computed using self-consistent calculation for a series of fixed volumes of their respective unit cells. Where necessary, the c0/a0 and b0/a0 ratios have also been optimized. The SCAN optimized unit cells of all the ABO3 compounds are subsequently used for computing the electronic and optical properties. For computing the mechanical properties, we have utilized the Elastic Constants for Cubic Cases (ELAS) program provided within the WIEN2k package.26 For the computation of the vibrational properties of the ABO3 compounds (using a 40-atom supercell), the frozen phonon approximation was employed using the phonopy code.28 For all the calculations involving phonons, a force convergence criteria of 0.01 mRy a.u.−1 was used. In order to eliminate numerical noise in our phonon calculations, the charge density grid has been enlarged by a factor of 2, while symmetrization of the force constants was also taken into account during post processing of the forces with the phonopy code.29
m) structure of SrTiO3, BaTiO3, SrZrO3 and BaZrO3 perovskites and compute the structural properties using the SCAN functional. Since the energetic properties presented in this study also required computation of ground state properties of the oxygen molecule, elemental solids and binary oxides, all the structural parameters for these molecules and solids are also optimized using the SCAN functional. In the case of oxygen molecule, force minimization is performed for computing the optimized bond length. On the other hand, lattice parameters of elemental solids, binary oxides and ternary oxides are computed using self-consistent calculation for a series of fixed volumes of their respective unit cells. Where necessary, the c0/a0 and b0/a0 ratios have also been optimized. The SCAN optimized unit cells of all the ABO3 compounds are subsequently used for computing the electronic and optical properties. For computing the mechanical properties, we have utilized the Elastic Constants for Cubic Cases (ELAS) program provided within the WIEN2k package.26 For the computation of the vibrational properties of the ABO3 compounds (using a 40-atom supercell), the frozen phonon approximation was employed using the phonopy code.28 For all the calculations involving phonons, a force convergence criteria of 0.01 mRy a.u.−1 was used. In order to eliminate numerical noise in our phonon calculations, the charge density grid has been enlarged by a factor of 2, while symmetrization of the force constants was also taken into account during post processing of the forces with the phonopy code.29![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m)
m)![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m)
m)![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m)
m)![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m)
m) from the total energy of ABO3
from the total energy of ABO3 according to the relation42
according to the relation42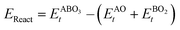
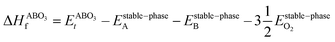
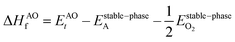

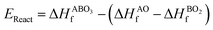
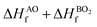 ), which indicates that the structure of the cubic perovskite oxides is energetically stable.49 Since experimental studies have shown the existence of BaTiO3 in the cubic phase,51,52 our calculated values of the enthalpies of the formation of BaTiO3, BaO and TiO2 clearly satisfy
), which indicates that the structure of the cubic perovskite oxides is energetically stable.49 Since experimental studies have shown the existence of BaTiO3 in the cubic phase,51,52 our calculated values of the enthalpies of the formation of BaTiO3, BaO and TiO2 clearly satisfy 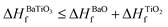 , showing that the SCAN meta-GGA functional has good agreement with experimental observations which have earlier been satisfied only through the use of the semi-empirically corrected GGA+U method.42
, showing that the SCAN meta-GGA functional has good agreement with experimental observations which have earlier been satisfied only through the use of the semi-empirically corrected GGA+U method.42

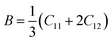
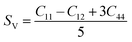
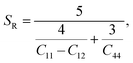
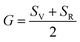
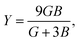



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 88
88