Epitaxial growth of perovskite oxide films facilitated by oxygen vacancies

Abstract

Single-crystal epitaxial films of technologically important and scientifically intriguing multifunctional ABO₃ perovskite-type metal oxides are essential for advanced applications and understanding of these materials. In such films, a film-substrate misfit strain enables unprecedented crystal phases and unique properties that are not available in their bulk counterparts. However, the prerequisite growth of strained epitaxial films is fundamentally restricted by misfit relaxation. Here we demonstrate that introduction of a small oxygen deficiency concurrently stabilizes epitaxy and increases lattice strain in thin films of archetypal perovskite oxide SrTiO₃. By combining experimental and theoretical methods, we found that lattice distortions around oxygen vacancies lead to anisotropic local stresses, which interact with the misfit strain in epitaxial films. Consequently, specific crystallographic alignments of the stresses are energetically favorable and can facilitate epitaxial growth of strained films. Because anisotropic oxygen-vacancy stresses are inherent to perovskite-type and many other oxides, we anticipate that the disclosed phenomenon of epitaxial stabilization by oxygen vacancies is relevant for a very broad range of functional oxides.

---

Introduction

Perovskite ABO₃-type metal oxides possess a variety of unique properties: they exhibit electronic behavior that can range from insulator to superconductor; they display ordering of charge, magnetic spins, and/or electric dipoles; and they demonstrate strong responses to external stimuli. This rich diversity of properties enables numerous emerging and commercial applications of perovskite oxides in different sectors of electronics, photonics, and related fields.^1,2

Single-crystal-type epitaxial films of perovskite oxides represent an essential part of modern research.^3–11 Beyond usage in advanced integrated devices and as high-quality crystals for basic investigations, epitaxial films bring a plethora of remarkable novel phenomena that stem from couplings between film with underlying substrate. Elastic coupling is especially important. In epitaxial films, elastic strain arises from the film-substrate mismatch in lattice symmetries, parameters, and/or thermal expansion coefficients. Epitaxial strained films can adopt unprecedented crystal phases and possess unique properties that are not available in their unstressed bulk counterparts.^12–18 Correspondingly, understanding and control of epitaxial growth of perovskite oxide films are vital for the exploration and applications of these materials.

The epitaxial growth of a film experiencing a substrate-imposed misfit strain is restricted by an elastic energy that increases with increasing film thickness.¹⁹ A film can grow in full coherency with the substrate to a certain critical thickness, at which strain relaxation starts. For many perovskite oxides, the critical thickness is a few tens of nanometers at a strain magnitude of about 1%, and smaller at larger strains. Most commonly, the strain relaxation involves the formation of dislocations and other structural imperfections that are detrimental for important functional responses. For instance, structural imperfections often cause unwanted optical or dielectric losses in wide-bandgap insulators or increased resistivity in conductors. The growth of coherent strained epitaxial films of sufficiently large thickness is highly desirable but fundamentally limited.

Here we demonstrate that introducing a small oxygen deficiency can stabilize epitaxy, significantly raise the critical thickness, and enlarge the lattice strain in perovskite oxide films. In this work we selected SrTiO₃(STO) as a representative, well studied perovskite oxide. We note that epitaxial STO films can be grown on commercial silicon substrates, which is of immense practical importance.^4,20 The substrate-induced biaxial in-plane misfit strain is compressive in thin STO films on Si, where the substrate-ensured in-plane lattice parameter is ∼3.840 Å. In this work, we use (001)(La_0.3Sr_0.7)(Al_0.65Ta_0.35)O₃ (LSAT) substrates to enable an in-plane lattice parameter of 3.868 Å and cube-on-cube epitaxial growth of in-plane compressed STO films, resembling those on Si.

By varying the pressure of oxygen during pulsed laser deposition, we found that even a minor oxygen deficiency can raise the critical thickness from ∼60 nm to at least 150 nm, whereas significantly reduce the optical losses in the STO/LSAT films. Our analysis of the measured lattice parameters of the strained films revealed strong and anisotropic chemical expansion in unstressed oxygen-deficient material within each film. Using first-principles calculations, we established that atomic displacements around oxygen vacancies produce strains leading to anisotropic stresses. We suggest that these stresses interact with the misfit strain field. The interaction enables a peculiar spatial arrangement of the stresses and a reduction of the total elastic energy. Such mechanism leads to an anisotropic chemical expansion, an increased critical thickness, and a large residual strain.

Anisotropic lattice distortions around oxygen vacancies are intrinsically inherent to all perovskite oxides. Therefore, we anticipate that the interaction of oxygen-vacancy stresses with substrate-induced strain fields is general for epitaxial perovskite oxide films. We also expect that, apart from stabilizing epitaxial growth, this interaction can lead to unusual functional behaviour. The results of our work can have broad implications in the field of technologically important and scientifically intriguing perovskite oxides.

Methods

Experimental

Thin STO films were grown by pulsed laser deposition using an excimer KrF laser (wavelength 248 nm, pulse duration 20 ns, repetition rate 5 Hz). A dense ceramic STO target was synthesized at the Institute of Solid State Physics, University of Latvia. The target-to-substrate distance was 35 mm, the area of the irradiated spot and energy density on the target surface were 3 mm² and 2 J cm⁻², respectively. Mechanical scanning included rotation, precession, and translation of the target and the substrate holder. Epitaxially polished (001) LSAT substrates were purchased from MTI Corp. A substrate temperature of 973 K was kept during deposition and lowered at a rate of 5 K min⁻¹ during post-deposition cooling. The oxygen pressure was kept constant during deposition and post-deposition cooling, and varied from 0.1 Pa to 20 Pa for different samples. The thickness of the films was regulated by number of laser pulses.

The crystal structure of the films was studied by high-resolution X-ray diffraction on a D8 DISCOVER diffractometer (Bruker corporation) using Cu Kα radiation. Θ–2Θ scans in the range of 2Θ = (10–130) deg and reciprocal space maps (RSM) in the vicinity of the perovskite (002) and (303) diffractions were acquired. The in-plane (parallel to substrate surface) and out-of-plane (normal to substrate surface) lattice parameters were estimated from the positions of the diffraction maxima using LSAT as a reference. The thickness of the films was determined by X-ray reflectometry on the diffractometer. The diffraction and reflectometry data were fitted using LEPTOS software.

The chemical composition of the films was characterized by X-ray photoelectron spectroscopy (XPS) using a NanoESCA instrument (Oxford Instruments Omicron Nanoscience) and CasaXPS software and by energy dispersive X-ray spectroscopy on a FEI QUANTA scanning electron microscope (ThermoFisher).

The optical properties and thicknesses of the films were inspected using variable angle spectroscopic ellipsometry (VASE). The measurements were performed on a J. A. Woollam VUV ellipsometer at room temperature, in dry nitrogen atmosphere, and at photon energies of (0.75–8.8) eV. The data were processed using a commercial WVASE32 software package.

First-principles analysis

The first-principles (ab initio) computations were performed using the CRYSTAL17 computer code within the linear combination of atomic orbitals (LCAO) approximation.²¹ The B1WC advanced hybrid exchange–correlation functional of the density-functional-theory (DFT) was employed. More computational details can be found in our previous papers on simulations of (Ba,Sr)TO₃ and (Ba,Ca)TiO₃ solid solutions,^22–24 as well as BTO/STO heterostructures.^23,25 Note that in the studies ref. 23 and 24 we used and compared three hybrid functionals (PBE0, B1WC and B3LYP) for the perovskite systems simulations and established that B1WC functional demonstrated the most reliable results.

The neutral and charged oxygen vacancies were treated as point defects whose introduction into cubic STO (space group SG 221) lowers its symmetry. The tetragonal phase (SG 99) was considered for the systems with defects. For the neutral oxygen vacancies, we took into account various possible spin states of the system and applied unrestricted (open shell) method of calculations.²¹ More detailed description of the neutral oxygen vacancies computations is presented in our paper,²⁶ where the local structure, as well as charge and spin distribution near these vacancies are considered in tetragonal BTO (SG 99) and STO (SG 140) systems. For the charged vacancies, we employed the ionic basis sets and restricted (closed shell) calculations. The defect charge was compensated by homogeneously distributed counter-charge in the supercell.

The 2 × 2 × 2 and 3 × 3 × 3 supercells (SC) with periodic boundary conditions were adopted to simulate different concentrations of defects. The concentrations of oxygen vacancies (relative to the stoichiometric number of oxygen atoms) were 4.17% (SC 2 × 2 × 2) and 1.23% (SC 3 × 3 × 3).

Results and discussion

Epitaxial films

The theoretical STO/LSAT biaxial in-plane misfit strain s_a is compressive (s_a = a_SUB/a₀ − 1) ≈ −0.95%. Here a_SUB = 3.868 Å and a₀ = 3.905 Å are the lattice parameters of LSAT and unstressed STO, respectively. For a cube-on-cube-type epitaxial coherent strained STO film, the in-plane lattice parameters are similar and equal to (a = b = a_SUB). The out-of-plane strain (s_c), the out-of-plane lattice parameter (c), the unit-cell volume (V), and the tetragonality (t = c/a) of the strained film are elastically related to the in-plane strain [S1 and expressions (1–6), ESI†]. Thus, for the coherent STO/LSAT film, the theoretically expected parameters are a = 3.868 Å and c = 3.927 Å. As found before,²⁷ such tetragonal fully strained STO/LSAT films can grow to thickness of ∼60 nm, above which the misfit relaxation occurs.

Here, perovskite STO/LSAT films with thicknesses of 150 nm and 80 nm were grown by pulsed laser deposition (PLD) at different oxygen pressures. We note that parameters of laser radiation (wavelength, pulse duration, pulse repetition rate) and irradiation conditions (such as size and symmetry of irradiated spot on the target surface, energy density in this spot, and target-to-substrate distance), together with the nature and pressure of gas ambience, determine the dynamics of laser-stimulated plasma and, consequently, the deposition kinetics and metal stoichiometry in PLD of multicomponent materials.^28–32 Here, the deposition rate was practically pressure-independent, implying pressure-independent growth kinetics and, hence, pressure-independent metal composition in the films [S2 and Fig. S2, ESI†]. The direct assessment of composition did not reveal observable changes of the Sr : Ti ratio with oxygen pressure either.

Cube-on-cube-type epitaxial STO films were obtained at all pressures [Fig. 1 and Fig. S3–S5, ESI†]. In agreement with the previous study,²⁷ we observe strain relaxation in the 150 nm-thick film deposited at 20 Pa [Fig. 1(a)]: the film contains a strained fraction and a relaxed fraction. The lattice parameters of the strained tetragonal fraction are close to theoretical estimates, whereas the relaxed fraction is cubic and similar to unstressed STO. We note that such a relaxed fraction is not seen in a thinner film deposited at the same pressure: the 80 nm-thick film is strained tetragonal [Fig. S6, ESI†]. Remarkably, with decreasing oxygen pressure, only coherent growth is detected in the 150 nm-thick films [Fig. 1(b)–(f)]. The critical thickness for misfit relaxation is then at least 150 nm.

Fig. 1 Epitaxy. Reciprocal space maps around (303) lattice points in the 150 nm-thick STO/LSAT films deposited at different pressures of oxygen. Coordinates are expressed in reciprocal lattice units of LSAT.

We underline that strain relaxation has negative implications on the optical transparency of the STO films for wavelengths of 400–1500 nm. The extinction coefficient in the relaxed 150 nm-thick film deposited at 20 Pa is significantly higher than that in the coherent 80 nm-thick film deposited at the same pressure [Fig. S7(a), ESI†]. Importantly, the extinction coefficient in the strained 150 nm-thick film deposited at a lower pressure (10 Pa) is as small as that in the in the coherent 80 nm-thick film deposited at 20 Pa [Fig. S7(b), ESI†]. These observations imply that structural imperfections are critical for optical losses and should be avoided in thin films for photonic applications. To achieve epitaxial oxide photonic films of sufficiently large thickness, introducing oxygen deficiency may be a counterintuitive solution.

To get better insight into the perfect epitaxy of oxygen deficient films, we compared the lattice parameters, tetragonality, and unit-cell volume of the 150 nm films with the theoretical values, which were estimated using elastic considerations [S1 and expressions (1–6), ESI†]. The out-of-plane lattice parameter c is very close to theoretical in the strained fraction of the film deposited at 20 Pa [Fig. 2(a)]; the unit-cell volume and tetragonality of this fraction are also close to theoretical estimations [Fig. 2(b) and (c)]. For the films deposited at lowered pressures (oxygen deficient films), the in-plane parameters coincide with those of the substrate a = b ≈ 3.868 Å, but the out-of-plane parameter clearly exceeds that estimated for the coherent strained STO/LSAT film [Fig. 2(a)]. Moreover, both the unit-cell volume and tetragonality increase concurrently with decreasing pressure and are noticeably larger than the theoretical values [Fig. 2(b) and (c)]. This behavior is schematically illustrated in Fig. 2(d).

Fig. 2 Crystal lattice. (a) Out-of-plane lattice parameter, (b) unit-cell volume, and (c) tetragonality as a function of pressure in the 150 nm-thick films. (d) Schematics of unit cells in the STO crystal and STO/LSAT films.

The increased parameters c, V, and t can be related to a chemical expansion of the unstressed oxygen deficient material of the films. First, we considered a commonly accepted isotropic chemical expansion, i.e. an increase of the parameter a₀ of the cubic cell (tetragonality t₀ = 1) of the material [schematics in Fig. 3(a)]. Using the measured lattice parameters of the 150 nm-thick films and elastic relationships [Fig. S1 expressions (1–6), ESI†], we extracted the lattice parameter a₀, the unit-cell volume V₀, and the film-substrate misfit strain s_a as a function of oxygen pressure for such an isotropically expanded material.

Fig. 3 Chemical expansion. (a and e) Schematics of (a) isotropically and (e) anisotropically expanded unit cells of unstressed material of the films and the corresponding (b and f) unit-cell volume, (c and g) tetragonality, and (d and h) in-plane strain for such cells as a function of pressure.

The unit-cell volume V₀ as large as 60.6 ų is extracted for low pressures [Fig. 3(b)]. This large volume suggests a gigantic chemical expansion of 1.8% (volumetric, or 0.6% linear). Such a massive expansion has never been reported for bulk STO, nor for other perovskite oxides. Assuming, nevertheless, that cationic or oxygen off-stoichiometry could cause this expansion, we deduced off-stoichiometry using the theoretical chemical expansion coefficients for cationic or oxygen vacancies in STO (see ref. 33 and references therein). The volumetric chemical expansion of 1.8% corresponds to either a deficit or excess of Sr, with the Sr/Ti ratio of 0.8 or 1.05, respectively; or to an oxygen deficit of x = 6 in SrTiO_3−x. These cationic off-stoichiometries are unrealistic for the stability of the perovskite phase and the oxygen deficit is nonsensical. Especially important here, the extracted magnitude of the in-plane material-substrate compressive strain increases with decreasing pressure and reaches 1.5% [Fig. 3(d)]. This increase is in striking conflict with the observed better stabilization of epitaxy at lower pressures. Regarding an assumed isotropic chemical expansion, the critical thickness should have become smaller, and, hence, more efficient strain relaxation should have occurred at lower pressures. Therefore, an isotropic chemical expansion is improbable here.

Next, we assumed that the chemical expansion is anisotropic such that the material is tetragonal, whereas its unit-cell volume remains equal to that of unstressed STO [Fig. 3(e) and (f)]. Again, using the elastic relationships [S5 and expressions (7–12), ESI†] and the measured lattice parameters of the films, we extracted the tetragonality of the material [Fig. 3(g)] and the magnitude of the in-plane compressive misfit strain [Fig. 3(h)]. In contrast to the isotropic expansion, the assumed anisotropic expansion gives a significant decrease of the misfit-strain magnitude [compare Fig. 3(d) and (h)]. This decrease is in excellent agreement with the coherent epitaxial growth at lowered pressures.

Thus, anisotropic, out-of-plane directed, chemical expansion can explain the stabilization of coherent epitaxial growth of compressively strained oxygen deficient STO films. The lattice parameters of the anisotropically expanded material differ from that of bulk unstressed STO [Fig. S8, ESI†]: the in-plane parameters shrink (a₀ < a_STO) and the out-of-plane parameter increases (c₀ > a_STO). To find a physical mechanism, leading to such an anisotropic expansion, we applied first-principles analyses to scrutinize the local lattice distortions around oxygen vacancies in STO.

Oxygen vacancies

We note that the previous first-principles analyses of oxygen vacancies in STO were performed using several different approaches (see ref. 34–36 and references therein). Most of these studies focused on the electronic structure of neutral vacancies as important shallow donors, whereas less attention was paid to the charged vacancies (see, e.g.ref. 37 and 38). Also calculations of the local distortions and charge redistribution around both types of vacancies are rare. Here, the neutral and charged vacancies were analyzed within the same approach (DFT hybrid functional B1WC, see Methods section), which ensured high accuracy and allowed for reliable quantitative comparison of both types of vacancies. Note that depending on such conditions as temperature, presence of dopants, and position of the Fermi level, one or another type of vacancies is thermodynamically more stable.³⁹

When an oxygen atom is removed from STO and a neutral vacancy is formed, each of the two nearest Ti atoms receives one unpaired electron, whose possible spin states were taken into account. The systems with different spin states (S = 0 and S = 1) were considered. In contrast, removal of an oxygen anion produces the doubly charged oxygen vacancy, around which all chemical bonds remain closed. The distances between ions and the effective charges of ions were calculated both for the neutral and charged vacancies as well as for the reference stoichiometric STO. The supercells of 2 × 2 × 2 unit cells (SC 2) and of 3 × 3 × 3 unit cells (SC 3) containing 40 and 135 atoms, correspondingly, were employed. The calculated elastic properties demonstrated high accuracy when compared to experiment [S7, ESI†].

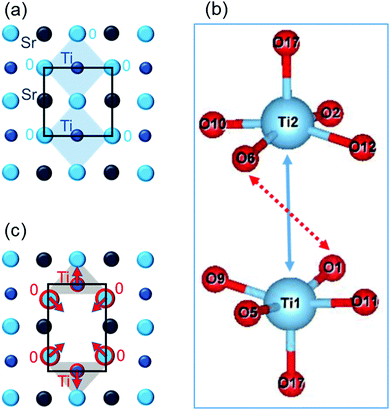
Compared to the high-symmetry TiO₆-octahedra in stoichiometric cubic STO [Fig. 4(a)], local anisotropic lattice distortions arise around an oxygen vacancy V_O [Fig. 4(b) and (c)]. The neighboring Ti ions (Ti–V_O–Ti) are displaced away from the vacancy, whereas the closest O ions are shifted towards the vacancy. The calculated Ti–Ti distance [Ti–V_O–Ti between Ti1 and Ti2 as shown by solid arrow in Fig. 4(b)] and the distances between “corner” O ions [O–V_O–O between O1 and O6 as shown by the dashed arrow in Fig. 4(b), and alike O2–O5, O9–O12, and O10–O11] are summarized in Table 1.

Fig. 4 Oxygen vacancy. Schematics of ionic positions in (a) regular STO and (b and c) around an oxygen vacancy in STO. In (c), the arrows mark directions of ionic displacements around vacancy compared to regular STO.

Table 1 Distances between ions and effective charges of ions for stoichiometric STO and around oxygen vacancies (V_O) in STO

	STO	VO
		Neutral		Charged
		S = 0	S = 1	SC 2	SC 3
Distance (Å)
Ti1–Ti2	3.884	4.139	4.136	4.032	4.116
O1–O6; O2–O5; O9–O12; O10–O11	5.493	5.149	5.262	5.082	5.069
Effective charge (e)
Ti	+2.32	+2.23	+2.13	+2.25	+2.25
O17	−1.40	−1.32	−1.34	−1.29	−1.32
O (except O17)	−1.40	−1.42	−1.45	−1.37	−1.41

---

Compared to stoichiometric STO, introducing an oxygen vacancy leads to a significant increase (4–6.5%) of the Ti–Ti distance and a simultaneous decrease (4–7.5%) of the distances between oxygen ions. These changes persist in all cases, although the distances are sensitive to the vacancy type, spin state, and supercell dimensions. Overall, the lattice strongly expands along the Ti–V_O direction [Fig. 4(c)].

The lattice distortions around oxygen vacancy are responsible for local stresses, which are commonly described using a second rank tensor, or elastic dipole tensor. A strongly anisotropic elastic dipole tensor is produced by oxygen vacancy.³³ Note that cationic vacancies are unable to give such strongly anisotropic elastic dipoles.³³ In bulk unstressed STO, the presence of anisotropic oxygen vacancy stresses does not lead to a macroscopic anisotropic chemical expansion because different crystallographic orientations of elastic dipole tensors are energetically similar, randomly distributed, and averaged. However, in epitaxial films, the presence of substrate and substrate-imposed strain can determine peculiar spatial arrangement of the stresses, or of the oxygen-vacancy elastic dipole tensors.

In cube-on-cube epitaxial STO films, oxygen vacancies can be located in the [SrO]-planes parallel to the substrate surface, i.e. in the (001)[SrO] plane, as illustrated in Fig. 5(a). The lattice is then locally out-of-plane elongated (in-plane contracted) and the elastic dipole tensor is out-of-plane oriented. For oxygen vacancies in the [TiO]-plane parallel to the substrate surface, i.e. in the (001)[TiO] planes, the lattice is locally out-of-plane contracted (in-plane elongated) and the elastic dipole tensor is in-plane oriented [schematics in Fig. 5(b)].

Fig. 5 Oxygen-vacancy stresses in epitaxial film. Schematics of different orientations of the elastic dipole tensors for oxygen vacancies in the (a) (001)[SrO]-plane and (b) (001)[TiO]-plane.

The local stresses interact with the strain field that is produced by the film-substrate misfit (in-plane biaxial strain s_a and out-of-plane strain s_c). For the out-of-plane and in-plane components of the dipole tensor λ_c and λ_a, respectively, the interaction energy E_int can be estimated as [E_int = −(λ_cs_c + 2λ_as_a)].⁴⁰ For the compressive in-plane misfit strain s_a < 0 (s_c > 0), the interaction energy is negative if λ_c > 0 and λ_a < 0. This condition corresponds to a vacancy position in the (001)[SrO] plane, with the out-of-plane orientation of the oxygen-vacancy stress tensor [Fig. 5(a)]. The interaction energy turns positive for s_a < 0 (s_c > 0), when λ_c < 0 and λ_a > 0, i.e. if the vacancy is located in the (001)[TiO] plane [Fig. 5(b)]. Therefore, the in-plane compressive misfit strain favors the location of oxygen vacancies in the (001)[SrO] planes and not in the (001)[TiO] planes. This selective vacancy location is qualitatively comprehensible because the in-plane Ti–V_O–Ti elongations “work” against the in-plane misfit compression, which is energetically unfavorable. The strain-defined selective location and correspondingly, the alignment of the local lattice Ti–V_O–Ti elongations produces anisotropic chemical expansion of the film.

We note that the selective location of defects and anisotropic expansion are caused by interaction of anisotropic stresses of these defects with misfit strain. Because such elastic interaction is general, then any defect possessing anisotropic elastic dipole tensor can principally contribute to epitaxial stabilization. For instance, our first-principles calculations showed that the STO/LSAT strain can lead to the formation energy for vacancy in the (001)[TiO] plane being smaller than in the (001)[SrO] plane by 0.6–1.4 eV depending on the spin state of the system. If this difference dominates and vacancies are preferably formed in the (001)[TiO] planes, then anisotropic elastic dipole tensor may be produced by displacements of Sr ions arising due to local distortions around oxygen vacancy. More detailed theoretical analyses of this and other scenarios are in progress.

For the theoretical oxygen-vacancy elastic dipole tensor³³ and STO/LSAT misfit strain, each vacancy in the (001)[SrO] plane reduces the total energy by ∼65 meV, whereas each vacancy in the (001)[TiO] plane raises the energy by ∼35 meV [S8 and expressions (13 and 14), ESI†]. Assuming that non-interacting oxygen vacancies in the (001)[SrO] planes fully compensate elastic energy, which is associated with the STO/LSAT misfit strain, the maximum concentration of such vacancies can be ∼1 at % only [S8 expressions (15 and 16), ESI†]. Considering the measured in-plane strain in oxygen deficient films [Fig. 3(h)], the concentration of oxygen vacancies may be even smaller than 1 at % therein. Such small concentrations are impossible to measure directly using state-of-the-art techniques. Thus, even a minor concentration of oxygen vacancies can significantly increase the critical thickness in strained epitaxial films.

Remarkably, the presence of vacancies enhances the total lattice strain. The out-of-plane lattice strain is enlarged to 1.5% in oxygen deficient films compared to the purely substrate-induced strain of 0.5% [Fig. 2(a) and Fig. S8, ESI†]. This enhancement can be understood as a result of interactions between the aligned stresses and the rest of the material.

We expect that multiscale theoretical modelling can establish precise mechanisms for epitaxial stabilization and strain enhancement in oxygen deficient films. However, qualitatively, the driving force for the formation of oxygen-vacancy stresses is an increased Coulomb repulsion between the B-site cations in the presence of an oxygen vacancy between them, which is thus valid for all ABO₃ perovskites. In cube-on-cube-type epitaxial films with a compressive misfit strain, the elastic dipole tensors will align along the out-of-plane direction, whereas for a tensile misfit strain, there are two in-plane invariants for the orientation. The effect can be sensitive to the type of cations and may be stronger for compressed films. In any case, the aligned oxygen-vacancy stresses can stabilize epitaxy, enhance lattice strain, and thus enable perovskite oxide films with novel properties. Moreover, because anisotropic elastic dipole tensors may be associated with oxygen vacancies in many other metal oxides,^41–44 we anticipate a broad ubiquity of the phenomenon disclosed here. We also anticipate that oxygen-vacancy stabilized films can demonstrate new advanced properties and further expand usage of oxygen vacancies in oxide electronics and photocatalysis.^45,46 The results of our work can have wide implications in the field of technologically important perovskite-structure and other oxides.

Conclusions

In conclusion, combining the experimental and theoretical approaches, we demonstrated that local stresses, which are produced by anisotropic lattice distortions around oxygen vacancies in an archetypal perovskite oxide, SrTiO₃, interact with substrate-induced misfit strain in epitaxial films. The interaction results in a peculiar spatial alignment of the vacancy stresses, enables anisotropic chemical expansion, facilitates epitaxy, and enhances lattice strain. Because anisotropic oxygen-vacancy stresses are inherent to perovskite-type and many other oxides, the revealed phenomenon of epitaxial stabilization by oxygen vacancies is of high importance for a very broad range of functional oxides.

Author contributions

M. T. conceived the project, planned and organized experiments, analyzed the data, and drafted the manuscript. L. R. and E. K. performed the first-principles calculations and analysis. M. T. and L. R. finalized the manuscript. O. P. carried out X-ray diffraction studies and T. K. grew the films. M. T. and A. D. supervised technical work at the Institute of Physics.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank P. Yudin for valuable discussions, N. Nepomniashchaia for VASE studies, and S. Cichon for XPS analysis. The authors acknowledge support from the Czech Science Foundation (Grant No. 19-09671S), the European Structural and Investment Funds and the Ministry of Education, Youth and Sports of the Czech Republic through Programme “Research, Development and Education” (Project No. SOLID21 CZ.02.1.01/0.0/0.0/16-019/0000760), and ERA NET project Sun2Chem (E. K. and L. R.). Calculations have been done on the LASC Cluster in the ISSP UL.

References

1. M. Lorenz, M. S. Ramachandra Rao, T. Venkatesan, E. Fortunato, P. Barquinha, R. Branquinho, D. Salgueiro, R. Martins, E. Carlos, A. Liu, F. K. Shan, M. Grundmann, H. Boschker, J. Mukherjee, M. Priyadarshini, N. DasGupta, D. J. Rogers, F. H. Teherani, E. V. Sandana, P. Bove, K. Rietwyk, A. Zaban, A. Veziridis, A. Weidenkaff, M. Muralidhar, M. Murakami, S. Abel, J. Fompeyrine, J. Zuniga-Perez, R. Ramesh, N. A. Spaldin, S. Ostanin, V. Borisov, I. Mertig, V. Lazenka, G. Srinivasan, W. Prellier, M. Uchida, M. Kawasaki, R. Pentcheva, P. Gegenwart, F. Miletto Granozio, J. Fontcuberta and N. Pryds, J. Phys. D: Appl. Phys., 2016, 49, 433001.
2. M. Coll, J. Fontcuberta, M. Althammer, M. Bibes, H. Boschker, A. Calleja, G. Cheng, M. Cuoco, R. Dittmann, B. Dkhil, I. El Baggari, M. Fanciulli, I. Fina, E. Fortunato, C. Frontera, S. Fujita, V. Garcia, S. T. B. Goennenwein, C.-G. Granqvist, J. Grollier, R. Gross, A. Hagfeldt, G. Herranz, K. Hono, E. Houwman, M. Huijben, A. Kalaboukhov, D. J. Keeble, G. Koster, L. F. Kourkoutis, J. Levy, M. Lira-Cantua, J. L. MacManus-Driscoll, J. Mannhart, R. Martins, S. Menzel, T. Mikolajick, M. Napari, M. D. Nguyen, G. Niklasson, C. Paillard, S. Panigrahi, G. Rijnders, F. Sánchez, P. Sanchis, S. Sanna, D. G. Schlom, U. Schroeder, K. M. Shen, A. Siemon, M. Spreitzer, H. Sukegawa, R. Tamayo, J. van den Brink, N. Pryds and F. Miletto Granozio, Appl. Surf. Sci., 2019, 482, 1–93.
3. H. Wei, C. Yang, Y. Wu, B. Cao, M. Lorenz and M. Grundmann, J. Mater. Chem. C, 2020, 8, 15575–15596.
4. M. Spreitzer, D. Klement, R. Egoavil, J. Verbeeck, J. Kovac, A. Zaloznik, G. Koster, G. Van Tendeloo, D. Suvorov and G. Rijnders, J. Mater. Chem. C, 2020, 8, 518–527.
5. D. H. Kim, S. Ning and C. A. Ross, J. Mater. Chem. C, 2019, 7, 9128–9148.
6. P.-C. Wua and Y.-H. Chu, J. Mater. Chem. C, 2018, 6, 6102–6117.
7. X. Cao, Z. Liu, L. R. Dedon, A. J. Bell, F. Esat, Y. Wang, P. Yu, C. Wang and P. Jin, J. Mater. Chem. C, 2017, 5, 7720–7725.
8. J. M. Vila-Fungueiriño, B. Rivas-Murias, J. Rubio-Zuazo, A. Carretero-Genevrier, M. Lazzari and F. Rivadulla, J. Mater. Chem. C, 2018, 6, 3834–3844.
9. L. W. Martin, Y.-H. Chu and R. Ramesh, Mater. Sci. Eng., R, 2010, 68, 89–133.
10. Epitaxial Growth of Complex Metal Oxides, ed. G. Koster, M. Huijben, G. Rijnders, Elsevier, 2015.
11. J. L. MacManus-Driscoll, M. P. Wells, C. Yun, J.-W. Lee, C.-B. Eom and D. G. Schlom, APL Mater., 2020, 8, 040904.
12. N. A. Pertsev, A. G. Zembilgotov and A. K. Tagantsev, Phys. Rev. Lett., 1998, 80, 1988.
13. D. G. Schlom, L.-Q. Chen, C.-B. Eom, K. M. Rabe, S. K. Streiffer and J.-M. Triscone, Annu. Rev. Mater. Res., 2007, 37, 589–626.
14. J. Li, Z. Shan and E. Ma, MRS Bull., 2014, 39, 108–114.
15. B. Yildiz, MRS Bull., 2014, 39, 147–156.
16. D. G. Schlom, L.-Q. Chen, C. J. Fennie, V. Gopalan, D. A. Muller, X. Pan, R. Ramesh and R. Uecker, MRS Bull., 2014, 39, 118–130.
17. J. Hwang, Z. Feng, N. Charles, X. R. Wang, D. Lee, K. A. Stoerzinger, S. Muy, R. R. Rao, D. Lee, R. Jacobs, D. Morgan and Y. Shao-Horn, Mater. Today, 2019, 31, 100–118.
18. R. Ramesh and D. G. Schlom, Nat. Rev. Mater., 2019, 4, 257–268.
19. M. Ohring, Materials Science of Thin Films, Academic Press, San Diego, 2nd edn, 2002.
20. A. McKee, F. J. Walker and M. F. Chisholm, Phys. Rev. Lett., 1998, 81, 3014.
21. R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D’Arco, M. Llunell, M. Causà, Y. Noël, L. Maschio, A. Erba, M. Rerat and S. Casassa, CRYSTAL17 User's Manual, University of Torino, Torino, 2017.
22. L. L. Rusevich, G. Zvejnieks, A. Erba, R. Dovesi and E. A. Kotomin, J. Phys. Chem. A, 2017, 121, 9409–9414.
23. L. L. Rusevich, G. Zvejnieks, E. A. Kotomin, M. Maček Kržmanc, A. Meden, Š. Kunej and I. D. Vlaicu, J. Phys. Chem. C, 2019, 123, 2031–2036.
24. L. L. Rusevich, G. Zvejnieks and E. A. Kotomin, Solid State Ionics, 2019, 337, 76–81.
25. G. Zvejnieks, L. L. Rusevich, D. Gryaznov and E. A. Kotomin, Phys. Chem. Chem. Phys., 2019, 21, 23541–23551.
26. L. L. Rusevich, E. A. Kotomin, G. Zvejnieks and A. I. Popov, Low Temp. Phys., 2020, 46, 1185–1195.
27. T. Yamada, B. Wylie-van Eerd, O. Sakata, A. K. Tagantsev, H. Morioka, Y. Ehara, S. Yasui, H. Funakubo, T. Nagasaki and H. J. Trodahl, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 214101.
28. M. Tyunina, J. Wittborn, C. Björmander and K. V. Rao, J. Vac. Sci. Technol., A, 1998, 16, 2381.
29. M. Tyunina, J. Levoska and S. Leppävuori, J. Appl. Phys., 1998, 83, 5489.
30. M. Tyunina, K. Sreenivas, C. Bjormander, J. Wittborn and K. V. Rao, J. Appl. Surf. Sci., 1996, 96, 831.
31. M. Tyunina, J. Levoska and S. Leppävuori, J. Appl. Phys., 1999, 86, 2901.
32. M. Tyunina and S. Leppävuori, J. Appl. Phys., 2000, 87, 8142.
33. D. A. Freedman, D. Roundy and T. A. Arias, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 064108.
34. Yu. F. Zhukovskii, E. A. Kotomin, R. A. Evarestov and D. E. Ellis, Int. J. Quantum Chem., 2007, 107, 2956–2985.
35. J. Carrasco, F. Illas, N. Lopez, E. A. Kotomin, Yu. F. Zhukovskii, R. A. Evarestov, Yu. A. Mastrikov, S. Piskunov and J. Maier, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 064106.
36. R. Evarestov, E. Blokhin, D. Gryaznov, E. A. Kotomin, R. Merkle and J. Maier, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 174303.
37. C. Ricca, I. Timrov, M. Cococcioni, N. Marzari and U. Aschauer, Phys. Rev. Res., 2020, 2, 023313.
38. A. Janotti, J. B. Varley, M. Choi and Ch. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 085202.
39. C. Mitra, C. Lin, J. Robertson and A. A. Demkov, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 155105.
40. E. Clouet, C. Varvenne and T. Jourdan, Comput. Mater. Sci., 2018, 147, 49–63.
41. A. Janotti, J. B. Varley, P. Rinke, N. Umezawa, G. Kresse and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085212.
42. A. Janotti and C. G. Van de Walle, Appl. Phys. Lett., 2005, 87, 122102.
43. D. Gryaznov, E. Blokhin, A. Sorokine, E. A. Kotomin, R. A. Evarestov, A. Bussmann-Holder and J. Maier, J. Phys. Chem. C, 2013, 117, 13776–13784.
44. I. Chatratin, F. P. Sabino, P. Reunchan, S. Limpijumnong, J. B. Varley, C. G. Van de Walle and A. Janotti, Phys. Rev. Mater., 2019, 3, 074604.
45. F. Gunkel, D. V. Christensen, Y. Z. Chen and N. Pryds, Appl. Phys. Lett., 2020, 116, 120505.
46. H. Tan, Z. Zhao, W. Zhu, E. N. Coker, B. Li, M. Zheng, W. Yu, H. Fan and Z. Sun, ACS Appl. Mater. Interfaces, 2014, 6, 19184–19190.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0tc05750a

---