Open Access Article
Open Access ArticleTransformation of Co3O4 nanoparticles to CoO monitored by in situ TEM and predicted ferromagnetism at the Co3O4/CoO interface from first principles†
Xiaodan
Chen‡
 a,
Heleen
van Gog‡
a,
Heleen
van Gog‡
 *b and
Marijn A.
van Huis
*b and
Marijn A.
van Huis
 *a
*a
aSoft Condensed Matter, Debye Institute for Nanomaterials Science, Utrecht University, Princetonplein 5, 3584 CC Utrecht, The Netherlands. E-mail: m.a.vanhuis@uu.nl
bEngineering Thermodynamics, Process & Energy Department, Faculty of Mechanical, Maritime and Materials Engineering, Delft University of Technology, Leeghwaterstraat 39, 2628 CB Delft, The Netherlands. E-mail: h.vangog@tudelft.nl
First published on 27th March 2021
Abstract
Nanoparticles of Co3O4 and CoO are of paramount importance because of their chemical properties propelling their applications in catalysis and battery materials, and because of their intriguing magnetic properties. Here we elucidate the transformation of Co3O4 nanoparticles to CoO into nanoscale detail by in situ heating in the transmission electron microscope (TEM), and we decipher the energetics and magnetic properties of the Co3O4/CoO interface from first principles calculations. The transformation was found to start at a temperature of 350 °C, and full conversion of all particles was achieved after heating to 400 °C for 10 minutes. The transformation progressed from the surface to the center of the nanoparticles under the formation of dislocations, while the two phases maintained a cube-on-cube orientation relationship. Various possibilities for magnetic ordering were considered in the density functional theory (DFT) calculations and a favorable Co3O4/CoO {100}/{100} interface energy of 0.38 J m−2 is predicted for the lowest-energy ordering. Remarkably, the DFT calculations revealed a substantial net ferromagnetic moment originating from the interface between the two antiferromagnetic compounds, amounting to approximately 13.9 μB nm−2. The transformation was reproduced ex situ when heating at a temperature of 400 °C in a high vacuum chamber.
1. Introduction
Co3O4 nanocrystals are materials of great importance to many applications. Cobalt oxide nanoparticles and their reduced derivatives are used as catalysts in the well-known Fischer–Tropsch process for the production of hydrocarbon fuels, but are also considered as catalysts for water splitting.1–4 Furthermore, cobalt oxide is one of the most frequently used materials in Li-ion batteries5,6 powering cell phones and other electronic equipment, and is used in gas sensors as well.7 Understanding the reduction process and its mechanism at the nanoscale is essential for controlling the nanoparticle properties in these applications. The reduction of Co3O4 under different chemical and physical conditions has been extensively investigated, as will be discussed in more detail below. A two-stage reduction process has been reported by many researchers,8–10 where spinel Co3O4 first transforms to rock salt CoO and subsequently to elemental Co,| Co3O4 → CoO → Co. | (1) |
Elemental Co adopts the hexagonal close packed (hcp) crystal structure in the bulk phase, but adopts the face centered cubic (fcc) structure with a lattice parameter of 0.354 nm when the particle size is less than 30 nm.11 The crystal structures of Co3O4 and CoO are both cubic and the lattice parameter of Co3O4 is approximately twice as large as the lattice parameter of CoO.
Fig. 1 shows their schematic structure. Co3O4 has the spinel crystal structure. Cobalt atoms are in the interstices of the distorted fcc lattice of oxygen atoms. Co2+ cations occupy tetrahedral interstitial sites and Co3+ cations occupy octahedral interstitial sites. In contrast, CoO has a rock salt structure with Co2+ cations on one of the interpenetrating fcc sublattices and O2− anions on the other fcc sublattice.
The thermal stability of the Co–O system has been investigated in several ways. The thermodynamic properties of both solid and liquid phases of the Co–O system were calculated by Chen et al.12 In a study employing interatomic potentials obtained by machine learning, Kong et al. showed that only CoO and Co3O4 are stable compositions in the Co–O system and that the transition between cubic CoO and Co3O4 is reversible.13 Navrotsky et al. calculated phase diagrams for both the bulk Co–O system and the nanoscale Co–O system, and showed that the range where the CoO phase is stable (in terms of partial oxygen pressure and temperature) is considerably narrower for 10 nm sized nanoparticles in comparison with the CoO range of stability in the bulk phase diagram.14
The reduction processes have been investigated experimentally under a H2 atmosphere4,8,10,15,16 and under plasma exposure.17 Ward et al. observed the reduction using environmental transmission electron microscopy (ETEM) under low hydrogen pressures, and found that Co3O4 nanoparticles reduced to CoO predominantly at a temperature of 350 °C and at a hydrogen pressure of 0.1 mbar (10 Pa), while the formation of pure Co was only observed upon further heating at 450 °C at a higher hydrogen pressure of 0.3 mbar (30 Pa).18 Bulavchenko et al. investigated the transformation at standard pressure (1.0 × 105 Pa) using X-ray diffraction (XRD) and reported the two-stage process, but in addition they also reported a one-step process where the Co3O4 particles could be reduced directly to metallic Co, without intermediate formation of CoO, when the samples were exposed to pure H2.9 The standard enthalpy of reduction of Co3O4 to CoO was reviewed and investigated experimentally by Mayer et al.19 A detailed high-resolution study of the nanoscale structural transformation during heating under vacuum conditions in the absence of any reducing agents has not yet been performed, though. The rapidly developing in situ transmission electron microscopy (TEM) technique now enables the direct observation of phase transformations at atomic resolution,20 which greatly benefits a detailed investigation of the reduction process.
The Co3O4 and CoO phases have also been extensively studied because of their interesting electronic and magnetic structures, which have been the subject of a lively debate in the literature.21–25 The rock salt CoO phase undergoes a Jahn–Teller distortion at low temperature, rendering it a monoclinic phase that is still pseudo-rock-salt type.23 The magnetic ground state is antiferromagnetic (AFM), where spins of equal sign are arranged in the cubic (111) planes of Co atoms, and the spin-up/spin-down alternation is along the [111] stacking direction of these Co atomic planes. This AFM type is referred to as AFM2.22 The magnetic moment of the Co2+ atoms is approximately 3 μB21,22 and the Néel temperature is TN = 287 K.21,26 The material is a semiconductor both below and above that temperature; reported values for the band gap are about 2.5–2.7 eV.23,27
In the spinel-type Co3O4 phase the trivalent Co3+ ions are nonmagnetic while the Co2+ ions carry a magnetic moment. At low temperature the Co3O4 phase is antiferromagnetic (AFM) with the Co2+ ions following conventional AFM ordering with alternating magnetic moments along the cubic axes (AFM1 ordering). The experimentally determined magnetic moment of the Co2+ ions is 3.26 μB and the Néel temperature is TN = 40 K.24 Co3O4 is a semiconductor, with reported values for the band gap varying from 0.74 eV (ref. 25) to 1.5–2.5 eV.24,28
The electronic and magnetic properties of CoO and Co3O4 nanoscale particles can differ dramatically from the properties discussed above for CoO and Co3O4 bulk compounds. That the Néel temperature of both bulk compounds is below room temperature while our experiments are performed at room temperature, does not necessarily imply that the nanoparticles under investigation in the present study will not be magnetic. In general, due to finite size effects, and surface and interface effects, the magnetization and magnetic anisotropy of nanoparticles can be much larger than the magnetization and magnetic anisotropy of their bulk counterparts, and the Curie and Néel temperatures can vary by hundreds of degrees.29 Typically, magnetic nanoparticles consist of only one magnetic domain, which explains their generally higher anisotropy in comparison with multi-domain bulk structures. Furthermore, below a critical size nanoparticles can become superparamagnetic, in which case the atomic magnetic moments in the nanoparticles will be continuously fluctuating when an external magnetic field is absent but respond with high levels of magnetization when an auxiliary magnetic field is applied.29 The magnetic ordering temperature of a nanomaterial is generally lower than the bulk phase value, but this effect can be masked or reversed by crystallographic parameters or composition.29 For CoO and Co3O4 nanoparticles, a reduction of the Néel temperature was observed; this reduction has been found to increase with decreasing particle size.30–32 At the same time, the literature on CoO and Co3O4 nanoparticles reports the observation of net ferromagnetism at room temperature;32–35 this net-ferromagnetic effect is generally attributed to surface effects. Room-temperature ferromagnetism has also been reported for Co3O4/CoO core/shell particles; in their case, the net-ferromagnetism was attributed to interface effects.36
The experiments performed in this work established that the Co3O4 and CoO phases are in a cube-on-cube orientation relationship with respect to each other. We therefore employed density functional theory (DFT) calculations to investigate the {100}/{100} interface between the two phases. This particular interface orientation is observed in Co3O4/CoO nanocrystals in the present study, and was also described experimentally by Tung et al. in Co3O4/CoO core/shell nanocubes.37 Various possible input magnetic configurations were considered for the DFT calculations. The interface energy of the lowest-energy {100}/{100} interface between the Co3O4 and CoO phase was calculated. We also aim to answer the interesting question of whether the overall magnetism and the magnetic ordering changes when the two phases are brought into contact with each other.
In the present study, we first investigate the thermal reduction of Co3O4 to CoO nanocrystals experimentally by means of in situ vacuum heating in the TEM. The transformation was monitored both by real-space imaging and by electron diffraction (ED) to identify the formation of new phases and their crystal structures. The reduction started at a temperature of 350 °C, and full reduction of all particles was achieved at 400 °C. During the transition, the two phases were found to be in a cube-on-cube orientation relationship. Next, the interface between Co3O4 and CoO is investigated by means of DFT calculations, to calculate the interface energy of the interface and to study the effect of the interface on the magnetic properties of the multiphase configuration.
2. Experimental section
Sample preparation and TEM characterization
The Co3O4 nanocrystals (NCs) were purchased from Sigma-Aldrich and had a broad size distribution of 5–50 nm as shown in Fig. 1(c). The Electron Diffraction (ED) and in situ TEM investigations were conducted using a TFS TalosF200X TEM operating at 200 kV with a point-to-point resolution of approximately 1.1 Å in bright-field TEM imaging mode. An overview TEM image of the pristine samples is shown in Fig. 1(c). High-resolution imaging was also conducted with a double aberration corrected TFS Spectra300 TEM, operated at 300 kV and with a point-to-point resolution of 50 pm in TEM mode, on partially transformed particles to show high resolution details of the heterogeneous nanostructures. The TEM specimens were prepared by drop casting the Co3O4 solution onto a DENSsolutions MEMS heating chip containing electron-transparent 15 nm thick SiN membranes, which we will refer to as the ‘windows’ on the chip.X-ray diffraction (XRD)
The crystal structure of Co3O4 in the pristine samples was confirmed by XRD measurements (shown in Fig. S1, ESI†). The XRD was conducted using a PW 1729 Philips diffractometer, equipped with a Cu Kα X-ray source (1.79026 Å). The Co3O4 powder was uniformly dispersed on an aluminum substrate for the XRD measurement.In situ TEM heating
The heating chips were subsequently mounted on a DENSsolutions single tilt heating holder. The Co3O4 nanocrystals were first heated from room temperature to 900 °C with 50 °C increments to monitor their evolution with temperature. It was established that reduction took place at 350–400 °C. The transformation took place everywhere, also in areas on the heating chip that were not previously exposed to the electron beam. A control experiment was also performed where the NCs were heated to 400 °C and then cooled down gradually, to verify that the NCs did not transform into a structure other than CoO rocksalt after cooling to room temperature, which was not the case.Ex situ heating experiments
Several ex situ control experiments were performed. Ex situ heating experiments were conducted in tube furnaces under air flow, N2 flow, and under vacuum. For these experiments, the complete heating chips with the sample, prepared in the same way as for the in situ heating experiments, were inserted in the oven. The samples heated under air and under N2 flow were heated at a rate of 5 °C min−1. The samples were kept at 400 °C for 10 minutes and allowed to cool down naturally to room temperature. The samples were also heated with the heating holder in air, and with the heating holder inserted in a high vacuum chamber (Gatan pumping station Model 655), applying the same rate as in the in situ heating experiments. The pressure in the high vacuum chamber was approximately 1.0 × 10−7 Torr. After holding the temperature at 400 °C for 10 minutes, the sample was cooled down fast to room temperature and swiftly inserted in the TEM for subsequent analysis.3. Computational section
Density functional theory (DFT) calculations were employed to study the CoO/Co3O4 {100}/{100} interface. First, the CoO and Co3O4 bulk phases were calculated separately, to obtain bulk phase reference energies and equilibrium lattice parameters, and to establish the magnetic ground state of the bulk phases. Four multiphase supercells with various magnetic orderings for the constituent bulk phase slabs were then constructed to calculate the interface energy of four different magnetic configurations. A Bader analysis38 was performed to investigate if, and how, the magnetism changes when the two phases are brought into contact.Computational method
The calculations were performed using the plane-wave VASP code39,40 employing the projector augmented wave (PAW) scheme41,42 and the generalized gradient approximation (GGA) with the exchange–correlation functional by Perdew, Burke and Ernzerhof (PBE).43 For the bulk phases, the DFT+U approach44 was considered as well. In the DFT+U approach, the Hubbard U potential has the effect of lowering the energies of the d electron bands and as such compensates for the deficiency of standard DFT in describing strongly correlated systems. The use of hybrid functionals such as HSE06 or PBE0 was not considered as these methods are computationally prohibitively expensive for the large interface supercells considered in this work. The energy cutoff and the density of the k-meshes were tested to ensure energy convergence well within 2 meV per atom. All calculations were performed in reciprocal space as calculations in real space were often found not to converge properly electronically. The required cutoff energy of the wave functions found from the energy convergence tests was 700 eV, which is higher than the energy cutoffs typically reported in the literature (500–600 eV). A cutoff energy of 980 eV was used for the augmentation functions. The electronic wave functions were sampled using the Monkhorst and Pack scheme,45 on 6 × 6 × 6 k-grids for both the conventional Co3O4 unit cell and the 2 × 2 × 2 supercell of the conventional CoO unit cell that is required to accommodate the AFM2 magnetic ordering of the latter (see Fig. 1(d and e)). For the interface supercells, 6 × 6 × 1 k-grids were used.All simulation cells were structurally optimized, relaxing atomic positions and lattice parameters, to yield lower-energy configurations. For the ionic relaxation loop, accumulative energy and atomic force convergence criteria of 10−5 eV and 0.01 eV Å−1, respectively, were applied for the bulk phase calculations; for the interface calculations, accumulative criteria of 10−4 eV and 0.01 eV Å−1 were used. For all calculations, an energy convergence criterion of 10−6 eV was set for the electronic convergence loop. For the spin-polarized calculations, the initial magnitude of the magnetic moment was always set to 4 μB for the atoms carrying a magnetic moment (i.e., for all Co2+ atoms), and to 0 for all other atoms. The magnetic moments were not fixed but allowed to relax (to reduce in magnitude, and even to change in sign) during the electronic self-consistent calculation. The Bader analysis, performed to determine the charge distribution among the atoms and to calculate the magnetic moments on the atoms, was carried out using the approach by Henkelman et al.46 All calculations are valid for a temperature of 0 K and a pressure of 0 Pa. Zero-point vibration contributions have been neglected. Non-collinear magnetism has not been considered.
CoO and Co3O4 reference phases
Most DFT calculations in the literature have been performed using the primitive cells of the cubic phases of CoO and Co3O4, while Dalverny et al. performed calculations on the Jahn–Teller distorted monoclinic phase of CoO.23 In the present work, we performed calculations and parameter testing on the conventional unit cells as these are more representative for the interface supercells we wish to construct. For the CoO phase, input configurations with antiferromagnetic AFM1 and AFM2, ferromagnetic (FM), and nonmagnetic (NM) magnetic orderings were considered. Here, AFM1 represents the alternation of spin-up and spin-down Co (100) planes, whereas AFM2 represents the alternation of spin-up/spin-down Co (111) atomic planes as depicted in Fig. 1(d and e); we here follow the nomenclature by Deng et al.22 For the Co3O4 phase, AFM1 (as depicted in Fig. 1(a and b)), FM, and NM magnetic orderings were considered as input. All configurations were calculated both with standard DFT, i.e., using the GGA-PBE exchange–correlation functional, and with DFT+U. In the literature reporting DFT+U results on CoO and Co3O4 phases, in general Ueff values between 4 and 5 eV are chosen.21–25 Here, for our DFT+U calculations, we used an identical value of Ueff = 4.4 eV for all Co atoms in the two compounds, as we wish not to distinguish between Co2+ and Co3+ when interfaces are created.CoO/Co3O4 supercells and interface energy
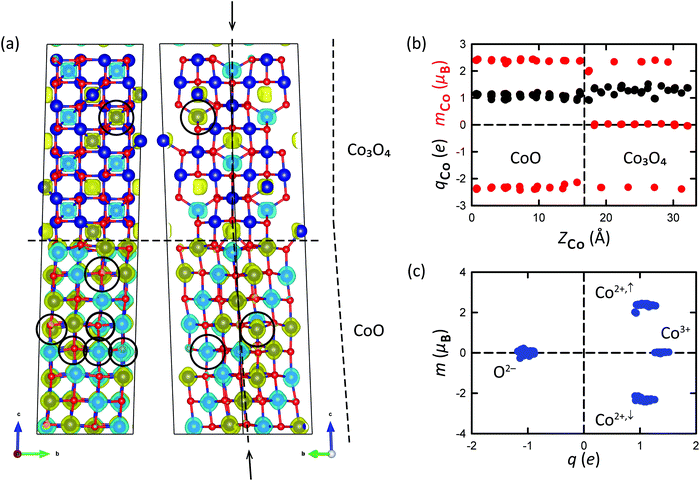
Fig. 2 shows the interface supercells with the various configurations of the magnetic orderings that were used as input for the calculations. The designation of the magnetic orderings applies to the CoO/Co3O4 {100}/{100} interface simulated by a supercell of which the bottom half consists of a 2 × 2 × 4 supercell of the conventional CoO unit cell and the top half consists of a 1 × 1 × 2 supercell of the conventional Co3O4 unit cell, adding up to a total of 240 atoms per interface supercell. Besides a fully nonmagnetic (NM/NM) and a fully ferromagnetic (FM/FM) input configuration, two antiferromagnetic input configurations were considered. In the antiferromagnetic configurations, the interface is formed by a bottom CoO slab that has either AFM1 or AFM2 ordering and a top Co3O4 slab that is always AFM1 ordered, which results in the AFM1/AFM1 and AFM2/AFM1 configurations depicted in Fig. 2(c)–(e).After full relaxation of the supercells, the interface energy γint was calculated for each of the interfaces as:
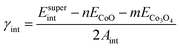 | (2) |
4. Results and discussion
In situ and ex situ TEM investigations
The in situ heating experiments conducted on the Co3O4 NCs were performed as described in the Experimental section. An XRD spectrum confirming the Co3O4 phase of the pristine nanosamples can be found in Fig. S1 of the ESI.† First, the particles as dropcast on the heating chip were heated from room temperature to 900 °C with increments of 50 °C. Bright-field TEM images and selected area electron diffraction (SAED) patterns were recorded at every heating step. Fig. 3 shows TEM images of the cobalt oxide nanoparticles in two different areas at room temperature, at 400 °C, and at 800 °C. The particles agglomerated at room temperature after drying on the TEM supports. After heating at a temperature of 400 °C, the surfaces of the nanocrystals became uneven and more faceted. This indicates that particular crystallographic facets are preferentially exposed, driven by minimization of the total surface energy. As the onset of faceting coincides with the transformation to CoO, which will be become clear from the SAEDs in Fig. 4, this is possibly caused by CoO NPs having more distinct facet-dependent surface energies than Co3O4 NPs. In addition, stronger diffraction contrast also appeared on the particles, which we attribute to the phase transformation to CoO as also evidenced by the SAED results of Fig. 4 and Fig. S2 (ESI†). At 800 °C, the particles coalesced and fused as is clear from the bottom-right panel in Fig. 3, which corroborates of the results of the SAED patterns showing fewer but stronger peaks at temperatures of 600 °C and higher (Fig. S2 of the ESI†). | ||
| Fig. 3 Bright-field TEM images of (initially) Co3O4 NPs at room temperature, at 400 °C and at 800 °C. The surfaces of the NPs become uneven at 400 °C, while diffraction contrast increases. | ||
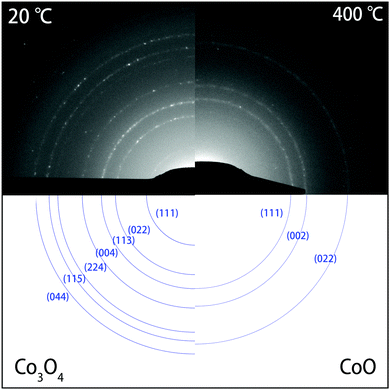 | ||
| Fig. 4 SAED patterns (top) of Co3O4 NPs before heating at 20 °C (left), and after heating for 10 min at 400 °C (right). At 20 °C, the diffraction rings in the DP corresponded to the Co3O4 phase. After heating at 400 °C, only three rings remained that correspond to the highly symmetric CoO phase. The rings in the experimental SAED patterns (top) are indexed in blue (bottom). Please note that the (hkl) indexing of the diffraction rings refers to reflections at {hkl} families of lattice planes. The complete DPs are shown in Fig. S2 of the ESI.† | ||
While bright-field TEM imaging provides information about changes in morphology and in the size of the NCs, the SAED patterns uniquely identify the crystal structure of the NCs during the heating experiments. Fig. S2 of the ESI† shows the diffraction patterns (DPs) recorded during the whole heating process. At room temperature and after heating at temperatures of up to 300 °C, the SAED patterns corresponded to the Co3O4 crystal structure. Upon annealing at 350 °C, however, the patterns started to change, and after keeping the sample at 400 °C for 10 minutes, only three rings remained that are indicative of the highly symmetric CoO phase.
In Fig. 4, a comparison is shown between the SAED patterns at 20 °C (left) and at 400 °C (right). The rings in the DPs were indexed and found to correspond to the Co3O4 phase and to the CoO phase, respectively. Table S2 (ESI†) shows the corresponding lattice spacings of the rings in both diffraction patterns. Fig. S3 (ESI†) shows the integrated DPs at 20 °C, 350 °C, 400 °C and 400 °C after 10 minutes, clearly showing the transformation as well. From 350 °C onwards, peaks corresponding Co3O4 started to disappear or became weaker, whereas a new peak corresponding to the (002) reflection of CoO appeared. Finally at 400 °C, only peaks corresponding to CoO were found, indicating that the transformation of the NPs was complete. Clearly, the SAED patterns show that the transformation to CoO took place from 350 °C onwards and was completed after heating to 400 °C for 10 minutes. Above 400 °C, the rings in the DPs did not change any more, indicating no further reduction. From 600 °C onwards, there are fewer spots on the rings due to coalescence and alignment of the nanocrystals, which consequently became larger and fewer in number.
Four ex situ reference experiments were conducted for comparison with the in situ heating experiments. Ex situ heating was conducted in a tube oven in air (1), in a tube oven under N2 flow (2), using the heating holder while kept in ambient air outside the TEM (3), and using the heating holder in a high vacuum chamber (4). The results are shown in Fig. S4 (ESI†). The SAED patterns after heating in the vacuum chamber clearly indicate the CoO structure, showing that the phase transformation to CoO also took place ex situ under low pressure conditions. The SAED patterns after heating under standard pressure and under N2 flow still show the Co3O4 structure, i.e., the transformation did not take place under these ex situ conditions, which implies that the transformation from Co3O4 to CoO requires a very low partial oxygen pressure. The cooling processes in the microscope is typically much faster than in regular furnaces, so that high-temperature phases might be quenched to room temperature. As an additional control experiment, the NCs were heated in situ from 20 °C to 400 °C (transforming completely to CoO) and subsequently cooled down very slowly to verify that no other structures than CoO are formed during cooling down. The resulting SAEDs are shown in Fig. S5 (ESI†). Both diffraction patterns show a CoO rocksalt crystal structure. High resolution TEM images (shown in Fig. S6, ESI†) also show that the particles remain in the CoO phase after heating and cooling down. Consequently, the transformation to CoO that is observed in situ must be caused by the combination of elevated temperature and the very low partial oxygen pressure under vacuum conditions.
The results of the ex situ experiments conducted in air and under nitrogen flow are in good agreement with the Co–O phase diagrams that Navrotsky et al. calculated for bulk and nanoscale cobalt oxide.14 For 10 nm sized anhydrous Co3O4 nanoparticles, these authors predicted that the partial oxygen pressure needs to be extremely low (p(O2/1 atm) < 10−20) for reduction to take place at a temperature of 650 K (∼350 °C). Consequently, during conditions of annealing ex situ at standard pressure either in air or under (not 100% pure) nitrogen flow, the partial oxygen pressure will not be sufficiently low for the Co3O4 NPs to be reduced. The transformation was observed, though, during heating in the in situ experiments and when heating ex situ in the high vacuum chamber. The partial oxygen pressure in these high vacuum environments is unfortunately not known but must be considerably lower than the total pressure in the column of the TEM and in the vacuum chamber, which is approximately 1.0 × 10−5 Pa. Therefore, as the total partial pressure (with respect to atmospheric pressure) is 1.0 × 10−10, the partial oxygen pressure will be considerably lower. The thermodynamic modelling as performed by Navrotsky et al. is only valid for systems in equilibrium, though. From a thermodynamic point of view, vacuum annealing in situ in the TEM or in a high vacuum chamber is always an out-of-equilibrium condition as oxygen molecules are continuously removed from the system through the work done by the vacuum pumps, thereby driving the dissociation from Co3O4 to CoO; there is no equilibrium with any gas. For a thermodynamic assessment of the reduction reaction under equilibrium conditions, we refer to the excellent review by Mayer et al.19 and to the work of Navrotsky et al. who also incorporated nanosize effects.14
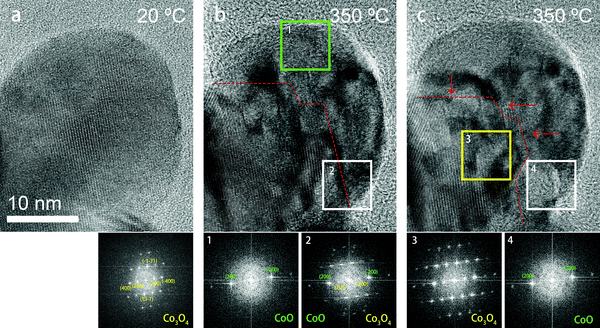
In Fig. 5, high-resolution TEM (HRTEM) images of a particle at room temperature and at 350 °C are shown, revealing details of the phase transformation. In Fig. 5(a), the particle is single crystalline being observed in a [013]-zone axis at room temperature. At 350 °C (Fig. 5(b) and (c)), multiple smaller areas displaying a different contrast appeared on the particle, which indicates that the particle was no longer single crystalline at this temperature. The inset images show the Fast Fourier Transforms (FFTs) of the corresponding smaller areas. The FFT images in Fig. 5(b) and (c) show that at 350 °C the central area of this particle is still in the Co3O4 phase while the surface area has transformed to CoO. The area marked by the green square in Fig. 5(b) displays the CoO phase while the white area contains both Co3O4 and CoO phases. However, the white square area transformed to CoO after a few minutes of continued annealing (shown in Fig. 5(c)), which means that the relative fraction of the CoO phase increased during heating, while the area marked with the yellow square in Fig. 5(c) was still in the Co3O4 phase, indicating that the transformation had not proceeded yet into the most central area of the particle. Fig. 5 also shows that at 350 °C the spots corresponding to the (200) fringes of CoO are crystallographically aligned with the (400) fringes of Co3O4. This reveals that during the transformation, there is a cube-on-cube orientation relationship between the Co3O4 parent nanocrystal and the Co product nanocrystals.
In Fig. 6, aberration-corrected TEM (AC-TEM) images are shown of a particle that had partially transformed to CoO, where the particle is imaged in a [001] projection. The image was taken after swiftly cooling down from 400 °C to room temperature. Fig. 6(c) and (d) are the FFT patterns indicating a central area (c) that is still in the Co3O4 phase and an area at the edge (d) that has transformed into the CoO phase. The two phases are in a cube-on-cube orientation relationship, in good agreement with the results shown in Fig. 5. Fig. 6(b) shows a magnified HRTEM image of the central area of the particle (marked by the white rectangle in panel (a)), with the Co3O4 phase at the left hand side and the CoO phase at the right hand side. Atomic overlays have been drawn to indicate the atomic structures. At the right hand side, the atomic columns match the CoO structure well. Very distinctively, in the Co3O4 part of the structure there are additional columns of atoms standing out that are generating a ‘diagonal’ pattern that is rotated 45° with respect to the cubic CoO structure. These atomic columns are the Co2+ ions in Co3O4. The inset in Fig. 6(b) shows a simulated image of Co3O4 (using QSTEM, for a thickness of 71.3 Å and a defocus value of 10 nm) where this feature is very strong, which confirms the presence of the Co3O4 structure in the central areas of the partially transformed nanoparticles. Due to changes in thickness, and possibly some mistilt, the contrast of the Co3O4 part in the images varies to some extent and the interfaces between both phases is not atomically sharp. This may also be caused by the fact that the TEM images are a projection of a 3D structure, while many of these particles display a core–shell structure (with a Co3O4 core and a CoO shell), so that in projection the central part is in fact a superposition of both phases including interfaces between them. Both {100}/{100} and {110}/{110} interfaces can be distinguished where the transition seems to be gradual. An additional HRTEM image of another particle, showing very similar features, is shown in Fig. S7 of the ESI.†
In Fig. 7, HRTEM images of a larger nanoparticle are shown. At room temperature, spots corresponding to Co3O4 (220)-lattice fringes can be clearly observed in the TEM image (panel (a)) and the corresponding FFT pattern (panel (d)). After heating to 400 °C, spots corresponding to (331) lattice fringes appeared, and new pairs of spots also appeared that are very close to the Co3O4(440) spots, but which deviate by a small tilt angle and have a slightly smaller k-spacing. These pairs of spots correspond to the {220} lattice fringes of CoO, which implies that the surface layer of the particle was reduced to CoO, and that this layer is slightly tilted with respect to the Co3O4 crystal lattice at the interior of the NP. Similarly small mistilts between the two phases were reported by Ward et al.,18 who studied the reduction of Co3O4 nanoparticles in a chemically reducing H2 atmosphere. Combining the result of Fig. 5 and 6, both phases are observed from 350 °C to 400 °C, which is in good agreement with the result of the DPs. This means that the transformation started from 350 °C onwards, and progressed inwards from the surface to the center of the particles until complete conversion is achieved at 400 °C.
A moiré pattern also appears at the bottom part of the particle, shown in Fig. 7(b), which confirms the multi-layer structure. Fig. 7(f) shows the inverse FFT image of a mask applied around the (220) spots of CoO in Fig. 7(e), showing that dislocations are formed during the reduction. In Fig. 7(b), some voids displaying bright contrast appeared on the particle, which was single crystalline at room temperature before heating. The dislocations and voids are likely formed due to the release of oxygen atoms during the reconstruction of the Co3O4 structure into the CoO structure. The dissociation reaction can be written as
 | (3) |
The oxygen sublattices of Co3O4 and CoO are nearly identical, both being fcc sublattices and having a very commensurate lattice parameter (Fig. 1). As 25% of the O atoms are released during reduction, the oxygen sublattice and therefore the volume of the nanoparticle itself has to reduce by about 25% (the positioning and occupation of the Co atoms in the lattices is not limiting their volume). If the shrinkage of the nanoparticle does not proceed fast enough to match the release of oxygen atoms and molecules, the formation of voids and dislocations can be expected.
DFT study of the CoO/Co3O4 interface
Density functional theory (DFT) calculations were conducted on CoO and Co3O4 reference bulk phase unit cells and on CoO/Co3O4 interface supercells, as described in the Computational details section. To investigate the performance of the DFT (PBE) and DFT+U (PBE+U) methods considered in this study in describing the CoO and Co3O4 phases, the unit cells of these phases were calculated both with DFT and DFT+U. Table 1 summarizes the obtained lattice parameters and band gaps, and the relative energetic stability of the various magnetic geometries. As expected, the Hubbard U correction leads to increased band gap values, and even opened up band gaps for the AFM1 and FM CoO configurations, making these configurations no longer metallic and half-metallic as predicted by PBE but semiconducting instead. Surprisingly, it was found that DFT+U incorrectly predicts the magnetic ground state (MGS) of CoO to be AFM1 rather than AFM2. The deviation of our results from earlier DFT+U findings in this regard may be related to the higher (and presumably more accurate) energy cutoff used in this work, and to the fact that we performed our calculations on conventional unit cells rather than on the primitive cells. Standard DFT did predict AFM2 to be the lowest-energy phase of CoO, in agreement with experiment. Both DFT and DFT+U correctly predict the MGS of Co3O4 to be AFM1, although in these cases the ferromagnetic (FM) solution was found to be only slightly less favorable than AFM1. In a combined theoretical and experimental study by Qiao et al., who investigated the electronic structure of Co3O4 with DFT calculations for a range of Ueff parameters for both Co2+ and Co3+ ions, it was shown that DFT+U leads to a severe distortion of the top of the valence band in Co3O4 due to strong downward bending of the band edge corresponding to Co3+ 3d orbitals,25 which makes a sensible prediction of the electronic band gap cumbersome. The authors of that study found from their experiments that the fundamental band gap of Co3O4 is substantially lower (0.74 eV) than typically reported (1.5–2.5 eV), and concluded from their DFT calculations that standard GGA-PBE without U correction is best capable of describing the electronic structure of Co3O4.25| Method | Magnetism | Relative energy (meV per atom) | Lattice parameter (Å) | Band gap (eV) | |||
|---|---|---|---|---|---|---|---|
| CoO | Co3O4 | CoO | Co3O4 | CoO | Co3O4 | ||
| DFT | AFM2 | 0 | — | 4.218 | 4.043 | 0.52 | — |
| AFM1 | 113 | 0 | 4.223 | 4.043 | M | 0.31 | |
| FM | 75 | 4 | 4.247 | 4.046 | HM: 1.08 | 0.16 | |
| NM | 257 | 95 | 4.101 | 4.014 | M | M | |
| DFT+U | AFM2 | 345 | — | 4.246 | 4.068 | 1.57 | — |
| AFM1 | 0 | 0 | 4.295 | 4.068 | 0.91 | 2.14 | |
| FM | 435 | 1 | 4.241 | 4.069 | 2.02 | 2.16 | |
| NM | 857 | 481 | 4.088 | 4.009 | M | M | |
In the present work we are particularly interested in a sufficiently reliable calculation of the total energies for calculating the interface energy between the two phases, and a reliable prediction of the magnetism at the interface. Considering the misidentification of the magnetic ground state for CoO and the distortion of the valence band of Co3O4 when using DFT+U, there are no good reasons to choose DFT+U for the present study, and we performed the interface calculations using standard DFT only. For the (lowest-energy) AFM2 CoO and AFM1 Co3O4 phases, Table 2 summarizes the electric charges and magnetic moments on the Co2+, Co3+, and O2− atoms, as obtained from standard DFT and Bader volume analysis. Values obtained for the magnetic moments are ±2.30 μB for the Co2+ ions in Co3O4 and ±2.42 μB for the Co2+ ions in CoO, in agreement with previously reported values in the literature.22,24
| a 0 (Å) | MGS | M (μB) | q (e) | m (μB) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Co2+ | Co3+ | O2− | Co2+ | Co3+ | O2− | ||||
| CoO | 4.218 | AFM2 | 0.000 | +1.31 | — | −1.31 | ±2.42 | — | 0.00 |
| Co3O4 | 4.043 | AFM1 | 0.000 | +1.33 | +1.44 | −1.05 | ±2.30 | 0.00 | ±0.07 |
Next, the four interface supercells with the magnetic ordering shown in Fig. 2 were fully relaxed. The interface energy of the various interfaces was calculated according to eqn (2) and using the energetically most favorable (AFM2) CoO and (AFM1) Co3O4 phases as obtained from the bulk phase unit cell calculations as reference phases. Table 3 provides the calculated interface energies and the net magnetic moments of the supercells. The precise supercell dimensions of the obtained output configurations are provided in Table S1 of the ESI.†
| Interface CoO/Co3O4 | E 0 (eV) | A int (Å2) | γ int (eV Å−2) | γint (J m−2) | M (μB) | Mismatch (%) |
|---|---|---|---|---|---|---|
| AFM2/AFM1 | 0.00 | 67.84 | 0.024 | 0.38 | 18.9 | 4.2 |
| AFM1/AFM1 | 3.11 | 63.58 | 0.050 | 0.80 | 6.5 | 4.4 |
| FM/FM | 2.76 | 63.87 | 0.047 | 0.75 | 158.9 | 4.8 |
| NM/NM | 26.70 | 62.78 | 0.239 | 3.82 | 0.0 | 2.1 |
The atomic output configurations are shown in Fig. 8 and in Fig. S8 of the ESI.† The atomic models are overlaid with isosurfaces of the spin-polarization density, where yellow represents excess spin-up electron density and blue represents excess spin-down electron density. Graphs with an analysis of the Bader evaluated electric charges and magnetic moments on the atoms in the interface supercells are included as well. In Fig. 8(a), the first notable observation is that the magnetic ordering of the AFM2/AFM1 supercell at both sides of the interface is distorted. The (bottom) CoO slab of the supercell indeed displays an AFM2 ordering, and the (top) Co3O4 slab an AFM1 ordering; there are, however, clearly a number of Co2+ atoms whose magnetic moment changed sign during relaxation (excess spin-up electron density becoming excess spin-down electron density for these atoms, and vice versa), as indicated with black circles in Fig. 8(a). This can easily be seen by comparing with the input magnetic ordering displayed in Fig. 2(d and e). Remarkably, these atoms with flipped magnetic moments are found not only close to the interface, but also quite far away (at distances of up to 4 atomic layers) from the interface.
As can be seen from Table 3, the AFM2/AFM1 ordered input configuration resulted in the energetically most favorable interface configuration; i.e., the two bulk components forming the interface, preferably follow the same magnetic ordering as the separate bulk phases. In absolute terms, the interface energy of 0.38 J m−2 is quite favorable, in particular considering the 4.2% lattice mismatch. The NM/NM interface, with the highest total energy and an interface energy of 3.82 J m−2, is clearly unfavorable, despite the lower lattice mismatch of 2.1%; the higher energy difference is caused by the fact that here the structure is forced to be nonmagnetic while magnetic solutions are preferred. Fig. 8(a) shows the atomic output configuration for the (lowest-energy) AFM2/AFM1 interface supercell. The output configurations of all interface supercells can be found in Fig. S8 of the ESI.† The charges and magnetic moments on the Co atoms in the relaxed AFM2/AFM1 supercell are shown in Fig. 8(b), where they are plotted as a function of the Z-coordinate (height in the supercell). Fig. S8(d) (ESI†) includes the charges and magnetic moments on the O atoms. The correlation between the charges on the atoms and their magnetic moments is nicely visualized in Fig. 8(c). Clearly, the CoO phase only contains Co2+ ions with either positive or negative magnetic moments, whereas the Co3O4 phase also contains nonmagnetic Co3+ ions (Fig. 8(b)). The charges and the magnetic moments on the atoms in the supercell in general follow the same trend as the charges and magnetic moments obtained for the atoms in the CoO and Co3O4 bulk phase compounds (Table 2). As can be seen from Fig. 8(c), the nonmagnetic Co3+ ions have a somewhat higher positive charge of +1.38e in comparison with the Co2+ ions, which carry an (either spin-up or spin-down) magnetic moment of ±2.34 μB and have Bader charges of +1.09e (all averaged values; the Co2+ atoms with upward magnetic moments actually have an averaged magnetic moment that is slightly larger, namely +2.37 μB, than the corresponding value for the magnetically downwardly orientated Co2+ atoms, which was found to be −2.31 μB on average). There is one Co layer (the Co layer closest to the interface at Zrel ≈ 1/2, in the Co3O4 component of the supercell) where the Co2+ ions have slightly smaller magnetic moments and Bader charges of +1.99 μB and +0.92e. For the Co2+ atoms of which the magnetic moment changed sign during relaxation, slightly larger values of the magnetic moment were found, of +2.42 μB on average, at Bader charges of +1.05e.
The constituting bulk phases of the AFM2/AFM1 supercell are both AFM-type with zero net magnetic moment (Table 2). Remarkably, the formation of the interface leads to a substantial net ferromagnetic moment of 18.9 μB over the entire AFM2/AFM1 supercell (Table 3). The supercell as a whole is therefore ferrimagnetic. The net ferromagnetic moment that arises from the formation of the interface between the two antiferromagnetic compounds can for the largest part be retraced to the flipping of magnetic moments of Co2+ atoms at both sides of the interface. In total 9 ions changed the sign of their magnetic moment, 6 upwardly and 3 downwardly: in the (bottom) CoO slab, 3 Co2+ ions changed the sign of their magnetic moment from up to down, and 5 changed their sign from down to up; and in the (top) Co3O4 slab, one Co2+ ion changed its sign from down to up. The resulting net contribution of these atoms to the magnetization of the supercell amounts to the equivalence of 3 of their upwardly orientated atomic magnetic moments, and is accompanied by a net contribution of an equal number of (unflipped) atomic magnetic moments from the Co2+ sublattice, where the upwardly orientated magnetic moments of three Co2+ atoms due to the flipping are now no longer matched and counterbalanced by originally downwardly orientated but now flipped magnetic moments. The contribution to the net magnetic moment of the entire supercell due to the flipping of magnetic moments can therefore be estimated to be 3 × (2.42 + 2.37) = 14.4 μB. A smaller part (2.0 μB) of the magnetization of the supercell is caused by the difference in magnetic moment between the spin-up and spin-down Co2+ atoms. Note that the two Co2+ atoms at the interface with the smaller magnetic moments will lower the magnetization (their contribution to the net magnetization of the supercell is −0.6 μB). The remainder of the supercell magnetization stems from low levels of spin-polarization at the nonmagnetic O2− and Co3+ atoms, which were found to have very small atomic magnetic moments after relaxation (of ±0.08 μB and ±0.03 μB on average and adding up to a net contribution of 2.7 μB and 0.4 μB, respectively). Magnetic moments can change sign as a result of the exchange interaction between magnetic moments. In the present case, apparently the broken symmetry and disorder induced by the presence of the interface causes individual magnetic moments at the interface to change in sign, which consecutively causes the adjacent magnetic moment to change in sign as well, eventually leading to flipped magnetic moments quite far away from the interface.
By analogy with the definition of the interface energy (eqn (2)), the net ferromagnetization of the supercell can be expressed per unit of interfacial area as 13.9 μB nm−2; the larger part of the magnetization, to a value of 10.3 μB nm−2, occurs in the constituting CoO component, whereas a magnetization of 3.6 μB nm−2 was found for the Co3O4 slab. In the literature, net ferromagnetism in antiferromagnetic nanoparticles was experimentally observed to persist even at room temperature for compounds having a bulk Néel temperature below room temperature, which has generally been attributed to surface and interface effects.32–36 The present calculations predict that this is indeed also the case for the CoO/Co3O4 {100}/{100} interface geometry investigated here. We suggest that a follow-up study could study experimentally whether partially converted composite Co3O4/CoO nanoparticles exhibit stronger ferromagnetism than pure Co3O4 NPs or pure CoO NPs.
The second notable observation that can be made from Fig. 8(a) is that the relaxed AFM2/AFM1 supercell is clearly skewed, most likely under the influence of the directionality along 〈111〉 of the antiferromagnetic ordering in the CoO phase. Please note that when both phases are nonmagnetic (NM/NM), skewing of the supercell does not occur as can been seen in Fig. S8(a) of the ESI.† (The precise dimensions of the supercells can be found in Table S1, ESI.†) As is indicated by arrows and illustrated schematically at the right-hand side of Fig. 8(a), relaxation resulted in a mistilt of approximately 4° between the Z-axes of the two cubic phases. We point out that a lattice mistilt between the two phases was sometimes also observed in the experiments, as evidenced by the electron diffraction pattern of Fig. 7(e), and by the study by Ward et al. who reduced Co3O4 in an H2 atmosphere. In theory, the experimentally observed mistilt could be explained from the magnetic interactions between the two phases. As explained in the Introduction, magnetism is often found for nanoparticles above the Curie or Néel temperature of their corresponding bulk phases because of size effects and surface and interface effects.29 In addition, there is quite a strong magnetic field present in the electron microscope with field strengths up to 2 Tesla,47 which can easily induce magnetization. Nonetheless, we consider that, whereas the skewing and mistilt observed in the simulations are most likely related to the different directionality of the magnetic ordering of the two phases, the most plausible explanation for the experimentally observed lattice mistilt is the formation of dislocations in the oxygen sublattice, as revealed by the real-space HRTEM observations.
5. Conclusion
The thermal reduction process of Co3O4 nanoparticles to CoO was investigated by in situ heating in the TEM under vacuum conditions. The results show that transformation of the Co3O4 NPs starts at 350 °C and that the NPs are completely converted after heating at 400 °C for 10 min. Upon heating to higher temperatures, up to 900 °C, no further reduction was observed. The reaction proceeds from the surface to the center of the particle, where the parent Co3O4 and the product CoO nanoparticles are in a cube-on-cube orientation relationship of their crystal lattices. The CoO reduced surface layer was sometimes slightly tilted with respect to the Co3O4 interior, which is likely associated with the formation of dislocations as the volume of the NPs has to reduce by 25% due to oxygen release. The transformation did not take place during ex situ heating experiments conducted in air and under nitrogen flow, however the transformation was achieved ex situ when heating in a high vacuum chamber; vacuum conditions, equivalent to a very low partial oxygen pressure, are necessary for achieving the transformation to CoO at a temperature of 400 °C.The energetics and magnetic structure of the interface were investigated by density functional theory (DFT) calculations predicting a favorable CoO/Co3O4 {100}/{100} interface energy of 0.38 J m−2. The antiferromagnetic orderings of the two phases at both sides of the interface, AFM2 for CoO and AFM1 for Co3O4, correspond to those of the lowest-energy bulk phases. It was also found, however, that the magnetic ordering is distorted as several atoms have magnetic moments with a sign that is opposite to the sign that would yield the perfect magnetic order. The distortion in the antiferromagnetic ordering takes place at the interface but also leads to flipping of magnetic moments at a considerable distance (∼1 nm) from the interface, likely due to exchange coupling. The flipping in sign of the magnetic moments leads to a considerable net ferromagnetic moment of 18.9 μB over the entire supercell, which corresponds to a net magnetization of approximately 13.9 μB nm−2. We suggest that verifying experimentally whether the presence of the Co3O4/CoO interface indeed enhances the ferromagnetism of NPs with respect to pure Co3O4 or pure CoO NPs, would be an interesting topic for an experimental follow-up study. Both in the experiments and in the simulations, a small mistilt between the two cubic phases was found. In the simulations, this is likely related to stress fields originating from different directionalities of the antiferromagnetic orderings in CoO and Co3O4. In the experiments, this is likely due to the formation of dislocations in the oxygen sublattice during the thermal reduction. In the present work we show that the formation of an interface leads to ferromagnetism in otherwise only antiferromagnetic materials. Although we demonstrate this solely for the Co3O4/CoO interface, this effect can be expected to take place in many other transition metal oxide systems as well. The implication of the current findings is that it could be very beneficial to reduce transition metal oxide nanoparticles only partially, in order to boost ferromagnetism at their interfaces. This would be an interesting topic for an experimental follow-up study, as generating ferromagnetism simply by partial reduction would make these nanoparticles interesting to a much wider range of applications including magnetic recording media, sensing, and biomedical applications.48–50
Author contributions
MAvH conceived the experimental part of the study. XDC performed and analyzed the in situ and ex situ heating experiments. HvG conceived the computational part of the study and performed and analyzed the DFT calculations. XDC and HvG wrote the manuscript. All authors commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
MAvH acknowledges funding by the European Research Council through an ERC Consolidator Grant (Grant No. 683076). Part of this work was carried out on the Dutch national e-infrastructure with the support of SURF Cooperative. Figures of atomic structural models and spin-polarization density plots were produced using VESTA.51 We thank Bo van den Bosch, who participated in the experiments within the framework of the ‘Research Traineeship’ 2nd year Bachelor course at Utrecht University. We thank Albert Grau Carbonell and Hans Meeldijk for EM support, and Profs. Alfons van Blaaderen and Petra de Jongh for useful discussions.References
- R. Zhang, Y. C. Zhang, L. Pan, G.-Q. Shen, N. Mahmood, Y.-H. Ma, Y. Shi, W. Jia, L. Wang, X. Zhang, W. Xu and J.-J. Zou, ACS Catal., 2018, 8, 3803 CrossRef CAS.
- F. Song, L. Bai, A. Moysiadou, S. Lee, C. Hu, L. Liardet and X. Hu, J. Am. Chem. Soc., 2018, 140, 7748 CrossRef CAS PubMed.
- B. Ernst, A. Bensaddik, L. Hilaire, P. Chaumette and A. Kiennemann, Catal. Today, 1998, 39, 329 CrossRef CAS.
- L. J. Garces, B. Hincapie, R. Zerger and S. L. Suib, J. Phys. Chem. C, 2015, 119, 5484 CrossRef CAS.
- P. A. Connor and J. T. S. Irvine, Electrochim. Acta, 2002, 47, 2885 CrossRef CAS.
- D. Su, S. Dou and G. Wang, Sci. Rep., 2014, 4, 5767 CrossRef PubMed.
- W. Y. Li, L. N. Xu and J. Chen, Adv. Funct. Mater., 2005, 15, 851 CrossRef CAS.
- R. Dehghan, T. W. Hansen, J. B. Wagner, A. Holmen, E. Rytter, Ø. Borg and J. C. Walmsley, Catal. Lett., 2011, 141, 754 CrossRef CAS.
- O. A. Bulavchenko, S. V. Cherepanova, V. V. Malakhov, L. S. Dovlitova, A. V. Ishchenko and S. V. Tsybulya, Kinet. Catal., 2009, 50, 192 CrossRef CAS.
- D. Potoczna-Petru and L. Kępiński, Catal. Lett., 2001, 73, 41 CrossRef CAS.
- O. Kitakami, H. Sato, Y. Shimada, F. Sato and M. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 13849 CrossRef CAS.
- M. Chen, B. Hallstedt and L. J. Guackler, J. Phase Equilibr., 2003, 24, 212 CrossRef CAS.
- F.-C. Kong, Y.-F. Li, C. Shang and Z.-P. Liu, J. Phys. Chem. C, 2019, 123, 17539 CrossRef CAS.
- A. Navrotsky, C. Ma, K. Lilova and N. Birkner, Science, 2010, 330, 199 CrossRef CAS PubMed.
- B. Tomić-Tucaković, D. Majstorović, D. Jelić and S. Mentus, Thermochim. Acta, 2012, 541, 15 CrossRef.
- G. Ji, S. Smart, S. K. Bhatia and J. C. Diniz da Costa, Sep. Purif. Technol., 2015, 154, 338 CrossRef CAS.
- K. C. Sabat, R. K. Paramguru, S. Pradhan and B. K. Mishra, Plasma Chem. Plasma Process., 2015, 35, 387 CrossRef CAS.
- M. R. Ward, E. D. Boyes and P. L. Gai, ChemCatChem, 2013, 5, 2655 CrossRef CAS.
- N. A. Mayer, D. M. Cupid, R. Adam, A. Reif, D. Rafaja and H. J. Seifert, Thermochim. Acta, 2017, 652, 109 CrossRef CAS.
- M. A. van Huis, N. P. Young, G. Pandraud, J. F. Creemer, D. Vanmaekelbergh, A. I. Kirkland and H. W. Zandbergen, Adv. Mater., 2009, 21, 4992 CrossRef CAS PubMed.
- T. Archer, R. Hanafin and S. Sanvito, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 014431 CrossRef.
- H.-X. Deng, J. Li, S.-S. Li, J.-B. Xia, A. Walsh and S.-H. Wei, Appl. Phys. Lett., 2010, 96, 162508 CrossRef.
- A.-L. Dalverny, J.-S. Filhol, F. Lemoigno and M.-L. Doublet, J. Phys. Chem. C, 2010, 114, 21750 CrossRef CAS.
- J. Chen, X. Wu and A. Selloni, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 245204 CrossRef.
- L. Qiao, H. Y. Xiao, H. M. Meyer, J. N. Sun, C. M. Rouleau, A. A. Puretzky, D. B. Geohegan, I. N. Ivanov, M. Yoon, W. J. Weber and M. D. Biegalski, J. Mater. Chem. C, 2013, 1, 4628 RSC.
- F. B. Lewis and N. H. Saunders, J. Phys. C: Solid State Phys., 1973, 6, 2525 CrossRef CAS.
- E. Z. Kurmaev, R. G. Wilks, A. Moewes, L. D. Finkelstein, S. N. Shamin and J. Kunes, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 165127 CrossRef.
- V. R. Shinde, S. B. Mahadik, T. P. Gujar and C. D. Lokhande, Appl. Surf. Sci., 2006, 252, 7487 CrossRef CAS.
- Y. A. Koksharov, in Magnetic Nanoparticles, ed. S. P. Gubin, Wiley, Weinheim, 2009, ch. 6, pp. 197–254 Search PubMed.
- S. Sako, K. Ohshima, M. Sakai and S. Bandow, Surf. Rev. Lett., 1996, 3, 109 CrossRef CAS.
- L. He, C. Chen, N. Wang, W. Zhou and L. Guo, J. Appl. Phys., 2007, 102, 103911 CrossRef.
- S. R. Gawali, A. C. Gandhi, S. S. Gaikwad, J. Pant, T.-S. Chan, C.-L. Cheng, Y.-R. Ma and S. Y. Wu, Sci. Rep., 2018, 8, 249 CrossRef PubMed.
- L. Zhang, D. Xue and C. Gao, J. Magn. Magn. Mater., 2003, 267, 111–114 CrossRef CAS.
- G. Yang, D. Gao, Z. Shi, Z. Zhang, J. Zhang, J. Zhang and D. Xue, J. Phys. Chem. C, 2010, 114, 21989 CrossRef CAS.
- C. Nethravathi, S. Sen, N. Ravishankar, M. Rajamathi, C. Pietzonka and B. Harbrecht, J. Phys. Chem. B, 2005, 109, 11468 CrossRef CAS PubMed.
- Z.-A. Li, N. Fontaíña-Troitiño, A. Kovács, S. Liébana-Viñas, M. Spasova, R. E. Dunin-Borkowski, M. Müller, D. Doennig, R. Pentcheva, M. Farle and V. Salgeuiriño, Sci. Rep., 2015, 5, 7997 CrossRef CAS PubMed.
- C.-W. Tung, Y.-Y. Hsu, Y.-P. Shen, Y. Zheng, T.-S. Chan, H.-S. Sheu, Y.-C. Cheng and H. M. Chen, Nat. Commun., 2015, 6, 8106 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, UK, 1990 Search PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- G. Henkelman, A. Arnaldsson and H. A. Jónsson, Comput. Mater. Sci., 2006, 36, 354 CrossRef.
- N. Shibata, Y. Kohno, A. Nakamura, S. Morishita, T. Seki, A. Kumamoto, H. Sawada, T. Matsumoto, S. D. Findlay and Y. Ikuhara, Nat. Commun., 2019, 10, 2308 CrossRef CAS PubMed.
- S. Singamaneni, V. N. Bliznyuk, C. Binek and E. Y. Tsymbal, J. Mater. Chem., 2011, 21, 16819 RSC.
- H. Lai, F. Xu and L. Wang, J. Mater. Sci., 2018, 53, 8677 CrossRef CAS.
- Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dohson, J. Phys. D: Appl. Phys., 2003, 36, R167 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0tc05727d |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2021 |



![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] projection in (e). Panel (e) is included so that the AFM2 ordering in the CoO phase,
10] projection in (e). Panel (e) is included so that the AFM2 ordering in the CoO phase,