Triphenylamine- and triazine-containing hydrogen bonded complexes: liquid crystalline supramolecular semiconductors

Abstract

Despite the fact that triphenylamine derivatives have been widely explored as hole-transporting materials, studies on charge transport properties in the liquid crystal phase have been overlooked. Here, it is reported that triphenylamine liquid crystals can attain very high hole mobility values in a hexagonal columnar mesophase, up to μ ≈ 5 cm² V⁻¹ s⁻¹. The columnar liquid crystalline phase was obtained by a proper design of a supramolecular mesogen, and this is unprecedented for triphenylamine liquid crystals. In fact, the supramolecules were formed by hydrogen-bonded 1 : 3 complexes of a star-shaped triazine core and three triphenylamine peripheral units. The resulting hexagonal columnar mesophase acts as a successful scaffold that confines TPA units at the periphery of columns. Challenging DFT theoretical investigations into a model based on such supramolecular systems involving a large number of atoms were undertaken to explore the stability and geometry of the complexes and their electronic properties.

---

Introduction

As a paradigm of assemblies with order-dependent properties, liquid crystals (LCs) constitute a successful tool to engineer the assembly of appropriately designed molecules and implement novel functional materials.¹ Among the different LC organizations, columnar mesophases² are of special interest because of their 1D nanostructured architecture, which makes them interesting for charge transport and semiconducting behavior.³

Because of its electroactive and photoactive properties, triphenylamine shows up as a valuable unit to challenge its inclusion in columnar liquid crystalline architectures with improved charge-carrier mobility. On the one hand, triphenylamine, TPA, has a strong electron-donor character. The hole mobility values measured in amorphous films of TPA derivatives are usually in the range 10⁻⁵–10⁻² cm² V⁻¹ s⁻¹.^4–14 Accordingly, TPA has been widely used in the design of molecules that provide materials for hole injection and hole transport layers in optoelectronic devices,⁴ such as OLEDs,¹⁵ OFETs,¹⁶ or solar cells.^5,6,17,18 On the other hand, TPA adopts a propeller shape in which the phenyl rings are rotated by around 41° with respect to the plane defined by the three N–C bonds.^19,20 This is the reason why TPA usually promotes amorphous glasses with good film-forming properties and this favors its inclusion in materials for thermodynamically stable optoelectronic devices.^15,21 Nevertheless, there are outstanding studies that concern the possibility of employing TPA as a structural unit to obtain ordered supramolecular architectures,²² thus leading to enhanced conductivity in the aggregate.²³ In this respect, it has been proven that some TPA-derivatives containing amide groups aggregate in solvents to form supramolecular polymers with chirality amplification,^24–27 photoinduced self-assembly due to the formation of radical cation species in the presence of chlorinated solvents,^24,28 or supramolecular electropolymerization.²⁹ However, few examples have been described in which TPA is part of a mesogen that arranges in a columnar LC phase.^30–33 In addition, charge transport properties in the LC phase have not been reported to date.

In the route from a molecule, i.e. TPA, to a functional LC material, the correct design of constituent molecules is essential but also the control of intermolecular interactions responsible for the supramolecular architecture and the properties.^34–36 In this respect, a myriad of mesogens have been built through hydrogen-bonding interactions between complementary units, thus forming defined supramolecules that, in turn, self-organize into a mesophase architecture. Such a possibility provides an efficient bottom-up methodology to attain hierarchically organized supramolecular materials based on LCs,^37–39 and yield successfully supramolecular semiconductors.^40,41

In order to prepare TPA-containing semiconductors we designed a hydrogen bonded complex formed by two complementary units, a star-shaped triazine, T3C₄ (blue in Fig. 1), and three benzoic acid derivatives bearing the TPA unit, A-2BnOC₁₂-TPAnC₁₂ (n = 2, 4, 6), (Fig. 1). As for the acid, the high tendency of 3,4,5-tris(4-alkoxybenzylozy)benzoic acids to promote the formation of columnar liquid crystalline organizations on their own,⁴² and particularly forming 1 : 3 complexes with T3C₄,^39d,e inspired us to design the acids A-2BnOC₁₂-TPAnC₁₂ (n = 2, 4, 6). The aim was to ensure the stability of the complexes and compensate for the lack of planarity of TPA, which could disturb the stacked arrangement. Thus, three complexes were prepared and characterized, and their LC behaviour studied. Charge mobility measurements were carried out on T3C₄-2BnOC₁₂-TPA2C₁₂, which showed a hexagonal columnar mesophase that was stable at room temperature. DFT theoretical calculations were also undertaken in a model system to explore the stability and geometry of the new supramolecules, their electronic properties and the main parameters that control the charge transport. The theoretical analysis of a proposed new molecular material is playing an ever-increasing role in research. Although the comparison between theoretical and experimental results might not be straightforward,⁴³ it highlights trends and explains the measured properties from an electronic point of view. Here, it is worth emphasizing that the size of the theoretical model applied here (402 atoms, which in the calculation of the transfer integral required a dimer of 804 atoms) exceeded, to the best of our knowledge, previous theoretical studies on LCs,⁴⁴ and involved a significant challenge.

Fig. 1 Chemical structure of the three H-bonded complexes formed by T3C₄ and three triphenylamine-containing benzoic acids with different number of peripheral dodecyloxy chains.

Results and discussion

Synthesis and characterization

The triazine core, T3C₄, was synthesized by a previously reported procedure.^39d The synthesis of acids A-2BnOC₁₂-TPA2C₁₂ (11a), A-2BnOC₁₂-TPA4C₁₂ (11b) and A-2BnOC₁₂-TPA6C₁₂ (11c) is presented in Scheme 1. The acids consist of a triphenylamine moiety and a 3,5-dibenzyloxybenzoic acid moiety linked together by a flexible n-hexamethylene spacer. The triphenylamine moiety 4a–c was synthesized in high yields, ca. 80%, by a Buchwald–Hartwig C–N coupling⁴⁵ between para-benzyloxyaniline (1) and the corresponding aryl halide 3a–c.⁴⁶ Benzyl cleavage in 4a–c provided a triphenylamine moiety with a hydroxy group and peripheral dodecyloxy chains (5a–c), with yields around 90%. The introduction of 6-bromohexanol gave rise to the triphenylamine-containing alcohol 6a–c, which was coupled with methyl 4-hydroxy-3,5-bis(tert-butyldimethylsilyloxy)benzoate (7) under Mitsunobu conditions, reaching yields between 55% and 80%. Subsequent deprotection of the hydroxyl groups at positions 3 and 5 of intermediates 8a–c, using tetrabutylammonium fluoride, gave quantitatively the corresponding derivatives with free hydroxyl groups (9a–c), which allowed the introduction of the para-dodecyloxybenzyl group⁴⁷ by means of a Williamson reaction and moderate yields, ca. 37%. Hydrolysis of the methyl esters 10a–c gave the acid components A-2BnOC₁₂-TPA2C₁₂, A-2BnOC₁₂-TPA4C₁₂ and A-2BnOC₁₂-TPA6C₁₂, with moderate-high yields between 57% and 71%. Details of the synthesis and characterization of these acids are collected in the ESI.†

Scheme 1 Synthesis of the acids.

The supramolecular complexes were prepared by dissolving the components, T3C₄ core and the acid, in a 1 : 3 ratio, in dichloromethane and evaporating the solvent. The solutions of the mixtures were prepared in amber-coloured vials to avoid possible oxidation processes of the triphenylamines promoted by light in chlorinated solvents and characterized by NMR (Fig. S2, ESI†).²⁸

A thermal treatment, in which the mixtures were heated to the isotropic liquid state and then allowed to cool down to room temperature, was carried out with the aim of improving the homogeneity and favouring the formation of the supramolecular complexes.

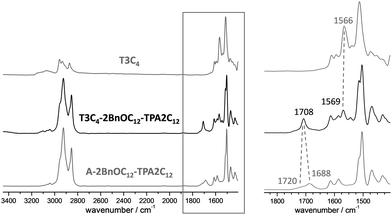
The three complexes were studied by FTIR at room temperature on samples cooled from the isotropic liquid (Fig. 2, and Fig. S3, S4, ESI†). A comparison between the spectra of the complex T3C₄-2BnOC₁₂-TPA2C₁₂ and its two components is provided in Fig. 2. The spectrum of the supramolecular complex shows bands corresponding to the heterocyclic rings of T3C₄ at slightly higher wavenumbers (1569–1573 cm⁻¹) than those in the free core (1566 cm⁻¹). More importantly, the spectrum of the complex shows a C=O stretching band at 1708 cm⁻¹ in contrast with the spectrum of the acid that presents a C=O stretching band corresponding to the dimeric form at 1688 cm⁻¹, and a shoulder at 1720 cm⁻¹ that can be attributed to the open dimer form of the acid.⁴⁸ These changes are consistent with the formation of the proposed H-bonded complex between T3C₄ and the corresponding acid.^39d,e,41

Fig. 2 FTIR spectra measured on KBr pellets at r.t. of T3C₄, the acid A-2BnOC₁₂-TPA2C₁₂ and the corresponding supramolecular complex T3C₄-2BnOC₁₂-TPA2C₁₂.

Liquid crystalline properties

The thermal properties and liquid crystalline behaviour of the H-bonded complexes were studied by POM, TGA, DSC and X-ray diffraction and the results are collected in Table 1.

Table 1 Thermal properties of the supramolecular complexes. Lattice parameters of the corresponding hexagonal columnar mesophase

Complex	T (°C) [ΔH (kJ mol^−1)]^a	Colh lattice parameter
a Phase transitions (I: isotropic liquid, Colh: hexagonal columnar mesophase) from the second cooling cycle recorded at a rate of 10 °C min^−1. All temperatures correspond to the peak maximum.
T3C4-2BnOC12-TPA2C12	I 37 [2.7] Colh	a = 46.2 Å
T3C4-2BnOC12-TPA4C12	I 76 [3.7] Colh	a = 54.3 Å
T3C4-2BnOC12-TPA6C12	I 50 [2.2] Colh	a = 55.1 Å

---

All the complexes appeared under the POM as homogeneous materials, which were thermally stable within the liquid crystalline temperature interval as confirmed by thermogravimetric analysis (Fig. S5, ESI†). The complexes have improved mesomorphic properties with respect to those of the precursor acids (Fig. S6–S9 and Table S1, ESI†). The acid A-2BnOC₁₂-TPA2C₁₂ showed a hexagonal columnar mesophase, but acids A-2BnOC₁₂-TPA4C₁₂ and A-2BnOC₁₂-TPA6C₁₂ showed a complex thermal behavior and their diffractogram contained a few reflections that could not be indexed unequivocally to any defined columnar arrangement (Fig. S10 and Table S2, ESI†).

All three supramolecular complexes showed textures consistent with columnar mesomorphism when cooled from the isotropic liquid (Fig. 3 and Fig. S11, ESI†). T3C₄-2BnOC₁₂-TPA2C₁₂ is an enantiotropic liquid crystal that shows a single mesophase that is stable at room temperature, as confirmed by its DSC thermogram (Table 1 and Fig. S12, ESI†). Although complexes T3C₄-2BnOC₁₂-TPA4C₁₂ and T3C₄-2BnOC₁₂-TPA6C₁₂ appeared to be mesomorphic at room temperature when observed on cooling from the isotropic liquid, their DSC thermograms showed respective cold crystallization processes during the second heating (Fig. S13 and S14, ESI†), and subsequent melting temperatures higher than those corresponding to the transition between the isotropic liquid and the mesophase on cooling. These findings indicate that their mesophase is thermodynamically unstable and both are monotropic liquid crystals.

Fig. 3 Photomicrograph of the texture observed by POM for T3C₄-2BnOC₁₂-TPA2C₁₂ at r.t., on cooling from the isotropic liquid at 0.1 °C min⁻¹.

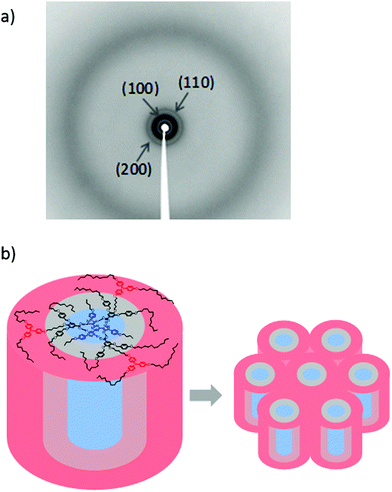
The structural features of the mesophases were studied by X-ray diffraction at room temperature on samples cooled from the isotropic liquid. The diffractograms of the three supramolecular complexes T3C₄-2BnOC₁₂-TPA2C₁₂, T3C₄-2BnOC₁₂-TPA4C₁₂ and T3C₄-2BnOC₁₂-TPA6C₁₂ (Fig. 4 and Fig. S15, ESI†) contain several reflections in the low angle region, at distances consistent with the relationship d, d/√3, d/√4, which is characteristic of hexagonal columnar mesophases, and corresponding to reflections (100), (110) and (200) of the hexagonal network, respectively (Table S3, ESI†). The high-angle region contains a diffuse halo that is characteristic of the liquid crystal state, thus confirming that these supramolecular complexes can maintain the mesophase at room temperature, at least during the time of the XRD experiments. The number of complex molecules per unit cell (Z) was estimated from the data obtained by XRD experiments. Since a clear outer reflection indicative of a periodic stacking distance along the columns was not observed for any of the complexes, a stacking distance c = 3.4 Å was considered as observed in related complexes between T3C₄ and benzoic acids.^39d Assuming a density value of 1 g cm⁻³, Z = 1 was deduced for the three complexes. The columnar arrangement is formed then by the stacking of one supramolecular complex. In such a way the columns have different coaxial circular regions (Fig. 4b), with the T3C₄ moiety occupying the centre of the column (blue area), the dendritic part in the middle (grey area) and the TPA units radially distributed at the periphery (red area).

Fig. 4 (a) X-ray diffractogram taken at r.t. for the supramolecular complex T3C₄-2BnOC₁₂-TPA2C₁₂ cooled from the isotropic liquid: (b) model for the organization of the supramolecular complexes in the Col_h mesophase.

Electrochemical properties

In order to determine the redox potentials and the HOMO and LUMO levels of the complexes, their electrochemical properties were studied by cyclic voltamperommetry in solution and in film.

The voltamperograms of the complexes in dichloromethane solution showed a reversible oxidation wave at around 0.46–0.57 V (relative to the Ag/AgCl electrode), which corresponds to the oxidation of the triphenylamine units to the radical cation (Table 2).⁴⁹ The presence of the electron-donating alkoxy chains in the triphenylamine units causes a decrease in the oxidation potential with respect to derivatives without such substituents (1.25 V).⁴⁹ This allows a HOMO value of around −4.9 eV to be calculated. The TPA radical cation can be oxidized to a dication and undergo subsequent chemical reactions.^49–51 As a consequence, additional oxidation waves were observed for all complexes at more positive potentials on measuring larger potential windows (Fig. S16, ESI†). In addition, due to the presence of T3C₄, which is an electron acceptor, a reduction wave was also observed in the voltamperograms of the complexes. This signal corresponds to reduction potentials between −1.66 V and −1.68 V and allows a similar LUMO value of −2.7 eV to be calculated for all complexes.⁴¹

Table 2 Electrochemical data for the supramolecular complexes T3C₄-2BnOC₁₂-TPA2C₁₂, T3C₄-2BnOC₁₂-TPA4C₁₂ and T3C₄-2BnOC₁₂-TPA6C₁₂

Complex	E ^red (V) vs. Ag/AgCl	E ^ox1/2 (V) vs. Ag/AgCl	E ^red (V) vs. FOC	E ^ox1/2 (V) vs. FOC	HOMO^c (eV)	LUMO^d (eV)
a In dichloromethane solution. b E 1/2 = 0.42 V vs. Ag/AgCl. c E HOMO = −e[E^ox1/2vs. FOC + 4.8 V]. d E LUMO = −e[E^redvs. FOC + 4.8 V]. e Thin film in acetonitrile. f E 1/2 = 0.43 V vs. Ag/AgCl.
T3C4-2BnOC12-TPA2C12	−1.68	0.50	−2.10	0.08	−4.88	−2.70
T3C4-2BnOC12-TPA4C12	−1.66	0.46	−2.08	0.04	−4.84	−2.72
T3C4-2BnOC12-TPA6C12	−1.66	0.57	−2.08	0.15	−4.95	−2.72
T3C4-2BnOC12-TPA2C12	−1.67	0.78	−2.10^f	0.35^f	−5.15	−2.70

---

Given the stability of the hexagonal columnar mesophase at room temperature, the electrochemical properties of the complex T3C₄-2BnOC₁₂-TPA2C12 were also studied in a film deposited onto the disk electrode and immersed in a non-solvent containing the electrolyte (acetonitrile). In this case the voltamperogram (Table 2 and Fig. S17, ESI†) shows an oxidation wave with maximum at 0.78 V and a reduction wave at −1.67 V. The voltamperograms of the precursory acids under the same conditions (solution or film) only showed oxidation processes at similar potentials to the complexes (Tables S4, S5 and Fig. S18, S19, ESI†). This indicates independent behaviour of the TPA and T3C₄ units.

Cyclic voltammetry measurements on the supramolecular complexes are consistent with the electron-donor character of the TPA units and the electron-acceptor character of T3C₄. In addition, the HOMO and LUMO values calculated from these measurements may be suitable to give rise to ambipolar transport properties in the columnar organization of these complexes.

Charge carrier mobility measurements

Given the HOMO energy level of T3C₄-2BnOC₁₂-TPA2C₁₂, E_HOMO = −5.15 eV, this compound is ideally suited for an evaluation of its hole transport properties via the Space Charge Limited Current (SCLC) method, using Au as an injecting electrode with ohmic contact (Fig. S20, ESI†). Samples were prepared as described in the ESI† and a description of the measurements is also included (Fig. S21, ESI†).

The SCLC method probes charge drift across the whole thickness of the samples, in our case typically of the order of 10 μm. As a consequence, in anisotropic media the observed mobility value is highly dependent on the size of the ordered domains and on their orientation with respect to the direction of measurement. As assessed by POM (Fig. S22, ESI†), the director distribution was never homogeneous in the samples of T3C₄-2BnOC₁₂-TPA2C₁₂, not even on a submillimeter-scale. Nonetheless, a mobility in the range 10⁻⁹–10⁻⁸ cm² V⁻¹ s⁻¹, which is typical of amorphous phases, was measured in numerous different areas of samples obtained after slow cooling from the melt.

The situation changed when thermal treatments were carried out as described in the ESI.† Even though the POM analysis did not show any marked variation in the homogeneity of the director distribution, it was possible to measure much higher mobility values, albeit ranging within 4–5 orders of magnitude between 10⁻⁴ and more than 1 cm² V⁻¹ s⁻¹. The results of a typical set of measurements in different areas of the same sample are shown in Fig. 5. We attribute the width of the range of the measured mobility values to different orientational environments. The evident alignment of the highest measured values of mobility towards a limiting maximum is suggestive of a disorder limited mobility: in this view, the limiting value could be considered as the hole mobility along the columns when the orientational disorder and the effect of traps at grain boundaries is minimized. Considering the highest values measured on different samples, which seem to lie nicely within a limited range, we obtain a mobility μ ≈ 5 cm² V⁻¹ s⁻¹. These SCLC results indicate that the order of magnitude of hole mobility when TPA units are embedded within columnar phases can be much higher than in amorphous TPA phases, if orientational disorder is minimized.

Fig. 5 A typical example of hole mobilities measured in different areas (labelled A1, A2, etc.) of the same sample of T3C₄-2BnOC₁₂-TPA2C₁₂ after thermal treatment.

In order to evaluate electron mobility, samples were prepared in which a ∼5–10 μm thick layer of T3C₄-2BnOC₁₂-TPA2C₁₂ was sandwiched between two ITO electrodes covered with a thin layer of ZnO. However, regardless of the type of thermal treatment carried out, currents were always low, although SCLC regimes were often obtained. The resulting electron mobility, of the order of 10⁻⁹–10⁻⁸ cm² V⁻¹ s⁻¹, should then be taken as lower limit, probably a consequence of the poor injection from the ZnO layer.

Theoretical calculations

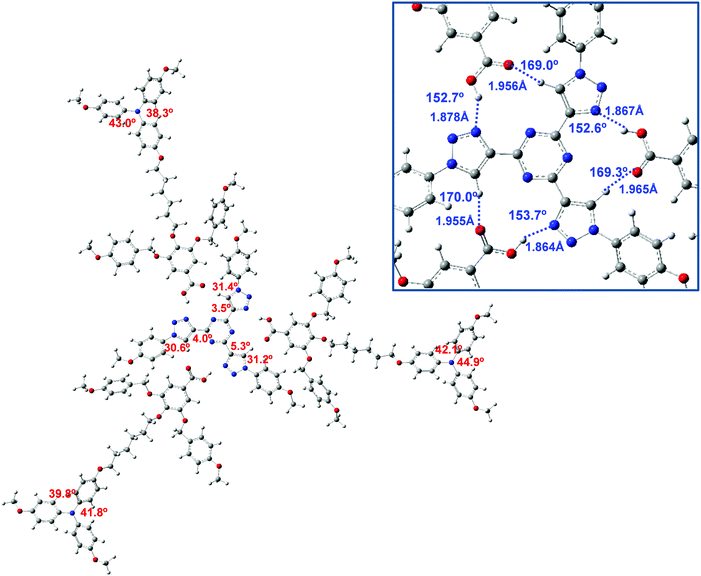
The star-shaped T3C₄ core was theoretically studied in a previous work at the B3LYP-D3/6-31G** level of theory and the C₃ conformation was computed to be more stable than the asymmetric one.^39e In addition, the H-bond interaction between the core and benzoic acid was scrutinized in order to draw conclusions about the most stable host–guest supramolecular structure.^39e In this work, we considered these previous results to calculate the structure and properties of the supramolecular complex between T3C₄ and the TPA-derived benzoic acid. Since the hydrogen bonds established between the T3C₄ core and three benzoic acid molecules play an important role in the stability of the complex, and hence in the self-assembly of the columnar mesophase, it was interesting to explore theoretically the structure and stability of the complex geometry. Taking into account the larger size of the complex studied in this work, a simplified model complex, T3C1-2BnOC₁-TPA2C₁, which is an analog of T3C₄-2BnOC₁₂-TPA2C₁₂ but with methoxy groups in the core and the TPA unit, was fully optimized at the ωB97XD/6-31G** level of theory without symmetry constraints. This long-range functional includes dispersion corrections and has proven to be suitable in similar studies in which π–π interactions and hydrogen bonds are present.⁵²

The optimized structure of the T3C₁-2BnOC₁-TPA2C₁ complex is shown in Fig. 6. The directionality of the H-bonds is a key parameter to describe the strength of these non-covalent interactions, which have a high impact on the self-assembly of liquid crystals and their structure–property relationships.⁵³ According to Jeffrey's criteria,⁵⁴ our theoretical calculations predict that the hydrogen bonds in T3C₁-2BnOC₁-TPA2C₁ could be classified as moderate. A zoomed view of the T3C₁-2BnOC₁-TPA2C₁ scaffold is shown in Fig. 6 and it can be seen that each triazole ring is bonded to a benzoic acid moiety via two nonlinear hydrogen bonds, i.e., less than 180 degrees, with angles for the C–H⋯O contacts that are more directional than those for O–H⋯N.

Fig. 6 Optimized T3C₁-2BnOC₁-TPA2C₁ complex at the ωB97XD/6-31G** level of theory.

The mean values for the C–H⋯O and O–H⋯N bond angles are 169.4° and 153°, respectively, while the H⋯O interaction is predicted to be longer than H⋯N, with values of 1.959 Å and 1.870 Å, respectively. These results are consistent with distances calculated at the B3LYP-D3/6-31G** level for a complex between T3C₄ and a 3,4,5-(4-alkoxybenzyloxy)benzoic acid (2.033 and 1.801 Å, respectively).^39e

Several relevant dihedral angles for the T3C₄ core are also included in Fig. 6. The triazole ring is almost coplanar with triazine (<6°) while it is significantly twisted with respect to the peripheral benzene groups, with dihedral angles of around ∼31°. This structure is consistent with our previous theoretical studies on the T3C₄ molecule – either alone or complexed with benzoic acids^39e – performed at the B3LYP-D3/6-31G** level of theory. In addition, the dihedral angles for two phenyl rings of the triphenylamine moiety are also included in Fig. 6, with angles in the range 38–45°, in agreement with the twisted structure of TPA.⁵⁵

The HOMO and LUMO molecular orbitals for the optimized structure are shown in Fig. 7, together with their corresponding energy levels. It is clear that LUMO and LUMO+1 are degenerate and the same applies to HOMO, HOMO−1 and HOMO−2. The HOMO and LUMO wavefunctions are highly localized on the three electron-donor triphenylamine units and the electron-acceptor tris(triazolyl)triazine core, respectively, although the propeller shape of these units could be to the detriment of the hole and electron charge transport through the columnar mesophase. As a result of the different physical localization of the HOMO and LUMO, holes and electrons could flow independently through different charge transport molecular wires along the columnar mesophase.

Fig. 7 Shapes of the frontier molecular orbitals for T3C₁-2BnOC₁-TPA2C₁ calculated at the ωB97XD/6-31G** level of theory in the gas phase (isocontour plots (0.02 a.u.)).

To gain a more comprehensive understanding of the semiconductor properties of the T3C₁-2BnOC₁-TPA2C₁ complex, typical electronic properties such as electron affinity, ionization potential, reorganization energy and transfer integral were calculated to estimate the efficiency of charge injection and charge transport. The calculations were also performed on the T3C₁ core and the TPA3C₁ as references (see Fig. S23, ESI†). Inspection of the calculated properties shown in Table 3 indicates that both moieties determine to a large extent the electronic properties of the final complex.

Table 3 Hole (λ₊) and electron (λ₋) reorganization energies, Adiabatic Ionization Potential (AIP) and Electron Affinities (in eV) for T3C₁, TPA3C₁ and T3C1-2BnOC₁-TPA2C₁ complex calculated at the ωB97XD/6-31G** level of theory in the gas phase

Compound	λ +	λ −	AIP	AEA
T3C1	0.775	0.519	7.533	0.312
TPA3C1	0.297	0.397	5.875	−1.388
T3C1-2BnOC1-TPA2C1	0.310	0.688	5.698	0.720

---

TPA has fascinated researchers as a p-type semiconductor that has many applications in organic electronics despite the fact that its non-planar structure hinders the molecular orbital overlap for charge transport. Our theoretical results for TPA are in agreement with those previously calculated by Lin et al.⁵⁵ using B3LYP/6-31G* and with those by Cias et al. on a series of para-substituted triphenylamines at the B3LYP/TZVP level of theory,⁵⁶ although the results are not rigorously comparable due to the different functional and basis set used. In the case of the tris(triazolyl)triazine core, it is worth noting that this is the first theoretical study concerning its semiconductor-related properties.

The reorganization energy calculated for the T3C₁-2BnOC₁-TPA2C₁ complex shows that hole transport would be more favoured than electron transport, with λ₊ being almost half (0.310 eV) of λ₋ (0.688 eV). The relative value λ₋/λ₊ ∼ 2 for T3C₁-2BnOC₁-TPA2C₁ is close to that calculated by Lin et al.⁵⁵ for the TPA unit using B3LYP/6-31G*. However, higher values for both λ₋ and λ₊ were obtained for the T3C₁ core and λ₋ < λ₊ is consistent with its electron acceptor character.

The ionization potential and electron affinity were also calculated for T3C₁-2BnOC₁-TPA2C₁ (see Table 3) and the results show that hole injection would be favored over electron injection. Thus, the predicted value for the ionization potential is in the range of typical p-type semiconductors such as TPA,⁵⁶ while the electron affinity calculated for the T3C₁-2BnOC₁-TPA2C₁ complex and the T3C₁ core is far from the limit of 3 eV for typical n-type semiconductors.⁵⁷

In order to estimate the molecular orbital overlap and charge transfer integral between two T3C₁-2BnOC₁-TPA2C₁ units, a full geometry optimization was performed on a stacked dimer of the complex. The dimer was built using the optimized molecular geometry of the isolated complex (Fig. 6). The initial stacking distance was 3.5 Å, based on a typical interdisk distance in columnar liquid crystals.² One disk was slightly rotated relative the other (10°) to prevent steric repulsion. The optimized structure of the dimer is represented in Fig. 8a and it can be seen that the T3C₁ cores are rotated by around 15° with respect to each other, with an interdisk distance between the two centers of the triazine rings of around 3.4 Å, which is in agreement with our previous results.^39d,e One important consequence of such a limited rotation angle is that TPA units of adjacent complexes in the same column end up close enough in space to interact with each other.

Fig. 8 Top and side views of the optimized dimer of the T3C₁-2BnOC₁-TPA2C₁ complex at the ωB97XD/6-31G** level of theory. Two different colors are used to highlight the two complexes that form the dimer. The expanded view shows bond distances and angles for the hydrogen bonding interactions.

An expanded view of the two T3C₁ cores in the optimized dimer is also presented in Fig. 8 along with bond distances and angles for the hydrogen bonds, which are similar to those obtained for the optimized isolated complex. An enlarged view of the stacked TPA regions is shown in Fig. 9 including the distances between the centers of phenyl rings (in red) and also some distances between carbon atoms (in black). It could be expected that the most advantageous arrangement for molecular orbital overlap would be in the a region in which the two TPA units stack one on top of the other although large distances were predicted (4.5–4.7 Å) which would be in detriment of the charge transport. A more favored situation is found in c where two phenyl rings could become closer (3.9 Å) being a bit away from the typical π-stacking distance (3.5 Å). However, shorter distances were predicted between some carbon atoms (3.2–3.4 Å) in favor of the molecular orbital overlap.

Fig. 9 Enlarged view of the TPA regions showing distances between the centers of phenyl rings (in red) and some distances between carbon atoms (in black).

The charge transfer integral was estimated at the ωB97XD/6-31G** level of theory for the stacked dimer with values of 0.029 eV (t₊) and 0.110 eV (t−) obtained for holes and electrons, respectively. According to the Marcus equation, the calculated hopping rate constant was k₊ = 1.24 × 10¹² s⁻¹ and k₋ = 3.02 × 10¹¹ s⁻¹, thus suggesting better hole transport than electron transport (k₊ > k₋). As previously stated, the calculated AEA is far from those of typical n-type semiconductors, and this is related to easy electron injection.^58,59 Besides, the interface between the injection layer and the semiconductor is usually treated as a Mott–Schottky barrier, where the barrier height is given by the difference between the metal work function (Φ) and the (gas) semiconductor LUMO level.⁶⁰ In order to obtain a good ohmic contact between semiconductor materials and electrodes, potential barriers lower than 0.2–0.3 eV are generally expected.^60,61

Taking into account the fact that the metal work function of ZnO is 4.3 eV, the predicted barrier height should be 4.3 − 0.176 = 4.1 eV. Thus, our calculations support the hypotheses that the difficulty in obtaining electron mobility values may not be attributable to the intrinsic properties of the material, but probably to poor charge injection.

Conclusions

It has been demonstrated in a new precedent that a known hole transport unit, TPA, can be organized in LC phases with semiconducting properties using a supramolecular approach. The preparation of hydrogen bonded 1 : 3 complexes of a star-shaped triazine acceptor core and three TPA donor peripheral units gave rise to columnar LC phases. The columnar phase shows high hole mobility after thermal treatment, with very high mobility values, up to μ ≈ 5 cm² V⁻¹ s⁻¹, that can be considered as a mobility along the columns when the effects of static defects and grain boundaries are minimized.

Generally, charge transport in columnar LC phases can be traced back to the stacking of the central part of the columns, while the external section, with a higher number of conformational degrees of freedom, mainly plays a space filling role and it is referred to as the insulating area. However, in the present case, the measured hole mobility can be ascribed to the TPA units present in the external, more flexible section of the columns. Here the phase structure acts as a scaffold used to position TPA units close enough to each other to promote charge transfer while at the same time preventing crystallization. The local degree of order of the columnar phase, related to the organization of the central cores, is thus of secondary importance for charge mobility, while the length scale of the long range orientational uniformity, i.e. the average size of the orientational domains, plays a more dominant role.

DFT theoretical investigations on such supramolecular systems were undertaken despite the large size of the complex. An optimized structure was identified for which molecular orbitals could be studied. In addition, this is the first theoretical study on 2,4,6-tris(triazolyl)-1,3,5-triazine semiconductor properties and also unprecedented on the theoretical study of triphenylamine-containing supramolecules. As a result of the different physical localization of the HOMO and LUMO, holes and electrons could flow independently along the columns. The calculations for a stacked dimer suggest better hole transport than electron transport, but this is not attributable to the intrinsic properties of the material and is probably due to poor charge injection, as also evidenced by experimental results.

This work is one of the few examples that show a combined experimental and theoretical approach for the design and evaluation of complex supramolecular systems for organic semiconductors. Although further work aimed at modeling through molecular dynamics calculations could shed light on the details of the stacking geometry of TPA groups, including the effects of intercolumnar interactions, and thus provide further insight regarding the reasons of the improved mobility, the evidence presented here already indicates that a certain degree of order, like the one typical of a columnar organization, contributes to enhance hole mobility in TPA based compounds.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the MICIU-FEDER funds (project PGC2018-093761-B-C31), the Gobierno de Aragón-FSE (E47_20R and B. F. grant B084/13), the Consejería de Economía y Conocimiento, Junta de Andalucía (FQM-337), and the Universidad de Jaén (Acción 1). A. G. thanks support from the ELIOTROPO project (PON03PE_00092_2). R. T. was supported by the MERAVIGLIE project (CUP J28C17000080006). The authors would like to thank the Centro de Servicios de Informática y Redes de Comunicaciones (CSIRC), Universidad de Granada, for providing the computing time and the Servicios Generales de Apoyo a la Investigación-SAI and CEQMA, Universidad de Zaragoza-CSIC. We acknowledge support of the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI).

References

1. T. Kato, J. Uchida, T. Ichikawa and T. Sakamoto, Angew. Chem., Int. Ed., 2018, 57, 4355–4371.
2. T. Wöhrle, I. Wurzbach, J. Kirres, A. Kostidou, N. Kapernaum, J. Litterscheidt, J. C. Haenle, P. Staffeld, A. Baro, F. Giesselmann and S. Laschat, Chem. Rev., 2016, 116, 1139–1241.
3. T. Kato, M. Yoshio, T. Ichikawa, B. Soberats, H. Ohno and M. Funahashi, Nat. Rev. Mater., 2017, 2, 17001.
4. Y. Shirota and H. Kageyama, Chem. Rev., 2007, 107, 953–1010.
5. J. Y. Wang, K. Liu, L. C. Ma and X. W. Zhan, Chem. Rev., 2016, 116, 14675–14725.
6. P. Agarwala and D. Kabra, J. Mater. Chem. A, 2017, 5, 1348–1373.
7. U. Bach, K. De Cloedt, H. Spreitzer and M. Gratzel, Adv. Mater., 2000, 12, 1060–1063.
8. H. Ohishi, M. Tanaka, H. Kageyama and Y. Shirota, Chem. Lett., 2004, 33, 1266–1267.
9. H. H. Fong, A. Papadimitratos and G. G. Malliaras, Appl. Phys. Lett., 2006, 89, 172116.
10. A. Cravino, S. Roquet, O. Aleveque, P. Leriche, P. Frere and J. Roncali, Chem. Mater., 2006, 18, 2584–2590.
11. Y. B. Song, C. A. Di, X. D. Yang, S. P. Li, W. Xu, Y. Q. Liu, L. M. Yang, Z. G. Shuai, D. Q. Zhang and D. B. Zhu, J. Am. Chem. Soc., 2006, 128, 15940–15941.
12. T. Malinauskas, M. Daskeviciene, G. Bubniene, I. Petrikyte, S. Raisys, K. Kazlauskas, V. Gaidelis, V. Jankauskas, R. Maldzius, S. Jursenas and V. Getautis, Chem. – Eur. J., 2013, 19, 15044–15056.
13. R. J. Li, H. X. Li, Y. B. Song, Q. X. Tang, Y. L. Liu, W. Xu, W. P. Hu and D. B. Zhu, Adv. Mater., 2009, 21, 1605–1608.
14. W. M. Zhang, J. Smith, R. Hamilton, M. Heeney, J. Kirkpatrick, K. Song, S. E. Watkins, T. Anthopoulos and I. McCulloch, J. Am. Chem. Soc., 2009, 131, 10814–10815.
15. Y. Shirota, J. Mater. Chem., 2005, 15, 75–93.
16. S. Allard, M. Forster, B. Souharce, H. Thiem and U. Scherf, Angew. Chem., Int. Ed., 2008, 47, 4070–4098.
17. Z. Ning and H. Tian, Chem. Commun., 2009, 5483–5495.
18. C. Rodríguez-Seco, L. Cabau, A. Vidal-Ferran and E. Palomares, Acc. Chem. Res., 2018, 51, 869–880.
19. A. N. Sobolev, V. K. Belsky, I. P. Romm, N. Y. Chernikova and E. N. Guryanova, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1985, 41, 967–971.
20. M. Malagoli and J. L. Bredas, Chem. Phys. Lett., 2000, 327, 13–17.
21. P. Strohriegl and J. V. Grazulevicius, Adv. Mater., 2002, 14, 1439–1452.
22. E. Moulin, J. J. Armao and N. Giuseppone, Acc. Chem. Res., 2019, 52, 975–983.
23. V. Faramarzi, F. Niess, E. Moulin, M. Maaloum, J.-F. Dayen, J.-B. Beaufrand, S. Zanettini, B. Doudin and N. Giuseppone, Nat. Chem., 2012, 4, 485–490.
24. J. Kim, J. Lee, W. Y. Kim, H. Kim, S. Lee, H. C. Lee, Y. S. Lee, M. Seo and S. Y. Kim, Nat. Commun., 2015, 6, 6959.
25. T. Kim, T. Mori, T. Aida and D. Miyajima, Chem. Sci., 2016, 7, 6689–6694.
26. B. Adelizzi, I. A. W. Filot, A. R. A. Palmans and E. W. Meijer, Chem. – Eur. J., 2017, 23, 6103–6110.
27. A. Osypenko, E. Moulin, O. Gavat, G. Fuks, M. Maaloum, M. A. J. Koenis, W. J. Buma and N. Giuseppone, Chem. – Eur. J., 2019, 25, 13008–13016.
28. E. Moulin, F. Niess, M. Maaloum, E. Buhler, I. Nyrkova and N. Giuseppone, Angew. Chem., Int. Ed., 2010, 49, 6974–6978.
29. T. K. Ellis, M. Galerne, J. J. Armao IV, A. Osypenko, D. Martel, M. Maaloum, G. Fuks, O. Gavat, E. Moulin and N. Giuseppone, Angew. Chem., Int. Ed., 2018, 57, 15749–15753.
30. Y. Domoto, E. Busseron, M. Maaloum, E. Moulin and N. Giuseppone, Chem. – Eur. J., 2015, 21, 1938–1948.
31. (a) K. C. Majumdar, N. Pal, P. Debnath and N. V. S. Rao, Tetrahedron Lett., 2007, 48, 6330–6333; (b) K. C. Majumdar, B. Chattopadhyay, P. K. Shyam and N. Pal, Tetrahedron Lett., 2009, 50, 6901–6905.
32. T. D. Choudhury, N. V. S. Rao, R. Tenent, J. Blackburn, B. Gregg and I. I. Smalyukh, J. Phys. Chem. B, 2011, 115, 609–617.
33. Y. J. Wang, H. S. Sheu and C. K. Lai, Tetrahedron, 2007, 63, 1695–1705.
34. D. B. Amabilino, D. K. Smith and J. W. Steed, Chem. Soc. Rev., 2017, 46, 2404–2420.
35. Functional Supramolecular Materials: From Surfaces to MOFs, ed. R. Banerjee, RSC, 2017.
36. Supramolecular Soft Matter: Applications in Materials and Organic Electronics, ed. T. Nakanishi, Wiley, 2011.
37. T. Kato, J. Uchida, T. Ichikawa and B. Soberats, Polym. J., 2017, 50, 149.
38. T. Kato and Y. Kamikawa, Hydrogen-Bonded Systems: Discrete Defined Aggregates by Intermolecular H-Bonding, Amides, Carboxylic Acids, and Heterocycles (Chapter 10), in Handbook of Liquid Crystals, ed. J. W. Goodby, P. J. Collings, T. Kato, C. Tschierske, H. Gleeson, P. Raynes, Wiley-VCH Verlag GmbH & Co. KGaA, 2nd edn, 2014, vol. 5, p. 513.
39. (a) F. Vera, R. M. Tejedor, P. Romero, J. Barberá, M. B. Ros, J. L. Serrano and T. Sierra, Angew. Chem., Int. Ed., 2007, 46, 1873–1877; (b) F. Vera, J. Barberá, P. Romero, J. L. Serrano, M. B. Ros and T. Sierra, Angew. Chem., Int. Ed., 2010, 49, 4910–4914; (c) A. A. Vieira, E. Cavero, P. Romero, H. Gallardo, J. L. Serrano and T. Sierra, J. Mater. Chem. C, 2014, 2, 7029–7038; (d) B. Feringán, P. Romero, J. L. Serrano, R. Giménez and T. Sierra, Chem. – Eur. J., 2015, 21, 8859–8866; (e) B. Feringán, J. Cerdá, B. Diosdado, J. Aragó, E. Ortí, R. Giménez and T. Sierra, Chem. – Eur. J., 2020, 26, 15313–15322.
40. B. Feringán, C. L. Folcia, R. Termine, A. Golemme, J. M. Granadino-Roldán, A. Navarro, J. L. Serrano, R. Giménez and T. Sierra, Chem. – Eur. J., 2018, 24, 17459–17463.
41. B. Feringán, P. Romero, J. L. Serrano, C. L. Folcia, J. Etxebarria, J. Ortega, R. Termine, A. Golemme, R. Giménez and T. Sierra, J. Am. Chem. Soc., 2016, 138, 12511–12518.
42. V. C. Percec, H. Ahn, W. D. Cho, A. M. Jamieson, J. Kim, T. Leman, M. Schmidt, M. Gerle, M. Moller, S. A. Prokhorova, S. S. Sheiko, S. Z. D. Cheng, A. Zhang, G. Ungar and D. J. P. Yeardley, J. Am. Chem. Soc., 1998, 120, 8619–8631.
43. H. Oberhofer, K. Reuter and J. Blumberger, Chem. Rev., 2017, 117, 10319–10357.
44. (a) S. M. Said, M. S. Mahmood, M. N. Daud, M. F. M. Sabri and N. A. Sairi, Liq. Cryst., 2016, 43, 2092–2113; (b) Y. Zhang, D. A. Hanifi, M. P. Fernández-Liencres, L. M. Klivansky, B. Ma, A. Navarro and Y. Liu, ACS Appl. Mater. Interfaces, 2017, 9, 20010–20019.
45. (a) B. H. Yang and S. L. Buchwald, J. Organomet. Chem., 1999, 576, 125–146; (b) J. F. Hartwig, M. Kawatsura, S. I. Hauck, K. H. Shaughnessy and L. M. Alcazar-Roman, J. Org. Chem., 1999, 64, 5575–5580.
46. A. Sakalyte, J. Simokaitiene, A. Tomkeviciene, J. Keruckas, G. Buika, J. V. Grazulevicius, V. Jankauskas, C. P. Hsu and C. H. Yang, J. Phys. Chem. C, 2011, 115, 4856–4862.
47. V. Percec, D. Schlueter, Y. K. Kwon, J. Blackwell, M. Moller and P. J. Slangen, Macromolecules, 1995, 28, 8807–8818.
48. A. González, L. Irusta, M. J. Fernández-Berridi, J. J. Iruin, T. Sierra and L. Oriol, Vib. Spectrosc., 2006, 41, 21–27.
49. E. T. Seo, R. F. Nelson, J. M. Fritsch, L. S. Marcoux, D. W. Leedy and R. N. Adams, J. Am. Chem. Soc., 1966, 88, 3498–3503.
50. K. Y. Chiu, T. X. Su, J. H. Li, T. H. Lin, G. S. Liou and S. H. Cheng, J. Electroanal. Chem., 2005, 575, 95–101.
51. R. Reynolds, L. L. Line and R. F. Nelson, J. Am. Chem. Soc., 1974, 96, 1087–1092.
52. (a) L. M. da Costa, S. R. Stoyanov, S. Gusarov, X. Tan, M. R. Gray, J. M. Stryker, R. Tykwinski, J. W. de, M. Carneiro, P. R. Seidl and A. Kovalenko, Energy Fuels, 2012, 26, 2727–2735; (b) J. Kim, J. Lee, W. Y. Kim, H. Kim, S. Lee, H. C. Lee, Y. S. Lee, M. Seo and S. Y. Kim, Nat. Commun., 2015, 6, 6959.
53. M. Pfletscher, S. Hölscher, C. Wölper, M. Mezger and M. Giese, Structure-Property Relationships in Hydrogen-Bonded Liquid Crystals, Chem. Mater., 2017, 29, 8462–8471.
54. (a) G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, Oxford, 1997; (b) T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76; (c) A. Shahi and E. J. Arunan, J. Chem. Sci., 2016, 128, 1571–1577.
55. B. C. Lin, C. P. Cheng and Z. P. M. Lao, J. Phys. Chem. A, 2003, 107, 5241–5251.
56. P. Cias, C. Slugovc and G. Gescheidt, J. Phys. Chem. A, 2011, 115, 14519–14525.
57. Y.-C. Chang, M.-Y. Kuo, C.-P. Chen, H.-F. Lu and I. Chao, J. Phys. Chem. C, 2010, 114, 11595–11601.
58. C. R. Newman, C. D. Frisbie, D. A. da Silva Filho, J. L. Brédas, P. C. Ewbank and K. R. Mann, Chem. Mater., 2004, 16, 4436–4451.
59. Y. Wang, S. R. Parkin, J. Gierschner and M. D. Watson, Org. Lett., 2008, 10, 3307–3310.
60. P. S. Davids, I. H. Campbell and D. L. Smith, J. Appl. Phys., 1997, 82, 6319–6325.
61. H. A. Al Attar and A. P. Monkman, Adv. Funct. Mater., 2006, 16, 2231–2242.

---

Footnote

† Electronic supplementary information (ESI) available: Synthetic procedures, chemical characterization data, liquid crystalline properties, electrochemical studies, charge mobility measurements, theoretical characterization. See DOI: 10.1039/d0tc05186a

---