The mechanism underlying the functionalisation of cobalt nanoparticles by carboxylic acids: a first-principles computational study

Abstract

The promise of biocompatible magnetic nanoparticles with high magnetic saturation in the implementation as drug carriers and hyperthermia agents has generated significant interest in functionalised cobalt nanoparticles. Carboxylic acid coatings on metallic nanoparticles have been shown as an attractive option owing to their respectable stability and biocompatibility. However, only limited information is available on the molecular mechanism leading to the formation of such protective coatings. In this study, ab initio molecular dynamics simulations have been used to unravel the functionalisation mechanism starting from a neutral cobalt cluster and valeric acid molecules. Three stages were detected in the coating process: (i) rapid initial adsorption of acid molecules, (ii) simultaneous adsorption of new molecules and dissociation of those already interacting with the cluster, and, finally, (iii) grouping of dissociated hydrogen atoms and subsequent desorption of acid molecules. The fate of the hydrogen atoms was probed through a combination of static and dynamic ab initio modelling approaches, which predicted H₂ generation with favourable energetics. A better understanding of the functionalisation and interaction mechanisms will aid the rational design of biocompatible cobalt nanoparticles for various applications.

---

1 Introduction

The unique electronic, magnetic, and chemical properties of particles at the nanoscale are, by now, well established, and, together with the extensive opportunities for their manipulation, they have shaped a growing range of nanoparticles (NP) applications, from energy generation (catalysis, batteries, solar cells) to biomedicine (drug delivery, magnetic nanoparticle hyperthermia).^1–8 Magnetic nanoparticle hyperthermia (mNPH) has been a promising player on the frontline of cancer treatment for about a decade, with many NP materials for this therapy being overshadowed by highly biocompatible iron oxides.^9,10 However, despite much research into shape and composition, the advantage of the biological harmlessness of magnetite, maghemite, and many other metal oxides lost its magnitude under the ineffectiveness of insufficient magnetisation, which has fostered interest into highly magnetic metal NPs.^11,12 Originating from the popularity of innocuous iron oxides, Fe NPs were a natural first choice and their smaller size and improved magnetic properties have suggested that iron-based magnetic carriers would be superior to the existing maghemite and magnetite NPs.¹³ Combinations of Fe with other metals, such as FePt,^14–16 FeNi,^17,18 and FeCo^19–21 nanoalloys, also appeared attractive. However, the high magnetic moment of cobalt NPs gives them an intrinsic advantage over the aforementioned materials, which can be exploited specifically in mNPH, where a combination of magnetisation and small diameters is crucial for the desired performance. Experimentally obtained heat generation capabilities of various metals and metal oxides have identified Co NPs to have the highest heating capacity for NP diameters under 10 nm.^22–24

Nevertheless, considerable challenges exist in adapting these metallic systems into pragmatic, functional biomaterials. The most important practical question regarding the design of metallic NPs for use in biomedicine is how to ensure a sufficiently long lifetime of NPs in the organism. This not only requires that the NPs do not disintegrate, aggregate, or lose their integrity otherwise, but also that they are not removed by the immune system. Additionally, for mNPH the NPs should maintain high levels of magnetisation throughout the duration of the therapy. These are significant impediments based on the interactions amongst NPs, as well as between the NPs and the biological environment, and it is suggested that they can be solved through NP functionalisation prior to administration.^25,26 Usually, functionalisation is achieved by applying an organic surfactant which is effective in adjusting the reactivity of metal NPs without affecting their magnetic properties, and preparation of stable colloidal suspensions of functionalised metal NPs in organic fluids has already been reported by different groups for Co,^27–29 Fe,³⁰ and FeCo NPs.³¹ The majority of published techniques for the effective stabilisation and bio-incorporation of Co NPs rely on acid surfactants, owing to their strong interaction established through the binding of the carboxyl group, with oleic acid being a paramount choice in the literature.^32–35 Only a limited number of studies considered other types of ligands, such as polymers.^36,37 Acid-encapsulated Co NPs have been tested for heating applications, including mNPH,^23,38 and as contrast agents for MRI,³⁹ and the results of these studies suggest that protected Co NPs show great potential as an alternative to iron oxides.

However, the multi-parameter nature of the stability of functionalised nanocomposites in respect to the physiological environment and phenomenological explanations at the atomic level are hardly accessible experimentally. The impact of the interplay between the NP core and ligands on the properties of coated NPs^40–42 makes it all the more important to fully understand these mechanisms and to be able to predict the structure of a proposed organic coating-magnetic core design. Theoretical simulations can be an important contributor in such cases, where quantum and atomistic calculations have already helped to reveal interactions in several systems that were unclear from experiment, as well as suggesting multiple NP materials for novel applications.^43–45 Gold has gathered by far the most interest for biomedical applications, owing to its inertness, radio-sensitizing capabilities, and easy functionalisation with thiols. Information collected on Au NPs both experimentally and theoretically ranges from the dependence of structural changes on the size of NPs,^46,47 through the mechanism of formation,^48–50 layout,^51,52 and influence of thiolate coatings on the membrane penetration,^53–55 to the irradiation of Au–SH nanocomposites and their performance in radiotherapy or drug delivery.⁵⁶ Despite their promising qualities, Co NPs remain under-explored, with only a few studies on their reactivity and functionalisation. Our recent work has revealed that size and strain effects govern the alternations of geometrical shape with the increase in size of Co NPs.⁵⁷ The follow-up study was focused on resolving contradictory experimental findings on the nature of the ligand-NP interactions in acid-functionalised Co NPs, assigning bridging bidentate as the preferential binding mode.^32,33,58 However, virtually nothing is known regarding the functionalisation mechanism or reactivity of coated Co NPs beyond this basic information. The ability of the chosen ligand to function according to the biological requirements depends largely on the structure of the coating which is a complicated function of the surface density and type of the molecule in combination with material, size, and shape of the NP core, whereas the functionalisation mechanism can be a determining factor.

To explore the mechanism behind the functionalisation of Co NPs with carboxylic acids, we have performed ab initio molecular dynamics (AIMD) simulations of the process of coating with the molecules of valeric acid. The structure and stability of the formed nanocomposite were traced throughout the simulation with a particular focus on the changes in the adsorption rate and binding modes of adsorbed molecules. After the three stages of the functionalisation process were identified, the detected reactivity changes caused by the increased acid coverage and carboxyl hydrogen dissociation paved the way towards simulations of H₂ generation and desorption. From the calculated energy barriers, it appears that the formation of hydrogen gas can be expected within the process of carboxylic acid functionalisation of Co NPs, similar to the results of studies carried on thiol-protected Au NPs.

2 Models and methods

The characteristic length scales of functionalised NPs are of the order of a few nanometres with the number of atoms often beyond a few thousands. This puts constraints on the simulations, as the complexity of the system in terms of size by far exceeds the practical limits of precise ab initio methods which explicitly treat the electron dynamics of the system. With the interest of spanning the dynamics of the ligand molecules while also gaining electronic-level information to monitor the energetic effects, ab initio molecular dynamics offered the best compromise in terms of system size and accuracy.

Inclusion of regions with increased activity, such as edges and vertices, through a cluster model increases the accuracy when predicting the dynamics of ligand molecules, compared to the limited movement possibilities on a flat surface. The size of the NP model was determined to mimic behaviour of experimentally realistic systems as closely as possible, while staying within the size ranges that can be simulated by the AIMD approach. For the purposes of functionalisation of Co NPs, a 57-atom cluster (approximately 1 nm in diameter) was shown to be at the lower limit of large nano-particulate behaviour regarding both electronic properties and carboxylic acid adsorption process.⁵⁸ Therefore, in this work, 57-atom hcp Co cluster, with two (0001) and twelve (101̄1) facets, was utilised to represent the Co NPs, and valeric acid with its 5-C atom chain, CH₃(CH₂)₃COOH, was used as a ligand.

As a baseline for simulating the functionalisation mechanism, the reference case of a single particle in the presence of acid molecules was established. The previously optimised 57-atom Co cluster was placed in the simulation box together with 14 molecules of valeric acid (corresponding to a coverage of one molecule per facet if all molecules were to be adsorbed). The real density of the liquid was inaccessible to model by AIMD. AIMD simulations were performed using CP2K^59,60 with the PBE⁶¹ exchange–correlation functional and the Goedecker, Teter, and Hutter (GTH) Gaussian basis set.⁶² The chosen system was simulated in the NVT ensemble during 10.00 ps of Born–Oppenheimer molecular dynamics. A Nosé–Hoover thermostat⁶³ was set at the synthesis temperature of T = 500 K,^33,34,64 and a time step of 1.0 fs was used for the integration of the equations of motion.

Hydrogen dissociation and the formation of H₂ were studied by both density functional theory (DFT) and metadynamics simulations. Nudged Elastic Band (NEB) calculations⁶⁵ were performed using the Vienna Ab Initio Simulation Package (VASP)⁶⁶ within the generalized gradient approximation (GGA) of the PBE functional. The DFT-D3 method with Becke–Johnson damping was used to include the long-range dispersion interactions⁶⁷ and the k-point grid contained only the Γ point. In order to gauge the relevance of the size of the NP which was captured for the thiol-gold system,⁶⁸ H₂ generation on the 57-atom cluster was compared to the same process on a 13-atom counterpart with well-established gas-phase stability.⁶⁹ In addition, a comparison in energy barriers of carboxyl and thiol ligands was carried out. To reduce the computational cost, smaller acetic acid and ethanethiol molecules were employed in these calculations. All intermediate and transition states were fully optimised and Hessian calculations were performed to verify the existence of one imaginary frequency for the transition states. CP2K was used instead for metadynamics trajectories, where Gaussian hills with a height of 0.01 Hartree and a width of 0.05 were deposited every 50 fs. VMD was used for post-processing.⁷⁰

3 Results

3.1 Functionalisation mechanism

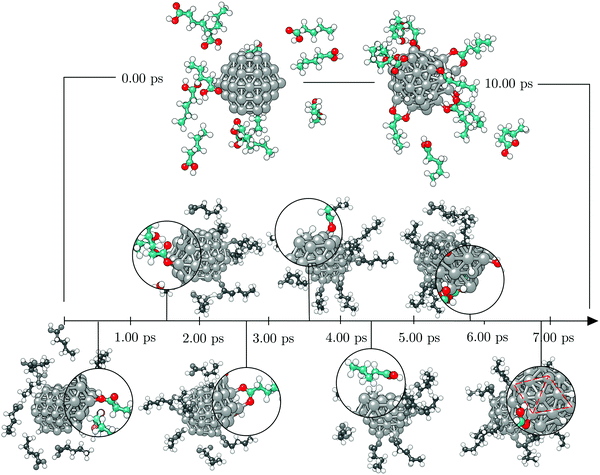
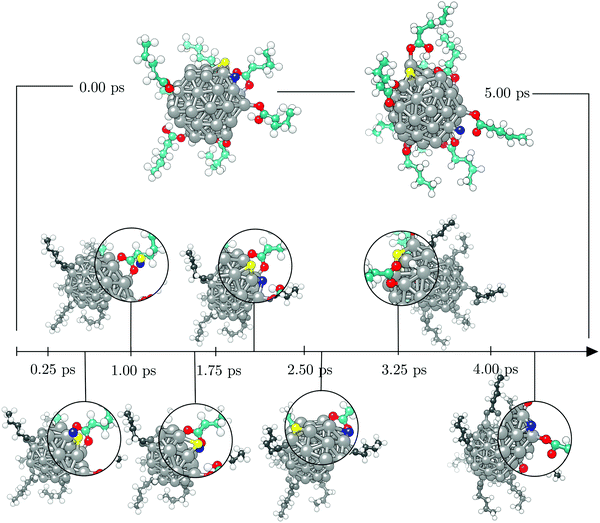
To investigate the functionalisation mechanism of Co NPs coated with carboxylic acids, a single 57-atom Co cluster was surrounded by 14 valeric acid molecules and AIMD relaxation was performed in a duration of 10.00 ps. Starting arrangement and optimised geometry after 10.00 ps are shown in the top panel of Fig. 1. The bottom panel of Fig. 1 contains the stimulation timescale with a few intermediate configurations capturing key events.

Fig. 1 Timeline of the 10.00 ps ab initio molecular dynamics run of the [57-atom Co NP – 14 valeric acid molecules] system with initial geometry given on the top left, the final geometry on the top right, and seven key events featured at the bottom in the order of their occurrence, i.e. first adsorption (0.60 ps), first dissociation (1.60 ps), formation of a bridging bidentate (2.50 ps), pairing of dissociated H atoms (3.20 ps), first desorption (4.40 ps), further grouping of dissociated H atoms (5.75 ps), cluster adopts icosahedral shape (6.80 ps). Grey, teal, red, and white spheres represent cobalt, carbon, oxygen, and hydrogen atoms, respectively.

Initially, the cluster and the randomly oriented acid molecules were separated by a distance of about 8 Å. Acid molecules immediately started to move towards the cluster and were progressively captured on the surface via a monodentate interaction, which is characterised by a single bond between one Co atom and one O atom of the –COOH group. Adsorption of the first molecule occurred after just half a picosecond. The molecule adsorbed onto the vertex Co atom of the (101̄1) surface through the –COOH oxygen atom which was bound to the carboxyl hydrogen. Shortly after, a second adsorbate molecule bound to another (101̄1) surface vertex, but this time the bond was established between the Co atom and the freestanding oxygen of carboxyl functional group. At 1.00 ps, a total of five molecules had already interacted with the cluster, one of them forming a bond with the (0001) surface vertex atom. Interestingly, regardless of the initial orientation, the acid molecules showed no preference for adsorption by one or other of the oxygen atoms of the carboxyl group; even if the –OH part was initially further away than the corresponding freestanding O atom of the –COOH group, some molecules interacted through the former. Within the next picosecond, half of the molecules attached to the cluster, mostly to vertex Co atoms, but still no pattern was observed regarding the oxygen atom through which the monodentate adsorption took place. There were also instances where an interchange of the oxygen atom interacting with the cluster would occur within the acid molecule. The coating at this point could have been characterised as isotropic, i.e. adsorbed molecules were found at isolated positions and no aggregation took place. Just before the simulation time reached 2.00 ps, one carboxyl hydrogen dissociated from its parent acid and less than 0.15 ps later a second dissociation happened. Each of the dissociated molecules formed two Co–O bonds with two available cluster atoms, thus adsorbing in a bridging bidentate mode. The dissociated hydrogen atoms effortlessly moved across the cluster through available bridge and hollow sites. As the simulation proceeded, within the next two picoseconds two more acids lost their carboxyl hydrogen atoms, while two previously unbound molecules adsorbed forming single Co–O bonds with the cluster. Even though a portion of adsorbed acid molecules was still interacting through the oxygen atom that was connected to the carboxyl hydrogen, dissociation happened in all four occasions on acids that were binding through the freestanding oxygen atom of the –COOH group. Dissociated acids were observed to quickly form bridging bidentate modes of interaction, typically within 0.25 ps after dissociation. In one instance, intermediate chelate state, where both oxygen atoms bind the same Co atom, was observed. At this point, the movement of dissociated hydrogen atoms started to be more localised, with a pair from the two earliest dissociations pulsing around the same vertex Co atom, simply interchanging amongst each others positions. This caused the nearby acid molecule, which was actively interacting with the cluster for over two picoseconds, to desorb at about 4.00 ps, followed by the adsorption of another acid molecule at an available site farther away. Grouping of the other pair of dissociated hydrogen atoms was also captured just after 4.50 ps on the vertex on the opposite side of the cluster. At the end of the 5.00 ps, nine acid molecules were attached to the surface of the cluster and four had dissociated and were interacting in a bridging bidentate mode. The remaining five molecules were adsorbed undissociated in a monodentate binding mode. No significant disruption in the shape of the cluster was observed thus far, as indicated by minimal changes in the radius of gyration, r_g, shown in Fig. 2.

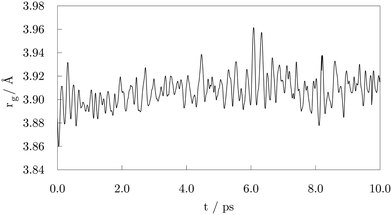Fig. 2 Radius of gyration, r_g, after the 10.00 ps of the ab initio molecular dynamics run of the functionalisation of 57-atom Co cluster with valeric acid.

Except for the constant repositioning of released hydrogen atoms, no further events were observed within the next half picosecond when an additional valeric acid molecule was adsorbed. With almost 40% of Co atoms on the surface of the cluster now directly interacting with oxygen atoms of adsorbed valeric acid molecules, shape of the cluster started to distort. Throughout the change, captured average values of the radius of gyration were around 3.96 Å, Fig. 2. Just after 6.00 ps, another dissociation occurred and it took almost a full picosecond for this latest dissociated carboxylic acid to establish a bridging bidentate interaction with the cluster because of the pulsating hydrogen atoms that were limiting the availably of surface Co atoms. This event was followed by the dissociation of yet another valeric acid at 7.00 ps, at which point the newly released H atom quickly paired with the hydrogen atom from the previous dissociation. By the time this acid formed a bridging bidentate mode with two Co atoms, the shape of the cluster had become icosahedral, and initial r_g values were retrieved, Fig. 2. The next dissociation was observed at 7.70 ps, followed by subsequent grouping of hydrogen atoms and the desorption, just before 8.25 ps, of yet another valeric acid molecule, whose adsorption was observed in the early stages of simulation (at 0.45 ps). Last dissociation happened just after 8.75 ps of the simulation time, where the final picosecond was marked as the longest period without the occurrence of any events, before the simulation was terminated at 10.00 ps.

At the end of the 10.00 ps run, ten acid molecules were attached to the surface of the cluster, eight of which had dissociated and were interacting through the bridging bidentate mode. The remaining two molecules were adsorbed undissociated in the monodentate binding mode, one bonding to the vertex Co atom and the other to the edge Co atom. One of the O–Co bonds was established through the oxygen atom interacting directly with the carboxyl hydrogen. That specific valeric acid molecule underwent multiple attempts to form a permanent bond with the cluster (average O–Co bond of interacting acid molecules being 1.9 Å), however, for the majority of the simulation time it was at a 2.2–2.4 Å distance from the cluster's surface, giving place to dissociated hydrogen atoms. The adsorbed acid molecules were distributed evenly across the whole cluster and both (0001) and (101̄1) surface areas, with the exception of the vertex sites where the dissociated hydrogen atoms resided.

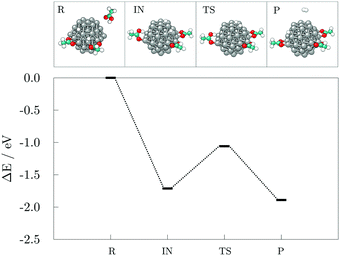
To evaluate the stability of the adsorption system, potential energy during the 10.00 ps run was plotted in Fig. 3. The figure illustrates a significant decrease in the potential energy of the system during the early stage of the simulation up to 1.00 ps followed by a relatively stable period of about 0.50 ps. Another noticeable drop in energy occurred at approximately 2.00 ps also followed by a stagnant trend and a more subtle decline that extends to 4.25 ps when the first occurrence of a loss in stability can be seen. After about 0.25 ps, the negative slope of the potential energy curve is restored. These alternations in stability occurred throughout the remaining time of the simulation, whereas the on-going decrease in the potential energy faded away after 7.00 ps, seemingly reaching equilibrium state in the number of adsorbed carboxylic acid molecules. Two additional striking drops at 7.10 ps and 8.75 ps correspond to the stability gained through the shape modification, and a further adsorption event as a response to the hydrogen-grouping triggered desorption destabilisation.

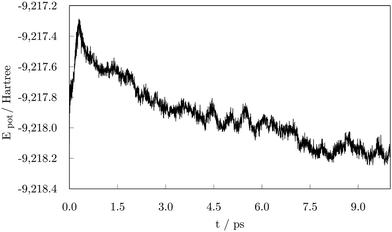Fig. 3 Potential energy as a function of time during the 10.00 ps ab initio molecular dynamics run on the 57-atom Co NP – 14 valeric acid molecules system.

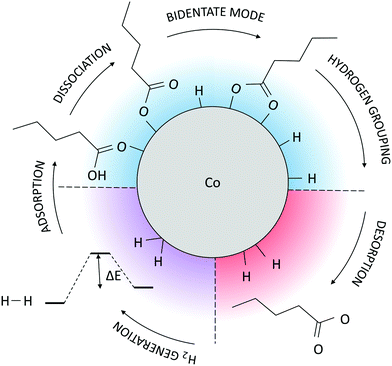
As the potential energy trend displays, the cluster functionalisation process can be divided into three distinct stages. Stage 1, in which a decrease in the potential energy is solely due to the effective adsorption of valeric acid molecules across the surface of the cluster at a relatively constant adsorption rate (first two picoseconds). In stage 2, the rate of adsorption is slowed down, and fluctuations in the potential energy of the system are caused by hydrogen dissociations and the establishment of bridging bidentate binding modes (between 2.00 ps and 4.50 ps). Finally, stage 3 comprises of alternating destabilisation and re-stabilisation periods characterised by desorption of valeric acid molecules near the locations of dissociated hydrogen atoms and counter-adsorption/dissociation of previously non-adsorbed/non-dissociated acid molecules at distinct sites of the cluster. In this final stage, the adsorption rate has reached the plateau, and adsorption is only induced in the instances of hydrogen-caused acid detachment to regain the equilibrium state of the system.

A schematic representation of the AIMD-predicted reaction mechanism is shown in Fig. 4. Considering that the available literature on the binding of carboxylic ligands to monometallic and bimetallic NPs and surfaces reports the bridging bidentate as the preferred mode of interaction in most cases with the occasional dominance of the chelate biding,^71–75 it is likely that the proposed functionalisation mechanism, or certain aspects of it, are also applicable to those systems. The true mechanisms for the acid functionalisation of other metallic NPs are, however, subject to future research efforts.

Fig. 4 Schematic representation of the AIMD-predicted mechanism for the acid-functionalisation of Co NPs. Colour scheme is as follows: steps shaded in blue are spontaneous and stabilising, steps shaded in red are destabilising, and steps shaded in purple are hindered by an energy barrier, but, once overcome, they lead to further stabilisation of the system.

In light of the proposed acid-functionalisation mechanism, follow-up experimental preparation and analysis via infrared (IR) and X-ray photoelectron spectroscopy (XPS), and evaluation of zeta potentials, could be employed to capture the effective surface charge and Co:C atomic ratio of functionalised NPs for a more accurate estimation of the carboxylic acid saturation rate, binding conformation, and packing density.^76–78 Changing the ionic strength of the medium might be a good strategy to obtain higher coating densities within the collapsed-site defects on the NP surface, as demonstrated on the example of Au NPs.⁷⁹

The observed behaviour, together with the comprehension that such organic coatings are often synthesised with the loss of hydrogen, indicates that the path of hydrogen should also be investigated. Throughout the simulation time, as more acid molecules lost their carboxyl hydrogen atoms, desorption started to occur, thereby destabilising the system. Since it is very unlikely that hydrogen atoms would detach from the cluster on the timescale of the AIMD simulations, a combination of NEB and ab initio metadynamics was chosen to model the occurrence and energetics of this rare event.

3.2 Fate of dissociated hydrogen

Very little is known about the reaction pathways of hydrogen atoms dissociated during the conjugation of organic surfactants with metal NPs. Even in the case of well-investigated thiol-gold systems, there are only a few very recent theoretical studies of the hydrogen transfer mechanism to support an experimentally suggested release of H₂ in the functionalisation process.^50,80 A previous AIMD work⁸¹ has shown that interaction of two thiols with a four-atom gold cluster results in the production of H₂ and formation of substructures containing adatom-like gold atoms pulled away from the cluster surface with almost linear RS–Au–SR bonding patterns. Such gold adatom-mediated substructures with alternating gold and sulphur atoms were first detected within the self-assembly of alkanethiolates on the Au(111) surface⁸² and are now known as staple motifs.^83,84 Later, the interaction of small gold clusters with one to 38 atoms was examined in a DFT study, which confirmed the thermodynamics of the H₂ generation and subsequent staple motif formation.⁶⁸ To the best of our knowledge, no information is available on cobalt-organic surfactant systems. To provide a greater understanding of the functionalisation mechanism of cobalt NPs by carboxylic acids, nudged elastic band algorithm was employed to investigate the dissociation, transfer, and recombination of hydrogen atoms associated with the carboxyl group, and the study was further extended to thiol ligands for comparison. To reduce the computational cost of expensive NEB calculations, 2C-atom chain ligands were used, i.e. acetic acid CH₃COOH, and ethanethiol CH₃CH₂SH, instead of the initially adopted 5-C atom counterparts. The effects of coverage and finite temperature were tested through metadynamics simulations on the original system.

3.2.1 Single-molecule adsorption. Adsorption energies of single molecules of acetic acid and ethanethiol at various available sites of the 13- and 57-atom Co clusters can be found in Table 1. Adsorption is spontaneous for all investigated positions, with the strongest interaction on the 13-atom cluster leading to the adsorption energies of −1.59 eV for acetic acid and −1.81 eV for ethanethiol. The 57-atom cluster is characterised by two (0001) and twelve (101̄1) surface areas, and adsorption was probed in available positions on both surfaces. Adsorption on the facet site of the surfaces was shown to be only half as strong as adsorption on the vertex Co atoms, with adsorption energies of −0.57/−0.53 and −1.08/−1.07 eV for facet and vertex adsorption of acetic acid on the (0001)/(101̄1) surface, respectively. Adsorption energies of ethanethiol were found to be −1.13/0.90 eV for the (0001)/(101̄1) facet adsorption sites, and −1.19 eV for adsorption on either of the cluster's vertices.

Table 1 Adsorption energies, E_ads, and Co–O distances, d_Co–O, after the adsorption of acetic acid and ethanethiol on 13- and 57-atom Co clusters as calculated by DFT

N	Position	Acetic acid		Ethanethiol
		E ads/eV	d Co–O/Å	E ads/eV	d Co–O/Å
13	Vertex	−1.59	1.944	−1.81	2.167
57	0001 facet	−0.57	2.104	−1.13	2.216
	0001 vertex	−1.08	1.956	−1.19	2.187
	101̄1 facet	−0.53	2.039	−0.90	2.222
	101̄1 vertex	−1.07	2.026	−1.19	2.197

---

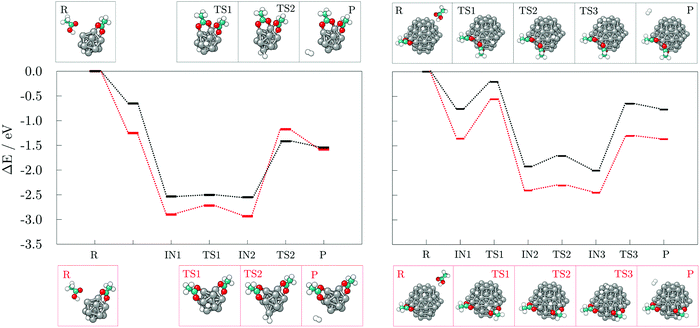
Next, the reaction pathways from the adsorption of acetic acid and ethanethiol on cobalt clusters to the formation of H-Co-OOCCH₃ and H-Co-SCH₂CH₃ complexes were calculated to determine the rate-limiting step. The reaction pathways, together with optimised structures, are shown in Fig. 5 for acetic acid and Fig. 6 for ethanethiol, on both 13- and 57-atom clusters.

Fig. 5 Reaction pathways and accompanying optimised structures of single acetic acid adsorption, dissociation, and subsequent hydrogen movement on the 13- (left) and 57-atom Co cluster (right). Two mechanisms on the 57-atom cluster distinguish between the adsorption on the (0001) and (101̄1) facets, with depicted structures corresponding to the (101̄1) surface. R, IN(1,2), TS(1,2), and P stand for reactants, intermediate and transition states, and products, respectively. Grey, teal, red, and white spheres represent cobalt, carbon, oxygen, and hydrogen atoms, respectively.

Fig. 6 Reaction pathways and accompanying optimised structures of single ethanethiol adsorption, dissociation, and subsequent hydrogen movement on the 13- (left) and 57-atom Co cluster (right). R, IN(1,2), TS(1,2), and P stand for reactants, intermediate and transition states, and products, respectively. Grey, teal, yellow, and white spheres represent cobalt, carbon, sulphur, and hydrogen atoms, respectively.

For acetic acid, the first transition state involves in both cases the transfer of the carboxyl hydrogen from acid molecule over a Co–Co bridge towards the nearest available three-fold adsorption site on the cluster. The interaction mode thus formed has no cobalt atoms shared between the dissociated hydrogen and bonding carboxyl oxygen atoms. Considering the limited size of the 13-atom cluster, the only possible transition is over the clusters edge, with the energy barrier of 0.70 eV. Extended surface areas of the 57-atom cluster allow transfer of hydrogen along the same facet during dissociation, which considerably reduces the energy barrier to 0.15 eV in the case of the (0001) surface, and to 0.13 eV in the case of the (101̄1) surface. Once the hydrogen is dissociated from the acid molecule, it is relatively free to move around the cluster over sites which are not saturated by Co–O interactions. This is shown by transition barriers of the subsequent hydrogen movement which were calculated to be 0.09 eV on the 13-atom cluster, and 0.20, and 0.18 eV on the (0001) and (101̄1) surfaces of the 57-atom cluster. Upon dissociation, the acid molecule proceeds to interact in a bridging bidentate adsorption mode.

The transition state of ethanethiol dissociation is characterised by a similar transfer of thiol hydrogen atom over a Co–Co bridge, with the rest of the molecule tilting in the opposite direction to form a second S–Co bond with the nearest cobalt atom. The difference compared to the acetic acid case is that the hydrogen atom adsorbs at the closest three-fold hollow adsorption site by sharing one of the cobalt atoms which interacts with the sulphur. This transition state lies 0.26 eV above the undissociated ethanethiol-13-atom cluster complex, and 0.44 eV above the undissociated ethanethiol-57-atom cluster complex. Energy barriers for the movement of dissociated hydrogen are still relatively low, i.e. 0.22 and 0.33 eV for the 13- and 57-atom cobalt cluster, respectively.

The dissociation transition state lies significantly below the energy of separated reactants and, thus, this reaction should proceed easily, as seen in the AIMD simulations, where spontaneous dissociation of valeric acid was observed on the 57-atom Co cluster.

3.3 Two-molecule adsorption

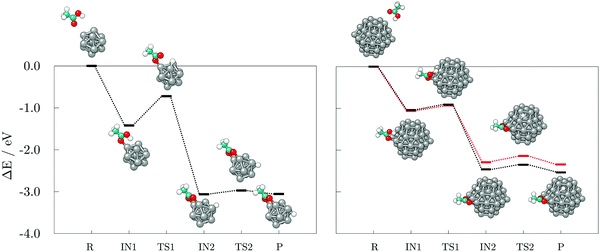
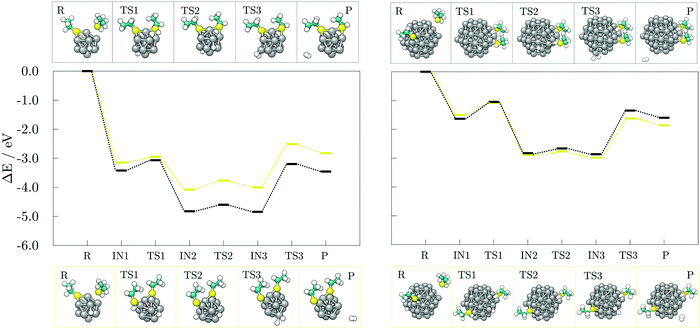
To develop an understanding of the formation of H₂ from dissociated hydrogen atoms, a second adsorbate molecule is required. Adsorption of the second adsorbate onto the site which is already coordinated, such that the two molecules both bind to the same atom of the cluster, was shown to be preferred in the case of thiol adsorption on the gold cluster, and it was accompanied by the rearrangement into a staple motif.⁶⁸ The formation of such motifs, as well as the influence of the adsorption sites of the second molecule on the generation of H₂, were probed on the 13- and 57-atom Co clusters.

The reaction mechanism for the adsorption and dissociation of the second acetic acid molecule at both uncoordinated and coordinated sites, and recombination of the pair of dissociated hydrogen atoms on the 13-atom Co cluster is shown in the left panel of Fig. 7. The dissociation of the second acid molecule is spontaneous and the movement of the dissociated hydrogen atom is unhindered, similar to the adsorption of a single acid molecule. The transition barrier is 0.18 eV when the second acid is adsorbed at the uncoordinated site on the cluster, and 0.03 eV when it is adsorbed at the coordination site of the first acid. However, desorption of H₂ requires for two hydrogen atoms to interact within a single vertex cobalt atom, which is followed by a slight pull-out of the interacting Co atom. This transition state requires overcoming a rather large energy barrier of 1.76 eV when two acids are adsorbed on remote sites of the cluster, but 1.13 eV if they are coordinated to the same Co atom. Adsorption of the second acetic acid onto the uncoordinated cobalt atom (E_ads = −1.25 eV) is favoured over sharing the interaction site (E_ads = −0.65 eV) by 0.60 eV in the undissociated state, and by approximately 0.35 eV after dissociation. Once the hydrogen molecule is formed, the cluster-acid complexes have similar stabilities. However, the reaction energy for the production of hydrogen gas starting from the adsorption of the second acid at the uncoordinated site is −0.33 eV, which almost triples to −0.89 eV when one cobalt atom is shared between the two adsorbed acids.

Fig. 7 Reaction pathways and accompanying optimised structures of the adsorption and dissociation of second acetic acid and subsequent recombination of hydrogen atoms into hydrogen gas on the 13-atom (left) and on the (101̄1) surface of the 57-atom (right) Co cluster. Red pathway corresponds to the adsorption of second acid molecule at the uncoordinated site on the cluster, while black pathway corresponds to the adsorption at the coordination site of the initially adsorbed acid. R, IN(1,2,3), TS(1,2,3), and P stand for reactants, intermediate and transition states, and products, respectively. Grey, teal, red, and white spheres represent cobalt, carbon, oxygen, and hydrogen atoms, respectively.

The 57-atom cluster offers many distinct uncoordinated adsorption sites, but since the vertex atoms showed significantly favoured adsorption, only vertex positions will be considered for the adsorption of the second acid. There is no obvious preference between the (0001) and (101̄1) surfaces when it comes to the adsorption of the second acid in a position that is remote from the cluster site already interacting with previously adsorbed acid molecule, with the difference in the E_ads of only 0.06 eV (E_ads(0001) = −1.20 eV and E_ads(101̄1) = −1.26 eV). Optimisation of the two acids adsorbed to a common vertex atom of the (0001) surface has led to repositioning of one of the acids, resulting in their adsorption more remotely at the cluster. Adsorption on the uncoordinated portion of the cluster remains favoured by 0.60 eV over the shared Co atom site on the (101̄1) surface (E_ads = −0.67 eV), as it was the case on the 13-atom cluster.

The subsequent reaction mechanism for the dissociation of the second acetic acid and H₂ generation at the (101̄1) surface of the 57-atom cluster is shown in the right panel of Fig. 7. In contrast to to the 13-atom cluster, the dissociation barrier for the second acetic acid is 0.80 eV when adsorbed at the uncoordinated site and 0.55 eV when sharing the adsorption site with the other acid. These energy barriers are considerably higher than the 0.15 eV barrier found for the initially adsorbed molecule, although dissociation of multiple acids was indeed observed in the AIMD functionalisation run. The subsequent movement of dissociated hydrogen remained relatively unconstrained with energy costs of 0.10–0.25 eV. The desorption and formation of H₂ upon the adsorption of two acetic acid molecules at remote sites of the 57-atom cluster is accompanied by an energy barrier of 1.15 eV. The barrier is thus reduced by 0.61 eV compared to the same adsorption arrangement on the 13-atom cluster. Structural distortion of the desorption cobalt site is also significantly less pronounced. Where two acids are coordinated to share the interacting cobalt atom, desorption of hydrogen atoms is energetically more restricted, with a barrier of 1.35 eV, which is 0.22 eV higher than on the cluster with 13 Co atoms. Another pronounced difference between the two cluster sizes is the stability of formed acid-cluster complexes, with the shared coordination site complex on the 57-atom cluster being 0.60 eV less stable compared to its counterpart with two acids at distinct adsorption sites. The reaction energy of H₂ generation in reference to the acid-cluster complex with one dissociated and one undissociated acetic acid is −0.010 eV and it remains almost unchanged at −0.012 eV when the molecules share the adsorption site.

Results for the adsorption at the uncoordinated site of the (0001) surface are fairly similar to the (101̄1) surface and a detailed description has thus been omitted. The energy barrier for the dissociation of the second acid is calculated at 0.63 eV and that of the hydrogen movement at 0.18 eV. Transition state for H₂ desorption is 1.17 eV higher in energy compared to the preceding intermediate state.

Finally, a third acid molecule was adsorbed onto the 57-atom Co cluster. Based on the previous findings, only the interaction on a distinct (101̄1) facet of the cluster was considered, with the first two acids not sharing their adsorption sites. The sole adsorption of another acid in an undissociated form did not alter the barrier of H₂ generation and desorption, which was found to be 1.21 eV. However, upon dissociation, the energy barrier was reduced to 0.65 eV with a reaction energy for hydrogen recombination of −0.18 eV, Fig. 8.

Fig. 8 Reaction pathway and accompanying optimised structures of the adsorption and dissociation of the third acetic acid and subsequent recombination of hydrogen atoms into hydrogen gas on the (101̄1) surface of the 57-atom Co cluster. R, IN, TS, and P stand for reactants, intermediate and transition states, and products, respectively. Grey, teal, red, and white spheres represent cobalt, carbon, oxygen, and hydrogen atoms, respectively.

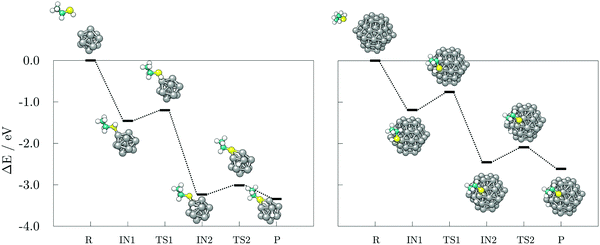
Hydrogen gas generation was probed for ethanethiol as well, at both uncoordinated and coordinated adsorption sites, with the reaction mechanisms presented in Fig. 9. The transition state barrier for the dissociation of the second ethanethiol molecule on the 13-atom cluster is 0.20 eV when adsorbed at the uncoordinated site, and 0.36 eV in the case of a shared Co atom interaction between the two molecules, which is similar to the dissociation of the first ethanethiol molecule. Likewise, the dissociated hydrogen atom can move around the cluster with minimal effort, the movement barrier being around 0.20 eV regardless of the adsorption site. The energy barrier and reaction energy for production and desorption of H₂ are, however, much more sensitive to the adsorption site of the second ethanethiol molecule. For hydrogen gas to form and leave the cluster, a barrier of 1.49 eV needs to be overcome if the second adsorbate molecule adsorbs at a remote adsorption site. The energetic cost increases to 1.65 eV when the two adsorbate molecules interact within shared cobalt atom. However, a difference in the reaction energy to obtain the products owing to the initially adsorbed state of the two molecules has greater impact; adsorption within the same site lowers the reaction energy from the endothermic value of uncoordinated site adsorption of 0.32 eV to the slightly exothermic value of −0.03 eV. Thus, compared to the acetic acid, the adsorption of two molecules of ethanethiol on the 13-atom Co cluster is more favourable for H₂ formation when they share the adsorption site. Formation of a staple motif is not as pronounced as on the gold clusters, but Co atom positioned between the two sulphur atoms is slightly dislocated from the cluster and the distance to the central atom is lengthened by 5.8%.

Fig. 9 Reaction pathways and accompanying optimised structures of the adsorption and dissociation of second ethanethiol and subsequent recombination of hydrogen atoms into hydrogen gas on the 13-atom (left) and on the (101̄1) surface of the 57-atom (right) Co cluster. Yellow pathway corresponds to the adsorption of second ethanethiol molecule at the uncoordinated site on the cluster, while black pathway corresponds to the adsorption at the coordination site of the initially adsorbed ethanethiol. R, IN(1,2,3), TS(1,2,3), and P stand for reactants, intermediate and transition states, and products, respectively. Grey, teal, yellow, and white spheres represent cobalt, carbon, sulphur, and hydrogen atoms, respectively.

Adsorption energies for the second ethanethiol molecule on the 57-atom Co cluster at the uncoordinated and at the site of the initially adsorbed ethanethiol are −1.97 and −2.04 eV, respectively. However, the energetic preference for interaction within the same Co atom is lost upon the dissociation of the second ethanethiol molecule, which is characterised by a 0.42 eV barrier when the two molecules are adsorbed separately, but a 0.58 eV barrier if they are adsorbed at the same adsorption site. The transition of hydrogen from one available three-fold site of the cluster to another is energetically less consuming, 0.12–0.17 eV. The transition state for the desorption of the dissociated hydrogen atoms in the form of a hydrogen molecule is accompanied by energy barriers of 1.36 eV for the two ethanethiol molecules at separate adsorption sites, and 1.52 eV for the staple-like arrangement of the pair of ethanethiol molecules. The barriers are reduced by 0.10 eV in average in comparison to the 13-atom cluster. Nevertheless, the reaction energy for the hydrogen recombination process is much more favourable when two adsorbates are not directly interacting within the same cobalt atom (−0.36 eV) than when they share the interaction site (0.03 eV), which is in a sheer contrast to the 13-atom cluster thiol complexes.

3.4 H₂ generation metadynamics

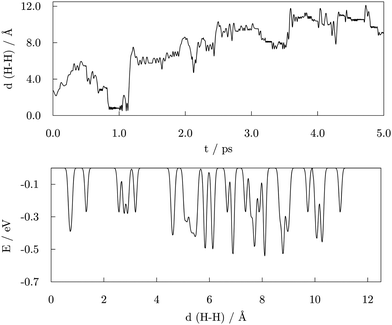
A 5.00 ps metadynamics run was carried out to completely explore the free energy landscape, with the distance between the two dissociated –COOH hydrogen atoms implemented as a collective variable to capture the transition barriers for H₂ generation more realistically. The starting geometry was taken from the AIMD functionalisation run, prior to the first acid desorption event. The observed H–H distances and the resulting free energy landscape as a function of the H–H distance are shown in Fig. 10.

Fig. 10 Top: H–H distance progression during the 5.00 ps metadynamics run for the system comprising of 57-atom Co NP and 14 valeric acid molecules; Bottom: Resulting free energy landscape as a function of the H–H distance as a collective variable.

Initially, the two hydrogen atoms were bridging the same vertex Co atom at a mutual distance of 2.76 Å, where they were observed to interchange positions for a significant period of time throughout the AIMD run, as depicted on the top left of the Fig. 11. The same interchanging trend was continued in the majority of the first picosecond of the metadynamics simulation, with H atoms ‘orbiting’ around the vertex Co atom through hollow and bridge sites. Just before the simulation time reached 1.00 ps, the H–H distance approached that of the H₂ bond and the newly formed hydrogen molecule detached from the cluster, also shown in Fig. 11. The system existed in this state for about 0.30 ps, followed by a dissociation of the H₂ entity and re-adsorption of the H atoms at a site of the cluster which did not coincide with the detachment point. The hydrogen atoms briefly maintained a shared type of interaction within the same Co atom before exploring distant parts of the cluster away from each other. In the period between 3.50 and 4.00 ps, additional dissociations of two carboxylic acids were observed, inducing independent movement of the two H atoms of interest towards remote, newly dissociated H atoms to form new grouping sites. At about 4.50 ps, the two H atoms of one of the new H–H pairs formed the transition state previously observed for the two initial hydrogen atoms of interest and desorbed shortly after from the cluster in the form of H₂. This event was taken as the termination point of the simulation, and it is depicted in the top right area of Fig. 11.

Fig. 11 Timeline of the 5.00 ps metadynamics run on the [57-atom Co NP – 14 valeric acid molecules] system with initial geometry given on the top left, the final geometry on the top right, and seven key events featured an the bottom in the order of their occurrence during the simulation. Acid molecules adsorbed on the front of the cluster were hidden for clarity. The two hydrogen atoms of interest, whose H–H distance was taken as a collective variable, are distinguished as yellow and blue spheres. Grey, teal, red, and white spheres represent cobalt, carbon, oxygen, and remaining hydrogen atoms, respectively.

The bottom panel of Fig. 10 depicts the free energy landscape as spanned over the H–H distance collective variable. The numerous minima captured for distances above 2.00 Å correspond to the positioning of two dissociated hydrogen atoms in various hollow and bridge positions available around the cluster. With energies between −0.28 and −0.53 eV, different combinations of hydrogen atoms situated in hollow and/or bridge positions presented similar energetic favourability. The alternating environment of available sites (proximity of edges, vertices, and adsorbed acid molecules) also affects the energetics of obtained minima. The energy barriers for the transitions between these combinations range from as low as 0.03 eV up to 0.50 eV, which confirms the low energy cost of hydrogen movement over the surface of the cluster, as predicted by DFT. A minimum with energy of −0.27 eV at a 1.32 Å H–H distance corresponds to the structure where the two H atoms have left favourable multi-fold positions and have each formed a single bond with the same Co atom, which resembles the transition state structures obtained by DFT. However, in contrast to the DFT geometry, the interacting Co atom was not pulled out from the cluster structure during the metadynamics simulation. Finally, another minimum is observed for the H–H distance of 0.75 Å, which corresponds to the bond length of a diatomic H₂ molecule, with an energy of −0.39 eV. Hence, the transition from the simultaneous interaction of both H atoms within the same vertex of the cluster to the generation and detachment of the H₂ molecule is predicted to have an energy cost of around 0.27 eV. This is a notably lower energy barrier than that calculated by DFT, which gives an indication of the influence that the presence of adsorbed valeric acid molecules and the experimental temperature conditions have on the strain and electronic properties of the cluster.

Metadynamics investigation of H₂ formation within the thiol-protected four-atom gold cluster captured a rearrangement of gold atoms, followed by an energy barrier of 1.21 eV for the desorption of the hydrogen molecule.⁸¹ However, a model of this size has only a limited capability to predict the behaviour of NPs. DFT calculations at 0 K have already shown significant differences in the energetics as the cluster size grows and a transition barrier of H₂ generation and detachment on a 12-atom Au cluster was predicted at 0.67 eV, around half that of the four-atom one.⁶⁸ This trend correlates with the reduction in the transition barrier obtained when going from the 13- to the 57-atom cobalt cluster predicted by our DFT calculations. The lower energy barrier of Au clusters compared to Co clusters emanates from the formation of thiolate staple motifs, which were not found to be as favourable and as geometrically pronounced for cobalt. Additionally, it is well-known that hydrogen binds more weakly to cobalt than to gold clusters,^85,86 offering a compromise in the energy costs despite the failure to form highly stable staple motifs. Overall, the 57-atom Co cluster used in this study is considered to offer a fairly good representation for the NP behaviour. The energy barrier for the detachment of H₂ obtained in the metadynamics simulations is found to be lower than what has been reported by DFT calculations for gold clusters, which can be explained by the differences in the binding energy of hydrogen and the increased number of adsorbate molecules present.

When considering adsorption strengths of hydrogen on the NPs and surfaces of different metals, calculated binding energies can vary by up to ±1.50 eV, which could significantly alter the energy costs of H₂ formation and desorption.^87–89 In addition, most favourable adsorption sites are also case-dependent, and hence the fate of dissociated hydrogen atoms captured here for the acid-functionalised Co NPs is not expected to be maintained across the transition metal row. Moreover, bimetallic alloying at the nanoscale is an increasingly popular strategy to tune material properties, and it could possibly provide a transparent solution for the reduction of hydrogen desorption barriers in cases where the established interaction is too strong on monometallic NPs, with examples of modified hydrogen binding available in the literature.^90–92

4 Conclusions

The mechanism of functionalisation of cobalt NPs by carboxylic acids was probed with AIMD, which has shown that the process can be resolved in three stages: (i) stage of sole adsorption, (ii) stage of concurrent dissociation of adsorbed molecules and adsorption of non-interacting molecules, and (iii) stage of alternating dissociation, desorption, and counter-adsorption processes with the stagnant potential energy and extensive aggregation of dissociated hydrogen atoms. The latter has been shown to prevent any further adsorption of acid molecules and hinder the formation of a protective coating of higher density, despite 40% of surface atoms still being accessible.

The investigation of H₂ formation and detachment from the cluster's surface revealed energetically feasible barriers for the generation of hydrogen gas within the functionalisation process and reduction of the barrier is observed for larger metal clusters. Furthermore, the desorption energy of H₂ from Co clusters has similar trends as the well-studied thiol-gold systems when predicted by DFT, while metadynamics simulations, which incorporated synthesis temperature and multiple ligand molecules, showed a significant reduction in the energy barriers. The insights into carboxylic acid functionalisation provided by this study will help design cobalt NPs suitable for a range of biomedical applications.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

BF is grateful to Cardiff University for support through a Research Scholarship from the School of Chemistry. We acknowledge the Engineering and Physical Sciences Research Council (Grant no. EP/R512503/1 and EP/K009567/2) for funding. This work was performed using the computational facilities of the Advanced Research Computing @ Cardiff_(ARCCA) Division, Cardiff University. Via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work made use of the facilities of ARCHER, the UK's national high-performance computing service, which is funded by the Office of Science and Technology through EPSRC's High End Computing Programme. Information on the data underpinning the presented results, including how to access them, can be found in the Cardiff University data catalogue at http://doi.org/10.17035/d.2020.0121356877.

References

1. E. A. Coronado, E. R. Encina and F. D. Stefani, Optical properties of metallic nanoparticles: manipulating light, heat and forces at the nanoscale, Nanoscale, 2011, 3, 4042–4059.
2. Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J Applications of magnetic nanoparticles in biomedicine, J. Phys. D: Appl. Phys., 2003, 36, R167–R181.
3. E. C. Dreaden, A. M. Alkilany, X. Huang, C. J. Murphy and M. A. El-Sayed, The golden age: gold nanoparticles for biomedicine, Chem. Soc. Rev., 2012, 41, 2740–2779.
4. M. Angelakeris, Magnetic nanoparticles: a multifunctional vehicle for modern theranostics, Biochim. Biophys. Acta, Gen. Subj., 2017, 1861, 1642–1651.
5. T. A. Rocha-Santos, Sensors and biosensors based on magnetic nanoparticles, TrAC, Trends Anal. Chem., 2014, 62, 28–36.
6. D. Astruc, Introduction: Nanoparticles in Catalysis, Chem. Rev., 2020, 120, 461–463.
7. J. Balach, J. Linnemann, T. Jaumann and L. Giebeler, Metal-based nanostructured materials for advanced lithium-sulfur batteries, J. Mater. Chem. A, 2018, 6, 23127–23168.
8. T. S. Rodrigues, A. G. Da Silva and P. H. Camargo, Nanocatalysis by noble metal nanoparticles: controlled synthesis for the optimization and understanding of activities, J. Mater. Chem. A, 2019, 7, 5857–5874.
9. S. Laurent, S. Dutz, U. O. Häfeli and M. Mahmoudi, Magnetic fluid hyperthermia: focus on superparamagnetic iron oxide nanoparticles, Adv. Colloid Interface Sci., 2011, 166, 8–23.
10. R. R. Shah, T. P. Davis, A. L. Glover, D. E. Nikles and C. S. Brazel, Impact of magnetic field parameters and iron oxide nanoparticle properties on heat generation for use in magnetic hyperthermia, J. Magn. Magn. Mater., 2015, 387, 96–106.
11. Z. Nemati, J. Alonso, L. M. Martinez, H. Khurshid, E. Garaio, J. A. Garcia, M. H. Phan and H. Srikanth, Enhanced Magnetic Hyperthermia in Iron Oxide Nano-Octopods: Size and Anisotropy Effects, J. Phys. Chem. C, 2016, 120, 8370–8379.
12. A. Espinosa, R. Di Corato, J. Kolosnjaj-Tabi, P. Flaud, T. Pellegrino and C. Wilhelm, Duality of Iron Oxide Nanoparticles in Cancer Therapy: Amplification of Heating Efficiency by Magnetic Hyperthermia and Photothermal Bimodal Treatment, ACS Nano, 2016, 10, 2436–2446.
13. E. E. Carpenter, Iron nanoparticles as potential magnetic carriers, J. Magn. Magn. Mater., 2001, 225, 17–20.
14. S. Maenosono and S. Saita, Theoretical assessment of FePt nanoparticles as heating elements for magnetic hyperthermia, IEEE Trans. Magn., 2006, 42, 1638–1642.
15. M. S. Seehra, V. Singh, P. Dutta, S. Neeleshwar, Y. Y. Chen, C. L. Chen, S. W. Chou and C. C. Chen, Size-dependent magnetic parameters of fcc FePt nanoparticles: applications to magnetic hyperthermia, J. Phys. D: Appl. Phys., 2010, 43, 145002.
16. C. L. Chen, L. R. Kuo, S. Y. Lee, Y. K. Hwu, S. W. Chou, C. C. Chen, F. H. Chang, K. H. Lin, D. H. Tsai and Y. Y. Chen, Photothermal cancer therapy via femtosecond-laser-excited FePt nanoparticles, Biomaterials, 2013, 34, 1128–1134.
17. K. L. McNerny, Y. Kim, D. E. Laughlin and M. E. McHenry, Chemical synthesis of monodisperse γ-Fe-Ni magnetic nanoparticles with tunable Curie temperatures for self-regulated hyperthermia, J. Appl. Phys., 2010, 107, 10–13.
18. A. Salati, A. Ramazani and M. Almasi Kashi, Deciphering magnetic hyperthermia properties of compositionally and morphologically modulated FeNi nanoparticles using first-order reversal curve analysis., Nanotechnology, 2019, 30, 025707.
19. L. M. Lacroix, R. B. Malaki, J. Carrey, S. Lachaize, M. Respaud, G. F. Goya and B. Chaudret, Magnetic hyperthermia in single-domain monodisperse FeCo nanoparticles: evidences for Stoner-Wohlfarth behavior and large losses, J. Appl. Phys., 2009, 105, 023911.
20. Y. Jing, H. Sohn, T. Kline, R. H. Victora and J. P. Wang, Experimental and theoretical investigation of cubic FeCo nanoparticles for magnetic hyperthermia, J. Appl. Phys., 2009, 105, 07B305.
21. Ö. Çelik and T. Frat, Synthesis of FeCo magnetic nanoalloys and investigation of heating properties for magnetic fiuid hyperthermia, J. Magn. Magn. Mater., 2018, 456, 11–16.
22. L. Kafrouni and O. Savadogo, Recent progress on magnetic nanoparticles for magnetic hyperthermia, Prog. Biomater., 2016, 5, 147–160.
23. M. Zeisberger, S. Dutz, R. Müller, R. Hergt, N. Matoussevitch and H. Bönnemann, Metallic cobalt nanoparticles for heating applications, J. Magn. Magn. Mater., 2007, 311, 224–227.
24. A. H. Habib, C. L. Ondeck, P. Chaudhary, M. R. Bockstaller and M. E. McHenry, Evaluation of iron-cobalt/ferrite core–shell nanoparticles for cancer thermotherapy, J. Appl. Phys., 2008, 103, 07A307.
25. R. A. Bohara, N. D. Thorat and S. H. Pawar, Role of functionalization: strategies to explore potential nano-bio applications of magnetic nanoparticles, RSC Adv., 2016, 6, 43989–44012.
26. H. Heinz, C. Pramanik, O. Heinz, Y. Ding, R. K. Mishra, D. Marchon, R. J. Flatt, I. Estrela-Lopis, J. Llop and S. Moya, et al., Nanoparticle decoration with surfactants: molecular interactions, assembly, and applications, Surf. Sci. Rep., 2017, 72, 1–58.
27. M. Wagener, B. Günther and E. Blums, Preparation of oxidation resistant cobalt oil colloids, J. Magn. Magn. Mater., 1999, 201, 18–22.
28. X. X. Zhang, G. H. Wen, G. Xiao and S. Sun, Magnetic relaxation of diluted and self-assembled cobalt nanocrystals, J. Magn. Magn. Mater., 2003, 261, 11–28.
29. H. Bönnemann, W. Brijoux, R. Brinkmann, N. Matoussevitch, N. Waldöfner, H. Palina and N. Modrow, A size-selective synthesis of air stable colloidal magnetic cobalt nanoparticles., Inorg. Chim. Acta, 2003, 350, 617–624.
30. R. Mendoza-Reséndez, O. Bomati-Miguel, M. P. Morales, P. Bonville and C. J. Serna, Microstructural characterization of ellipsoidal iron metal nanoparticles, Nanotechnology, 2004, 15, S254–S258.
31. A. Hütten, D. Sudfeld, I. Ennen, G. Reiss, K. Wojczykowski and P. Jutzi, Ferromagnetic FeCo nanoparticles for biotechnology, J. Magn. Magn. Mater., 2005, 293, 93–101.
32. N. Wu, L. Fu, M. Su, M. Aslam, K. C. Wong and V. P. Dravid, Interaction of Fatty Acid Monolayers with Cobalt Nanoparticles, Nano Lett., 2004, 4, 383–386.
33. S. M. Ansari, R. D. Bhor, K. R. Pai, D. Sen, S. Mazumder, K. Ghosh, Y. D. Kolekar and C. V. Ramana, Cobalt nanoparticles for biomedical applications: facile synthesis, physiochemical characterization, cytotoxicity behavior and biocompatibility, Appl. Surf. Sci., 2017, 414, 171–187.
34. H. T. Yang, C. M. Shen, Y. G. Wang, Y. K. Su, T. Z. Yang and H. J. Gao, Stable cobalt nanoparticles passivated with oleic acid and triphenylphosphine, Nanotechnology, 2004, 15, 70–74.
35. S. Sun and C. B. Murray, Synthesis of monodisperse cobalt nanocrystals and their assembly into magnetic superlattices (invited), J. Appl. Phys., 1999, 85, 4325–4330.
36. C. Dobbrow and A. M. Schmidt, Improvement of the oxidation stability of cobalt nanoparticles, Beilstein J. Nanotechnol., 2012, 3, 75–81.
37. L. Tan, B. Liu, K. Siemensmeyer, U. Glebe and A. Böker, Synthesis of thermo-responsive nanocomposites of superparamagnetic cobalt nanoparticles/poly(N-isopropylacrylamide), J. Colloid Interface Sci., 2018, 526, 124–134.
38. R. Hergt, S. Dutz, R. Müller and M. Zeisberger, Magnetic particle hyperthermia: nanoparticle magnetism and materials development for cancer therapy, J. Phys.: Condens. Matter, 2006, 18, S2919.
39. L. M. Parkes, R. Hodgson, L. T. Lu, L. D. Tung, I. Robinson, D. G. Fernig and N. T. K. Thanh, Cobalt nanoparticles as a novel magnetic resonance contrast agent-relaxivities at 1.5 and 3 Tesla, Contrast Media Mol. Imaging, 2008, 3, 150–156.
40. P. Crespo, R. Litrán, T. C. Rojas, M. Multigner, J. M. De La Fuente, J. C. Sánchez-López, M. A. García, A. Hernando, S. Penadés and A. Fernández, Permanent magnetism, magnetic anisotropy, and hysteresis of thiolcapped gold nanoparticles, Phys. Rev. Lett., 2004, 93, 049903.
41. O. Margeat, C. Amiens, B. Chaudret, P. Lecante and R. E. Benfield, Chemical control of structural and magnetic properties of cobalt nanoparticles, Chem. Mater., 2005, 17, 107–111.
42. M. J. Hartmann, J. E. Millstone and H. Häkkinen, Surface Chemistry Controls Magnetism in Cobalt Nanoclusters, J. Phys. Chem. C, 2016, 120, 20822–20827.
43. A. Vincent, S. Babu, E. Heckert, J. Dowding, S. M. Hirst, T. M. Inerbaev, W. T. Self, C. M. Reilly, A. E. Masunov and T. S. Rahman, et al., Protonated nanoparticle surface governing ligand tethering and cellular targeting, ACS Nano, 2009, 3, 1203–1211.
44. R. Velu, E. J. Padma Malar, V. T. Ramakrishnan and P. Ramamurthy, Acridinedione-functionalized gold nanoparticles and model for the binding of 1,3-dithiol linked acridinedione on gold clusters, Tetrahedron Lett., 2010, 51, 5680–5685.
45. S. R. Suryawanshi, V. Kaware, D. Chakravarty, P. S. Walke, M. A. More, K. Joshi, C. S. Rout and D. J. Late, Pt-nanoparticle functionalized carbon nano-onions for ultra-high energy supercapacitors and enhanced field emission behaviour, RSC Adv., 2015, 5, 80990–80997.
46. F. Baletto, C. Mottet and R. Ferrando, Growth simulations of silver shells on copper and palladium nanoclusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155420.
47. J. M. Rahm and P. Erhart, Beyond Magic Numbers: Atomic Scale Equilibrium Nanoparticle Shapes for Any Size, Nano Lett., 2017, 17, 5775–5781.
48. A. L. Garden, A. Pedersen and H. Jónsson, Reassignment of 'magic numbers' for Au clusters of decahedral and FCC structural motifs, Nanoscale, 2018, 10, 5124–5132.
49. A. I. Frenkel, S. Nemzer, I. Pister, L. Soussan, T. Harris, Y. Sun and M. H. Rafailovich, Size-controlled synthesis and characterization of thiolstabilized gold nanoparticles, J. Chem. Phys., 2005, 123, 184701.
50. J. Petroski, M. Chou and C. Creutz, The coordination chemistry of gold surfaces: formation and far-infrared spectra of alkanethiolate-capped gold nanoparticles, J. Organomet. Chem., 2009, 694, 1138–1143.
51. H. Grönbeck, Thiolate induced reconstruction of Au(111) and Cu(111) investigated by density functional theory calculations, J. Phys. Chem. C, 2010, 114, 15973–15978.
52. Y. Xue, X. Li, H. Li and W. Zhang, Quantifying thiol-gold interactions towards the efficient strength control., Nat. Commun., 2014, 5, 4348.
53. J. Lin, H. Zhang, Z. Chen and Y. Zheng, Penetration of lipid membranes by gold nanoparticles: insights into cellular uptake, cytotoxicity, and their relationship, ACS Nano, 2010, 4, 5421–5429.
54. F. Simonelli, D. Bochicchio, R. Ferrando and G. Rossi, Monolayer-Protected Anionic Au NanoparticlesWalk into Lipid Membranes Step by Step, J. Phys. Chem. Lett., 2015, 6, 3175–3179.
55. G. Rossi and L. Monticelli, Simulating the interaction of lipid membranes with polymer and ligand-coated nanoparticles, Adv. Phys.: X, 2016, 1, 276–296.
56. A. Torchi, F. Simonelli, R. Ferrando and G. Rossi, Local Enhancement of Lipid Membrane Permeability Induced by Irradiated Gold Nanoparticles, ACS Nano, 2017, 11, 12553–12561.
57. B. Farkaš and N. H. de Leeuw, Towards a morphology of cobalt nanoparticles: size and strain effects, Nanotechnology, 2020, 31, 195711.
58. B. Farkas, U. Terranova and N. H. De, Leeuw, Binding modes of carboxylic acids on cobalt nanoparticles., Phys. Chem. Chem. Phys., 2020, 22, 985–996.
59. J. Vandevondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Quickstep: fast and accurate density functional calculations using a mixed Gaussian and plane waves approach, Comput. Phys. Commun., 2005, 167, 103–128.
60. J. Hutter, M. Iannuzzi, F. Schiffmann and J. Vandevondele, J. Cp2k: atomistic simulations of condensed matter systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25.
61. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
62. J. VandeVondele and J. Hutter, Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases, J. Chem. Phys., 2007, 127, 114105.
63. S. Nosé, unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519.
64. T. L. Tan, L. L. Wang, J. Zhang, D. D. Johnson and K. Bai, Platinum nanoparticle during electrochemical hydrogen evolution: adsorbate distribution, active reaction species, and size effect, ACS Catal., 2015, 5, 2376–2383.
65. G. Henkelman and H. Jónsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, J. Chem. Phys., 2000, 113, 9978–9985.
66. G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
67. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465.
68. B. M. Barngrover and C. M. Aikens, Oxidation of gold clusters by thiols, J. Phys. Chem. A, 2013, 117, 5377–5384.
69. Y. Jia and Z. Luo, Thirteen-atom metal clusters for genetic materials, Coord. Chem. Rev., 2019, 400, 213053.
70. W. Humphrey, A. Dalke and K. Schulten, VMD - Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33–38.
71. M. Moskovits and J. S. Suh, Conformation of Mono- and Dicarboxylic Acids Adsorbed on Silver Surfaces, J. Am. Chem. Soc., 1985, 107, 6826–6829.
72. H. G. Bagaria, E. T. Ada, M. Shamsuzzoha, D. E. Nikles and D. T. Johnson, Understanding mercapto ligand exchange on the surface of FePt nanoparticles, Langmuir, 2006, 22, 7732–7737.
73. D. S. Kilin, O. V. Prezhdo and Y. Xia, Shape-controlled synthesis of silver nanoparticles: ab initio study of preferential surface coordination with citric acid, Chem. Phys. Lett., 2008, 458, 113–116.
74. J. Petroski and M. A. El-Sayed, FTIR study of the adsorption of the capping material to different platinum nanoparticle shapes, J. Phys. Chem. A, 2003, 107, 8371–8375.
75. T. Hachisu, T. Yotsumoto, A. Sugiyama and T. Osaka, Surface Modification of Chemically Synthesized FePt Nanoparticles, ECS Trans., 2019, 16, 199–206.
76. S. Alexander, V. Gomez and A. R. Barron, Carboxylation and Decarboxylation of Aluminum Oxide Nanoparticles Using Bifunctional Carboxylic Acids and Octylamine, J. Nanomater., 2016, 7950876.
77. A. A. Baharuddin, B. C. Ang, N. A. Abu Hussein, A. Andriyana and Y. H. Wong, Mechanisms of highly stabilized ex situ oleic acid-modified iron oxide nanoparticles functionalized with 4-pentynoic acid, Mater. Chem. Phys., 2018, 203, 212–222.
78. M. R. Ivanov, H. R. Bednar and A. J. Haes, Investigations of the mechanism of gold nanoparticle stability and surface functionalization in capillary electrophoresis, ACS Nano, 2009, 3, 386–394.
79. A. A. Volkert, V. Subramaniam, M. R. Ivanov, A. M. Goodman and A. J. Haes, Salt-mediated self-assembly of thioctic acid on gold nanoparticles, ACS Nano, 2011, 5, 4570–4580.
80. J. E. Matthiesen, D. Jose, C. M. Sorensen and K. J. Klabunde, Loss of hydrogen upon exposure of thiol to gold clusters at low temperature, J. Am. Chem. Soc., 2012, 134, 9376–9379.
81. V. Rojas-Cervellera, E. Giralt and C. Rovira, Staple motifs, initial steps in the formation of thiolate-protected gold nanoparticles: how do they form?, Inorg. Chem., 2012, 51, 11422–11429.
82. P. Maksymovych, D. C. Sorescu and J. T. Yates, Gold-adatom-mediated bonding in self-assembled short-chain alkanethiolate species on the Au(111) surface, Phys. Rev. Lett., 2006, 97, 146103.
83. P. D. Jadzinsky, G. Calero, C. J. Ackerson, D. A. Bushnell and R. D. Kornberg, Structure of a Thiol Monolayer-Protected Gold Nanoparticle at 1.1 A Resolution, Science, 2007, 318, 430–433.
84. D. E. Jiang, M. L. Tiago, W. Luo and S. Dai, The “staple” motif: a key to stability of thiolate-protected gold nanoclusters, Phys. Rev. Lett., 2008, 130, 2777–2779.
85. H. W. Ghebriel and A. Kshirsagar, Adsorption of molecular hydrogen and hydrogen sulfide on Au clusters, J. Chem. Phys., 2007, 126, 244705.
86. K. García-Díez, J. Fernández-Fernández, J. A. Alonso and M. J. López, Theoretical study of the adsorption of hydrogen on cobalt clusters, Phys. Chem. Chem. Phys., 2018, 20, 21163–21176.
87. P. Nordlander, S. Holloway and J. K. Nørskov, Hydrogen adsorption on metal surfaces, Surf. Sci., 1984, 136, 59–81.
88. L. Kristinsdóttir and E. Skúlason, A systematic DFT study of hydrogen difiusion on transition metal surfaces, Surf. Sci., 2012, 606, 1400–1404.
89. P. Ferrin, S. Kandoi, A. U. Nilekar and M. Mavrikakis, Hydrogen adsorption, absorption and difiusion on and in transition metal surfaces: a DFT study, Surf. Sci., 2012, 606, 679–689.
90. M. Hu, D. P. Linder, M. Buongiorno Nardelli and A. Striolo, Hydrogen adsorption on platinum-gold bimetallic nanoparticles: a density functional theory study, J. Phys. Chem. C, 2013, 117, 15050–15060.
91. I. A. Pašti, N. M. Gavrilov and S. V. Mentus, Hydrogen adsorption on palladium and platinum overlayers: DFT study, Adv. Phys. Chem., 2011, 2011, 305634.
92. M. G. Sandoval, R. Luna, G. Brizuela, A. O. Pereira, C. R. Miranda and P. Jasen, Theoretical Study of Hydrogen Adsorption on Au@Pd Icosahedral Nanoparticle, J. Phys. Chem. C, 2017, 121, 8613–8622.

---