Open Access Article
Open Access ArticleElucidating the formation and active state of Cu co-catalysts for photocatalytic hydrogen evolution†
Jasmin S.
Schubert
a,
Leila
Kalantari
a,
Andreas
Lechner
a,
Ariane
Giesriegl
a,
Sreejith P.
Nandan
a,
Pablo
Alaya
a,
Shun
Kashiwaya
b,
Markus
Sauer
 c,
Annette
Foelske
c,
Johanna
Rosen
b,
Peter
Blaha
a,
Alexey
Cherevan
c,
Annette
Foelske
c,
Johanna
Rosen
b,
Peter
Blaha
a,
Alexey
Cherevan
 *a and
Dominik
Eder
*a and
Dominik
Eder
 *a
*a
aInstitute of Materials Chemistry, Technische Universität Wien (TU Wien), Getreidemarkt 9, 1060, Vienna, Austria. E-mail: alexey.cherevan@tuwien.ac.at; dominik.eder@tuwien.ac.at
bMaterials Design, Department of Physics, Chemistry, and Biology (IFM), Linköping University, 58183, Linköping, Sweden
cAnalytical Instrumentation Center, Technische Universität Wien (TU Wien), Lehargasse 6, 1060 Vienna, Austria
First published on 6th September 2021
Abstract
The design of active and selective co-catalysts constitutes one of the major challenges in developing heterogeneous photocatalysts for energy conversion applications. This work provides a comprehensive insight into thermally induced bottom-up generation and transformation of a series of promising Cu-based co-catalysts. We demonstrate that the volcano-type HER profile as a function of calcination temperature is independent of the type of the Cu precursor but is affected by changes in oxidation state and location of the copper species. Supported by DFT modeling, our data suggest that low temperature (<200 °C) treatments facilitate electronic communication between the Cu species and TiO2, which allows for a more efficient charge utilization and maximum HER rates. In contrast, higher temperatures (>200 °C) do not affect the Cu oxidation state, but induce a gradual, temperature-dependent surface-to-bulk diffusion of Cu, which results in interstitial, tetra-coordinated Cu+ species. The disappearance of Cu from the surface and the introduction of new defect states is associated with a drop in HER performance. This work examines electronic and structural effects that are in control of the photocatalytic activity and can be transferred to other systems for further advancing photocatalysis.
Introduction
Photocatalysis can contribute to the development of environmentally-friendly processes relevant to water purification technologies, antibacterial applications, CO2 reduction as well as the energy sector.1–4 As such, photocatalytic water splitting towards light-driven hydrogen generation has the capability to be part of the solution to overcome the energy-related challenges of our times. To engineer the most efficient photocatalyst, heterogeneous photocatalysis has shown to be an advantageous approach, as it can combine a solid-state semiconductor – able to absorb light, generate electron–hole pairs and transfer their energy to the catalytic sites – and a co-catalyst with more suitable catalytic properties, which enables the desired oxidation and reduction half-reactions.2,3,5 Additionally, the co-catalysts can act as a driving force for quick separation of photoexcited charge carriers, by extracting the charge carriers from the bulk and preventing their recombination, leading ultimately to enhanced charge separation and photocatalytic activity.6 The use of tailor-made co-catalysts deposited on the photocatalyst surface thus, provides a means to control the catalytic sites to enhance and tune efficiency and adsorption–desorption equilibria of the reaction of interest.6 Therefore, co-catalyst engineering has emerged as one of the most promising strategies to achieve high photocatalytic performance.The light-to-hydrogen conversion efficiency of the final photocatalyst strongly depends on the electronic interaction and band alignments between the two components, as the photogenerated charge carries need to be effectively transferred between the semiconductor substrate and the catalytic sites.6 Besides, the accessibility of the co-catalyst to the reactants also defines the final rate of the charge consumption by the desired reaction. Hence, the overall photocatalytic activity is often limited by the degree of electronic communication between the semiconductor and the co-catalyst, and the accessibility of the catalytic active sites. In order to provide more control over the co-catalyst/semiconductor interface, co-catalyst species are often generated on the support surface via bottom-up methods such as photodeposition, chemical deposition and growth as well as a selective surface reaction.6–12 In many cases, the synthesis is accompanied by thermal treatments aiming to generate the desired co-catalyst species via oxidation or reduction. However, temperatures can facilitate otherwise kinetically hindered diffusion processes leading to possible growth of the co-catalyst species or their chemical interaction with the substrate. These processes can reduce the accessibility of the catalytic centers to the reactants and lead to doping which often creates charge recombination centers and introduces localized inter-bandgap states resulting in lower photocatalytic performance.13,14 It thus becomes important to control the location, chemical state and morphology of the co-catalyst species in the final photocatalytic system, for which more detailed investigations are often desired.
This work examines a series of Cu-based co-catalysts supported on anatase TiO2 as a model substrate and provides a comprehensive insight into the side effects of thermal pre-treatments on their photocatalytic performance. The results reveal a surprising effect of the heat-treatment temperature on the hydrogen evolution reaction (HER) activity: the HER rates decrease at higher calcination temperatures, while the maximum activity is achieved for the non- and low-temperature treated samples, in contrast to other works.10,15,16 Aiming to unveil optimal synthetic parameters, we prepared a set of Cu/TiO2 composites via wet-chemical deposition of Cu species and characterized systematically their oxidation state, location and loading. To elucidate and understand the mechanism responsible for the photocatalytic performance, we correlated the rates of HER with the data obtained via photoelectron spectroscopy (XPS and UPS), infrared-, Raman- and diffuse reflectance spectroscopy (DRS), as well as microscopic techniques (TEM) and X-ray diffraction (XRD), among others. Overall, our results reveal that higher calcination temperatures (>200 °C) can trigger migration of the Cu species from the TiO2 surface to its sub-surface and bulk. The disappearance of active sites as well as the introduction of defect sites can both be responsible for the observed HER decline. This work illustrates the importance of considering potential side effects of thermal treatments in the preparation and activation of non-noble-metal-containing co-catalysts and provides a quantitative measure for their impact on photocatalytic performance.
Results and discussion
We investigated the hydrogen evolution reaction (HER) for a series of nanoparticulate anatase TiO2 powders impregnated with ∼1 at% of Cu as a function of thermal treatment. Two sample sets were prepared using different Cu precursors: copper acetate, Cu(ac)2, and copper nitrate, Cu(NO3)2. The as-prepared Cu(ac)2/TiO2 and Cu(NO3)2/TiO2 powders were subjected to temperature-treatments ranging from room temperature (RT) – i.e. no thermal treatment – to 400 °C and evaluated with regard to their HER performance (Fig. 1a). The photocatalytic data revealed a clear trend for both sample sets: the activity first increased with calcination temperature to reach a maximum at 100 °C/150 °C, then by further increasing the temperature a gradual decrease of the HER takes place. The subsequent decrease at higher calcination temperatures, however, was surprising, considering that thermal treatments at those temperatures constitute a standard method required to either eliminate the anion residue, generate the corresponding oxides, or enhance the interaction between the substrate and co-catalyst.7,8,10–12,17,18 Yet, our data show that the calcination protocol of the Cu/TiO2 composites has a detrimental effect on photocatalytic performance. In addition, a similar HER trend was observed for isothermal treatments performed at 250 °C for different periods of time (see Fig. S2†). Hence, not only does the temperature of the treatment play a role but also the time of calcination. For simplicity, as both parameters – temperature and time – led to similar behavior, in this work we focused on the effect of temperature, and thus we set a constant calcination time of 2 h for each thermally treated sample.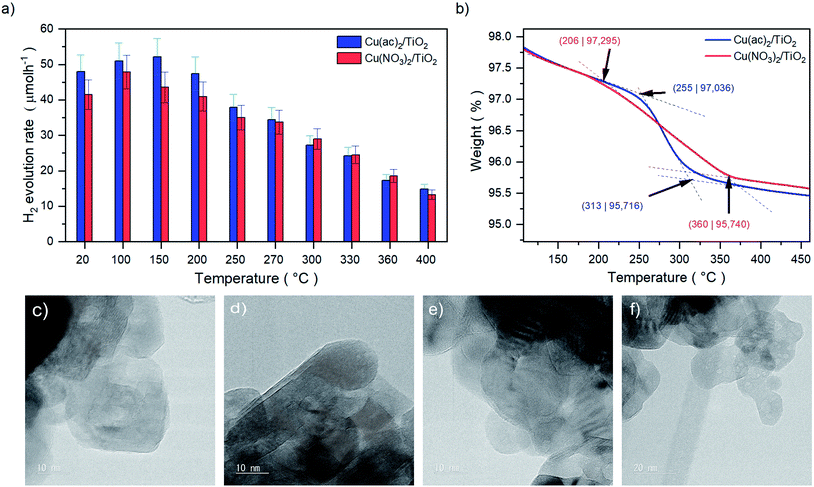 | ||
| Fig. 1 (a) Values of the HER rates achieved after 20 minutes of illumination of Cu(ac)2/TiO2 and Cu(NO3)2/TiO2 composite series prepared at different temperatures. Full HER evolution profiles over time and illumination are shown in Fig. S1 and Table S1,† HER stability (long-term HER performance) discussion can be found in Fig. S3,† (b) TGA profiles of the Cu(ac)2/TiO2 and Cu(NO3)2/TiO2 composites showing the decomposition ranges from 206 to 360 °C and 255 to 313 °C, respectively. Full profiles from room temperature to 800 °C are shown in Fig. S4.† (c) HRTEM images of anatase-TiO2, (d) the non-calcined, (e) 400 °C (10 nm) and (f) 400 °C calcined (20 nm) Cu/TiO2 composites. Further TEM and complementary SEM micrographs are shown in Fig. S5 and S6.† | ||
The observed HER decline in Fig. 1a can originate from several phenomena: (a) sintering of the Cu species on the TiO2 surface, (b) generation of less or non-active Cu species (change in the oxidation state/morphology) or (c) diffusion of Cu into the TiO2 lattice, which may lead to (d) reduced availability of the Cu sites at the solid–liquid interface, (e) formation of thermally induced defects that act as charge recombination centers (doping) or (f) changes of the band gap structure (electronic effect), among others.6,9–11,13,14,19–21 In order to elucidate the responsible factors for the observed HER trends, we thoroughly characterized and investigated both sample sets, Cu(ac)2/TiO2 and Cu(NO3)2/TiO2, with a plethora of methods.
Thermal and morphological analysis
The thermal gravimetric analysis (TGA) in Fig. 1b of the composites revealed that the decomposition of the anions takes place between 206 °C and 360 °C for Cu(NO3)2/TiO2 and 255 °C to 313 °C for Cu(ac)2/TiO2. The beginning of the anion decomposition coincides well with the start of the HER activity decline, which thus may be related to the precursor transformation. Yet, it is well known that the thermal treatment can also induce sintering of the Cu species that can lead to reduced activity.19 High-resolution transmission electron microscopy (HRTEM) revealed that no Cu-based clusters or nanoparticles (NP) are present on the TiO2 surface, independent of the precursor type and the temperature of the thermal treatment (Fig. 1c–f). This suggests that Cu is homogeneously distributed on the TiO2 support at the nanoscale as atomic layers/species without forming TEM-visible clusters, even at high-temperature treatments. This eliminates sintering as a significant reason for the observed activity drop.Structural and compositional analysis
The Raman spectrum in Fig. 2a shows only features that correspond to a pure anatase phase with the typical Eg (145.3 cm−1), B1g (397.5 cm−1), A1g + B1g (517.5 cm−1) and Eg (641.1 cm−1) bands, which belong to the O–Ti–O symmetric stretching, symmetric bending and antisymmetric bending vibrations, respectively.22,23 This indicates that neither the transition to rutile nor the formation of a separate Cu phase took place in any of the samples (further confirmed by XRD, see Fig. S7†). Furthermore, a gradual decrease of the TiO2 band intensities with increasing calcination temperatures occurred for both samples, accompanied by a broadening of their FWHM, yet with some fluctuations (Fig. 2b and c). The loss of Raman band intensity can be related to a decrease in polarizability and symmetry of the vibrational modes and suggests a crystal lattice distortion of TiO2, which is more pronounced at higher temperatures.22,24–30 The slight FWHM broadening of the Cu/TiO2 samples – in contrast to bare TiO2 – further confirms this assumption (Fig. 2d).22,25,26 Furthermore, recent DFT studies revealed that Cu incorporation (via interstitial or substitutional Cu:TiO2 doping) does not result in a strong TiO2 lattice distortion.31 Hence, these observations point to the possible formation of thermally induced Cu–TiO2 lattice defects, via Cu surface-to-bulk diffusion, which – being a kinetically hindered process – can be activated at higher temperatures.27–29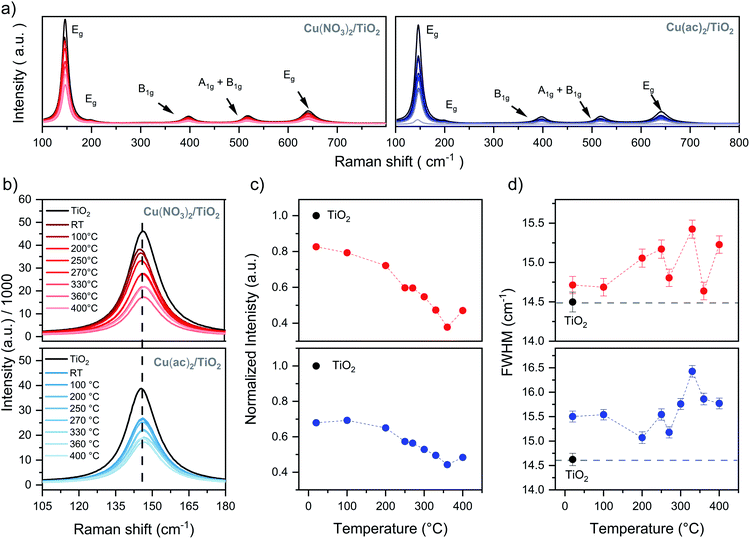 | ||
| Fig. 2 Raman data of the Cu(NO3)2/TiO2 (red) and Cu(ac)2/TiO2 (blue) composites as a function of post-thermal treatment temperature: (a) full range of the Cu(NO3)2/TiO2 and Cu(ac)2/TiO2 composites, (b) Eg band profiles, (c) normalized Eg band intensity – to bare TiO2 to exclude instrumental artifacts – and (d) Eg band FWHM changes. Details in Table S2.† | ||
Attenuated total reflection infrared (ATR-IR) spectroscopy of the composites, Fig. 3, indicates chemisorption of the Cu precursor species on the TiO2 surface already after impregnation (RT samples). This is evident from the red-shifted COO modes of the acetate ligand (around 1490 and 1600 cm−1), the appearance (1558 cm−1) and decrease (1419 cm−1) of a new acetate binding mode, and the pronounced rise of the intensity of the bidentate bridging nitrate coordination at 1620 cm−1, typical artifacts of surface-binding.32 Furthermore, at 400 °C we see a complete decomposition of the nitrate and acetate ligands, in line with TGA.
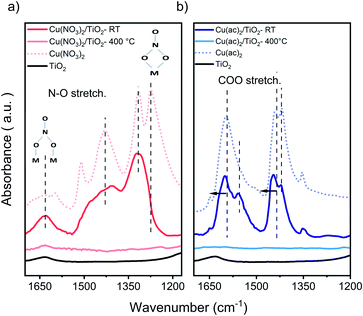 | ||
| Fig. 3 FTIR-ATR of (a) Cu(NO3)2/TiO2 and (b) Cu(ac)2/TiO2 samples. Main nitrate and acetate peaks, showing the new binding modes and band shift for the non-calcined (RT) and calcined at 400 °C composites vs. the pure precursors and TiO2. Samples contained 5 at% of Cu, to obtain a better visualization. The full range of the pure precursor, 5 at% Cu and 1 at% Cu samples are shown in Fig. S8 and S9.† | ||
Fig. 1a shows that the highest photocatalytic activity was obtained at 150 °C for Cu(ac)2/TiO2 and 100 °C for Cu(NO3)2/TiO2. Based on the discussion above, Raman signal changes are already visible at these temperatures and ATR-IR indicates strong binding of the precursor species, yet no Cu diffusion is expected at those temperatures. Hence, we suggest that such mild thermal treatments enact densification of the adsorbed precursor layer, resulting in Cu species that are bound more strongly to the TiO2 surface. This in turn induces a slight crystal distortion at the Cu/TiO2 interface (inducing the Raman signal changes) but concomitantly enhances the electronic communication between the support and the co-catalyst, leading to a better overall HER performance.
Surface-to-bulk diffusion
In order to further investigate a possible formation of Cu–TiO2 lattice defects upon calcination (indicated by Raman spectroscopy), we analyzed the samples with X-ray photoelectron spectroscopy (XPS). The idea is that diffusion of Cu from the surface into the bulk would lead to a decreased Cu concentration on the substrate surface and hence to a weaker Cu signal in the surface-sensitive XPS. Moreover, XPS also allows for identifying changes in the oxidation state of Cu and Ti.The survey spectra acquired show the expected Cu 2p, Cu Auger, Ti 2p, C 1s and O 1s signals for all measured samples. The detail spectra of C 1s and O 1s show the typical carbon species as well as the oxygen from TiO2 (Fig. S10–S13†). The Ti 2p3/2 signal (458.8 eV) corresponds to Ti4+ in all samples, with no detectable contribution of Ti3+ (Fig. 4e). The Cu 2p signals, however, are more complex and surprising, as no characteristic Cu2+ satellite features (generally around 942 eV) were detectable, despite Cu2+ precursors being used in the synthesis (Fig. 4a and b).33–35 Thus, the Cu 2p3/2 peaks, seen in all samples (932.5 eV for Cu(NO3)2/TiO2 and 932.3 eV for Cu(ac)2/TiO2), indicate the presence of Cu+, Cu0 or more likely a combination of both. However, considering the low signal intensity – due to the low (∼1 at%) Cu content – and the slight asymmetric broadening of the signal, the presence of small amounts of Cu2+ cannot be fully excluded. In fact, DRS – discussed later in the manuscript – confirms the presence of Cu2+. To further clarify the Cu oxidation states in the composites, we also analyzed the Cu LMM Auger signals shown in Fig. 4c. However, it was only possible to obtain a reliable signal for the non-calcined and 250 °C treated samples. Furthermore, as the binding energy and Auger parameters are sensitive to the ligand nature and small particle size, only qualitative analysis was performed to confirm the Cu 2p3/2 signal analysis.34,35 The data reveal a sharp and intense peak at 915.1 eV kinetic energy (K.E.), which corresponds to Cu+.33,36 At 918 eV K.E. a clear shoulder, typical of Cu0, is visible for the non-calcined Cu(ac)2/TiO2; the shoulder, however, almost disappears after the 250 °C treatment. Besides, as Cu2+ generally appears around ∼917 eV, the broadening in that region of the spectrum further indicates the presence of Cu0 and Cu2+. Overall, we conclude, that a mixture of Cu2+, Cu+ and Cu0 is present in all the Cu/TiO2 samples with Cu+ being the most abundant. The presence of a mixed oxidation state implies that a reduction of the original Cu2+ precursor takes place already during impregnation most probably induced by the photoelectrons of TiO2 generated under ambient light (further discussion in the optoelectronic analysis and DFT sections) and by the set of our synthetic conditions (i.e. use of vacuum and ethanol).
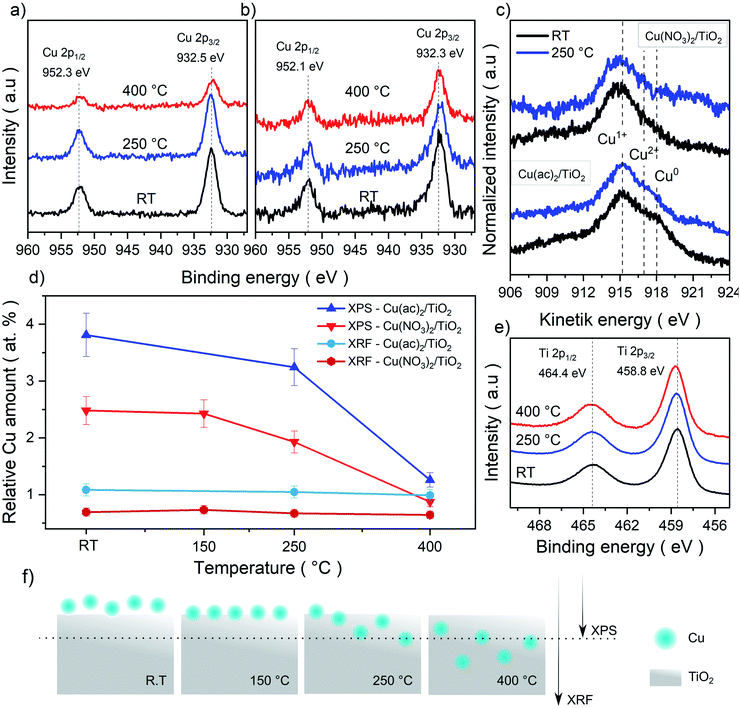 | ||
| Fig. 4 XPS Cu 2p detail spectra of the (a) Cu(NO3)2/TiO2 and (b) Cu(ac)2/TiO2 composites subjected to various temperature treatments. (c) Cu LMM Auger spectra for both composites non-calcined (RT) and at 250 °C. The Cu2+, Cu+ and Cu0 reference values were taken from literature reports.33–35 (d) Elemental Cu contents (Cu-to-Ti ratio in at%) derived from bulk sensitive XRF and surface-sensitive XPS survey data. Absolute values are shown in Table S5.† (e) Ti 2p spectra of the composites and (f) graphical representation of the proposed thermally induced diffusion mechanism and depth penetration of XPS and XRF. | ||
To further elaborate on the hypothesis of possible Cu diffusion into the substrate lattice, we compared the Cu amounts quantified from XPS (a surface-sensitive method) against the elemental quantification obtained using X-ray fluorescence (XRF) spectroscopy (a bulk-sensitive method, considering the nanometer-sized composites), shown in Fig. 4d and f. The XRF Cu signal of ∼1 at% is consistent for all composites (non-calcined and calcined at 150, 250 and 400 °C), while the Cu content in XPS decreased strongly from 2.5 to 0.9 Cu at% (Ti is set to 100% and Cu content is provided in relation to it). Overall, while XRF confirms that no Cu loss from the sample takes place upon calcination, these complementary sets of data suggest that Cu undergoes diffusion into the TiO2 lattice at higher calcination temperatures.
Analysis of the optoelectronic properties
The DRS data in Fig. 5a and b reveal a strong absorption band below 400 nm, which corresponds to the ligand-to-metal charge transfer (LMCT) of oxygen (O2−) to Ti4+ and Cun+ (n = 0, 1 or 2).37,38 Next, all samples show a shoulder in the range of 400 to 500 nm, absent in pure TiO2. The nature of this band is strongly debated in literature and has been attributed to localized surface plasmon resonance (LSPR) effects of Cu0 nanoparticles (NP), d–s transition of Cu0 (d10s1), interfacial charge transfer (IFCT) from the TiO2 valence band (VB) to the Cu2+ ions or CuxO-clusters as well as to Cu+ metal-to-ligand charge transfer (MLCT) absorption.38–43 In our case, TEM micrographs show no visible Cu nanoparticles. Thus, NP LSPR effects can be excluded. DFT calculations revealed that this shoulder originates from inter-band gap states of Cu-d orbitals caused by Cu0, Cu+ and Cu2+ (see the corresponding section for further discussion). The strong absorption between 550 and 900 nm is characteristic of Cu2+ d–d transitions (d9s0) (see pure Cu2+ precursors reference in Fig. 5a and b).37,39,44 This further corroborates the presence of Cu2+ in the composites. Furthermore, the d–d Cu2+ band intensity decreases by increasing temperature. This reveals that Cu2+ vanishes from the composites at higher calcination temperatures, in line with the heat-induced diffusion of Cu into TiO2, indicated by XPS and XRF as well as DFT models discussed later.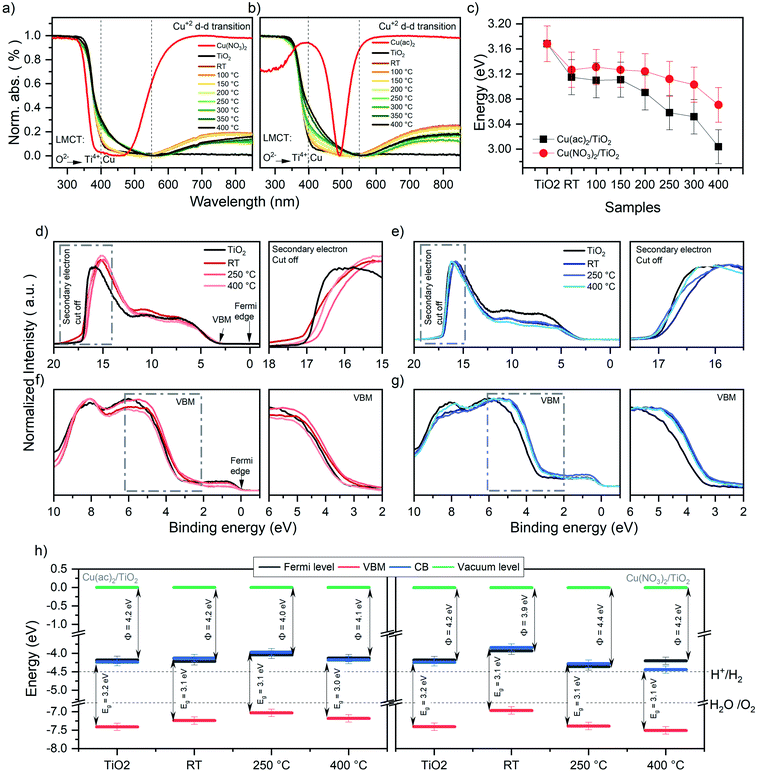 | ||
| Fig. 5 Normalized DRS data for the (a) Cu(NO3)2/TiO2 and (b) Cu(ac)2/TiO2 composites subjected to various thermal treatments along with the pure anatase TiO2 and the original Cu precursors. (c) Band gap (Eg) values of the Cu(NO3)2/TiO2 and Cu(ac)2/TiO2 composites as a function of post-treatment temperature. The data is extracted via Tauc plot analysis of the DRS spectra. RT = non-calcined sample, LMCT = ligand to metal charge transfer. Further details, absolute values of the composites and thermal evolution of the pure precursors are shown in Fig. S15, S16 and Table S6.† (d) UPS signals of Cu(NO3)2/TiO2 and (e) Cu(ac)2/TiO2 composites prepared at different temperatures. (f) VB-XPS of Cu(NO3)2/TiO2 and (g) Cu(ac)2/TiO2 composites. (h) Energy diagram (energy (eV) vs. vacuum level) of Cu(ac)2/TiO2 and Cu(NO3)2/TiO2 constructed from the corresponding UPS, XPS and DRS data (further detail in Fig. S17 and Table S7†) of the bare TiO2-anatase, the non-calcined sample and the composites obtained via calcination at different temperature. H+/H2 and H2O/O2 potential values taken at standard conditions.52,53 Note that the values are referenced to the vacuum level (Evac = 0 eV). | ||
The optical band gaps constructed from the corresponding DRS data, determined by using Tauc plots (Fig. 5c), revealed a clear band gap decrease with increasing temperature.45 Yet, already a decrease for the non-calcined samples takes place from 3.17 eV, for bare TiO2, to 3.12 eV and 3.13 eV for Cu(ac)2/TiO2 and Cu(NO3)2/TiO2, respectively. This also confirms the presence of Cu inter-band gap states and suggests that electronic communication between TiO2 and Cu was established immediately after impregnation – in line with Raman spectroscopy – and gets more pronounced with increasing temperature. These findings align well with the hypothesis of thermally induced diffusion of the Cu species into the TiO2 lattice and previously reported studies on Cu doped TiO2.46,47
The work function and valence band maximum (VBM) of the samples were determined using UPS and XPS (see Fig. 5d–h and for further detail about the method Fig. S17†).48 The data show strong fluctuations in the work function values, without following a clear trend, while the VBM shows a decrease for all samples except Cu(NO3)2/TiO2 at 400 °C, which increases (see Table 1). Furthermore, the energy diagrams, constructed based on XPS, UPS and DRS, show that the Fermi level of all samples, except Cu(NO3)2/TiO2 calcined at 400 °C, is in the same range as the conduction band minimum (CB) (see Fig. 5h), indicating an n-type conductivity of all samples. This can be related to an electron accumulation on the surface, which induces a downward band bending, attributed to defects (oxygen vacancies, titanium interstitials, etc.), adsorbed species (type and density of those species), UHV conditions or doping.49–52 This electron accumulation on the TiO2 surface would explain the reduction of Cu2+ to Cu+ and Cu0 seen in XPS even for the non-thermally treated Cu/TiO2 composites. Furthermore, to fully understand the work function differences between the composites prepared using different Cu precursors is beyond the scope of this study, yet it is well known that the work function depends on the surface structure and nature of the adsorbates.48,49 Hence, the presence of the different physisorbed anions (nitrate and acetate, that have different charge density and dipole moments), the products of the anion thermal decomposition and the different state and location of Cu is likely to affect the work function differently giving rise to these fluctuations.48 By correlating these data with the photocatalytic performance, we conclude that the position of the CB levels thermodynamically required to drive proton reduction remains suitable for all composites and does not seem to correlate with the observed HER trend. Yet, doping is known to induce defects that act as charge recombination centers; thus, the observed HER activity decrease can be governed by the Cu-induced defects which increase by increasing temperature, rather than the change in the optoelectronic properties.13,51,53
| Cu(NO3)2/TiO2 | Cu(ac)2/TiO2 | |||||
|---|---|---|---|---|---|---|
| Cut off | Work function | VBM | Cut off | Work function | VBM | |
| TiO2 | 17.0 | 4.2 | 3.2 | — | — | — |
| RT | 17.3 | 3.9 | 3.0 | 17.0 | 4.2 | 3.0 |
| 250 °C | 16.8 | 4.4 | 3.0 | 17.2 | 4.0 | 3.0 |
| 400 °C | 17.0 | 4.2 | 3.3 | 17.1 | 4.1 | 3.1 |
Analysis of the Cu–TiO2 linkage strength
Diffusion of Cu into the interior of the TiO2 particles will reduce their accessibility and improve their stability towards leaching into solution. Therefore, we performed washing experiments and analyzed the samples with DRS and XRF. DRS in Fig. 6a shows that the absorption band characteristic of Cu2+ (550 to 900 nm) decreased significantly after washing with water for the non-treated sample and those heated at low temperature, suggesting a significant portion of weakly bound Cu2+ species. In contrast, a far smaller amount of Cu-species detached in the samples treated at temperatures above 250 °C. XRF (Fig. 6b) confirmed that 62.5% and 86.3% of Cu was removed from the non-calcined samples for Cu(ac)2/TiO2 and Cu(NO3)2/TiO2, respectively, while the corresponding amounts for the samples treated at 350 °C were only 16.0% and 17.2%, respectively.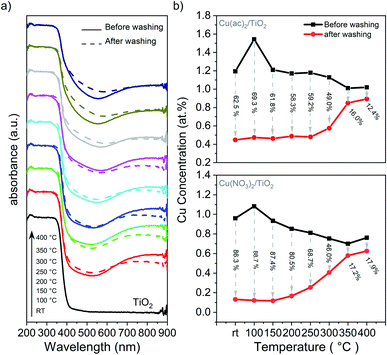 | ||
| Fig. 6 Washing experiments of the Cu/TiO2 composites: (a) DRS of the Cu(ac)2/TiO2 sample before and after washing. The corresponding DRS data of the Cu(NO3)2/TiO2 sample, showing the same behaviour, is shown in Fig. S18.† (b) XRF analysis of the Cu content before and after washing with the amount of Cu washed out (in % regarding the original content). Further details are shown in Table S8.† | ||
These results indicate that most of the Cu species are weakly bound on the surface and that the lower extent of leaching at high temperatures is a result of Cu surface-to-bulk diffusion. However, the observed band gap narrowing, VBM position shifts, as well as FTIR and Raman band changes indicate that Cu-to-support interactions exist to some extent already for the non-calcined sample. Hence, despite Cu being weakly chemisorbed after impregnation, this interaction appears to be strong enough to establish efficient electronic communication with the supporting TiO2. Accordingly, the HER maximum for the catalysts calcined at mild temperatures can be associated with densification of the adsorbed species on the surface, which leads to a stronger binding that facilitates charge transfer from TiO2 to the catalytic center, Cu. The increase of calcination temperature above 200 °C, however, triggers Cu diffusion into the TiO2 lattice, which consequently increases the number of charge recombination centers within TiO2 and reduces the number of Cu centers available on the surface.13,14 Previous reports have shown that Cu undergoes redox shuttling between the reactant and the TiO2 surface by going into solution and redepositing by electron transfer from the TiO2 CB to Cu.9,54 Additional photodeposition experiments indicate that this mechanism is relevant to our system (further discussion in ESI and Fig. S19†). Therefore, we can conclude that both, the reduced availability of Cu sites on the surface as well as the introduction of new trap and recombination states in TiO2 lattice, contribute to the HER performance decline.
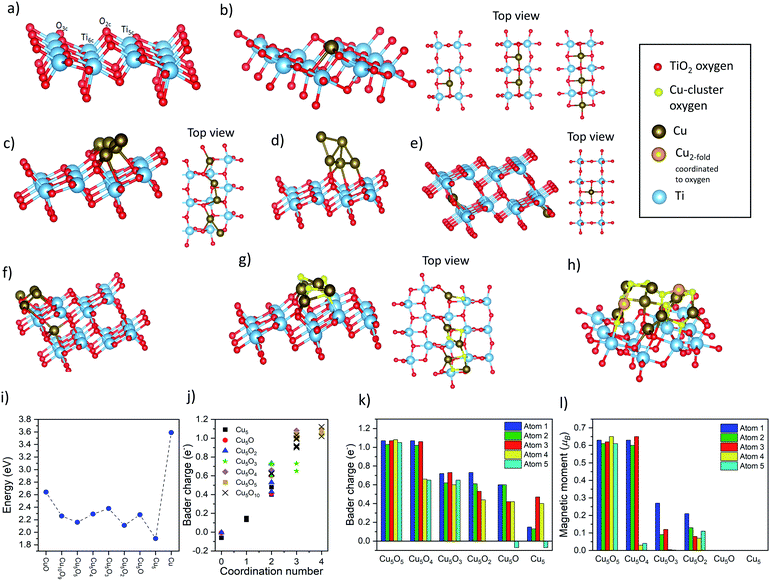
DFT calculations
For a single Cu atom, the results show that Cu prefers to adsorb at the bridge site between two unsaturated oxygen atoms (O2c, see Fig. 7a and b) with an almost linear O2c–Cu–O2c bond angle of 161°, similar to findings of previous studies.55–57 The adsorption energy (Eads) for one single Cu atom on TiO2 is 2.24 eV, which agrees well with literature.55–57 Furthermore, the two shortest Cu–O bonds of 1.87 Å are close to the Cu2O bond length (1.85 Å) but much shorter than for bulk-CuO (1.98 Å) (Table S10†), and the vanishing magnetic moments and the Bader charge of +0.68 (Fig. 7j–l) indicate a Cu-oxidation state of +1. For small Cux clusters (x = 1, 2, 3, and 5), when 2 or 3 Cu atoms are added to the surface, the most stable structures are still obtained for a Cu–O2c bridge sites (Fig. 7b). This indicates that Cu can form infinite almost linear Cu–O chains on the TiO2 surface. Yet, the further addition of Cu atoms tends to destroy the symmetric chain-like 3-atom structure and results in an irregular 3D-like Cu5 array (Fig. 7c and d). This is more stable than the corresponding chain-like Cu5 structures and has the highest Eads of all considered Cux-clusters (Table S11†). Furthermore, the charge transfer from Cu5 to TiO2 (in the DFT model each time a neutral Cu atom is added to the TiO2 surface) is in general smaller. As a result, Cu atoms of Cu5 clusters remain mainly neutral (Bader charges of −0.06 to 0.17), except for the Cu atoms directly attached on TiO2, which have still very short Cu–O bonds or are coordinated by 2 O2c atoms (Bader charge of 0.41 to 0.66), indicating ionized Cu.
For the CuxOy (x = 5, y = 0–5) clusters, we started from the chain-like Cu5 structure and gradually added oxygen atoms until a fully oxidized Cu cluster has been obtained (Fig. 7g and h). We calculated the Eads of different metal oxide clusters on the surface and computed the cohesive energies of bulk Cu and CuO for comparison (Fig. 7i). For all studied clusters, the obtained Eads are much smaller than the cohesive energy of bulk Cu, while showing more similar values to CuO. The Eads depends only weakly on the oxygen content (or the cluster size); thus, the oxygen partial pressure and kinetic effects will determine the specific oxidation state. Furthermore, a +1 Bader charge and 0.6 μB magnetic moments of Cu atoms in the Cu5Oy structures, indicate that for the Cu5O5 cluster Cu is in a +2 state. However, when the number of oxygen atoms gradually decreases, the ionicity also decreases. The largest Cu10O9 cluster has 8 Cu2+ and 2 Cu+ ions and 3 out of the 8 Cu2+ ions have already flipped their spin indicating the preferred antiferromagnetic order of CuO. This is further shown by analyzing the dependency of the Cu charge state with the number of O neighbors (coordination number – a bond is counted when the Cu–O distance is below 2.16 Å) shown in Fig. 7j. For simplicity, only the coordination number versus the Bader charge is shown, however, also bond angle or bond distances just below/above the cutoff criterion had some minor influence. This shows that Cu without or with one direct O neighbor is neutral, with two it is in the +1 state (Bader charge of ∼0.5) and with 3 or 4 coordinated oxygen atoms Cu is in a +2 state. Hence, by increasing oxygen content, the Cu ionicity increases.
To check the possibility of Cu diffusion into the bulk, we constructed DFT models in which one Cu atom migrates from the surface to different positions in the subsurface. Based on the calculated Eads values, Fig. 7e and f shows the most stable structures of subsurface Cu derived from two different configurations: the single Cu atom and the most stable 3D-like Cu5 cluster. As expected, when a single Cu atom diffuses into the subsurface there is a small energy loss (Eads decreases from 2.24 eV to 1.90 eV), which suggests that a single Cu atom is not prone to diffusion into the TiO2 lattice but is rather stable on the surface. Yet, for the larger cluster, migration of a single Cu atom yields virtually no energy difference (1.90 eV to 1.84 eV), which supports the possibility of Cu diffusion into the bulk. In both cases, the most preferable state of Cu incorporation in the subsurface is to be 4-fold coordinated by O and present in the Cu+ state, which is in line with our DRS and XPS results that indicated the reduction of the Cu2+ content.
Overall, the DFT results indicate that differently sized Cu clusters of a few atoms can indeed be stabilized on the TiO2 surface. Analysis of the Cu oxidation state shows that Cu+ and Cu0 species are likely to form at the solid–solid interface, while Cu2+ species can only be formed as an outer cluster layer when enough oxygen is present, in line with the experimental data and the washing experiments. Furthermore, the models show that the generation of interstitial Cu+ – surrounded by 4 O atoms of TiO2 lattice – is the most stable species that can be formed via diffusion in thermally treated samples. Such Cu incorporation results in a minimal crystal structure change, and thus is in line with the Raman and XRD data.
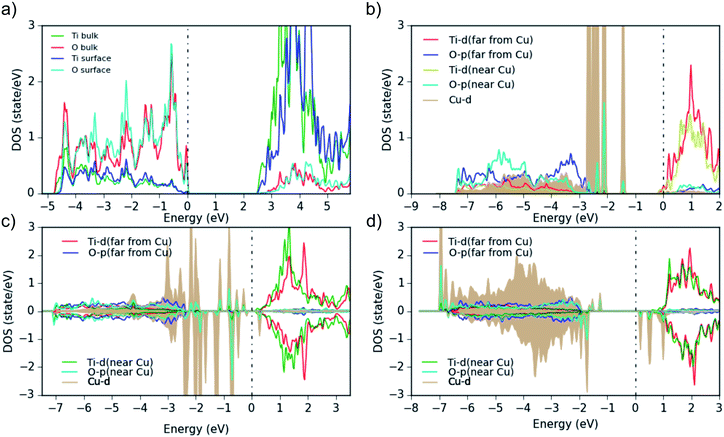
The bare TiO2 surface (Fig. 8a) exhibits a band gap of 2.5 eV (which is lower than the experimental value of 3.2 eV due to the well-known DFT shortcomings), the surface Ti-d states are a bit higher in energy than in the bulk and the Ti–O covalency is reduced (see reduced Ti-surface contribution at the bottom of the valence band). Furthermore, as this TiO2 model represents an ideal surface without defects, it shows p-type conductivity in contrast to the experimental TiO2 samples. Then, when a neutral Cu atom is added on the TiO2-anatase (101) surface (Fig. 8b), the Fermi level moves to the conduction band (the added Cu is in a neutral state, thus, by adding it on the ideal-TiO2 surface, Cu transfers negative charge to TiO2) and the system becomes formally metallic (n-type conductivity). Additionally, the Cu-d states show some hybridization with the O-p orbitals closest to the Cu atoms. This is evident in the difference of the O-PDOS of O atoms close/far to Cu atoms, from which in general a downward/upward shift of O-p states for atoms close/far to Cu can be observed. In any case, the main Cu-d peaks are located above the VBM within the TiO2 band gap and are fully occupied. Larger Cu clusters or Cu diffused into the subsurface (Cu5O2 and Cu5O5, Fig. 8c and d), show that the Cu-PDOS behaves qualitatively similarly. When more oxygen is added to the Cu5Ox clusters, no electron transfer takes place anymore from the Cu 4s (and partly 3d) to the Ti-d states at the CBM, but to the additional O atoms and the Fermi level moves down to the top of the Cu-d bands within the TiO2 gap. In addition, spin-polarization sets in, magnetic moments on (some) Cu atoms appear, and the Hubbard U shifts fully (partially) occupied Cu-d states down (up) in energy (Fig. 8d), indicating typical Cu2+ behavior. This moves a lot of Cu-d states down into the O-p band (e.g. in Cu5O2 and Cu5O4, Fig. 8c) and eventually in Cu5O5 leads to clear lower (below the O-p band) and upper (above EF) Hubbard bands with all Cu in the +2 state.
We conclude, the band gap reduction and the adsorption band between 400 and 550 nm of Cu(NO3)2/TiO2 and Cu(ac)2/TiO2 – compared to pure TiO2 – is related in all cases to Cu-d states in the band gap of the composites. In the case of Cu5O5, where Cu is mainly in the +2 state, we can also see some d states above the Fermi level, which can cause d–d excitations. The transitions from the highest occupied Cu-d states into the TiO2 conduction band may also explain the observed adsorption above 600 nm in Fig. 5a, b and 6.
Proposed diffusion mechanism and active Cu state
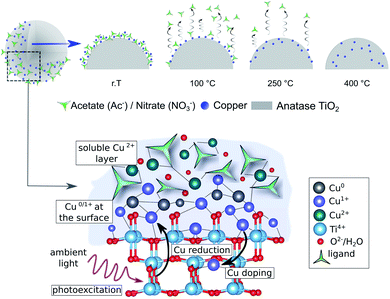
The combined experimental and theoretical results confirm that thermal pretreatment can indeed initiate the diffusion of Cu species into the TiO2 lattice, and that this process plays a key role in decreasing the photocatalytic activity towards HER. Moreover, Cu diffusion induces charge recombination centers, and results in lower availability of the Cu sites for the HER. Additionally, a mixed oxidation state of Cu+, Cu2+ and Cu0 is found to be in the composites at any thermal treatment; while Cu2+ is only weakly bound to the outer surface and can leach when in solution. Thus, we propose the following formation mechanism, which is summarized in Fig. 9: first, during the synthesis, the Cu2+ precursor species are weakly chemisorbed onto the TiO2 surface in a multilayer manner, in which the Cu atoms directly attached to the surface get reduced to Cu+ and Cu0, facilitated by the reduction with electrons accumulated on the TiO2 surface. The low-temperature treatments of the as-prepared composites (≤150 °C) densify the network and enhance the electronic coupling between the Cu and the substrate resulting in increased HER performance (peak activity). Higher calcination temperatures (>150 °C) induce the decomposition of precursor anions and facilitate the diffusion of Cu+ species into the TiO2 lattice, which in turn introduces charge recombination centers and reduces the accessibility of the Cu co-catalyst at the catalyst–reactant interface leading to a strong decrease in the photocatalytic performance.13,58Conclusions
This work sheds light on the thermally induced Cu diffusion into the TiO2 lattice that has a detrimental effect on photocatalytic performance. We show that calcination temperatures below 200 °C enhance the HER activity, yet treatments at higher temperatures have a surprisingly detrimental effect. Using a comprehensive set of experimental and theoretical state-of-the-art techniques, we critically examined various possible reasons for this observation. HRTEM and XPS showed that sintering and change in the oxidation state of the Cu species can be excluded, as they reveal the absence of larger Cu clusters on the TiO2 substrate even for the high-temperature treated samples, and all samples show a mixed Cu oxidation state – Cu0, Cu+ and Cu2+ – even for high-temperature calcined samples under air. Washing experiments show that at lower calcination temperatures Cu is weakly bounded and can leach off by 88.7%, yet at temperatures above 250 °C the percentage drops down to 12.4% of leached Cu. The combined assessment of XPS and XRF indicates that the drop of HER activity is not induced by leaching, but by diffusion of Cu into the TiO2 lattice, as XRF – a bulk sensitive method, considering the nanometer-sized composites – shows a constant Cu concentration for all samples, while XPS – a surface-sensitive method – reveals a strong drop of the Cu amount on the surface. This is further supported by Raman, DRS and DFT calculations. Furthermore, the data demonstrate that a reduction of the Cu2+ precursor to mainly Cu+ and partially to Cu0 takes place already after impregnation – without any further post-treatment – which indicates a photoreduction of the precursor species by TiO2 and that Cu+ is stabilized as an interstitial dopant. From the results, we propose a mechanism as follows: (a) after impregnation Cu2+ is weakly bound on the substrate and get reduced by TiO2 to Cu+ and Cu0, (b) by increasing temperature Cu densifies on the substrate and (c) at temperatures >200 °C Cu+ diffuses into the TiO2 lattice. The drop in photocatalytic performance is thus related to the diffusion of the co-catalyst species into the substrate, which generates charge recombination centers and depletes the number of co-catalyst species available on the surface for the redox reaction. This work demonstrates that mild thermal treatments of photocatalytic systems are considerably more complex than previously believed. Thus, future studies on other co-catalysts and materials need to consider the potential side effects induced by calcination.Experimental
Synthesis of the composites
All materials used for the syntheses were obtained from commercial suppliers. As such, anatase TiO2 from Sigma-Aldrich, Cu(ac)2 (98% pure) and Cu(NO3)2 from Sigma Aldrich (98% pure). The used solvent for the syntheses was absolute ethanol (from Chem-Lab NV) and for photocatalytic experiments deionized water and HPLC-gradient grade methanol (from VWR). The composites were synthesized by a wet impregnation method with a post-synthesis thermal treatment. The general synthesis procedure used for all samples included (a) suspending the TiO2 powder (400 mg, 5 mmol) in ethanol (20 mL); (b) stirring the suspension for 5 minutes; (c) adding the corresponding precursor salt: Cu(ac)2/Cu(NO3)2 (0.05 mmol) and stirring for another 5 min, (d) subjecting the resulting suspension to sonication to assist salt dissolution and homogenization of the suspension components for 15 minutes, (e) the resulting mixture was left stirring for 30 minutes; and (f) the ethanol was extracted under vacuum. The remaining powder was then ground. Afterwards, the samples were heat-treated at the corresponding temperature with a heating ramp of 2 h until reaching the desired temperature, in ambient air.Characterisation methods
Transmission electron microscopy (TEM) images were obtained using FEI TECNAI F20 transmission electron microscope equipped with a field emission gun in bright field mode using 200 kV acceleration voltage. The sample was prepared from an ethanol suspension, using a copper holey carbon-coated grid (Plano, 200 mesh). X-ray diffraction (XRD) was performed using an XPERT III: PANalytical XPert Pro MPD (θ–θ Diffractometer) for the in situ experiments and an XPERT II: PANalytical XPert Pro MPD (θ–θ Diffractometer) for the ex situ experiments. The sample was placed on a sample holder and irradiated with a Cu X-ray source (8.04 keV, 1.5406 Å). The signal was acquired with Bragg–Brentano θ/θ-diffractometer geometry ranging from 5° to 80° degrees. The detector system was a semiconductor X'Celerator (2.1°) detector. The in situ experiment was performed under air flow and temperatures ranging from 25 °C to 800 °C. The ex situ experiments were performed with a Si NIST certified standard reference material (SRM 640d) as an internal standard. The internal standard was required in order to detect the crystal parameter changes of the samples. Refinements were done according to the instruction provided by the standard. The thermogravimetric (TGA) measurements were carried out on a PerkinElmer Thermogravimetric Analyser TGA 8000. The samples were placed into an Al2O3 crucible and heated with a dynamic method at a heating rate of 5 °C min−1 under air from 25 °C to 800 °C. The chemical composition of the samples was obtained with two different X-ray photoelectron spectroscopy (XPS) machines. The Auger spectra were determined using a Thermo Fisher Microlab 310/350-spectrometer equipped with a twin anode Al/Mg-Kα X-ray source (XR3) and a hemispherical analyzer. Pass energies of 70 eV and 20 eV, as well as energy resolutions of 1 eV and 100 meV, were used for survey and detail spectra respectively (excitation energy: 1486.6 eV/1253.6 eV, beam power: 100 W, angle: 60° to sample surface normal, base pressure: 2 × 10−8 mbar, pressure during measurements: 3 × 10−8 mbar). All measurements were carried out with the sample in normal emission angle with respect to the analyzer. The samples were mounted onto the sample holder using double-sided carbon tape. The XPS spectra were acquired using an Axis Ultra DLD instrument from Kratos Analytical (UK) with the base pressure during spectra acquisition better than 1.1 × 10−9 torr (1.5 × 10−7 Pa), achieved by a combination of turbomolecular and ion pumps. Monochromatic Al-Kα radiation (hν = 1486.6 eV) is employed with the anode power set to 150 W. All spectra are collected at normal emission angle. Ultraviolet photoemission spectroscopy (UPS) experiment was carried out in home-built MOSES spectrometer under a base pressure of 5 × 10−10 mbar equipped with a monochromatic He-I radiation source (hν = 21.22 eV). All spectra were collected at normal emission and at room temperature. The total resolution of UPS is about 0.1 eV estimated from the width of the Fermi edge of a sputter-cleaned Au film. The signal was calibrated by using the Fermi edge of this sputtered Au. To extract sample work function, a bias of −50 V was applied to the sample during the UPS measurement. Data analysis was done using the CasaXPS Version 2.3.19PR1.0 software package employing Shirley/Shirley Tougaard backgrounds and Scofield sensitivity factors.59,60 Curve fits using combined Gaussian–Lorentzian peak shapes (GL(30)) were used to discern the components of detail spectra if not stated otherwise. For the peak analysis a charge correction was applied to the adventitious carbon peak (C–C peak) shifting to 284.8 eV binding energy (BE) due to the absence of a clear Fermi edge and for comparison to literature values, while for the VBM, where the indium foil was used, a charge correction was done to the Fermi level. All content values shown are in units of a relative atomic percent (at%), where the detection limit in survey measurements usually lies around 0.1–0.5 at%, depending on the element. The accuracy of XPS measurements is around 10–20% of the values shown. Assignment of different components was primarily done using ref. 61 and 62. For the attenuated total reflection Fourier-transform infrared spectroscopy (ATR-FTIR) measurements a PerkinElmer FTIR Spectral UATR-TWO with a spectrum two Universal ATR (Single Reflection Diamond) accessory was used. Raman measurement was conducted with LabRAM HR800 (HORIBA Co. Ltd). Ne:YAG diode was used as 532 nm laser source and the characteristic Raman peak of Si at 520.8 cm−1 was used as the calibration peak. The laser intensity was kept at 5 mW. The obtained signal intensity was normalized to the anatase sample to avoid measuring artifacts. The X-ray Fluorescence Spectroscopy (XRF) chemical quantification analysis was performed with an Atomika 8030C X-ray fluorescence analyzer in total reflection geometry (XRF) with a molybdenum X-ray source (monochromatized Kα-line). The excitation conditions were 50 kV and 47 mA for 100 s irradiation time and an energy-dispersive Si(Li)-detector was employed. For the sample preparation, all reflectors were washed thoroughly and measured to account for true blanks. 1 mg of the solid nano-powder was loaded on the clean reflectors and sealed with 5 μL of a 1% PVA solution to avoid contamination of the detector. After drying for 5 min on a hot plate and cooling, the reflectors with the loaded samples were measured. For the data evaluation, Ti was set as a matrix with 100% (wt%) and relative amounts of Cu were acquired (wt%). The Diffuse Reflectance Ultra-violet Spectroscopy (DRS or DR-UV-vis) a Jasco V-670 UV-Vis photo spectrometer has been used to measure diffusive reflectance spectra. The optical band gap was determined with the Tauc plots and with the exponent value, n = 1/2 for direct allowed transition.Photocatalytic experiments
Hydrogen evolution experiments were performed using a top irradiation flow-reactor (total volume of 100 mL) equipped with an LED light source with incident light intensity of 0.488 W centred at 365 nm ± 15 nm (192 mW cm−2, Thorlabs SOLIS). In a single experiment, the powdered photocatalyst (10 mg) was dispersed in 40 mL 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 vol% MeOH–water solution. During the experiment, the reactor was continuously purged with argon (flow rate of 30 mL min−1, controlled with a mass flow controller from MCC-Instruments) to deliver the gaseous products to the online gas analyzer (X-Stream®, Emerson Process Management) equipped with a thermal conductivity detector (TCD) for H2 quantification with an unmatchable sensitivity (down to ppm level) and time-resolution (one data point per second, see Fig. S1†). A typical H2 evolution profile obtained with our flow reactor includes an “induction” period (increasing H2 evolution rate during the first minutes) that is purely related to the fact the H2 gas first needs to fill the dead volume (e.g., reactor volume, tubing volume) to reach the detector. The temperature of the reactor was kept constant through a water-cooling system (Lauda).
1 vol% MeOH–water solution. During the experiment, the reactor was continuously purged with argon (flow rate of 30 mL min−1, controlled with a mass flow controller from MCC-Instruments) to deliver the gaseous products to the online gas analyzer (X-Stream®, Emerson Process Management) equipped with a thermal conductivity detector (TCD) for H2 quantification with an unmatchable sensitivity (down to ppm level) and time-resolution (one data point per second, see Fig. S1†). A typical H2 evolution profile obtained with our flow reactor includes an “induction” period (increasing H2 evolution rate during the first minutes) that is purely related to the fact the H2 gas first needs to fill the dead volume (e.g., reactor volume, tubing volume) to reach the detector. The temperature of the reactor was kept constant through a water-cooling system (Lauda).
Computational methods
To understand the experimental observations regarding the influence of the copper oxidation state on H2 production activity, spin-polarized DFT calculations of the model CuxOy clusters (x = 1, 2, 3, 5, 10 and y = 0, 1, …, 5, 9) adsorbed on the anatase TiO2 (101) surface were performed using the full-potential augmented plane wave plus local orbitals method as implemented in the WIEN2k code.63–65 The TiO2-anatase (101) surface was chosen as it is the most abundant and stable anatase surface.66,67 We employed the PBEsol exchange–correlation functional, which is a generalized gradient approximation (GGA) and yields lattice parameters of bulk anatase TiO2, a = b = 3.77 Å and c = 9.54 Å which are in good agreement with experimental data.68 In order to treat the correlated 3d electrons a Hubbard U correction was used.69 A value of Ueff = U − J = 5 eV has been used for Cu 3d e−, which is chosen deliberately smaller than what is typically used in strongly correlated Cu oxides, since in our case also less ionic (neutral) clusters were investigated and the correlation may not be always so strong. The (101) surface was modeled by a symmetric slab with a thickness of three layers of TiO2 (Fig. S20†), where only one layer is shown for better visibility and a vacuum region of 16 Å between the slabs. In order to reduce the interactions between the adsorbed clusters in neighboring cells, a 1 × 3 supercell was used for all surfaces with adsorbed clusters. Moreover, such a supercell is also helpful to release the interfacial strain energy and find more stable configurations. A 2 × 2 × 1 Γ-centered mesh of k-points was used during relaxation (a 5 × 4 × 1 mesh for the final results) and a basis-set size corresponding to RminMTKmax = 7 was used for the Cux models (atomic sphere radii RMT of Ti = 1.7, Cu = 1.65, O = 1.4 bohr), while the CuxOy models used RminMTKmax = 5.45, because the O spheres had to be reduced to 1.09 bohr. All surface models were relaxed until the residual forces were below 1 mRy bohr−1. Consistent RMT and RminMTKmax values were used for calculating the adsorption energy per atom Eads of clusters on the anatase surface, which is defined as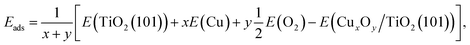 | (1) |
Author contributions
Jasmin S. Schubert: methodology, validation, formal analysis, investigation, writing – original draft, data curation, visualization. Leila Kalantari: investigation, formal analysis, writing – review & editing, data curation, software, visualization. Andreas Lechner: investigation, formal analysis, visualization. Ariane Giesriegl: investigation. Sreejith P. Nandan: investigation. Pablo Alaya: investigation. Shun Kashiwaya: investigation, writing – review & editing. Markus Sauer: writing – review & editing, resources. Annette Foelske: writing – review & editing, resources. Johanna Rosen: writing – review & editing. Peter Blaha: supervision, writing – review & editing. Alexey Cherevan: conceptualization, methodology, supervision, project administration, writing – review & editing. Dominik Eder: conceptualization, supervision, writing – review & editing, project administration, funding acquisition, resources.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the facilities of the Technische Universität Wien (TU Wien) for technical support and fruitful discussions: X-Ray Center (XRC) and especially Werner Artner and Klaudia Hradil; Analytical Instrumentation Center (AIC), Electron Microscopy Center (USTEM) and TU Wien Atominstitute, Tushar Gupta for supplementary TEM measurements, Jia Wang for the Raman measurements, Grzegorz Greczynski for the XPS measurements and Xianjie Liu for the UPS measurements. We further thank the SSF Foundation (EM16-0004), Austrian Science Fund (FWF, Project number P32801) and acknowledge support by the TU-D doctoral college (TU Wien). The authors acknowledge the TU Wien Bibliothek for financial support through its Open Access Funding Program.References
- T. Jafari, E. Moharreri, A. S. Amin, R. Miao, W. Song and S. L. Suib, Molecules, 2016, 21, 900 CrossRef PubMed.
- A. Kudo and Y. Miseki, Chem. Soc. Rev., 2008, 38, 253–278 RSC.
- X. Li, J. Yu, J. Low, Y. Fang, J. Xiao and X. Chen, J. Mater. Chem. A, 2015, 3, 2485–2534 RSC.
- I. Roger, M. A. Shipman and M. D. Symes, Nat. Rev. Chem., 2017, 1, 0003 CrossRef CAS.
- B. M. Hunter, H. B. Gray and A. M. Müller, Chem. Rev., 2016, 116, 14120–14136 CrossRef CAS PubMed.
- S. Bai, W. Jiang, Z. Li and Y. Xiong, ChemNanoMat, 2015, 1, 223–239 CrossRef CAS.
- M.-K. Jeon, J.-W. Park and M. Kang, J. Ind. Eng. Chem., 2007, 1, 84–91 Search PubMed.
- N.-L. Wu and M.-S. Lee, Int. J. Hydrogen Energy, 2004, 29, 1601–1605 CrossRef CAS.
- A. J. J. Lennox, P. Bartels, M.-M. Pohl, H. Junge and M. Beller, J. Catal., 2016, 340, 177–183 CrossRef CAS.
- M. Jung, J. Scott, Y. H. Ng, Y. Jiang and R. Amal, Int. J. Hydrogen Energy, 2014, 39, 12499–12506 CrossRef CAS.
- Y. Wu, G. Lu and S. Li, Catal. Lett., 2009, 133, 97 CrossRef CAS.
- H.-J. Choi and M. Kang, Int. J. Hydrogen Energy, 2007, 32, 3841–3848 CrossRef CAS.
- M. Nolan, A. Iwaszuk, A. K. Lucid, J. J. Carey and M. Fronzi, Adv. Mater., 2016, 28, 5425–5446 CrossRef CAS PubMed.
- L. Zhang, Q. Zheng, Y. Xie, Z. Lan, O. V. Prezhdo, W. A. Saidi and J. Zhao, Nano Lett., 2018, 8 Search PubMed.
- Q. Hu, J. Huang, G. Li, Y. Jiang, H. Lan, W. Guo and Y. Cao, Appl. Surf. Sci., 2016, 382, 170–177 CrossRef CAS.
- M. Jung, J. N. Hart, J. Scott, Y. H. Ng, Y. Jiang and R. Amal, Appl. Catal., A, 2016, 521, 190–201 CrossRef CAS.
- J. Yu, Y. Hai and M. Jaroniec, J. Colloid Interface Sci., 2011, 357, 223–228 CrossRef CAS PubMed.
- J. Bandara, C. P. K. Udawatta and C. S. K. Rajapakse, Photochem. Photobiol. Sci., 2005, 4, 857–861 CrossRef CAS PubMed.
- T. Akita, P. Lu, S. Ichikawa, K. Tanaka and M. Haruta, Surf. Interface Anal., 2001, 31, 73–78 CrossRef CAS.
- N. Waiskopf, Y. Ben-Shahar and U. Banin, Adv. Mater., 2018, 30, 1706697 CrossRef PubMed.
- F. A. L. Laskowski, S. Z. Oener, M. R. Nellist, A. M. Gordon, D. C. Bain, J. L. Fehrs and S. W. Boettcher, Nat. Mater., 2020, 19, 69–76 CrossRef CAS PubMed.
- A. El Mragui, Y. Logvina, L. Pinto da Silva, O. Zegaoui and J. C. G. Esteves da Silva, Materials, 2019, 12(23), 3874 CrossRef CAS PubMed.
- T. Ohsaka, F. Izumi and Y. Fujiki, J. Raman Spectrosc., 1978, 7, 321–324 CrossRef.
- W. Li, L. Fang, G. Qin, H. Ruan, H. Zhang, C. Kong, L. Ye, P. Zhang and F. Wu, J. Appl. Phys., 2015, 117, 145301 CrossRef.
- A. Chanda, K. Rout, M. Vasundhara, S. R. Joshi and J. Singh, RSC Adv., 2018, 8, 10939–10947 RSC.
- J. I. Garza-Arévalo, I. García-Montes, M. H. Reyes, J. L. Guzmán-Mar, V. Rodríguez-González and L. H. Reyes, Mater. Res. Bull., 2016, 73, 145–152 CrossRef.
- A. A. Kashale, A. S. Rasal, G. P. Kamble, V. H. Ingole, P. K. Dwivedi, S. J. Rajoba, L. D. Jadhav, Y.-C. Ling, J.-Y. Chang and A. V. Ghule, Composites, Part B, 2019, 167, 44–50 CrossRef CAS.
- M. R. Joya, K. M. Fonseca and J. Barba-Ortega, AIP Conf. Proc., 2014, 1627, 42–45 CrossRef CAS.
- P. Colomban and A. Slodczyk, Acta Phys. Pol., A, 2009, 116, 7 CrossRef CAS.
- J. Halim, M. R. Lukatskaya, K. M. Cook, J. Lu, C. R. Smith, L.-Å. Näslund, S. J. May, L. Hultman, Y. Gogotsi, P. Eklund and M. W. Barsoum, Chem. Mater., 2014, 26, 2374–2381 CrossRef CAS PubMed.
- A. M. Alotaibi, B. A. D. Williamson, S. Sathasivam, A. Kafizas, M. Alqahtani, C. Sotelo-Vazquez, J. Buckeridge, J. Wu, S. P. Nair, D. O. Scanlon and I. P. Parkin, ACS Appl. Mater. Interfaces, 2020, 12, 15348–15361 CrossRef CAS PubMed.
- M. Y. Mihaylov, V. R. Zdravkova, E. Z. Ivanova, H. A. Aleksandrov, P. St. Petkov, G. N. Vayssilov and K. I. Hadjiivanov, J. Catal., 2021, 394, 245–258 CrossRef CAS.
- V. Krylova and M. Andrulevičius, Int. J. Photoenergy, 2009, 2009, e304308 CrossRef.
- M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson, R. St and C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730 CrossRef CAS.
- M. C. Biesinger, Surf. Interface Anal., 2017, 49, 1325–1334 CrossRef CAS.
- J. Y. Park, Y. C. Kang, K. A. Lim and R. D. Ramsier, Bull. Korean Chem. Soc., 2011, 32, 3395–3399 CrossRef CAS.
- L. P. Bevy, Focus on Catalysis Research, Nova Publishers, 2006 Search PubMed.
- X. Qiu, M. Miyauchi, K. Sunada, M. Minoshima, M. Liu, Y. Lu, D. Li, Y. Shimodaira, Y. Hosogi, Y. Kuroda and K. Hashimoto, ACS Nano, 2012, 6, 1609–1618 CrossRef CAS PubMed.
- S. Pande, M. G. Weir, B. A. Zaccheo and R. M. Crooks, New J. Chem., 2011, 35, 2054–2060 RSC.
- A. Dikhtiarenko, P. Villanueva-Delgado, R. Valiente, J. R. García and J. Gimeno, Polymers, 2016, 8(2), 48 CrossRef PubMed.
- B. Viswanathan, Catalysis: Principles and Applications, CRC Press, 2002 Search PubMed.
- H. Irie, K. Kamiya, T. Shibanuma, S. Miura, D. A. Tryk, T. Yokoyama and K. Hashimoto, J. Phys. Chem. C, 2009, 113, 10761–10766 CrossRef CAS.
- H. Irie, S. Miura, K. Kamiya and K. Hashimoto, Chem. Phys. Lett., 2008, 457, 202–205 CrossRef CAS.
- K. Wang, L. Yang, W. Zhao, L. Cao, Z. Sun and F. Zhang, Green Chem., 2017, 19, 1949–1957 RSC.
- P. Makuła, M. Pacia and W. Macyk, J. Phys. Chem. Lett., 2018, 9, 6814–6817 CrossRef PubMed.
- I. Ganesh, P. P. Kumar, I. Annapoorna, J. M. Sumliner, M. Ramakrishna, N. Y. Hebalkar, G. Padmanabham and G. Sundararajan, Appl. Surf. Sci., 2014, 293, 229–247 CrossRef CAS.
- S. Mathew, P. Ganguly, S. Rhatigan, V. Kumaravel, C. Byrne, S. J. Hinder, J. Bartlett, M. Nolan and S. C. Pillai, Appl. Sci., 2018, 8, 2067 CrossRef CAS.
- A. Kahn, Mater. Horiz., 2015, 3, 7–10 RSC.
- S. Kashiwaya, J. Morasch, V. Streibel, T. Toupance, W. Jaegermann and A. Klein, Surfaces, 2018, 1, 73–89 CrossRef.
- S. Moser, L. Moreschini, J. Jaćimović, O. S. Barišić, H. Berger, A. Magrez, Y. J. Chang, K. S. Kim, A. Bostwick, E. Rotenberg, L. Forró and M. Grioni, Phys. Rev. Lett., 2013, 110, 196403 CrossRef CAS PubMed.
- K. Ozawa, M. Emori, S. Yamamoto, R. Yukawa, S. Yamamoto, R. Hobara, K. Fujikawa, H. Sakama and I. Matsuda, J. Phys. Chem. Lett., 2014, 5, 1953–1957 CrossRef CAS PubMed.
- S. Selcuk and A. Selloni, Nat. Mater., 2016, 15, 1107–1112 CrossRef CAS PubMed.
- U. Diebold, Surf. Sci. Rep., 2003, 48, 53–229 CrossRef CAS.
- D. Spanu, A. Minguzzi, S. Recchia, F. Shahvardanfard, O. Tomanec, R. Zboril, P. Schmuki, P. Ghigna and M. Altomare, ACS Catal., 2020, 10, 8293–8302 CrossRef CAS.
- S. K. Iyemperumal, T. G. Fenton, S. L. Gillingham, A. D. Carl, R. L. Grimm, G. Li and N. A. Deskins, J. Chem. Phys., 2019, 151, 054702 CrossRef.
- A. Alghannam, C. L. Muhich and C. B. Musgrave, Phys. Chem. Chem. Phys., 2017, 19, 4541–4552 RSC.
- N. Seriani, C. Pinilla and Y. Crespo, J. Phys. Chem. C, 2015, 119, 6696–6702 CrossRef CAS.
- Z. Lin, D. Han and S. Li, J. Therm. Anal. Calorim., 2012, 107, 471–475 CrossRef CAS.
- S. Tougaard, Surf. Interface Anal., 1997, 25, 137–154 CrossRef CAS.
- D. A. Shirley, Phys. Rev. B: Solid State, 1972, 5, 4709–4714 CrossRef.
- C. D. Wagner, A. V. Naumkin, A. Kraut-Vass, J. W. Allison, C. J. Powell and J. R. Rumble, NIST standard reference database, 2003, vol. 20, ch. 3, pp. 251–252 Search PubMed.
- G. Beamson and D. Briggs, Anal. Chem., 1992, 64, 1729–1736 CrossRef.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka, J. Luitz, R. Laskowsk, F. Tran, L. Marks and L. Marks, WIEN2k: An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, Techn. Universitat, 2019 Search PubMed.
- D. J. Singh and L. Nordstrom, Planewaves, Pseudopotentials, and the LAPW Method, Springer US, 2nd edn, 2006 Search PubMed.
- P. Blaha, K. Schwarz, F. Tran, R. Laskowski, G. K. H. Madsen and L. D. Marks, J. Chem. Phys., 2020, 152, 074101 CrossRef CAS PubMed.
- M. Lazzeri, A. Vittadini and A. Selloni, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 155409 CrossRef.
- M. Lazzeri, A. Vittadini and A. Selloni, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 119901 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954 CrossRef CAS PubMed.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, New York, 1994 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta05561e |
| This journal is © The Royal Society of Chemistry 2021 |