Open Access Article
Open Access ArticleMechanism of Li nucleation at graphite anodes and mitigation strategies†
Chao
Peng
 *abd,
Arihant
Bhandari
*abd,
Arihant
Bhandari
 cd,
Jacek
Dziedzic
cd,
Jacek
Dziedzic
 cde,
John R.
Owen
cd,
Chris-Kriton
Skylaris
cde,
John R.
Owen
cd,
Chris-Kriton
Skylaris
 cd and
Denis
Kramer
cd and
Denis
Kramer
 *bdf
*bdf
aMultiscale Crystal Materials Research Center, Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China. E-mail: chao.peng@siat.ac.cn
bSchool of Engineering, University of Southampton, Southampton SO17 1BJ, UK. E-mail: D.Kramer@soton.ac.uk
cSchool of Chemistry, University of Southampton, Southampton SO17 1BJ, UK
dThe Faraday Institution, Quad One, Becquerel Avenue, Harwell Campus, Didcot, OX11 0RA, UK
eFaculty of Applied Physics and Mathematics, Gdańsk University of Technology, Gdańsk 80-233, Poland
fFaculty of Mechanical Engineering, Helmut-Schmidt University, Hamburg, 22043, Germany
First published on 20th July 2021
Abstract
Lithium metal plating is a critical safety issue in Li-ion cells with graphite anodes, and contributes significantly to ageing, drastically limiting the lifetime and inducing capacity loss. Nonetheless, the nucleation mechanism of metallic Li on graphite anodes is still poorly understood. But in-depth understanding is needed to rationally design mitigation measures. In this work, we conducted First-Principles studies to elucidate the Li nucleation mechanism on graphite surfaces. These large-scale density-functional-theory (DFT) calculations indicate that nano-particulate Li forms much more readily than classical nucleation theory predicts. Further, our calculations indicate a crucial role of topological surface states near the zigzag edge, lowering the nucleation barrier by a further 1.32 eV relative to nucleation on the basal plane. Li nucleation, therefore, is likely to initiate at or near the zigzag edges of graphitic particles. Finally, we suggest that chemical doping with a view to reducing the effect of the topological surface states might be a potential mitigation strategy to increase nucleation barriers and reduce the propensity to plate Li near the zigzag edge.
Introduction
Lithium-ion batteries (LIBs) have attracted considerable attention in recent decades due to the significant progress in industrial applications such as energy storage.1–9 However, there are still some challenges that limit battery performance and durability, such as battery degradation and safety.10–12 One of the highly problematic issues is the formation and growth of metallic lithium on the graphite anode.13 The formation of metallic lithium, also known as Li deposition or Li plating, is detrimental to battery operation, leading to a low coulombic efficiency and serious safety issues due to the possibilities of short-circuits and catastrophic failure.13,14The graphite anode is particularly vulnerable to lithium deposition during charging, because of the very low margin between the thermodynamic potential required for full charge based on the LiC6 stoichiometry at 0.065 V vs. Li+/Li and the threshold for Li plating at 0.000 V. Therefore, the overpotentials generated by the high current densities applied for fast charging can often cause Li deposition.11 Charging at low temperature further increases the risk of Li plating, as the required overpotential increases with the charge transfer resistance Rct, (∝![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kT) according to the Arrhenius law).15 Li plating thus becomes increasingly competitive with Li intercalation at lower temperatures. Furthermore, slower diffusion of Li from the grain edges to the bulk can lead to greater non-uniformities of composition and overpotentials across the surfaces.16 Li plating has been widely studied both experimentally and through theoretical modelling.10,17–19 Experimentally, the applicability of graphite anodes, indeed, becomes lower with decreasing temperature.15,20,21 In-depth understanding of Li nucleation and growth is, therefore, important to suppress Li deposition on graphite anodes.
exp(−Ea/kT) according to the Arrhenius law).15 Li plating thus becomes increasingly competitive with Li intercalation at lower temperatures. Furthermore, slower diffusion of Li from the grain edges to the bulk can lead to greater non-uniformities of composition and overpotentials across the surfaces.16 Li plating has been widely studied both experimentally and through theoretical modelling.10,17–19 Experimentally, the applicability of graphite anodes, indeed, becomes lower with decreasing temperature.15,20,21 In-depth understanding of Li nucleation and growth is, therefore, important to suppress Li deposition on graphite anodes.
Li nucleation has been studied in some depth on graphene surfaces by Fan et al.,18 and Liu et al.22 using density-functional-theory (DFT) simulations of atomic Li cluster formation. The nucleation barrier was found to be highly dependent on the Li concentration.22 DFT studies showed that Li prefers spreading out on the graphene sheet at low Li concentrations (i.e. Li/C ratio = 1/64) but starts to nucleate as Li concentration increases.18 The lattice mismatch between Li clusters and the carbon substrate was identified as a factor for pushing the nucleation energy upwards and hinders uniform plating of Li.23 Although Li nucleation in the graphene system has been studied in some depth, to the best of our knowledge, there are few studies exploring the Li nucleation mechanism in the graphite system at the atomistic level, especially considering the edge effect of graphite that has a strong impact on Li intercalation kinetics.16,24
In the present work, we extend the consideration to multi-layered graphite, with the important addition of a variable lithium concentration in a (partially) intercalated layer between two graphene sheets, as a first effort to model the vastly more important case of lithium plating on graphite. Also, we perform a First-Principles study to investigate the nucleation of Li clusters with consideration of the graphite edge effect with the aim of identifying likely Li nucleation sites at graphite anodes and to propose rational strategies to suppress specific modes of Li plating.
Computational details
Theoretical method
Spin-polarized DFT calculations were performed by using the Vienna Ab initio Simulation Package (VASP).25,26 The Perdew–Burke–Ernzerhof (PBE) functional within the Generalized Gradient Approximation (GGA) was chosen for the treatment of exchange-correlation.26–28 The core electrons were described by the projector-augmented wave (PAW) method.29,30 The valence electronic states were expanded in plane-wave basis sets with a cutoff energy of 450 eV. The force convergence criterion was set to 0.03 eV Å−1. The DFT-D3 method with Becke–Johnson (BJ) damping was applied to account for dispersion interactions.31,32 Born–Oppenheimer ab initio molecular dynamics (AIMD) was conducted to sample low energy configurations for different sized Li clusters with a time step of 0.5 fs and a total sampling time of 6 ps. Three low-energy configurations were picked from the AIMD simulation for each cluster size after an initial equilibration period. Geometry optimization was performed for those three configurations, and the lowest energy configuration was selected as a representative shape model for nucleation energy calculations.Structural model
A p(8 × 8) two graphene-layer graphite basal plane (a = b = 19.73 Å, c = 25.03 Å; α = β = 90°, γ = 120°) was constructed by cutting the (001) plane of the unit cell of AB stacked graphite (a = b = 2.47 Å, c = 6.71 Å; α = β = 90°, γ = 120°) as shown in Fig. S1 of the ESI.† The convergence test for system size and number of layers of graphite is shown in Fig. S2.† A p(8 × 2) hydrogen-terminated zigzag-edged graphite (a = 23.41 Å, b = 22.19 Å, c = 57.72 Å; α = β = γ = 90°) was constructed to simulate Li nucleation near the edge. For the zigzag-edged LiC6, a p(3 × 4) (a = 24.43 Å, b = 22.42 Å, c = 57.40 Å; α = β = γ = 90°) supercell was constructed. A 15 Å vacuum padding was added in all configurations to minimize interactions between periodic slabs. During geometry optimization, all atoms were relaxed with the unit cell dimensions being fixed. We used a k-mesh of (3 × 3 × 1) to optimize the structure of the graphite basal plane and a k-mesh of (2 × 2 × 1) for the geometry optimization of zigzag-edged graphite.Li nucleation energy
The nucleation energy (ΔGnucleation) of Li is defined as:22,23| ΔGnucleation = μ(Lin) − nμ(Li) | (1) |
| μ(Lin) = G(Lin|C) − G(C) | (2) |
| μ(Li) = G(Li|C) − G(C) | (3) |
Because all the configurations are solids, the free energy can be approximated by the total energy.23 Therefore, the nucleation energy and the chemical potentials (μ(Lin) and μ(Li)) can be rephrased as:33
| Enucleation = μ(Lin) − nμ(Li) | (4) |
| μ(Lin) = E(Lin|C) − E(C) | (5) |
| μ(Li) = E(Li|C) − E(C) | (6) |
Results and discussion
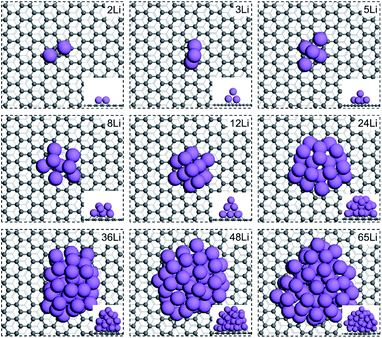
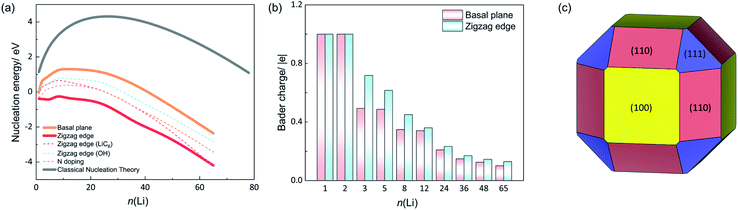
We first address Li nucleation on the basal plane of graphite. The AIMD results indicate that Li prefers nucleation as a cluster instead of forming a thin film on the basal plane. The first Li atom (n = 1) adsorbs on the hollow site of the carbon hexagon with an average C–Li bond length of 2.24 Å and forms the nucleus (see Fig. S1†). When the second Li approaches the basal plane (n = 2), it adsorbs at the nearest neighboring site to the first adsorbed Li, producing a Li2 dimer configuration as shown in Fig. 1. The Li–Li distance is 2.86 Å, shorter than the Li–Li distance (3.03 Å) in bulk Li metal. The shorter Li–Li distance mainly results from the lattice mismatch between the carbon hexagons and the Li metal lattice. For n = 3, the AIMD simulations show that Li nucleates in a triangle shape with two Li atoms binding with the surface carbons below. The third Li atom is sitting on top of the other two Li atoms and not adhering to the surface carbons. The formed triangle plane is approximately perpendicular to the basal plane rather than parallel to the surface. The bond lengths between the top Li atom and those two surface Li atoms are 2.94 and 2.91 Å respectively, which is longer than the bond length between the two surface Li atoms (2.85 Å) and closer to the Li–Li bond length (3.03 Å) in Li metal. Thus, it is the lattice mismatch with the carbon substrate and the weak C–Li interaction that drives up the Li triangle plane. With n rising to five, the Li cluster forms in a pentahedron shape stacked with two Li layers. The bottom layer consists of four Li atoms, arranged in the vertices of a parallelogram. The upper layer is only composed of one Li atom sitting on top of the center of the parallelogram. With n increasing from 8 to 65, the shape of the cluster becomes irregular. There are no visible perfect crystal facets exposed on the Li clusters.The nucleation energies (Enucleation) of different Li clusters were also examined. Fig. 2a shows the Enucleation of various sized Li clusters on the basal plane (orange line). With Li cluster growth, Enucleation shows first an increasing and afterwards a decreasing trend. As shown in eqn (4), we take the chemical potential of an adsorbed Li atom on the basal plane (μLi) as the reference for calculating the nucleation energy (−0.33 V vs. Li+/Li). Thus, the Enucleation at n = 1 is 0 eV. Bader charge analysis shows the charge of the Li adatom to be +1|e| (see Fig. 2b). The Li atom is thus a full electron donor that donates its electron to the graphene sheet. Hence, an ionic bond is generated for Li–C. With n = 2, Enucleation rises rapidly to 0.64 eV with the formation of the Li2 dimer. The charges for both Li atoms are +1|e| each. The less favorable geometry resulting from the lattice mismatch and strong charge repulsion between the two Li ions are likely the reason for the markedly higher Enucleation at n = 2. Enucleation increases dramatically with Li cluster size growth, reaching a critical point at n = 12. The nucleation barrier is, thus, 1.32 eV on the basal plane of graphite. Afterwards, Enucleation decreases gradually and becomes negative with n larger than 36. Fig. 2a indicates that the growth of small Li clusters (n < 48) is thermodynamically unfavourable due to the positive nucleation energies determined by the high surface energy of Li clusters even if the Li chemical potential is large enough for atomic adsorption of Li on the basal plane. Naturally, the nucleation energy becomes favourable for larger cluster where the bulk energy becomes the driving force. Therefore, the small cluster growth on the basal plane is the rate-limiting step.
We also investigated Li nucleation near the zigzag edge at which a topological surface state at the edge carbons was previously shown to strongly stabilize Li adsorption near the edge.16,24 Because AIMD simulations are prohibitively expensive for large systems, we collected the most stable Li configuration of each Li cluster on the basal plane sampled from the AIMD simulations and transferred them to the zigzag-edged systems to construct Li clusters deposited near the zigzag edge, followed by geometry optimization. The geometries of the composite systems are shown in Fig. S3.† The first adsorbed Li (n = 1) sits at the center of the carbon hexagon of the edge site. When n increases to two, Li also forms a Li2 dimer configuration, similar to the basal plane. But the Li–Li distance in the Li2 dimer elongates to 3.21 Å which is 0.35 Å longer than that on the basal plane. The Li3 cluster shows a different nucleation symmetry to that on the basal plane. The three Li atoms still nucleate as a triangle, but all of them adhere to the surface with two Li atoms binding at the edge sites and the third Li atom adsorbing at the subsurface site. The different nucleation behavior of Li3 clusters is likely due to the strong interaction between the surface carbons and Li atoms induced by the topological surface state favoring Li nucleation on the surface. With n increasing to five, the Li cluster forms in a pentahedron shape with one Li sitting on top of the parallelogram below, consisting of four Li atoms at each vertex. The facets of Li clusters are not specifically recognizable with n larger than eight because clusters are still too small to generate well-defined crystal facets, but it is clear that the clusters accumulate in multiple layers rather than film on the graphite surface.
In contrast to the nucleation energy on the basal plane of graphite, Li nucleation near the zigzag edge becomes much more favorable as shown in Fig. 2a (red curve). From the first Li adsorption at the edge site to a considerable size of Li cluster, the nucleation energies are negative, indicating that it is a barrier-free process of Li nucleation near the zigzag edge as soon as single atom adsorption becomes thermodynamically favorable. Fig. 2b shows the average charge of Li at both the basal plane and the zigzag edge. For the first Li and Li2 dimer systems, all the Li atoms have a +1|e| charge due to the ionic bonding between Li and graphite.
However, with the continuous growth of Li clusters (n > 2), the zigzag-edged system shows a higher average charge of Li than the basal plane system. For example, the Li3 cluster system presents an average charge of Li of +0.72|e|, while on the basal plane it is +0.50|e|. The trend of a higher positive charge on the Li clusters at the zigzag edge compared to the basal plane prevails even for n up to 65. This indicates that the Li clusters near the zigzag edge donate more electrons to the graphite substrate. As a consequence, Li clusters have stronger chemical interactions with the zigzag edge, which lowers the nucleation energies. Therefore, Li nucleation is more likely to occur at the zigzag edge and suppressing Li nucleation at that edge is worthy of attention.
When Li clusters grow and approach macroscopic dimensions, the crystal facets become well-defined, and the energy of Li cluster growth can be accurately described by classical nucleation theory (CNT). In that limit, the nucleation energy consists of the Li bulk energy (Ebulk), the surface energy of the Li cluster (Esurface) and the interface energy (Einterface) between the attached Li cluster and the graphite substrate. Thus, the nucleation energy can be expressed as:
| Enucleation = Ebulk + Esurface − Einterface | (7) |
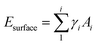 | (8) |
The nucleation energy as given by CNT is represented by the grey curve in Fig. 2a. CNT substantially overestimates the nucleation energy compared to finite-size Li clusters (n ≤ 65). The nucleation barrier from CNT is 4.31 eV at n = 28, which is much higher than the 1.32 eV obtained for the basal plane system from DFT calculations of actual nanoparticles. Notably, all the three curves show negative nucleation energies when Li clusters grow into larger particles. This is a direct consequence of our choice for μLi. Single Li atom adsorption at the basal plane defines a chemical potential of 0.33 eV above metallic Li and a voltage of −0.33 V vs. Li+/Li. Therefore, there is always a negative thermodynamic driving force once a cluster contains a sufficient number of bulk-like Li atoms.
During battery charging, the Li concentration within the graphite anode increases, which also has an impact on Li nucleation energies. Therefore, we studied fully lithiated graphite as well, particularly, the zigzag-edged LiC6 graphite intercalation compound (GIC). In Fig. 2a the dark-blue dashed line shows Li nucleation energies as a function of n(Li) in LiC6. The nucleation barrier rises to 0.71 eV with critical n at eight (see structures in Fig. S5†). Clearly, the nucleation barrier increases with rising Li concentration. This is attributed to the filled surface state at the zigzag edge reducing interactions of edge carbons with Li clusters at the surface, thereby raising the nucleation energy on LiC6. Notably, this 0.71 eV barrier is still much lower than that on the basal plane of Li-free graphite (1.32 eV). This highlights the crucial role of the zigzag edge for initial Li nucleation at graphite anode and also at the end of charging (LiC6). Different oxidized terminations co-exist at the edge of graphite anodes, because of the chemical reactions between the electrolyte and graphite surfaces.34,35 Thus, we considered the effect of other possible terminations on Li nucleation. The oxygen groups were reported to be critical to the formation of the solid electrolyte interphase (SEI) layer.36 Thus, OH-termination was investigated and compared with H-termination (see the structure in Fig. S6†).24,37 The light-blue dashed curve in Fig. 2a presents the nucleation energy at OH-terminated zigzag edges. The nucleation barrier is 0.86 eV, which is also lower than that of the basal plane case due to the prevalence of topological surface states in OH-terminated zigzag-edged graphite, as explained in our recent work.16 The nucleation trend is, therefore, similar to the H-terminated zigzag edge system with a slight increase in nucleation energy.
On the basis of those findings, it appears much more feasible to initiate Li plating near the zigzag edge than on the basal plane. The zigzag edge is, therefore, more detrimental to the safety of LIBs because it might facilitate Li plating and dendrite formation and associated degradation and capacity loss. Suppressing Li nucleation at the zigzag edge is, therefore, highly desirable, and for this purpose here we investigated chemical doping at the zigzag edge. A recent experimental study showed that Li nucleation can be effectively suppressed via a facile interfacial modification of the graphite electrode.38 Nitrogen (N) doping at the zigzag edge was considered (cf. Fig. S6†). Fig. 2a shows the nucleation energy of the N-doped zigzag edge system (dashed pink line). The nucleation barrier increases by 0.41 eV relative to the pristine zigzag edge. Introducing N dopant fills the surface state at edge carbons, which reduces Li–C interactions, thereby raising the Li nucleation energy. Chemical doping, thus, could be a promising approach to inhibit Li nucleation. Naturally, the overpotential during charging plays a critical role as well. Fig. 3a and b show the changes of the nucleation curve as a function of applied potential vs. Li+/Li. On the basal plane, the nucleation barrier is 2.99 eV at −0.26 V vs. Li+/Li. However, the barrier is lowered significantly to only 1.07 eV when the potential is reduced to −0.36 V vs. Li+/Li (cf.Fig. 3a). Applying an excess overpotential at the electrode does not only increase the thermodynamic driving force for Li plating, it also considerably reduces the nucleation barrier. Therefore, large overpotentials applied at the electrode for purposes like fast charging seriously increase the risk of Li plating by exponentially increasing the nucleation rate. At the zigzag edge, an analogous nucleation trend at different potentials is identified (cf.Fig. 3b). The nucleation barrier is as high as 1.22 eV when the potential is −0.26 V vs. Li+/Li. If an extra 0.07 V overpotential is applied to the graphite electrode, the nucleation barrier dramatically reduces to 0 eV (−0.33 V vs. Li+/Li). This indicates that Li can spontaneously nucleate near the zigzag edge at that potential. Furthermore, a good correlation complying with qualitative expectations from CNT is found between the nucleation barrier and the potential for both the basal plane system and the zigzag system (cf.Fig. 3c). CNT predicts a nucleation barrier Ea proportional to 1/μ2. Due to that relation, the nucleation rate (rnucleation) equation can be written as:
 | (9) |
Conclusions
We conducted First-Principles calculations to investigate the Li nucleation mechanism on graphite. On the basis of AIMD sampling of Li depositing on graphite, we found that the graphite edge has a substantial impact on the Li nucleation behavior. The detailed findings are:(1) The zigzag edge is crucial for the finite-size Li nucleation due to the “beneficial” role of the topological surface states. These lower the Li nucleation barrier by more than 1 eV compared to the basal plane.
(2) Classical nucleation theory parametrized by surface energies and a Wulff construction indicates a barrier of Li nucleation on the basal plane of 4.32 eV and overestimates the actual nucleation barrier for the initial Li nucleation process. The much lower barrier of the finite-size metallic Li cluster formation implies that inhibiting small Li cluster formation is of importance in order to prevent undesirable Li plating.
(3) The nucleation barrier increases at higher degree of lithiation, but the zigzag edge is still much more favorable for Li nucleation than the basal plane.
(4) Chemical doping of nitrogen can drive the nucleation barrier upward and could be a possible way to suppress Li nucleation.
(5) Nucleation rate depends exponentially on the square of the applied potential. Therefore, careful potential control of the graphite anode is not only important to keep the thermodynamic driving force for Li plating low, it also allows to keep the nucleation rate low. Indeed, one could argue that the potential where the nucleation barrier becomes zero or at least lower than the activation energy for intercalation defines an important limit for charging batteries safely.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support from the Faraday Institution and EPSRC (https://www.faraday.ac.uk; EP/S003053/1) with grant number of FIRG003. We are grateful for access to the Iridis5 Supercomputer of the University of Southampton, the Michael Supercomputer of the Faraday Institution, the Tryton Supercomputer at the TASK Academic Computer Centre (Gdańsk, Poland) and the UK Materials and Molecular Modelling Hub for computational resources, partially funded by the EPSRC (Grant No. EP/P020194/1 and EP/T022213/1).Notes and references
- A. Van der Ven, Z. Deng, S. Banerjee and S. P. Ong, Chem. Rev., 2020, 120, 6977–7019 CrossRef CAS PubMed.
- S. Chae, S.-H. Choi, N. Kim, J. Sung and J. Cho, Angew. Chem., Int. Ed., 2020, 59, 110–135 CrossRef CAS PubMed.
- R. V. Salvatierra and J. M. Tour, Nat. Nanotechnol., 2019, 14, 500–501 CrossRef CAS PubMed.
- Y. Li, Y. Lu, P. Adelhelm, M.-M. Titirici and Y.-S. Hu, Chem. Soc. Rev., 2019, 48, 4655–4687 RSC.
- M. Li, J. Lu, Z. Chen and K. Amine, Adv. Mater., 2018, 30, 1800561 CrossRef PubMed.
- G. E. Blomgren, J. Electrochem. Soc., 2016, 164, A5019–A5025 CrossRef.
- N. Nitta, F. Wu, J. T. Lee and G. Yushin, Mater. Today, 2015, 18, 252–264 CrossRef CAS.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- M. S. Whittingham, Chem. Rev., 2004, 104, 4271–4302 CrossRef CAS PubMed.
- M. Petzl, M. Kasper and M. A. Danzer, J. Power Sources, 2015, 275, 799–807 CrossRef CAS.
- N. Legrand, B. Knosp, P. Desprez, F. Lapicque and S. Raël, J. Power Sources, 2014, 245, 208–216 CrossRef CAS.
- J. Vetter, P. Novák, M. R. Wagner, C. Veit, K. C. Möller, J. O. Besenhard, M. Winter, M. Wohlfahrt-Mehrens, C. Vogler and A. Hammouche, J. Power Sources, 2005, 147, 269–281 CrossRef CAS.
- X. Qin, M. Shao and P. B. Balbuena, Electrochim. Acta, 2018, 284, 485–494 CrossRef CAS.
- X.-G. Yang, Y. Leng, G. Zhang, S. Ge and C.-Y. Wang, J. Power Sources, 2017, 360, 28–40 CrossRef CAS.
- T. Waldmann, B.-I. Hogg and M. Wohlfahrt-Mehrens, J. Power Sources, 2018, 384, 107–124 CrossRef CAS.
- C. Peng, M. P. Mercer, C.-K. Skylaris and D. Kramer, J. Mater. Chem. A, 2020, 8, 7947–7955 RSC.
- P. Bai, J. Li, F. R. Brushett and M. Z. Bazant, Energy Environ. Sci., 2016, 9, 3221–3229 RSC.
- X. Fan, W. T. Zheng, J.-L. Kuo and D. J. Singh, ACS Appl. Mater. Interfaces, 2013, 5, 7793–7797 CrossRef CAS PubMed.
- L. Guo and P. C. Searson, Electrochim. Acta, 2010, 55, 4086–4091 CrossRef CAS.
- T. Waldmann, B.-I. Hogg, M. Kasper, S. Grolleau, C. G. Couceiro, K. Trad, B. P. Matadi and M. Wohlfahrt-Mehrens, J. Electrochem. Soc., 2016, 163, A1232–A1238 CrossRef CAS.
- R. V. Bugga and M. C. Smart, ECS Trans., 2019, 25, 241–252 CrossRef.
- M. Liu, A. Kutana, Y. Liu and B. I. Yakobson, J. Phys. Chem. Lett., 2014, 5, 1225–1229 CrossRef CAS PubMed.
- J. Cui, S. Yao, M. Ihsan-Ul-Haq, J. Wu and J.-K. Kim, Adv. Energy Mater., 2019, 9, 1802777 CrossRef.
- E. G. Leggesse, C.-L. Chen and J.-C. Jiang, Carbon, 2016, 103, 209–216 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. C. Valero, P. Raybaud and P. Sautet, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 045427 CrossRef.
- P. Bernardo, J. M. Le Meins, L. Vidal, J. Dentzer, R. Gadiou, W. Märkle, P. Novák, M. E. Spahr and C. Vix-Guterl, Carbon, 2015, 91, 458–467 CrossRef CAS.
- H. Buqa, A. Würsig, J. Vetter, M. E. Spahr, F. Krumeich and P. Novák, J. Power Sources, 2006, 153, 385–390 CrossRef CAS.
- S. H. Ng, C. Vix-Guterl, P. Bernardo, N. Tran, J. Ufheil, H. Buqa, J. Dentzer, R. Gadiou, M. E. Spahr, D. Goers and P. Novák, Carbon, 2009, 47, 705–712 CrossRef CAS.
- M. Fujita, K. Wakabayashi, K. Nakada and K. Kusakabe, J. Phys. Soc. Jpn., 1996, 65, 1920–1923 CrossRef CAS.
- K. R. Tallman, B. Zhang, L. Wang, S. Yan, K. Thompson, X. Tong, J. Thieme, A. Kiss, A. C. Marschilok, K. J. Takeuchi, D. C. Bock and E. S. Takeuchi, ACS Appl. Mater. Interfaces, 2019, 11, 46864–46874 CrossRef CAS PubMed.
- J. Dziedzic, A. Bhandari, L. Anton, C. Peng, J. C. Womack, M. Famili, D. Kramer and C.-K. Skylaris, J. Phys. Chem. C, 2020, 124, 7860–7872 CrossRef CAS.
- A. Bhandari, L. Anton, J. Dziedzic, C. Peng, D. Kramer and C.-K. Skylaris, J. Chem. Phys., 2020, 153, 124101 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta03447b |
| This journal is © The Royal Society of Chemistry 2021 |