Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Suppressing void formation in all-solid-state batteries: the role of interfacial adhesion on alkali metal vacancy transport†
Ieuan David
Seymour
 * and
Ainara
Aguadero
* and
Ainara
Aguadero
Department of Materials, Imperial College London, Exhibition Road, SW7 2AZ London, UK. E-mail: ids08@imperial.ac.uk
First published on 9th June 2021
Abstract
All-solid-state batteries containing a solid electrolyte and a lithium (Li) or sodium (Na) metal anode are a promising solution to simultaneously increase the energy density and safety of rechargeable batteries. However, problems remain with the stripping of alkali metal from the alkali metal/solid-state electrolyte interface during discharge in which void formation and loss of contact can occur. A novel bond breaking model is developed in this work to understand the relationship between alkali metal vacancy segregation and interfacial adhesion at the alkali metal/solid-state electrolyte interface. The bond breaking approach is tested against density functional theory (DFT) calculations of pristine Li and Na metal surfaces and interfaces between Li and Na metal and model substrate structures (LiCl, Li3OCl, LiMg, Li2O, γ-Li3PO4, AlSc, NaCl and NaBr). The activation barrier for surface to subsurface vacancy diffusion was found to be considerably larger than bulk diffusion in Li and Na slabs. At the alkali metal/solid-state electrolyte interface, the preference for alkali metal vacancy segregation is shown to be intimately linked to the interfacial work of adhesion (Wad) and alkali metal surface energy, σm. Suppression of alkali vacancy segregation to the interface is found to occur when Wad ≥ 2σm. The role of interfacial structure on the vacancy segregation energy is demonstrated for both coherent and incoherent Li/LiCl interfaces. This work provides novel guidelines for the materials engineering of new solid-state electrolyte and interlayer materials that can suppress void formation in all-solid-state batteries with alkali metal anodes.
Introduction
All-solid-state batteries (ASSB) containing fast ion conducting, solid-state electrolyte (SSE) materials are at the forefront of rechargeable battery technology, particularly for the next generation of electric vehicle applications. The replacement of flammable organic liquid electrolytes with non-flammable SSE materials provides a significant improvement in battery safety. The introduction of a SSE may also enable the use of a pure lithium or sodium metal anode, which would increase the practical volumetric and gravimetric energy density of ASSB relative to conventional liquid electrolyte batteries.1,2 However, challenges relating to the dynamic stability of the alkali metal/SSE interface under fast rates of discharge and charge still need to be addressed to facilitate the adoption of ASSBs with alkali metal anodes.Due to the strongly reducing nature of alkali-metal anodes, only a limited number of SSE systems including Li7La3Zr2O12 (LLZO) garnets,3–6 antiperovskite Li3OCl7–9 and Na β′′-alumina,10–12 have been shown to be either thermodynamically stable or kinetically stabilised, with very small driving forces for reaction, against alkali metals. The majority of commonly studied SSE materials are thermodynamically unstable and can react with alkali metals to form secondary interphases.13,14 Two types of interphase are commonly distinguished: (i) a kinetically self-limiting interphase that is ionically conducting, but electronic insulating or (ii) a reactive, unstable interphase that is a mixed ionic and electronic conductor.15,16 In the latter case, continuous degradation of the SSE will occur leading to poor electrochemical performance.
In addition to having high stability under static conditions, the alkali metal/SSE interface is also required to display an interfacial resistance (<10 Ω cm2) to facilitate rapid alkali metal stripping and plating during discharge and charge, respectively.16 Although a full understanding of all of the atomistic processes that affect the interfacial resistance has not been established, it has been demonstrated that the adhesion between the alkali metal and SSE plays a crucial role.17,18 The interfacial adhesion or ‘wetting’ at the alkali metal/SSE interface is related to the surface chemistry and nature of bonding between the materials. Experimentally, contact angle measurements are commonly used to determine the work of adhesion (Wad) between a liquid and solid phase in which a hemispherical droplet of liquid, such as an alkali metal, forms an angle of θ on a solid substrate.
For an as-synthesised and polished LLZO substrate, a high contact angle of θ = 142° with molten Li was previously observed indicating poor metal–ceramic adhesion at the interface.17 After high temperature heat treatment, a lower contact angle of θ = 95° was found which was ascribed to the removal of contaminants, such as Li2CO3, that were present on the as-synthesised material. For the LLZO family of materials, it has been demonstrated that the intrinsic charge transfer resistance across the Li/LLZO interface is very small once contaminant layers have been removed.17,19–21 Analogously, in the Na β′′-alumina system, the removal of hydroxyl and carbon contaminants through heat treatment in an inert atmosphere was found to lead to very small (<10 Ω cm2) interfacial resistances with Na metal.12 Improvement of the wetting between alkali metals and SSE surfaces has been achieved in several studies through the addition of a thin, metallic interlayer phase.22–24 The interlayer materials typically form an alloy with Li (Na) that acts as an alkali conducting buffer that displays strong adhesion with both the Li (Na) metal and the SSE.
The reactivity of molten Li and Na with environmental contaminants such as O2 and CO2 make experimental contact angles measurements challenging, and as such, only a limited amount of quantitative data is currently available on the work of adhesion with different SSE materials. Density functional theory (DFT) calculations are particularly powerful for understanding the structure and adhesion of alkali metal/SSE interfaces. In the case of LLZO, DFT calculations have been used to show that the work of adhesion of Li metal on a LLZO substrate (Wad = 0.67 J m−2) was considerably larger than on a Li2CO3 (0.1 J m−2) substrate, in agreement with experimental contact measurements.17 In a separate study, the work of adhesion of Li with LLZO was found to be dependent on the coordination of Zr ions on the surface, with low coordination environments leading to strong wetting.25 A strong dependence of the work of adhesion on the surface chemistry was also shown for the Li3OCl system, in which O terminated surfaces displayed considerably stronger adhesion (0.77 J m−2) with Li metal compared to Cl terminated surfaces (0.09 J m−2).26 For the Na β′′-alumina system, it was demonstrated through ab initio molecular dynamics simulations that the addition of caesium lowered the contact angle and increased the work of adhesion of Na droplets on the surface of Na β′′-alumina.27
Even though materials such as LLZO and Na β′′-alumina display minimal thermodynamic driving force for reaction with Li and Na metal, high interfacial resistances are still observed during stripping (discharge) and plating (charge) of solid Li and Na metal at high current densities.28,29 The origin of this large interfacial resistance on stripping has been attributed to the loss of contact between the alkali metal (Li or Na) and SSE material.30 During discharge, Li (Na) atoms are stripped from the Li (Na) metal surface and inserted into the SSE as a Li+ (Na+) ion, leaving behind a vacancy in the Li (Na) metal.16,31 The rate of injection of Li (Na) vacancies into the Li (Na) metal is controlled by the applied current. The accumulation of Li (Na) vacancies can lead to the formation of voids at the interface, which reduces the contact between the Li (Na) metal and SSE and increases the interfacial resistance.
To suppress void formation, the rate of Li (Na) transfer from the bulk Li (Na) metal to the Li (Na)/SSE interface must be faster than the rate of vacancy creation. Two main mechanisms lead to alkali metal transport to the interface: stress driven creep and vacancy diffusion.32 In the case of creep, when stripping of Li (Na) atoms occurs under an applied pressure, deformation of the Li (Na) can occur below the yield stress which drives Li (Na) to the interface and closes voids. Power law creep, involving dislocation climb was proposed to be the dominant creep mechanism for Li.33 However, it has been shown that critical stack pressures on the order of 10 MPa are required to suppress void formation in Li and Na systems at current densities on the order of 1 mA cm−2.28,29,34 The application of high pressures in practical battery devices with Li or Na metals anodes poses a significant challenge.
In the case of vacancy diffusion, vacancies created at the interface can either diffuse into the bulk of the Li (Na) metal or be annihilated at features such as dislocations at the interface.30 The rate of vacancy diffusion away from the interface into the bulk depends on the fundament transport mechanisms present within the Li (Na) metal. Self-diffusion in alkali metals has previously been proposed to be an important factor dictating the growth of dendrites on alkali metal surfaces.35,36 Experimental and computational studies have shown that the self-diffusion mechanism in bulk Li and Na metal is dominated by monovacancy transport.37 Under thermal equilibrium, the overall activation energy for self-diffusion, ESDVm = EfVm + EmVm, is given as the sum of the vacancy formation energy, EfVm, and the activation energy, EmVm. DFT calculations have indicated that the activation energies of monovacancies in Li 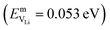 and Na
and Na 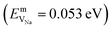 are considerably smaller than the formation energies (
are considerably smaller than the formation energies (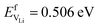 and
and 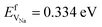 ).38 The DFT computed values of ESDVm are in good agreement with experimental NMR and radiotracer measurements of the diffusion coefficient in Li and Na, indicating that vacancy formation is rate limiting in Li and Na.39,40 The very small EmVm values for Li and Na indicate that once created, vacancies in Li and Na are expected to move rapidly in the bulk, even at room temperature. For Li metal, based on the diffusion coefficient for monovacancy self-diffusion, vacancy supersaturation and void formation is predicted to occur at the Li metal/SSE interface, even for small currents of 50–200 μA cm−2.30
).38 The DFT computed values of ESDVm are in good agreement with experimental NMR and radiotracer measurements of the diffusion coefficient in Li and Na, indicating that vacancy formation is rate limiting in Li and Na.39,40 The very small EmVm values for Li and Na indicate that once created, vacancies in Li and Na are expected to move rapidly in the bulk, even at room temperature. For Li metal, based on the diffusion coefficient for monovacancy self-diffusion, vacancy supersaturation and void formation is predicted to occur at the Li metal/SSE interface, even for small currents of 50–200 μA cm−2.30
Importantly, alkali metal transport via both creep and vacancy diffusion limits the current density of alkali metals in the solid state. However, it has recently been shown for the Na/Na β′′-alumina system that when Na metal is in the liquid state, significantly higher (1000×) current densities can be applied without loss of contact.41 Void formation at the Li/LLZO interface was also recently shown to be suppressed by the introduction of a thin liquid Na–K alloy layer.42 It should also be highlighted that metal vacancy assisted void formation is not unique to all-solid-state batteries and is a common phenomenon observed other fields including radiation induced voids in bimetallic composites43 and cavity formation during oxide film growth.44,45
Little is known about how the activation barrier for vacancy migration changes at the solid–solid alkali metal/SSE interface, even though this is of crucial importance for understanding the formation of voids during alkali metal stripping. In a recent kinetic Monte Carlo (KMC) study by Tewari and Mukherjee, it was demonstrated that when the strength of the bonding between Li and a model 2D SSE was greater than or equal to the strength of the Li–Li bonding in Li metal, voids were suppressed during Li metal deposition.46 In another study by Yang et al., large-scale molecular dynamics calculations were used to show how both the work of adhesion and pressure affect void formation at a model Li metal/SSE interface.47 It was demonstrated that a work of adhesion Wad > 0.7 J m−2 was required to suppress voids at the BCC Li (100)/SSE interface with the application of a moderate pressure (10–20 MPa).47 A fundamental difference was also observed in this study between coherent and incoherent Li metal/SSE interfaces, in which lower Li vacancy diffusion into the Li bulk was observed in the latter case.
In the current study, we develop a bond breaking model in combination with DFT calculations to understand the fundamental relationship between alkali metal vacancy diffusion and the work of adhesion at the alkali metal/SSE interface. The segregation energy of Li and Na metal vacancies from the alkali metal bulk to both a free metal surface and coherent Li (Na)/SSE interface is qualitatively captured with the bond breaking model, providing mechanistic insight about the role of interfacial bonding on vacancy segregation. The model is further developed to understand how incoherency at the Li (Na)/SSE interface affects the vacancy segregation. The results from this work provide novel insights about the links between interfacial adhesion and alkali metal surface energy on the transport of alkali metal vacancies, providing simple criteria for rational design of SSE materials that have higher tolerance to void formation.
Methodology
Computational details
Density functional theory (DFT) calculations were performed in this work with the Vienna Ab initio Simulation Package, using the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional.48,49 Projector-augmented wave (PAW) pseudopotentials were used for all species, with a plane wave cut off of 500 eV.50 To minimise the computational cost of studying large interface structures, the softest PAW pseudopotentials from each element were adopted from the VASP 5.4.4 distribution, which are labelled Li, Na, P, Al, Mg, Sc, Cl, Br, S and O_s. Tests of pseudopotentials containing additional valence electrons did not result in qualitative differences to bulk unit cell structures. Non-spin polarised calculations were used throughout, with an electronic energy convergence of 1 × 10−6 eV or better. Methfessel–Paxton smearing was used for all calculations with a smearing width of 0.1 eV.51 The unit cell parameters and atomic positions of alkali metal and substrate unit cells were optimised without symmetry constraints until the force on any atom fell below 0.01 eV Å−1. For slab calculations, the lattice parameters were fixed to the optimised unit cell parameters and the atomic positions relaxed to a force tolerance of 0.01 eV Å−1.Gamma centred k-point meshes with grids of 8 × 8 × 8 and 11 × 11 × 5 were used to sample the Brillouin zone of body centred cubic (BCC) Li and Na and hexagonal the close packed (HCP) Li unit cells, respectively, which resulted in a total energy convergence of <5 meV per atom. The lattice parameters of the BCC and HCP phases are shown in Table S1.† Gamma centred k-point meshes were also used for substrate unit cells in which the same k-point mesh density as used for the BCC or HCP alkali metal unit cells was adopted. The same reciprocal space k-point mesh density used for the unit cell structures was also used for supercell calculations in the ab plane parallel to the surface/interface, and a single k-point was used along the c vacuum direction. For surface and interface slab calculations, a vacuum thickness of 15 Å or greater was used in all cases. Activation barrier calculations on Li and Na slabs were performed with the climbing image nudged elastic band (NEB) method with 3 intermediate images along the band.52,53 Optimisation of the NEB images was performed under fixed cell conditions until the force on any atom fell below 0.01 eV Å−1 for each image. All structural images in this work were produced using the Vesta visualization software.54
Surface slab generation
A series of model interface structures were generated in this study to investigate the segregation of alkali metal vacancies at solid–solid interfaces in both Li and Na metal all-solid-state batteries (ASSB). At room temperature, Li and Na metal are commonly indexed with the body centred cubic (BCC) structure,55,56 although the energy of the BCC, hexagonal close packed (HCP) and face centred cubic (FCC) structures are almost degenerate from DFT calculations.57,58 In this work, the BCC structure was used for Na metal and both the BCC and HCP structures were investigated for Li, depending on the type of substrate. A series of representative model compounds LiCl (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), NaCl (Fm
m), NaCl (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), NaBr (Fm
m), NaBr (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), Li2O (Fm
m), Li2O (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), Li3OCl (Pm
m), Li3OCl (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), γ-Li3PO4 (Pnma), LiMg (Pm
m), γ-Li3PO4 (Pnma), LiMg (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), AlSc (Pm
m), AlSc (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), with very different electronic structures were selected to form interfaces with Li or Na metal. The alkali metal and substrate unit cell structures are shown in Fig. S1.† With the exception of LiMg and γ-Li3PO4, as detailed further in the ESI Methods section,† all of the model substrate phases in this work are predicted to be thermodynamically stable against Li or Na metal, based on DFT calculated reaction energies obtained from the Materials Project.59 All substrate phases contained a fully occupied Li or Na sublattice to minimise the computational complexity associated with partial alkali ion occupation. Symmetric surface slabs were generated in this work using the pymatgen python package.60,61 Further discussion about the choices of substrate structures studied in this work and the surface terminations of alkali metal and substrate slabs used can be found in the ESI Methods section.†
m), with very different electronic structures were selected to form interfaces with Li or Na metal. The alkali metal and substrate unit cell structures are shown in Fig. S1.† With the exception of LiMg and γ-Li3PO4, as detailed further in the ESI Methods section,† all of the model substrate phases in this work are predicted to be thermodynamically stable against Li or Na metal, based on DFT calculated reaction energies obtained from the Materials Project.59 All substrate phases contained a fully occupied Li or Na sublattice to minimise the computational complexity associated with partial alkali ion occupation. Symmetric surface slabs were generated in this work using the pymatgen python package.60,61 Further discussion about the choices of substrate structures studied in this work and the surface terminations of alkali metal and substrate slabs used can be found in the ESI Methods section.†
The surface energy (σ) of the alkali metal and substrate phases was calculated as:
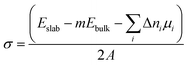 | (1) |
The surface energies of alkali metal slabs were calculated both under zero strain conditions and under strain within the surface plane, required to match the lattices parameters of substrate phases. The surface energy, σ, in eqn (1) is therefore dependent on the magnitude of the strain. The strain contribution to the surface energy of the alkali metal slabs was partially cancelled by applying the same strain to the slab when calculating the reference bulk energy Ebulk. For both strained and unstrained alkali metal slabs, Ebulk was calculated using the method of Vincenzo and Methfessel, in which the energies of 5 slabs with different thickness in the c-direction were calculated.62 Additional corrections to the alkali metal surface energy such as those in ref. 63 were not included, although they are expected to be small for Li and Na from previous work.64 For the substrate phases, which were not subjected to a strain, the bulk energy, Ebulk, was calculated from fully optimised, periodic unit cell structures of each material.
Interface generation
Coherent interface structures were formed by performing supercell transformations of the Li and Na metal slabs to match the atomic positions of the substrate slabs (Tables S2–S4†). Alkali metal/substrate interface pairings were only considered between interfaces that had similar atomic arrangements on the surface. The lattice parameters of the Li or Na slabs were then strained to match the lattice parameters of the substrates and both slabs were combined into a single supercell with the addition of a vacuum region.The LiCl, LiMg and AlSc (100) surfaces were paired with the BCC Li (100) surface. The NaCl and NaBr surfaces were paired with the BCC Na (100) surface. The Li3OCl (100) surface was paired with both the BCC Li and Na (100) surfaces, as the lattice parameter of Li3OCl (3.886 Å) was intermediate between BCC Li (3.436 Å) and BCC Na (4.194 Å). The cation sublattice of γ-Li3PO4 adopts the same structure as HCP Li. The (100) surface of the Pnma γ-Li3PO4 structure was therefore paired with the analogous (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface of the HCP Li structure. The Li2O (111) surface was paired with the (0001) basal surface of HCP Li, as both surfaces have a close packed Li configuration.
0) surface of the HCP Li structure. The Li2O (111) surface was paired with the (0001) basal surface of HCP Li, as both surfaces have a close packed Li configuration.
The orientation relationship between the alkali metal slab and the substrate was set by the atomic arrangement of the surface planes, although relative translations, both parallel (ab plane) and perpendicular (c direction) to the interface are still possible. To limit the number of configurations under study, initial structures were generated in which the alkali atoms in the alkali metal slabs were aligned above the anion sites in the substrate. For metallic phases (LiMg and AlSc), the Li atoms in the Li slab were aligned above the hollow sites on the substrate surface. The initial separation between the slabs in the c direction was approximately chosen based on the separation between planes in the substrate material. Supercell expansions of the a and b lattice parameters were then applied to minimise the interactions between periodic images. All atoms in both slabs were then allowed to fully relax and the interface separation to adopt an optimal value. The resulting interface structures for all systems are shown in Fig. S2.†
The work of adhesion (Wad) between an alkali metal slab and a substrate slab was evaluated as:
| Wad = (Em + Esub − Eint)/A | (2) |
Vacancy formation
Alkali metal vacancies were introduced into the alkali metal slabs and alkali metal/substrate interfaces by removing a single alkali metal atom from different positions along the c direction to investigate the energetic preference for vacancy segregation. The alkali metal vacancy formation energy for a slab (or interface) containing i alkali metal atoms is defined as:| EVm = Eslab,i−1 − Eslab,i + Ebulk | (3) |
The energy of a single alkali atom in the bulk, Ebulk, is taken from the previous calculation of the surface energy in eqn (1). Analogous to the surface energy, EVm is dependent on the strain applied to the alkali metal slab. Removal of alkali atoms from the SSE substrate was not considered as the focus of this work is on void formation on the alkali metal side of the interface. The barrier for alkali ion insertion into the SSE is important for understanding the interfacial charge transfer as previously shown by Gao et al., for LLZO, however, it is beyond the scope of the current study.65
Results and discussion
Bond breaking model
In the following section, a simple bond breaking model based on the previous study by Kumar et al.66 is developed to understand the relationship between the segregation of alkali metal vacancies at the metal–solid interface and the interfacial work of adhesion (Wad).The creation of an alkali metal surface requires the breaking of Ns alkali metal bonds, with bond energy, em–m and a surface density, ρ. The corresponding surface energy is:
| σm = Nsem–mρ | (4) |
An analogous surface energy can be defined for a ceramic or metal substrate:
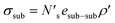 | (5) |
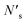 bonds between substrate atoms are broken with a bond energy and surface density of esub–sub and ρ′, respectively. The absolute number of bonds broken and the corresponding energy is more challenging to define in metals compared to ionic solids, as it has previously been established that the bonding energy has a dependence on square root of the density in metals.67,68 In the current model, as energy differences are taken between structures with similar alkali metal coordination environments, the simple bond breaking approach without a square root density dependence still provides qualitatively correct results, as will be shown later in comparison with DFT calculations.
bonds between substrate atoms are broken with a bond energy and surface density of esub–sub and ρ′, respectively. The absolute number of bonds broken and the corresponding energy is more challenging to define in metals compared to ionic solids, as it has previously been established that the bonding energy has a dependence on square root of the density in metals.67,68 In the current model, as energy differences are taken between structures with similar alkali metal coordination environments, the simple bond breaking approach without a square root density dependence still provides qualitatively correct results, as will be shown later in comparison with DFT calculations.
The interfacial energy between an alkali metal and a substrate (ceramic or metal) is given by:
| γi = σm + σsub − 2Niem–subρ | (6) |
| Wad = σm + σsub − γi = 2Niem–subρ | (7) |
The energy to form a vacancy in the bulk of an alkali metal (i.e. away from the interface) involves breaking Nb alkali metal bonds:
| EBulkVm = Nbem–m | (8) |
At a free metal surface in the absence of a substrate, Ns bonds have already been broken per atom, so the formation energy to form a vacancy is smaller:
| EFreeVm = (Nb − Ns)em–m | (9) |
The energy to form a vacancy at the alkali metal/substrate interface requires breaking additional alkali metal–substrate bonds:
| EIntVm = Niem–sub + (Nb − Ns)em–m | (10) |
Combining eqn (4), (7), (8) and (10), the energy difference between an alkali metal vacancy at the bulk and interface, subsequently referred to as the segregation energy, is:
| ΔEBulk–IntVm = EBulkVm − EIntVm = Nbem–m − Niem–sub = (σm − Wad/2)/ρ | (11) |
The energy difference between an alkali metal vacancy at the bulk and free surface is:
| ΔEBulk–FreeVm = EBulkVm − EFreeVm = Nbem–m − (Nb − Ns)em–m = σm/ρ | (12) |
An important result from the relationship in eqn (11) is that when Wad = 2σm, the segregation energy is ΔEBulk–IntVm = 0, i.e. there is no preference for the segregation of vacancies. When Wad < 2σm, there is an energetic preference for alkali metal vacancies to reside at the interface and when Wad > 2σm there is an energetic preference for vacancies to be injected into the bulk. That is, suppression of alkali vacancy segregation to the interface occurs when Wad ≥ 2σm.
Although the use of a simple bond breaking model may be a simplification of the nature of bonding in metallic systems, it should be highlighted that the criteria Wad = 2σm becomes exact in the trivial case of a coherent interface between an alkali metal and a substrate of the same metal with the same orientation, i.e. in the bulk. As indicated in the Introduction, contact angle measurements are commonly used experimentally to determine the value of Wad for a material system. Wad is related to the metal surface energy, σm, and the contact angle θ via the Young–Dupré equation, Wad = σm(1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). Inserting the criteria of Wad = 2σm into the Young–Dupré equation leads to the result that a contact angle of θ = 0° between the substrate and liquid alkali metal is required to suppress the energetic preference for vacancy segregation to the interface.
θ). Inserting the criteria of Wad = 2σm into the Young–Dupré equation leads to the result that a contact angle of θ = 0° between the substrate and liquid alkali metal is required to suppress the energetic preference for vacancy segregation to the interface.
In the following sections, the bond breaking model in eqn (11) and (12) is tested first on free metal surfaces and then using a series of model ceramic and metallic substrate materials relevant to all-solid-state-batteries.
Free alkali metal surfaces
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) and (0001) surfaces of HCP Li were calculated with unstrained surface slabs, as shown in Table S5.† The surface energies of 0.463 and 0.230 J m−2 for relaxed BCC Li and Na (100) slabs, respectively, are in good agreement with previous studies.64 A very small difference in the energy was observed between the as-cleaved and relaxed BCC (100) surfaces for both Li and Na. The (10
0) and (0001) surfaces of HCP Li were calculated with unstrained surface slabs, as shown in Table S5.† The surface energies of 0.463 and 0.230 J m−2 for relaxed BCC Li and Na (100) slabs, respectively, are in good agreement with previous studies.64 A very small difference in the energy was observed between the as-cleaved and relaxed BCC (100) surfaces for both Li and Na. The (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) and (0001) surfaces of HCP Li are higher in energy per unit area than the (100) surface of BCC Li. However, for the bond breaking model in eqn (11) and (12), the surface energy per surface atom, σm/ρ, is also important. For the basal (0001) plane, the Li atoms are in a close packed arrangement with a high density of 12.26 atoms per nm2. For the (10
0) and (0001) surfaces of HCP Li are higher in energy per unit area than the (100) surface of BCC Li. However, for the bond breaking model in eqn (11) and (12), the surface energy per surface atom, σm/ρ, is also important. For the basal (0001) plane, the Li atoms are in a close packed arrangement with a high density of 12.26 atoms per nm2. For the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface, Li atoms in layer 1 and 2 experience a reduction in first nearest neighbour (1nn) coordination from 12 to 8 and 10, respectively, and so both types of atoms are included in the surface atom density, ρ. When normalised per surface atom, both the (0001) (0.290 eV per atom) and (10
0) surface, Li atoms in layer 1 and 2 experience a reduction in first nearest neighbour (1nn) coordination from 12 to 8 and 10, respectively, and so both types of atoms are included in the surface atom density, ρ. When normalised per surface atom, both the (0001) (0.290 eV per atom) and (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) (0.253 eV per atom) Li HCP surfaces have lower energies than the BCC Li (100) surface (0.341 eV per atom).
0) (0.253 eV per atom) Li HCP surfaces have lower energies than the BCC Li (100) surface (0.341 eV per atom).
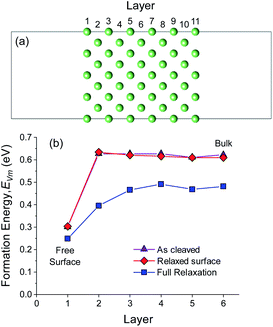
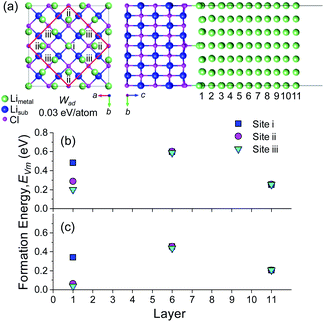
The diffusion of a metal vacancy from the surface (layer 1) to the bulk (layer 6) was studied for each structure. The results for an 11 Li layer slab of the BCC Li (100) surface are shown in Fig. 1a and b, and the results for BCC Na (100) and HCP Li are shown in Fig. S3–S5.† The bond breaking model described previously does not explicitly take into account the effect of structural relaxation on the on the vacancy formation energy, EVm. The role of relaxation of the BCC Li (100) surface and of the neighbouring atoms around the vacant Li site on EVm was probed using three separate DFT calculations at each vacancy position. In the first set of calculations, the energy of vacancies in the unrelaxed, ‘as-cleaved’ Li (100) slab structure were calculated. In the second set, the pristine Li (100) slab was first fully relaxed after which vacancies were introduced at different positions without further relaxation, subsequently referred to as ‘relaxed-surface’. In the final case, all atoms at the surface and around the vacant site were relaxed. The resulting vacancy formation energies are shown in Fig. 1b.
For the ‘as-cleaved’ and ‘relaxed surface’ structures in which no relaxation around the vacancy was allowed, it can be seen from Fig. 1b that the energy to form a vacancy at the BCC Li (100) surface layer (EFreeVm ∼ 0.3 eV) is approximately half that in the bulk (EBulkVm ∼ 0.6 eV). Beyond the top surface layer (layer 1), EVm rapidly reaches the bulk value, suggesting that the preference for vacancy formation at the surface is a highly localised effect that originates from the undercoordinated nature of the Li atoms within the surface plane. The vacancy formation energy has previously been shown to be surface dependent where low index surface planes such as the (210) surface of BCC Li are expected to have even lower EFreeVm values than the (100) surface.64 A EFreeVm value of ∼0 eV is expected to occur at a surface kink site. The segregation energies, ΔEBulk–FreeVm, as outlined in eqn (12) for the ‘as-cleaved’ and ‘relaxed surface’ cases are 0.321 eV and 0.302 eV, respectively. These values are in agreement with the as cleaved (σm = 0.343 eV per atom) and relaxed (σm = 0.341 eV per atom) (100) surface energies of BCC Li, normalised per atom, indicating that the result ΔEBulk–FreeVm = σm/ρ obtained from the bond breaking model is in qualitative agreement with the current DFT calculations.
When relaxation of the atoms around the vacancy is included, the vacancy formation energy at all positions decreases. The formation energy of a Li vacancy in the centre of the slab EBulkVm = 0.482 eV is consistent with previous DFT calculations on bulk Li systems.37,38 For the (100) surface of BCC Li, the decrease in EVm after vacancy relaxation is slightly larger in the bulk (0.13 eV) compared to the surface layer (0.06 eV). This difference leads to a smaller ΔEBulk–FreeVm value for the relaxed vacancy case (0.233 eV) compared to the ‘as-cleaved’ and ‘relaxed surface’ systems. The largest change in vacancy formation energy after vacancy relaxation was observed in layer 2, in which the presence of the free surface facilitated a substantial relaxation of the neighbouring Li sites as shown in Fig. S6.†
The same analysis was also performed for the Na BCC (100) surface and HCP Li (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) and (0001) as shown in Fig. S3–S5.† The results for the Na BCC (100) surface are in close agreement with BCC Li (100), in which relaxation around the vacancy leads to a decrease in the energy of all sites by >0.12 eV. The largest energy change after relaxation was again observed for a vacancy in layer 2. The ΔEBulk–FreeVm values of for the ‘as-cleaved’ (0.182 eV), ‘relaxed surface’ (0.176 eV) and ‘fully relaxed case (0.182 eV), are more similar for Na BCC (100) compared to Li BCC (100) as the change in EVm after relaxation in the former case was almost identical at the surface (layer 1) and the bulk (layer 6).
0) and (0001) as shown in Fig. S3–S5.† The results for the Na BCC (100) surface are in close agreement with BCC Li (100), in which relaxation around the vacancy leads to a decrease in the energy of all sites by >0.12 eV. The largest energy change after relaxation was again observed for a vacancy in layer 2. The ΔEBulk–FreeVm values of for the ‘as-cleaved’ (0.182 eV), ‘relaxed surface’ (0.176 eV) and ‘fully relaxed case (0.182 eV), are more similar for Na BCC (100) compared to Li BCC (100) as the change in EVm after relaxation in the former case was almost identical at the surface (layer 1) and the bulk (layer 6).
For the HCP Li (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) and (0001) systems, a much smaller energy difference between the as cleaved and relaxed vacancy energies was observed for all sites compared to the BCC Li (100) system. The smaller vacancy relaxation of the HCP Li structure over the BCC Li structure is likely due to the higher packing density in the former material, which was previously shown to have an important impact on the relaxation of vacancies on different Al surfaces.69 For the (0001) slab, the unrelaxed/relaxed values of ΔEBulk–FreeVm (0.360–0.375 eV) are in good agreement with the as cleaved (0.300 eV per atom) and relaxed (0.290 eV per atom) surface energies. Unlike in the BCC structure, during relaxation, the vacancy in layer 2 of the (0001) slab spontaneously relaxed to the surface layer, suggesting that the first subsurface layer is an unstable position for vacancies in the HCP Li (0001) surface.
0) and (0001) systems, a much smaller energy difference between the as cleaved and relaxed vacancy energies was observed for all sites compared to the BCC Li (100) system. The smaller vacancy relaxation of the HCP Li structure over the BCC Li structure is likely due to the higher packing density in the former material, which was previously shown to have an important impact on the relaxation of vacancies on different Al surfaces.69 For the (0001) slab, the unrelaxed/relaxed values of ΔEBulk–FreeVm (0.360–0.375 eV) are in good agreement with the as cleaved (0.300 eV per atom) and relaxed (0.290 eV per atom) surface energies. Unlike in the BCC structure, during relaxation, the vacancy in layer 2 of the (0001) slab spontaneously relaxed to the surface layer, suggesting that the first subsurface layer is an unstable position for vacancies in the HCP Li (0001) surface.
As discussed previously, for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface, the Li atoms in layers 1 and 2 have a lower 1nn coordination than the bulk. From Fig. S5,† it can be seen that the EVm for a vacancy in layer 2 (∼0.46 eV) is in-between that in layer 1 (∼0.18 eV) and layer 6 (∼0.62 eV). To approximate the value of EFreeVm for the (10
0) surface, the Li atoms in layers 1 and 2 have a lower 1nn coordination than the bulk. From Fig. S5,† it can be seen that the EVm for a vacancy in layer 2 (∼0.46 eV) is in-between that in layer 1 (∼0.18 eV) and layer 6 (∼0.62 eV). To approximate the value of EFreeVm for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) structure, an average of the EVm was taken. The resulting ΔEBulk–FreeVm values of 0.295–0.311 eV are in good agreement with the as cleaved (0.258 eV per atom) and relaxed (0.253 eV per atom) (10
0) structure, an average of the EVm was taken. The resulting ΔEBulk–FreeVm values of 0.295–0.311 eV are in good agreement with the as cleaved (0.258 eV per atom) and relaxed (0.253 eV per atom) (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface energies.
0) surface energies.
The activation barriers for diffusion between layers 5 and 6 in the bulk of the Li and Na slabs are very small at 0.037 and 0.040 eV, respectively, which are on the same order as thermal energy at T = 300 K (kBT = 0.026 eV). The barrier for diffusion from the BCC (100) surface (layer 1) to the subsurface (layer 2) in Li and Na is considerably larger at 0.238 and 0.182 eV, respectively, which suggests that the dynamics of isolated vacancies will be dominated by this surface to subsurface step. As the activation barrier of ‘bulk’ vacancies is so small, the total activation barrier for surface to bulk diffusion can be approximated as the difference between the energy of a vacancy at the surface compared to the bulk, i.e. ΔEBulk–FreeVm, which for the BCC Li (100) and Na (100) surfaces are, 0.233 eV and 0.182 eV, respectively. The lower value for ΔEBulk–FreeVm for Na compared to Li indicates that Na will have intrinsically faster vacancy dynamics which will lead to a higher resistance to void formation.
The Li vacancy activation barriers from the surface to the bulk of (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) and (0001) HCP Li slabs were also calculated as shown in Fig. S6.† For the (10
0) and (0001) HCP Li slabs were also calculated as shown in Fig. S6.† For the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) and (0001) slabs, vacancy hops were considered perpendicular to the surface between adjacent sites along 〈10
0) and (0001) slabs, vacancy hops were considered perpendicular to the surface between adjacent sites along 〈10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0〉 and 〈2
0〉 and 〈2![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 03〉 directions, respectively. For the (0001) surface, as a vacancy in layer 2 was previously found to be unstable, a longer ranged hop between a vacancy in layer 1 and layer 3 was considered for the surface to subsurface step. Larger barriers of 0.125 and 0.118 eV were observed for Li vacancy hops in the bulk of the (10
03〉 directions, respectively. For the (0001) surface, as a vacancy in layer 2 was previously found to be unstable, a longer ranged hop between a vacancy in layer 1 and layer 3 was considered for the surface to subsurface step. Larger barriers of 0.125 and 0.118 eV were observed for Li vacancy hops in the bulk of the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) and (0001) HCP Li slabs, respectively, as compared to the BCC Li (100) structure. For both the (10
0) and (0001) HCP Li slabs, respectively, as compared to the BCC Li (100) structure. For both the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) (0.444 eV) and (0001) (0.438 eV) slabs, the surface to subsurface barrier was found to be considerably larger than the bulk activation barrier, as was the case BCC Li and Na systems. This result indicates that regardless of the structure, the surface to subsurface vacancy activation barrier plays a dominant role in the vacancy dynamics in alkali metals.
0) (0.444 eV) and (0001) (0.438 eV) slabs, the surface to subsurface barrier was found to be considerably larger than the bulk activation barrier, as was the case BCC Li and Na systems. This result indicates that regardless of the structure, the surface to subsurface vacancy activation barrier plays a dominant role in the vacancy dynamics in alkali metals.
Alkali metal/substrate interfaces
From Table S6,† the magnitude of Wad is correlated with the substrate surface energy, σsub, as expected from eqn (7).
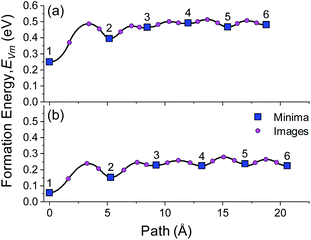
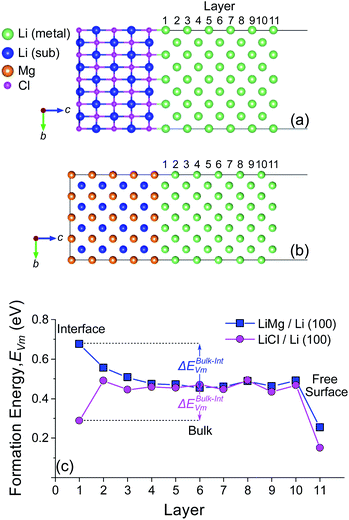
The vacancy formation energy, EVm, at different distances from the BCC Li (100) surface was initially tested for the Li (100)/LiCl (100) (Fig. 3a) and Li (100)/LiMg (100) (Fig. 3b) interfaces. Analogous to the free metal surfaces described previously in Fig. 1 and S3–S5,† the effect of relaxation on the vacancy segregation energy ΔEBulk–IntVm was evaluated with two separate calculations for each interface. In the first set of calculations, alkali vacancies were introduced into the previously relaxed alkali metal-interface structure, either on the alkali metal side of the alkali-metal interface or in the alkali metal bulk, without further relaxation (unrelaxed vacancy). In the second case, the atoms around the vacancy were allowed to relax (relaxed vacancy). The results for the unrelaxed and relaxed vacancy cases are shown in Fig. S8† and 3c, respectively.
It can be seen from Fig. 3c that the energy, EIntVm, to form a (relaxed) Li vacancy at the Li (100)/LiMg (100) interface is significantly larger than at the Li (100)/LiCl (100) interface, which is consistent with the larger Wad value of the Li (100)/LiMg (100) interface (0.978 eV per atom) compared to the Li (100)/LiCl (100) interface (0.199 eV per atom). The same trend is observed without relaxation of the Li vacancies in Fig. S7,† although the absolute scale of EVm is higher than with relaxation, as expected. In Fig. 3c, EIntVm at the Li (100)/LiCl (100) interface is higher than the value at the free surface, EFreeVm, but lower than the bulk value, EBulkVm, leading to a positive vacancy segregation energy of ΔEBulk–IntVm = 0.180 eV. The positive value of ΔEBulk–IntVm highlights that there is an energetic preference for the Li vacancy to reside at the interface relative to the bulk. For the Li (100)/LiMg (100) system, EIntVm is higher than EBulkVm, leading to a negative vacancy segregation energy of ΔEBulk−IntVm = −0.223 eV. A vacancy created at the interface will rapidly migrate into the bulk until it encounters a free surface or another feature such as a dislocation or free interstitial.
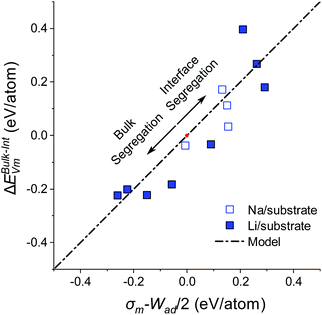 | ||
| Fig. 4 Plot of vacancy segregation energy (ΔEBulk–IntVm) with surface energy, σm, and work of adhesion Wad, for coherent alkali metal/substrate interfaces. The bond breaking model from eqn (11) is shown as a dot-dash line. Li and Na metals systems are shown with closed and open symbols. For all structures, ΔEBulk–IntVm is calculated after vacancy relaxation. The origin where Wad = 2σm and ΔEBulk–IntVm = 0 is marked with a red dot. The arrows indicate the regions of the bond breaking model in which there is an energetic preference for alkali metal vacancy segregation in the alkali metal bulk or alkali metal/substrate interface. | ||
It can be seen from Fig. 4 that for the majority of the systems studied, the simple bond breaking model in eqn (11) accurately describes the relationship between the vacancy segregation energy ΔEBulk–IntVm and the surface energy work of adhesion difference, σm − Wad/2. The good agreement between the model and the diverse range of interfacial structures suggests that the σm − Wad/2 relationship is universal for alkali metal systems, regardless of the structure and alkali metal species. As indicated previously, vacancy relaxation has a larger effect on the energy for BCC than HCP systems, however the difference in ΔEBulk–IntVm for the relaxed and unrelaxed systems appears to be small compared to the overall energy scale set by Wad and σm. This result is discussed further in the General discussion section below.
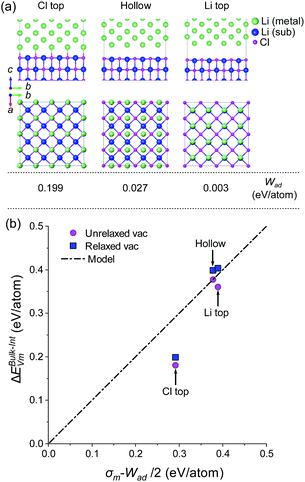
This approach was adopted to investigate how semicoherency affects Wad and ΔEBulk–IntVm at the interface for the BCC Li (100)/LiCl (100) system. The a and b parameters of the BCC (100) surface were initially strained by +5.7%, followed by a 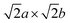 expansion to match the lattice parameters and lattice sites in the LiCl (100) structure. A 4 × 4 supercell expansion of strained-Li (100)/LiCl (100) interface was then used to minimise the interactions between periodic images. Three translations of the Li (100) surface relative to the LiCl (100) substrate were studied, as shown in Fig. 5a, in which the surface atoms of BCC Li metal were aligned: on top of the Cl ions of LiCl (Cl top), on top of the Li ions in LiCl (Li top) and at and intermediate hollow site. The Cl top configuration was previously used in Fig. 3. In each case, all atoms in both phases were allowed to relax and adopt the most favourable interfacial separation.
expansion to match the lattice parameters and lattice sites in the LiCl (100) structure. A 4 × 4 supercell expansion of strained-Li (100)/LiCl (100) interface was then used to minimise the interactions between periodic images. Three translations of the Li (100) surface relative to the LiCl (100) substrate were studied, as shown in Fig. 5a, in which the surface atoms of BCC Li metal were aligned: on top of the Cl ions of LiCl (Cl top), on top of the Li ions in LiCl (Li top) and at and intermediate hollow site. The Cl top configuration was previously used in Fig. 3. In each case, all atoms in both phases were allowed to relax and adopt the most favourable interfacial separation.
The largest Wad (0.199 eV per atom) was observed for the Cl-top structure in which the Li atoms of BCC Li metal are directly above the Cl ions of LiCl. The hollow and Li top structures had very low Wad values (0.003 and 0.027 eV per atom), indicating that very weak binding is present across the interface for these configurations. Using the same methodology as used in Fig. 4, the vacancy segregation ΔEBulk–IntVm was calculated for each of the structures, as shown in Fig. 5b. As expected from the bond breaking model, the higher work of adhesion of the ‘Cl top’ configuration results in a lower ΔEBulk–IntVm compared to the ‘hollow’ and ‘Li top’ configurations, which have ΔEBulk–IntVm values that are very similar to the free Li surface.
The role of misfit was further investigated by explicitly modelling an incoherent BCC Li (100)/LiCl (100) interface. Coincidence site lattice (CSL) theory in the MPInterfaces code74 was used to find a supercell in which the lattice mismatch between Li (100) and LiCl (100) was minimised. An interface formed from a 3a × 3b expansion of BCC Li (100) and 2a × 2b expansion of LiCl (100) resulted in a lattice mismatch of <−0.05%, requiring minimal strain of the Li lattice. A 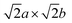 supercell expansion of the resulting interface structure was produced, followed by a relaxation of all atoms. The optimised interface structure is shown in Fig. 6a.
supercell expansion of the resulting interface structure was produced, followed by a relaxation of all atoms. The optimised interface structure is shown in Fig. 6a.
The presence of the LiCl (100) substrate breaks the symmetry of the BCC Li (100) surface and results in three different Li environments ((i), (ii) and (iii)) in the first layer (layer 1), as shown in Fig. 6a. After relaxation, Li site (i), was located directly above a Cl ion, analogous to the ‘Cl-top’ site in Fig. 5a. Li site (ii) was located in between the Cl top site and the hollow site and Li site (iii) was located in between the Li top site and the hollow site. A small, total Wad of 0.03 eV per atom was calculated for this incoherent Li (100)/LiCl (100) interface, which is consistent with the larger fraction of Li-top (4/9) and hollow sites (4/9) over Cl-top sites (1/9). The total value of Wad, however, is an average over all surface atoms, which does not capture the individual bonding contributions of the different sites. The vacancy formation energy at the different sites was therefore calculated without vacancy relaxation and with vacancy relaxation as is shown in Fig. 6b and c, respectively. The presence of the LiCl (100) surface also resulted in three symmetrically distinct Li sites in the central layer (layer 6) and on the free Li surface (layer 11) and the vacancy formation energy of each of these sites was also calculated for reference.
The distribution of vacancy formation energies in the bulk (layer 6) and free Li surface (layer 11) both before and after relaxation are very small, whereas the distribution of the formation energies at the Li (100)/LiCl (100) interface (layer 1) are considerable. In Fig. 2b and c, Li site (i) at a Cl top site in layer 1 displays the highest vacancy formation energy before (0.483 eV) and after (0.342 eV) vacancy relaxation, with a ΔEBulk–IntVm value of ∼0.11 eV. Before relaxation, Li sites (ii) (0.287 eV) and (iii) (0.201 eV) at the Li (100)/LiCl (100) interface have similar vacancy formation energies to the average vacancy formation energy at the free surface (layer 11) of 0.254 eV. After relaxation, the EVm values of site (ii) (0.063 eV) and (iii) (0.039 eV) are considerably smaller than at the free surface (0.206 eV). The low values of EVm for these sites stems from the lack of electrostatic interaction with Cl sites at the interface and structural distortions from neighbouring sites. The fact that Li sites (ii) and (iii) in layer 1 have lower EVm values than the free surface suggests that vacancy accumulation at the Li (100)/LiCl (100) interface would be significant.
An important conclusion from this result is that the average value of Wad in (J m−2 or eV per atom), which is often calculated with DFT for incoherent interfaces, is not a sufficient metric to understand the vacancy segregation at a semicoherent or incoherent interface. Instead, the value of ΔEBulk–IntVm at the weakest binding site, such as the centre of a misfit dislocation core has to be ΔEBulk–IntVm ≤ 0 to eliminate the preference for vacancy segregation. The criteria of Wad = 2σm, however still serves as a lower bound for semi/incoherent interfaces.
General discussion
The simple bond breaking model developed in this work provides a mechanistic understanding of previous experimental and computational results of vacancy diffusion and allows for the rational design of new materials to suppress void growth. In the molecular dynamics study by Yang et al.,47 it was demonstrated that a work of adhesion of Wad > 0.7 J m−2 was required to suppress voids at a model incoherent BCC Li (100)/SSE interface, with the application of a pressure on the order of 10–20 MPa. Without the application of pressure, a Wad > 1.8 J m−2 was required. An embedded atom (EAM) potential was used in that study for Li from a previous work by Nichol and Ackland.75 The surface energy predicted for the Li (100) surface using the EAM potential is σm = 0.368 J m−2, from NIST online repository.76 The results from this previous study are in good agreement the results from our model which predicts that interfacial vacancy segregation will be suppressed when Wad ≥ 2σmi.e. Wad = 2 × 0.368 = 0.736 J m−2. The requirement for pressure to be applied for average Wad values of 0.7–1.8 J m−2 may be consistent with the incoherent nature of the interface in which a distribution of ΔEBulk–IntVm values will exist for the average Wad value.The bond breaking model in this work is also in qualitative agreement with a recent kinetic Monte Carlo (KMC) study by Tewari and Mukherjee, in which it was demonstrated that void formation during plating is suppressed when the strength of the Li-substrate interaction is equal to or greater than the Li–Li interaction.46 From eqn (4) and (7), the criteria Wad ≥ 2σm can be written in terms of the bond energies as em–sub ≥ Ns/Niem–m. Assuming that the number of bonds formed at the interface is similar to the number of bonds broken at the metal surface, (Ns ≈ Ni) then the criteria of Wad ≥ 2σm is met when em–sub ≥ em–m, in good agreement with the previous KMC results. In the current study, only sharp alkali metal/SSE interfaces were considered from DFT calculations, whereas in real systems, significant reconstruction or amorphization of the alkali metal at the interface may occur.47,70,77 The simple bond breaking model is still likely to be applicable for these systems, as was the case for incoherent interfaces, although care must be taken to accurately model the distribution of possible EIntVm and EBulkVm values in systems with lower crystallinity. Due to the large cost of DFT calculations of explicit interfaces, only single, isolated alkali metal vacancies were considered in this study to understand the fundamental relationship between interfacial adhesion and vacancy segregation. The model could be extended in future studies to include the role of alkali metal vacancy clusters in larger scale void formation using computationally cheaper approaches such as EAM or machine-learning potentials.
The criteria of Wad ≥ 2σm and associated contact angle of θ = 0°, leads to a significant challenge for the selection appropriate SSE ceramic materials for alkali metal anode batteries. A key criteria of SSE materials is that they are either thermodynamically stable against alkali metals or decompose to form passivating secondary phases that are stable, otherwise continuous degradation of the SSE will occur. In the case of decomposition, for example in the argyrodite system with reaction Li6PS5Cl + 8Li → 5Li2S + Li3P + LiCl,78 the criteria of Wad ≥ 2σm also needs to be met by the secondary phases formed in situ. The average value of Wad was calculated for incoherent interfaces of the (111) surface of Li2S and (001) surface of Li3P with the (100) surface of BCC Li, as shown in Fig. S10 and S11.† As can be seen from Table S7,† the average Wad for the BCC Li (100)/Li3P (001) interface is higher (Wad = 0.435 eV per atom) than the BCC Li (100)/Li2S (111) interface (Wad = 0.266 eV per atom), due to the semiconducting nature of Li3P leading to a more metallic like bonding interaction with Li. As was the case for the BCC Li (100)/LiCl (100) interface, for Li3P and Li2S, Wad < 2σm and θ > 0°, indicating that there is still a preference for vacancy segregation to the interface. This result also highlights that the spatial distribution of the LiCl, Li3P and Li2S phases formed during decomposition is of critical importance as the phase in contact with Li metal will control the adhesion and void formation. Further development of experimental probes of the local structure, such as cryogenic electron microscopy (TEM), is required to understand how the phases formed during decomposition of SSE materials in contact with alkali metals are spatially distributed, as was recently shown for the LiPON system.79
Previous computational models have indicated that the bonding between metals and highly ionic ceramics is typically weak as the interfacial bonding is primarily electrostatic in nature.80 This is consistent with the small Wad values observed for the LiCl, NaCl, NaBr and Li2O interfaces (Table S5†). The weak bonding between ionic ceramics and alkali metals is also consistent with the large contact angles measured for systems such as carbonates Li2CO3 (θ = 142°) and oxides including Li2O (θ > 120° below 250 °C).17,81 However, the nature of the surface termination/interfaces of secondary phases formed at the alkali metal chemical potential may also be significantly different to those under synthesis conditions, as was recent shown computationally for Li2O.70
Previous DFT calculations have indicated that Li7La3Zr2O12 garnet materials, which are stable against Li metal, have larger average works of adhesion, approaching or exceeding the Wad = 2σm (θ = 0°) criteria for Li metal (σm = 0.471 J m−2).17,25 The larger Wad values for Li7La3Zr2O12 may be related to the open d-shell structure of Zr, which has previously been shown to increase adhesion in other metal ceramic systems.82 The design of interlayer materials containing open d-shell cations such as Zr, Sc and Y or the substitution of open d-shell cations in conventional oxide or sulphide SSE materials may be a general strategy to improve the interfacial adhesion with alkali metals. However, as discussed in the introduction, during experimental electrochemical measurement, voids are still observed at the Li/LLZO interface in the absence of large pressures.28 As indicated previously, the average work of adhesion predicted with DFT calculations of incoherent interfaces may not be fully sufficient to understand vacancy segregation. In a previous DFT study by Gao et al., the formation energy of Li metal vacancies at an incoherent Li/LLZO interface was found to vary by up to 0.55 eV.65 This result highlights the importance of understanding ΔEBulk–IntVm for Li/Na metal sites at the interface in addition to calculating the average Wad value.
The bond breaking model suggests that metallic interlayer materials are some of the most promising systems to suppress void formation between alkali metals and ceramic solid electrolytes. The Wad ≥ 2σm criterion is readily met for interfaces between alkali metals and metal interlayer and substrates, such as LiMg and AlSc studied in this work, due to the large surface energy of metallic phases and the formation of strong metallic bonds at the interface. Li–Mg alloys were demonstrated to effectively suppress Li pore formation, although chemical diffusion of Li in the alloy was a limiting factor.83 In both liquid electrolyte and all-solid-state systems, the in situ formation of a metallic secondary phases through decomposition of oxides against Li metal has been utilised to improve the work of adhesion.84,85 The formation of thin, metallic interfacial layers, through decomposition or ‘reactive wetting’, that can conduct Li may therefore be an important strategy to reach the Wad ≥ 2σm criterion. The use of metallic alloys in the liquid state, as recently demonstrated for a Li/LLZO system containing a thin liquid Na–K alloy layer, is another promising avenue to achieve both good adhesion and fast Li transport.42 The strong interaction between alkali metals and metallic substrates is also an important consideration for the selection of current collectors, particularly for alkali metal free designs, in which alkali metal is directly deposited from the SSE onto the current collector (CC).86 The simple bond breaking model presented in the current study could be further extended to understand the preference for void formation at the Li/SSE versus Li/CC interfaces.
As indicated previously, only a limited number of high-quality measurements of the alkali metal contact angle, θ, have been performed for SSE or interlayer materials due to the high reactivity of Li and Na metal. Increasing experimental efforts should be dedicated to the measurement of alkali contact angles on well-defined sample surfaces. Experimental contact angle measurements on oriented, thin film samples would allow for more direct comparison with the facet dependent contact angles measured from DFT calculations and allow for the rational selection of materials with criteria (θ = 0°). Careful atmospheric control of O2 must be strictly maintained throughout these measurements which requires careful control of the experimental setup, as previously described by Liu et al.87 The development of in operando methodologies to visualise changes in the local structure of interfaces during stripping and plating is of paramount importance to gain a deeper understanding of the structural and chemical changes taking place.
Finally, the current work clearly shows that the selection of ceramic solid-electrolyte materials with large values of Wad is desirable to suppress vacancy segregation and void formation. However, it has previously been postulated that materials with high values of Wad can result in the preferential formation of metal Li dendrites at SSE grain boundaries, assuming that the SSE grain boundary energy is proportional to the SSE surface energy.88 Selective surface modifications of SSE materials, such as the introduction of conductive interlayers with strong Wad, that do not alter the grain boundary energetics may help to decouple these effects.
Conclusions
The suppression of voids at the alkali metal/solid-state electrolyte (SSE) interface that results from alkali metal vacancy accumulation is one of the most important challenges that needs to be solved to allow for the fast discharging of alkali metal anodes in all-solid-state-batteries. In this study, we have demonstrated using a novel bond breaking model coupled with DFT calculations that the segregation of alkali metal vacancies at the alkali metal/solid electrolyte interface is intimately related to the interfacial structure and adhesion.The activation barrier for Li and Na vacancies to migrate from the surface to the first subsurface layer in Li and Na metal slabs was shown to be considerably larger than the bulk activation barrier from DFT calculations. The energetic preference for vacancy segregation to alkali metal surfaces was shown to be a localised effect driven by the undercoordination of alkali atoms at the surface layer and is qualitatively captured by a bond breaking approach. DFT calculations demonstrate the formation of alkali metal–substrate bonds at the alkali metal/SSE interface critically alters the energy landscape for alkali metal vacancy segregation.
The bond breaking model highlights the critical link between the work of adhesion (Wad) at the alkali metal/SSE interface and the metal surface energy σm. It leads to the result that for coherent interfaces, when Wad ≥ 2σm, or analogously a contact angle of θ = 0°, there is a driving force for alkali metal vacancies to be injected into the alkali metal bulk instead of remaining at the interface. This was demonstrated to be widely applicable to a range of ASSB relevant materials. DFT calculations of Li/LiCl interfaces highlight that incoherency can have a significant impact on the local vacancy formation energy of alkali metal sites at the interface which are not captured by the average Wad value.
This work highlights that the criteria of Wad ≥ 2σm (θ = 0°) is not readily met by experimentally studied SSE materials, such as Li7La3Zr2O12 or commonly observed SSE decomposition products such as Li2O and LiCl. Metal alloys are a particularly appealing choice for interlayers due to their high surface energy and intrinsically strong metal bonding between dissimilar metals, however sufficient alkali conductivity through the interlayers must still be maintained. The current model highlights the importance of interfacial adhesion on isolated vacancy transport at sharp alkali metal/SSE interfaces, however, more work is required to develop novel computational methods to study alkali vacancy transport at extended structural features, such as dislocations and grain boundaries. A deeper understanding of the role of interfacial adhesion on the vacancy segregation and void formation more broadly within the all-solid-state battery field will require more systematic experimental studies of the contact angle, surface energies and work of adhesion for a range of solid electrolyte and interlayer materials. Finally, the results from the bond breaking model in this work may have more general applications in other fields including void formation during high temperature oxidation and radiation induced voids at bimetallic interfaces.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
I. D. S. and A. A. acknowledge funding for their research from EPSRC Platform Grant EP/R002010/1. I. D. S. acknowledges the Imperial College Research Computing Service (10.14469/hpc/2232), and associated support services used during this work. We are grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1, EP/T022213/1, EP/P003532/1 and ICSF EP/R024006/1). I. D. S. and A. A. would like to thank Professor Michael Finnis, Professor Graeme Henkelman, Edouard Quérel and Dr Rowena Brugge for valuable discussions during the initial stages of this project.References
- J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 1–4 CrossRef.
- J. Betz, G. Bieker, P. Meister, T. Placke, M. Winter and R. Schmuch, Adv. Energy Mater., 2019, 9, 1803170 CrossRef.
- R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778–7781 CrossRef CAS PubMed.
- F. Han, Y. Zhu, X. He, Y. Mo and C. Wang, Adv. Energy Mater., 2016, 6, 1501590 CrossRef.
- J. Wolfenstine, J. L. Allen, J. Read and J. Sakamoto, J. Mater. Sci., 2013, 48, 5846–5851 CrossRef CAS.
- J. G. Connell, T. Fuchs, H. Hartmann, T. Krauskopf, Y. Zhu, J. Sann, R. Garcia-Mendez, J. Sakamoto, S. Tepavcevic and J. Janek, Chem. Mater., 2020, 32, 10207–10215 CrossRef CAS.
- Y. Zhao and L. L. Daemen, J. Am. Chem. Soc., 2012, 134, 15042–15047 CrossRef CAS PubMed.
- X. Lü, G. Wu, J. W. Howard, A. Chen, Y. Zhao, L. L. Daemen and Q. Jia, Chem. Commun., 2014, 50, 11520–11522 RSC.
- X. Lü, J. W. Howard, A. Chen, J. Zhu, S. Li, G. Wu, P. Dowden, H. Xu, Y. Zhao and Q. Jia, Adv. Sci., 2016, 3, 1500359 CrossRef PubMed.
- S. Wenzel, T. Leichtweiss, D. A. Weber, J. Sann, W. G. Zeier and J. Janek, ACS Appl. Mater. Interfaces, 2016, 8, 28216–28224 CrossRef CAS PubMed.
- R. O. Ansell, J. Mater. Sci., 1986, 21, 365–379 CrossRef CAS.
- M. C. Bay, M. Wang, R. Grissa, M. V. F. Heinz, J. Sakamoto and C. Battaglia, Adv. Energy Mater., 2020, 10, 1902899 CrossRef CAS.
- W. D. Richards, L. J. Miara, Y. Wang, J. C. Kim and G. Ceder, Chem. Mater., 2016, 28, 266–273 CrossRef CAS.
- Y. Xiao, Y. Wang, S. H. Bo, J. C. Kim, L. J. Miara and G. Ceder, Nat. Rev. Mater., 2020, 5, 105–126 CrossRef CAS.
- S. Wenzel, T. Leichtweiss, D. Krüger, J. Sann and J. Janek, Solid State Ionics, 2015, 278, 98–105 CrossRef CAS.
- T. Krauskopf, F. H. Richter, W. G. Zeier and J. Janek, Chem. Rev., 2020, 120, 7745–7794 CrossRef CAS PubMed.
- A. Sharafi, E. Kazyak, A. L. Davis, S. Yu, T. Thompson, D. J. Siegel, N. P. Dasgupta and J. Sakamoto, Chem. Mater., 2017, 29, 7961–7968 CrossRef CAS.
- M. Wang and J. Sakamoto, J. Power Sources, 2018, 377, 7–11 CrossRef CAS.
- H. Huo, J. Luo, V. Thangadurai, X. Guo, C. W. Nan and X. Sun, ACS Energy Lett., 2020, 5, 252–262 CrossRef CAS.
- R. H. Brugge, F. M. Pesci, A. Cavallaro, C. Sole, M. A. Isaacs, G. Kerherve, R. S. Weatherup and A. Aguadero, J. Mater. Chem. A, 2020, 8, 14265–14276 RSC.
- F. M. Pesci, A. Bertei, R. H. Brugge, S. P. Emge, A. K. O. Hekselman, L. E. Marbella, C. P. Grey and A. Aguadero, ACS Appl. Mater. Interfaces, 2020, 12, 26 CrossRef PubMed.
- K. K. Fu, Y. Gong, B. Liu, Y. Zhu, S. Xu, Y. Yao, W. Luo, C. Wang, S. D. Lacey, J. Dai, Y. Chen, Y. Mo, E. Wachsman and L. Hu, Sci. Adv., 2017, 3, e1601659 CrossRef PubMed.
- M. M. Gross, L. J. Small, A. S. Peretti, S. J. Percival, M. A. Rodriguez and E. D. Spoerke, J. Mater. Chem. A, 2020, 8, 17012–17018 RSC.
- W. Luo, Y. Gong, Y. Zhu, Y. Li, Y. Yao, Y. Zhang, K. K. Fu, G. Pastel, C. F. Lin, Y. Mo, E. D. Wachsman and L. Hu, Adv. Mater., 2017, 29, 1606042 CrossRef PubMed.
- B. Gao, R. Jalem and Y. Tateyama, ACS Appl. Mater. Interfaces, 2020, 12, 16350–16358 CrossRef CAS PubMed.
- K. Kim and D. J. Siegel, ACS Appl. Mater. Interfaces, 2019, 11, 39940–39950 CrossRef CAS PubMed.
- X. Lu, G. Li, J. Y. Kim, D. Mei, J. P. Lemmon, V. L. Sprenkle and J. Liu, Nat. Commun., 2014, 5, 1–8 Search PubMed.
- J. Kasemchainan, S. Zekoll, D. Spencer Jolly, Z. Ning, G. O. Hartley, J. Marrow and P. G. Bruce, Nat. Mater., 2019, 18, 1105–1111 CrossRef CAS PubMed.
- M. J. Wang, R. Choudhury and J. Sakamoto, Joule, 2019, 3, 2165–2178 CrossRef CAS.
- T. Krauskopf, H. Hartmann, W. G. Zeier and J. Janek, ACS Appl. Mater. Interfaces, 2019, 11, 14463–14477 CrossRef CAS PubMed.
- T. Krauskopf, B. Mogwitz, H. Hartmann, D. K. Singh, W. G. Zeier and J. Janek, Adv. Energy Mater., 2020, 10, 2000945 CrossRef CAS.
- M. Wang, J. B. Wolfenstine and J. Sakamoto, Electrochim. Acta, 2019, 296, 842–847 CrossRef CAS.
- W. S. LePage, Y. Chen, E. Kazyak, K.-H. Chen, A. J. Sanchez, A. Poli, E. M. Arruda, M. D. Thouless and N. P. Dasgupta, J. Electrochem. Soc., 2019, 166, A89–A97 CrossRef CAS.
- D. Spencer Jolly, Z. Ning, J. E. Darnbrough, J. Kasemchainan, G. O. Hartley, P. Adamson, D. E. J. Armstrong, J. Marrow and P. G. Bruce, ACS Appl. Mater. Interfaces, 2020, 12, 678–685 CrossRef CAS PubMed.
- M. Jäckle and A. Groß, J. Chem. Phys., 2014, 141, 174710 CrossRef PubMed.
- M. Jäckle, K. Helmbrecht, M. Smits, D. Stottmeister and A. Groß, Energy Environ. Sci., 2018, 11, 3400–3407 RSC.
- V. Schott, M. Fähnle and P. A. Madden, J. Phys.: Condens. Matter, 2000, 12, 1171–1194 CrossRef CAS.
- P. W. Ma and S. L. Dudarev, Phys. Rev. Mater., 2019, 3, 063601 CrossRef CAS.
- M. Mali, J. Roos, M. Sonderegger, D. Brinkmann and P. Heitjans, J. Phys. F: Met. Phys., 1988, 18, 403–412 CrossRef CAS.
- M. Neumann, P. Scharwaechter, A. Seeger, W. Frank, K. Freitag, M. Konuma and G. Majer, Defect Diffus. Forum, 1997, 143–147, 85–90 CAS.
- D. Landmann, G. Graeber, M. V. F. Heinz, S. Haussener and C. Battaglia, Mater. Today Energy, 2020, 18, 100515 CrossRef.
- R. J.-Y. Park, C. M. Eschler, C. D. Fincher, A. F. Badel, P. Guan, M. Pharr, B. W. Sheldon, W. C. Carter, V. Viswanathan and Y.-M. Chiang, Nat. Energy, 2021, 6, 314–322 CrossRef CAS.
- S. Zheng, S. Shao, J. Zhang, Y. Wang, M. J. Demkowicz, I. J. Beyerlein and N. A. Mara, Sci. Rep., 2015, 5, 1–8 Search PubMed.
- C. M. Wang, A. Genc, H. Cheng, L. Pullan, D. R. Baer and S. M. Bruemmer, Sci. Rep., 2015, 4, 1–6 Search PubMed.
- R. P. Oleksak, M. Kapoor, D. E. Perea, G. R. Holcomb and Ö. N. Doğan, npj Mater. Degrad., 2018, 2, 25 CrossRef.
- D. Tewari and P. P. Mukherjee, J. Phys. Chem. C, 2021, 125, 2221–2229 CrossRef CAS.
- M. Yang, Y. Liu, A. M. Nolan and Y. Mo, Adv. Mater., 2021, 33, 2008081 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- G. J. Ackland, M. Dunuwille, M. Martinez-Canales, I. Loa, R. Zhang, S. Sinogeikin, W. Cai and S. Deemyad, Science, 2017, 356, 1254–1259 CrossRef CAS.
- M. Hanfland, I. Loa and K. Syassen, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 1841091–1841098 CrossRef.
- A. R. Natarajan and A. Van Der Ven, Chem. Mater., 2019, 31, 8222–8229 CrossRef.
- D. Gaissmaier, M. van den Borg, D. Fantauzzi and T. Jacob, ChemSusChem, 2020, 13, 771–783 CrossRef CAS PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- W. Sun and G. Ceder, Surf. Sci., 2013, 617, 53–59 CrossRef CAS.
- V. Fiorentini and M. Methfessel, J. Phys.: Condens. Matter, 1996, 8, 6525–6529 CrossRef CAS.
- T. R. Mattsson and A. E. Mattsson, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 1–8 CrossRef.
- K. S. Nagy, S. Kazemiabnavi, K. Thornton and D. J. Siegel, ACS Appl. Mater. Interfaces, 2019, 11, 7954–7964 CrossRef CAS.
- J. Gao, X. Guo, Y. Li, Z. Ma, X. Guo, H. Li, Y. Zhu and W. Zhou, Adv. Theory Simul., 2019, 2, 1900028 CrossRef.
- A. Kumar, H. Barda, L. Klinger, M. W. Finnis, V. Lordi, E. Rabkin and D. J. Srolovitz, Nat. Commun., 2018, 9, 1–8 CrossRef CAS PubMed.
- M. W. Finnis and J. E. Sinclair, Philos. Mag. A, 1984, 50, 45–55 CrossRef CAS.
- Q. Jiang, H. M. Lu and M. Zhao, J. Phys.: Condens. Matter, 2004, 16, 521–530 CrossRef CAS.
- S. S. Gupta, M. A. Van Huis, M. Dijkstra and M. H. F. Sluiter, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 085432 CrossRef.
- J. S. Lowe and D. J. Siegel, ACS Appl. Mater. Interfaces, 2020, 12, 46015–46026 CrossRef CAS PubMed.
- N. D. Lepley and N. A. W. Holzwarth, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 214201 CrossRef.
- A. Alavi and D. N. Seidman, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 16094–16102 CrossRef.
- R. Benedek, D. N. Seidman and C. Woodward, J. Phys.: Condens. Matter, 2002, 14, 2877–2900 CrossRef CAS.
- K. Mathew, A. K. Singh, J. J. Gabriel, K. Choudhary, S. B. Sinnott, A. V. Davydov, F. Tavazza and R. G. Hennig, Comput. Mater. Sci., 2016, 122, 183–190 CrossRef CAS.
- A. Nichol and G. J. Ackland, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 184101 CrossRef.
- NIST Material Measurement Laboratory, Interatomic Potentials Repository Project, https://www.ctcms.nist.gov/potentials/, accessed, 6 April 2021 Search PubMed.
- X. Wang, G. Pawar, Y. Li, X. Ren, M. Zhang, B. Lu, A. Banerjee, P. Liu, E. J. Dufek, J. G. Zhang, J. Xiao, J. Liu, Y. S. Meng and B. Liaw, Nat. Mater., 2020, 19, 1339–1345 CrossRef CAS PubMed.
- S. Wenzel, S. J. Sedlmaier, C. Dietrich, W. G. Zeier and J. Janek, Solid State Ionics, 2018, 318, 102–112 CrossRef CAS.
- D. Cheng, T. A. Wynn, X. Wang, S. Wang, M. Zhang, R. Shimizu, S. Bai, H. Nguyen, C. Fang, M. c. Kim, W. Li, B. Lu, S. J. Kim and Y. S. Meng, Joule, 2020, 4, 2484–2500 CrossRef CAS.
- M. W. Finnis, J. Phys.: Condens. Matter, 1996, 8, 5811–5836 CrossRef CAS.
- S. A. Krat, A. S. Popkov, Y. M. Gasparyan, A. A. Pisarev, P. Fiflis, M. Szott, M. Christenson, K. Kalathiparambil and D. N. Ruzic, Fusion Eng. Des., 2017, 117, 199–203 CrossRef CAS.
- E. A. Jarvis and E. A. Carter, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 1001031–1001034 CrossRef.
- T. Krauskopf, B. Mogwitz, C. Rosenbach, W. G. Zeier and J. Janek, Adv. Energy Mater., 2019, 9, 1902568 CrossRef CAS.
- Y. Chen, Z. Wang, X. Li, X. Yao, C. Wang, Y. Li, W. Xue, D. Yu, S. Y. Kim, F. Yang, A. Kushima, G. Zhang, H. Huang, N. Wu, Y. W. Mai, J. B. Goodenough and J. Li, Nature, 2020, 578, 251–255 CrossRef CAS PubMed.
- J. Jia, Z. Tang, Z. Guo, H. Xu, H. Hu and S. Li, Chem. Commun., 2020, 56, 4248–4251 RSC.
- M. J. Wang, E. Carmona, A. Gupta, P. Albertus and J. Sakamoto, Nat. Commun., 2020, 11, 1–9 Search PubMed.
- T. Liu, P. Sen and C. J. Kim, J. Microelectromech. Syst., 2012, 21, 443–450 CAS.
- G. Li and C. W. Monroe, Phys. Chem. Chem. Phys., 2019, 21, 20354–20359 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta03254b |
| This journal is © The Royal Society of Chemistry 2021 |